Kinetics of small molecule interactions with membrane proteins in single cells measured with mechanical amplification

Small-molecule interactions with membrane proteins in single cells are measured with a mechanical amplification method.

Abstract

Measuring small molecule interactions with membrane proteins in single cells is critical for understanding many cellular processes and for screening drugs. However, developing such a capability has been a difficult challenge. We show that molecular interactions with membrane proteins induce a mechanical deformation in the cellular membrane, and real-time monitoring of the deformation with subnanometer resolution allows quantitative analysis of small molecule–membrane protein interaction kinetics in single cells. This new strategy provides mechanical amplification of small binding signals, making it possible to detect small molecule interactions with membrane proteins. This capability, together with spatial resolution, also allows the study of the heterogeneous nature of cells by analyzing the interaction kinetics variability between different cells and between different regions of a single cell.

INTRODUCTION

Advances in structural biology have led to an exponential growth in the number of membrane proteins with determined three-dimensional (3D) structures (1). However, to understand the cellular functions of membrane proteins, it is also necessary to determine the interaction kinetics of the membrane proteins with various molecules. This is because cells perform many functions, including communication, through the interactions of their membrane proteins with molecules in the extracellular medium. Quantifying membrane protein interactions with molecules is also critical for discovering and validating drugs because most drug targets are membrane proteins (2, 3). However, measuring the interactions of molecules with membrane proteins in the natural lipid environment has been a difficult task.

The traditional method for studying molecular interactions uses radioactive or fluorescent labels. These end-point assays do not provide kinetic constants that are needed to quantify the membrane receptor interactions relevant to biological functions (4, 5). To determine the kinetic information, the current practice involves extracting membrane proteins from cells, purifying them from the extracts, immobilizing the purified proteins on a solid surface, and then exposing them to a ligand for kinetic study (6). The procedures are not only laborious but also prone to alteration of the native functions of membrane proteins, especially integral membrane proteins that are permanently attached to the membrane. Furthermore, the isolation of membrane proteins from their native cellular environment prevents the study of the allosteric effect in the molecular interactions (7) and the examination of the heterogeneous nature of cells (8, 9). Measurement of the binding kinetics of membrane proteins on cells (10) or lipid bilayers (11, 12) has been demonstrated with surface plasmon resonance (SPR) and SPR with novel nanostructures, such as nanoparticles and nanopores. However, the limitation of these technologies is that the detection signal diminishes with the mass of the molecule, thus leading to difficulty in detecting small molecules, which play many important roles in cellular functions and represent the vast majority of the existing drugs.

Here, we report an observation of mechanical deformation of cells upon interactions of the cellular membrane proteins with molecules in the extracellular medium, and demonstrate a real-time analysis of the interactions in single cells by analyzing the mechanical deformation with subnanometer resolution. Various methods have been developed for measuring cell membrane deformation, including optical tweezers (13, 14), quantitative phase imaging (15, 16), and atomic force microscopy (AFM) (17–19). Our measurement is based on a differential detection method that provides subnanometer accuracy to monitor cell edge deformation. Using this capability, we have monitored the kinetics of both large and small molecule interactions with membrane proteins, including glycoproteins and ion channels in intact cells (fixed or living), and obtained the binding kinetic constants. For large molecules, the kinetic constants agree with those obtained with a plasmonic imaging technique. For small molecules, the present method represents the first kinetic measurement, and direct comparison with other techniques is not possible, but the equilibrium constants extracted from the present method are consistent with those obtained with end-point radioactive labeling assays. The imaging capability allowed us to reveal cell-to-cell variability and region-to-region variability within the same cell.

RESULTS

The principle and experimental setup to measure the mechanical deformation in the cellular membrane associated with the binding of molecules with the membrane proteins are illustrated in Fig. 1. The mechanical deformation is expected because the law of thermodynamics predicts that when molecules bind to a surface, the surface tension changes, leading to a mechanical response in the cell membrane (Fig. 1E). According to thermodynamics, the surface concentration (Γ) of molecules bound on the membrane surface is given by

$$\mathrm{Г}=-\frac{\mathit{d}\mathrm{\gamma }}{\mathit{d}\mathrm{\mu }}$$ (1)

at a constant temperature and pressure, where γ is the surface tension and μ is the chemical potential of the molecules. For ideal solutions, the chemical potential is related to the bulk concentration, c, according to

$$\mathit{d}\mathrm{\mu }=\mathit{R}\mathit{T}\mathit{d}(\text{ln} \mathit{c})$$ (2)

where R is the gas constant and T is temperature. From Eqs. 1 and 2, at a given concentration of analyte, molecular binding is directly proportional to the surface tension change, and thus, the molecular interactions with the membrane proteins can be determined by measuring the mechanical deformation in the membrane (Fig. 1C). Note that, according to Eq. 1, the mechanical deformation detected here does not scale with the size of the molecule, so the method works, in principle, for both large and small molecules. We will return to this in Discussion.

Fig. 1. Detection of molecular interactions with membrane proteins in cells through mechanical amplification.

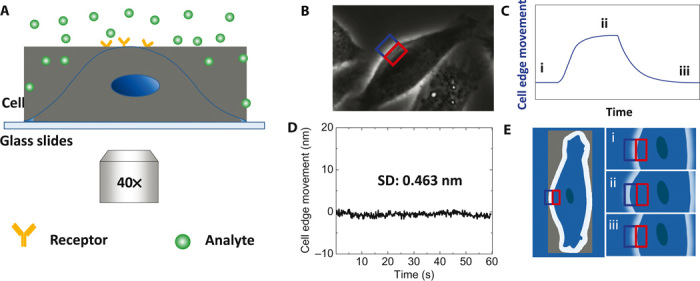
(A) Schematic illustration of the experimental setup based on an inverted phase-contrast microscope with a 40× phase 2 objective. (B) Differential optical detection for accurate tracking of cell edge changes induced by analyte-receptor interaction. (C) Schematic of a typical binding curve as determined from the cell edge movement. (D) The root mean square of the fixed cell edge change is 0.46 nm. (E) Illustration of cell edge changes over time during the binding process, where i, ii, and iii correspond to the stages marked in (C). Blue and red rectangles in (B) and (E) are the ROIs for differential detection.

To detect the binding of a small amount of molecules, it is critical to be able to measure small mechanical deformations in the cell membrane. Although AFM could, in principle, be used to measure cell deformation (17–19), we developed a simple method by tracking the edge movement of a cell with an optical microscope using a differential detection algorithm. Compared to AFM, it is noninvasive and fast, allowing multiple cells to be measured simultaneously. The differential detection algorithm allowed us to achieve a detection limit of 0.5 nm of cell edge movement (the size of an atom) with millisecond temporal resolution [limited only by the frame rate of the charge-coupled device (CCD) camera].

Figure 1A shows a schematic illustration of the experimental setup based on an inverted optical microscope. The edge of a cell is clearly revealed with conventional phase-contrast imaging, as shown in Fig. 1B. A rectangular region of interest (ROI) is defined such that the edge of a cell passes through the center of the rectangle, dividing the ROI into two equal halves: one half is inside of the cell and the second half falls outside of the cell. We denote the intensities of the two halves as A and B. If the cell expands upon molecular binding (Fig. 1C), then A decreases and B increases (Fig. 1E). We measure differential image intensity, (A − B)/(A + B), and use it to determine the movement of the cell edge at each location. The relation between the cell edge movement and (A − B)/(A + B) is calibrated using the procedure described in the Supplementary Materials. By following the cell edge movement, we obtain the binding kinetics as illustrated in Fig. 1C.

We refer to this method of edge tracking as differential optical detection. The differential optical detection subtracts out common noise in the optical system, thus providing a superior detection limit. Figure 1D plots the noise level over time, showing an SD of 0.46 nm. Although we focus on phase-contrast imaging in the present work, this optical detection algorithm can be readily applied to other optical imaging modes, such as bright-field (20) and SPR imaging (21, 22).

To demonstrate the capability of the method for detecting and quantifying the interactions of molecules with the membrane proteins, we first studied molecular binding to glycoproteins. Glycoproteins are the most abundant membrane proteins with sugar groups extended into the extracellular space of the cells, which is critical in cell recognition and communication with various signaling molecules via specific interactions (23). An important example of the specific interactions is between lectins (proteins that bind to and recognize specific sugar structures) and glycoproteins on the cell membranes. We studied wheat germ agglutinin (WGA; molecular weight, 36 kD), a lectin that can specifically recognize N-acetylglucosamine (GlcNAc) and sialic acid groups on Barrett’s esophagus–derived CP-D (CP-18821) cells.

Figure 2 (A and B) shows the phase-contrast images of CP-D cells attached to a glass slide. The measurement was carried out by first flowing 1× phosphate-buffered saline (PBS) over the cells at a flow rate of 350 μl/min for 30 s to obtain a baseline. WGA in 1× PBS was then introduced for 90 s to allow the binding (association) of WGA with the glycoproteins on the cell surface. During the association process, the cell edge moved outward as shown in Fig. 2, C and D. After the association process, the WGA solution was switched to 1× PBS to allow the bound WGA to dissociate from the cells. Figure 2 (C and D) shows that the cell edge moved back to the original position during the dissociation process. Mechanical responses in the cell membranes to the binding of WGA using micropipettes have been reported (24, 25), which supports the present observation. By globally fitting the data with the first-order kinetics, the association rate constant (k_on), dissociation rate constant (k_off), and dissociation constant (K_D) were found to be 1.09 ± 0.02 × 10⁵ M⁻¹ s⁻¹, 2.20 ± 0.01 × 10⁻³ s⁻¹, and 19.0 ± 0.5 nM, respectively. The binding kinetics of WGA and glycoprotein on more cells are shown in table S1. WGA binding to glycoproteins on live cells was also detected with the same method (fig. S1 and table S2). The results from both fixed and live cells are in agreement with those obtained with the plasmonic imaging method recently reported by us (10). Another example is the binding of anti–epidermal growth factor receptor (EGFR) antibody (molecular weight, 134 kD) to EGFR on A431 cells (fig. S2), which is described in section S-2 of the Supplementary Materials. Unlike the plasmonic imaging method, which is not well suited for measuring small molecules (26, 27), the present mechanical amplification can detect both large and small molecules.

Fig. 2. Large molecule interactions: WGA interaction with glycoproteins.

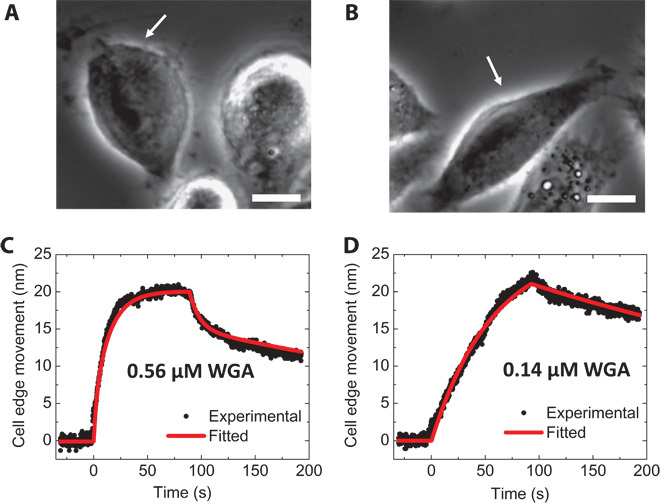
(A and B) Phase-contrast images of fixed CP-D cells with binding of WGA [0.56 μΜ (20 μg/ml) (A) and 0.14 μM (5 μg/ml) (B)]. The white arrows mark the cells under analysis. (C and D) Averaged cell edge movement over the whole cell (black dots) and global fitting (red curves) for 0.56 μΜ (20 μg/ml) (C) and 0.14 μM (5 μg/ml) (D) WGA, respectively. Scale bars, 10 μm.

To demonstrate the small molecule binding detection capability of the present method, we studied the binding of acetylcholine (molecular weight, 146.2 daltons) with nicotinic acetylcholine receptors (nAChRs) using engineered SH-EP1 cells that expressed human α4β2 (hα4β2) receptors. nAChRs are among the most studied membrane receptors because of their critical role in neurotransmission and nicotine addiction (28, 29). Determining the binding kinetics of neurotransmitters, such as acetylcholine, with nAChR in neurons is important for basic neuroscience and for the clinical evaluation of nicotine addiction (30). The neurotransmitter-receptor binding affinity cited in textbooks and literature was obtained with the radioactive labeling method, which requires lysis of the neurons (31) and incubation with the neurotransmitters, and thus cannot measure the binding affinity of each individual cells. Because radioactive or other labeling methods are end-point assays, they do not provide kinetic constants.

The image of SH-EP1-hα4β2 cells is shown in Fig. 3A, where the white arrow marks the cell under analysis. Buffer (1× PBS) was first introduced to flow over the cell for 25 s, and then the buffer was switched to an acetylcholine solution in 1× PBS. After association, the acetylcholine solution at each concentration was switched back to 1× PBS to allow for dissociation. The above procedure was repeated for different acetylcholine concentrations. As shown in Fig. 3B, the cell edge expands during the association phase and retracts during the dissociation phase. Figure 3B also shows that the amount of cell expansion during the association process increases with the acetylcholine concentration, which is expected for first-order binding kinetics. The association (k_on) and dissociation (k_off) rate constants were found to be 1.20 ± 0.01 × 10⁻⁶ M⁻¹ s⁻¹ and 1.96 ± 0.02 × 10⁻² s⁻¹, respectively, which represent the first direct measurement of the kinetic constants for the binding of the neurotransmitter to the nAChRs in intact cells. From k_on and k_off, the equilibrium dissociation constant (K_D = k_off/k_on) was determined to be 16.4 ± 0.2 nM. By plotting the equilibrium response versus acetylcholine concentrations (Fig. 3C), the equilibrium constant (K_D) was found to be ~ 26 nM, which is consistent with that obtained by kinetics measurement. Because this is the first kinetic measurement of acetylcholine binding to nAChRs, we cannot compare our findings to other reference technologies or prior data. However, the equilibrium dissociation constant determined here is in agreement with the average K_i determined with radioligand binding assays, which involved centrifugation and formation of cell pellets (31, 32).

Fig. 3. Small-molecule interactions: Acetylcholine interaction with nAChRs in cells.

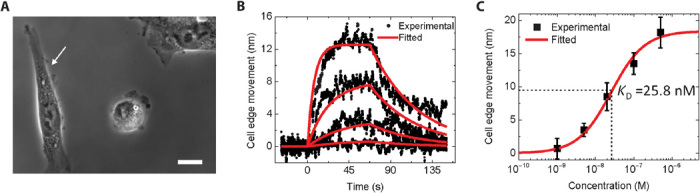
(A) Phase-contrast image of fixed hα4β2-transfected SH-EP1 cells, where the white arrow marks the cell under analysis. Scale bar, 20 μm. (B) Averaged cell edge movement over the whole cell (black dots) and global fitting results (red curves) during the binding process for acetylcholine of different concentrations (from bottom to top: 1, 5, 20, and 100 nM). (C) Cell edge movement at equilibrium versus acetylcholine concentration. The equilibrium constant (K_D) was determined to be ~26 nM by fitting the data with the Langmuir isotherm.

As a control experiment, we carried out the measurement with fixed wild-type SH-EP1 cells, which do not have nAChRs expressed on the cell surface, and observed no deformation in the cell membrane (fig. S3). The expression levels of nAChRs in the engineered and wild-type cells were confirmed with immunofluorescence imaging, which showed high coverage of nAChRs in the SH-EP1-hα4β2 cells and little coverage in the wild-type SH-EP1 cells (fig. S4). The nAChR expression level was estimated to be 110 nAChRs/μm² on transfected SH-EP1-hα4β2 cells (31). These results demonstrated that the mechanical deformation in the engineered SH-EP1 cells was indeed due to the specific binding of acetylcholine to the expressed nAChRs.

Not only can the present method quantify the binding kinetics of small-molecule interactions with membrane proteins in single cells, but it can also examine cell-cell variations in the binding kinetics. Figure 4 (A and C) shows phase-contrast images of SH-EP1-hα4β2 cells, where the numbers in circles mark the cells under analysis. Cells 1 and 2 were cultured on one glass slide, and cells 3 and 4, on a second glass slide. The responses of these cells to 100 nM acetylcholine are shown in Fig. 4, B and D, and the corresponding kinetic constants are given in Table 1, which show significant differences in the binding kinetics among the cells (binding kinetics on more cells are shown in table S2). The method also allows us to examine the binding kinetics at different locations of the same cell. Figure 4E plots the binding kinetic curves of acetylcholine to nAChRs at various locations of a cell, which show large variations in binding. Figure 4F shows the maximum membrane deformation along the edge of a cell, where the color represents the deformation in nanometers. Heterogeneous distribution of membrane protein receptors in cells plays an important role in cellular functions, including interactions between different cells (8, 9).

Fig. 4. Heterogeneity of small-molecule interactions with cell membrane receptors.

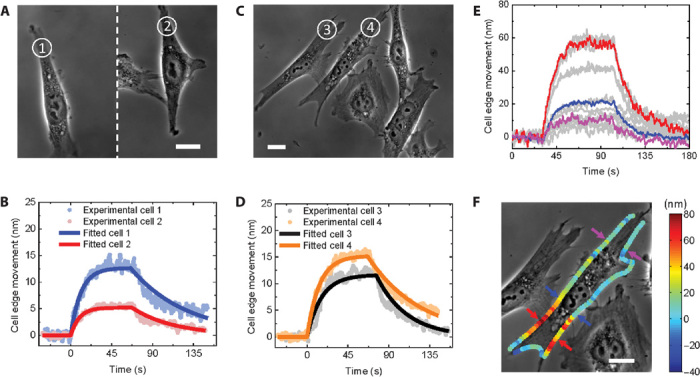
(A and C) Phase-contrast images of fixed hα4β2-transfected SH-EP1 cells, where the numbers mark the cells under analysis. Scale bars, 20 μm. (B) Binding kinetics of cells 1 and 2 (100 nM acetylcholine). (D) Binding kinetics of cells 3 and 4 (100 nM acetylcholine). (E) Binding kinetics at different locations of the cell in (F) (100 nM acetylcholine). (F) Phase-contrast image of a fixed hα4β2-transfected SH-EP1 cell. The color represents the amount of cell membrane edge deformation. Scale bar, 20 μm.

Table 1. Association rate constants (k_on), dissociation rate constants (k_off), and equilibrium constants (K_D) for four cells as shown in Fig. 4, A to D.

	kon (M−1 s−1)	koff (s−1)	KD (nM)
Cell 1	7.3 ± 0.2 × 105	1.61 ± 0.02 × 10−2	22.0 ± 0.6
Cell 2	8.3 ± 0.3 × 105	2.17 ± 0.03 × 10−2	26.1 ± 0.7
Cell 3	3.4 ± 0.2 × 105	2.98 ± 0.03 × 10−2	88.0 ± 4.0
Cell 4	5.8 ± 0. 9 × 105	1.72 ± 0.01 × 10−2	29.9 ± 0.5
Mean	6.2 × 105	2.12 × 10−2	41.5
SD	2.1 × 105	0.62 × 10−2	31.2

DISCUSSION

The importance of studying molecular interactions with membrane proteins has motivated many efforts to develop label-free detection technologies for real-time analysis of the interaction kinetics. Examples include quartz crystal microbalance (33) and SPR techniques (10). However, the signals of these methods are proportional to the mass of the molecule, making the kinetic measurement of small-molecule interactions with membrane proteins difficult. Localized SPR in metal nanoparticles enhances the detection limit (34), and the extraordinary optical transmission (EOT) effect from nanopores in a metal film offers unique plasmonic characteristics (35), which show promise for sensitive detection of molecular interactions. However, these approaches have not been applied to study molecular interactions with membrane proteins in cells, and their sensitivities scale with the molecular mass, thus making molecular interaction studies increasingly difficult for small molecules. To our knowledge, the present work is the first direct and real-time measurement of the binding kinetics of small molecules with membrane proteins in intact cells without labeling.

The method is based on the law of thermodynamics, which is general and applicable to analyzing the interactions of both large and small molecules with membrane proteins. However, the amount of membrane deformation depends on membrane mechanical properties, which is not considered in Eq. 1. Mechanical contributions to the free energy of the cell membrane include the Helfrich bending energy and tension (36). In the presence of membrane proteins with concentration ϕ, the free energy also includes the entropic contribution of the membrane proteins [f(ϕ)], and the interactions between the membrane proteins (ΛHϕ) and the membrane, given by (37)

$$\mathit{F}={\displaystyle \int }[\frac{\mathrm{\kappa }}{2}{(2\mathit{H}-{\mathit{C}}_0)}^2+\mathrm{\sigma }-\mathrm{\Lambda }\mathit{H}\mathrm{\phi }+\mathit{f}(\mathrm{\phi })]\mathit{d}\mathit{A}$$ (3)

where κ is the bending modulus, H is the mean membrane curvature, C₀ is the spontaneous curvature, and Λ is the coupling coefficient. The presence of the membrane proteins (last terms in Eq. 3) affects the membrane modulus, leading to an effective bending modulus of

$${\mathrm{\kappa }}_{\text{eff}}=\mathrm{\kappa }-\frac{{\mathrm{\Lambda }}^2}{{\mathrm{\kappa }}_{\mathrm{B}}\mathit{T}}\mathrm{\phi }$$ (4)

which indicates a change in the membrane bending modulus in the presence of proteins. This protein binding–induced membrane deformation has been observed in different membrane systems (38–40).

Ligand binding–induced membrane deformation is also expected from the molecular-scale consideration. In general, ligand binding to a protein receptor in the cell membrane leads to a conformational change in the receptor, which affects the receptor’s interaction with the surrounding lipid molecules and thus induces a membrane deformation. For example, in the case of acetylcholine binding to nAChRs, the conformational changes of nAChRs include moving of hydrophobic residues away from the pore, rotation of hydrophilic residues toward the pore, and an increase in pore size from ~3 to ~8 Å (30). The redistribution of hydrophobic/hydrophilic residues and the expansion in the size of the receptor are expected to distort the cell membrane through the receptor-lipid coupling term (ΛHϕ) in Eqs. 3 and 4. On the basis of these considerations, the binding signal detected with the present approach depends on the specific ligand-receptor and receptor-lipid interactions and overall membrane mechanical properties, which do not necessarily scale with the size of the ligand. For binding kinetics studies, one needs only to assume that the membrane deformation is proportional to the amount of ligand binding to the membrane receptor, which is expected to be true when the ligand density is low. The observed agreement between the present study and literature validates the assumption for the systems studied here.

In addition to mechanical amplification, the subnanometer resolution offered by the differential detection algorithm provides sensitive detection of molecular binding in single cells, which is also essential for the success of the present method. The subnanometer-scaled detection limit can be further improved by removing noise from different sources. Figure S5 shows the noise power spectrum of the cell edge movement of a cell. At low frequencies (<10 Hz), the power spectrum can be fitted with a linear function with a slope close to −2, indicating Brownian motion as the major source of noise. However, at higher frequencies, it deviates significantly from the Brownian noise behavior, which shows that noise from other sources, such as light source and camera, is important. The mechanical deformation measured here depends on the binding strength and membrane protein surface coverage, as well as on the mechanical properties of the cell membrane. In the present study, the detection limits of detecting WGA and acetylcholine are estimated to be 1.5 nM for CP-D cells and 1.4 nM for SH-EP1-hα4β2 cells, based on the criterion of 3 SDs.

The spatial resolution at a single cell level allows us to quantify not only cell-to-cell variation in the binding kinetics (Fig. 4, A to D) but also region-to-region variation within a single cell. For example, Fig. 4F shows relative larger binding signals of a cell in the regions where the cell interacts with a neighboring cell (red color in Fig. 4F). Similarly, the corresponding regions of the neighboring cell also show larger binding signals than other regions (fig. S6A). This phenomenon has also been observed in other cells (fig. S6B). We attribute the observed region-to-region variations to the local variations in the membrane protein coverage and mechanical properties of the cell.

The present method shows a capability for studying the binding kinetics of small molecules to membrane proteins on fixed and living cells. Fixation with paraformaldehyde (PFA) is a common practice to fix cells and has been widely used in immunofluorescence and enzyme-linked immunosorbent assays. Literature has also shown that PFA fixation does not affect the binding of nAChRs (α4β2) (41). We found similar binding kinetics for fixed and living cells (41) and that the binding kinetics or equilibrium constants obtained with the present method are consistent with the literature reports (10, 31, 32). These observations indicate that fixation did not affect the binding kinetics for the systems studied here. However, fixation, in general, may affect protein activities and should be considered in the interpretation of data. The similarity in the binding kinetics of fixed and living cells also suggests that the downstream effect in the cells studied here did not significantly affect the binding kinetics. Despite the success, molecular binding–induced downstream effects, such as cytoskeletal rearrangements (42), must be considered when applying the present method to study molecular binding in living cells.

Finally, the method is based on optical microscopy, which is simple and compatible with various optical imaging techniques, including fluorescence imaging. These capabilities will benefit the screening of drugs and the analysis of various cellular processes that involve membrane proteins. The latter is especially important because as the number of 3D structures of membrane proteins exponentially increases, studying the interaction kinetics of molecules with membrane proteins becomes increasingly important.

MATERIALS AND METHODS

Materials

WGA and acetylcholine chloride were purchased from Sigma-Aldrich. Anti-EGFR monoclonal antibody was purchased from EMD Millipore (cat. no. 05-101). Primary rat monoclonal antibody to nAChR α4 subunit (clone 299) and Alexa Fluor 488 goat anti-rat immunoglobulin G (IgG) were purchased from Abcam Inc. For all binding experiments, 1× PBS (pH 7.4) was used as buffer. All samples were prepared in 1× PBS buffer.

Cell cultures

SH-EP1-hα4β2 cells were cultured in a humidity incubator at 37°C with 5% CO₂ and 70% relative humidity. The cells were cultured in a 25-cm² flask containing Dulbecco’s modified Eagle’s medium (DMEM; Lonza) with 10% fetal bovine serum (Life Technologies) and penicillin-streptomycin (BioWhittaker). When about 80% confluency was reached, the cells were passaged with 0.05% trypsin-EDTA (Life Technologies).

CP-D cells were cultured in an incubator at 37°C with 5% CO₂ and 70% relative humidity. The cells were cultured in a 25-cm² flask containing 1× Keratinocyte-SFM (Life Technologies) and penicillin-streptomycin (BioWhittaker). When about 80% confluency was reached, the cells were passaged with 0.05% trypsin-EDTA (Life Technologies).

A431 cells were cultured in an incubator at 37°C with 5% CO₂ and 70% relative humidity. The cells were cultured in a 25-cm² flask containing DMEM (Lonza) with penicillin-streptomycin (BioWhittaker). When about 80% confluency was reached, the cells were passaged with 0.05% trypsin-EDTA (Life Technologies).

For the experiments, cells were cultured overnight on bare glass slides (22 × 60 –mm micro cover glass, VWR) placed on top of a silicone well (FlexiPERM, Greiner Bio-One) to allow cells to attach on the surface. Cells on glass slides were also cultured in an incubator at 37°C with 5% CO₂ and 70% relative humidity. Cells were incubated in 4% PFA for 10 min at room temperature for fixation and further analysis. Before measurement, the small silicone well was changed to a homemade polydimethylsiloxane (PDMS) well 2 cm in length, 1 cm in width, and 1 cm in height.

For measuring binding kinetics on live cells, cells were also cultured overnight on bare glass slides on a silicone well and placed in an incubator at 37°C with 5% CO₂ and 70% relative humidity. Before the experiment, the small silicone well was changed to a homemade PDMS well with larger dimensions. The measurement was carried out immediately after the culture medium was changed to live cell imaging solution (Life Technologies) to maintain cell viability.

Optical imaging setup

An inverted microscope (Olympus X81) equipped with a phase 2 condenser and a 40× phase 2 objective was used with illumination from the top of the sample cells. For the acetylcholine experiment, an extra 0.5× zoom lens was used with the CCD camera.

Immunofluorescence microscopy

For nAChR immunofluorescence, cells were fixed with 4% PFA in PBS for 10 min at room temperature and then rinsed three times with 1× PBS. The fixed cells were incubated in 1% bovine serum albumin in PBS at 37°C for 1 hour to block the cell surface. The primary antibody was added, and the cells were incubated for 30 min at 37°C. The cells were rinsed three times with PBS buffer, then the Alexa Fluor 488–labeled secondary antibody was added, and the cells were incubated for another 30 min. The fluorescence image was captured on the same setup for phase-contrast image after the well was rinsed three times with PBS. A set of optical filters (excitation, 420 to 480 nm; emission, 515 nm) was used for the immunofluorescence analysis.

Calibration of the differential optical detection of cellular edge movement

The relation between the cell edge movement and the measured differential image intensity change was determined and calibrated using the following procedure. To reduce digital noise associated with the finite pixel size, the pixel density of each image was increased five times by adding additional pixels with a bilinear interpolation approach. The distance between two pixels in the interpolated image was 37 nm (Pike F032B CCD, Allied Vision Technologies). The edge of one cell was manually chosen, and the centroid (O) of the cell was determined (fig. S7A). A polar coordinate system was set up with the centroid serving as the pole. The cell edge movement was calculated at every 1 μm starting from 0° (fig. S7, B and C). The ROI (1.85 × 3.70 μm) at a certain point of the cell edge (point A) was shifted by different numbers of pixels from the outside to the inside of the cell (fig. S7D) (perpendicular to the tangential line at point A), and the corresponding changes in the differential image intensity were determined (fig. S7E). The relation between the differential image intensity and the cell edge movement (pixels) was found to be linear within a certain range (fig. S7E, between two red dashed lines), which served as a calibration curve to determine the cell edge movement (mechanical deformation) from the differential image intensity (fig. S7F). Note that each pixel corresponds to 0.037 μm, which allowed us to convert movement in terms of pixels to micrometers.

The overall procedure of the differential detection method for cell edge movement tracking is shown in fig. S8. First, the cell edge was manually defined. Then, the calibration curve at each location along the cell edge was obtained using the procedure described earlier. Using these calibration curves, we determined the edge movements at different cell edge locations. Although we manually selected the cell boundary in the current study, the result is insensitive to the selection as long as the boundary is within the linear region of fig. S7E, which is about 20 pixels (0.74 μm). It typically takes around 5 min to analyze one cell, including selection of the cell boundary, calibration, edge tracking, and kinetic data, with a laptop. Automatic selection of the cell boundary and more efficient calculation are possible in the future.

Data analysis

The binding kinetics k_on, k_off, and K_D were obtained by fitting the experimental kinetic curves with a first-order kinetic model (least square fitting), and the errors are the fitting errors. The average value and SD of binding kinetics among different cells were also calculated and shown in Table 1 and tables S1 to S3. The variability in the binding kinetics among different cells is much larger than the fitting errors.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/1/9/e1500633/DC1

WGA and glycoprotein interactions in a live cell

Fig. S1. WGA and glycoprotein interactions in a live cell.

Anti-EGFR antibody interaction with EGFR in fixed A431 cells

Fig. S2. Anti-EGFR antibody interaction with EGFR in fixed A431 cells.

Negative control for nAChR and acetylcholine interaction

Fig. S3. Negative control for nAChR and acetylcholine interaction.

nAChR immunofluorescence

Fig. S4. Phase-contrast and immunofluorescence images of nAChR-positive and nAChR-negative cells.

Noise power spectrum of cell edge movement of a fixed CP-D cell

Fig. S5. Noise power spectrum of cell edge movement of a fixed CP-D cell.

Molecular binding–induced membrane deformation along cell edges

Fig. S6. Molecular binding–induced membrane deformation along cell edges.

Calibration of the differential imaging intensity and cell edge movement

Fig. S7. Calibration of the differential detection of cellular edge movement.

Differential detection method

Fig. S8. Diagram illustrating the procedure of the differential detection method.

Statistic analysis of WGA and glycoprotein interactions on fixed CP-D cells

Table S1. Binding kinetics between WGA and glycoprotein on different fixed CP-D cells.

Statistic analysis of WGA and glycoprotein interactions on live CP-D cells

Table S2. Binding kinetics between WGA and glycoprotein on different live CP-D cells.

Statistic analysis of acetylcholine and nAChR interaction on fixed SH-EP1-hα4β2 cells.

Table S3. Binding kinetics between acetylcholine and nAChRs on different fixed SH-EP1-hα4β2 cells.

Reference (43)