Efficient Search and Fit Methods to Find Nerve Stimulation Parameters for Multi-Contact Electrodes

Abstract

This paper describes a method to efficiently sample EMG recruitment space over a wide range of pulse amplitude (PA) and pulse width (PW). A gradient based search method is developed to find high information areas of a recruitment surface. This search method is first examined in the context of simulated EMG recruitment data and its ability to sample and subsequently fit Gompertz-Function-inspired surfaces to it. The search method is then used to determine parameters when stimulating through an 8 contact flat interface nerve electrode (FINE). The recorded EMG recruitment data are then used to validate the Gompertz surface fitting method as well as the search method.

I. Introduction

The aim of a functional electrical stimulation (FES) system is to restore or improve the function of individuals with neurological compromise, especially those with upper motor neuron (UMN) involvement. FES has been shown to be effective in restoring basic lower extremity motor function in individuals with stroke or spinal cord injury [1]. In the past, stimulation at the femoral nerve using the flat interface nerve electrode (FINE) has been shown to be effective in recruiting muscles in a selective fashion [2]. This muscle selectivity is important to stimulate the proper muscles during different phases of gait and also to delay fatigue by alternating stimulation of functionally synergistic muscles [3]. To test the efficacy of nerve cuffs prior to implantation, intraoperative testing has been performed on patients while recording recruitment of muscles using electromyography (EMG) [2]. As the number of contacts on a cuff increases, stimulation can better activate the desired muscles without recruiting unwanted ones that would be counter-productive to the intended movement [4], but it also becomes more time consuming to discover the best stimulation parameters--in this case, pulse amplitude (PA) and pulse width (PW)--to achieve this selectivity. Thus, it is important to intelligently choose which parameter sets to use in intraoperative testing as the number of stimulating contacts increases.

Previous methods to find nerve stimulation parameters generally focus on recording EMG recruitment along one dimension at a time (often modulating PW at a set PA) [5]. Here, we examine search methods of stimulation parameters across the full space of both PA and PW. As well, we explore the validity of fitting Gompertz-Function-inspired surfaces to EMG response data to predict muscle responses to any set of stimulation parameters. These Gompertz surfaces are tested by fitting and validating using separate EMG datasets elicited after bilateral stimulation of proximal femoral nerves. Together, these methods can gather data efficiently to allow for more effective testing of nerve cuffs to be used for restoration of function after UMN injury.

II. Methods

The process we explore for efficiently determining nerve stimulation parameters starts with simulating EMG recruitment surfaces. These surfaces are used to test the efficiency of methods to collect data points which provide information about the shape of the surfaces. These points are then validated against the simulated dataset by fitting a surface to the sampled points and calculating the coefficient of determination (R²) over the full simulated space (Matlab, Natick, MA). After determining the efficiency of this process, the search method was used to characterize EMG recruitment over PA and PW during the acute application of a FINE to the bilateral proximal femoral nerves. To validate the surface fitting procedure and thus the search method described below, the EMG recruitment data were randomly divided into separate datasets for surface fitting and testing.

A. Surface Creation

The primary set of simulated EMG recruitment surfaces were modeled as an analogy to a Gompertz function. The Gompertz function is often used to model population growth, for instance, in tumors [6]. It is appealing to use this function to describe the recruitment of a population of axons. As well, the Gompertz function was chosen since it has been shown to fit human EMG recruitment data well along a single dimension (pulse amplitude modulation or pulse width modulation) [7]. The Gompertz surfaces were created based on 5 parameters: A, to control overall amplitude, B to control shifting of the curve along PA or PW, and three variables (C_PA, C_PW, C_PAPW) to control the rate of rise in each the direction of PA, PW, and the product of PA and PW. The form of the surface follows:

$$A{e}^{Be(C_{PA}{P}_A+C_{PW}{P}_W+C_{PAPW}{P}_A{P}_W)}.$$ (1)

The 5 parameters used in Eq. 1 were varied independently of each other for each surface created based on separate independent uniform distributions. Some parameters could vary from approximately ten-fold (for instance, A) to one-hundred-fold (C_PA) or more (B) so that the surfaces produced would rise at values of (PA, PW) that covered the full space available. The parameters controlling rise were all negative, as was B, while A was always positive. The function used a sum of parameters in the second exponent as this was required to control rise of the sigmoid independently along PA, PW, and their product across the space of PA and PW.

To ensure robust behavior with expected EMG signals, noise was added to all simulated surfaces. The added noise was Gaussian with a mean of zero and a standard deviation ranging from 0.01 to 0.2 of the maximum simulated EMG value. To ensure further robustness, search and fit methods were also tested against surfaces that were created only with the assumption that they must be monotonically increasing in PA and PW. These surfaces were created by randomly increasing recruitment with each step in PA or PW.

B. Search Methods

The pulse space search method aims to isolate areas with a high gradient and to cover all values between a predetermined high (0.9) and low (0.1) thresholds, which are normalized to the highest point on the surface. Thus, density of search points positively correlates to the gradient of the surface. In addition, if there is a large change in recruitment values between any two PA, PW pairs, the algorithm will explore the recruitment values at PA and PW values between the original PA, PW pair.

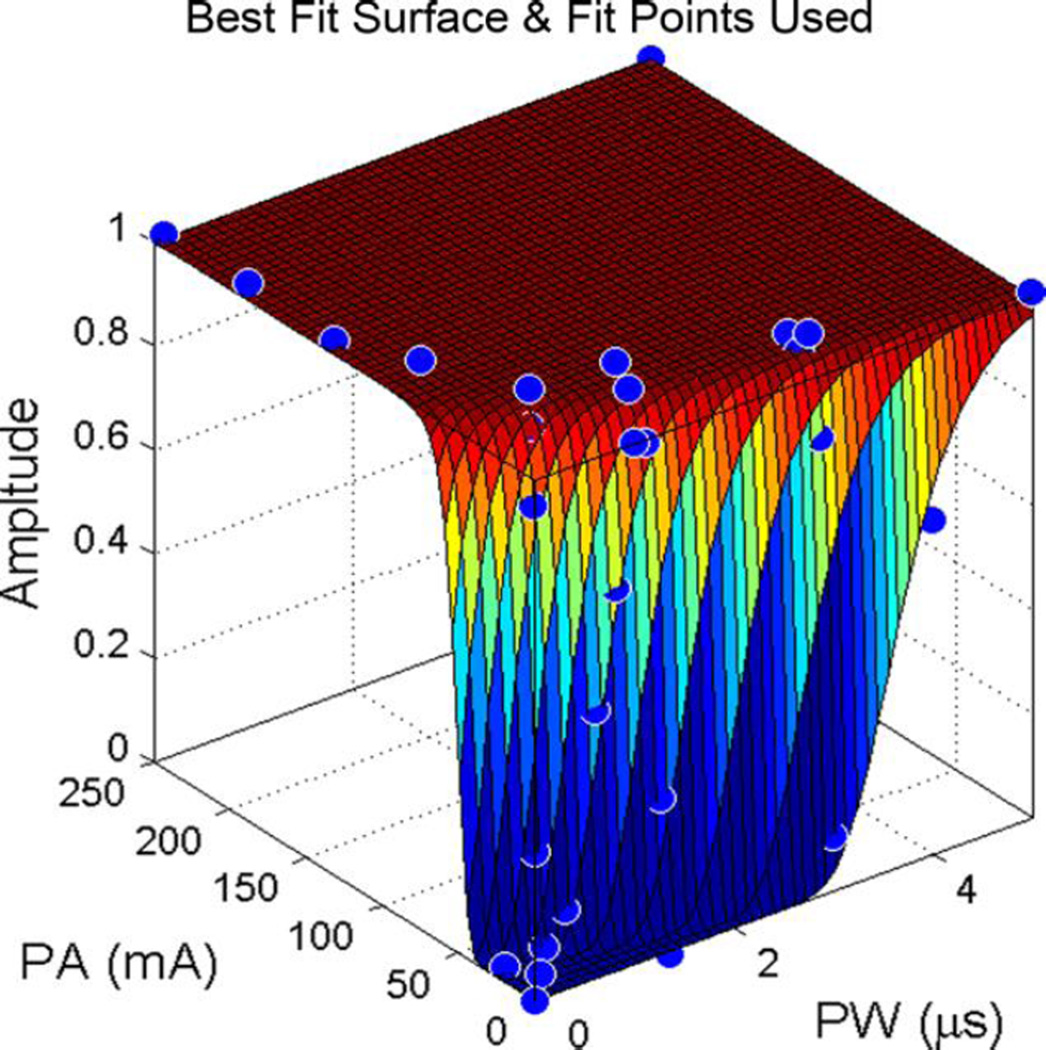
The search is conducted as follows. First the value of the surface at maximum PA and PW is found. Second, the search starts at the highest value in PA and the lowest value in PW. If the surface at this point is below lower threshold, a recruitment curve is searched along PW at the current value in PA. The rate of movement along this curve depends on the gradient found from the previous two sampled points such that points are sampled more closely when gradients are higher. This local search stops when all muscles’ EMG data is above upper threshold. Conversely, if the lower threshold was not passed, PA is lowered until the criterion is met and then a curve is found along PW at a lower PA. Third, PA is again lowered for another search along PW. This search begins at the PW where upper threshold was passed on the previous curve (it is assumed that at lower PA the point will likely be below upper threshold) and occurs both in increasing and decreasing directions to pass upper and lower thresholds, respectively. This repeats until two curves are produced. Fourth, the local searches are repeated in the opposite direction (starting at high PW and low PA to create curves that search along PW). Figure 1 illustrates an example of the results of this process and shows that points are closer together where the surface rises steeply.

Fig. 1.

Example of Pulse Space Search Method and Resulting Surface Fit on Simulated EMG Recruitment Data. Blue dots show sampled points in the simulated EMG recruitment surface. Note that the pulse space search method sampled few points in the plateau of this surface.

The pulse space search method was compared to a method of collecting samples consisting of a predefined grid over the space of PA and PW. This method requires minimal computational overhead but is unable to increase resolution in specific areas as needed.

C. Surface Fitting

Search methods were evaluated by how well they provided points to fit a surface to the simulated EMG data. This was compared using the calculated R² between the simulated surface and the fitted surface across every defined point (all PA and all PW) in the recruitment surface space.

During each fit iteration, the R² value for the points sampled by the algorithm was calculated. If this R² value was low, the fit was rerun with randomized initial guess parameters. Through initial testing, it was clear that some surfaces (such as surfaces only assuming random monotonic increase in recruitment) required more control over the dependence of recruitment surface on PA and/or PW. Thus, four more parameters were introduced including a parameter on each of PA and PW to control the power to which each value was raised and a parameter on each of PA and PW to control a shift in the value of each variable. Figure 1 shows an example of a surface fitted using this method.

D. EMG Recording

An 8 contact FINE was used to validate the pulse space search method. Two FINEs were implanted bilaterally around the proximal femoral nerves of a volunteer with motor-complete spinal cord injury. The nerve cuff electrode was connected to a stimulator which could deliver a monopolar, charge-balanced, biphasic stimulus independently to each contact with a range of PA from 0.1 mA to 5 mA and PW from 1 µs to 255 µs. Stimulus pulses were delivered 3 times at each (PA, PW) point. EMG signals from rectus femoris, vastus lateralis, vastus intermedius, vastus medialis, and sartorius were recorded with needle electrodes. The EMG signal was amplified and low pass filtered at 1,000 Hz and sampled at 2,500 Hz. The signal was then rectified and integrated from 3 ms to 40 ms, and this value was normalized by the maximum EMG recording for a given channel. The pulse space search method was utilized to determine which points in PA and PW to sample.

Informed consent was acquired prior to all experimental procedures and all human testing protocols were approved by the Institutional Review Board of MetroHealth Medical Center, Cleveland, OH.

E. Surface Fitting Validation

75 EMG Recruitment surfaces were collected using the pulse space search method (5 muscles over 15 contacts). These surfaces were randomly divided into separate data sets so that one was used to fit surfaces to the recruitment data and the other set was used to verify the fit. As well, these 75 surfaces were placed into three groups based on the ratio of the normalized mean to the standard deviation of the signal at a given point (3 samples were taken at each point). This is noted here as low, medium, and high SNR groups

Goodness of fit was determined using coefficient of determination (R²) of both datasets and also by examining what proportion of surfaces correctly predicted the PW at which EMG threshold (determined as 10% of maximal recruitment) was passed at PA of 0.8 mA and 1.4 mA. The PW threshold predictions were deemed correct if they fell within the range of PW that was found during implantation when binary search along PW at these amplitudes was carried out on the same muscle and contact.

III. Results

A. Fitting Surfaces with Different Sampling Methods

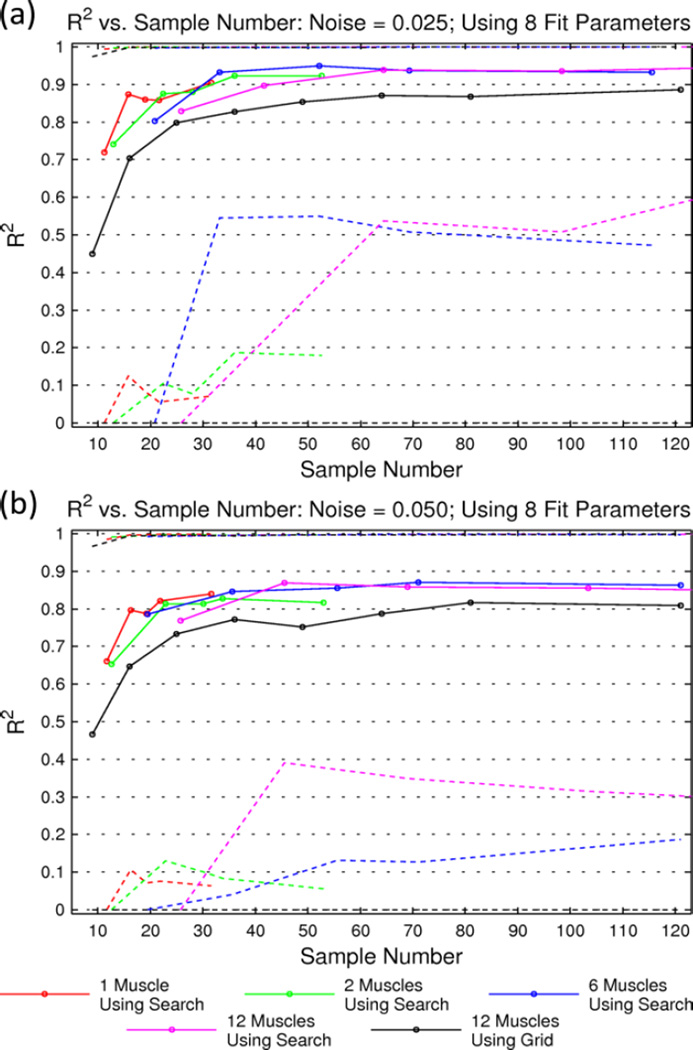
Figure 2 provides an overview of the data initially collected when sampling from and then fitting surfaces to simulated EMG data. Using the pulse space search method on 1 surface at a time achieves a high value of R² with much fewer points than a search on 12 surfaces at a time. This is expected since there are fewer high-information areas in space to sample. However, this difference disappears quickly as number of surfaces increases such that searching 12 surfaces at a time only requires a small increase in sample size compared to 6 surfaces at a time. Also of note is that a predefined grid method for choosing points is consistently less reliable at fitting a surface with a given number of samples. This is obvious when examining the worst fits from both methods: the 2.5^th percentile using the grid method is generally quite low.

Fig. 2.

Goodness of Fit of Simulated EMG Recruitment Surfaces Pulse Using Space Search and Grid-Based Method. Coefficient of determination (R²) mean (solid lines) and 2.5^th and 97.5^th percentiles (dashed lines) vs. sample number. Results are shown for noise added with a standard deviation of 2.5% of signal (a) and 5% of signal (b).

Based on these simulated surfaces, using the pulse space search method, about 15 samples can fit a single Gompertz surface with 0.025 and 0.05 standard deviation noise. To classify the recruitment for 12 surfaces at once (stimulating 12 muscles with one electrode), this search method needs about 45 samples. The grid method reaches a plateau at about the same number of samples as the search method on 12 surfaces. However, the mean of the R² value is about 0.05 lower and the 2.5^th percentile is up to 0.5 lower. The grid method also never reaches the same R² values that the search method does, likely due to imprecision during surface fitting. It is also of note that this search and fit method is relatively robust to simulated noise (Figure 2 a and b).

B. Efficient Nerve Stimulation Parameter Selection

During implantation, the pulse space search method was able to characterize EMG recruitment surfaces well using an average of 58 sample points (a range of 29 to 103 over all contacts). This required approximately 1 minute of time to characterize each channel. As well, this could have been achieved with fewer points, since extra sampling was required for validation datasets.

C. Validation of Fitting Recruitment Surfaces

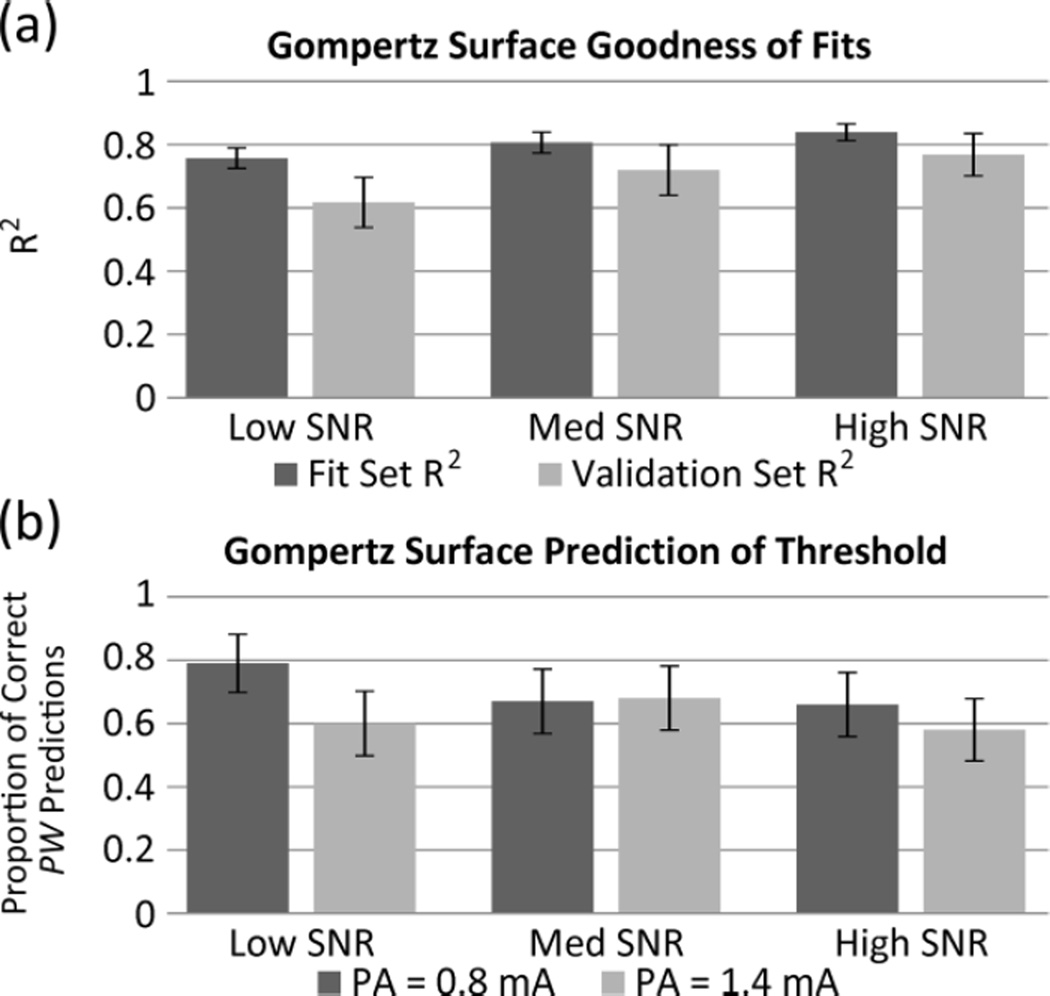
To validate the previous results which used simulated recruitment surfaces, EMG data from the subject with bilateral proximal femoral nerve cuffs were fit and validated (Figure 3). The goodness of fit was dependent on the quality of the recorded EMG signal from the muscle being stimulated. For this reason, the 75 recruitment surfaces fit in this study were divided into three groups based on sum of the ratio of normalized mean to standard deviation at each point (SNR in Figure 3). While a relationship between R² and SNR is noted, differences are not significant. It is believed they would be with more subjects.

Fig. 3.

Evaluation of Gompertz Surfaces Fit to Experimental EMG Recruitment Data. EMG data were divided into equally sized groups of 25 surfaces based on the ratio of the normalized mean to standard deviation of signal at a given point (low, medium, high SNR groups). Goodness of fit was evaluated by mean R² value (a) of both the fit and validation data sets and proportion of predictions of threshold PW (10% of maximum) that fall within the binary searches (b) at different values of PA. Error bars represent standard error of the mean.

The best R² values are over 0.8 for the dataset being fit, and over 0.75 for the validation dataset. This does drop as SNR drops, especially in the validation set. This same trend is not noted when the fitted Gompertz surfaces are used to predict the PW at which threshold (10% of maximum) occurs. This is likely due to the Low SNR group of surfaces having high recruitment only at higher PA, PW values (thus the average mean over the sample collected is lower and so SNR is lower). This results in the PW range of thresholds being larger and thus easier to predict. There may be difference between threshold prediction results at PA of 0.8 mA and 1.4 mA but this is not significant in these results.

IV. Discussion

Based on the initial analysis of fitting simulated muscle recruitment surfaces, fitting a surface to adaptively-chosen (as in the pulse space search) points presents a promising method of characterizing muscle recruitment as it relates to changes in PA and PW. As well, the pulse space search method works quickly and provides samples to fit recruitment surfaces well. The sampling method is much more efficient at acquiring recruitment data than previous methods involving modulation of a single stimulation parameter at a time. In the amount of time that previous methods characterized two to three curves along PW, this method characterizes a full surface over PA and PW. The method will be faster if validation datasets are not required. In the future, it may also be beneficial to examine possible benefits of weighting certain areas in the PA, PW space more highly than others. These areas would ideally be found by examining many recruitment surfaces and finding areas of significantly elevated or decreased information. As well, future comparison to other sequential sampling methods, such as particle filters, could be fruitful. Surface fitting appears promising but could be improved. More time allowed for computation iterations can give better fitting results. Assuming that recruitment should monotonically increase over PW and PA, it may be possible to weight areas that are presumed to be known (such as high or low plateaus). This may provide more reliable fitting in fewer iterations by ensuring the proper surface shape even if only a few points in the high or low plateaus are sampled.

The analysis performed on EMG data provides strong evidence that recruitment surfaces can be well characterized using Gompertz surfaces. Muscles that are highly recruited by a given contact are fit very well. However, there remains concern with poorer fitting of less-strongly recruited muscles with lower SNRs. In the future, running similar surface fitting validation with results from a patient with a chronically-implanted nerve electrode (where thousands of data points could be obtained at one time) could be very useful to further confirm the validity of these methods.