Deducing acidification rates based on short-term time series

Abstract

We show that, statistically, the simple linear regression (SLR)-determined rate of temporal change in seawater pH (β_pH), the so-called acidification rate, can be expressed as a linear combination of a constant (the estimated rate of temporal change in pH) and SLR-determined rates of temporal changes in other variables (deviation largely due to various sampling distributions), despite complications due to different observation durations and temporal sampling distributions. Observations show that five time series data sets worldwide, with observation times from 9 to 23 years, have yielded β_pH values that vary from 1.61 × 10⁻³ to −2.5 × 10⁻³ pH unit yr⁻¹. After correcting for the deviation, these data now all yield an acidification rate similar to what is expected under the air-sea CO₂ equilibrium (−1.6 × 10⁻³ ~ −1.8 × 10⁻³ pH unit yr⁻¹). Although long-term time series stations may have evenly distributed datasets, shorter time series may suffer large errors which are correctable by this method.

Ocean acidification is an unavoidable consequence of increasing atmospheric CO₂¹,²,³,⁴,⁵. Understanding how fast the oceans acidify is critical to examining and predicting the impact of ocean acidification on the aquatic ecosystem. Invaluable decadal ocean time series measurements of carbonate chemistry parameters can now be used for this purpose. Observations show that surface ocean pH under in situ temperature (pH_insitu) has strong seasonal variations, with a high pH_insitu in winter and a low pH_insitu in summer. Long-term decreasing trends are superimposed on the regular seasonal variations⁶,⁷,⁸.

To investigate how fast the oceans acidify, the widely used first-order simple linear regression (SLR) method has been used to model the long-term temporal changes in pH_insitu (β_pH)²,⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³. The SLR model in general form is as follows,

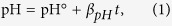where pH° is the intercept, β_pH is the slope, and t is time in the pH_insitu vs. t plot.

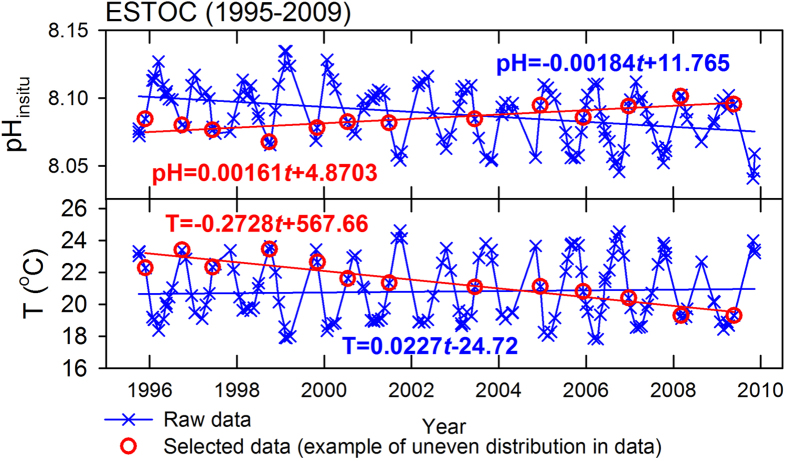
The β_pH, the so-called acidification rate, refers to an average rate of temporal change in pH_insitu. Conventional wisdom has it that the longer the pH_insitu time series (e.g., over a decade) the better the estimation of the β_pH. Bermuda Atlantic Time Series Study (BATS) and the Hawaii Ocean Time Series (HOT) (see Fig. 1 for the station locations) are two examples of long-term time series with even sampling distribution, and their β_pH values fairly reflected the acidification rates due to the increased atmospheric CO₂ concentrations⁶,⁷. However, in a time series with short observation years (e.g., less than a decade), the small long-term temporal change in pH_insitu due to the increase in atmospheric CO₂ could be easily masked by the strong seasonal variations, especially in the case of uneven sampling distribution. The pH_insitu and seawater temperature (T) time series at the European Station for Time Series in the Ocean Canary Islands (ESTOC) between 1995–2009 are shown as examples (Fig. 2). The raw data (blue cross), when fitted by the SLR, result in a negative β_pH of −1.84 ± 0.39 × 10⁻³ pH unit yr⁻¹ and positive SLR-determined rate of temporal change in T (β_T) of 0.023 ± 0.039 °C yr⁻¹ (Fig. 2). The red circles represent an extreme example of uneven sampling distribution, with the sampling time gradually shifting from summer to winter. As a result, these data now would have a positive β_pH of 1.61 ± 0.37 × 10⁻³ pH unit yr⁻¹ and a negative β_T of −0.273 ± 0.036 °C yr⁻¹. Moreover, the slopes of the regression lines would increase with a shift in sampling time from summer to winter within a shorter observation period. This shows that β_pH is highly sensitive to the temporal distribution, and the duration, of time series data.

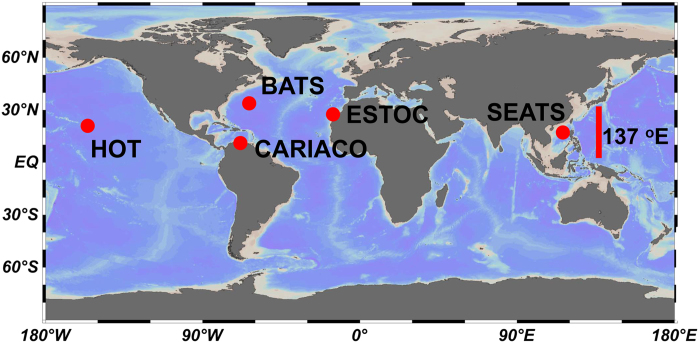
Figure 1. Station locations of the time series, including Bermuda Atlantic Time Series Study (BATS), Carbon Retention in a Colored Ocean Project (CARIACO), European Station for Time Series in the Ocean Canary Islands (ESTOC), Hawaii Ocean Time Series (HOT), South East Asia Time Series Study (SEATS), and 137°E repeated hydrographic line (137°E).

The map was generated using Ocean Data View 4.6.2. Schlitzer, R., Ocean Data View, odv.awi.de, 2015.

Figure 2. Time series of pH_insitu and T at ESTOC.

The blue crosses and lines show the raw data and the regression lines. The red circles and lines show a case of selected data, and the regression lines. Data taken from Gonzalez-Davila and Santana-Casiano¹⁹.

It has been suggested that the effect of seasonal variations on β_pH could largely be reduced when pH anomaly data (observed data minus seasonal average) are used². However, this method may not be applicable to time series with short observation periods and uneven sampling distribution, which do not have sufficient data to generate effective seasonal means, resulting in errors. Furthermore, the reported low values of the coefficient of determination (R²), ranging from 0.09 to 0.55, indicate that these time series data were still poorly fitted by SLR lines². Consequently, estimating β_pH using only t introduces a deviation due to the influence of strong temporal variations. As a result, it remains unclear whether the observed rates at which surface seawater pH_insitu changes differ are due to the changing carbonate chemistry of seawater at different time series stations or to deviation using SLR.

In this study, we propose a simple statistical method for reducing deviations of β_pH under the influence of strong temporal variations. We show that when pH is expressed as a linear function of t and the other variables, β_pH can be expressed as a linear combination of a constant (an estimated rate of temporal change in pH) and SLR-determined rates of temporal changes in the selected variables (deviation largely due to various sampling distributions under the strong seasonal pH variability), despite complications due to different observation durations and temporal sampling distributions. Using this method, we demonstrate that β_pH differs from the observations from five time series stations (the BATS, Carbon Retention in a Colored Ocean Project (CARIACO), ESTOC, HOT, and the South East Asia Time Series Study (SEATS, with bottom depth >3700m)) mainly due to deviations under various sampling distributions rather than changing seawater chemistry. Average summer and winter β_pH values from 31 stations along the 137°E repeated hydrographic line (137°E) likely contain the same deviation.

There are few reported acidification rates for the world’s oceans, as there are only a handful of stations with decadal time series of carbonate parameters. Time series studies with high temporal variations and few observation years can benefit from our approach to find the fair estimation in the rate of temporal change in pH_insitu.

Results

Decomposition of β _pH and its physical meaning

Statistically, for any pH_insitu time series, β_pH is defined as follows¹⁴,

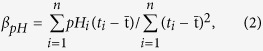where pH_i and t_i are pH and t, respectively at t = t_i, and is the average t.

As t can only be used to model the linear temporal change in pH_insitu, it cannot be used to model the strong seasonal variations. Suppose that other variables (e.g. T, dissolved oxygen, nutrients), x₁, …, x_n, are added to model the temporal variations in pH_insitu, which can be expressed as follows,

where m₁ ~ m_k are constants, t° is a reference point of t, and are x₂ ~ x_k at t = t°, respectively.

Substituting Eq (3) into Eq (2), Eq (2) can be rewritten as follows,

As and 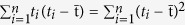, the equation above can be simplified as follows,

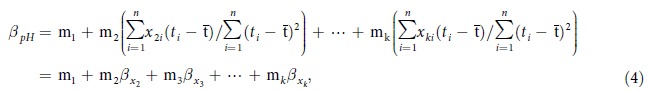where 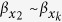are SLR-determined rates of temporal changes in x₂ ~ x_k, respectively (see the definition shown in Eq (2)).

Equation (4) shows that in fact, β_pH can be expressed as a linear combination of a constant (m₁) and rates of temporal changes in the other regression variables (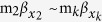). Thus, although differences in the number of observation years and temporal distribution of sampling yield different β_pH and 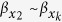, values for 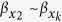change with β_pH, whereas m₁ remains unchanged. Statistically, if x₂ ~ x_k in the above equation have no long-term trends of changes, 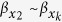are expected to be zero. Non-zero 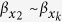refers to the consequence of various sampling distributions under seasonal variations in x₂ ~ x_k. If the long-term trends of changes in x₂ ~ x_k have no collinearities with that of pH_insitu, any long-term trends of changes in x₂ ~ x_k would not affect β_pH.

Notably, m₁ is defined as the amount of pH_insitu change as t changes. Therefore, if long-term changes in 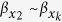do not vary with that of t or pH_insitu, m₁ refers to the estimated rate of temporal change in pH_insitu due to different physical and biological forcings (e.g. changes in anthropogenic CO₂ concentration, productivity, microbial respiration rate, etc.), whereas 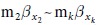refers to the deviation due to the temporal variation. Notably, the deviation due to uneven sampling distribution under strong temporal variations can be quantified using rates of temporal changes in other variables.

Verifications and criteria of additional regression variables

To verify Eq (4), additional variables need to be added to the regression model shown in Eq (3). These variables must be strong in seasonal variations and weak in long-term changes, so that they can be used to model the seasonal variations in the pH_insitu. At the same time they should have weak collinearities with t. Seawater T may serve this purpose, as pH_insitu is related to T and observations show that the T time series routinely mirrors the pH_insitu time series⁶,⁷. Furthermore, modelled results from recent studies show that the surface ocean pH_insitu has no observable change under a long-term change in T¹⁵,¹⁶.

To verify the appropriateness of using t and T in modeling pH_insitu, Eq (3) is simplified as follows,

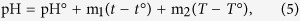where T^o is T when t = t^o.

Using the initial year of t° = 1988 as a reference, the multiple linear regression (MLR) model of Eq (5) is then applied to the surface ocean pH_insitu from five time series stations. The results are shown in Fig. 3 and Table 1.

Figure 3. The surface seawater pH_insitu at various time series stations.

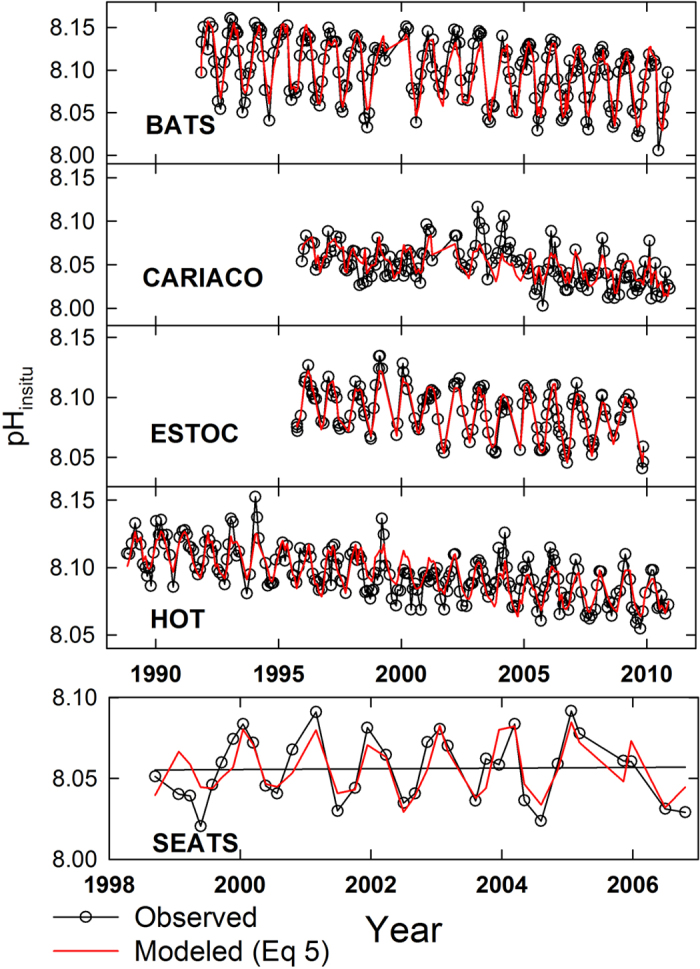
The black and red lines show, respectively, the observed values and the values modeled by Eq (5).

Table 1. MLR coefficients of Eq (5) of seawater pH_insitu from various time series studies. The pH° and T° are determined using the SLR method when t° = 1988 (see Supplementary Table S2).

		Eq (5) pH = pH° + m1(t−t°) + m2(T−T°)
Station	Year	pHO	T°	m1 x10−3 pH unit yr−1	m2 x10−3 pH unit oC−1	Standard Error	R2	n
BATS	1991–2010	8.1297	22.85	−1.8 ± 0.2	−9.9 ± 0.3	0.0135	0.86	215
CARIACO	1995–2010	8.0835	24.82	−1.5 ± 0.3	−7.0 ± 0.7	0.0155	0.51	144
ESTOC	1995–2009	8.1155	20.46	−1.6 ± 0.1	−9.6 ± 0.2	0.0053	0.94	144
HOT	1988–2010	8.1172	24.68	−1.7 ± 0.1	−9.3 ± 0.5	0.0088	0.77	222
SEATS	1998–2006	8.0531	30.63	−1.5 ± 0.9	−7.7 ± 1.0	0.0123	0.66	35
Average		8.0998 ± 0.0311	24.69 ± 3.76	−1.6 ± 0.1	−8.7 ± 1.4	0.011 ± 0.004	0.75 ± 0.17	5

Linearity between pH_insitu, t, and T.

Figure 3 shows the observed pH_insitu time series and the modeled results using MLR at various time series stations. The regression results match well with the annual, interannual, and long-term variations in observations. The m₁ and m₂ of −1.6 ± 0.1 × 10⁻³ pH unit yr⁻¹ and −8.7 ± 1.4 × 10⁻³ pH unit °C⁻¹, respectively, are similar among the time series stations. The R² values are increased from 0.09 ~ 0.55 to 0.51 ~ 0.94, with all sites averaging 0.75 ± 0.17. The differences between the measured and the MLR results are at most approximately twice the pH calculation error of ±0.0062, based on the carbonate system using total alkalinity (TA) and dissolved inorganic carbon¹⁷, suggesting the validation of Eq (5). Consequently, Eq (4) can now be simplified as follows,

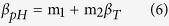It is important to point out that the linearity between pH_insitu and T is a lump sum of various physical and biological forcings. Based on this linearity, the change in β_pH due to various sampling distributions under the strong seasonal variability is reflected in m₂β_T. The fact is that, changes in pH_insitu and T owing to other factors (e.g. global warming, enhanced upwelling, etc.) may not equal to m₂, resulting in residuals. The standard errors of Eq (5) shown in Table 1 possibly reflect the errors from minor disturbances and from the measurements. Since Eq (6) is generated from Eq (5), Eq (6) contains the same kind of errors as Eq (5) does. Fortunately, the standard errors are relatively small. Therefore, m₁ is the estimated rate of temporal change in pH_insitu, and m₂β_T is the deviation largely due to the various sampling distributions under the strong seasonal pH_insitu variability. In addition, any parameter, having linearity with pH_insitu and having no observable temporal collinearities with t or pH_insitu, can technically be used in the same way as T does to quantify the deviation of β_pH due to various sampling distributions under strong seasonal pH_insitu variability.

Linearity between β _pH vs. β _T and the deviation (m₂ β _T )

To quantify Eq (6), observations from five time series with varying numbers of observation years (9–23 years) are examined with the average β_pH of 31 time series stations along the 137 ^oE line in the winter and summer (Fig. 4; detailed information are shown in Supplementary Fig. S1 Supplementary Information Table S1). Determined by SLR on the observed pH_insitu and T time series, the results show that the observed β_pH values vary from +1.61 × 10⁻³ pH unit yr⁻¹ to −2.5 × 10⁻³ pH unit yr⁻¹. The slope (m₂) of the regression line of −9.7 ± 0.7 × 10⁻³ pH unit °C⁻¹ is consistent with the MLR determined m₂, with an average of −8.7 ± 1.4 × 10⁻³ pH unit °C⁻¹ for the five time series (Table 1). Although no reported average values in m₁ and m₂ are given, the result in Fig. 4 shows that the average β_pH values at the 137 ^oE likely have m₁ and m₂ values similar to that of the other five time series.

Figure 4.

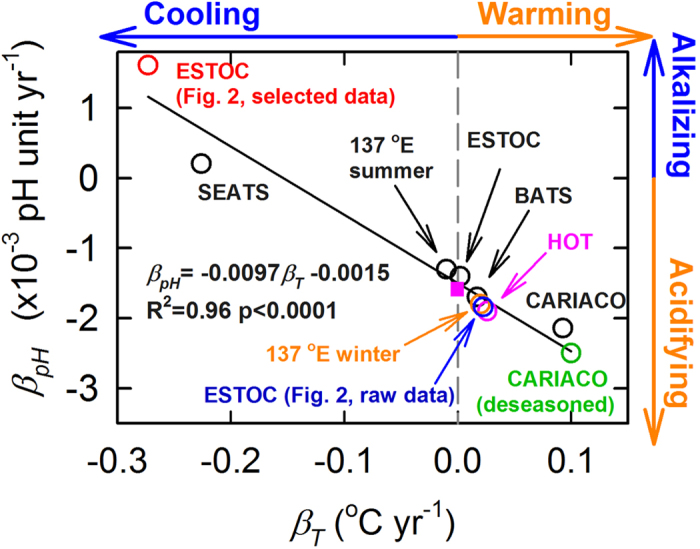
The observed surface seawater β_pH vs. β_T at various time series stations. The solid line shows the linear regression result. The pink solid square shows the expected acidification rate based on the assumption of air-sea CO₂ equilibrium. The vertical dashed line represents zero β_T. See the text for the names of the time series studies.

Assuming an air-sea CO₂ equilibrium, the surface ocean has slight regionally distributed differences in acidification rates owing to differences in seawater carbonate chemistry¹⁸. Based on thermodynamic calculations using the average carbonate parameters at each station, the acidification rate among the five time series stations and the 137 ^oE line are similar between −1.6 × 10⁻³ and −1.8 × 10⁻³ pH unit yr⁻¹. As β_pH is negatively correlated with β_T, the deviation (m₂β_T) is equal to zero when β_T is zero. Indeed, the regression line in Fig. 4 yields a β_pH of −1.5 ± 0.1 × 10⁻³ pH unit yr⁻¹ at β_T = 0. This value agrees with the MLR-determined m₁ of −1.6 ± 0.1 × 10⁻³ pH unit yr⁻¹, and with the expected acidification rate of −1.6 × 10⁻³ ~ −1.8 × 10⁻³ pH unit yr⁻¹, when considering only the observed global atmospheric pCO₂ increments during the studied periods. Notably, the assumed, extreme case of uneven sampling distribution shown in Fig. 2 agrees well with the regression line (Fig. 4, red circle). As shown for the first time, and having the shortest observation years and the largest deviation from the expected acidification rate (positive β_pH), the SEATS site is used as an example to illustrate the influence of sampling distribution on the β_pH in the following discussion. At the SEATS site, the observed β_pH, m₂, and β_T of the nine year study are 0.21 × 10⁻³ pH unit yr⁻¹, −7.7 × 10⁻³ pH unit °C⁻¹, and −0.23 °C yr⁻¹, respectively (Fig. 4, Table 1). It is important to note that the estimated rate of temporal change in pH_insitu (m₁) is β_pH – m₂β_T = (0.21 × 10⁻³pH unit yr⁻¹)−(−7.7 × 10⁻³ pH unit ^oC⁻¹) × (−0.23 °C yr⁻¹) = −1.6 × 10⁻³ pH unit yr⁻¹, which is statistically indistinguishable from the expected acidification rate, assuming the air-sea CO₂ equilibrium.

Discussion

The results above show that the β_pH among the studied time-series, at β_T = 0, reflects the increasing atmospheric CO₂, while deviations from that value are mainly due to different deviations of m₂β_T under various distributions of sampling points in the studied areas. In short, β_pH at ESTOC with only selected data (an extreme case of uneven sampling distribution), and at SEATS and CARIACO, deviates so much from the expected acidification rate due to increasing atmospheric CO₂ because of the deviation indicated by the apparent decrease in the observed T at ESTOC and SEATS (positive deviation) and the apparent increase in T at CARIACO (negative deviation). The long-term time-series, such as BATS and HOT, have the β_pH statistically indistinguishable from the expected rate of −1.6 × 10⁻³ ~ −1.8 × 10⁻³ pH unit yr⁻¹ assuming air-sea CO₂ equilibrium. That is, although long-term time series may have evenly distributed datasets and negligible deviations in β_pH, shorter time series may suffer large errors which are correctable by this method.

It has been suggested that the anomaly (observed pH_insitu or T minus climatology mean) be used to reduce seasonal variations, as it has been reported that β_pH is sensitive to these². Comparing deseasoned β_pH from Bates, et al.² and deseasoned β_T from Astor, et al.⁹, based on pH_insitu and T anomalies at the CARIACO site, the deseasoned β_pH is similar to the observed β_pH that contains a deviation of m₂β_T (Fig. 4, green circle). The reason why the β_pH and the deseasoned β_pH contain similar deviations needs further investigation.

The observed slope of −9.7 ± 0.7 × 10⁻³ pH unit °C⁻¹ shown in Fig. 4 can only be due to changing seawater chemistry, and not to deviations, if the following two conditions are satisfied. First, β_T is a fair estimation of changing T. Second, the change in pH_insitu under long-term change in T is equal to the m₂ of −9.7 ± 0.7 × 10⁻³ pH unit °C⁻¹. However, the second assumption contradicts with our thermodynamic calculation that the change in pH_insitu as T changes (m₂) is in fact just approximately −1.1 × 10⁻³ pH unit ^oC⁻¹, which is based on the assumptions of air-sea CO₂ equilibrium and constant TA. This is consistent with recent studies showing that the change in surface ocean pH_insitu under long-term change in T (m₂) is close to zero¹⁵,¹⁶. Seasonal changes in T are much larger than long-term changes in T, such that the observed m₂ of −8.7 ± 1.4 × 10⁻³ and −9.7 ± 0.7 × 10⁻³ pH unit °C⁻¹ shown in Table 1 and Fig. 4, respectively, largely represents the values of seasonal change in pH_insitu as T changes. Notably, uneven sampling generates a deviation in β_T as well. Although deducing the deviation in β_T under uneven sampling distribution is beyond the scope of this study, this does not change a fact that based on Eq (6), in the case of uneven distribution of sampling the slope of β_pH vs. β_T plot should be approximately equal to m₂ = −8.7 ± 1.4 × 10⁻³pH °C⁻¹. In contrast, the slope of fair estimation is expected to be just about −1.1 × 10⁻³ pH unit °C⁻¹. The factor of −9.7 ± 0.7 × 10⁻³ β_T shown in Fig. 4 is actually a deviation of the acidification rate largely owing to various distributions of sampling points, rather than an effect on the acidification rate due to warming or cooling.

In the marine carbonate system, the TA concentration should remain constant if the change in pH_insitu is solely caused by the air-sea CO₂ exchange. To examine the temporal change in the TA concentration, it is normalized to a particular salinity (S), such as at S = 35 (nTA = TA/S×35), to reduce the influences of precipitation or evaporation on the TA concentration. At the ESTOC and the 137 °E line, the nTA concentrations have reportedly remained unchanged over the study regions and periods⁸,¹². The rates of temporal change in nTA (β_nTA) among the rest of the four sites are also found to be insignificant within the uncertainties of the data (see Supplementary Table S1 for detail). Further, changes in TA through precipitation or evaporation have insignificant influences on β_pH among those time series stations. For instance, at the HOT site, a change in TA as S changes (11 × 10⁻³ S unit yr⁻¹) yields a β_pH of only 0.091 × 10⁻³ pH unit yr⁻¹. Such a magnitude of change is less than 5% of the reported β_pH at the HOT site. In fact, the constant nTA among the studied time series leads to the conclusion that m₁ of −1.6 × 10⁻³ pH unit yr⁻¹ in Table 1 and −1.5 × 10⁻³ pH unit yr⁻¹ in Fig. 4 indeed reflect the increasing atmospheric CO₂ concentration.

To conclude, long-term time series with even sampling distribution contains negligible deviation. However, a short duration of observation years, low sampling frequency, and high seasonal variations in the pH_insitu time series tend to result in a temporal change with a large deviation. For instance, due to its high seasonal variation in pH_insitu and short duration, in the SEATS study, the temporal increase in pH_insitu due to uneven distributions of data is large enough to compensate for decreasing pH_insitu caused by increased atmospheric CO₂. T is used as an example to quantify the deviation. Once the deviation is eliminated, seawaters at the studied stations are acidified at a rate statistically indistinguishable from the expected rate under the air-sea CO₂ equilibrium. Our results indicate that the differences in β_pH among the studied time series are due to deviations using SLR. As our approach is not so limited by the number of observation years or the sampling distribution, time series studies with high seasonal variations and short duration times can benefit from our approach, achieving a fair estimation of the rate of temporal change in pH_insitu.

Methods

The data sets (see Fig. 1 for station locations) used in this study are from five published time series studies (the BATS⁶, CARIACO²,⁹, ESTOC⁸,¹⁹, HOT⁷, and the 137°E¹²) and an unpublished, open access pH time series study (the SEATS). In this study, the up-to-date CO₂ System Calculations Program (version 2.1) developed by Pierrot, et al.²⁰ and the recommended dissociate constants of carbonate chemistry for best practices²¹,²² were used to calculate the carbonate system. The pH is in the total scale at the in situ temperature. Numbers are expressed as the value ± one standard error.

Additional Information

How to cite this article: Lui, H. K. and Chen, C. T. A. Deducing acidification rates based on short-term time series. Sci. Rep. 5, 11517; doi: 10.1038/srep11517 (2015).