Divergent selection along climatic gradients in a rare central European endemic species, Saxifraga sponhemica

Abstract

Background and Aims The effects of habitat fragmentation on quantitative genetic variation in plant populations are still poorly known. Saxifraga sponhemica is a rare endemic of Central Europe with a disjunct distribution, and a stable and specialized habitat of treeless screes and cliffs. This study therefore used S. sponhemica as a model species to compare quantitative and molecular variation in order to explore (1) the relative importance of drift and selection in shaping the distribution of quantitative genetic variation along climatic gradients; (2) the relationship between plant fitness, quantitative genetic variation, molecular genetic variation and population size; and (3) the relationship between the differentiation of a trait among populations and its evolvability.

Methods Genetic variation within and among 22 populations from the whole distribution area of S. sponhemica was studied using RAPD (random amplified polymorphic DNA) markers, and climatic variables were obtained for each site. Seeds were collected from each population and germinated, and seedlings were transplanted into a common garden for determination of variation in plant traits.

Key Results In contrast to previous results from rare plant species, strong evidence was found for divergent selection. Most population trait means of S. sponhemica were significantly related to climate gradients, indicating adaptation. Quantitative genetic differentiation increased with geographical distance, even when neutral molecular divergence was controlled for, and Q_ST exceeded F_ST for some traits. The evolvability of traits was negatively correlated with the degree of differentiation among populations (Q_ST), i.e. traits under strong selection showed little genetic variation within populations. The evolutionary potential of a population was not related to its size, the performance of the population or its neutral genetic diversity. However, performance in the common garden was lower for plants from populations with reduced molecular genetic variation, suggesting inbreeding depression due to genetic erosion.

Conclusions The findings suggest that studies of molecular and quantitative genetic variation may provide complementary insights important for the conservation of rare species. The strong differentiation of quantitative traits among populations shows that selection can be an important force for structuring variation in evolutionarily important traits even for rare endemic species restricted to very specific habitats.

INTRODUCTION

Selection, drift and gene flow shape genetic variation within and among natural populations and their study is important for conservation and evolutionary biology (Merilä and Crnokrak, 2001; Leinonen et al., 2008, 2013). Habitat destruction and fragmentation affect these processes by reducing the size and increasing the isolation of populations (Ellstrand and Elam, 1993; Schemske et al., 1994). Plants in small and isolated populations often have a lower performance than those in larger, interconnected populations due to increased inbreeding (Ellstrand and Elam, 1993; Fischer and Matthies, 1998; Kéry and Matthies, 2004). They have lower levels of genetic variation, limited evolutionary potential (Schemske et al., 1994; Young et al., 1996; Willi et al., 2006; Aguilar et al., 2008; Weber and Kolb, 2014) and they are more strongly threatened by random environmental fluctuations (Matthies et al., 2004). As a consequence, fragmented populations have a higher risk of becoming extinct (Young et al., 1996).

A recent meta-analysis confirmed a generally positive relationship between the size, the molecular genetic variation and the fitness of plants in populations (Leimu et al., 2006). Neutral molecular genetic variation has been studied extensively, but it is often not or only weakly correlated with adaptive variation and does not inform about the evolutionary potential of populations (Reed and Frankham, 2001; Vitt and Havens, 2004; Volis et al., 2005; Leinonen et al., 2008). Knowledge of the potential for adaptation to changing environmental conditions is particularly important for rare and threatened species in order to plan appropriate conservation management (Ye et al., 2013; Weber and Kolb, 2014), but there are very few studies of quantitative genetic variation in rare plants (Kramer and Havens, 2009).

Genetic variation in quantitative traits of plants can be studied by growing plants from different seed families and populations in a common garden (Vitt and Havens, 2004). Moreover, combining studies of adaptive quantitative plant traits (Q_ST) and of non-adaptive molecular markers (F_ST) makes it possible to estimate the relative contributions of drift and selection to the overall genetic differentiation among populations (Spitze, 1993; Merilä and Crnokrak, 2001). When Q_ST and F_ST are similar, genetic drift alone can account for the observed genetic differentiation, whereas if Q_ST and F_ST differ, selection has also shaped differentiation among populations. If Q_ST is larger than F_ST, the quantitative genetic differentiation is larger than expected by drift alone, and the difference could be assigned to divergent selection and adaptation to local environments, but, if Q_ST is smaller, convergent spatially uniform selection could have favoured the same genotypes at different sites (Volis et al., 2005). Although Q_ST–F_ST comparisons have been criticized (e.g. Goudet and Martin, 2007; Whitlock, 2008; Edelaar et al., 2011), studies based on Q_ST–F_ST comparisons have provided valuable insights into the causes of spatial genetic divergence among populations, and the number of studies is growing (Leinonen et al., 2008). Recent meta-analyses have shown that Q_ST values are on average higher than F_ST values (Leinonen et al., 2008; De Kort et al., 2013), suggesting an important role for directional selection in natural populations.

Evidence for unifying selection (Q_ST < F_ST) is scarce, but has been found in the rare plant species Clarkia dudleyana (Podolsky and Holtsford, 1995), Brassica insularis (Petit et al., 2001), Scabiosa columbaria (Scheepens et al., 2010a) and Psilopeganum sinense (Ye et al., 2013). Quantitative variation may be similar to molecular genetic variation if selection has not had enough time to drive divergence (Whitlock and McCauley, 1999). In small and isolated populations, Q_ST tends to equal F_ST because drift is enhanced and the effectiveness of selection is reduced (Gravuer et al., 2005; Johansson et al., 2007). In the rare Liatris scariosa var. novae-angliaea, Q_ST values similar to F_ST were found for most traits, possibly due to increased drift and a lower responsiveness to selection (Gravuer et al., 2005). In contrast, a recent study of Ranunculus reptans found enhanced directional selection and drift in small populations (Willi et al., 2007). In spite of their usefulness for detecting variation among populations in traits important for evolutionary responses to environmental changes, Q_ST–F_ST comparisons have only rarely been used in a conservation context (Gravuer et al., 2005; Leamy et al., 2014). Furthermore, to assess the potential of rare species to respond to global change, it will be necessary to know whether traits that are strongly differentiated among populations and are important for adaptation to local conditions maintain sufficient variation (evolvability) within populations. However, little is known about the relationship between the evolvability and among-population differentiation of traits in rare species.

Our model species Saxifraga rosacea Moench subsp. sponhemica (C.C.Gmel.) D.A.Webb. (hereafter referred by its synonym S. sponhemica C.C.Gmel.) is a rare endemic of Central Europe. Because of its disjunct distribution and its stable and specialized habitat type (treeless screes and cliffs), the species is considered to be an ice age relict (Thorn, 1960; Walter and Straka, 1970). Because populations of S. sponhemica have evolved in long-term fragmented habitats they provide a suitable study system to investigate the joint effects of drift, gene flow and selection in naturally fragmented populations. Moreover, due to its narrow habitat requirements, S. sponhemica is a good model species for studying the effect of climatic gradients on genetic differentiation in rare plants, because there is likely to be little variation in habitat conditions apart from climate. A previous study using random amplified polymorphic DNA (RAPD) markers has shown that isolated S. sponhemica populations have preserved considerable levels of molecular genetic diversity, presumably because the taxon is long lived (Walisch et al., 2014). Levels of among-population variation of molecular marker loci were also high. Here, we present the results of a study of the quantitative genetic variation within and among S. sponhemica populations and the performance of plants in a common garden to address the following questions. (1) What has been the relative importance of drift and selection in shaping the distribution of quantitative genetic variation? In particular, is there evidence for adaptive differentiation along climatic gradients for the rare S. sponhemica? (2) Do the fitness of plants, quantitative genetic variation, molecular genetic variation and population size correlate positively? (3) Is the differentiation of a trait among populations and its evolvability positively correlated?

MATERIALS AND METHODS

Study species

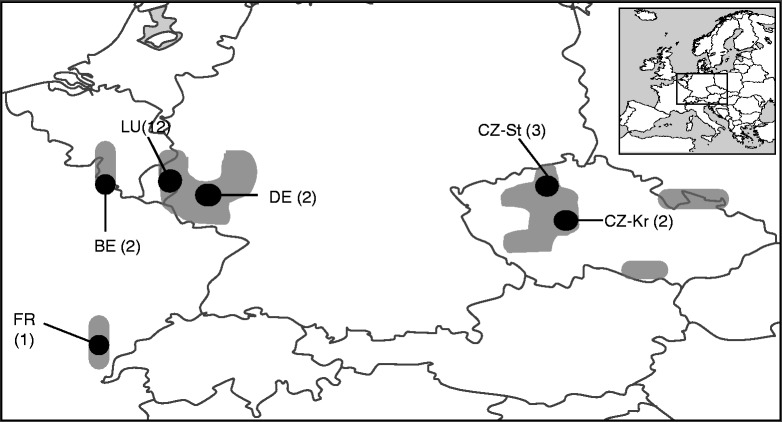
Saxifraga sponhemica C.C.Gmel. is a perennial cushion plant of rocks and screes whose habitat is naturally fragmented. Flowers of S. sponhemica are strongly protandrous. Self-pollination within a flower is possible and geitonogamy is probably quite common (Webb and Gornall, 1989). According to a recent study in a large population in Luxembourg, S. sponhemica has a mixed mating system with a moderate selfing rate (T. J. Walisch et al., unpubl. res.). Saxifraga sponhemica has a disjunct distribution in Europe. It occurs in three separate areas: (1) in the Belgian Ardennes, the Luxembourg Oesling and the German Rhineland; (2) in some isolated locations in the French Jura; and (3) in the Czech Bohemian low mountains (České středohoří) and the Czech Bohemian Karst region (Českŷ kras), with isolated populations in the south of Moravia and in the Polish Sudetes (Fig. 1; Webb and Gornall, 1989; Jalas et al., 1999). In most parts of its distribution, S. sponhemica is considered to be extremely rare or critically endangered, and is legally protected (Korneck et al., 1996; Holub and Procházka, 2000; Colling, 2005; Mirek et al., 2006). Saxifraga sponhemica is listed as a species of conservation priority in Central Europe (Schnittler and Günther, 1999).

Fig. 1.

Distribution areas (grey) of Saxifraga sponhemica (modified from Jalas et al., 1999). The sampling regions are marked as black dots on the map, and the numbers of study populations are given in parentheses. LU, Luxembourg; DE, Germany; BE, Belgium; FR, France; and five populations in two regions of the Czech Republic: three in České středohoří (CZ-St) and two in Český kras (CZ-Kr).

Study populations and bioclimatic variables

In summer 2002 and 2003, we visited 22 populations of S. sponhemica, 12 in Luxembourg, two in Belgium, two in Germany, one in France and five in the Czech Republic (Fig. 1; Table 1). We determined the position of each population with a GPS, counted the number of cushions, noted whether it occurred on a rock face, a scree or a stone wall, and estimated its main orientation as the absolute deviation from north in degrees. In small populations, we determined the number of plants by counting all cushions, while in large populations the total number of plants was estimated by extrapolating counts from parts of the total population area. In subsequent analyses, we combined walls and scree habitats, because in some sites walls had been built at the bottom of screes to hold them, and in these sites plants occurred in both habitat types (Table 1).

Table 1.

Populations of Saxifraga sponhemica sampled in Belgium (BE), Germany (DE), Luxembourg (LU) and the Czech Republic (CZ)

Geographical region	Population and habitat	N	Nfam	No. of plants per family	Orientation (°)	Location(latitude/longitude)
Oesling (LU)	Bettel, rock	465	12	6·1	25	49·923N/6·218E
	Bettel-Vianden, rock	536	10	6·4	15	49·923N/6·219E
	Kautenbach, rock	300	11	5·0	10	49·952N/6·016E
	Michelau-Erpeldange, scree	10	11	7·3	46	49·945N/6·027E
	Michelau-Erpeldange, scree and wall	250	12	7·4	9	49·894N/6·115E
	Michelau-Erpeldange, rock	188	12	6·1	30	49·893N/6·115E
	Unterschlinder, wall	9600	12	7·7	63	49·892N/6·112E
	Unterschlinder, rock	326	13	7·5	34	49·926N/6·076E
	Vianden parking, rock	100	13	7·3	20	49·922N/6·072E
	Vianden–Roth, rock	157	14	6·6	68	49·935N/6·198E
	Vianden tower, wall	66	12	6·3	10	49·929N/6·225E
	Vianden castle, wall	1100	7	7·4	57	49·933N/6·208E
Mid-Rhine (DE)	Loreleifels, rock	14	6	6·7	30	49·680N/7·288E
	Hammerstein crossroads, rock	58	10	5·8	40	49·690N/7·289E
Jura (FR)	Planches-sur-Arbois, scree	50	9	5·8	30	46·879N/5·813E
Ardennes (BE)	Bouillon below castle, rock	199	6	6·0	68	49·793N/5·064E
	Bouillon Bastion Bretagne, wall	27	7	4·3	5	49·797N/5·069E
České středohoří (CZ)	Ostrý, scree	405	9	3·7	20	50·532N/13·951E
(CZ-St)	Boreč, scree	90	6	6·5	35	50·515N/13·990E
	Blešno, scree	125	7	4·7	10	50·482N/13·906E
Český kras (CZ-Kr)	Voškov, rock	150	6	6·3	17	49·918N/14·197E
	Tetínské Skály, rock	600	5	5·0	37	49·950N/14·107E

N, number of plants in the population; N_fam, number of seed families in the garden; No. of plants per family, number of plant per seed family grown in the garden; orientation, absolute deviation from north.

We obtained the following bioclimatic variables for each study site (interpolations of observed climate data, representative of 1950–2000) in a grid size of about 1 km² (30 arc s) from the Worldclim database version 1.4. (Hijmans et al., 2005): mean annual temperature, minimum temperature of the coldest month, maximum temperature of the warmest month, mean diurnal temperature range, temperature annual range, temperature seasonality (SD), annual precipitation, precipitation of the wettest month, precipitation of the driest month and precipitation seasonality (CV). Because these variables were intercorrelated, we identified three principal components (PCs) by principal component analysis (PCA) with varimax rotation (Table 2). The correlations of the PCs with the climatic variables indicated that the first PC (PC CONTIN, 57·6 % of the variation) represented continentality, the second (PC SUMMWARM, 24·7 % of variation) summer warmth and the third PC (PC PRECIP, 15·6 % of variation) a gradient of precipitation. Continentality was related to the longitude east of the sites of origin (r = 0·91, P < 0·001) whereas summer warmth (r = −0·49, P < 0·05) and precipitation decreased with increasing latitude (r = −0·61, P < 0·01).

Table 2.

Correlations between climatic variables and three principle components extracted from these variables (varimax rotation)

Climate variable	PC1, CONTIN	PC2, SUMMWARM	PC3, PRECIP
Temperature seasonality (SD)	0·97	0·04	−0·21
Min. temperature of coldest month	−0·96	0·24	0·08
Temperature annual range	0·92	0·35	−0·14
Precipitation seasonality (CV)	0·91	0·07	−0·35
Mean annual temperature	−0·72	0·68	0·09
Max. temperature of warmest month	−0·11	0·98	−0·10
Mean diurnal temperature range	0·28	0·92	0·07
Precipitation of wettest month	0·02	−0·03	0·99
Annual precipitation	−0·56	0·01	0·82
Precipitation of driest month	−0·65	0·03	0·75

The three principle components accounted for 97·6 % of the variation.

The strongest correlations (|r| > 0·7) are in bold.

Collection of seeds and cultivation of plants

In 2002–2003 we sampled 5–14 plants (cushions) depending on the number of accessible plants along a transect of 10–15 m length in each of the 22 populations (Table 1). Within each transect, we recorded the distances among the sampled plants in each transect. If possible, samples were taken from plants that were at least 100 cm apart to ensure that each sample came from a different individual. For comparisons between trait values in the field and in the common garden, we determined for each plant its diameter, the total number of flowering stems and the mean length of up to four randomly selected flowering stems from their base to the uppermost flower. One ripe capsule, if available, and the top part of one rosette were collected from each plant. The rosette was placed in a small paper bag and immediately frozen in liquid nitrogen. The samples were then stored at −80 °C for molecular genetic analysis. The capsules were stored in paper bags in a plastic box with silica gel at 6 °C. At the end of February 2007, two batches of 25 seeds per capsule were placed in Petri dishes on moist filter paper and stored in a growth chamber at 20 °C under a 12 h day/12 h night light regime. Petri dishes were randomized every 3–4 d. Seeds were checked for germination every 2 weeks, and up to 15 seedlings per seed family (hereafter referred to as family) of about 1 cm length were selected at random and transplanted into soaked peat pellets (‘Jiffy pots’). The plants were randomly placed into trays and received light from fluorescent tubes (Gro-Lux®, 28 W, Osram Sylvania, USA). In June 2007, the plants were transplanted into square pots of 8 × 8 cm filled with low-nutrient soil (138 mg L⁻¹ N; 108 mg L⁻¹ P₂O₂; 158 mg L⁻¹ K₂O) and 1322 plants were cultivated outdoors in the common garden of the Musée national d’histoire naturelle, Luxembourg.

Measurement of quantitative traits

In May 2008, several traits were measured on plants cultivated in the common garden: diameter of the plants and of the largest rosette, number of rosettes, and the reproductive traits number of flowers, number of flowering stems and length of the longest stem. From mid-April 2009 onwards, the onset of flowering of the plants was recorded every 3 d, and one flower in the female stage on a secondary branch was collected per flowering plant. The flowers were put into holes in PCR microplates without overlapping of the petals and photographed with a digital camera (Nikon Coolpix 995, 3·34 Megapixels). At least two petals per flower were attached to black cardboard sheets and were scanned at a resolution of 600 dpi. Furthermore, one leaf was collected from the base of the longest stem of each plant. The leaves were fixed to a cardboard sheet with self-adhesive tape and scanned at a resolution of 600 dpi together with a length standard. The leaves were then dried and weighed individually.

Using the scans and photo images, we counted the number of leaf lobes and determined the length, width, perimeter and area of leaves and petals with ImageJ 1.42 (National Institute of Health, USA). In addition, we calculated the variables shape of the leaves and petals as the ratio between their perimeter and area, leaf narrowness as the ratio between leaf length and width, number of flowers per rosette as the ratio between the number of flowers and the number of rosettes of a plant, and specific leaf area (SLA) as the ratio between leaf area and mass. As several of the variables were correlated, we extracted two PCs each from a PCA with varimax rotation of the reproductive and vegetative traits (Table 3). The PCs were treated as quantitative traits. For certain analyses, we divided both vegetative and reproductive traits into morphological and fitness-related life-history traits (Table 3). Of the traits not listed in Table 3, SLA and leaf narrowness were treated as morphological traits and flowering time as a life-history trait.

Table 3.

Loadings of reproductive and vegetative traits of S. sponhemica on principal components derived from (a) vegetative (73·7 % of variation) and (b) reproductive traits (80·0 % of variation) after varimax rotation

(a) Vegetative traits		PC LEAFSIZE (M)	PC PLANTSIZE (Lh)
(M)	Leaf area (sqrt)	0·97	−0·01
(M)	Leaf perimeter	0·93	0·01
(M)	Leaf length	0·87	0·05
(M)	Leaf width	0·86	−0·01
(M)	Number of leaf lobes	0·61	0·17
(M)	Leaf shape (log)	−0·82	−0·02
(Lh)	Plant diameter (sqrt)	0·04	0·93
(Lh)	Number of rosettes (sqrt)	−0·15	0·86
(M)	Diameter of largest rosette	0·28	0·74
(b) Reproductive traits		PC PETALSIZE (M)	PC REPRO (Lh)
(M)	Petal perimeter	0·99	0·05
(M)	Petal area	0·99	0·04
(M)	Petal shape (log)	−0·97	-0·05
(M)	Petal length	0·89	0·07
(M)	Petal width	0·84	0·02
(M)	Diameter of flower	0·76	0·05
(Lh)	Number of flowers per plant (sqrt)	−0·05	0·97
(Lh)	Number of flowering stems (sqrt)	−0·07	0·90
(Lh)	Number of flowers per rosette (sqrt)	0·08	0·84
(Lh)	Length of the longest flowering stem	0·21	0·73

The strongest correlations (|r| > 0·6) are in bold.

For some analyses, traits were also divided into morphological (M) and life-history (Lh) traits.

RAPD-PCR

Molecular genetic data for plants from all study populations were available from a genetic study (Walisch et al., 2014). For the current study, we used only the data from the sub-set of populations for which quantitative genetic data were available (Table 1). After removing nine band positions that had been identified as putative non-neutral loci (Walisch et al., 2014), we obtained a final matrix of 287 samples and 52 neutral loci for our 22 study populations. Genetic diversity within populations was estimated with AFLP-SURV as Nei’s gene diversity (expected heterozygosity H_eN) according to the method of Lynch and Milligan (1994). We calculated F_ST, its standard error and genetic distances as pairwise F_ST values in AFLP-SURV, and calculated 95 % confidence intervals from the standard error of F_ST.

Statistical analysis

We studied the effects of population size, habitat type, orientation and of the three principal bioclimatic PCs CONTIN, PRECIP and SUMMWARM on mean vegetative and reproductive traits in populations of S. sponhemica. For each plant trait, we calculated the Bayesian information criterion (BIC) of all possible models using the leaps package (version 2.9; Lumley, 2009) in R (version 3.0; R core team, 2014). We selected the model for which the BIC was minimal and studied the relationship between each plant trait and explanatory variables by multiple regression. We performed a correlation analysis between the following traits of plants that had been measured in a population in the field and in the common garden: plant diameter and the number and mean length of flower stems.

Analyses of variance (ANOVAs) with population and family as factors were conducted for all traits. According to the hierarchical design, the effect of population was tested against the variation between families. Before the analyses, all traits were checked for normally distributed residuals. Leaf area, plant diameter, number of rosettes, number of flowers per plant, number of flowering stalks and the number of flowers per rosette were square-root transformed, and leaf shape and petal shape were log-transformed. To estimate between-population genetic variation (Q_ST), heritability (h₂) and evolvability (genetic coefficient of variation, CV_genetic; Houle 1992), we calculated variance components between populations (V_pop), between families within populations (V_fam) and between individuals within families (V_error) for each trait by restricted maximum likelihood with the varcomp function of the R-package ape version 3.1-4 (Paradis et al., 2004). Heritability (h₂) was calculated as h₂ = (V_fam/2θ)/(V_fam + V_error), and the evolvability (genetic coefficient of variation) as CV_genetic = √(V_fam/2θ)/mean, where θ is a measure of the kinship of the plants. We used untransformed values to calculate mean evolvability as suggested by Hansen et al. (2011). For selfed plants, θ is 0·5, for full-sibs it is 0·25 and for half-sibs it is 0·125 (Jimenez-Ambriz et al., 2007). We estimated a selfing rate of 47 % after Charlesworth (1988) from the multiplicative fitness function number of flowers per seed calculated for offspring from selfed, open-pollinated and outcrossed flowers in a large population of S. sponhemica in Luxembourg (T. J. Walisch et al., unpubl. res.). Knowing that about 50 % of our plants originated from selfings, we assumed that the other half were full-sibs and used a value of 0·375 for θ. The assumption of full-sibs in the case of unknown relationships between offspring from a family provides conservative estimates of quantitative genetic parameters (Podolsky and Holtsford, 1995). Q_ST was thus computed as

$$V_{\text{pop}}/\left[\text{2}\left(V_{\text{fam}}/\text{2}\theta \right)+V_{\text{pop}}\right]=V_{\text{pop}}/\left(\text{2}.\text{67}{V}_{\text{fam}}+V_{\text{pop}}\right)$$

We estimated 95 % confidence intervals for Q_ST by the jackknife technique following O’Hara and Merilä (2005). We calculated the mean Q_ST of the reproductive and vegetative traits as the sum of the numerators divided by the sum of the denominators of the individual Q_ST values, after standardizing the sums of the variance components for each trait to 1 as suggested by Chapuis et al. (2007) to avoid some traits having an undue influence on the overall average. We used regressions to study the relationship between mean evolvability and mean heritability of each trait over all populations, as well as the relationship between mean evolvability and mean heritability per population over all traits.

We estimated the genetic variability of quantitative traits as mean evolvability (CV_genetic) over vegetative and over reproductive traits, and studied the relationship between quantitative genetic variability and molecular genetic variability by regressions. We also studied the effects of population size, rock as a habitat, orientation and the three bioclimatic PCs CONTIN, PRECIP and SUMMWARM on the mean evolvability of vegetative and reproductive traits and their PCs. For each plant trait, we calculated the BIC for all possible models using the leaps package in R (Lumley, 2009; R core team, 2014). We selected the model for which the BIC was minimal and studied the relationship between each plant trait and the explanatory variables by multiple regressions.

As a measure of quantitative genetic distances, Mahalanobis distances were calculated for morphological and for life-history traits averaged over families. Mahanalobis distances measure distance in multivariate space taking into account correlations among traits and are independent of the scale of the traits (Legendre and Legendre, 1998). We compared the pairwise quantitative genetic distance matrix with the geographic distance matrix while controlling for the effect of neutral genetic drift as measured by pairwise F_ST (partial Mantel tests). Significance levels were obtained after performing 1000 random permutations for the Mantel test. Significant partial Mantel correlations suggest that clinal variation in quantitative traits cannot be explained by non-adaptive (i.e. isolation-by-distance) mechanisms alone. We also analysed if there was a relationship between quantitative genetic distances and climatic distances calculated as pairwise euclidian distances based on the three bioclimatic PCs CONTIN, PRECIP and SUMMWARM. All Mantel tests were calculated using the program zt version 1.1 (Bonnet and Van de Peer, 2002) with 1000 permutations. All statistical analyses, if not stated otherwise, were carried out with SPSS 19.0 (IBM Corp., 2010)

RESULTS

Principal component analysis of vegetative traits identified two main components. The first component (PC LEAFSIZE) explained 49·8 % of the total variation and correlated closely with leaf traits (Table 3). The second component (PC PLANTSIZE) accounted for 23·9 % of the variation and was closely related to variables that measured the size of the plants. The first component (PC PETALSIZE) from the PCA of reproductive traits accounted for 50·7 % of the variance and was closely related to petal traits such as petal area and perimeter (Table 3). The second component (PC REPRO) explained 29·3 % of the variation and correlated strongly with variables such as the number of flowers and the length of the flowering stalks.

Variation among trait means

The variation among populations and among families within the populations of S. sponhemica grown was highly significant for all vegetative and reproductive traits, and for the four components extracted from these traits (all P < 0·01). To study possible causes of the differences among populations, regression analyses of the influence of habitat characteristics of the populations of origin on the four trait PCs and on three traits that were not related to these components (leaf narrowness, SLA and start of flowering) were carried out.

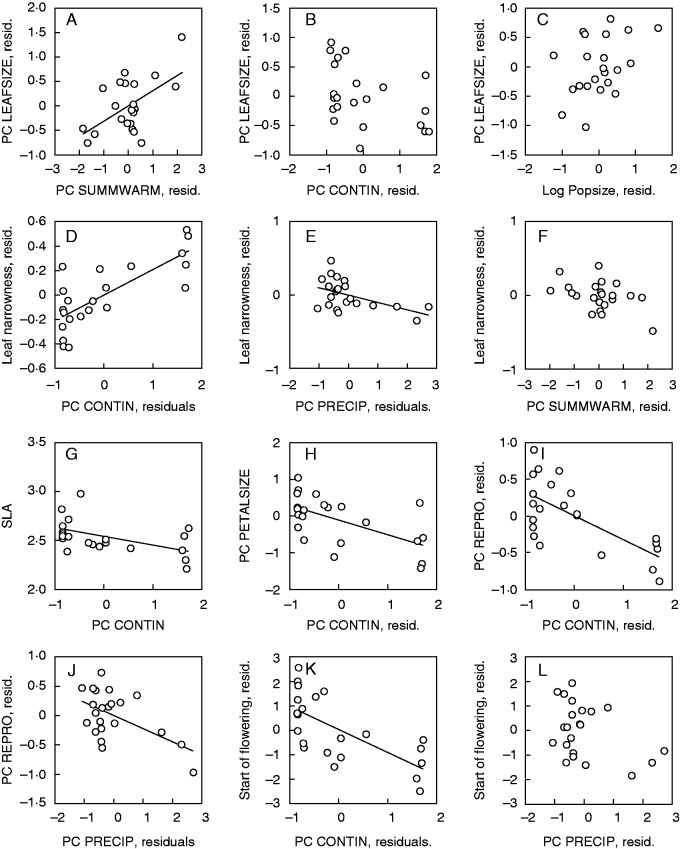
The size of leaves increased with summer warmth (Fig. 2A) and decreased with continentality of a site (Fig. 2B; Table 4), and PC LEAFSIZE was the only trait for which the best set of predictors included the size of the populations of origin (Fig. 2C). However, in single linear regressions, only plant diameter in the common garden was related to population size (r = 0·45, P < 0·05). In contrast to leaf size, leaf narrowness decreased with summer warmth (Fig. 2F) and increased with continentality (Fig. 2D), but was also related negatively to precipitation at a site (Fig. 2E). SLA (Fig. 2G), petal size (Fig. 2H), reproduction (Fig. 2I) and the starting date of flowering (Fig. 2K) were all related negatively to continentality. In addition, reproduction (Fig. 2J) and the starting date of flowering (Fig. 2L) decreased with precipitation. Both the mean length of the longest stem in a population in the field and in the common garden (r = 0·53, P < 0·05) and the number of flower stems per rosette (r = 0·54, P < 0·01) in a population in the field and the common garden were correlated (see Supplementary Data Fig. S1).

Fig. 2.

Relationships between (A–C) PC LEAFSIZE, (D–F) leaf narrowness, (G) SLA, (H) PC PETALSIZE, (I, J) PC REPRO, (K, L) start of flowering of Saxifraga sponhemica and significant explanatory variables. Shown are regression plots (G, H) in the case of single explanatory variables and partial regression plots (A–F, I–L) in the case of several explanatory variables. For statistical analysis see Table 4.

Table 4.

The effects of habitat characteristics of the population of origin and its size on mean trait values of plants of Saxifraga sponhemica grown in a common garden

Dependent variable	r2	d.f.	F	Explanatory variable	β	t-value
Vegetative traits
PC LEAFSIZE	0·44	18	4·68*	PC SUMMWARM	0·52	2·84*
				PC CONTIN	−0·36	−2·04
				Log Popsize	0·33	1·83
Leaf narrowness	0·66	18	11·75***	PC CONTIN	0·68	5·00***
				PC PRECIP	−0·33	−2·43*
				PC SUMMWARM	−0·29	−2·09
SLA (sqrt)	0·26	20	6·94*	PC CONTIN	−0·51	−2·63*
Reproductive traits
PC PETALSIZE	0·35	20	10·67**	PC CONTIN	−0·59	−3·27**
PC REPRO	0·57	19	12·49***	PC CONTIN	−0·62	−4·10***
				PC PRECIP	−0·43	−2·86**
Start of flowering	0·51	19	10·06**	PC CONTIN	−0·65	−4·06***
				PC PRECIP	−0·31	−1·91

The models for which the Bayesian information criterion is minimal are presented. Possible explanatory variables were the principal components PC SUMMWARM, PC CONTIN, PC PRECIP and rock habitat (rock faces = 1, walls and screes = 0), orientation (absolute deviation from north) and population size. No significant relationship to any of the variables was found for PC PLANTSIZE.

Only PCs and dependent variables not strongly correlated with the PCs (see Table 2) were studied.

*P < 0·05; **P < 0·01; ***P < 0·001.

Genetic differentiation among populations

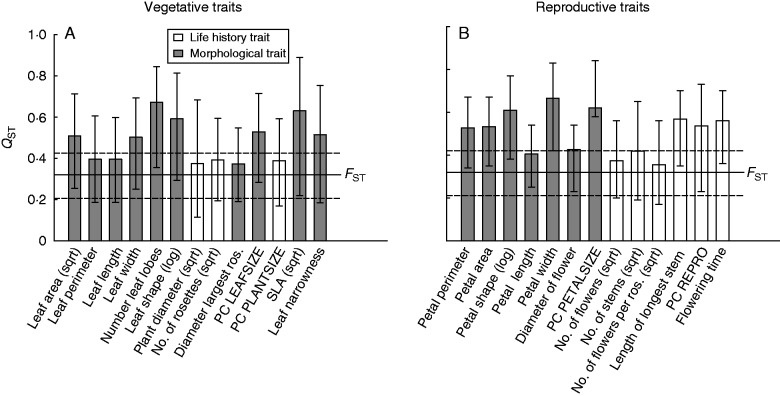
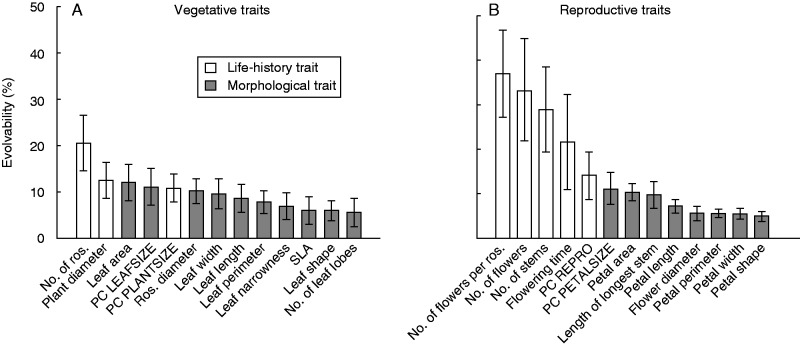
We divided both vegetative and reproductive traits into morphological and life-history traits (Table 2; Fig. 3). Quantitative genetic differentiation among populations (Q_ST) was mostly higher for morphological than for life-history traits, both for vegetative (Fig. 3A) and for reproductive traits (Fig. 3B). The Q_ST values of all individual traits and the mean Q_ST value (0·49) were higher than the F_ST value (0·32), suggesting diversifying selection. The mean difference between Q_ST and F_ST was more pronounced for morphological traits (0·20) than for life-history traits (0·13). However, for only two of the reproductive morphological traits (petal width and PC PETALSIZE) did the 95 % confidence intervals of the Q_ST and the F_ST values not overlap. The coefficients of determination for the most supported regression models relating trait means and explanatory habitat characteristics were positively correlated with the genetic differentiation among populations (Q_ST) (r = 0·39, Fig. 4), indicating that for traits with a high Q_ST habitat characteristics were a better predictor of trait means than for traits with a lower Q_ST.

Fig. 3.

Mean genetic differentiation in quantitative traits between populations (Q_ST) for (A) vegetative and (B) reproductive traits of Saxifraga sponhemica. Vertical error bars indicate 95 % confidence limits of Q_ST. Life-history traits and morphological traits are indicated. Horizontal dotted lines show the 95 % confidence limits of F_ST.

Fig. 4.

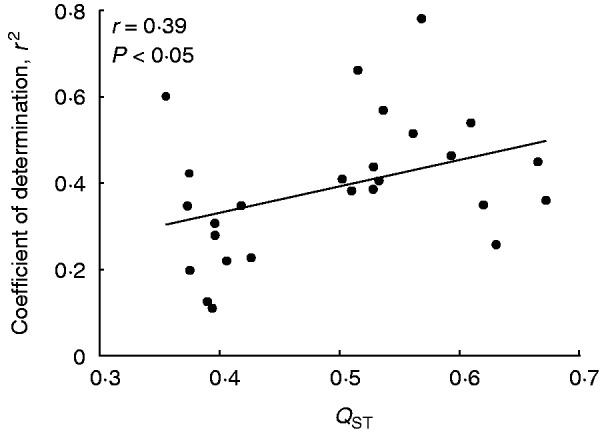
The relationship between the coefficient of determination, i.e. the amount of variation in a trait that could be explained by environmental differences between sites (r²) and the quantitative genetic differentiation (Q_ST) between populations for that trait. r² values were taken from regression analyses for which the Bayesian information criterion was minimal.

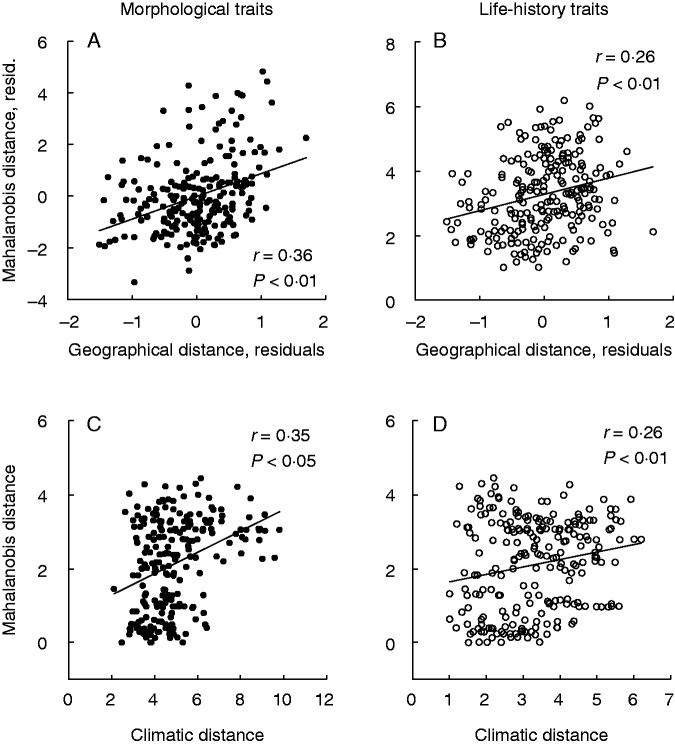
The pairwise quantitative genetic distance (Mahalanobis distance) and the molecular genetic distance (pairwise F_ST value) were correlated for both life-history traits (r = 0·30, P < 0·01; Mantel test) and morphological traits (r = 0·28, P = 0·06; Mantel test). In a partial Mantel test, the pairwise quantitative genetic distance increased with geographical distance both for morphological and for life-history traits, controlled for the effect of neutral molecular divergence (Fig. 5A, B). This indicates that the quantitative genetic differentiation among populations cannot be explained by non-adaptive (i.e. isolation-by-distance) mechanisms alone but that local adaptation due to diversifying selection also plays a role. Climatic distance between populations also increased with geographical distance (r = 0·83, P < 0·001), indicating a clinal variation in climate. Furthermore, quantitative genetic distance was correlated with climatic distance, suggesting that climate is a diversifying selective force (Fig. 5C, D).

Fig. 5.

Relationships of pairwise quantitative–genetic distances between populations of S. sponhemica based on (A, C) morphological traits (filled symbols) and (B, D) life-history traits (open symbols) and (A, B) pairwise geographical distances and (C, D) pairwise climatic distances. In (A) and (B), partial regression plots are presented, in which the effects of geographical distance are adjusted for those of molecular genetic distance (pairwise F_ST).

Quantitative genetic variation within populations

Quantitative genetic diversity, estimated as evolvability (CV_genetic), was significantly larger than zero in all traits and was on average higher for reproductive traits (15·0 %) than for vegetative traits (9·9 %), and particularly high for reproductive traits related to the life-history of the plants, such as the number of flowers and flowering stems per plant and start of flowering (Fig. 6). In contrast, the evolvability of morphological traits such as leaf and petal shape was particularly low. Heritabilities of vegetative traits ranged from 0·095 (SLA) to 0·204 (leaf width) and those of reproductive traits from 0·154 (length of longest stem) to 0·308 (flowering time), and were significantly larger than zero in all traits but did not differ among life-history and morphological traits.

Fig. 6.

Mean evolvability ± 95 % confidence limits of (A) vegetative and (B) reproductive traits of S. sponhemica. White bars indicate life-history traits and grey bars morphological traits.

In multiple regressions, the main influences on the genetic diversity of quantitative traits within populations were the summer warmth in the populations of origin and whether populations were growing on rocks or on screes and walls (Table 5). Genetic variability of leaf narrowness, of petal perimeter and of petal area increased with summer warmth, while that of the start of flowering decreased. Genetic variability of populations from rock habitats was higher for several traits related to petal size and shape than that of populations from screes and walls. Leaf width was the only trait whose evolvability was related (negatively) to population size. The evolvability of all other traits was not significantly related to population size (all r < 0·21, all P > 0·12) in simple linear regressions.

Table 5.

The effects of habitat characteristics of the population of origin and its size on the evolvability of quantitative traits (genetic coefficient of variation) of Saxifraga sponhemica grown in a common garden

Dependent variable	r2	d.f.	F	Explanatory variable	β	t-value
Vegetative traits
Leaf width	0·19	19	4·54*	Log Popsize	−0·43	−2·13*
Leaf narrowness	0·45	19	7·90**	PC SUMMWARM	0·72	3·93***
				Rock habitat	−0·38	−2·06
Reproductive traits
Petal perimeter	0·46	19	8·13**	Rock habitat	0·44	2·43*
				PC SUMMWARM	0·37	2·06
Petal area	0·44	19	7·54**	Rock habitat	0·46	2·51*
				PC SUMMWARM	0·33	1·79
Petal shape (log)	0·28	20	7·84*	Rock habitat	0·53	2·80*
Diameter of flower	0·32	20	9·45**	Rock habitat	0·57	3·07**
No. of flowers per rosette	0·25	20	6·64*	PC CONTIN	0·50	2·58*
Start of flowering	0·24	19	5·84*	PC SUMMWARM	−0·48	−2·42*

The models for which the Bayesian information criterion is minimal are presented. Possible explanatory variables were the principal components PC SUMMWARM, PC CONTIN, PC PRECIP and rock habitat (rock faces = 1, walls and = 0), orientation (absolute deviation from north) and population size. No significant relationship with any of the variables was found for the vegetative traits PC LEAFSIZE, PC PLANTSIZE, leaf area, leaf perimeter, leaf length, number of leaf lobes, leaf shape, plant diameter, number of rosettes, SLA and rosette diameter; and the reproductive traits PC PETALSIZE, petal length, petal width, number of flowers, number of stems and length of longest stem.

*P < 0·05; **P < 0·01; ***P < 0·001.

Heritability (h²) and evolvability of each trait in the populations were strongly correlated (all r > 0·84, all P < 0·001). Averaged over all traits per population, mean evolvability of traits in the populations varied from 7 to 35 %. There was a strong positive relationship between mean evolvability and mean heritability of a trait (averaged over all populations) (r = 0·93, P < 0·001), but no relationship between the mean evolvability and heritability of all traits per population (r = 0·20, P = 0·33). Mean genetic variation of quantitative traits in a population (mean evolvability) did not increase with molecular genetic variability (Nei’s gene diversity) per population, either for vegetative traits (r = −0·16, P = 0·48) or for reproductive traits (r = −0·21, P = 0·36). Molecular genetic variation in the populations was also not positively correlated with evolvability of the individual vegetative (r from −0·39 to 0·10, P > 0·075) or reproductive traits (r from −0·33 to 0·03, P > 0·13). Evolvability and heritability were both negatively related to among-population differentiation (Q_ST) of a trait, but the relationship was significant for evolvability only (r = −0·52, Fig. 7).

Fig. 7.

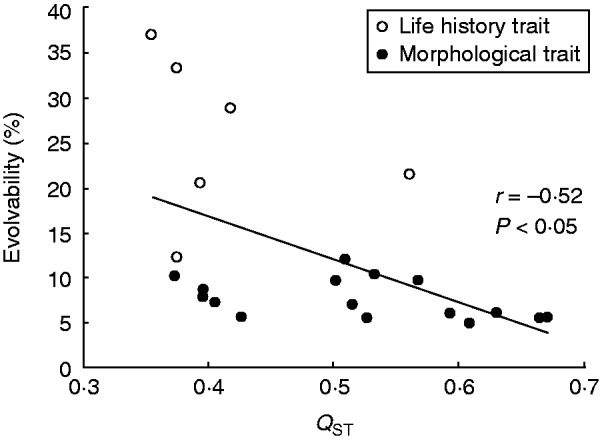
The relationship between mean evolvability of a trait and its differentiation between populations (Q_ST) for life-history traits and morphological traits (see key) of S. sponhemica. The fitted line is based on both types of traits.

Relationships between fitness-related traits and estimates of genetic diversity

All fitness-related traits increased in the common garden with the molecular genetic diversity of the population of origin (see Supplementary Data Fig. S2): PC PLANTSIZE (r = 0·53, P < 0·05), plant diameter (r = 0·44, P < 0·05), number of rosettes (r = 0·52), number of flowers (r = 0·56) and PC REPRO (r = 0·52; all P < 0·05). In contrast, traits that were not related to fitness did not correlate with the molecular genetic diversity of the population. Moreover, there was no significant correlation between the mean of any trait and its mean evolvability or heritability in a population (all |r| < 0·3, all P > 0·30), indicating that performance and morphology were not related to quantitative genetic variation. Fitness traits did not correlate with the mean of the evolvabilities of all measured traits per population (all |r| < 0·3, all P > 0·30).

DISCUSSION

Evidence for selection

Several lines of evidence suggest that selection shaped the quantitative genetic structure of populations of the rare and highly fragmented Saxifraga sponhemica. Most population trait means of S. sponhemica were significantly related to climate gradients, suggesting adaptive genetic differentiation in quantitative traits among populations (see Whitlock, 2008). Such patterns could also result from non-selective processes such as genetic drift (Vasemägi, 2006; Kawakami et al., 2011), which is considered to be the primary evolutionary force leading to population divergence among fragmented populations (Lynch, 1986; Ye et al., 2013). However, we found significant relationships between overall quantitative genetic distances between populations as measured by Mahalanobis distances and geographical distances, even after controlling for differentiation in neutral molecular genetic variation in partial Mantel tests. This shows that the quantitative genetic differentiation between populations was higher than could be explained by neutral processes. In line with this, we also found for some traits that Q_ST was significantly higher than F_ST.

In contrast to our results, previous studies of quantitative genetic variation in rare species either found that non-selective processes were sufficient to explain the observed differentiation in quantitative traits among populations, or even found evidence for uniform selection (Scabiosa canescens, Waldmann and Andersson, 1998; Centaurea corymbosa and Brassica insularis, Petit et al., 2001; Liatris scariosa, Gravuer et al., 2005; Primula sieboldii, Yoshida et al., 2008; Psilopeganum sinense, Ye et al., 2013). In small fragmented populations, the effectiveness of selection can be reduced and, because rare species often have a narrow ecological niche, their populations may be exposed to homogeneous selective forces that result in low population differentiation in quantitative traits (Petit et al., 2001; Ye et al., 2013). Saxifraga sponhemica also has a very restricted range of habitats, but nevertheless showed strong population differentiation related to climate gradients. This could be due to the fact that the maximum distance between the populations of S. sponhemica was much larger than in previous studies of rare species. Our study populations were thus exposed to different climatic conditions exerting divergent selective pressures.

Plants from sites with a harsher, more continental climate had smaller, narrower and thicker leaves and smaller petals, flowered earlier and reproduced less than those from more Atlantic sites. Smaller and thicker leaves could be an adaptation to reduce water loss during warm and dry spells (Scheepens et al., 2010b) at the continental sites. Early flowering could be an adaptation to avoid heat or drought periods (Latta and Gardner, 2009; Franks, 2011), which may be exacerbated by the dark rock faces or screes in S. sponhemica habitats that strongly absorb solar radiation. The earlier timing of reproduction and the harsher climate may have led to the observed lower reproduction and reduced petal size (Obeso, 2002) at the more continental sites. A further indication that climatic differences among sites drive local adaptation is given by the positive correlation between quantitative genetic and climatic distances.

Evolvability of traits and its relationship to differentiation among populations

The genetic variability (evolvability) of quantitative traits varied among populations. The larger evolvability of petal size traits of plants which originated from rock faces was possibly due to more spatially variable selection (e.g. Kelly, 1992; McLeod et al., 2012) and restricted gene flow within S. sponhemica populations (Walisch et al., 2014), resulting in small-scale local adaptation (Knight and Miller, 2004; Paccard et al., 2013). Likewise, the larger evolvability of petal size and leaf narrowness could be caused by a spatially or temporally varying selection due to environmental heterogeneity (e.g. Schemske and Horvitz, 1989; Kelly, 1992; Siepielsky et al., 2009) at sites with warmer summers. Conversely, the evolvability of the start of flowering decreased with warmer summers, and the evolvability of leaf narrowness was lower in rock habitats, suggesting that less adapted genotypes have been filtered out by selection. The loss of genetic variability within populations due to selection is in agreement with quantitative genetic theory (Bulmer, 1971; Visscher et al., 2008).

The degree of differentiation among S. sponhemica populations (mean Q_ST value) decreased with the evolvability of a trait within populations. Heritability showed the same trend as evolvability. In contrast, previous studies of the relationship between heritability and Q_ST of traits found non-significant negative (Steinger et al., 2002), non-significant positive (Podolsky and Holtsford, 1995; Bonnin et al., 1996) or significant positive correlations (Andersson, 1991; Yang et al., 1996; Lynch et al., 1999). A positive relationship has been interpreted as support for the hypothesis that traits with a high evolvability respond more strongly to divergent selective forces (Lynch et al., 1999; Hansen et al., 2011). In contrast, the negative relationship between evolvability and Q_ST found for S. sponhemica could be the result of differences in the strength of selection for individual traits. Traits under strong selection will tend to show little variability within populations (low evolvability), but will vary strongly among populations (high Q_ST) due to local adaptation to strongly diverging environmental conditions. Our results thus suggest that selection shaped quantitative genetic variation not only among, but also within populations of S. sponhemica.

Variation in morphological traits was more strongly affected by selection than variation in life-history traits, as shown by the lower evolvability and larger mean Q_ST– F_ST differences for morphological traits. Furthermore, morphological traits were more strongly correlated with geographic and climatic distances than life-history traits, reinforcing the conclusion that life-history traits showed a weaker response to directional selection than morphological traits. Stronger differentiation among populations for morphological than life-history traits has also been found in other empirical studies (Merilä and Crnokrak, 2001; Leinonen et al., 2008, 2013; De Kort et al., 2013). It has been suggested that life-history traits respond more slowly to selection because they are influenced by multiple genes of small effect and by interactions among genes that result in non-additive genetic effects (Kruuk et al., 2008; Morrissey et al., 2012).

Mean evolvability and mean heritability of a trait averaged over all populations correlated strongly, whereas the means over all traits per population did not correlate. The first result is in contrast and the second lends support to the general conclusion of reviews by Houlé (1992) and Hansen et al. (2011) that evolvability and heritability are generally not correlated. It has been suggested that this is due to positive relationships between additive genetic variances and other components of variance (Hansen et al., 2011).

Quantitative genetic variation and its relationship to molecular genetic variation and fitness

Quantitative and molecular genetic variation are both subject to drift and are predicted to decline in small populations (Schemske et al., 1994; Lynch, 1996; Young et al., 1996; Aguilar et al., 2008). However, neither molecular (Walisch et al., 2014) nor quantitative genetic variation in S. sponhemica was related to population size. There are several non-mutually exclusive explanations for the absence of an effect of population size on quantitative variation. Either stabilizing or divergent selection within populations may have over-ridden the effects of genetic drift (Reed and Frankham, 2001), effective population sizes may have been different from census sizes (Lynch and Hill, 1986), and there may have been insufficient generations at a small size to reduce genetic diversity in the long-lived S. sponhemica (Walisch et al., 2014). Other field studies have produced varying results. Salvia pratensis and Scabiosa columbaria (Ouborg et al., 1991), Ranunculus reptans (Willi et al., 2007) and Phyteuma spicatum (Weber and Kolb, 2014) showed an increase in phenotypic variation with increasing population size, whereas for Senecio integrifolius quantitative genetic variation was larger in a small sub-divided population than in a large interconnected population (Widén and Andersson, 1993). In several other species, no relationship between heritability and population size was detected (Widén and Andersson, 1993; Waldmann and Andersson, 1998; Podolsky, 2001; Steinger et al., 2002; Widén et al., 2002; Gravuer et al., 2005; Ellmer et al., 2011).

The fitness of plants tends to be reduced in small and fragmented populations (Fischer and Matthies, 1998; Leimu et al., 2006), because of genetic erosion (Young et al., 1996; Aguilar et al., 2008) and increased inbreeding (Ellstrand and Elam, 1993). In S. sponhemica, all fitness traits were significantly reduced in populations with low molecular variability, suggesting inbreeding depression. In contrast, plant fitness did not correlate with the evolvability of a trait or with the mean evolvability of all traits per population. Molecular variation appears to be a better predictor of inbreeding effects in populations than variation in quantitative traits.

Neither mean evolvability nor the evolvability of individual traits was related to the molecular genetic diversity of S. sponhemica. Because of the strong influence of selection on variation in quantitative traits observed in S. sponhemica, this is not surprising. Our results contribute to the increasing body of evidence that studies of molecular variation provide little insight into variation of traits important for adaptation to changing conditions (Reed and Frankam, 2001; McKay and Latta, 2002; Steinger et al., 2002; Vitt and Havens, 2004; Gravuer et al., 2005). To assess the amount of adaptive genetic variation present in populations of rare species, conservation studies should thus investigate quantitative traits and not molecular markers.

Conclusions

We found that selection has strongly influenced the variation in quantitative traits within and among populations of S. sponhemica. This is in agreement with the conclusions of general meta-analyses of the role of selection for population differentiation in plants (Merilä and Crnokrak, 2001; Leinonen et al., 2008, 2013; De Kort et al., 2013), but in contrast to the results of other studies on rare plant species (Gravuer et al., 2005). Our results indicate that selection can be an important force for structuring variation in evolutionarily important traits even for rare endemic species restricted to very specific habitats, if climatic conditions vary. The negative relationship between the differentiation of a trait among populations of S. sponhemica and its evolvability indicates that those traits that are important for adaptation to a changing climate have the least evolutionary potential within populations. Adaptation to climate change in S. sponhemica may thus require gene flow between populations, which is, however, unlikely due to the strong fragmentation of the populations.

We found no significant relationships between the genetic variability of any of the quantitative traits and molecular genetic variability. Our results thus support the conclusion that molecular genetic variation is not suitable to predict the short-term evolutionary potential of populations or population divergence, because of the importance of selection for the variation in quantitative traits (Reed and Frankham, 2001). Quantitative traits in relation to environmental conditions should therefore be studied to assess the potential for adaptation (Vitt and Havens, 2004; Whitlock, 2008). In contrast, low molecular genetic variability appears to be a better indicator for the risk of inbreeding depression than low variability in quantitative traits. We conclude that studies of genetic variation of molecular markers and of quantitative traits may provide complementary insights important for the conservation of rare species.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Figure S1: relationships between population means of the length of stems and the number of flower stems per rosette of plants measured in the field and in the common garden. Figure S2: relationships between plant diameter, number of rosettes, PC PLANTSIZE, number of flowers and PC REPRO in populations and their molecular diversity, H_eN.