Abstract
The hydrogen isotope (2H/1H) ratio of lipids from phytoplankton is a powerful new tool for reconstructing hydroclimate variations in the geologic past from marine and lacustrine sediments. Water 2H/1H changes are reflected in lipid 2H/1H changes with R2 > 0.99, and salinity variations have been shown to cause about a 1‰ change in lipid δ2H values per unit (ppt) change in salinity. Less understood are the effects of growth rate, nutrient limitation and light on 2H/1H fractionation in phytoplankton. Here we present the first published study of growth rate effects on 2H/1H fractionation in the lipids of coccolithophorids grown in continuous cultures. Emiliania huxleyi was cultivated in steady state at four growth rates and the δ2H value of individual alkenones (C37:2, C37:3, C38:2, C38:3), fatty acids (C14:0, C16:0, C18:0), and 24-methyl cholest-5,22-dien-3β-ol (brassicasterol) were measured. 2H/1H fractionation increased in all lipids as growth rate increased by 24‰ to 79‰ (div d-1)-1. We attribute this response to a proportional increase in the fraction of NADPH from Photosystem I (PS1) of photosynthesis relative to NADPH from the cytosolic oxidative pentose phosphate (OPP) pathway in the synthesis of lipids as growth rate increases. A 3-endmember model is presented in which lipid hydrogen comes from NADPH produced in PS1, NADPH produced by OPP, and intracellular water. With published values or best estimates of the fractionation factors for these sources (αPS1 = 0.4, αOPP = 0.75, and αH2O = 0) and half of the hydrogen in a lipid derived from water the model indicates αlipid = 0.79. This value is within the range measured for alkenones (αalkenone = 0.77 to 0.81) and fatty acids (αFA = 0.75 to 0.82) in the chemostat cultures, but is greater than the range for brassicasterol (αbrassicasterol = 0.68 to 0.72). The latter is attributed to a greater proportion of hydrogen from NADPH relative to water in isoprenoid lipids. The model successfully explains the increase in 2H/1H fractionation in the sterol 24-methyl-cholesta-5,24(28)-dien-3β-ol from marine centric diatom T. pseudonana chemostat cultures as growth rate increases. Insensitivity of αFA in those same cultures may be attributable to a larger fraction of hydrogen in fatty acids sourced from intracellular water at the expense of NADPH as growth rate increases. The high sensitivity of α to growth rate in E. huxleyi lipids and a T. pseudonana sterol implies that any change in growth rate larger than ~0.15 div d-1 can cause a change in δ2Hlipid that is larger than the analytical error of the measurement (~5‰), and needs to be considered when interpreting δ2Hlipid variations in sediments.
Introduction
Discovered in 1931 by Harold Urey [1], deuterium (2H) accounts for 0.0156% of hydrogen atoms on Earth, or about one of every 6,420. Since deuterium has twice the mass of protium (1H or H), chemical bonds to 2H have significantly lower vibrational frequencies than those to H, and as a result, require more energy to break. Reactions involving C-2H bonds therefore occur some 5–10 times more slowly than those involving C-H bonds [2,3]. This gives rise to a large kinetic isotope effect and ensuing isotopic fractionations that are much larger than for any other stable isotope system. This characteristic makes the stable hydrogen isotopes particularly sensitive tracers of biological and environmental processes.
Analytical advances in the separation of small molecules by capillary gas chromatography, their pyrolytic reduction to H2 gas, and the introduction of that H2 into a dual inlet mass spectrometer by a stream of helium by Alex Sessions and others in the 1990s provided a means of precisely (ca. +/- 5‰) measuring 2H/1H ratios on sub-microgram quantities of individual lipids, or biomarkers [4–6]. Sauer et al. (2001) subsequently demonstrated that the 2H/1H ratio of microalgal lipids co-varied with that of the water in which the algae grew [7], a relationship borne out by culture studies [8–10].
Because the hydrogen isotopic composition of lake or ocean surface waters is sensitive to local evaporation and precipitation rates [11–13], reconstructions of water isotope variations in the geologic past are possible by measuring 2H/1H ratios of microalgal lipids in lake or ocean sediment cores [8,14–20]. This technique is analogous to the widely used oxygen isotope method in calcium carbonate microfossils. It can be used where such fossils are non-existent, such as in many lacustrine settings and in parts of the ocean where calcium carbonate is not well preserved. Unlike the oxygen isotopic ratio of biogenic CaCO3, which is generally within a few parts per thousand of the water in which the shell was grown after accounting for the effect of temperature, δ2H values of lipids are 100‰ to 400‰ depleted in deuterium compared to the water in which the microalgae grew [4,9,21]. What’s more, the 2H-depletion in algal lipids varies as a function of taxa [9], lipid type [4,9], growth phase [22,23], and environmental conditions [10,24–27]. This large 2H-depletion in algal lipids was presciently attributed by Estep and Hoering (1981) to a very low δ2H value of hydride in nicotinamide adenine dinucleotide phosphate (NADPH) [28].
Much of what is known about hydrogen and deuterium cycling within cells comes from 2H NMR studies that provide 2H/1H ratios of individual hydrogen atoms within molecules [29,30], on the one hand, and comparative studies of the hydrogen isotopic composition of different biochemical constituents of plants, microalgae and bacteria under different growth conditions on the other (i.e., autotrophic, heterotrophic and mixotrophic) [28,31,32]. The conclusion common to all these studies is that photosynthetically-produced NADPH is the probable source of the large 2H-depletion in lipids relative to environmental water [28,29,31–33].
The other key inference from the 2H NMR studies [29,30] and the Lemna gibba (duckweed) growth experiments by Yakir and DeNiro (1990) [32] is that rapid and extensive non-enzyme-catalyzed exchange of hydrogen occurs between intracellular water and organic hydrogen. This effect was confirmed and quantified by Kreuzer-Martin et al. (2006 & 2012) [34,35], who measured the hydrogen isotopic composition of intracellular water and fatty acids in bacterial and mammalian cells following growth on 2H-labeled water. They concluded that ~50% of the hydrogen in intracellular water had cycled through the organic hydrogen pool in exponentially growing cells, and about half that amount in stationary-phase cells [34,35].
A so-called “vital effect” several times the magnitude of the environmental signal might at first seem untenable for a paleoenvironmental proxy. Yet a growing number of studies continue to find systematic and reproducible variations of algal lipid δ2H values not only with water δ2H values, but other environmental parameters as well, such as salinity [10,22,24–27,36].
Because a detailed mechanistic understanding of the source of 2H-depletion in algal lipids is lacking it is difficult to know a priori how particular environmental or growth conditions will manifest in the δ2H value of lipids. Through empirical studies performed first by Schouten et al. (2006) [10], it was shown that 2H/1H fractionation increased as growth rate increased in batch cultures of the marine coccolithophorids Emiliania huxleyi and Gephyrocapsa oceanica. Growth rates varied in those experiments in response to changes in salinity and temperature. The extent to which salinity and/or temperature themselves caused the observed changes in 2H/1H fractionation, independent of changes in growth rate, was difficult to diagnose. Furthermore, in a batch culture, the biomass, light intensity, nutrient concentrations, waste products, and consequently the cellular environment, are always changing. Motivated by the high sensitivity of 2H/1H fractionation to growth rate implied by the Schouten et al. (2006) experiments [10], we set out to quantify the 2H/1H fractionation response in coccolithophorid and diatom lipids to changes in growth rate using continuous culturing techniques that permit controlled, steady-state growth to be maintained. The first of these results were published by Zhang et al. (2009) [37] based on just two continuous cultures of the diatom Thalassiosira pseudonana. They observed greater 2H/1H fractionation at the higher growth rate in the sterol 24-methyl-cholesta-5,24(28)-dien-3β-ol but not in three fatty acids. The results from T. pseudonana in the present study generally confirm the earlier findings, but slight differences in culturing conditions preclude a direct comparison.
We find that 2H/1H fractionation in alkenones, fatty acids and a sterol from the coccolithophorid Emiliania huxleyi, and a sterol from the marine diatom Thalassiosira pseudonana increases as growth rate increases, by 20–79‰ (div d-1)-1. We attribute this large and systematic hydrogen isotope effect on lipids from growth rate to (i) changing contributions of NADPH from photosynthesis on the one hand, and the oxidative pentose phosphate pathway and tricarboxylic acid cycle on the other, as well as (ii) the relative contributions of hydrogen from intracellular water and NADPH, and potentially, (iii) changes in the 2H/1H ratio of intracellular water as growth rate changes.
Materials and Methods
Culture Methods
E. huxleyi
Cultures of E. huxleyi (CCMP Strain 374) were obtained from the Provasoli-Guillard National Center for Marine Algae and Microbiota (NCMA), formerly the National Center for Culture of Marine Phytoplankton (CCMP). Information provided by NCMA indicates strain collection on 6/23/1989 from a water depth of 5 m in the Gulf of Maine area by P. Holligan with isolation and deposition at CCMP by T. Skinner (9/1/1990 and 10/22/90, respectively). The axenic culture is maintained at NCMA at 18–22°C in f/2-Si or L1-Si media.
Growth media for the batch and four continuous cultures of E. huxleyi utilized seawater collected from Puget Sound between October, 2006 and June, 2007 from a range of locations bounded by the Straits of Juan de Fuca on the north and Elliot Bay on the South. Seawater salinity in these collections ranged between 30.19 and 31.37, with an average of 30.70. Nutrient composition of the stock seawater was as follows (average ± 1 SD, for N = 4): 2.40 ± 0.21 μM PO4 3-, 27.49 ± 3.36 μM NO3 1-, 0.25 ± 0.21 uM NO2 1-, 2.24 ± 1.91 μM NH4 1+, and 70.06 ± 27.00 μM Si(OH)4 (aq). The seawater was sterilized by filtration through Millipore 0.45 um Type HA filters followed by autoclaving. Growth media for the two continuous cultures under nutrient replete (NR) conditions used this seawater enriched as per the f/2-Si (silicate addition excluded) formulation [38,39] resulting in a molar N/P ~ 24:1 in the feed media. In order to establish N-limited (N2L) growth rates in two continuous cultures, nitrate and phosphate additions were modified from the f/2-Si recipe to attain a molar N/P ratio of <1.5. The calculated concentrations of nitrogen in the growth (feed) media and the associated N:P ratios for all four E. huxleyi continuous cultures are summarized in Table 1.
Table 1. Growth conditions for continuous cultures of E. huxleyi and T. pseudonana.
| Media Type | Number of Generations | Division Rate (div day-1) | Cell Density (cells mL-1) /106 | Feed Media Nitrate (μM) | Feed Media Molar N/P Ratio | Residual Nitrate (μM) | Residual Phosphate (μM) | Residual Molar N/P Ratio |
|---|---|---|---|---|---|---|---|---|
| E. huxleyi | ||||||||
| N2L | 3.53 | 0.20 | n.d. | 30.5 | 1.42 | 3.03 ± 0.07 (2) | 11.85 ± 0.01 (2) | 0.256 ± 0.006 (2) |
| N2L | 4.01 | 0.69 | n.d. | 24.6 | 1.16 | n.d. | n.d. | n.d. |
| NR | 4.44 | 0.89 | n.d. | 958 | 23.7 | n.d. | n.d. | n.d. |
| NR | 4.09 | 0.99 | n.d. | 951 | 23.6 | n.d. | n.d. | n.d. |
| T. pseudonana | ||||||||
| N2L | 4.20 | 0.52 | 2.08 ± 0.20 (8) | 98.0 | 5.18 | 0.04 ± 0.05 (7) | 1.34 ± 0.25 (7) † | 0.034 ±0.046 (7) † |
| N2L | 5.08 | 1.41 | 1.95 ± 0.10 (5) | 98.0 | 5.18 | 0.60 ± 0.25 (4) | 1.76 ± 0.32 (4) † | 0.346 ± 0.153 (4) † |
| N2L | 5.81 | 2.07 | 1.73 ± 0.13 (4) | 98.0* | 5.18* | 6.66 ± 1.98 (3) | 7.60 ± 0.56 (3) | 0.870 ± 0.211 (3) |
Cell densities for T. pseudonana are presented as average ± SD (number of samples), where each sample represents the density measured on the days before harvesting. The symbol n.d. means no data available. The feed media nitrate concentrations and N/P ratios were calculated from the mass of nutrient salts added to the media.
* The measured nitrate concentration and molar N/P ratio for the N2L feed media in this T. pseudonana culture were 96.79 ± 2.77 μM and 5.81 ± 0.07, respectively, close to the values determined from based on the mass of nutrient salts added to the media.
† These residual phosphate concentrations and associated molar N/P ratios represent minimum and maximum values, respectively, owing to the potential loss of phosphate during sample storage (as discussed in Materials and Methods: Culture Methods: T. pseudonana).
Upon receipt from NCMA, the E. huxleyi strain was revived by batch culturing with f/2-Si media (NR) in capped 25 mL glass culture tubes under light and temperature conditions representative of those to be used for continuous cultures. In vivo fluorescence measurements were used to monitor biomass increase in the batch cultures. Sequential and multiple transfers of the strain to fresh media by subsampling and inoculation during exponential phase of growth ensured acclimation and a valid determination of the maximum growth rate attainable under the provided conditions. With batch culturing in NR media, this CCMP Strain 374 of E. huxleyi attained a maximum growth rate of 1.31 ± 0.05 div d-1 (specific growth rate of 0.91) for N = 4 samples.
All tubing and culture vessels used in this study were sterilized by autoclaving. The continuous cultures of E. huxleyi were grown at ~ 20°C in 15L polycarbonate culture vessels illuminated continuously by four 48” Cool White Fluorescent 40 Watt Bulbs and gently stirred (50 to 60 rpm) with either a Lightning stirrer with impeller or a Nalgene Magnetic Carboy Stirrer coupled with a magnetic stir plate. Light intensity in the growth chamber area, based on previous measurements in our similarly illuminated studies, was 200 ± 20 μmol m-2 s-1 [37]. The cultures were supplied medical grade air by gentle bubbling just below the media surface. Sterile growth media of either type NR or N2L was fed to the culture vessel using a peristaltic pump, and the media volume (7 L) in the culture vessel was kept constant by positioning a media withdrawal tube at an appropriate height in the vessel and connected to a second peristaltic pump.
For E. huxleyi, each of the four continuous cultures was inoculated with algae from either the NR or N2L batch culture; and the respective population was allowed to reach a healthy cell density, as indicated by significant in vivo fluorescence, before the peristaltic pumps were turned on. Under steady-state conditions of nutrient-limited growth rate and constant algal cell density (ln of fluorescence), the specific growth rate (d-1) is equivalent to the dilution rate D of the culture, ie. D = Fm/Vc where Fm and Vc are the inflow of the media and the volume of the culture, respectively. The cell division rate, the unit of growth rate used in this study, is provided by D/ln(2). The media feeds were set to provide a range of nutrient-limited growth rates by adjusting the inflow peristaltic pump. E. huxleyi cell division rates achieved in this study were 0.99 and 0.89 div d-1 for the NR-based cultures, and 0.69 and 0.20 div d-1 for the N2L-based cultures (Table 1).
The inflows to the culture vessel were measured daily and the inflow peristaltic pump was adjusted to keep a constant dilution rate. Simultaneous monitoring of in vivo fluorescence on samples of the continuous culture withdrawn daily provided an estimate of cell density and the degree of stabilization of the algal population at a specific growth rate. Once the cell density stabilized, the continuous culture was allowed to run a minimum of 3.5 generations, after which the algal culture was harvested.
Comparison of the nitrate (3.03 μM) and phosphate (11.85 μM) concentrations measured in the culture media of the lowest growth rate (0.20 div d-1) E. huxleyi continuous culture at steady-state represent 10- and 2-fold reductions from their concentrations in the feed media, respectively, and a reduction in molar N/P ratio from 1.4 to 0.26 (Table 1).
T. pseudonana
The T. pseudonana cultures were obtained from the School of Oceanography, University of Washington [37]. Growth media for the batch and three (3) continuous cultures of this second species utilized artificial seawater made by dissolving sea salt (Instant Ocean® Aquarium Mixture) in Milli-Q water to attain a salinity of 32. The measured nutrient composition of the artificial seawater was: 0.03 μM PO4 3-; 1.11 μM NO3 1-; 0.15 uM NO2 1-; 0.36 μM NH4 1+; and 4.14 μM Si(OH)4. The seawater was gravity-filtered through a 142 mm GF/F filter followed by a 0.8/0.2 μm Supor® AcroPak™ cartridge filter (Pall Life Sciences). Both NR and N2L versions of the feed media were based on the f/2 medium [38,39] with component stock solutions added sterilely by syringe outfitted with a 25 mm 0.2 um SFCA syringe filter (Thermos Scientific™ Nalgene™). The macronutrient enrichments were modified from the f/2 medium recipe to provide the following nominal concentrations for the NR medium: 38 μM PO4 3-, 891 μM NO3 1-, 106 μM Si(OH)4; and the N2L medium: 19 μM PO4 3-, 98 μM NO3 1-, 201 μM Si(OH)4. This provided molar N/P ratios of 23 and 5.2 for the NR and N2L media, respectively.
Batch culturing of T. pseudonana in the NR media described above was used to sustain the culture until chemostat inoculation. The highest growth rate observed in NR media was 2.98 div d-1 for n = 3 samples, which is comparable to the previously reported rate of 2.89 div d-1 with a different growth media [37] (see S1 Appendix).
All three continuous cultures of T. pseudonana used the N2L formulation of diatom-required media, but the same illumination, similar growth temperatures (20 to 22°C) and similar inoculation, maintenance, and sampling protocols as those described for E. huxleyi. The flow rate of the N2L feed media was adjusted to obtain T. pseudonana cell division rates of 2.07, 1.41, and 0.52 div d-1 for culture volumes of 6.8, 6.8, and 9.8 L, respectively, and the cells were harvested after 4.2 to 5.8 generations of steady-state conditions (constant fluorescence and cell density). The cell densities observed during steady-state were 1.73, 1.95, and 2.08 x 106 cells mL-1, respectively (Table 1).
The residual concentration of nitrate (6.66 μM) and phosphate (7.60 μM) in the T. pseudonana continuous culture media at the highest division rate (2.07 div d-1) represented a 15-fold reduction from their concentrations in the feed media, whereas this reduction was 2.5-fold in the slowest growing (0.52 div d-1) chemostat (Table 1). This resulted in a reduction of the molar N/P ratios from 5.2 to 0.87 in the highest growth-rate culture (Table 1).
Residual nutrients in the two lowest growth rate T. pseudonana cultures were measured after long-term storage of the frozen samples. Clementson and Wayte (1992) reported that while nitrate concentration exhibited no significant change in concentration after 24-months of frozen storage, phosphate steadily decreased after 4 months [40]. In this study, comparison of replicate residual nutrient samples of the 2.07 div d-1 culture confirmed the likely loss of phosphate but preservation of the nitrate during long-term freezing. Therefore, while the residual phosphate concentrations of 1.34 and 1.76 μM in the two lowest growth rate cultures should be considered minimum amounts, the residual nitrate concentrations are representative.
Lipid extraction, purification and derivatization
The phytoplankton cells were isolated from the continuous cultures by either gravity or vacuum-assisted gravity filtration through pre-combusted 142 mm Whatman GFF filters (GE Healthcare Bio-Sciences, Pittsburgh, Pennsylvania, USA). The filters were frozen and kept at ≤ -10°C until further subsampling and analysis.
Lipids were extracted from the freeze-dried filter subsamples utilizing a Accelerated Solvent Extraction System 200 (Dionex ASE-200, Thermo Scientific, Sunnyvale, California, USA) and a 9:1 (v/v) mixture of dichloromethane:methanol as extraction solvent.
The lipids were separated into a non-polar (NP) and a polar, fatty-acid containing fraction (FA) using solid-phase extraction (SPE) on an aminopropyl column. The NP fraction contained the long-chain alkenones, alkenoates, and the 24-methyl cholest-5,22-dien-3β-ol sterol (brassicasterol) from the E. huxleyi and the 24-methyl-cholesta-5,24(28)-dien-3β-ol sterol from the T. pseudonana culture extracts. The latter sterol was isolated in sufficiently pure form for hydrogen isotope analysis using further separation of the appropriate NP fraction on an SPE column packed with 5% deactivated silica gel.
Long-chain di- and tri-unsaturated C37 and C38 alkenones and brassicasterol were isolated from the NP fractions of the T. pseudonana extracts by semi-preparative high-performance liquid chromatography—mass spectrometry (HPLC-MS) using the alkenone purification method previously described [41] modified to facilitate simultaneous isolation of brassicasterol and for optimal utilization of NP lipid SPE fractions from algal culture extracts (as described in the S2 Appendix).
The fatty acids were methylated for both quantification and hydrogen isotope analysis using methanolic HCl The contribution of introduced methyl group hydrogens to the δ2H values of the fatty acids was determined by simultaneous methylation of a Na-phthalate standard of known δ2H value (-95.5 ± 2.2, Dr. Arndt Schimmelmann, Indiana University). The fatty acid δ2H values reported herein have been corrected for the added methyl hydrogens of δ2H = 156.2, and represent those of the free carboxylate anions.
Aliquots of each NP SPE fraction containing the alkenones and brassicasterol and each silica-gel SPE subfraction containing the 24-methyl-cholesta-5,24(28)-dien-3β-ol were silylated (BSTFA + 1% TMCS), after addition of an internal standard (5α-cholestane), to allow for quantification of the alkenones and sterols by GC-FID.
Derivatization of sterols for hydrogen isotope analysis requires a product highly resistant to decomposition and the ability to correct the δ2H of the sterol for hydrogens added, neither of which is adequately provided by silylation. The HPLC isolates of brassicasterol and the SPE fraction containing the 24-methyl-cholesta-5,24(28)-dien-3β-ol were acetylated using acetic anhydride with a known δ2H value of -133.2 ± 2.1‰ (Dr. Arndt Schimmelmann, Indiana University). The hydrogen isotope values reported for the sterols have been corrected for the hydrogens added by the acetyl group and represent the sterols without the hydroxyl hydrogen atom.
Detailed descriptions of the lipid extraction, purification, and derivatization methods are available in the S2–S4 Appendices.
GC-FID and GC-MS analyses
The alkenone, sterol, and fatty acid compositions of the continuous cultures were evaluated and quantified by gas chromatography—flame ionization detection (GC-FID) by comparing their area responses with that of the added 5α-cholestane internal standard. Quantification of fatty acids (as methyl esters) proceeded similarly but were additionally corrected for procedural recovery (~70%) using a known mass of heneicosanoic acid added to the culture extract before SPE.
Analysis of the HPLC-isolated alkenones and test fractions by GC-FID, with 5α-cholestane internal standard added, provided confirmation of adequate HPLC purification and appropriate dilution amounts for subsequent hydrogen isotope analyses by GC-IRMS. Silylation of test fractions bracketing the HPLC elution time of brassicasterol confirmed that the combined vials contained all of the compound. Aliquots of the acetylated sterols and methylated fatty acids were similarly quantified to determine the mass isolated and dilution required for subsequent GC-IRMS analysis.
Gas chromatography—mass spectrometry (GC-MS) analysis was used for compound identifications, qualitative analysis of the HPLC fractions, and confirmation of GC-FID results.
Additional details of the GC-FID and GC-MS methods are available in the S5 Appendix.
Hydrogen isotope analysis of lipids and water
The stable hydrogen isotopic compositions of the purified alkenones, brassicasterol, 24-methyl-cholesta-5,24(28)-dien-3β-ol and fatty acids were determined using gas chromatography—isotope ratio mass spectrometry (GC-irMS; instrument details in the S6 Appendix).
The H3 + factor was determined daily or between batches of runs using 10 injections of H2 reference gas of known δ2H, and this correction typically ranged from 4 to 6. Consistent operation of the irMS component of the system was ensured by monitoring its response to the reference gas injected at the beginning and end of each analysis. The overall performance of the combined GC-irMS and consistency in δ2H measurements was ensured by daily injections of a series of n-C14 to n-C44 n-alkanes of known hydrogen isotope composition (Schwab and Sachs, 2009) [41] and instrument maintenance was scheduled accordingly. Hydrogen isotope data was processed using ISODAT 2.5 software.
In order to quantitatively compensate for the potential drifts in measured δ2H values as a result of changes in GC elution time, column aging, thermal conversion efficiency, and instrument drift and/or memory effects during and between analyses, standards of known δ2H that bracket the retention times of the target compounds were coinjected. For the alkenones, n-C38 and n-C41 n-alkanes of known δ2H (-99.4‰ and -205.7‰, respectively; Dr. Arndt Schimmelmann, Indiana University) were coinjected. The n-C41 coinjection standard was used to correct the measured δ2H values via reprocessing with the onboard ISODAT software. The n-C38 coinjection standard was used only for a secondary quality control check (ISODAT calculated δ2H = -100.1 ± 5.1‰ for n = 27 sample runs). Coinjection of n-C32 and n-C36 n-alkanes of known δ2H (-225.9‰ and -212.7‰, respectively; [41] was used for similarly correcting the brassicasterol and the 24-methyl-cholesta-5,24(28)-dien-3β-ol δ2H values. Analogous corrections of the fatty acid measurements utilized coinjection of n-C14 and n-C26 n-alkanes of known δ2H (-68.8‰ and -57.7‰, respectively; Dr. Arndt Schimmelmann, Indiana University). Nominally, triplicate injections were averaged to arrive at the final δ2H values, with the values reported for brassicasterol and fatty acids corrected for hydrogen added during derivatization.
The δ2H values of the media water for the continuous cultures were obtained using a Thermo Finnigan High Temperature Conversion Elemental Interface (TC/EA) equipped with a CTC Analytics GCPal Autosampler and interfaced with the Delta V Plus irMS (described in the S6 Appendix). Thermal conversion of the water was conducted at a pyrolysis temperature of 1450°C. Six replicate analyses of each media sample allowed minimization of any memory effect of the system by exclusion of the first three samples from the final average. Measured values were referenced to Vienna Standard Mean Ocean Water (VSMOW) by calibration with a combination of secondary water standards and VSMOW, Greenland Ice Sheet Precipitation (GISP), and Standard Light Antarctic Precipitation (SLAP) primary standards.
Results
E. huxleyi
The marine coccolithophorid Emiliania huxleyi (CCMP Strain 374) was grown in continuous cultures at 0.99, 0.89, 0.69 and 0.20 div d-1 (Table 1). All conditions were held constant between the four treatments except for the rate at which fresh media was supplied and the nitrate-to-phosphate ratio of that media (Table 1). The concentration of the primary sterol (24-methyl cholest-5,22-dien-3β-ol, or brassicasterol), five fatty acids (myristic (C14:0), palmitic (C16:0), palmitoleic (C16:1), stearic (C18:0), oleic (C18:1)) and four alkenones (methyl ketones: C37:2, C37:3, C38:2, C38:3) in the cultures are given in Table 2. Alkenone concentrations varied between 9 and 270 ng mL-1 of culture and decreased as growth rates increased (Fig 1A). Brassicasterol concentrations were between 5 and 30 ng mL-1 of cultures and decreased as growth rates increased (Fig 1A). Fatty acid concentrations were between 2 and 55 ng mL-1 of culture and did not vary systematically with growth rate, with two increasing (C14:0, C16:0), one decreasing (C18:1), and two showing no trend (C16:1 and C18:0) (Fig 1B). As discussed below lipid concentrations are reported on a per-cell-basis for T. pseudonana cultures (Fig 2).
Table 2. Lipid concentrations in E. huxleyi chemostat cultures.
| Fatty Acids (ng mL-1) | Alkenones (ng mL-1) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Growth Rate (div d-1) | Sterol* (ng mL-1) | C14:0 | C16:1 | C16:0 | C18:1 | C18:0 | C37:2 | C37:3 | C38:2 | C38:3 | Uk' 37 | Uk’ 37-SST (°C) |
| 0.20 | 30.1 | n.d. | n.d. | n.d. | n.d. | n.d. | 235 | 105 | 270 | 45.6 | 0.690 | 19.2 |
| 0.69 | 5.09 | 23.5 | 3.6 | 19.1 | 2.9 | 2.8 | 109 | 40.0 | 135 | 14.3 | 0.733 | 20.4 |
| 0.89 | 17.8 | 25.3 | 1.5 | 9.9 | 2.3 | 2.8 | 131 | 61.9 | 106 | 19.9 | 0.680 | 18.8 |
| 0.99 | 7.67 | 54.9 | 3.7 | 34.9 | n.d. | 17.7 | 62.8 | 30.2 | 46.9 | 9.01 | 0.675 | 18.7 |
* Brassicasterol.
Concentrations of lipids in E. huxleyi chemostat cultures in ng per mL culture media. Alkenone unsaturation ratios (Uk’ 37) and inferred SST based on the Prahl et al. temperature calibration [42] are also provided. The symbol n.d. means no data available. Lipid concentration per cell was not calculated owing to a lack of cell counts.
Fig 1. Concentration of lipids as a function of growth rate in E. huxleyi cultures.
Concentrations presented in ng lipid per mL of culture media. (A) Alkenones and brassicasterol. (B) Fatty acids.
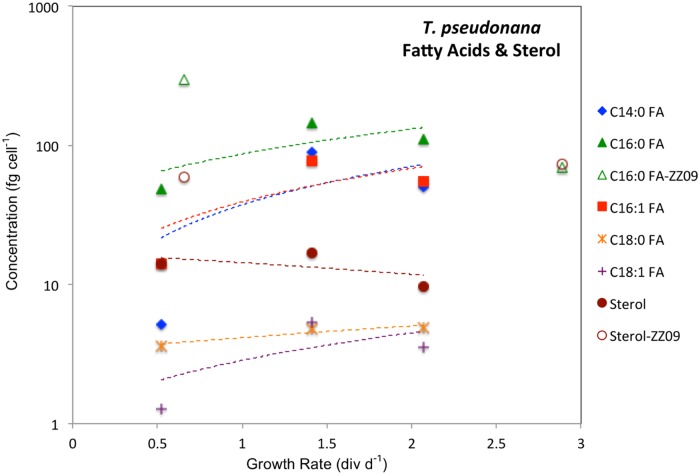
Fig 2. Concentration of lipids as a function of growth rate in T. pseudonana cultures.
Concentrations presented in 10−15 g (fg) cell-1. Open symbols represent estimates from [37]. Best fit lines in are curved owing to the log scale of the y-axis. The purpose of fitting lines to 3 data points is to demonstrate the positive slope for FAs and negative slope for 24-methyl-cholesta-5,24(28)-dien-3β-ol.
Hydrogen isotope ratios of lipids in the E. huxleyi chemostat cultures were between –337‰ for brassicasterol at 0.99 div d-1 and –188‰ for C18:0 at 0.2 div d-1 and generally decreased with increasing growth rate. δ2H values for lipids are listed in Table 3, except for C16:1 and C18:1, the concentrations of which were too low for δ2H analyses. Water δ2H values in the four cultures were -9.2‰, -6.4‰, -4.5‰, and -6.5‰, respectively, for the growth rates of 0.2, 0.69, 0.89, and 0.99 div d-1 (Table 3). δ2H values were generally highest for fatty acids (-254‰ to -188‰), intermediate for alkenones (-231‰ to -196‰), and lowest for brassicasterol (-298‰ to -337‰) at any particular growth rate. δ2H values were lower for tri-unsaturated alkenones than for di-unsaturated alkenones.
Table 3. Hydrogen isotope ratios and fractionation factors in E. huxleyi and T. pseudonana chemostat cultures.
| Lipid | Growth Rate(div d-1) | δ2H -H2O | SD-H2O | δ2H -Lipid | SD-Lipid | α | SD-α | N |
|---|---|---|---|---|---|---|---|---|
| E. huxleyi | ||||||||
| 0.2 | -9.2 | 0.4 | -196 | 7.41 | 0.811 | 0.00748 | 3 | |
| C37:2 | 0.69 | -6.4 | 1.4 | -219 | 1.59 | 0.786 | 0.00160 | 4 |
| 0.89 | -4.5 | 0.4 | -214 | 3.18 | 0.789 | 0.00320 | 4 | |
| 0.99 | -6.5 | 0.4 | -227 | 4.65 | 0.778 | 0.00468 | 3 | |
| 0.2 | -9.2 | 0.4 | -207 | 2.43 | 0.800 | 0.00245 | 3 | |
| C37:3 | 0.69 | -6.4 | 1.4 | -221 | 5.52 | 0.784 | 0.00555 | 3 |
| 0.89 | -4.5 | 0.4 | -216 | 2.80 | 0.787 | 0.00281 | 3 | |
| 0.99 | -6.5 | 0.4 | -227 | 6.88 | 0.778 | 0.00693 | 5 | |
| 0.2 | -9.2 | 0.4 | -196 | 2.81 | 0.811 | 0.00284 | 3 | |
| C38:2 | 0.69 | -6.4 | 1.4 | -211 | 3.48 | 0.794 | 0.00350 | 3 |
| 0.89 | -4.5 | 0.4 | -210 | 3.86 | 0.794 | 0.00388 | 3 | |
| 0.99 | -6.5 | 0.4 | -212 | 3.52 | 0.793 | 0.00355 | 3 | |
| 0.2 | -9.2 | 0.4 | -207 | 2.21 | 0.800 | 0.00223 | 3 | |
| C38:3 | 0.69 | -6.4 | 1.4 | -218 | 4.19 | 0.787 | 0.00422 | 3 |
| 0.89 | -4.5 | 0.4 | -225 | 13.1 | 0.778 | 0.0132 | 3 | |
| 0.99 | -6.5 | 0.4 | -231 | 11.7 | 0.774 | 0.0118 | 3 | |
| Brassi | 0.2 | -9.2 | 0.4 | -298 | 2.90 | 0.719 | 0.00275 | 3 |
| caster | 0.69 | -6.4 | 1.4 | -312 | 0.703 | 1 | ||
| ol | 0.89 | -4.5 | 0.4 | -319 | 2.18 | 0.695 | 0.00206 | 3 |
| 0.99 | -6.5 | 0.4 | -337 | 7.15 | 0.681 | 0.00675 | 3 | |
| 0.2 | -9.2 | 0.4 | -197 | 5.76 | 0.810 | 0.00712 | 3 | |
| C14:0 | 0.69 | -6.4 | 1.4 | -246 | 5.06 | 0.759 | 0.00588 | 4 |
| FA | 0.89 | -4.5 | 0.4 | -252 | 1.70 | 0.751 | 0.00209 | 3 |
| 0.99 | -6.5 | 0.4 | -254 | 2.34 | 0.751 | 0.00258 | 6 | |
| 0.2 | -9.2 | 0.4 | -193 | 20.4 | 0.814 | 0.0252 | 3 | |
| C16:0 | 0.69 | -6.4 | 1.4 | -225 | 7.25 | 0.781 | 0.00789 | 7 |
| FA | 0.89 | -4.5 | 0.4 | -224 | 11.4 | 0.779 | 0.0126 | 6 |
| 0.99 | -6.5 | 0.4 | -232 | 7.86 | 0.773 | 0.00846 | 8 | |
| 0.2 | -9.2 | 0.4 | -188 | 17.7 | 0.819 | 0.0253 | 2 | |
| C18:0 | 0.69 | -6.4 | 1.4 | -191 | 9.29 | 0.814 | 0.0105 | 5 |
| FA | 0.89 | -4.5 | 0.4 | -201 | 4.38 | 0.802 | 0.00508 | 4 |
| 0.99 | -6.5 | 0.4 | -214 | 6.48 | 0.791 | 0.00697 | 8 | |
| T. pseudonana | ||||||||
| 0.52 | -75.2 | 0.36 | -366 | 8.8 | 0.685 | 0.0095 | 3 | |
| Sterol | 1.41 | -74.3 | 0.46 | -387 | 4.0 | 0.662 | 0.0043 | 3 |
| 2.07 | -74.5 | 0.37 | -394 | 3.6 | 0.655 | 0.0038 | 3 | |
| C14:0 | 0.52 | -75.2 | 0.36 | -234 | 3.18 | 0.828 | 0.0034 | 3 |
| FA | 1.41 | -74.3 | 0.46 | -252 | 3.23 | 0.808 | 0.0034 | 3 |
| 2.07 | -74.5 | 0.37 | -243 | 2.71 | 0.818 | 0.0028 | 3 | |
| C16:0 | 0.52 | -75.2 | 0.36 | -238 | 1.86 | 0.824 | 0.0018 | 3 |
| FA | 1.41 | -74.3 | 0.46 | -237 | 3.26 | 0.825 | 0.0034 | 3 |
| 2.07 | -74.5 | 0.37 | -222 | 4.65 | 0.841 | 0.0049 | 3 | |
| C16:1 | 0.52 | -75.2 | 0.36 | -223 | 4.34 | 0.840 | 0.0046 | 3 |
| FA | 1.41 | -74.3 | 0.46 | -224 | 4.03 | 0.838 | 0.0043 | 3 |
| 2.07 | -74.5 | 0.37 | -214 | 1.36 | 0.849 | 0.0013 | 3 | |
SD = standard deviations of the tabulated averages. N = number of samples averaged. δ2Hlipid or H2O = [(2H/1H) lipid or H2O − (2H/1H) std]/(2H/1H) std*1000 with VSMOW as reference standard. α = (δ2H lipid + 1000)/(δ2H H2O + 1000).
Fractionation factors (α = (δ2Hlipid + 1000)/ (δ2HH2O + 1000)) were determined using the individual compound-specific δ2Hlipid measurements and an average value for the δ2HH2O of the respective culture water (see formulas in Table 3). The averages of these individual α values along with their associated standard deviations (SD-α) are presented in Table 3.
Fractionation factors (α) generally decreased, indicating greater 2H/1H fractionation between lipids and extracellular water, as growth rates increased for all lipids. The magnitude of the increase in fractionation as a function of growth rate was between 52 and 79‰ (div d-1)-1 for myristic (C14:0), palmitic (C16:0), and stearic (C18:0) fatty acids (Fig 3A), 44‰ (div d-1)-1 for brassicasterol (Fig 3A), and between 24 and 38‰ (div d-1)-1 for the four alkenones (Fig 3B).
Fig 3. Hydrogen isotope fractionation in lipids as a function of growth rate in E. huxleyi chemostat cultures.
(A) Fractionation factors (α) decreased, indicating greater 2H/1H fractionation between lipids and extracellular water, as growth rates increased by 44‰ (div d-1)-1 for brassicasterol, and 79‰ (div d-1)-1 for myristic acid (C14:0), 52‰ (div d-1)-1 for palmitic (C16:0), and 32‰ (div d-1)-1 for stearic acid (C18:0). (B) Fractionation factors (α) decreased, indicating greater 2H/1H fractionation between alkenones and extracellular water, as growth rates increased by 38‰ (div d-1)-1 for C37:2, and 25‰ (div d-1)-1 for C37:3, 24‰ (div d-1)-1 for C38:2, and 33‰ (div d-1)-1 for C38:3.
The alkenone unsaturation index, Uk’ 37, values in the E. huxleyi chemostat cultures were between 0.675 and 0.733 and did not vary systematically with growth rate (Table 2). These Uk’ 37 values correspond to water temperatures of 18.7°C to 20.4°C using the Prahl et al. (1988) temperature calibration [42], close to the growth temperature of 20°C.
T. pseudonana
The marine centric diatom Thalassiosira pseudonana (CCMP 1335) was grown in continuous cultures at 0.52, 1.41, and 2.07 div d-1 (Table 1). Concentrations of lipids were between 9.7 fg cell-1 and 17 fg cell-1 for 24-methyl-cholesta-5,24(28)-dien-3β-ol, and between 1.3 fg cell-1 and 110 fg cell-1 for C14:0, C16:0, C16:1, C18:0, C18:1 fatty acids (Fig 2 and Table 4). δ2H values were between -394‰ and -366‰, resulting in fractionation factors between 0.655 and 0.685 in the sterol, and between -252‰ and -214‰, resulting in fractionation factors between 0.808 and 0.849 in the fatty acids (Table 3 and Fig 4).
Table 4. Lipid concentrations in T. pseudonana chemostat cultures.
| Fatty Acids (fg cell-1) | ||||||
|---|---|---|---|---|---|---|
| Growth Rate (div d-1) | Sterol*(fg cell-1) | C14:0 | C16:1 | C16:0 | C18:1 | C18:0 |
| 0.52 | 14.1 | 5.16 | 14.0 | 48.4 | 1.27 | 3.60 |
| 1.41 | 16.8 | 89.6 | 77.7 | 145 | 5.39 | 4.83 |
| 2.07 | 9.68 | 50.5 | 55.3 | 112 | 3.54 | 4.92 |
* 24-methyl-cholesta-5,24(28)-dien-3β-ol.
Concentrations of lipids per cell in T.pseudonana chemostat cultures in fg (10−15 g) per cell.
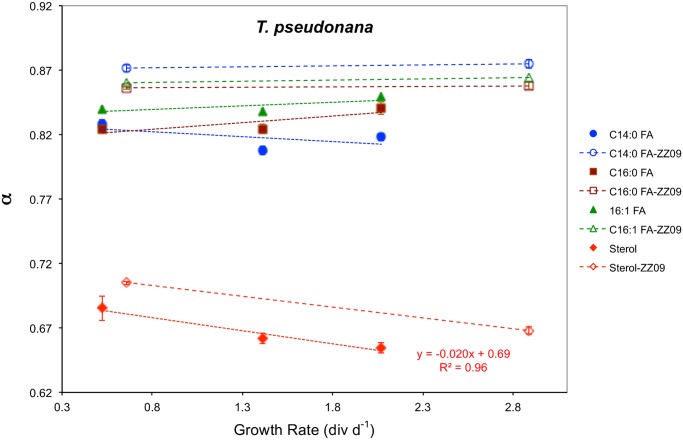
Fig 4. Hydrogen isotope fractionation in 24-methyl-cholesta-5,24(28)-dien-3β-ol and three fatty acids as a function of growth rate in T. pseudonana chemostat cultures.
Open symbols are results reported in [37]. Fractionation factors (α) decreased in the sterol, indicating greater 2H/1H fractionation between lipids and extracellular water, as growth rates increased by 20‰ (div d-1)-1, and nearly constant in C14:0, C16:0 and C16:1 fatty acids.
Discussion
Lipid concentration variations as a function of growth rate
The increase in sterol and alkenone concentrations in E. huxleyi (Fig 1A) as growth rate decreased is consistent with many studies showing that phytoplankton respond to nitrogen limitation by accumulating lipids [43–47]. Several studies have further demonstrated that alkenone concentrations increase under N limitation in E. huxleyi [48–51] and the related haptophyte species Gephyrocapsa oceanica [50] and Isochrysis galbana [49,52]. All of these studies were conducted with batch cultures, and N limitation was usually associated with the post-exponential or stationary phase of growth, making direct comparison with our results from continuous cultures of exponentially growing cells difficult. Nevertheless, the systematic increase in alkenone concentrations in haptophyte cells that are limited by nitrogen, regardless of growth phase or experimental treatment, implies a robust physiological response.
Some fatty acid concentrations decreased (C14:0, C16:0), while others increased (C18:1) in E. huxleyi (Fig 1B) as growth rate decreased. While there may have been a decline in fatty acid content of cells in T. pseudonana (Fig 2) as growth rate decreased the data are inconclusive with just 3 data points.
Hydrogen isotope variations as a function of growth rate in E. huxleyi
As E. huxleyi growth rates increased from 0.2 to 1 div d-1 the apparent lipid-water 2H/1H fractionation increased (i.e., α decreased) by 52 to 79 ‰ (div d-1)-1 in fatty acids, 44 ‰ (div d-1)-1 in brassicasterol (Fig 3A) and 24 to 38 ‰ (div d-1)-1 in alkenones (Fig 3B). We put forth two hypotheses to explain this response. The first calls upon an increase in the fraction of NADPH used for lipid synthesis from the oxidative pentose phosphate (OPP) pathway, relative to that from the light reactions of photosynthesis. The second hypothesis attributes the high sensitivity of hydrogen isotope fractionation in algal lipids to growth rate to increased cellular demand for energy (adenosine triphosphate, ATP) and reductant (NADPH) at higher growth rates and the exchange of hydrogen between sugars and intracellular water.
Varying sources of NADPH
By 1981 it was recognized that the primary source of deuterium depletion in microalgal biomass is the hydride derived from NADPH during biosynthetic reactions [28,29,31–33]. H- from NADPH produced photosynthetically by ferredoxin-NADP+ reductase in Photosystem I (PS1) is estimated to have a δ2H value about 600‰ lower than that of the water from which it was derived [53]. A fractionation factor (α) of 0.4 for hydride produced by photosynthetic oxidation of water is plausible according to Schmidt et al. (2003), in light of the theoretical α value of 0.36 derived from the dissociation constants for 2H2O relative to H2O, and the experimentally determined 2H/1H fractionation for water fission [29].
The central role that NADPH plays in imparting 2H-depletion to biomolecules appears to be independent of the Domain of Life or metabolism (e.g., heterotrophic, photoautotrophic, chemoautotrophic) of the organism [31]. Culture studies with photoautotrophic eukaryotic unicellular phytoplankton [9,21,28], photoautotrophic, photoheterotrophic and heterotrophic C3 plants [32], photoheterotrophic unicellular eukaryotes [54], heterotrophic, chemoautotrophic and photoautotrophic prokaryotes [31], and heterotrophic archaea [55] all conclude that hydride derived from NADPH is the principle source of 2H-depletion in lipids relative to environmental water.
Because NADPH and the associated reductant nicotinamide adenine dinucleotide (NADH) can be produced via multiple pathways, including the light reactions of photosynthesis (in photoautotrophs), the oxidative pentose phosphate (OPP) pathway, the tricarboxylic acid (TCA) cycle, glycolysis, and the glyoxylate cycle, the relative contributions of reductant to a biomolecule from these various pathways is likely to be an important source of H isotopic variation between different lipids in the same cell and between the same lipid in different cells [31,55]. Changing sources of NADPH within a cell in response to environmental conditions and/or metabolic state can therefore be expected to give rise to differing magnitudes of 2H-depletion in lipids.
NADPH derived from processes other than PS1 is expected to be enriched in 2H relative to that produced photosynthetically by ferredoxin-NADP+ reductase in PS1 [29], because it acquires hydride from metabolites rather than photooxidized water. For example, hexoses in the cytosol provide the hydride from which NADPH is produced in the cytosolic OPP pathway. Hydrogen in those hexoses derives ultimately from both intracellular water and NADPH. Assuming half of that hydrogen comes from each, as is the case for glyceraldehyde 3-phosphate (GAP) produced in the Calvin cycle, GAP and monosaccharides synthesized from it might be expected to have a δ2H value of approximately -300‰ (assuming δ2HNADPH/PS1 = -600‰ and δ2Hwater = 0‰). Normal isotope effects for glucose-6-phosphate dehydrogenase and 6-phosphogluconate, the enzymes catalyzing the reduction of NADP+ in the OPP pathway might result in NADPH with a δ2H value less than that on the one hand, but hydrogen exchange reactions between water and saccharides prior to and during the OPP pathway may increase their δ2H value. The latter effect could be exacerbated by the fact that deuterium is preferentially enriched in carbohydrates during hydrogen exchange with water [33]. For these reasons the apparent fractionation factor for non-photosynthetic NADPH is expected to be higher (less 2H/1H fractionation) than for photosynthetically produced NADPH, closer to 0.75 [29] than the 0.4 proposed for photosynthetic NADPH.
A secondary source of 2H-enrichment of hydride from both PS1 and the OPP pathway may be hydrogen exchange between intracellular water and NADPH-derived H- during its transfer to lipids via flavoproteins [29,31]. Hydride can be directly transferred to lipids from NADPH or it can first be transferred to a flavoprotein, and then to the lipid. Once associated with the flavin ring H- can exchange with water [56], resulting in 2H-enrichment assuming a normal isotope effect. The extent to which hydrogen exchange during hydride transfer via flavoproteins influences lipid δ2H values will depend on the enzymes involved with lipid and precursor synthesis since some enzymes are flavin-free, the type of lipid, and the species of phytoplankton. Since virtually nothing is known about the extent to which H- transfer via flavoproteins is likely to influence lipid δ2H values in phytoplankton we neglect this process in the following discussion and propose simply that it may act to decrease the δ2H difference between lipids and intracellular water.
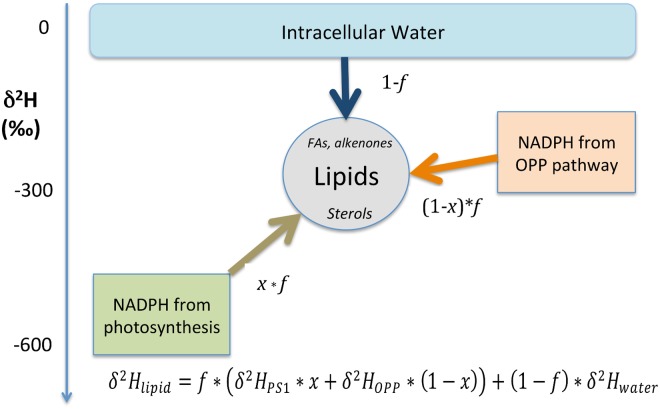
A simple mass balance model demonstrates the sensitivity of algal lipid δ2H values to changes in the relative proportion of H- derived from photosynthetic and non-photosynthetic NADPH (Fig 5). Here we assume that all of the hydrogen in lipids (fatty acids, alkenones and sterols in the case of E. huxleyi) derives from three sources: photosynthetic and non-photosynthetic NADPH and intracellular water. At the steady state condition represented by the continuous cultures the following mass balance yields the δ2H value of lipids:
| (1) |
where f is the fraction of hydrogen in lipids that comes from NADPH and x is the fraction of that NADPH produced in PS1 of photosynthesis. According to this model, when apparent fractionation factors for photosynthetic (0.4) and non-photosynthetic (0.75) NADPH are used, the δ2H value of intracellular water is assumed to be the same as that for extracellular water (0‰), and 50% of the hydrogen in lipids is assumed to come from each NADPH and intracellular water, δ2Hlipid is -213‰ and the fractionation factor (α) for lipids is 0.787. This is close to the average for acetogenic lipids (i.e., alkenones and fatty acids) in E. huxleyi cultures (Table 3, Fig 3).
Fig 5. Model of hydrogen isotopic relationships giving rise to observed δ2H values of lipids in E. huxleyi cells.
f is the fraction of hydrogen in lipids that comes from NADPH, 1-f is the fraction of hydrogen in lipids that comes from water, x is the fraction of hydrogen in lipids derived from PS1 of photosynthesis, 1-x is the fraction of hydrogen in lipids derived from the OPP pathway.
Based on this mass balance model we propose four relationships that can account for (i) the universal 2H-depletion in the lipids of phytoplankton relative to environmental water, (ii) the increase in 2H-depletion of lipids as growth rate increases, the (iii) 2H-depletion in isoprenoid lipids relative to acetogenic lipids, and (iv) the 2H-depletion in lipids relative to carbohydrates and protein:
| (2) |
| (3) |
| (4) |
| (5) |
The first relationship (Eq 2) states that the δ2H value of intracellular water is greater than that of hydride from NADPH produced via the OPP pathway, which in turn is greater than the δ2H value of H- produced in PS1, as described by Schmidt et al. (2003) [29]. The second (Eq 3) states that the relative proportion of NADPH from PS1 and the OPP pathway is proportional to growth rate, justified below, and explaining why α values decrease as growth rate increases (Fig 3). The third (Eq 4) states that there is a greater proportion of hydrogen derived from NADPH relative to water in isoprenoid lipids as compared to acetogenic lipids, explaining their greater 2H-depletion. The fourth (Eq 5) states that there is a greater proportion of hydrogen derived from NADPH relative to water in lipids as compared to other cellular biomass (i.e., carbohydrates plus proteins), explaining their greater 2H-depletion, as first observed by Estep et al. (1980) [21].
The utility of this model to explain the decrease in α as growth rate increased in E. huxleyi rests on the assumption that the proportion of H- from OPP increased at the expense of H- from PS1 as growth rate decreased. While we have no direct evidence for this assertion, a substantial body of literature on the response of phytoplankton cells to nitrogen limitation supports its plausibility. According to Hockin et al. (2012) “The down-regulation of photosynthesis is a universal response to nitrogen starvation among photosynthetic eukaryotes” [57]. Photochemical energy conversion efficiency decreases and genes associated with photosynthesis and carbon fixation are down-regulated [57–59]. In E. huxleyi Rokitta et al. (2014) concluded that “the photosynthetic light reactions were strongly decreased” under N-limitation based on the down regulation of genes associated with plastidic ATP and chlorophyll synthesis [60]. At the same time genes associated with the OPP pathway and TCA cycle are up-regulated in N-limited cells to increase the efficiency of intracellular nitrogen assimilation [57–59]. A decrease in photosynthesis combined with an up-regulation of OPP and TCA genes in response to N-limitation is likely to cause a shift in the proportion of NADPH derived from those processes, such that relatively-less-2H -depleted NADPH from OPP+TCA is produced at the expense of more-highly-2H -depleted NADPH from photosynthesis as N-limited growth rate decreases. A schematic representation of these metabolic changes is shown in Fig 6. At low rates of growth and/or under N-limited conditions genes associated with photosynthesis and carbon fixation are down-regulated, indicated in Fig 6B by smaller compartments for the light (LR) and dark (DR) reactions of photosynthesis, and a smaller flux of CO2 to the DR. At the same time genes associated with the OPP pathway and TCA cycle are up-regulated and cellular production of lipids is high. We propose that this constellation of metabolic activity results in a relatively larger proportion of NADPH used for lipid synthesis coming from OPP compared to PS1, and therefore a relatively higher δ2H value of those lipids. Conversely, we propose that at high rates of growth and/or under N-replete conditions genes associated with photosynthesis and carbon fixation are up-regulated, resulting in a relatively large flux of reductant from photosynthesis as compared to the OPP pathway for the synthesis of lipids (Fig 6A).
Fig 6. Proposed metabolic differences in E. huxleyi cells growing at different rates.
The two represented regimes are: (A) high rates of growth and/or in N-replete conditions, and (B) low rates of growth and/or in N-limited conditions (after [74], Fig 3). LR = Light Reactions of photosynthesis. DR = Dark Reactions (Calvin Cycle). OPP = Oxidative Pentose Phosphate pathway. TCA = Tricarboxylic Acid Cycle.
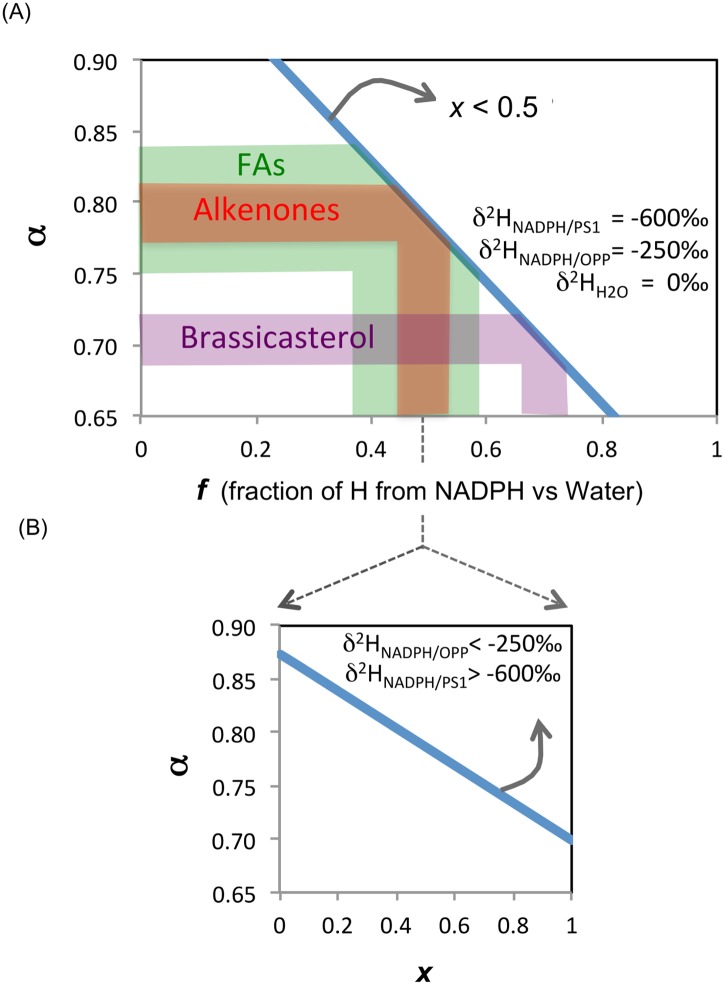
Fig 7 illustrates the sensitivity of α to changes in f, the fraction of lipid hydrogen derived from NADPH versus intracellular water, and x, the fraction of NADPH-derived hydrogen in lipids that comes from PS1 as opposed to the OPP pathway. 2H-depletion increases (α decreases) as both f (Fig 7A) and x (Fig 7B) increase. The sensitivity of α to f increases (i.e., the slope in Fig 7A increase) as the proportion of NADPH from PS1 decreases. The sensitivity of α to x decreases (i.e., the slope in Fig 7B decrease) if either δ2HNADPH/PS1 increases or δ2H NADPH/OPP decreases. When fractionation factors for NADPH from PS1 and OPP are set at 0.4 and 0.75, respectively, δ2HH2Oi is set at 0‰, and half of the NADPH used in lipid synthesis comes from PS1, the model predicts that roughly 40% to 60% of hydrogen in fatty acids, 45% to 55% of hydrogen in alkenones, and 65% to 75% of hydrogen in brassicasterol comes from NADPH, with the remainder coming from water (Fig 7A). These estimates are consistent with the assessment by [31] that about 50% of the hydrogen in fatty acids comes from NADPH, and 25% each from water and acetyl-CoA.
Fig 7. Sensitivity of the 2H/1H fractionation factor, α, to intracellular hydrogen source.
The fractionation factor, α, can respond to both (A) f, the fraction of lipid hydrogen derived from NADPH versus intracellular water, and (B) x the fraction of NADPH-derived hydrogen in lipids that comes from photosynthesis as opposed to the OPP pathway. δ2H values of NADPH/PS1 and NADPH/OPP are set at -600‰ and -250‰, respectively. Intracellular water δ2H is set at 0‰. The shaded areas in (A) indicate the range of α values measured for 3 lipid classes (fatty acids, FA-green; alkenones-red; brassicasterol-purple) in our E. huxleyi continuous cultures (Table 3). The slope of the relationship would increase if less than half of the NADPH-derived hydrogen in lipids came from photosynthesis (i.e., x < 0.5 In (B) it is assumed that half of the hydrogen in lipids is from NADPH and half from water (i.e., f = 0.5). A greater fraction of NADPH from photosynthesis (higher x) results in lower α values since photosynthetically produced hydride is 2H -depleted relative to NADPH produced via OPP in the cytosol. In (B) the sensitivity of α to changes in x decreases if either δ2H NADPH/PS1 > -600‰ or δ2H NADPH/OPP < -250‰.
2H-depletion of intracellular water at high growth rates
A second mechanism by which 2H/1H fractionation in lipids could increase with growth rate is a lowering of δ2HH2Oi from more rapid hydrogen exchange between relatively 2H-enriched cell water and relatively 2H-depleted organic hydrogen at higher growth rates. It has been shown that hydrogen from intracellular water is rapidly and extensively exchanged with certain hydrogen atoms in biomolecules, such as those bound to O, P and N [29,30,32]. Even hydrogen atoms that are bound to C can readily exchange in the aqueous medium of the cell when they occur adjacent to certain functional groups, such as ketones and aldehydes, via keto-enol tautomerism. The rates of non-enzymatic hydrogen exchange reactions are often much greater than for enzyme-mediated reactions [30].
In a series of 14C labeling experiments with the green alga Dunaliella tertiolecta, Halsey et al. (2011) showed that the turnover of polysaccharides was eight times faster in cells growing at 1.7 div d-1 than in cells growing at 0.17 div d-1 in the four hours following the introduction of DI14C [61]. This was attributed to rapid catabolism of carbohydrates in the TCA cycle and the OPP pathway in fast-growing cells. Based on these results, and the well-established relationship between metabolic rates and growth rates in plants and animals [62,63] it is reasonable to assume that the metabolic rates in the E. huxleyi cultures co-varied with growth rate.
Whether δ2HH2Oi scales with growth rate will then depend on whether the rate of hydrogen exchange between organic hydrogen and intracellular water scales with the metabolic rate. If so, then fast-growing cells ought to have δ2HH2Oi values that are lower than slow-growing cells as the H-exchange process transfers 2H-depleted hydrogen to the water. Experimental evidence for greater H-exchange at higher growth rates in prokaryotic and mammalian cells was provided by [34,35]. They demonstrated that the fraction of hydrogen in intracellular water that had been metabolically processed was about 50% in E. coli and rat fibroblast cells in the exponential phase of growth as compared to about 25% in cells at the stationary phase of growth [34,35]. Whether photoautotrophic cells such as E. huxleyi exhibit similar rates of H-exchange is unknown.
Any tendency to lower δ2HH2Oi via H-exchange with organic hydrogen would be countered by the 2H-enrichment of cell (specifically, plastidic) water that presumably accompanies water oxidation in PS1 and by the exchange of intra- and extra-cellular water. On the other hand, the exchange of hydrogen between carbohydrates and water enriches the carbohydrate in 2H, which would drive δ2HH2Oi lower. The net effect of H-exchange between organic hydrogen and intracellular water on δ2HH2Oi, and whether a lowering of δ2HH2Oi as growth rate increases is a viable mechanism for decreasing α as growth rate increases remain open questions. Future experiments ought to address these questions by measuring δ2HH2Oi.
Generality of growth rate influence on 2H/1H fractionation
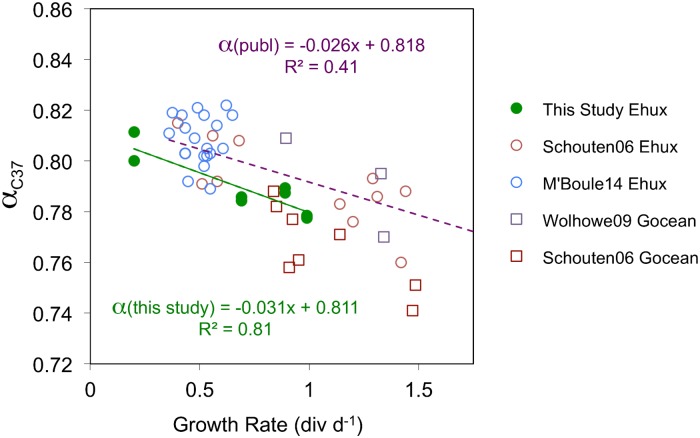
Since the optimal, or “Redfield” ratio of N:P is 16 we assume that all of the cultures grown in N2L media that had N:P ratios of 1 to 1.5 (E. huxleyi 0.2 and 0.69 div d-1), 2.4 (T. pseudonana 0.66 div d-1 [37]) or 5 (T. pseudonana 0.52, 1.41 and 2.07 div d-1) were N-limited and that the cultures grown in NR media that had molar N:P ratios of 24 (E. huxleyi 0.89 and 0.99 div d-1) or 16 (T. pseudonana 2.89 div d-1 [37]) were not N-limited [64,65]. It is possible therefore that growth rate itself, be it modulated by substrate limitation, temperature or salinity, rather than N-limitation, is fundamentally linked to 2H/1H fractionation. Support for this comes from published batch culture experiments in which growth rates of the coccolithophorids E. huxleyi and Gephyrocapsa oceanica were inferred to have changed as salinity and temperature were altered [10,36]. As growth rate increased in their E. huxleyi cultures the 2H/1H fractionation between C37 alkenones and growth water increased by 26‰ (div d-1)-1, within 20% of the increase observed in our E. huxleyi chemostats (31‰ (div d-1)-1) (Fig 8). This suggests that our 3-endmember model of hydrogen isotopes in phytoplankton lipids (Fig 5) and the metabolic differences in E. huxleyi cells at high (Fig 6A) and low (Fig 6B) growth rates may be equally valid whether the growth rate differences are induced by N-limitation, temperature or salinity.
Fig 8. Fractionation factor for C37 alkenones as a function of growth rate in E. huxleyi and G. oceanica cultures.
The presented results are from the following sources: E. huxleyi data: continuous cultures from this study (solid green circles), batch cultures from [10] (open brown circles) and [36] (open blue circles). G. oceanica data: batch cultures from [10] (open brown squares) and [23] (open purple squares). All data are from C37 methyl alkenones. The C37:2 and C37:3 alkenones were measured and plotted separately in this study, whereas they were combined and measured together in [10,23,36].
Growth rate influence on H isotope variations in T. pseudonana lipids
The results of the T. pseudonana chemostat experiments are not as conclusive as those for E. huxleyi owing to the fact that two of the five T. pseudonana chemostats were conducted using a different protocol (see [37]) than the three chemostats conducted as part of this study, apparently resulting in α values some 0.02 to 0.05 higher (Fig 4). Trace metal concentrations in particular were 16 to 44 times higher in the three chemostats conducted for this study than in the two chemostats reported in [37] except for molybdenum which was 25% of the concentration used in the previous study (Table A in S1 Appendix). Additionally, chemostat cultures grown for this study had 10% the EDTA concentration as those in [37]. The very different per cell sterol and C16:0 FA concentrations in the [37] cultures as compared to the three new cultures (Fig 2) is a good indication that the metabolic state of T. pseudonana cells in the two studies was different, irrespective of growth rate. If the lower trace metal concentrations in the earlier study were responsible for their higher α values, one possibility is that a smaller proportion of NADPH from PS1 relative to OPP is available for lipid synthesis when one or more trace metals are limiting.
Notwithstanding these differences in the two studies there appears to be a trend toward lower α values and greater 2H/1H fractionation at higher growth rates in the sterol (24-methyl-cholesta-5,24(28)-dien-3β-ol) (Fig 4), similar to the trend observed in E. huxleyi cultures (Fig 3). As in all E. huxleyi lipids, greater 2H/1H fractionation in the T. pseudonana sterol at higher growth rates can be explained by a proportional increase in the fraction of NADPH derived from PS1 relative to OPP as growth rate increases.
The seemingly anomalous finding is the lack of any clear trend in fatty acid α values as a function of growth rate in either of the two sets of T. pseudonana cultures, supporting the inference from [37] that 2H/1H fractionation in fatty acids from T. pseudonana is insensitive to growth rate (Fig 4). Based on the simple model we have proposed to explain hydrogen isotopic relationships of lipids in phytoplankton and their response to growth rate changes (Eqs 1–5, Fig 5) this lack of sensitivity of α to growth rate could be explained by an increasing fraction of hydrogen in fatty acids derived from (isotopically enriched) intracellular water (f) as growth rate increases that offsets the greater fraction of (isotopically depleted) NADPH from photosynthesis (x) that the model assumes. Evidence in support of this possibility comes from the overall decrease in cellular metabolism when T. pseudonana is deprived of nitrogen [59] coupled with the observations by [34,35] that the flux of hydrogen between intracellular water and metabolites is greater in exponentially growing cells than in stationary cells.
At this point it can be concluded that the mechanism put forth to explain increasing 2H/1H fractionation at higher growth rates in the T. pseudonana sterol by [37] is unlikely to be correct. They attributed greater fractionation at higher growth rates to the transfer of 2H-depleted isopentenyl diphosphate (IPP) from the plastid (where it is synthesized in the 1-deoxyxylulose 5-phosphate/2-C- methyl-D-erythritol 4-phospate (DOXP/MEP) pathway) to the cytosol to feed into the acetate mevalonic acid (MVA) pathway of sterol synthesis. This no longer seems viable because the sterol in T. pseudonana responds just like the fatty acids, alkenones and sterol in E. huxleyi, with a decrease in α as growth rate increases (Fig 3), and IPP is not involved in acetogenic lipid synthesis.
Implications for paleoclimate reconstructions
Owing to their source specificity and excellent preservation in the geologic record alkenone δ2H values are increasingly being used to reconstruct hydrologic conditions in paleoclimatology [8,14–16,19,20]. Our observation that δ2H values of alkenones decrease by approximately 30‰ (div d-1)-1 has the potential to complicate their interpretation as hydroclimate indicators. Relatively small growth rate changes of 0.1 to 0.2 div d-1 would be expected to cause alkenone δ2H differences of 3‰ to 6‰, which is approximately the analytical precision of the analysis. Larger (alkenone-producing) coccolithophorid growth-rate differences, either at one location over time, between locations, or between a location and the calibration set have the potential to influence results, especially if the differences are systematic.
For example, within the euphotic zone of the subpolar North Pacific Ocean the growth rate of alkenone-producing coccolithophorids varied between 0.9 div d-1 at 10 m and 0.1 div d-1 at 70 m in [66]. Most of that decline was attributed to decreasing light intensity [66]. If growth rate controlled by light affects 2H/1H fractionation in phytoplankton the same way other growth parameters do (e.g., N-limitation, temperature and salinity), alkenones produced at 10 m should have had a δ2H value about 25‰ less than those produced at 70 m. For comparison, that would be the same signal that would be expected from a 10 to 20 ppt change in salinity [22,36]. Thus, if alkenone δ2H values were used to reconstruct salinity changes from a sediment core at the subpolar location in [66] there could be as much as a 10–20 ppt uncertainty in reconstructed salinity depending on the depth at which the alkenones in the sediment were initially synthesized.
No influence of growth rate on alkenone unsaturation ratios
The relative abundances of the di- and tri-unsaturated C37 methyl alkenones, the Uk’ 37 ratio [67], showed no systematic change as a function of growth rate (Table 2). This result adds to the substantial body of literature supporting the robustness of the alkenone thermometer under a very wide range of environmental conditions [68–73]. On the other hand, [23] reported that batch cultures of both G. oceanica and E. huxleyi had systematically lower Uk’ 37 values at the stationary phase and “late-log” phase of growth compared to the exponential and “mid-log” phase of growth. Our continuous culture results do not conflict with those results as the growth phase under the two types of culture systems are distinctly different, with cells in the chemostats undergoing perpetual exponential growth. Nevertheless, the comparison does support the inference that the growth phase of cells that produce the alkenones ultimately buried in sediments could influence their Uk’ 37 value, independent of temperature. The use of core-top calibrations of the alkenone thermometer (e.g., [70]), rather than those from culture or suspended particles, ought to mitigate this effect. The fact that global core-top calibrations are virtually identical to those from culture (compare [70] to [42]) further implies that the effect of growth phase on Uk’ 37 is likely to be small compared to that of temperature.
Conclusion
Continuous culture experiments with the coccolithophorid Emiliania huxleyi revealed that hydrogen isotope fractionation in both isoprenoid and acetogenic lipids increases as growth rate increases. δ2H values decreased by 24 to 38‰ (div d-1)-1 in di-and tri-unsaturated C37 and C38 alkenones, 44‰ (div d-1)-1 in brassicasterol, and 32 to 79‰ (div d-1)-1 in myristic acid (C14:0), palmitic (C16:0), and stearic acid (C18:0). A simple 3-endmember mixing model in which hydrogen in lipids comes from NADPH produced in Photosystem 1 of photosynthesis with α ~ 0.4, NADPH produced by the cytosolic oxidative pentose phosphate pathway with α ~ 0.75, and intracellular water with α ~ 0 is used to explain these results. We propose that the fraction of NADPH from PS1 increases as growth rate increases, resulting in a lowering of α. Support for this mechanism comes from transcriptomic studies in which genes associated with photosynthesis and carbon fixation are down-regulated while those associated with OPP are up-regulated in N-limited cells. We hypothesize that the resulting constellation of metabolic changes causes a shift in the proportion of NADPH derived from PS1 and the OPP pathway, such that relatively less 2H-depleted NADPH from OPP is produced at the expense of more highly 2H-depleted NADPH from PS1 as N-limited growth rate decreases. The model can also account for the observations that isoprenoid lipids are depleted in 2H relative to acetogenic lipids and the δ2H values of lipids are lower than those of proteins and carbohydrates if the fraction of hydrogen from intracellular relative to NADPH is greater in acetogenic lipids, proteins and carbohydrates.
While the model successfully explains the increase in 2H/1H fractionation in the sterol 24-methyl-cholesta-5,24(28)-dien-3β-ol from T. pseudonana chemostat cultures as growth rate increases, an additional process must be invoked to explain the lack of sensitivity of 2H/1H fractionation in fatty acids to growth rate. An increase in the fraction of hydrogen in fatty acids that is derived from intracellular water at the expense of NADPH as growth rate increases is one possibility.
The ~30‰ decrease in the δ2H value of alkenones per unit (div d-1) increase of growth in our E. huxleyi chemostats is in line with published batch culture experiments showing a similar magnitude response. This needs to be considered when applying δ2H measurements of sedimentary alkenones in paleoclimate studies since any change in growth rate larger than about 0.15 div d-1 would cause a change in δ2Hlipid larger than the analytical error of the measurement, about 5‰.
Supporting Information
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Acknowledgments
We are grateful to Jeff Bowman, Amy Cash and Brittany Demianew for assisting with the culture experiments. Conversations with Ginger Armbrust and Ashley Maloney, Adrian Marchetti, and Josh Gregersen improved this manuscript. We are grateful to the editor and two anonymous reviewers whose comments helped to improve this manuscript.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This material is based upon work supported by the National Science Foundation under Grant No. OCE-1027079.
References
- 1. Urey HC, Brickwedde FG, Murphy GM (1932) A Hydrogen Isotope of mass 2 and its concentration. Physical Review 40: 1–15. [Google Scholar]
- 2. Westheimer FH (1961) The magnitude of the primary kinetic isotope effect for compounds of hydrogen and deuterium. Chemical Reviews 61: 265–273. [Google Scholar]
- 3. Northrop DB (1975) Steady-state analysis of kinetic isotope effects in enzymic reactions. Biochemistry 14: 2644–2651. [DOI] [PubMed] [Google Scholar]
- 4. Sessions AL, Burgoyne TW, Schimmelmann A, Hayes JM (1999) Fractionation of hydrogen isotopes in lipid biosynthesis. Organic Geochemistry 30: 1193–1200. [Google Scholar]
- 5. Hilkert AW, Douthitt CB, Schlüter HJ, Brand WA (1999) Isotope Ratio Monitoring Gas Chromatography/Mass Spectrometry of D/H by High Temperature Conversion Isotope Ratio Mass Spectrometry. Rapid Communications in Mass Spectrometry 13: 1226–1230. [DOI] [PubMed] [Google Scholar]
- 6. Sessions AL, Burgoyne TW, Hayes JM (2001) Determination of the H-3 factor in hydrogen isotope ratio monitoring mass spectrometry. Analytical Chemistry 73: 200–207. [DOI] [PubMed] [Google Scholar]
- 7. Sauer PE, Eglington TI, Hayes JM, Schimmelman A, Sessions AL (2001) Compound-specific D/H ratios of lipid biomarkers from sediments as a proxy for environmental and climatic conditions. Geochimica et Cosmochimica Acta 65: 213–222. [Google Scholar]
- 8. Englebrecht AC, Sachs JP (2005) Determination of sediment provenance at drift sites using hydrogen isotopes and unsaturation ratios in alkenones. Geochimica et Cosmochimica Acta 69: 4253–4265. [Google Scholar]
- 9. Zhang Z, Sachs JP (2007) Hydrogen isotope fractionation in freshwater algae: I. Variations among lipids and species. Organic Geochemistry 38: 582–608. [Google Scholar]
- 10. Schouten S, Ossebaar J, Schreiber K, Kienhuis MVM, Langer G, et al. (2006) The effect of temperature, salinity and growth rate on the stable hydrogen isotopic composition of long chain alkenones produced by Emiliania huxleyi and Gephyrocapsa oceanica . Biogeosciences 3: 113–119. [Google Scholar]
- 11. Craig H (1961) Isotopic variations in meteoric waters. Science 133: 1702–1703. [DOI] [PubMed] [Google Scholar]
- 12. Craig H, Gordon LI (1965) Deuterium and oxygen 18 variations in the ocean and the marine atmosphere In: Tongiorgi E, editor. Stable Isotopes in Oceanographic Studies and Paleotemperatures. Pisa: V. Lischi; pp. 9–130. [Google Scholar]
- 13. Gat JR (1996) Oxygen and hydrogen isotopes in the hydrologic cycle. Annual Reviews of Earth and Planetary Sciences 24: 225–262. [Google Scholar]
- 14. van der Meer MTJ, Baas M, Rijpstra WIC, Marino G, Rohling EJ, et al. (2007) Hydrogen isotopic compositions of long-chain alkenones record freshwater flooding of the Eastern Mediterranean at the onset of sapropel deposition. Earth and Planetary Science Letters 262: 594–600. [Google Scholar]
- 15. van der Meer MTJ, Sangiorgi F, Baas M, Brinkhuis H, Sinninghe DamstÈ JS, et al. (2008) Molecular isotopic and dinoflagellate evidence for Late Holocene freshening of the Black Sea. Earth and Planetary Science Letters 267: 426–434. [Google Scholar]
- 16. Pahnke K, Sachs JP, Keigwin LD, Timmermann A, Xie S-P (2007) Eastern tropical Pacific hydrologic changes during the past 27,000 years from D/H ratios in alkenones. Paleoceanography 22: PA4214. [Google Scholar]
- 17. Sachs JP, Sachse D, Smittenberg RH, Zhang Z, Battisti DS, et al. (2009) Southward movement of the Pacific intertropical convergence zone AD 1400–1850. Nature Geoscience 2: 519–525. [Google Scholar]
- 18. Smittenberg RH, Saenger C, Dawson MN, Sachs JP (2011) Compound-specific D/H ratios of the marine lakes of Palau as proxies for West Pacific Warm Pool hydrologic variability. Quaternary Science Reviews 30: 921–933. [Google Scholar]
- 19. Leduc G, Sachs JP, Kawka OE, Schneider RR (2013) Holocene changes in eastern equatorial Atlantic salinity as estimated by water isotopologues. Earth and Planetary Science Letters 362: 151–162. [Google Scholar]
- 20. Vasiliev I, Reichart G-J, Krijgsman W (2013) Impact of the Messinian Salinity Crisis on Black Sea hydrology—Insights from hydrogen isotopes analysis on biomarkers. Earth and Planetary Science Letters 362: 272–282. [Google Scholar]
- 21. Estep MF, Hoering TC (1980) Biogeochemistry of the stable hydrogen isotopes. Geochimica et Cosmochimica Acta 44: 1197–1206. [Google Scholar]
- 22. Chivall D, M’Boule D, Sinke-Schoen D, Sinninghe Damsté JS, Schouten S, et al. (2014) The effects of growth phase and salinity on the hydrogen isotopic composition of alkenones produced by coastal haptophyte algae. Geochimica et Cosmochimica Acta 140: 381–390. [Google Scholar]
- 23. Wolhowe M, Prahl F, Probert I, Maldonado M (2009) Growth phase dependent hydrogen isotopic fractionation in alkenone-producing haptophytes. Biogeosciences 6: 4165–4200. [Google Scholar]
- 24. Sachse D, Sachs JP (2008) Inverse relationship between D/H fractionation in cyanobacterial lipids and salinity in Christmas Island saline ponds. Geochimica et Cosmochimica Acta 72: 793–806. [Google Scholar]
- 25. Sachs JP, Schwab VF (2011) Hydrogen isotopes in dinosterol from the Chesapeake Bay estuary. Geochimica et Cosmochimica Acta 75: 444–459. [Google Scholar]
- 26. Nelson DB, Sachs JP (2014) The influence of salinity on D/H fractionation in alkenones from saline and hypersaline lakes in continental North America. Organic Geochemistry 66: 38–47. [Google Scholar]
- 27. Nelson DB, Sachs JP (2014) The influence of salinity on D/H fractionation in dinosterol and brassicasterol from globally distributed saline and hypersaline lakes. Geochimica et Cosmochimica Acta 133: 325–339. [Google Scholar]
- 28. Estep MF, Hoering TC (1981) Stable hydrogen isotope fractionations during autotrophic and mixotrophic growth of microalgae. Plant Physiology 67: 474–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Schmidt HL, Werner RA, Eisenreich W (2003) Systematics of 2H patterns in natural compounds and its importance for the elucidation of biosynthetic pathways. Phytochemistry Reviews 2: 61–85. [Google Scholar]
- 30. García-Martín ML, Paloma B, Cerdán S (2001) The metabolism of water in cells and tissues as detected by NMR methods. Progress in Nuclear Magnetic Resonance Spectroscopy 39: 41–77. [Google Scholar]
- 31. Zhang X, Gillespie AL, Sessions AL (2009) Large D/H variations in bacterial lipids reflect central metabolic pathways. Proceedings of the National Academy of Sciences 106: 12580–12586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Yakir D, DeNiro MJ (1990) Oxygen and Hydrogen Isotope Fractionation during Cellulose Metabolism in Lemna gibba L. Plant Physiology 93: 325–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Hayes JM (2001) Fractionation of carbon and hydrogen isotopes in biosynthetic processes. Stable Isotope Geochemistry 43: 225–277. [Google Scholar]
- 34. Kreuzer HW, Quaroni L, Podlesak DW, Zlateva T, Bollinger N, et al. (2012) Detection of Metabolic Fluxes of O and H Atoms into Intracellular Water in Mammalian Cells. PLoS One 7: e39685 10.1371/journal.pone.0039685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Kreuzer-Martin HW, Lott MJ, Ehleringer JR, Hegg EL (2006) Metabolic processes account for the majority of the intracellular water in log-phase Escherichia coli cells as revealed by hydrogen isotopes. Biochemistry 45: 13622–13630. [DOI] [PubMed] [Google Scholar]
- 36. M’boule D, Chivall D, Sinke-Schoen D, Sinninghe Damsté JS, Schouten S, et al. (2014) Salinity dependent hydrogen isotope fractionation in alkenones produced by coastal and open ocean haptophyte algae. Geochimica et Cosmochimica Acta 130: 126–135. [Google Scholar]
- 37. Zhang Z, Sachs JP, Marchetti A (2009) Hydrogen isotope fractionation in freshwater and marine algae: II. Temperature and nitrogen limited growth rate effects. Organic Geochemistry 40: 428–439. [Google Scholar]
- 38. Guillard RRL (1975) Culture of Phytoplankton for Feeding Marine Invertebrates In: Smith WL, Chanley MH, editors. Culture of Marine Invertebrate Animals. New York: Plenum Publishing Corporation; pp. 29–60. [Google Scholar]
- 39. Guillard RRL, Ryther JH (1962) Studies of marine planktonic diatoms: I. Cyclotella nana hustedt, and Detonula confervacea (cleve) gran. Canadian Journal of Microbiology 8: 229–239. [DOI] [PubMed] [Google Scholar]
- 40. Clementson LA, Wayte SE (1992) The effect of frozen storage of open-ocean seawater samples on the concentration of dissolved phosphate and nitrate. Water Research 26: 1171–1176. [Google Scholar]
- 41. Schwab VF, Sachs JP (2009) The measurement of D/H ratio in alkenones and their isotopic heterogeneity. Organic Geochemistry 40: 111–118. [Google Scholar]
- 42. Prahl FG, Muehlhausen LA, Zahnle DL (1988) Further evaluation of long-chain alkenones as indicators of paleoceanographic conditions. Geochimica et Cosmochimica Acta 52: 2303–2310. [Google Scholar]
- 43. Spoehr H, Milner HW (1949) The chemical composition of Chlorella; effect of environmental conditions. Plant physiology 24: 120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Collyer DM, Fogg GE (1955) Studies on fat accumulation by algae. Journal of Experimental Botany 6: 256–275. [Google Scholar]
- 45. Shifrin NS, Chisholm SW (1981) Phytoplankton lipids: interspecific differences and effects of nitrate, silicate and light‐dark cycles. Journal of Phycology 17: 374–384. [Google Scholar]
- 46. Rodolfi L, Chini Zittelli G, Bassi N, Padovani G, Biondi N, et al. (2009) Microalgae for oil: Strain selection, induction of lipid synthesis and outdoor mass cultivation in a low-cost photobioreactor. Biotechnology and Bioengineering 102: 100–112. 10.1002/bit.22033 [DOI] [PubMed] [Google Scholar]
- 47. Livne A, Sukenik A (1992) Lipid synthesis and abundance of acetyl CoA carboxylase in Isochrysis galbana (Prymnesiophyceae) following nitrogen starvation. Plant and cell physiology 33: 1175–1181. [Google Scholar]
- 48. Prahl FG, Sparrow MA, Wolfe GV (2003) Physiological impacts on alkenone paleothermometry. Paleoceanography 18: 1025. [Google Scholar]
- 49. Eltgroth ML, Watwood RL, Wolfe GV (2005) Production and cellular localization of neutral long-chain lipids in the haptophyte algae Isochrysis galbana and Emiliania huxleyi . Journal of Phycology 41: 1000–1009. [Google Scholar]
- 50. Conte MH, Thompson A, Lesley D, Harris RP (1998) Genetic and physiological influences on the alkenone/alkenoate versus growth temperature relationship in Emiliania huxleyi and Gephyrocapsa oceanica . Geochimica et Cosmochimica 62: 51–64. [Google Scholar]
- 51. Epstein BL, D'Hondt S, Quinn JG, Zhang J, Hargraves PE (1998) An effect of dissolved nutrient concentrations on alkenone-based temperature estimates. Paleoceanography 13: 122–126. [Google Scholar]
- 52. Chivall D, M’Boule D, Sinke-Schoen D, Sinninghe Damsté JS, Schouten S, et al. (2014) Impact of salinity and growth phase on alkenone distributions in coastal haptophytes. Organic Geochemistry 67: 31–34. [Google Scholar]
- 53. Luo Y-H, Steinberg L, Suda S, Kumazawa S, Mitsui A (1991) Extremely Low D/H Ratios of Photoproduced Hydrogen by Cyanobacteria. Plant Cell Physiol 32: 897–900. [Google Scholar]
- 54. Dirghangi SS, Pagani M (2013) Hydrogen isotope fractionation during lipid biosynthesis by Tetrahymena thermophila. Organic Geochemistry 64: 105–111. [Google Scholar]
- 55. Dirghangi SS, Pagani M (2013) Hydrogen isotope fractionation during lipid biosynthesis by Haloarcula marismortui . Geochimica et Cosmochimica Acta 119: 381–390. [Google Scholar]
- 56. Simon H, Kraus A (1976) Hydrogen isotope transfer in biological processes In: Buncel E, Lee CC, editors. Isotopes in organic chemistry vol 2. Amsterdam: Elsevier Science Publishers B.V; pp. 153–229. [Google Scholar]
- 57. Hockin NL, Mock T, Mulholland F, Kopriva S, Malin G (2012) The response of diatom central carbon metabolism to nitrogen starvation is different from that of green algae and higher plants. Plant physiology 158: 299–312. 10.1104/pp.111.184333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Tolonen AC, Aach J, Lindell D, Johnson ZI, Rector T, et al. (2006) Global gene expression of Prochlorococcus ecotypes in response to changes in nitrogen availability. Molecular systems biology 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Bender SJ, Durkin CA, Berthiaume CT, Morales RL, Armbrust EV (2014) Transcriptional responses of three model diatoms to nitrate limitation of growth. Frontiers in Marine Science 1. [Google Scholar]
- 60. Rokitta SD, Von Dassow P, Rost B, John U (2014) Emiliania huxleyi endures N-limitation with an efficient metabolic budgeting and effective ATP synthesis. BMC genomics 15: 1051 10.1186/1471-2164-15-1051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Halsey KH, Milligan AJ, Behrenfeld MJ (2011) Linking time‐dependent carbon‐fixation efficiencies in Dunaliella tertiolecta (chlorophyceae) to underlying metabolic pathways. Journal of Phycology 47: 66–76. [DOI] [PubMed] [Google Scholar]
- 62. Kleiber M (1975) The fire of life. New York: Robert E. Kreiger. [Google Scholar]
- 63. Niklas KJ, Enquist BJ (2001) Invariant scaling relationships for interspecific plant biomass production rates and body size. Proceedings of the National Academy of Sciences 98: 2922–2927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Redfield AC, Ketchum BH, Richards FA (1963) The influence of organisms on the composition of sea-water In: Hill MN, editor. The Sea. New York: Interscience; pp. 26–77. [Google Scholar]
- 65. Goldman JC, McCarthy JJ, Peavey DG (1979) Growth rate influence on the chemical composition of phytoplankton in oceanic waters. Nature 279: 210–215. [Google Scholar]
- 66. Popp BN, Bidigare RR, Deschenes B, Laws EA, Prahl FG, et al. (2006) A new method for estimating growth rates of alkenone-producing haptophytes. Limnology and Oceanography: Methods 4: 114–129. [Google Scholar]
- 67. Prahl FG, Wakeham SG (1987) Calibration of unsaturation patterns in long-chain ketone compositions for palaeotemperature assessment. Nature 330: 367–369. [Google Scholar]
- 68. Herbert TD (2001) Review of alkenone calibrations (culture, water column, and sediments). Geochemistry Geophysics Geosystems 2: 2000GC000055. [Google Scholar]
- 69. Sachs JP, Schneider RR, Eglinton TI, Freeman KH, Ganssen G, et al. (2000) Alkenones as paleoceanographic proxies. Geochemistry, Geophysics and Geosystems 1: 1035. [Google Scholar]
- 70. Müller PJ, Kirst G, Ruhland G, Storch IV, Rosell-Mele A (1998) Calibration of the Alkenone paleotemperature index Uk'37 based on core-tops from the eastern South Atlantic and the global ocean (60°N-60°S). Geochimica et Cosmochimica Acta 62: 1757–1772. [Google Scholar]
- 71. Rosell-Melé A, Prahl FG (2013) Seasonality of temperature estimates as inferred from sediment trap data. Quaternary Science Reviews 72: 128–136. [Google Scholar]
- 72. Prahl F, Popp B, Karl D, Sparrow M (2005) Ecology and biogeochemistry of alkenone production at Station ALOHA. Deep Sea Research Part I: Oceanographic Research Papers 52: 699–719. [Google Scholar]
- 73. Conte MH, Sicre M-A, Rühlemann C, Weber JC, Schulte S, et al. (2006) Global temperature calibration of the alkenone unsaturation index (UK′37) in surface waters and comparison with surface sediments. Geochemistry, Geophysics, Geosystems 7: Q02005. [Google Scholar]
- 74. Rokitta SD, John U, Rost B (2012) Ocean Acidification Affects Redox-Balance and Ion-Homeostasis in the Life-Cycle Stages of Emiliania huxleyi . PLoS ONE 7: e52212 10.1371/journal.pone.0052212 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.