Abstract
There is increasing recognition that genetic diversity can affect the spread of diseases, potentially affecting plant and livestock disease control as well as the emergence of human disease outbreaks. Nevertheless, even though computational tools can guide the control of infectious diseases, few epidemiological models can simultaneously accommodate the inherent individual heterogeneity in multiple infectious disease traits influencing disease transmission, such as the frequently modeled propensity to become infected and infectivity, which describes the host ability to transmit the infection to susceptible individuals. Furthermore, current quantitative genetic models fail to fully capture the heritable variation in host infectivity, mainly because they cannot accommodate the nonlinear infection dynamics underlying epidemiological data. We present in this article a novel statistical model and an inference method to estimate genetic parameters associated with both host susceptibility and infectivity. Our methodology combines quantitative genetic models of social interactions with stochastic processes to model the random, nonlinear, and dynamic nature of infections and uses adaptive Bayesian computational techniques to estimate the model parameters. Results using simulated epidemic data show that our model can accurately estimate heritabilities and genetic risks not only of susceptibility but also of infectivity, therefore exploring a trait whose heritable variation is currently ignored in disease genetics and can greatly influence the spread of infectious diseases. Our proposed methodology offers potential impacts in areas such as livestock disease control through selective breeding and also in predicting and controlling the emergence of disease outbreaks in human populations.
Keywords: quantitative genetics, complex traits, disease resistance, Bayesian statistics, infectivity
INFECTIOUS disease constitutes a ubiquitous threat to plants, livestock, and human populations. Apart from its obvious impact on health and welfare of affected species and its associated production losses, infectious disease in plants and livestock also jeopardizes human food security and international trade. Despite substantial advances in disease diagnostics and medical interventions over recent years, the need for effective prevention strategies continues to exist.
There is increasing recognition that host genetics play an important role in the spread of infections within and between populations (Springbett et al. 2003; O’Brien and Nelson 2004; Lively 2010) and that genetic disease control strategies may offer a viable complement to epidemiological interventions. Compared to most epidemiological interventions, genetic control strategies are long-term, proactive (rather than reactive), and less likely to cause undesirable side effects such as environmental spillover or emergence of highly virulent or antimicrobial resistant pathogen strains (Gibson and Bishop 2005; Kemper et al. 2013). Their potential benefits are enhanced through the advent of high-throughput genomics, which in principle allows identification of individuals with high genetic risk purely based on their genetic material without ever needing to expose them to infectious pathogens. It is therefore not surprising that genetic improvement of disease resistance has become a prime target in livestock and plant genomics (Bishop and Woolliams 2014; Brooks-Pollock et al. 2015) and that prediction of genetic disease risk has become the focus of human genome projects (Chapman and Hill 2012). Nevertheless, theoretical evidence strongly indicates that existing genetic analyses tools, which focus almost exclusively on host resistance, capture only a fraction of the genetic variation inherent in epidemiological data (Bishop et al. 2012; Lipschutz-Powell et al. 2012a; Bishop and Woolliams 2014).
Epidemiological theory points to two key host traits affecting the spread of infectious diseases: host susceptibility, i.e., the propensity to become infected upon contact with infectious material, and host infectiousness, i.e., an individual’s ability to transmit the infection (Lipschutz-Powell et al. 2014). The latter is composed of three traits under potential genetic control: contact rate, duration of infectious period, and infectivity, i.e., the ability to transmit infection per unit contact (Lloyd-Smith et al. 2006). Genetic-epidemiological models reveal that genetic heterogeneity in either trait can profoundly affect disease spread in populations (Nath et al. 2008; Doeschl-Wilson et al. 2011) and that a priori identification of highly susceptible or infectious individuals, e.g., by their genetic makeup, would constitute powerful means to prevent future disease outbreaks (Lloyd-Smith et al. 2005; Matthews et al. 2006). Using epidemiological tracing data, Lloyd-Smith et al. (2005) established a link between recent large-scale outbreaks and the presence of superspreaders characterized by a small proportion of highly infectious individuals, thus providing evidence for phenotypic, although not genetic, variation in infectiousness.
To date it is not known to what extent superspreading is genetically determined as genetic parameters for infectiousness cannot be accurately estimated with existing quantitative genetic models (Lipschutz-Powell et al. 2012a,b, 2014). In particular, infectivity is a trait expressed through social interactions, as it affects the disease phenotype of group members rather than that of the host expressing it. If subject to heritable variation, infectivity can be defined as an indirect genetic effect (IGE), also known as an associative or a social genetic effect (Griffing 1967). Similarly, as susceptible individuals are more likely to become infected and thus also to transmit infection relative to resistant individuals that do not become infected in the first place, an individual’s susceptibility can be considered as an IGE, as recently demonstrated by Anche et al. (2014). As such, quantitative genetic models that account for IGEs may be used to estimate genetic effects for either trait.
Although standard IGE models seem suitable to simultaneously evaluate whether susceptibility and infectivity are under genetic control, Lipschutz-Powell et al. (2014) showed that they underestimate infectivity genetic variances and therefore cannot fully capture the whole genetic variation underlying this trait: IGE models consider a linear relationship between the phenotype and its direct and indirect genetic effects and also assume that the phenotype of an individual is affected by the IGE of all the individual’s group members (Bijma et al. 2007a). However, the binary disease status (healthy/diseased) of an individual undergoing an epidemic is a function of the interaction of its susceptibility and the time-varying infection pressure exerted by the infected individuals (Keeling and Rohani 2008). Hence, the linearity and static nature of current IGE models are unrealistic assumptions when dealing with the stochastic nonlinear dynamics underlying disease transmission. Building upon these concepts of nonlinear disease dynamics, Lipschutz-Powell et al. (2014) developed a genetic-epidemiological link function that links the binary disease phenotype to underlying susceptibility and infectivity. However, using this link function for statistical inference has proved difficult (Doeschl-Wilson et al. 2014).
Due to the demand for large sample sizes that are characteristic of quantitative genetic studies and often expensive labor-intensive and inaccurate diagnostics, epidemiological data usually come in binary form (healthy/diseased), measured either once or several times throughout a fixed observation period. Thus, genetic parameter estimates for host susceptibility and infectivity would need to be inferred in the absence of information of exact infection time or individual infection status. Hierarchical Bayesian models have proved to be a powerful approach for dealing with missing information and for accommodating different layers of variation inherent in data (Lindley and Smith 1972; Gianola and Fernando 1986), and the development of Bayesian models together with related computational algorithms to analyze epidemiological data has gained momentum over the recent years (O’Neill and Roberts 1999; Dukic et al. 2012; Elderd et al. 2013; Brooks-Pollock et al. 2014; O’Hare et al. 2014). However, very few Bayesian models for epidemiological data incorporate genetic information.
We develop in this article the first statistical model and its Bayesian inferential method to accurately estimate host infectivity and susceptibility genetic parameters from incomplete epidemiological data, under the assumption that both traits are under polygenic control. The proposed model, hereafter denoted the dynamic nonlinear indirect genetic effects (dnIGE) model, takes into account the nonlinear dynamic interactions between susceptibility and infectivity and combines quantitative genetic IGE models with key epidemiological principles. For efficient estimation of the high-dimensional vector of the dnIGE model parameters, an adaptive MCMC algorithm is developed. Using data from simulated livestock epidemics, we demonstrate that the proposed dnIGE model provides accurate heritability estimates and predictions of genetic risk for both susceptibility and infectivity for a range of scenarios that are realistic for livestock populations, even when infection times are not accurately known. Additionally, we demonstrate that the dnIGE model can improve prediction of susceptibility genetic risks when compared to the same predictions provided by models that do not account for genetic variation in infectivity. Guidelines for data requirements and future applications are also provided.
Materials and Methods
Data structure, definitions, and assumptions
The dnIGE model applies to infectious diseases that spread by susceptible individuals becoming infected after an effective contact, which is the contact with infectious individuals or infectious material shed by the infected individuals, resulting in disease transmission. For simplicity of model development, it is assumed at first that individuals can be immediately diagnosed as infected upon infection and also that they become immediately infectious upon infection with no latency period and remain infected throughout the epidemic. These are the assumptions of the so-called susceptible-infective (SI) epidemiological models (Keeling and Rohani 2008). Extensions of the methodology to other epidemic scenarios are discussed later.
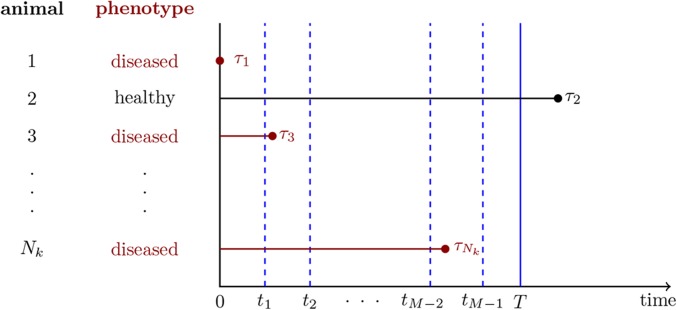
The proposed statistical model is fitted to infectious disease data from P closed groups in which individuals are allocated, We assume that the epidemics in all closed groups are observed within a fixed interval where time 0 is the start of the observation period and T is the final observation time. The observed epidemics in each group can be triggered in natural outbreaks by individuals that were infected before the start of the observation period or, in the case of experimental infections in individuals, by the introduction of artificially infected individuals in each group at time We define these individuals as index cases. Let be the infection time and the index case indicator of individual j, with and if j is an index case and and otherwise, Note that the infection time of an infected individual j can be observed only if For model development, it is assumed that disease status can be periodically recorded at times where M is the number of sampling times. A diagram with the structure of the infection data considered to develop the dnIGE model is shown in Figure 1 for one of the closed groups.
Figure 1.
Structure of the infection data considered to develop the proposed dnIGE model. Individual 1 is an index case, as Individual 2 is not observed as infected during the observation time, since Also, individual 3 is infected (diseased) at time between sampling times and while the infection time of individual is between sampling times and When the infection times cannot be exactly recorded, the model parameters can be estimated by using the disease status (healthy/diseased) recorded at each of the sampling times
Initially, we derive the method assuming that all infection times are exactly known, given by where I is the number of infecteds during in the population. After deriving the dnIGE model for known infection times, we extend it for the case where the individual disease states are observed only at sampling times
Modeling the infection events accounting for genetic heterogeneity in host susceptibility and infectivity: the dnIGE model
Suppose that, at any time, all susceptibles can have effective contacts with infectious individuals in the same group, where effective contacts are defined by contacts resulting in disease transmission. Assuming a homogeneous population, the number of effective contacts between a susceptible and an infectious individual can be modeled by a Poisson process with effective contact rate β. This effective contact rate is a transmission parameter, which combines several factors that affect disease transmission and represents the etiology of the infection process (Anderson and May 1991). The total number of effective contacts of a susceptible individual j with I infectious individuals is then the sum of individual Poisson processes with pairwise rate β, which is also a Poisson process with rate (Ross 1996).
To account for individual heterogeneity in the infection process due to differences in susceptibility and infectivity, we consider these traits as individual deviations from the (average) pairwise effective contact rate β. In other words, the effective contact rate between a susceptible individual j and an infectious individual m is represented by Furthermore, defining as the group number of individual j, with the time-varying infection rate of individual j, is
| (1) |
where represents the set of all group mates of j and if and 0 otherwise. Therefore, the time-varying infection rate of a susceptible individual is a function not only of the (population-level) transmission parameter β but also of its susceptibility and the infectivity of its previously infected group mates.
In homogeneous populations, if setting and to unity, in (1) represents the density-dependent force of infection (Keeling and Rohani 2008), which is the rate at which individuals get infected during an epidemic. The dnIGE model assumes that the time-varying infection rate defined in (1) is conditional on random frailty terms (Aalen et al. 2008) and which capture unobserved heterogeneity in host (relative) susceptibility and host (relative) infectivity, respectively. These frailty terms represent deviations from the population parameter β, therefore accounting for individual variation in the infection process. Hence, can be viewed as the individual force of infection at time t, and it captures individual heterogeneity, population-mean effects, and the nonlinear transmission dynamics of the infection process. The individual force of infection was also mathematically derived from first principles assuming binary disease phenotypes (healthy/diseased) in Lipschutz-Powell et al. (2014), where susceptibility and infectivity were represented as probabilities.
To decompose the individual force of infection into genetic and nongenetic components, variance component structures were assumed for and as follows. The susceptibility of an individual j was modeled as
| (2) |
where is the additive genetic effect for susceptibility of individual j and is its susceptibility environmental effect. Note that average susceptibility effects are captured by the population-level effective contact rate β in Equation 1. Since infected index cases do not express susceptibility within the observation period, Equations 1 and 2 are considered for every j such that Therefore, assuming index cases, the vector of dimension represents susceptibility additive genetic effects, with where is the relationship matrix excluding rows and columns related to index cases. Also, is a vector of dimension of susceptibility environmental effects, with where is an identity matrix of dimension
Similarly, a variance component model for the infectivity of an infected individual j was defined as
| (3) |
where is the infectivity additive genetic effect of j and is its infectivity environmental effect. Equation 3 is defined for each j who can express infectivity, and this is the case if there are remaining susceptibles in group after its infection. Defining as the number of individuals who can express infectivity in the population, represents the -dimensional vector of infectivity additive genetic effects such that and is the relationship matrix excluding rows and columns related to individuals who cannot express infectivity. Additionally, represents the -dimensional vector of infectivity environmental effects with where is an identity matrix of dimension Note that the assumption of normal distribution for the infectivity variance components implies that has a log-normal distribution, which can have a skewed shape and therefore can account for the observed occurrence of superspreaders (Lloyd-Smith et al. 2005).
Within this framework, the individual force of infection of the dnIGE model is equivalent to a hazard function (also called force of mortality in survival analysis) when accounting for unobserved heterogeneity using frailty terms. These frailty terms represent susceptibility and infectivity effects that can be captured from the data. In addition, β is the constant baseline hazard function, which can be viewed as a population mean effective contact rate. A particular case of the dnIGE model was presented in Korsgaard et al. (1998), who assumed a variance component structure for the log-normal frailty that can be related to susceptibility. The dnIGE model also extends the mixed survival model described in Ducrocq and Casella (1996) to estimate genetic parameters of time-to-event traits, where only one frailty term was considered.
Estimating the dnIGE model parameters using infection data
Likelihood function of the dnIGE model:
For a population where I individuals were recorded as infected within the observation period the likelihood of the dnIGE model defined in Equations 1–3 is a product of the probability of observing the infection times of the nonindex cases and the probability of not observing infections in the remaining susceptibles in the population, where the number of effective contacts of each individual follows a Poisson process.
Derivation of the likelihood function for individual-level Poisson processes in the context of infectious diseases can be found in Brown et al. (2014), and the main idea is as follows: a nonindex case individual j, if infected at contributes to the likelihood as the product of the probability of not observing infection up to (its actual time of infection) and the probability of observing an infection at On the other hand, if the individual j was not infected before the final observation time T, its contribution to the likelihood is the probability that its infection is observed after T. Note that the likelihood contributions of the index cases cannot be evaluated as their transitions from susceptible to (natural) infection cannot be observed. Therefore, defining as the vector of unknown model parameters, the likelihood function is
| (4) |
Substituting the individual infection rate defined in Equation 1 into Equation 4 and given the variance component models for susceptibility and infectivity defined in Equations 2 and 3, respectively, the log-likelihood can be written as
| (5) |
Bayesian inference:
A paternal risk (i.e., sire) model was adopted for the variance components of susceptibility and infectivity, such that if j is a nonindex case and if j can express infectivity, with representing the male parent of j, Let S be the number of male parents and let and be the S-dimensional vectors representing the corresponding paternal additive genetic effects. Assuming unrelated male parents and independence between susceptibility and infectivity, prior distributions of additive genetic effects are and where and is an identity matrix of dimension S. As defined in Modeling the infection events accounting for genetic heterogeneity in host susceptibility and infectivity: the dnIGE model, the priors for the environmental effects are and Inverse-gamma priors were considered for the paternal additive genetic variances, defined as and with hyperparameters defined to represent noninformative priors. Finally, a noninformative gamma prior with hyperparameters was used for the effective contact rate β.
Exploiting the hierarchical parameter structure of the dnIGE model, the joint posterior distribution of θ can be written as
| (6) |
The conditional density functions of the joint posterior distribution above were implemented into a hybrid MCMC scheme where the Gibbs sampling algorithm was applied to the parameters whose conditional densities have standard forms and the Metropolis–Hastings (MH) algorithm was used otherwise (Gelman et al. 2003). Particularly, the evaluation of the conditional density functions of the environmental effects and considered that susceptible and infected individuals contribute differently to the likelihood function defined in Equation 4. The conditional posterior densities derived from the posterior distribution in (6) can be found in Supporting Information, File S1.
Adaptive Metropolis–Hastings and data augmentation of unknown infection times:
The MH algorithm depends on proposal distributions to generate candidate values from posterior distributions of model parameters. Usually, variances of these proposals are manually tuned according to the acceptance rate of the MH algorithm (Gelman et al. 2003). As discussed in Rosenthal (2011), manually tuning proposal distributions is infeasible when dealing with high-dimensional vectors of individual parameters, which is the case for additive genetic effects and environmental effects. Nevertheless, automatic tuning of proposal distributions can be achieved using adaptive MH methods, which periodically update the proposal distribution based on acceptance rates over MCMC iterations in an adaptive way to maximize the efficiency of the sampling algorithm. For a review of adaptive MH methods, see Rosenthal (2011). In the MCMC algorithm to estimate the parameters of the dnIGE model, parent and individual environmental effects were sampled one at a time through a MH step based on a normal proposal distribution, whose mean was equal to the current value of the chain, and the proposal variance was tuned according to the algorithm presented in Roberts and Rosenthal (2009).
Additionally, Bayesian analysis of the dnIGE model initially assumed known infection times In practice, individual infection status is observed only at fixed sampling times, such that the true infection time lies within the interval ranging from the last sampling time that j was observed as noninfected to the first sampling time that j was observed as infected. Defining this interval as the missing infection time of each nonindex case infected individual j, can be treated as a latent variable and modeled through data augmentation techniques (Tanner and Wong 1987). This can be implemented through an additional MH step for each j with a uniform distribution on as a proposal distribution. A data augmentation approach based on the MH algorithm for unknown infection times was also developed in Brown et al. (2014).
Model validation using data from simulated epidemics for heterogeneous livestock populations
Although the methodology outlined in this section can be applied to infectious diseases in human or livestock populations, our validation focused on family and group structures that are typical for livestock, where we expect the initial implementation of the dnIGE model.
Family structure and stochastic simulation of the epidemics:
A Monte Carlo simulation study was carried out to evaluate the estimates provided by the dnIGE model over a range of scenarios that are realistic for livestock populations. The scenarios were defined by varying population and group size and frailty-scale heritabilities of susceptibility and infectivity (by setting the unknown environmental variance to one). Additionally, in practice infection data are seldom exactly observed, so we varied the observation period resulting in a variety of disease prevalences depending on the final observation time T. For the scenarios with unknown infection times, we also varied the frequency that the disease status of each individual was observed during the epidemic (sampling frequency). To evaluate the sampling variation of the model estimates, unless otherwise stated, 20 replicates of each scenario were generated, with each replicate representing a different simulated population where the infection data were generated and the dnIGE model was fitted. Table 1 presents all scenarios considered for evaluating the dnIGE model.
Table 1. Values of heritability, sample size, prevalence, group size, and sampling frequency (when infection time was assumed unknown) considered in the simulated epidemics for validation of the dnIGE model.
| Susceptibility and infectivity h2a,b | Infectivity h2c | Sample sizea | Prevalenced | Group sizeb | Sampling frequency for unknown infection timese |
|---|---|---|---|---|---|
| 0.2 | |||||
| 0.4 | 500 | 0.3 | 2 | ||
| 0.1 | 0.4 | 2 | |||
| 0.33 | 0.5 | 5 | |||
| 0.4 | 0.6 | 10 | 10 | ||
| 0.67 | 0.7 | 30 | |||
| 0.8 | 0.8 | 2000 | 0.8 | 60 | |
| 0.9 | 20 | ||||
| 1 |
The base scenario assumed the values in boldface type and known infection times. Unknown environmental variance was set at 1.
To evaluate the effect of heritability and sample size on estimates of heritability and effective contact rates (Figure 2 and Figure S1).
To evaluate the effect of heritability and group size on heritability estimates, prediction accuracies, and sire ranking (Figure 4 and Figure S2).
To evaluate the effect of genetic variation of infectivity on prediction accuracies (Figure 3).
To evaluate the effect of disease prevalence on prediction accuracies (Figure 5).
To evaluate the effect of sampling frequency on prediction accuracies (Figure 6).
The base population was simulated following a parental half-sib structure, where 100 sires were mated to 20 dams and all parents were unrelated. A polygenic model was considered for the genetic architecture of the traits, with additive genetic effects of the base population sampled from a normal distribution with additive genetic variances and for susceptibility and infectivity, respectively. Also, additive genetic effects of offspring were obtained by adding the mean of the additive genetic effects of their parents to a Mendelian sampling term, obtained from a normal distribution with zero mean and variance given by half of the trait additive genetic variance. It was generated one offspring per mating, resulting in a population of size 2000. To test whether the dnIGE model provides useful estimates for small populations, we also show results for (25 sires with 20 dams per sire). Offspring environmental effects were generated from a normal distribution with zero mean and unit variance for both susceptibility and infectivity. Then, the frailties associated with these two traits were calculated for the offspring population, using the variance component models defined in Equations 2 and 3.
The epidemics were simulated in the offspring population, where individuals were randomly allocated into groups of equal sizes. In each group, an individual was chosen at random to be the index case responsible to start the outbreak. No disease transmission was allowed between members of different groups. The transmission in each of these closed groups was simulated using Gillespie’s direct method (Gillespie 1977), where the times between infections were simulated from an exponential distribution with parameters given by the sum of the infection rates of the susceptibles, represented by in Equation 1. After specifying the time of each infection, the corresponding individual was chosen randomly from the pool of remaining susceptibles, using their infection rates as relative weightings. This iterative algorithm was independently run for each group until all the group members were infected. Populations with different disease prevalences were defined by setting the final observation time T according to predefined prevalences, corresponding to a time when a given proportion of individuals in the entire population were recorded as infected. Note that disease prevalences in each group at time T varied.
Fitting the dnIGE model to simulated infection data:
The paternal risk (sire) version of the dnIGE model was fitted to all simulated data sets, using the MCMC scheme described in Estimating the dnIGE model parameters using infection data. For each data set, two chains from the algorithm were generated to assess MCMC convergence, which was evaluated by looking at trace and autocorrelation plots as well as by computing the Gelman–Rubin statistic (Gelman et al. 2003). Each chain comprised iterations, such that its first values were discarded (the burn-in period), and every 100th value from the remaining iterations was used as draws from the posterior distribution of the parameter of interest.
dnIGE model validation criteria:
Currently, there is no available method that estimates heritabilities and genetic risks of susceptibility and infectivity from longitudinal disease data. To compare our model with existing methods and also to evaluate the effect of neglecting variation in infectivity, a restricted version of the model assuming variation only in susceptibility (hereafter denoted the alternative model) was also fitted to the simulated infection data. The alternative model is equivalent to the semiparametric log-normal frailty model proposed by Korsgaard et al. (1998) with a constant baseline hazard rate. Estimates of the susceptibility parameters of both models were then compared when varying the heritability in infectivity, with the goal of evaluating the effect of neglecting variation in this trait when modeling susceptibility only.
Prediction accuracies were defined by the correlation of the true (simulated) and estimated paternal additive genetic effects for each underlying trait. Narrow sense heritability estimates based on the paternal risk dnIGE model were defined as and for susceptibility and infectivity, respectively, where represents the variance estimate and the subscript S stands for sire. Additionally, we estimated the proportion of the best and worst 10% of male parents correctly identified by the model.
Data availability
The R code used to generate the data to evaluate the dnIGE model is available on request.
Results
Unless otherwise stated, the results presented in this section refer to 20 replicates of a base scenario where heritability was 0.8 for both susceptibility and infectivity, simulated populations consisted of 2000 individuals allocated in groups of size 10, and the observation period was sufficiently long so that the whole population was infected during the epidemic. Note that a heritability of 0.8 for susceptibility and infectivity frailties corresponds to a considerably lower heritability (≈0.2, as verified in simulation studies) for the recorded binary infection status, which is in line with the values recorded in the literature (Lipschutz-Powell et al. 2012a).
Model fit and comparison
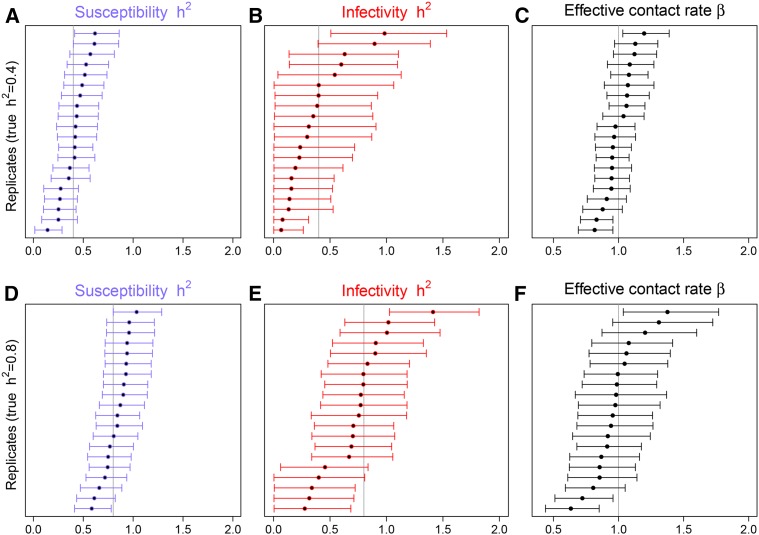
Posterior summaries of frailty-scale heritabilities and effective contact rates are presented in Figure 2, which shows the 90% credibility intervals for these parameters when fitting the dnIGE model to 20 replicates. About 85% of the replicate intervals cover the true heritability values used to simulate the populations, indicating that the model can provide calibrated interval estimates for this parameter (Little 2011). Credibility intervals for heritabilities of infectivity are wider than the ones for susceptibility, which shows that it is more difficult to capture genetic variation in infectivity. These intervals also strongly indicate that posterior distributions of population parameters provided by the dnIGE model tend to be symmetric, except for heritability credibility intervals of infectivity when the true value for this parameter was 0.4 (on the frailty scale), where most of the posterior distributions were right skewed. Furthermore, heritability posterior means of susceptibility and infectivity are significantly larger than zero for most of the replicates, showing that the dnIGE model can capture genetic variation in both traits, if it exists. As expected, uncertainty with respect to population parameter estimates was larger when using smaller population sizes, as reflected by much wider credibility intervals in most of the replicates of size 500 (see Figure S1). However, genetic signal of both traits could still be detected in this case.
Figure 2.
(A–F) Bayesian credible intervals for heritabilities of susceptibility (A and D), infectivity (B and E), and also for effective contact rate β (C and F), obtained by fitting the dnIGE model to 20 replicates of generated data sets of sample size 2000, using 10 individuals per group. Heritabilities used were 0.4 (A–C) and 0.8 (D–F). Gray lines indicate true heritabilities (A,B,D,E) and true effective contact rates (C,F). Dots represent posterior means.
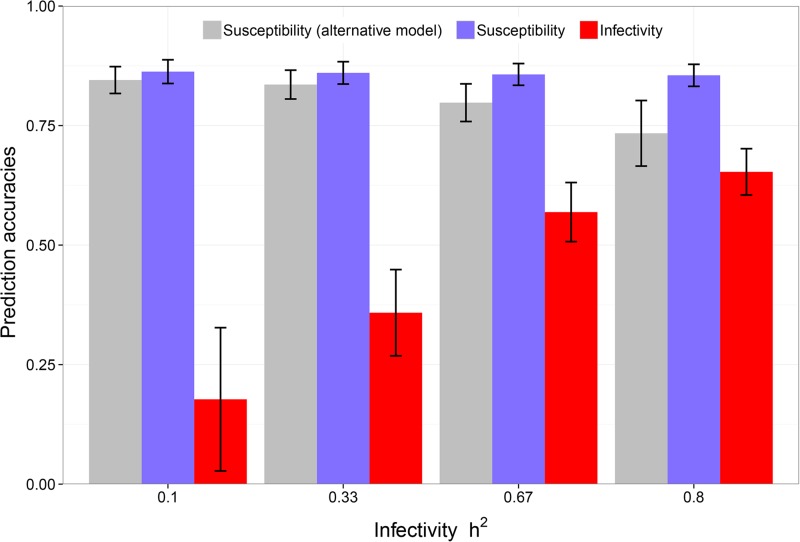
Figure 3 shows prediction accuracies for susceptibility and infectivity for different infectivity heritabilities obtained with the dnIGE model. The plot shows an increasing trend in prediction accuracies for infectivity, with increasing precision (reflected by smaller standard errors) as infectivity heritabilities increased. Also, predictions for susceptibility provided by the dnIGE model were not affected by variation in infectivity. On the other hand, when the alternative model ignoring variation in infectivity was used, genetic variation in infectivity reduced prediction accuracy of susceptibility in the alternative model as well as the precision of these estimates (Figure 3). These results show not only that variation in infectivity can negatively affect accuracies in models that account for genetic variation in susceptibility only, but also that the dnIGE model can predict the genetic effects in both traits, with the prediction accuracy of paternal genetic infectivity risk depending on the genetic variation of this trait.
Figure 3.
Influence of genetic variation in infectivity on prediction accuracies for susceptibility and infectivity additive genetic paternal effects obtained from the dnIGE model compared to the alternative approach (Korsgaard et al. 1998) that ignores genetic variation in infectivity. Bars in the plot represent mean prediction accuracy while the lines represent that estimate plus or minus its standard error over 20 replicates. Heritability of 0.8 was considered for susceptibility, with population size 2000 and group size 10.
Effect of underlying trait heritabilities and group size on heritability estimates and predictive accuracies
Figure 4 shows the effect of group size and genetic variation (represented by different heritability values) on the performance of the dnIGE model, where heritabilities for both susceptibility and infectivity were 0.4 and 0.8 for group sizes 2, 10, and 20. Greater genetic variation in susceptibility and infectivity led to higher prediction accuracies for both traits (Figure 4, A and B), but had little impact on the accuracy of heritability estimates (Figure 4, C and D). Also, the quality of the estimates was generally poorer for infectivity than for susceptibility, as demonstrated by lower mean accuracies and higher standard errors of heritability estimates associated with infectivity. Heritability estimates of both traits were severely upward biased for group size 2, but realistic for larger groups. Additionally, while prediction accuracies of susceptibility paternal genetic effects increased with increasing group size, the accuracy of infectivity paternal genetic effects followed the opposite trend, reflecting a trade-off between predicting infectivity and predicting susceptibility genetic effects with respect to group size.
Figure 4.
Effect of group size on model estimates. (A–D) Mean prediction accuracies of paternal effects (A and B, with lines representing plus or minus standard error of that mean over 20 replicates) and posterior mean heritabilities (C and D, with black lines representing plus or minus standard error of that mean over 20 replicates) obtained when fitting the dnIGE model to simulated data sets considering 2, 10, and 20 individuals per group, using heritabilities 0.4 (A and C) and 0.8 (B and D) for both susceptibility and infectivity. Gray lines in C and D indicate true heritabilities.
Heritability and group size also seem to affect the identification of best and worst male parents according to their predicted genetic merit, as shown in Figure S2. The proportion of correctly identified among best and worst 10% of male parents varied between 30% and 67% for susceptibility and between 25% and 47% for infectivity, showing that it is easier for the dnIGE model to identify the least and most genetically susceptibles than the least and most genetically infectious. Also, while heritability has a positive effect on the predictive ability of the dnIGE model for both traits, group size has a large impact on the proportion of correctly identified best and worst male parents according to susceptibility but little impact on the identification of least and most infectious male parents (Figure S2).
Model performance for different observation periods and sampling frequencies
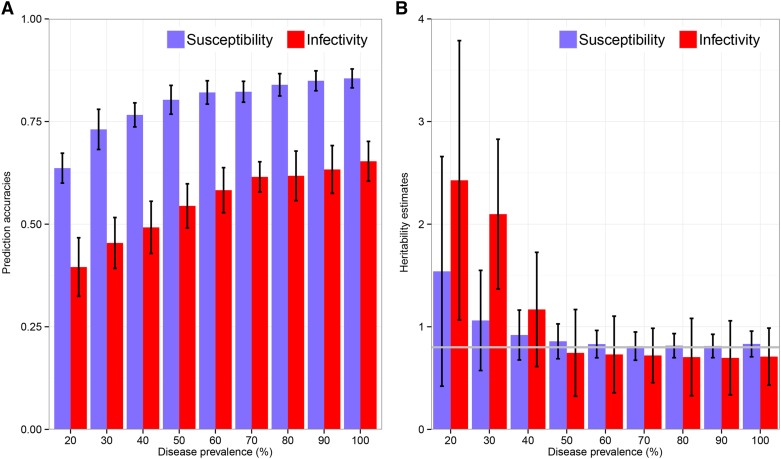
Figure 5 shows prediction accuracies of estimated paternal genetic effects and posterior mean heritability estimates, obtained when fitting the dnIGE model to simulated data sets that considered different observation periods such that disease prevalences in these data sets varied from to Heritability estimates for both susceptibility and infectivity were similar for disease prevalences but upward biased with large standard errors when disease prevalence was lower. The upward bias was particularly large for infectivity. These results suggest that, although it may not be possible to obtain reliable heritability estimates when using infection data with low disease prevalences, it is not required to observe the entire epidemics to accurately estimate susceptibility and infectivity genetic parameters. Figure 5 also shows that prediction accuracies of genetic risk increase with disease prevalence, with consistently greater prediction accuracies for susceptibility than for infectivity.
Figure 5.
Effect of disease prevalence on model estimates. (A and B) Mean prediction accuracies of paternal additive genetic effects (A) and posterior mean heritabilities (B) obtained when fitting the dnIGE model to simulated data sets, using group size 10, heritability 0.8, and population disease prevalence ranging from 0.2 to 1. Black lines in A and B represent plus or minus standard error of mean predictive accuracy and heritability, respectively, over 10 replicates. Gray line in B indicates true heritabilities.
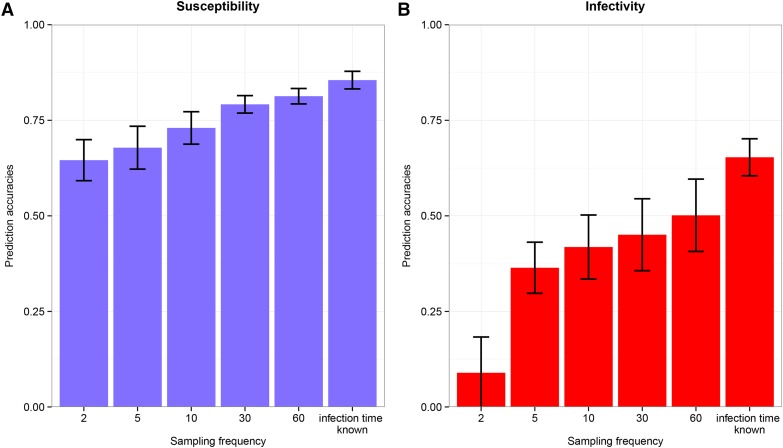
As would be expected, the highest prediction accuracies of additive genetic paternal risk were obtained if infection time was known, and they tend to increase with sampling frequency (Figure 6). Most importantly, prediction accuracies were relatively high even for low sampling frequencies, indicating that the epidemics do not need to be observed very frequently to obtain accurate predictions of genetic risk in becoming infected or transmitting infection. However, very low infectivity prediction accuracies were obtained when recording the disease status of individuals only twice (Figure 6B), and this accuracy was close to zero when cross-sectional data were used, where the disease status was observed only at the final observation time T (results not shown).
Figure 6.
Effect of sampling frequency on model estimates. (A and B) Prediction accuracies of susceptibility (A) and infectivity (B) paternal additive genetic effects obtained for model estimates from simulated data sets, using group size 10 and heritability 0.8 and for both known and unknown infection times. Sampling frequencies used for the unknown infection time case were 2, 5, 10, 30, and 60, with population disease prevalence 0.90. Lines in the plots represent mean estimate plus or minus its standard error over 10 replicates.
Discussion
Even though the effect of host heterogeneity on the severity of disease epidemics has long been recognized (Woolhouse et al. 1997; Lloyd-Smith et al. 2005; Doeschl-Wilson et al. 2011), there is currently no available methodology that can accurately disentangle the different sources of individual variation inherent in disease data such as susceptibility and propensity to infect group members. Our methodology combines previous quantitative genetic models of disease traits with nonlinear stochastic modeling of the individual-level infection process. Furthermore, by exploring modern Bayesian computational techniques, it results in the first statistical model that not only accounts for the frequently modeled variation in host susceptibility, but also can fully capture the usually neglected genetic variation in host infectivity. As highlighted by numerous authors (Lipschutz-Powell et al. 2012a,b; Anche et al. 2014; Brooks-Pollock et al. 2015), capturing genetic variation in infectivity in quantitative genetic models of infectious diseases has been so far an open challenge due to the lack of statistical methodologies to accurately estimate parameters associated with this trait. The lack of inference methods accounting for heterogeneity in infectivity has also been long recognized in the statistical literature (see, for example, Becker and Britton 1999). Therefore, the dnIGE model pushes forward the genetic analysis of infectious diseases by exploring the genetic variation in a trait whose individual effects are currently not estimated in disease genetic studies but greatly influence the spread of infectious diseases.
By identifying individuals with high genetic risk for contracting and transmitting infections, the dnIGE model offers previously recognized advances in livestock disease control through selective breeding and also for predicting and controlling the emergence of disease outbreaks in human populations. Lloyd-Smith et al. (2005) inferred the presence of superspreaders in all of the eight available data sets collected from recent disease outbreaks, indicating that superspreading is a common phenomenon. Since we used the log-normal distribution to represent the skewed distributions assumed for host infectivity and susceptibility, the dnIGE model can identify superspreaders. Most importantly, the fact that we could identify approximately half of the parental males with the highest additive genetic risk for infectivity in the simulation study demonstrates that the model has the capacity to infer whether superspreading is genetically controlled.
Existing models currently do not fully account for polygenic variation in infectivity, which may affect their estimates of genetic risk in susceptibility, especially if genetic superspreaders exist. Our results showed that, while accuracies of genetic risk in susceptibility from the dnIGE model remained robust regardless of the magnitude of the genetic variation in infectivity, estimates of genetic risk in susceptibility from an equivalent model accounting for this trait only were less accurate as genetic variation in infectivity increased. Hence, even when the interest is solely on estimates of genetic risk in susceptibility, it may be important to account for genetic variation in infectivity when modeling infectious disease data.
Following the overwhelming evidence emerging in genetic analyses of disease traits, our model assumes that host susceptibility and infectivity are polygenic traits, i.e., controlled by many genes with small effects (Bishop and Woolliams 2014). Alternative approaches that consider genetic variation in infectivity assume that this trait and susceptibility are fully controlled by single independent loci explaining all of the variation in them (see Lipschutz-Powell et al. 2012a; Anche et al. 2014; Pooley et al. 2014). Anche et al. (2014) argued that, since selection for disease traits aims to reduce epidemic risk and disease prevalence, genetic improvement should focus on reduction of the basic reproduction ratio (), which is a central parameter in epidemiology determining risk and size of an epidemic (Keeling and Rohani 2008), and defined as a function of susceptibility and infectivity allelic effects. Although this has allowed investigation of how selection response in is influenced by allele effects and other factors such as genetic relatedness, it would be difficult to extend their approach to polygenic traits.
Pooley et al. (2014) developed an algorithm to simultaneously estimate susceptibility and infectivity, also assuming major gene effects for both traits. Their model is an extension of the multitype epidemic models (Britton 1998), with different susceptible-infectious-recovered (SIR) models representing individual genotypes and an MCMC algorithm to estimate parameters of these coupled SIR processes. Although assuming major gene effects allows the search for candidate genes affecting susceptibility and infectivity and it also implies a small parameter space, therefore simplifying inference, extension of their methods to accommodate an infinitesimal genetic model is not straightforward, as the number of SIR processes included in their algorithm increases with the number of gene effects.
Validation of the dnIGE model for a variety of simulated scenarios provided valuable insights regarding requirements for experimental designs and data collection to obtain reliable genetic parameter estimates for both host susceptibility and infectivity. Our methodology can be applied to disease data from humans, plants, and livestock. The dnIGE model produced accurate estimates for additive genetic variance and paternal genetic risk for both contracting and transmitting infections for populations comprising 2000 individuals. Although this matches the typical requirements for quantitative genetic studies of disease traits, larger sample sizes might be possibly needed if interest is on estimated genetic variation in infectivity when heritability on this trait is very low. However, given that susceptibility and infectivity are indirect genetic effects, estimation of genetic parameters also requires related individuals to be distributed across different epidemiological groups (Muir 2005; Anche et al. 2014). In our simulations, paternal offspring were allocated randomly into equally sized groups comprising 2–20 individuals, corresponding to 1000–100 epidemic groups. Such stratification is more likely for livestock and fish than for human populations, as individual sires can have a large number (e.g., 20) of offspring in different herds or experimental groups. Therefore our model validation focused primarily on scenarios that are realistic for domestic livestock and fish, which we consider as the primary target (although not the single target as outlined below) for applying our newly developed methods.
In line with previous results of IGE models (Bijma 2010; Ødegård and Olesen 2011), group size was found to have a substantial, but opposite effect on genetic parameter estimates of susceptibility and infectivity. While few larger groups are favorable for estimating susceptibility, many small groups tend to produce better infectivity estimates. Intuitively, this can be explained as follows: as highly susceptible individuals tend to become infected at lower infection pressure and thus earlier relative to less susceptible individuals, and individual infection pressure increases with the number of infecteds, larger group sizes provide more information on the order of infection. This results in better accuracy and precision of susceptibility genetic parameter estimates. On the other hand, without detailed information on who infects whom, larger groups increase the potential confounding among the expressions of infectivity from different infected individuals, as it becomes more difficult to disentangle the individual infectivities from the infected individuals that might have transmitted the infection to the susceptibles as group size increases. This confounding is particularly severe at the later stages of infection when many individuals are infected. This may explain the deterioration of prediction accuracies and heritability estimates of infectivity in larger groups. Additionally, although our methodology works best for infection data with high disease prevalence, the dnIGE model can also provide reliable estimates of infectivity and susceptibility genetic parameters when fitted to data with low disease prevalence, where information for inference is reduced.
In domestic livestock, challenge infection experiments have proved useful for identifying genetic regulation of disease resistance (Vallejo et al. 1998; Lunney et al. 2011; Ødegård and Olesen 2011; Hamzic et al. 2014). In many of these studies all animals are infected with a given pathogen dose. However, this type of experiment is not suitable when interest is on improving both infectivity and susceptibility. To quantify genetic variation in both traits, it is necessary to observe how the disease is transmitted naturally in the population. Experimentally, this could be achieved by artificially infecting some animals (usually called donors), allocating them into closed groups with susceptible individuals (the recipients), and recording the disease status of the recipients in each group at multiple points in time.
Previous attempts to simultaneously estimate genetic parameters associated with infectivity and susceptibility focused on IGE models for binary data observed at a single time point during the epidemics (Lipschutz-Powell et al. 2012a,b) or at the equilibrium state of an epidemic (Anche et al. 2014). Several studies have demonstrated (e.g., Gitterle et al. 2006; Ødegård et al. 2007; Pérez-Cabal et al. 2009; Vazquez et al. 2009) that the predictive ability of quantitative genetic models of disease resistance can be improved by using longitudinal data rather than cross-sectional records of the dynamic infection process. Similar arguments apply for inferring infectivity estimates: sequential records of the binary disease phenotype provide richer information about the true infection times and thus about potential transmission routes. Assuming that longitudinal binary disease data are available, we considered time to infection as the disease phenotype for our models and we used data augmentation techniques to incorporate the uncertainty regarding unknown infection times into the model. Our results show that the dnIGE model can provide unbiased heritability estimates of infectivity, therefore fully capturing genetic variation in this trait from longitudinal disease records. It was also verified that heritability estimates of infectivity are largely dependent on sample size. Additionally, predictive ability of the dnIGE model is not severely compromised by having only few repeated measurements. Moreover, predictions for genetic risk based on inexact infection times were not drastically different from the predictions one would obtain if infection times were exact. Our results therefore suggest that, even though the population should be observed at multiple points in time to fully capture genetic variation in infectivity and susceptibility, the sampling frequency to observe the disease status of individuals does not need to be high.
The dnIGE model can be viewed as an extended class of IGE models that not only allows for nonnormally distributed traits and nonlinearity among genetic parameters, but also captures the dynamic interaction of the infection process. Since it was theoretically and empirically shown that accounting for indirect genetic effects increases the response to selection of a trait affected by social interactions (Muir 2005; Bijma et al. 2007a,b), including diseases (Lipschutz-Powell et al. 2012a), this would imply that many characteristics of IGEs also apply to infectivity, such as the need for related individuals across groups (also shown by Anche et al. 2014) and the negative effect on selection response if this trait is not accounted for. In addition, as was developed for linear IGE models (Bijma 2010; Ødegård and Olesen 2011; Anche et al. 2014), further research in optimizing experimental designs using group size and composition to maximize prediction accuracies is warranted. Particularly, it would be interesting to verify whether groups containing related individuals can increase predictive accuracy (as shown by Bijma 2010; Ødegård and Olesen 2011) when compared to random allocation of individuals into groups, which was used in this study.
For the development of the dnIGE model, we focused on simple epidemiological SI models that assume that animals remain infected once the disease has been transmitted to them. This holds for several important diseases in livestock such as Marek’s disease in chickens, infectious pancreatic necrosis in salmon, and bovine tuberculosis in cattle (Vallejo et al. 1998; Bishop and Woolliams 2014). Since the expression for individual infection rate in Equation 1 is based on a Poisson process for the number of infections that each animal can acquire, the dnIGE model falls into the class of recurrent event models in survival analysis (Kalbfleisch and Prentice 2011). Hence, the methodology proposed here can be also applied to diseases that allow recovery or recurrent infections. Our model can also be easily extended to accommodate other sources of genetic variation, such as recovery or contact rate, and to accommodate survival rather than infection data.
Further work is warranted to accommodate potentially additional sources of heritable variation into our model. We assumed that individuals can be immediately diagnosed as infected upon infection. However, this may not be the case when genetic variation in tolerance affects the time of onset of detectable symptoms, for example. Moreover, we assumed that infectivity and susceptibility are independent, which is the case where the model benefits most from accounting for variation in both traits. In the Bayesian analysis of the dnIGE model both genetic and environmental variances of susceptibility and infectivity were modeled using inverse gamma distributions. Although a straightforward generalization of these priors is an inverse Wishart distribution, Gelman and Hill (2006) point out that this distribution may not be flexible enough to express the lack of information about covariance matrices, since noninformative priors for their covariance components might significantly restrict the possible range of values of the variances. Hence, a detailed evaluation should be developed by comparing different prior distributions that can be considered to represent the uncertainty regarding putative dependencies between infectivity and susceptibility.
Estimates of paternal additive genetic effects (sire breeding values) and heritabilities provided by the dnIGE model were evaluated using a polygenic paternal risk (sire) model for both infectivity and susceptibility, where the male parents were assumed unrelated. We considered this approach as the model was evaluated using several replicates and a variety of scenarios by considering different heritabilities, sampling frequencies, and disease prevalences as well as group and sample sizes. The model could also be fitted assuming an animal model for these traits, as described in Equations 2 and 3. In this case, the computational costs associated with the MCMC algorithm would significantly increase to incorporate the genetic relationship matrix and additional progeny information into the conditional posterior distributions of the parameters.
Moreover, if genomic information from the population is available in the form of SNP markers, the proposed model can be applied to identify genetic loci affecting infectivity phenotypes. While important SNPs have already been found for susceptibility (Houston et al. 2008; Ødegård et al. 2011), the lack of statistical methods has hindered the search for infectivity genes. Moreover, application of the dnIGE model in livestock production using information from dense SNP markers would enable genomic selection based on the genomic breeding values for both susceptibility and infectivity, therefore avoiding constantly exposing animals to infection without the need to discover causative genetic variants of infectivity.
Finally, although the focus for our model applications has been primarily on livestock, we anticipate that the dnIGE model also has useful applications in the control of infectious diseases in humans. Modeling human genetic variation in infectivity it is an open challenge for infectious disease modelers, since current methods to estimate infectiousness and susceptibility in human disease outbreaks usually account for individual heterogeneity in these traits through population subgroups, defined by identifiable factors such as age and vaccination. To apply the proposed methodology to human epidemics the spreading mechanism must be incorporated into the dnIGE model. This can be done, for example, by assuming a community structure (such as the presence of households) or by using contact network models (Danon et al. 2011), which have been successfully applied in infectious disease modeling. In the first step toward disentangling human individual variation in susceptibility and infectivity the genetic variance structure of the model can be ignored, therefore avoiding the requirement of having related individuals in different groups. Thus, by extending the proposed methodology with existing methods to account for the nonhomogeneous contact structure in human epidemic data, the dnIGE model can offer potential impacts to public health by identifying individuals at high risk of becoming infected or transmitting infections.
In conclusion, our results suggest that the dnIGE model can reliably identify individuals with high genetic risk for contracting or transmitting infections from inexact information on time to infection. The model constitutes an important step in detecting genetic signal in noisy field disease data, therefore potentially affecting genetic disease control.
Supplementary Material
Acknowledgments
We thank Professor Paddy Farrington (Open University) for fruitful discussions about the derivation of the proposed model and two referees for their constructive and helpful comments on an earlier version of this manuscript. This work was carried out with funding from the Biotechnology and Biological Sciences Research Council Institute Strategic Programme grant ISP1 (to O.A., J.A.W., and A.B.D.-W.) and the European Union FP7 project FISHBOOST (KBBE-KBBE-7-613611) (to O.A., J.A.W., A.B.D.-W., and L.A.G.-C).
Footnotes
Communicating editor: G. A. Churchill
Supporting information is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.115.179853/-/DC1.
Literature Cited
- Aalen, O., O. Borgan, and H. Gjessing, 2008 Survival and Event History Analysis: A Process Point of View. Springer-Verlag, Berlin/Heidelberg, Germany/New York. [Google Scholar]
- Anche M. T., de Jong M. C. M., Bijma P., 2014. On the definition and utilization of heritable variation among hosts in reproduction ratio R0 for infectious diseases. Heredity 113: 364–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R., May R., 1991. Infectious Diseases of Humans: Dynamics and Control. Oxford University Press, Oxford. [Google Scholar]
- Becker N. G., Britton T., 1999. Statistical studies of infectious disease incidence. J. R. Stat. Soc. Ser. B Stat. Methodol. 61: 287–307. [Google Scholar]
- Bijma P., 2010. Estimating indirect genetic effects: precision of estimates and optimum designs. Genetics 186: 1013–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bijma P., Muir W. M., Arendonk J. A. M. V., 2007a Multilevel selection 1: quantitative genetics of inheritance and response to selection. Genetics 175: 277–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bijma P., Muir W. M., Ellen E. D., Wolf J. B., Arendonk J. A. M. V., 2007b Multilevel selection 2: estimating the genetic parameters determining inheritance and response to selection. Genetics 175: 289–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop S. C., Woolliams J. A., 2014. Genomics and disease resistance studies in livestock. Livest. Sci. 166: 190–198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop S. C., Doeschl-Wilson A. B., Woolliams J. A., 2012. Uses and implications of field disease data for livestock genomic and genetics studies. Front. Genet. 3: 114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britton T., 1998. Estimation in multitype epidemics. J. R. Stat. Soc. Ser. B Stat. Methodol. 60: 663–679. [Google Scholar]
- Brooks-Pollock E., Roberts G. O., Keeling M. J., 2014. A dynamic model of bovine tuberculosis spread and control in Great Britain. Nature 511: 228–231. [DOI] [PubMed] [Google Scholar]
- Brooks-Pollock E., de Jong M. C. M., Keeling M. J., Klinkenberg D., Wood J. L. N., 2015. Eight challenges in modelling infectious livestock diseases. Epidemics 10: 1–5. [DOI] [PubMed] [Google Scholar]
- Brown P. E., Chimard F., Remorov A., Rosenthal J. S., Wang X., 2014. Statistical inference and computational efficiency for spatial infectious disease models with plantation data. J. R. Stat. Soc. C 63: 467–482. [Google Scholar]
- Chapman S. J., Hill A. V. S., 2012. Human genetic susceptibility to infectious disease. Nat. Rev. Genet. 13: 175–188. [DOI] [PubMed] [Google Scholar]
- Danon L., Ford A. P., House T., Jewell C. P., Keeling M. J., et al. , 2011. Networks and the epidemiology of infectious disease. Interdiscip. Perspect. Infect. Dis. 2011: e284909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doeschl-Wilson A. B., Davidson R., Conington J., Roughsedge T., Hutchings M. R., et al. , 2011. Implications of host genetic variation on the risk and prevalence of infectious diseases transmitted through the environment. Genetics 188: 683–693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doeschl-Wilson A. B., Lipschutz-Powell D., Anacleto O., Lough G., Lengeling A., et al. , 2014. New methods for capturing unidentified genetic variation underlying infectious disease in livestock populations. Proceedings of 10th World Congress on Genetics Applied to Livestock Production, Vancouver, BC, Canada. [Google Scholar]
- Ducrocq V., Casella G., 1996. A Bayesian analysis of mixed survival models. Genet. Sel. Evol. 28: 505. [Google Scholar]
- Dukic V., Lopes H. F., Polson N. G., 2012. Tracking epidemics with Google Flu Trends data and a state-space SEIR model. J. Am. Stat. Assoc. 107: 1410–1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elderd B. D., Dwyer G., Dukic V., 2013. Population-level differences in disease transmission: A Bayesian analysis of multiple smallpox epidemics. Epidemics 5: 146–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman, A., and J. Hill, 2006 Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press, Cambridge, UK/London/New York. [Google Scholar]
- Gelman, A., J. Carlin, H. Stern, and D. Rubin, 2003 Bayesian Data Analysis, Ed. 2 (Chapman & Hall/CRC Texts in Statistical Science). Chapman & Hall/CRC, Boca Raton. [Google Scholar]
- Gianola D., Fernando R., 1986. Bayesian methods in animal breeding theory. J. Anim. Sci. 63: 217–244. [Google Scholar]
- Gibson J., Bishop S., 2005. Use of molecular markers to enhance resistance of livestock to disease: a global approach. Rev. Sci. Tech. 24: 343–353. [PubMed] [Google Scholar]
- Gillespie D. T., 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81: 2340–2361. [Google Scholar]
- Gitterle T., Ødegård J., Gjerde B., Rye M., Salte R., 2006. Genetic parameters and accuracy of selection for resistance to White Spot Syndrome Virus (WSSV) in Penaeus (Litopenaeus) vannamei using different statistical models. Aquaculture 251: 210–218. [Google Scholar]
- Griffing B., 1967. Selection in reference to biological groups i. Individual and group selection applied to populations of unordered groups. Aust. J. Biol. Sci. 20: 127–140. [PubMed] [Google Scholar]
- Hamzic, E., B. Bed’Hom, H. Juin, R. Hawken, M. Abrahamsen et al., 2014 Plasma components as traits for resistance to coccidiosis in chicken. Proceedings of 10th World Congress on Genetics Applied to Livestock Production, Vancouver, BC, Canada. [Google Scholar]
- Houston R. D., Haley C. S., Hamilton A., Guy D. R., Tinch A. E., et al. , 2008. Major quantitative trait loci affect resistance to infectious pancreatic necrosis in atlantic salmon (Salmo salar). Genetics 178: 1109–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalbfleisch, J. D., and R. L. Prentice, 2011 The Statistical Analysis of Failure Time Data. John Wiley & Sons, New York/Hoboken, NJ. [Google Scholar]
- Keeling, M. J., and P. Rohani, 2008 Modeling Infectious Diseases in Humans and Animals. Princeton University Press, Princeton, NJ. [Google Scholar]
- Kemper K. E., Goddard M. E., Bishop S. C., 2013. Adaptation of gastrointestinal nematode parasites to host genotype: single locus simulation models. Genet. Sel. Evol. 45: 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korsgaard I. R., Madsen P., Jensen J., 1998. Bayesian inference in the semiparametric log normal frailty model using Gibbs sampling. Genet. Sel. Evol. 30: 241. [Google Scholar]
- Lindley D. V., Smith A. F. M., 1972. Bayes estimates for the linear model. J. R. Stat. Soc. Ser. B Stat. Methodol. 34: 1–41. [Google Scholar]
- Lipschutz-Powell D., Woolliams J. A., Bijma P., Doeschl-Wilson A. B., 2012a Indirect genetic effects and the spread of infectious disease: Are we capturing the full heritable variation underlying disease prevalence? PLoS One 7: e39551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipschutz-Powell D., Woolliams J. A., Bijma P., Pong-Wong R., Bermingham M. L., et al. , 2012b Bias, accuracy, and impact of indirect genetic effects in infectious diseases. Front. Genet. 3: 215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipschutz-Powell D., Woolliams J. A., Doeschl-Wilson A. B., 2014. A unifying theory for genetic epidemiological analysis of binary disease data. Genet. Sel. Evol. 46: 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little R., 2011. Calibrated Bayes, for statistics in general, and missing data in particular. Stat. Sci. 26: 162–174. [Google Scholar]
- Lively C. M., 2010. The effect of host genetic diversity on disease spread. Am. Nat. 175: E149–E152. [DOI] [PubMed] [Google Scholar]
- Lloyd-Smith, J. O., S. J. Schreiber, and W. M. Getz, 2006 Moving beyond averages: individual-level variation in disease transmission, pp. 235–258 in Mathematical Studies on Human Disease Dynamics: Emerging Paradigms and Challenges. American Mathematical Society, edited by A. B. Gumel, C. Castillo-Chavez, R. E. Mickens, and D. P. Clemence, Washington, DC. [Google Scholar]
- Lloyd-Smith J. O., Schreiber S. J., Kopp P. E., Getz W. M., 2005. Superspreading and the effect of individual variation on disease emergence. Nature 438: 355–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunney J. K., Steibel J. P., Reecy J. M., Fritz E., Rothschild M. F., et al. , 2011. Probing genetic control of swine responses to PRRSV infection: current progress of the PRRS host genetics consortium. BMC Proc. 5: S30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews L., Low J. C., Gally D. L., Pearce M. C., Mellor D. J., et al. , 2006. Heterogeneous shedding of Escherichia coli O157 in cattle and its implications for control. Proc. Natl. Acad. Sci. USA 103: 547–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muir W. M., 2005. Incorporation of competitive effects in forest tree or animal breeding programs. Genetics 170: 1247–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nath M., Woolliams J. A., Bishop S. C., 2008. Assessment of the dynamics of microparasite infections in genetically homogeneous and heterogeneous populations using a stochastic epidemic model. J. Anim. Sci. 86: 1747–1757. [DOI] [PubMed] [Google Scholar]
- O’Brien S. J., Nelson G. W., 2004. Human genes that limit AIDS. Nat. Genet. 36: 565–574. [DOI] [PubMed] [Google Scholar]
- Ødegård J., Olesen I., 2011. Comparison of testing designs for genetic evaluation of social effects in aquaculture species. Aquaculture 317: 74–78. [Google Scholar]
- Ødegård J., Olesen I., Gjerde B., Klemetsdal G., 2007. Evaluation of statistical models for genetic analysis of challenge-test data on ISA resistance in Atlantic salmon (Salmo salar): prediction of progeny survival. Aquaculture 266: 70–76. [Google Scholar]
- Ødegård J., Baranski M., Gjerde B., Gjedrem T., 2011. Methodology for genetic evaluation of disease resistance in aquaculture species: challenges and future prospects. Aquacult. Res. 42: 103–114. [Google Scholar]
- O’Hare A., Orton R. J., Bessell P. R., Kao R. R., 2014. Estimating epidemiological parameters for bovine tuberculosis in British cattle using a Bayesian partial-likelihood approach. Proc. R. Soc. Lond. B Biol. Sci. 281: 20140248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Neill P. D., Roberts G. O., 1999. Bayesian inference for partially observed stochastic epidemics. J. R. Stat. Soc. Ser. A Stat. Soc. 162: 121–129. [Google Scholar]
- Pérez-Cabal M. A., de los Campos G., Vazquez A. I., Gianola D., Rosa G. J. M., et al. , 2009. Genetic evaluation of susceptibility to clinical mastitis in Spanish Holstein cows. J. Dairy Sci. 92: 3472–3480. [DOI] [PubMed] [Google Scholar]
- Pooley C., Marion G., Bishop S., 2014. Estimation of single locus effects on susceptibility, infectivity and recovery rates in an epidemic using temporal data. Proceedings of 10th World Congress on Genetics Applied to Livestock Production, Vancouver, BC, Canada. [Google Scholar]
- Roberts G. O., Rosenthal J. S., 2009. Examples of adaptive MCMC. J. Comput. Graph. Stat. 18: 349–367. [Google Scholar]
- Rosenthal, J. S., 2011 Optimal proposal distribution and adaptive MCMC, pp. 93–112 in Handbook of Markov Chain Monte Carlo, edited by S. Brooks, A. Gelman, G. Jones, and X.-L. Meng. CRC Press, Cleveland, OH/Boca Raton, FL. [Google Scholar]
- Ross, S. M., 1996 Stochastic Processes. John Wiley & Sons, New York/Hoboken, NJ. [Google Scholar]
- Springbett A. J., MacKenzie K., Woolliams J. A., Bishop S. C., 2003. The contribution of genetic diversity to the spread of infectious diseases in livestock populations. Genetics 165: 1465–1474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanner M. A., Wong W. H., 1987. The calculation of posterior distributions by data augmentation. J. Am. Stat. Assoc. 82: 528–540. [Google Scholar]
- Vallejo R. L., Bacon L. D., Liu H.-C., Witter R. L., Groenen M. A. M., et al. , 1998. Genetic mapping of quantitative trait loci affecting susceptibility to Marek’s disease virus induced tumors in F2 intercross chickens. Genetics 148: 349–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazquez A. I., Gianola D., Bates D., Weigel K. A., Heringstad B., 2009. Assessment of Poisson, logit, and linear models for genetic analysis of clinical mastitis in Norwegian Red cows. J. Dairy Sci. 92: 739–748. [DOI] [PubMed] [Google Scholar]
- Woolhouse M. E. J., Dye C., Etard J.-F., Smith T., Charlwood J. D., et al. , 1997. Heterogeneities in the transmission of infectious agents: implications for the design of control programs. Proc. Natl. Acad. Sci. USA 94: 338–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The R code used to generate the data to evaluate the dnIGE model is available on request.