Inter-allelic interactions play a major role in microsatellite evolution

Abstract

Microsatellite mutations identified in pedigrees confirm that most changes involve the gain or loss of single repeats. However, an unexpected pattern is revealed when the resulting data are plotted on standardized scales that range from the shortest to longest allele at a locus. Both mutation rate and mutation bias reveal a strong dependency on allele length relative to other alleles at the same locus. We show that models in which alleles mutate independently cannot explain these patterns. Instead, both mutation probability and direction appear to involve interactions between homologues in heterozygous individuals. Simple models in which the longer homologue in heterozygotes is more likely to mutate and/or biased towards contraction readily capture the observed trends. The exact model remains unclear in all its details but inter-allelic interactions are a vital component, implying a link between demographic history and the mode and tempo of microsatellite evolution.

1. Introduction

Microsatellites form an important genomic component and remain the genetic marker of choice in most non-human systems. Evolution occurs mainly through the gain and loss of single repeat units, leading to the widespread assumption of a simple stepwise mutation model (SMM) [1]. The SMM has several attractive properties, including a linear relationship between evolutionary divergence and time [2,3]. With increasingly large datasets of related individuals genotyped for extensive panels of microsatellite markers [4,5], estimates of microsatellite mutation rates are improving, allowing accurate dating of recent evolutionary splits [5]. However, on closer inspection, these large mutation studies raise as many questions as they answer.

In the largest study yet, Sun et al. identified almost 1500 mutations in confirmed pedigrees [5]. They constructed a refined microsatellite mutation model that incorporates: (i) a length-dependent mutation rate, (ii) higher mutation rates in males, and (iii) constraints that cause longer alleles within a locus usually to contract and shorter alleles usually to expand. Properties (i) and (ii) have been known about for some time [6–8]. Property (iii) has been reported before in almost identical form (see data in [4]) but has usually been overlooked when calculating genetic diversity and divergence rates, the exception being [5]. We refer to property (iii) as the centrally directed mutation (CDM) model, and it has a large impact on estimates of genetic divergence [5].

Sun et al. model the CDM by imposing a mutation bias that varies with an allele's length relative to the population mean, expressed as a Z-score [5]. This method readily captures the empirical pattern but cannot operate in nature because individual alleles have only the length of their homologue for reference. How alleles mutate in a way that correlates strongly with relative allele length therefore remains undetermined. A related issue is the steepness of the relationship between mutation bias and Z-score. According to Figure 2 in Sun et al., an allele with 20 repeats will contract 80% of the time if it is the longest allele at a short locus but only 20% of the time if it is the shortest at a long locus. As before, the mechanism that allows each allele to mutate appropriately for its locus is unclear.

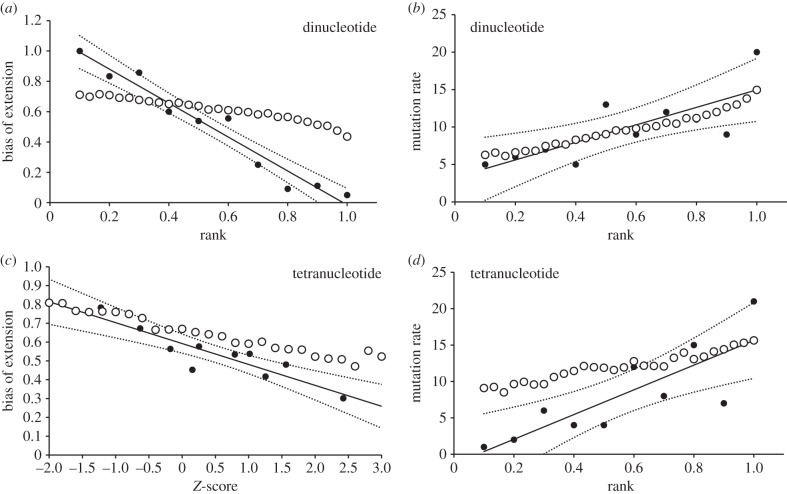
Figure 2.

Can simple allele interaction rules explain the observed local trends? Empirical local trends and panel order are as in figure 1. Open symbols show the results of a simple model where the longer of two alleles in a heterozygote is more likely to mutate (mutation rate) or to contract (mutation bias), applied to a large dataset of allele length frequency distributions (dinucleotides, Dib et al. [10]; tetranucleotides, Rosenberg et al. [11]). All models are symmetrical and have one parameter, P, the probability that the longer allele mutates/contracts, the shorter allele doing the same with probability 1-P. Best-fit values of P for each panel are: (a) 0.95, (b) 0.71, (c) 0.95, (d) 0.92. For mutation rate, mutations are four times as likely to occur in heterozygote genotypes compared with homozygotes.

Mutation rate also reveals a dependency on relative allele length when mutation data are plotted on a standardized scale. One study of largely tetranucleotide repeats reveals an approximately 20-fold increase in rate between the shortest and longest alleles [9] while a study of dinucleotides reveals a fourfold increase [4]. These values can be compared against the very large dataset generated by Sun et al., where mutation rate is plotted as a function of absolute repeat number. All three studies show broad agreement on average mutation rates. However, the slope of mutation rate against absolute repeat number implies differences in mutation rate between the shortest and longest alleles of only 2.8-fold and 1.8-fold for dinucleotides and tetranucleotides, respectively (assuming a locus with alleles ranging from 15 to 25 repeats), far less than the sevenfold increase obtained when data from the two published local trends are combined to yield a single, average trend. For clarity, hereafter we refer to trends based on absolute repeat number as ‘general trends’ while those based on length relative to other alleles at the same locus we refer to as ‘local trends’.

2. Results and Discussion

To explore these apparent contradictions more systematically, we first asked how much information an allele's own length carries about its rank order length. We used published data for a large number of dinucleotides [10], filtered to remove loci with multiple repeat types and converted to repeat units using primer sequences and e-PCR. These data were chosen as the largest publicly available dataset for microsatellites genotyped in Europeans. One allele was chosen at random from each of the 4775 qualifying microsatellites and its length expressed both as absolute repeat number and its Z-score, revealing an r² of only 22%. This rather small value makes intuitive sense because all but the smallest and largest repeat numbers can occur at almost any rank order length.

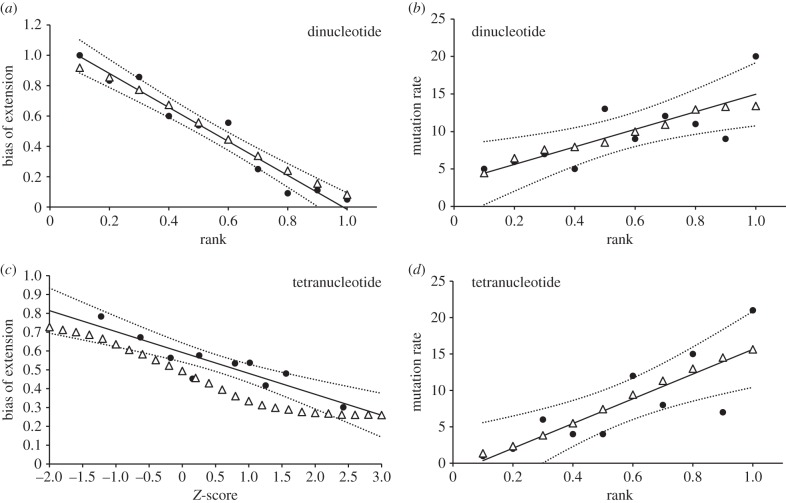
We next asked whether the observed general and local trends are self-consistent, beginning with mutation bias. An empirical general trend for mutation bias is not available, so we assumed the strongest possible relationship, with the proportion of expansion mutations falling from 100 to 0% across the range of repeat numbers generally found in markers: 10–35 repeats for dinucleotides and 5–20 repeats for tetranucleotides. Alleles below and above these ranges are assumed always to expand and contract, respectively. These general trends were then used to back-calculate the expected local trends for dinucleotides and tetranucleotides using the Centre d'Etudes du Polymorphisme Humain (CETH) reference data [10] and data for 513 tetranucleotides genotyped in Europeans [11], respectively. Specifically, each allele was assigned a length bin based on its standardized length relative to other alleles at the same locus. Within each bin, we calculated the expected number of mutations, N, as the sum of the frequencies of all qualifying alleles, and the expected number of expansion mutations, E, as the sum of these frequencies, each multiplied by the appropriate general trend bias. Local trend bias for each bin was calculated as E/N. To compare with published data, it is important to use the same method of standardization. Thus, dinucleotide data were standardized sensu Ellegren [9], whereby alleles are assigned their mid-point cumulative frequency, and tetranucleotide lengths were converted to Z-scores [5]. The calculated local trend for dinucleotides is far too shallow while the trend for tetranucleotides is only slightly too shallow compared with the empirical data (figure 1a and c, respectively). However, the relatively good fit for tetranucleotides is misleading. If the observed local trend is used to reconstruct the general trend, bias only falls from 69 to 43%, too shallow to reconstruct the local trend. Thus, the general and local trends are internally incompatible.

Figure 1.

Microsatellite mutation rate and mutation bias: a comparison between observed local trends and local trends derived from general trends. Local trends refer to trends where mutation rate or mutation bias is plotted as a function of allele length relative to other alleles at the same locus. General trends refer to trends where allele length is expressed as absolute repeat number. In each panel, the empirically derived local trend is shown in solid symbols, together with a best-fit linear trend (solid line) and its associated 95% envelope (dotted line). Open circles show local trends back-calculated from the relevant empirically derived general trend (for back-calculation details, see text). Panels are: (a,b) dinucleotides, (c,d) tetranucleotides, (a,c) mutation bias, and (b,d) mutation rate. Empirically derived local and general trends are redrawn/derived from: panel (a) (local trend, Huang et al. [4]; general trend, maximum possible); panel (b) (local trend, Huang et al. [4]; general trend, Sun et al. [5]); panel (c) (local trend, Sun et al. [5]; general trend, maximum possible); panel (d) (local trend, Ellegren [9]; general trend, Sun et al. [5]). To enable a fair, direct comparison with the empirical data, all back-calculated local trends are expressed on the scale used in the original publication (Rank = rank order sensu Ellegren [9], 0.1 = shortest 10% of alleles, 1 = longest 10% of alleles; Z-score is self-explanatory).

Turning to mutation rate, we used as reference the linear general trends given in Sun et al. Figure 2c, using the stated slopes and X-axis intercepts of 9.5 repeats (dinucleotides) and 3 repeats (tetranucleotides). Shorter alleles were assumed immutable. As with mutation bias, expected local mutation rates were determined by multiplying the frequency of each allele by the expected general trend mutation rate and then summing by standardized length sensu Ellegren [9]. For dinucleotides, the general trend approximately predicts the local trend: in the empirical data, the longest alleles are 3.4 times as mutable as the shortest alleles, compared with 2.4 times as mutable in local trends derived from the general trend (figure 1b). By contrast, for tetranucleotides, the empirical longest allele to shortest allele mutation rate ratio is much higher than for the local trend as predicted by the general trend (43 times compared to 1.7 times, figure 1d). Thus, a reasonable fit is obtained for dinucleotides but the reconstructed local trend for tetranucleotides is too shallow.

If local trends are sometimes too strong to be explained by the empirical general trends, how are they created? One possibility is that homologues interact. To test the plausibility of such a model, we explored the consequences of simple binary rules in which the longer of two alleles in a heterozygote is either more likely to contract or more likely to mutate. Specifically, we constructed symmetrical models with one parameter P. For mutation rate, if a genotype is selected to mutate, the longer allele in a heterozygote mutates with probability P and the shorter allele mutates with probability (1-P). For mutation bias, if an allele is selected to mutate the longer allele contracts with probability P and expands with probability (1-P). Conversely, shorter alleles contract with probability (1-P) and expand with probability P. In homozygotes, P = 0.5 in both models. As heterozygotes may be more mutable than homozygotes [12], we also explored the effect of having the mutation rate of alleles in homozygotes variously 1X, 0.5X and 0.25X as mutable as alleles in heterozygotes.

The above rules were applied separately to the two sets of allele length frequency data, assuming all genotypes occur in Hardy–Weinberg proportions. To see whether these simple models can plausibly recreate the empirical trends, P was varied between 0.5 and 1. When P is set in the range 0.7–0.92, three of the four local trends are captured well, the exception being mutation bias in tetranucleotides (figure 2). Here, the slopes are similar but the empirical data exhibit an overall positive bias, manifest as an upward shift on the Y-axis that cannot be captured by symmetrical models, where mutation bias must average parity. For mutation rate, the simple linear trends suggested by the empirical data are approximated much better if heterozygotes are made more mutable than homozygotes. Specifically, when heterozygotes and homozygotes are equally mutable, the relationship between standardized length and mutation rate becomes distinctly humped, with mutability dipping for the longest allele class instead of contributing the highest value (electronic supplementary material, figure S1).

Failure to find a perfect fit in all cases between empirical trends and the output of simple models indicates that one or more important elements are missing. This is expected for several reasons. First, empirical mutations identified in parentage data [9] involve unusually informative markers and may be less representative of microsatellites as a whole. This represents a special case of the more general issue that different studies use different sets of markers and markers represent only a subset of all microsatellites, potentially meaning that we are sometimes failing to compare like with like. Perhaps more importantly, there are several known properties of microsatellites that are not captured by our models. For example, while human microsatellite markers generally show a net positive mutation bias [5,9,13] our simple models suggest that relatively longer alleles are both more mutable and prone to contraction, implying the exact opposite trend. The true mutation rules are therefore likely to be more complicated. Possible additional elements include model asymmetry, a dependence on the length difference between alleles, an independent impact of repeat number and different behaviours between homozygotes and heterozygotes. If alleles interact, then the outcome may also vary depending on whether one or both alleles carry an interruption mutation. Given that good fits can be obtained with the simplest model, elucidating these more complicated aspects must await future work with larger numbers of verified mutations.

If local trends are too strong to be explained by the observed general trends, options for alternative models appear limited. Consider mutation bias. The key challenge is to find a mechanism by which most loci show the full range of mutation biases despite all alleles descending from a single common ancestor. If the ancestral allele has a positive bias such an allele must usually produce descendants that are both longer and have a negative bias, while a negatively biased ancestor must spawn shorter, positively biased alleles. Similarly, an unbiased ancestor must produce approximately equal numbers of longer and shorter descendants, carrying negative and positive biases, respectively. Such predictability cannot depend mainly on repeat number because absolute repeat number is a poor predictor of bias. Flanking sequences also seem unlikely because most carry far too little variability to account for the range of biases seen. Additionally, even if local trends do evolve, mutations must rapidly and predictably regenerate the properties of any lineages lost through drift. We feel that inter-allelic interactions offer one plausible solution.

In a broader context, inter-allelic interactions have already been implicated as factors that may influence mutation rate of both microsatellites and base substitutions [14,15]. The ‘heterozygote instability’ (HI) hypothesis suggests that mutations are more likely at and near heterozygous sites due to the extra round of DNA replication that occurs when such sites become the focus of gene conversion events in heteroduplex DNA formed during synapsis [16]. Importantly, the HI hypothesis has recently received strong support from whole genome sequencing of parents and progeny in Arabidopsis [17]. However, our current analysis suggests something beyond an influence on mutation rate. In microsatellites, interactions between alleles appear to act as cues that allow mutation behaviour to reflect relative length. Of course, the two processes may operate side by side, with homozygotes being the least mutable and the longer alleles in heterozygotes being the most. Elucidating the exact behaviours will again require further work.

Inter-allelic interactions have interesting implications for population genetics. Sun et al. have already shown how the CDM slows the rate of divergence relative to a strict SMM, with the result that any given level of average squared length difference between microsatellites implies a greater age of separation than previously assumed [5]. If, as our analysis suggests, the CDM depends on allelic interactions in heterozygotes, then loci carrying more heterozygotes will potentially behave differently from those carrying fewer. Interestingly, less variable loci would tend to evolve in a way that is closer to the SMM, so would diverge more rapidly than expected. Since heterozygosity changes over time and with demographic changes, these complexities call into question the idea of microsatellites following a molecular clock [2,3], particularly if rate is affected as well as bias. Just how big the effect sizes will be requires larger studies of pedigree-derived mutations, analysed to determine which rules fit best.

Ethics

All analyses are conducted on data that have already been published by others.

Authors' contributions

W.A. conceived the study, carried out the analyses and drafted the paper; D.K. conducted a wide range a simulations, many of which were not included, but that acted as critical background for the final draft, and helped write the manuscript; A.E. conducted further simulations and helped write the manuscript. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

We received no funding for this study.