Abstract
In the past decade the volvocine green algae, spanning from the unicellular Chlamydomonas to multicellular Volvox, have emerged as model organisms for a number of problems in biological fluid dynamics. These include flagellar propulsion, nutrient uptake by swimming organisms, hydrodynamic interactions mediated by walls, collective dynamics and transport within suspensions of microswimmers, the mechanism of phototaxis, and the stochastic dynamics of flagellar synchronization. Green algae are well suited to the study of such problems because of their range of sizes (from 10 μm to several millimetres), their geometric regularity, the ease with which they can be cultured and the availability of many mutants that allow for connections between molecular details and organism-level behavior. This review summarizes these recent developments and highlights promising future directions in the study of biological fluid dynamics, especially in the context of evolutionary biology, that can take advantage of these remarkable organisms.
I. VOLVOCINE ALGAE AND THE EVOLUTION OF MULTICELLULARITY
High on any list of fundamental questions in biology – a list surely led by the origin of life and the nature of consciousness – is one regarding evolutionary biology: What are the origins of multicellularity (Bonner, 1998)? That is, why and how did the simplest unicellular life forms first appearing on Earth evolve into multicellular organisms, which were not only larger but eventually exhibited cellular differentiation? In other words, what are the (fitness) advantages of being larger and of dividing up life’s processes into specialized cells, increasing complexity (Smith and Szathmáry, 1995; Szathmáry and Smith, 1995)? For microscopic life existing in a fluid environment, these questions unsurprisingly often involve physical processes such as transport (diffusion, mixing, and buoyancy), locomotion, and sensing, because the exchange of materials with the environment is one of the most basic features of life. For these reasons, physical scientists are beginning to move toward these problems in evolutionary biology with the hope of shedding light on these deep issues. As with all fundamental problems in biology, there are model organisms which by community consensus become the focus of research from many differing perspectives. Examples include the enteric bacterium Escherichia coli for sensing and locomotion, the fruit fly Drosophila melanogaster for genetics and development, and Arabidopsis thaliana for much of plant science. The purpose here is to discuss a class of organisms that has emerged as a model for many aspects of biological fluid dynamics. Caveat emptor: many of the problems discussed in this review can only be fully appreciated in their native biological context. Their ultimate solutions will most likely not involve just the application of fluid dynamics. Rather, they will require an interdisciplinary approach in which cell biology, genetics, microscopy, micromanipulation, and some applied mathematics together will unravel the underlying biological complexity. Fluid dynamics will have an important role, but the broader scientific method will be key.
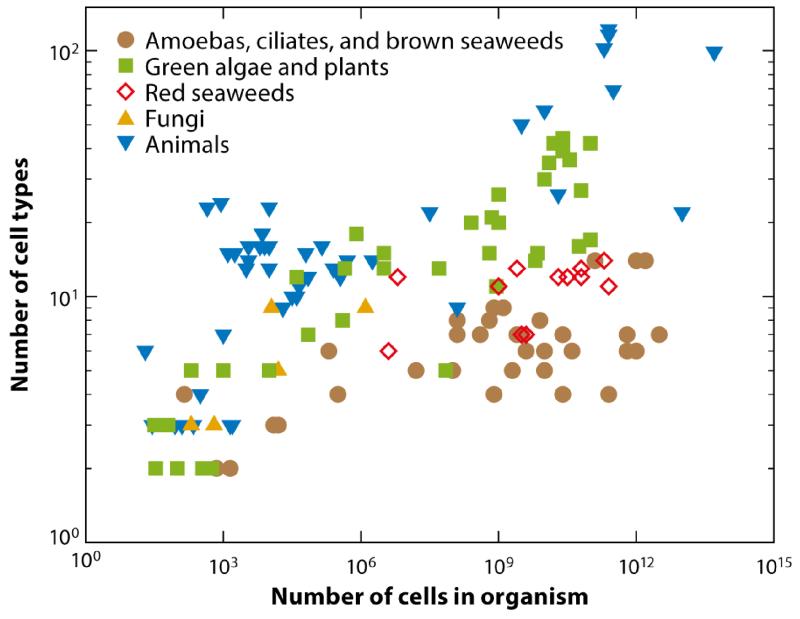
To put the problem of differentiation, complexity, and size into perspective, let us consider the data shown in Figure 1, which were first presented by Bell and Mooers (1997) and then revisited by Bonner (2004). For a range of organisms in the animal and plant world, this figure shows a double logarithmic plot of the number of distinct cell types found in an individual organism as a function of the total number of cells in the organism’s body. Although debate exists about the precise way to count distinct cell types in higher organisms, such subtleties are not important for the present, qualitative discussion. The archetypal unicellular organism, such as a bacterium, is located at (1, 1), whereas a human is just o the upper right of the graph at (1014, 210). (The figure 1014 can be rationalized by the volume of a human, ~ 0.1 m3, and the linear dimension of a typical cell of ~ 10 μm). There is a general trend that larger organisms are more complex, as measured by the number of cell types, but the data are noisy, and it would be unwise to try to find a meaningful power law. Rather, various arguments suggest that a good way to tackle the size-complexity relationship is to be very reductionist and begin at the lower left-hand corner of the graph, where organisms of ever-increasing cell number abruptly make the transition from one to two cell types.
FIG. 1.
The number of distinct cell types as a function of cells in an organism’s body. Figure adapted from Bell & Mooers (1997).
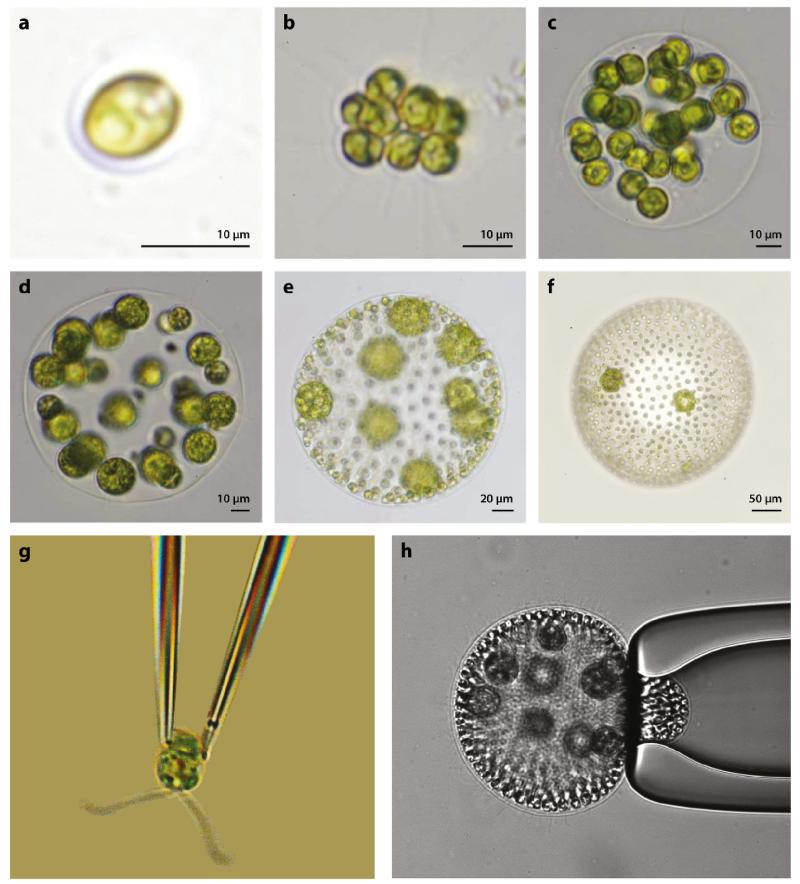
In the late 1800s the great biologist August Weismann (1892) suggested volvocine green algae as a class of model organisms for the study of the transition to multicellularity (Figure 2). Weismann was the originator of germ plasm theory, according to which the germ cells (gametes, from the Greek root meaning ‘spouse’) alone control heredity, whereas the sterile somatic cells (meaning ‘of the body’) in multicellular organisms play no role. This distinction is clearly seen in the volvocine algae, which derive from the unicellular biflagellate Chlamydomonas (Harris, 2009), and continues through species comprising ~ 2n (n ≲ 16) Chlamydomonas-like cells arranged in regular geometric structures, all the way to Volvox, of which there are species containing up to 50, 000 cells in a spheroid several millimeters in diameter (Kirk, 1998). This figure shows a sharp divide at Volvox, for all species shown in Figure 2a-d have cells of only one type that carry out all the functions of life, reproduction and everything else, whereas the species shown in Figure 2e,f have two cell types: sterile somatic cells (galley slaves) mounted in a transparent gel-like extracellular matrix (ECM) with their flagella pointing outwards, and specialized reproductive (germ) cells on the inside. This so-called germ-soma differentiation is the most basic distinction of cell types in biology and can be seen as a first step towards multicellularity. A natural question, returned to below, is why nature put the dividing line at Volvox: Is there something special about the size of Volvox or its cell number that suddenly makes it advantageous to have two cell types?
FIG. 2.
Examples of volvocine green algae: (a) unicellular Chlamydomonas reinhardtii, undifferentiated (b) Gonium pectorale (8 cells) and (c) Eudorina elegans (32 cells), (d) soma-differentiated Pleodorina californica (64 cells), and germ-soma differentiated (e)Volvox carteri (~ 1, 000 cells) and (f) Volvox aureus (~ 2, 000 cells). (g) C. reinhardtii and (h) V. carteri held on glass micropipettes. Panels a–f reproduced with permission from Solari et al. (2006a). Copyright 2006 by the National Academy of Sciences.
As summarized by Kirk (1998) in his celebrated book on Volvox, there are many reasons why this class of organisms is excellent for the study of multicellularity; it is an extant lineage spanning from unicellular to differentiated multicellular species, it is readily obtainable in nature, it has been studied from a variety of different perspectives (biochemical, developmental, genetic), its ecological niches are understood, it developed recently enough that its genome may retain traces of genetic changes in organization, it displays evidence of repeated genetic changes, and it is amenable to DNA transformation. Indeed, the genome of Volvox has recently been sequenced (Prochnik et al., 2010) and, in comparison with that of Chlamydomonas, is providing fascinating information about the genetic changes necessary for multicellularity. For fluid dynamicists theory becomes simpler because these colonies are quasi-spherical and their large size makes visualization easy. In addition, because their size spans from 10 μm to several millimeters, it may be possible to use these organisms to uncover scaling laws of physiology and behavior that underlie the transition to multicellularity (Short et al., 2006; Solari et al., 2006a, 2007, 2006b).
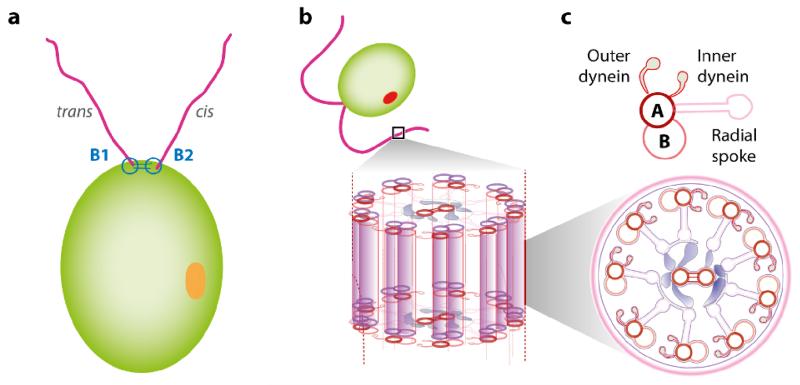
Volvox itself was discovered by Antony van Leeuwenhoek (1700), as described in a famous letter to the Royal Society. Its name was given by Linneaus (1758), in the last entry of his great book on taxonomy, based on the Latin word volvere (to roll) for its characteristic spinning motion around a body-fixed axis. That spinning is a consequence of the coordinated action of the thousands of flagella on its surface, each of which beat in a plane that is tilted approximately 15° from the anterior-posterior axis. All known species rotate in the same direction (clockwise when viewed from the anterior), but there are known inversion mutants that rotate in the opposite sense. These eukaryotic flagella, often called cilia when occurring in large numbers (as on protists such as Paramecium or Opalina) or when emanating from tissues within an organism (as in human respiratory and reproductive systems), must be distinguished from the prokaryotic flagella of bacteria. The latter are rigid, generally helical structures comprising the protein flagellin, turned by the proton-driven motion of rotary motors embedded in the cell wall. Eukaryotic flagella and cilia have a much more complex microstructure (Figure 3). The basic structure, known as the axoneme, consists of parallel microtubules (themselves polymerized tubulin protein monomers) arranged in the form of nine doublets around the periphery and two doublets in the center. This 9+2 arrangement is one of the most highly conserved structures in biology, such that the protein content in Chlamydomonas flagella, which appeared on Earth the better part of a billion years ago, is essentially identical to that in human cilia (Pazour et al., 2005). For this reason, the volvocine algae, and Chlamydomonas in particular, have long been model organisms in the study of human ciliopathies (Ibañez-Tallon et al., 2003). These filaments are cross-linked by proteins such as dyneins that undergo a conformational transition through the hydrolysis of adenosine triphosphate (ATP), so as to slide one filament relative to the other. Coordinated waves of such sliding under the constraint that the microtubule bases are held rigid lead to bending waves.
FIG. 3.
Chlamydomonas and the structure of the eukaryotic axoneme. (a) The two flagella are termed cis and trans based on their position relative to the eyespot (orange). (b) The axoneme consists a 9+2 arrangement of microtubule doublets on which dynein motors initiate interdoublet sliding and produce the flagellar beat. Figure adapted from Wan et al. (2014).
The anchoring of each axoneme occurs in a special structure called the basal body, which also serves as a microtubule organizing center during cell division. Microtubules emerging from each of the two centers are responsible for pulling the two pairs of chromosomes apart. Intriguingly, the dual roles for the organizing centers are mutually exclusive through what is known as the ‘flagellation constraint’, a prohibition against multitasking: Flagella are lost during cell division. It has been suggested that the associated loss of motility during cell division played a role in driving germ-soma differentiation (Koufopanou and Bell, 1993).
As there are several excellent historical and recent reviews on the swimming of microorganisms (Brennen and Winet, 1977; Guasto et al., 2012; Lauga and Powers, 2009), the present article focuses instead on a series of case studies in biological fluid dynamics from the past decade in which the volvocine green algae have been key to substantial progress. These include the first direct measurements of the flow fields around freely swimming microorganisms, studies of nutrient uptake at high Péclet numbers, findings on the nature of interactions of swimmers with surfaces, quantitative studies of how eukaryotic flagella synchronize, elucidation of the mechanism of phototaxis in multicellular swimmers, and exploration of the statistical properties of passive tracers in suspensions of motile microorganisms.
I close this section by pointing out that another set of organisms, the choanoflagellates, is emerging as a model for understanding the transition to multicellularity (King, 2004). Choanoflagellates are understood to be the closest living unicellular ancestor of current metazoans (animals) and can exist in both unicellular and multicellular forms. Their fluid dynamics is just beginning to be studied quantitatively (Orme et al., 2003; Pettitt et al., 2002; Roper et al., 2013).
II. FLOW FIELDS AROUND SWIMMING MICROORGANISMS
Our understanding of the swimming dynamics of microorganisms has advanced over the past few decades in part through the development of new technologies. Berg’s (1971) invention of the tracking microscope enabled the discovery of how the run-and-tumble locomotion of peritrichously flagellated bacteria such as Escherichia coli is coordinated to achieve chemotaxis (Berg and Brown, 1972). Rather than visualizing organisms through a low-magnification objective with a wide field of view, and hence with low spatial resolution, this device continuously re-centers the organism in a small field of view at high magnification, via feedback control of a motorized stage. Likewise, the advent of relatively inexpensive, high-sensitivity and high-speed video cameras and specialized fluorescent dyes has made it possible to study the rapid dynamics of flagellar bundling and unbundling at high temporal resolution, uncovering conformational transitions between different helical structures (Turner et al., 2000). These and many other innovations have made it possible to quantify the stochastic trajectories of bacteria and other swimming microorganisms.
Only recently, however, has attention turned to actually measuring the flow fields around individual organisms, using the method of particle image velocimetry (PIV) (Adrian, 1991). Although such measurements have been made for larger organisms, including fish (Müller et al., 1997) and copepods (Catton et al., 2007), extending the use of PIV down to the micrometer scale has a number of difficulties. First, there is the intrinsically stochastic nature of most microorganism swimming so that, even if the organism swims continuously within the focal plane, it is constantly changing direction. For example, in the run-and-tumble locomotion of E. coli, the cell swims in an approximately straight trajectory, with its multiple helical flagella bundled behind it, but changes direction after approximately 1 s through a tumble, when one or more motors reverse direction and the bundle flies apart. If we wish to use the motion of advected microspheres to trace the fluid flow, then it is necessary to change the local frame of reference to account for such turns. This can be dealt with (see below) but requires careful data analysis. Second, the organisms rarely stay within the microscope focal plane for long, particularly if undergoing run-and-tumble locomotion, thus requiring the acquisition of multitudes of very short video clips. To avoid this problem one can confine the swimmers to quasi-two-dimensional chambers, but wall effects can then become significant and difficult to incorporate into the analysis.
It is in this context that one can first appreciate the role of the green algae in biological fluid dynamics. Let us consider first the case of Volvox. The earliest measurements of flow fields around Volvox appear to be those of Hand and Haupt (1971), who were interested in the mechanism of phototactic response to light (discussed further in Section VI). Their manual tracking of the motion of suspended microspheres near spheroids yielded the first estimates of flow speeds near the colony surface when it is held in place on a microscope slide by a coverslip. To go beyond these crude measurements, researchers were motivated by the use of micropipettes to hold and study giant unilamellar vesicles (Evans and Rawicz, 1990), quasi-spherical lipid bilayer vesicles that can be tens of micrometers in diameter, and by the world of in vitro fertilization, in which oocytes are immobilized with holding pipettes that have been specially shaped to avoid damage to the specimens. It proves straightforward to hold Volvox colonies on micropipettes with gentle suction, or indeed to exert greater suction to investigate the mechanics of distortion of the ECM (see Fig. 2). Seeding the surrounding fluid with microspheres enabled a quantitative measurement of the velocity field as a function of position around the colony surface and its variation with colony size (Short et al., 2006; Solari et al., 2006a). The observed flows can exceed 500 μm/s, establishing that these organisms live in the regime of large Péclet numbers (Section III). Perhaps even more importantly, the observed dependence of the tangential fluid velocity field on the angular coordinate from the anterior to posterior pole was highly reminiscent of that in the celebrated squirmer model of Lighthill (1952). The existence of this biological realization of squirmers has made it possible to test many aspects of theoretical predictions arising from that model.
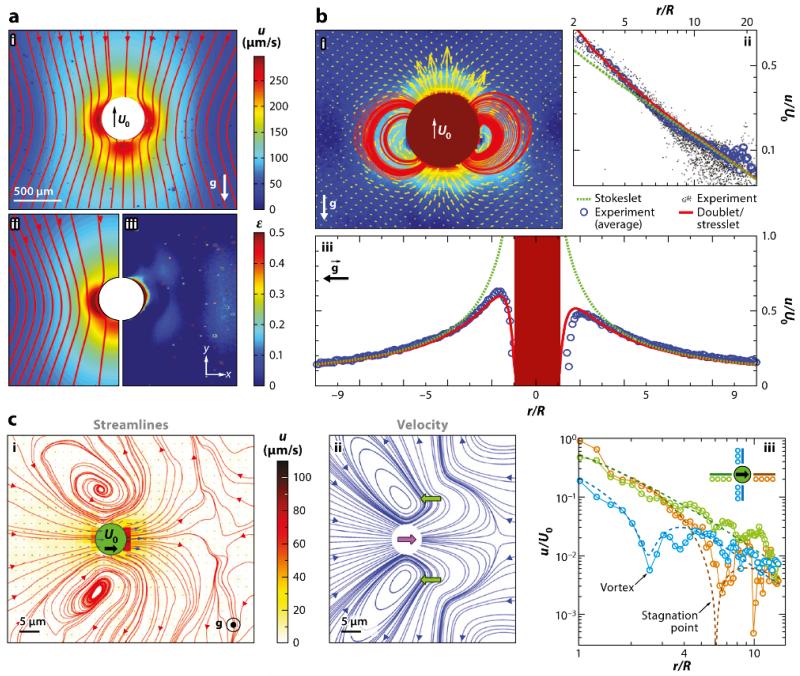
To go beyond measurements of the flows around immobilized colonies, one can take advantage of the bottom heaviness of Volvox, which results from the positioning of the daughter colonies in the posterior hemisphere of the spheroid (which is at the upper right of the colony shown in Fig. 2h). Such an asymmetrical distribution of mass is responsible for the phenomenon of gyrotaxis, the combination of swimming and reorientation by fluid vorticity (Pedley and Kessler, 1992). In the absence of any external fluid flow Volvox will right itself like a ship with a heavy keel and swim upward against gravity. A tracking microscope can then be built that uses a motorized microscope stage turned vertically to control the position of a lightweight video camera that visualizes an organism as it swims upward in a fixed chamber through fluorescent microspheres illuminated by a laser light sheet. This enables PIV in the frame of reference of the swimmer. The steadiness of Volvox swimming has allowed for averaging over up to 50,000 video frames to get extremely accurate flow fields (Drescher et al., 2010a) (Figure 4).
FIG. 4.
Flows around freely swimming green algae. (a) Velocity field around Volvox carteri in the laboratory frame. (i,ii) Magnitude and streamlines of u and theoretical fit, with a common color bar. (iii) The relative error of fit. The direction of gravity is indicated. (b) Near-field flow around V. carteri. (i) Magnitude, vector fields, and streamlines of u after subtracting a fitted Stokeslet, with the color bar as in part i of panel a. (ii) Velocity magnitude taken along a horizontal cross section through the center of a colony. An average Stokeslet (green dashed line) follows the observed decay (blue circles) averaged over the sample set of colonies (black dots). Deviations from a pure Stokeslet appear at distances less than ~ 5R and are accounted for by adding a source doublet and a stresslet (red solid line). (iii) Vertical section of u through the center of a colony, with symbols as in panel ii, showing front-back asymmetry due to the stresslet. (c) Average flow field of Chlamydomonas reinhardtii. (i) Streamlines (red) computed from velocity vectors (blue). Color scheme indicates flow speed magnitudes. (ii) Streamlines of the azimuthally averaged three-Stokeslet model. Flagellar thrust results from two Stokeslets (lateral green arrows), whose sum balances the drag on the cell body (central purple arrow). (iii) Decay of the velocity magnitude for the three directions indicated by separate colors in the inset compared to results from the three-Stokeslet model (dashed lines). Figure adapted with permission from Drescher et al. (2010a). Copyright 2010 by the American Physical Society.
For many swimming organisms (bacteria, spermatazoa, uniciellular algae), it is convenient to classify their structure based on the far-field behavior of the flow they produce, which is that of a stresslet [i.e. two force monopoles (Stokeslets) separated by a small distance]. Configurations with flagella behind the body are known as pushers, whereas those with flagella in front, such as Chlamydomonas, are pullers. Volvox has such a high degree of symmetry that it does not have an appreciable stresslet component; instead, the far field is dominated by the Stokeslet contribution owing to its significant density relative to the surrounding fluid. Higher-order singularities become important close to the colony surface. One of the key findings in the case of Volvox was that the Stokeslet is the dominant force singularity observed beyond approximately one body diameter. This finding turns out to be crucial in understanding the wall-mediated effects described in Section IV and in the problems of tracer statistics in suspensions discussed in Section VII. Recent work has explored the decomposition of these flows into irreducible representations (Ghose and Adhikari, 2014).
In extending such PIV measurements down to the unicellular level, Chlamydomonas has many advantages over bacteria. First, with a body size of 10 μm in diameter, it is straightforward to track at moderate magnification, thus eliminating the need for a true tracking microscope. Second, we know from three-dimensional tracking studies (Polin et al., 2009) (see Section V) that its two flagella, each 10 – 12 μm in length and beating at ~ 60 Hz in a characteristic breaststroke waveform, achieve synchrony persisting for a characteristic time on the order of 10 s. Measurements of the mean-square displacement of free-swimming cells show a crossover from ballistic behavior below this timescale to diffusive behavior beyond (Rafai et al., 2010). This long persistence time of straight swimming enormously increases the likelihood of in-focal-plane trajectories. Finally, cell bodies can be tracked via their natural autofluorescence, along with fluorescent microspheres used for PIV. Analysis of very large amounts of data yields the time-averaged velocity field shown in part i of Figure 4c. We can recall that Chlamydomonas spins around its axis at ~ 2 Hz (Harris, 2009), so the time average is over not only the flagellar waveform but also the orientation of the cell. There are several important features of this flow field. First, it is similar to that of a puller stresslet far away from the cell, pulling fluid in from the front and back, sending it out along the sides of the cell. But closer to the cell body there is more structure, including the swirls from the two flagella and a stagnation point in front of the cell. If we associate a point force with the cell body and one each at the midpoint of each flagellum, we arrive at the simplest singularity model of Chlamydomonas, whose flow field (part ii of Fig. 4c) is remarkably close to the measured one and exhibits the observed spatial decay (part iii of Figure 4c). This provides important evidence in support of point force models for flagella, particularly in the context of synchronization (Section V). In independent and contemporaneous work, Guasto et al. (2010) succeeded in measuring the time-resolved velocity fields around Chlamydomonas cells swimming in a thin free-standing fluid film. Using the standard result for the rate of power dissipated in a two-dimensional fluid of viscosity μ, P = ∫ dA2μE : E, where E = (1/2)[∇u + ∇uT] is the rate of the strain tensor, they found peak powers of approximately 15 fW and average powers through the cycle of approximately 5 fW. This is consistent with P = Fv, where F is the Stokes drag force F = 6πμRv ~ 10 pN on a sphere of radius 5 μm moving at a speed v ~ 100 μm/s, provided one accounts for the average of the dissipated power being approximately four times the dissipation from the average flow. These results are consistent with estimates of forces and powers based on analysis of the actual flagellar waveforms (Leptos et al., 2013). These numbers give interesting insight into the consumption of ATP by beating flagella. Using the peak power, the duration of the power stroke, and the hydrolysis energy per ATP molecule, one finds that the consumption of ATP molecules is on the order of 5,000 per axoneme per beat, or approximately 1 every few nanometers along the axoneme. Given the microstructure of the axoneme this is far less than full capacity.
Flow field measurements were ultimately extended to the case of bacteria (Drescher et al., 2011), using a smooth-swimming mutant of E. coli (HCB437) that does not tumble. This removes one of the key impediments to tracking but still requires the collection of many short-duration video clips. The resulting flow field is that of a pusher stresslet, with clear evidence of the r−2 decay of the flow field, and an amplitude of the stresslet characterized by a Stokeslet strength of 0.42 pN and a separation of 1.9 μm, very consistent with expectations for an organism the size of E. coli. By restricting measurements to trajectories close to a no-slip surface, one can also see the modifications to the flow field due to that boundary, which are fully consistent with calculations of stresslets near surfaces (Blake, 1971a), most importantly demonstrating the weaker r−3 decay and multilobed structure.
III. LIFE AT HIGH PÉCLET NUMBERS
All the organisms considered in this review live in a world of small or even ultrasmall Reynolds numbers, Re = UL/ν. Even for the largest Volvocales, with L ~ 0.1 cm and a swimming speed of at most U ~ 0.1 cm/s, we have Re ~ 1. But the neglect of advective contributions to momentum transport does not carry over to the transport of molecular species. In this case, the relative importance of advection to diffusion is given by the Péclet number, Pe = UL/D. Because the diffusivity D of small molecular species is typically ~ 10−5 cm2/s, three orders of magnitude smaller than the kinematic viscosity of water, the Péclet numbers are that much larger. Thus, even for Chlamydomonas we find Pe ~ 0.1 – 0.5 (Tam and Hosoi, 2011), whereas for Volvox, it can be several hundreds (Short et al., 2006; Solari et al., 2006a). This is a very different regime than that for the case of bacteria, with L ~ 1 – 5 μm and U ~ 10 – 40 μm/s, so Pe ~ 0.01 – 0.2, as emphasized by Berg and Purcell (1977) in their classical work on chemoreception.
One of the most basic possible implications for organisms living in a world in which advection matters is a change in the rate of nutrient uptake or waste dispersal, relative to the purely diffusive behavior. The first experimental evidence that fluid flow would matter for the metabolism of Volvox colonies came from comparative studies of germ cell growth under normal conditions (Solari et al., 2006a), deflagellation of the mother colony, the removal of germ cells in a quiescent fluid, and one in which artificial stirring was provided. It was shown that a lack of external fluid flow reduced germ cell growth, which could be rescued by stirring. Later work showed significantly stronger evidence of phenotypic plasticity in the flagellar apparatus in the presence of nutrient deprivation for Volvox than for Chlamydomonas (Solari et al., 2011).
Our discussion of theoretical approaches to nutrient uptake at large Pe begins by noting that the transport of a scalar quantity in the presence of flow is a classic problem in fluid mechanics, first studied in detail, with heat conduction providing a physical and mathematical analog for diffusion, using the method of matched asymptotics in the context of heat transport from a solid sphere in a laminar flow (Acrivos and Taylor, 1962). In a quiescent system, neglecting buoyancy effects, the current of heat Q is given by the diffusive flux, itself calculated from the gradient of the equilibrium temperature field deviation T(r) = T0(1 − R/r), so Q ~ R. At very large Pe, a boundary layer develops in which there are enhanced thermal gradients at the front of the sphere and a long trailing thermal wake. A balance between the local advective radial flow and diffusion leads to a boundary layer thickness δ ~ Pe−1/3 and the flux enhancement Q ~ RPe1/3.
Organisms such as Volvox have substantial fluid flow over their surfaces driven by flagella, and although there is a no-slip condition, one expects the uptake rate to be different than the non-self-propelled situation. The first such calculation was done by Magar and colleagues (Magar et al., 2003; Magar and Pedley, 2005) using both steady and unsteady squirmer models, with similar results found in a different model with a similar tangential velocity profile (Solari et al., 2006a). The alteration of the velocity field in the neighborhood of the surface leads to the scaling δ ~ Pe−1/2 and Q ~ RPe1/2.
A heuristic argument suggests a possible implication for this new scaling law. An organism with the architecture of the Volvocales has all or at least the vast majority of its cells on its surface, so its metabolic needs must scale as the surface area, ~ R2. Without flagella-driven flows the nutrient uptake rate scales as R, implying a bottleneck at some radius, suggesting that Volvox could not live by diffusion alone. Although difficult to estimate, this bottleneck size appears to be in the middle of the Volvocales size spectrum. Now, if we adopt a simple model for swimming, in which the total propulsive force from flagella is proportional to the number of somatic cells, and hence R2, while the drag is proportional to the radius R, we conclude that the swimming speed U ~ R, which in turn implies Pe ~ UR ~ R2, and hence Q ~ R2, removing the diffusive bottleneck. This result suggests that there is a fitness advantage per somatic cell to be in a larger colony that swims faster, providing a potential driving force for increased size, although other factors can surely play a role, such as the ability to escape from predators. It also suggests a reason for germ-soma differentiation, for if the cooperative swimming is needed to enhance nutrient acquisition then sequestering the germ cells inside the colony overcomes the lack of swimming during cell division (the flagellation constraint). This idea is complementary to the argument by (Koufopanou and Bell, 1993) that larger organisms will sink too far in the water column during cell division, again because of the flagellation constraint, without developing germsoma differentiation.
Looking more generally at the possible surface velocity profiles within squirmer models, Michelin and Lauga (2011) recently showed that optimizing swimming is equivalent to optimizing nutrient uptake for all Pe. Along with the work of Tam and Hosoi (2011) on optimizing waveforms of biflagellated algae for nutrient uptake, we can see the emergence of more quantitative mechanical analysis of problems in evolutionary biology.
IV. SURFACE INTERACTIONS
In their natural habitats, many swimming microorganisms find themselves close to surfaces, from bacteria in confined physiological environments to sperm cells in the fallopian tubes. On rather general grounds, it would be expected that nearby surfaces can induce long-range interactions with such swimmers, owing to the slow spatial decay of the low-order multipole flow fields of the Stokeslets and stresslets (Blake, 1971a; Blake and Chwang, 1974). The presence of a no-slip wall can also induce large-scale eddy currents that can assist feeding, as first discussed by Higdon (1979) and elaborated on more recently in several contexts (Orme et al., 2003; Pepper et al., 2010). This section considers two problems involving the swimming of organisms near surfaces to illustrate the role the volvocine algae have played in revealing new phenomena and in testing various theoretical predictions.
In 1963, Rothschild observed that sperm cells accumulate near the walls of a container, an effect seen more recently with bacteria (Berke et al., 2008). There have been two contrasting explanations for this effect: one based on long-range hydrodynamic interactions (Berke et al., 2008) and another based on contact interactions with the wall (Li and Tang, 2009). The first argument starts from the picture of sperm or bacteria as generating far-field flows associated with pusher stresslets, and examines the effects of a no-slip wall on both the orientation and distance from the wall. A straightforward calculation shows that cells swimming parallel to the wall experience an attractive interaction decaying with distance as z−3 and torques that will tend to turn non-parallel orientations toward parallelism, at a given separation. Assuming that the parallel orientations are achieved, it is possible to balance the attraction against diffusion to arrive at a steady-state profile that shows accumulation near walls, as in experiments, although the quantitative agreement at short distances is only fair.
The second approach argues that long-range hydrodynamics play little role: instead, the direct contact interaction with the surfaces is crucial. Here the picture is one in which the incoming and outgoing angles of a swimmer approaching and then leaving a wall are very different. If most incoming orientations lead to shallow outgoing angles, then cells will tend to accumulate near the walls, with rotational diffusion randomizing the outgoing trajectories.
Understanding when the effects of long-range hydrodynamic interactions on cellular reorientation dominate over rotational Brownian motion is an important general issue not only in cell-surface interactions, but also in cell-cell scattering. A simple argument suggests that there is a characteristic length scale, termed the hydrodynamic horizon, beyond which hydrodynamic effects are negligible relative to rotational diffusion (Drescher et al., 2011). Let us consider a bacterium at the origin, and the far-field velocity field around it,
| (1) |
where A = ℓF/8πμ is the stresslet amplitude, and d′ is the unit vector in the swimming direction. The position and orientation of a second swimmer, at position x and moving with speed V0 in direction d, obey
| (2) |
| (3) |
where ω is the vorticity, and Γ is a shape factor for rod-shaped cells. If we assume there is an interaction timescale τ between the two cells, the angular rotation of the second cell will be Δϕ ~ ωτ, where ω falls off as A/r3, so ⟨Δϕ(τ, r)2⟩H ~ A2τ2/r6. The corresponding mean squared angular deviation from rotational Brownian motion will be ⟨Δϕ(t)2⟩D = 4Drτ, and a balance between the two effects occurs at the length scale
| (4) |
Estimates for E. coli (Drescher et al., 2011) suggest that rH ≃ 3.3 μm, a value that would require a volume fraction of cells on the order of 5 – 10%, which approximates the limiting value at which collective effects are observed. This line of reasoning suggests therefore that in dilute suspensions and in the interaction of cells with surfaces long-range hydrodynamic interactions should play a minor role, and more local effects should be dominant.
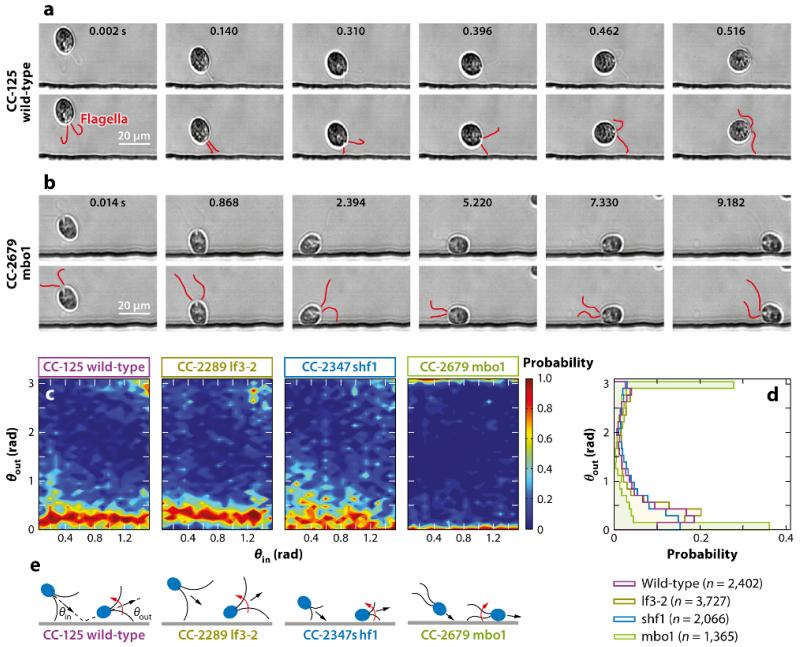
Kantsler et al. (2013) tested these ideas by directly visualizing the interactions between swimming microorganisms and surfaces in microfluidic chambers. They used bull spermatazoa as an example of pusher swimmers, and wild-type and mutant strains of Chlamydomonas were the chosen pullers. The essence of the results is contained in the scattering plots of outgoing versus incoming angles (Figure 5), which clearly show the strongly inelastic character of surface interactions. These can be attributed to purely geometric effects, in which the tail undulations for sperm trace out a wedge larger in amplitude than the head diameter, thus driving the head into the wall at a slight angle. This can be modified by changing the temperature, which alters the beat amplitude and correspondingly changes the probability distribution function. In the case of Chlamydomonas the high-speed videos show directly that cells interact with the wall through flagellar contact and depart from the wall at a shallow angle determined by the geometry of the flagellar waveform relative to the body size (Figure 5). Experiments with mutants having shorter flagella and those moving only backward are consistent with this geometric picture.
FIG. 5.
(a) Scattering process for wild-type Chlamydomonas CC-125: (top row) original images and (bottom row) flagella highlighted in red. Results for the long-flagella mutant lf3-2 and the short-flagella mutant shf1 appear qualitatively similar. The scale bar is 20 μm. (b) As in panel a but for the mutant pusher mbo1 (which moves backward only), which remains trapped for several seconds. (c) The conditional probability distributions P(θout|θin) indicating that, for all four strains, the memory of the incident angle is lost during the inelastic collision process owing to multiple flagellar contacts with the surface. (d) The cumulative scattering distribution P(θout) showing how cilia length and swimming mechanisms determine the effective surface-scattering law. (e) Schematic illustration of the flagella-induced scattering and trapping mechanisms. Figure adapted with permission from Kantsler et al. (2013).
Squires (2001) pointed out one of the more intriguing consequences of the presence of a no-slip boundary on a nearby Stokeslet (Blake, 1971a). Building on earlier work on hydrodynamically induced attractive interactions between colloidal particles near walls (Squires and Brenner, 2000), he observed that if it were possible to levitate a pair of spheres near the upper surface of a container, so that their individual Stokeslets (due to gravity) pointed away from the ceiling, there would be a weak attractive interaction between the two, mediated by the no-slip surface. Although he imagined something like an electrophoretic mechanism to achieve the levitation of passive particles, Volvox naturally swims upward because of its bottom heaviness and thus shares this behavior. Using a tracking system designed for protists, Drescher et al. (2009) stumbled upon a realization of Squires’ calculation while investigating the possibility of complex pairwise interactions between spherical swimmers, motivated by simulations on suspensions of squirmers (Ishikawa and Pedley, 2008).
As an aside, I note that the tracking system used for these experiments addresses some of the key difficulties encountered when studying the swimming of large protists. If one wishes to examine swimming far from walls, then the experimental chamber must be many times the organism’s diameter, approaching at least the centimeter scale. To avoid triggering a phototactic response by the organisms, one must use red light illumination, but this, combined with the larger chamber size, can produce thermal convection currents that overwhelm the swimming cells. Great care must be taken to avoid this by suitable stirring of an external heat bath.
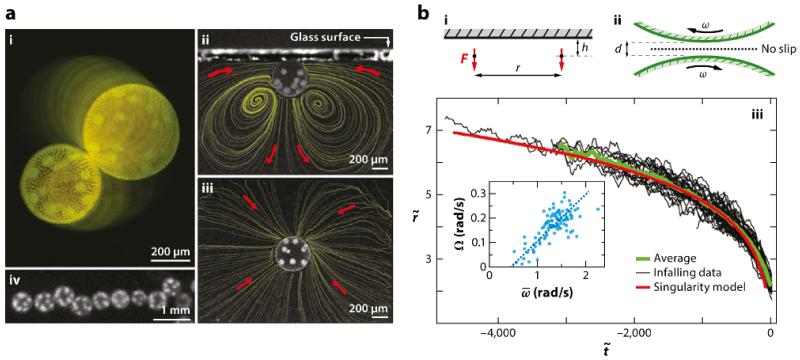
Drescher et al.’s discovery was termed a hydrodynamic bound state, and its basic properties are illustrated in Figure 6. Two nearby Volvox swimming up to the top surface of the chamber are attracted together and orbit each other in a stable state. Although the orbiting is a particular feature of Volvox, the infalling of the two colonies toward each other is in precise agreement with theory, provided one treats the interactions between the two colonies as those of two Stokeslets. The measurements of the flows around freely swimming Volvox discussed in Section II provide justification for this approximation. When the two Volvox are up against the chamber top, the only degrees of freedom are their lateral positions xi, which evolve according to , where u(xi) is the local velocity at colony i due to the second colony. The upswimming speed U of colonies can be readily measured, as can their settling speed V when deflagellated, so the Stokeslet strength is simply F = 6πμR(U + V), and the distance h of each Stokeslet from the wall is the colony radius R. If we rescale the radial distance between colonies as and time as , then the infalling trajectories obey
| (5) |
The excellent agreement with the data shown in Figure 6 is strong evidence for this wall-mediated flow mechanism. The analysis has been extended to account for the orbiting dynamics of the colonies by an application of lubrication theory, and a second type of bound state that occurs when colonies hover near the chamber bottom. Sophisticated conformal mapping methods have recently been developed to treat more complex examples of hydrodynamic bound states (Crowdy and Samson, 2011).
FIG. 6.
(a) Observations of the hydrodynamic bound state of Volvox. (i) View through the top of a glass chamber showing superimposed images taken 4 s apart, graded in intensity for clarity. (ii) Side and (iii) top views of a colony swimming against a coverslip, with fluid streamlines from particle image velocimetry. (iv) A linear cluster viewed from above. (b) Data and analysis of the hydrodynamic bound state of Volvox. Geometry of (i) two interacting Stokeslets (side view) against an upper no-slip surface and (ii) the gap between nearby spinning colonies. (iii) Radial separation r of infalling colonies, normalized by the mean colony radius, as a function of rescaled time for 60 events (black). The running average (green) compares well with predictions of the singularity model (red). (Inset) Orbiting frequency Ω versus mean spinning frequency , and the linear fit. Figure adapted with permission from Drescher et al. (2009b). Copyright 2009 by the American Physical Society.
V. SYNCHRONIZATION OF FLAGELLA
One of the long-standing issues in the swimming of microorganisms is the manner in which flagella synchronize. A key historical point is the observation by Gray (1928), Rothschild (1949), and others that nearby swimming sperm cells tend to synchronize their beating, and this was the motivation for Taylor’s (1951) celebrated model of waving sheets discussed below, although synchronization occurs in both prokaryotic and eukaryotic systems (Lauga and Goldstein, 2012). In the former case, the helical flagella of peritrichously flagellated bacteria bundle and unbundle as the rotary motors that turn them stochastically switch direction. In the unbundled state, a bacterium executes a tumble, whereas when bundled, the cell body moves forward in a straight line. This is the run-and-tumble locomotion that has been much studied. Although the underlying biochemistry of power generation and switching regulation is known in exquisite detail for bacteria, the bundling dynamics in vivo are not [although there are elegant macroscopic studies of this problem with mechanical models (Kim et al., 2003)]. The eukaryotic case is the precise opposite in many ways, for there is now emerging a detailed body of work on the synchronization dynamics, but the (admittedly more complex) biochemistry of beat generation and regulation is still unclear. We focus on the eukaryotic situation here.
No discussion of synchronization is complete without reference to the famous work of Huygens (1893) on the synchronization of pendulum clocks, reproduced in a modern setting by Bennett et al. (2002). Huygens discovered that nearby clocks supported on a common structure would phase lock, typically in antiphase, owing to vibrations in the structure. In modern language we would say that the two oscillators synchronized through a weak, presumably linear coupling. The fundamental question in the biological context can be stated as, What is the biological equivalent of the wall coupling Huygens’s clocks? One of the first key insights was provided by Taylor (1951), whose work sparked the search for a hydrodynamic mechanism.
Taylor’s work on waving sheets abstracted the problem of synchronization to the analysis of the fluid dynamics of two parallel, laterally-infinite sheets of an inextensible material subjected to sinusoidal traveling waves of vertical displacement. By calculating the rate of energy dissipation in the surrounding fluid as a function of the relative phase of the two waves he found that there is a minimum in the dissipation when the waves were nested (i.e., in phase). This was not a dynamical calculation by which synchronization was obtained from an arbitrary initial configuration, although later work has done this (Fauci, 1990), including that on the effects of sheet flexibility (Elfring and Lauga, 2011). Of course, the minimization of dissipation is not a general physical principle from which to derive behavior; it may be true in a given situation, but it is not a satisfactory approach in general. We expect that one needs to consider the response of the axoneme as a whole (motors, filaments) to forces and torques in order to understand synchronization. It is important to emphasize the distinction between the mechanism of the coupling (hydrodynamic, elastic) and the mechanism of response of the flagella to the forces and torques produced by a neighboring filament. The latter could be related to the molecular motors themselves, to mechanosensitive ion channels in the flagellum, or other as yet unknown biological features.
A. Pairs
The most important early work on the synchronization of eukaryotic flagella was done by Rüffer and Nultsch (1985, 1987, 1997a,b). Using high-speed imaging techniques of the day (images captured on film) and manual light-table tracings of individual movie frames, they established the essential features of flagellar synchronization for both wild-type and a mutant of Chlamydomonas. Although their methods lacked connection with the more recently developed viewpoint of stochastic nonlinear oscillator theory, and their observations were not fully quantitative, their essential findings are seminal.
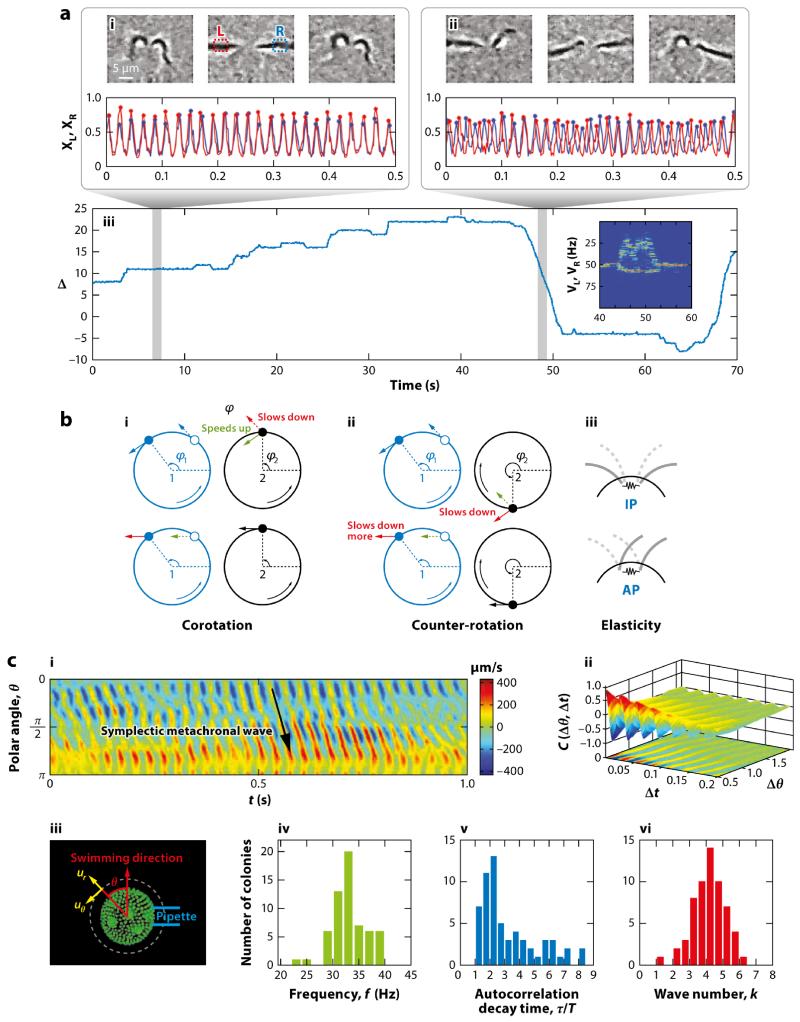
One of their most important findings was the existence of three distinct modalities of beating; synchrony, synchrony with transient interruptions, and asynchrony (Rüffer and Nultsch, 1987). The synchronous state (seen ~85% of the time) is the familiar breaststroke, in which there may be slight variations in the period from beat to beat, but the two flagella appear phase locked. The interrupted synchrony (~10%) took the form of several faster beats of one flagellum (trans; see Figure 3), which would then re-synchronize with the cis flagellum. In the asynchronous state (~5%), the two flagella had different frequencies and no phase locking. These observations were made with individual movies lasting only a few seconds, and the authors proposed that these different beating patterns corresponded to three distinct subpopulations of cells.
One of the features that makes Chlamydomonas so useful in the study of eukaryotic flagella is the relative ease with which it can be studied by micropipette manipulation, the method of choice for Rüffer & Nultsch. With digital high-speed video microscopy it is now possible to obtain long time series of flagellar beating and to quantify synchrony in a way that allows quantitative comparison with theory (Polin et al., 2009). Of the many ways to quantify the beating dynamics, the simplest and most straightforward is essentially a Poincaré section. Small interrogation windows are created within the digital images on either side of the cell body, and the pixel intensity in each is examined over time (Fig. 7). A criterion based on those intensities can be used to define the discrete times at which the phase angle θi of each flagellar oscillator reaches a multiple of 2π, with linear interpolation of the phases in between those times. From these, one can construct the normalized phase difference Δ = (θ1 − θ2)/2π. Periods of synchrony correspond to plateaus in Δ(t), steps up or down by integers correspond to the transient asynchronies (henceforth called slips) that Rüffer & Nultsch found, and asynchronous beating is marked by Δ(t) locally linear in time (termed drifts). Part iii of Figure 7a shows a typical trace of Δ(t) over a bit more than 1 min, and we see all three behaviors Rüffer & Nultsch found but in a single cell! Averaging over many cells shows the fraction of time spent in the three modes of beating to be 0.85: 0.10: 0.05 within experimental error. This is a state of a airs just like in statistical physics, where ensemble averages (over many cells) and time averages (on a single cell) yield the same results.
FIG. 7.
(a) Synchronization in Chlamydomonas. (i,ii, top) Images from a high-speed video of flagellar beating in synchrony and during asynchrony, with interrogation windows for Poincaré sections in part i. (i, ii, bottom) Time series of left and right pixel intensities in windows. (iii) Time series of phase difference Δ over 70 s, showing periods of synchrony, slips, and drifts. (Inset) Fourier transform during transition from synchrony into drift and back. Panel a adapted with permission from Polin et al. (2009). (b) Mechanisms of synchronization. In the elastohydrodynamic mechanism, (i) corotation leads to in-phase (IP) synchrony, and (ii) counter-rotation produces antiphase (AP) locking. (iii) Elastic couplings can provide a competing effect. Panel b adapted with permission from Leptos et al. (2013). (c) Metachronal waves in Volvox carteri. (i) Space-time illustration of a radial component of the fluid flow measured near the colony surface. (ii) Correlation function of waves. (iii) Confocal microscope image of Volvox, showing the colonial axis and the radius for velocity components (dashed). Histograms of (iv) beat frequencies, (v) decay times of the correlation function scaled by the beat period, and (vi) the metachronal wave number for 60 colonies. Panel c adapted with permission from Brumley et al. (2012).
In Figure 7, we can see that the synchronous periods are noisy. One can easily calculate the expected thermal fluctuations of a passive axoneme based on its length and stiffness and deduce that the observed noise level is much larger. This is biochemical noise associated with the underlying action of molecular motors distributed along the length of the axoneme. Whether one has a reduced description of flagellar dynamics in terms of phase angles or complete waveforms, a fundamental question is how to extract useful information about the underlying biomechanics of beating and synchronization from time series. We discuss here one analysis of phase-angle dynamics that has proven useful. In the absence of any coupling between the oscillators, their phase angles would evolve as , so , where δν is the intrinsic frequency difference (ω1 − ω2)/2π. Any coupling between the two oscillators must respect the periodicity of the angles and, in the simplest case, would depend only on the angle difference Δ. As seen above, the actual time series of Δ is noisy, and the equation of motion for Δ should be a stochastic ordinary differential equation (ODE), the simplest case being additive noise on top of a deterministic dynamics. An example of the latter is the famous Adler (1946) equation, first derived in the context of the synchronization of electronic oscillators. Introducing a random noise ξ(t), we obtain
| (6) |
where ϵ is a coupling parameter for the lowest-order periodic term. We take ⟨ξ⟩ = 0 and ⟨ξ(t)ξ(t′)⟩ = 2Teffδ (t−t′), where angular brackets denote an average over realizations of the noise and Teff can be thought of as an effective temperature.
To estimate δν, ϵ, and Teff from the time series, one notes that the stochastic Adler equation also reflects the motion of a Brownian particle on a tilted washboard potential. Periods of synchrony correspond to trajectories near one of the minima, slips correspond to thermally assisted hopping from one minimum to an adjacent one, and drifts are found in the regime in which the tilt is sufficiently large that there are no longer any minima, so the particle runs downhill. If the noise level is not too large, then the fluctuations near any given minimum occur in a potential well that is well approximated by a quadratic, and one can appeal to known results to obtain three independent observables from which to determine the unknowns. These are the amplitude and decay time of the autocorrelation function of Δ,
| (7) |
and the relative left-right hopping probability,
| (8) |
Analysis of large amounts of data yields intrinsic frequency differences that are smaller than a few percent in the synchronized regime but are as large as 20% during drifts. We conclude that Chlamydomonas is able to change the internal frequency difference between its two flagella. When it is small, the interflagellar coupling leads to synchronous behavior, and when it is large, there are drifts. A consistency check in this analysis is that the tilt of the washboard potential implies that there is a small shift in the phase of the locked state from zero, approximately one-eleventh of a cycle. This had independently been measured by Rüffer & Nultsch. Subsequent analysis showed that the noisy Adler equation is in quantitative agreement with the detailed dynamics of a phase slip (Goldstein et al., 2009).
These observations suggested that individual Chlamydomonas cells execute a eukaryotic equivalent of bacterial run-and-tumble locomotion which bacteria do by stochastically bundling and unbundling their flagella: run-and-turn locomotion. If this is the case, then a population should diffuse at a corresponding rate. Measurements of the diffusion of cells in a suspension yielded diffusivity D ~ 10−3 cm2/s. For a stochastic process of the type imagined, we expect D ~ u2τ, where u is a typical swimming speed and τ is the mean time between turns. For Chlamydomonas, we know that u ~ 100 μm/s, so τ should be ~ 10 s. Measurements of the trajectories of individual cells indeed showed that there is an exponentially distributed PDF of the time between sharp turns, with a time constant of 11 s (Drescher et al., 2009). Although models are now emerging to describe this run-and-turn locomotion from a microscopic picture of noisy flagellar orbits (Bennett and Golestanian, 2013), it must be emphasized that at present there is no understanding of the biochemical origin of this timescale.
Let us now consider some of the leading proposed mechanisms by which flagella can synchronize, and their corresponding models. There are two basic types of mechanisms proposed: (a) waveform compliance and (b) variable forcing. The easiest way to visualize these is to first adopt the point of view that the motion of flagella during a beat cycle can be represented by the motion of microspheres around closed trajectories. That this can be a faithful representation of real flagella is seen in the above discussion of the flow fields around individual Chlamydomonas cells, for which the three-Stokeslet model provides a surprisingly accurate representation of the time-averaged flow field (Drescher et al., 2010a). This provides ex post facto justification for many models of synchronization. With regard to waveform compliance, the work of Niedermayer et al. (2008) provides a particularly clear derivation of a key elastohydrodynamic effect. With the flagella modeled for analytic convenience as spheres driven around circular orbits by a constant tangential force, deviations from that ideal orbit are allowed by a spring whose equilibrium length is the unperturbed orbital radius. With a constant driving force, deflections of the sphere to a larger radius orbit lead to a decrease in the angular velocity, and deflections inward produce higher angular velocities. It is then straightforward to see how synchronization occurs when the spheres are coupled through the Stokeslet fields they create (Figure 7b). The predicted coupling strength then scales as ℓ3, as this is the stiffness of an elastic filament of length ℓ.
It is not easy to alter growth conditions to change the equilibrium length of flagella in any systematic way, but nature has provided us with a powerful mechanism to investigate the dependence of synchrony on the flagellar length. When flagella are subject either to a pH shock or to mechanical stress they often are shed and can grow back over an hour or two. This is an eternity on the timescale necessary for synchronization studies, so it is possible to investigate synchronization at discrete points in time throughout the regrowth phase (Goldstein et al., 2011). Results show a very strong dependence on the flagellar length which is consistent with the elastohydrodynamic mechanism.
Uchida and Golestanian (2011, 2012) proposed a second mechanism for synchronization. It is, in many ways, the converse of the elastohydrodynamic mechanism, which postulated a constant internal driving force and a flexible trajectory. Uchida &Golestanian studied the case of rigid cyclic trajectories with variable tangential drive along the path and arrived at general conditions under which synchronization is possible. From a biological point of view, there is no doubt that the intraflagellar forces vary considerably during a cycle, for Guasto et al.’s (2010) time-resolved tracking studies and more recent work (Brumley et al., 2014) have quantified the variation between the power and recovery strokes. The analysis of synchronization corresponds to that in the elastohydrodynamic picture, because the Stokeslet flow fields still influence each particle, but their speedup or slowdown happens within rigid orbits. Recent work using colloidal particles forced by time-dependent optical traps has tested these two ideas and shown their interplay (Bruot et al., 2012; Kotar et al., 2013).
More recently, it has been suggested that direct hydrodynamic interaction between flagella is not necessary for synchronization (Friedrich and Jülicher, 2012; Geyer et al., 2013); instead, the rocking of the cell body when flagella desynchronize can put them back into synchrony. This is an interesting idea, although some other mechanism, such as elastic couplings at the flagellar bases, must be invoked to explain the synchronization of flagella on pipette-held cells.
As is often the case in biological studies, key insight can be gained from the study of mutants. In the context of synchronization, ptx1, a mutant with deficient phototaxi, is of great interest. First isolated by Horst and Witman (1993), ptx1 is believed to lack the asymmetry between the way its two flagella respond to calcium, which is known to be essential to the phototactic response (see Section VI for a more detailed discussion). If its two flagella were nearly identical, ptx1 would be expected to exhibit distinct behavior from the wild type. Once again, Rüffer and Nultsch (1997a,b) provided important early studies, showing that ptx1 displays not only the ordinary breaststroke seen in the wild type, but also a second mode of so-called ‘parallel’ beating for the motion of the flagellar bases. This new mode occurs at a significantly higher frequency than the breaststroke, close to the instantaneous frequency during a phase slip of the wild type. Using modern high-speed imaging, Leptos et al. (2013) found that this state is precise antiphase synchronization, with stochastic transitions back and forth between in-phase and antiphase states. Selective deflagellation studies of the wild type show that one flagellum by itself can also execute the higher-frequency mode (Wan et al., 2014).
Some insight can be gained by re-examining the bead-spring model of Niedermayer et al. (2008), but allowing for the fundamental orbits to be of the opposite direction, as in Chlamydomonas. In this case, one finds that the natural synchronized state is in fact antiphase, whereas it is in phase for the ciliary case (two beads orbiting in the same sense) (Leptos et al., 2013). This implies that ptx1 is consistent with this basic elastohydrodynamic model and the wild type is the exceptional case. Clearly there must be more operating in Chlamydomonas synchronization than what is captured by these simple models. Perhaps elastic couplings at the flagellar bases are important, possibly involving the striated filaments that run between the basal bodies (Lechtreck and Melkonian, 1991). It should also be noted that the plausible assumption that an increase in radius produces a slow-down in angular velocity need not hold. If the reverse is true then it is possible to find antiphase synchronization for co-rotating orbits (Leoni and Liverpool, 2012). The path to solving this mystery will likely involve the continued use of mutants, genetics, and micromanipulation (Brumley et al., 2014) to isolate the crucial features of each mode of synchronization.
The above discussion of synchronization has neglected any detailed description of the flagellar waveform itself, but in many ways this is one of the most important outstanding problems in the field. Although there is consensus that the undulations are ultimately a consequence of microtubule doublets being slid past one another by the stepping of dynein motor proteins, the manner in which this translates into the observed waveform is still under debate (Mitchison and Mitchison, 2010). One promising approach (Riedel-Kruse et al., 2007) builds on the idea of spontaneous oscillations of active filaments (Brokaw, 1975; Camalet et al., 1999). Here, the coupling among motor stepping, probabilistic detachment, filament bending and viscous resistance leads to an eigenvalue problem for a Hopf bifurcation. This immediately shows that there is a discrete set of modes on the eukaryotic flagellum, each with a distinct waveform and frequency. Perhaps the wild-type breaststroke mode and the ptx1 antiphase mode are the first two rungs on this ladder. Intriguingly, Chlamydomonas is known to exhibit a photoshock response in which the two flagella undulate in the sinusoidal shape mode in front of the cell body, propelling it backwards away from intense light (Schmidt and Eckert, 1976). This beating occurs at yet higher frequencies. Determining whether this picture of discrete modes holds is an important goal for the next generation of experiments.
B. Multitudes
Some of the most important situations in which cilia and flagella drive fluid motion involve great numbers of them emanating from tissue. This is the case in the left-right organizer (LRO) that is involved in embryonic symmetry breaking (Hirokawa et al., 2009), in the respiratory tract and reproductive system of vertebrates, and in ciliates such as Paramecium and Opalina. The nodal cilia in the left-right organizer are short structures that whirl around, but in all the other examples we find longer cilia with well-defined power and recovery strokes, exhibiting metachronal waves. Despite decades of observation, there has been remarkably little quantitative study of the dynamics and fluid dynamics of metachronal waves (Knight-Jones, 1954). This is perhaps not surprising for the animal contexts, given the difficulty of visualization in vivo or even ex vivo. Volvox has again provided a way forward, for close observation has demonstrated that it displays robust metachronal waves (Brumley et al., 2012). Figure 7c shows a space-time illustration of one component of the fluid velocity of the metachronal waves of Volvox carteri just above the flagella tips, along with various statistical measures of the metachronal wave properties. A typical wavelength is on the order of 10 somatic cells, so the relative phase shift between neighbors is small.
One way to think about metachronal waves is to compare the behavior of pairs of flagella. If the basic coupling between Chlamydomonas flagella leads to precise phase locking, why does a carpet of flagella display long-wavelength modulations in phase? Is this a cumulative effect of interactions with multiple flagella? Does it arise from the presence of an underlying no-slip surface such as the extracellular matrix of Volvox or a tissue layer in the respiratory system? Although there are theoretical studies that take as a starting point the existence of metachronal waves and examine their consequences for swimming (Blake, 1971b; Brennen, 1974; Michelin and Lauga, 2010), only more recently have detailed proposals for the underlying mechanism been advanced. These include analyses of undulating filaments near no-slip surfaces (Guirao and Joanny, 2007; Guirao et al., 2010) and coupled orbiting spheres near surfaces (Brumley et al., 2012; Vilfan and Jülicher, 2006). In each case the common feature is the presence of the no-slip boundary, suggesting that the deflection of the flow by it produces the observed phase shift.
VI. PHOTOTAXIS
As photosynthetic organisms, the volvocine algae need light for survival, and evolution has endowed them with photoreceptors termed eyespots to enable steering toward the light (Jékely, 2009). Chlamydomonas has a single eyespot, as does each somatic cell of multicellular species such as Volvox. In the latter case, the eyespots tend to have a gradation in size, from large (~ 2.5 μm in diameter) at the anterior to small (~ 0.8 μm) near the posterior (Drescher et al., 2010b). In the volvocine algae these eyespots have a distinctive reddish color. Each eyespot lies inside the chloroplast of the cell and has a remarkable internal structure comprising multiple layers of proteins and membranes that function as a quarter-wave plate (Foster and Smyth, 1980). The result is a structure which is sensitive to light impinging on it in the hemisphere around the outward surface normal but insensitive to light from behind. This is a crucial property for the mechanism of phototactic steering.
As noted above, Volvox was given its name for its spinning motion, the frequency of which ranges from ~ 0.3 Hz for small, young colonies of V. carteri to 0.02 Hz for larger, older colonies. Those that are very phototactically active tend to have frequencies toward the upper range. Chlamydomonas also spins about its major axis as it swims, typically at frequencies of ~ 2 Hz. When coupled with the directionality of the eyespot, these motions give rise to light intensities at the eyespots that are periodic functions of time when the organism (single cell or colony) is not aligned with the incident light and that are nonmodulated signals when it is aligned. It appears therefore that nature has repeatedly found a biochemical mechanism to use periodic signals as a means to navigate in the sense that the existence of periodicity implies a lack of proper alignment. There are two clear questions that arise from these basic observations. First, what is the relationship between the light signals and flagellar beating? Second, how does this result in navigation toward light? It should be noted that the interplay of helical swimming and periodic signals appears to be more general than phototaxis, as there is evidence that sperm chemotaxis may operate similarly (Friedrich and Jülicher, 2007). The ubiquity of spiral swimming has been remarked upon for over a century (Jennings, 1901).
It is intuitive that, in the absence of light stimulus, an organism swimming along a straight trajectory through the symmetric action of its flagella can only deviate from that path by an asymmetry in its flagellar beating. In the case of Chlamydomonas, the synchronization described in earlier sections occurs despite the intrinsic differences between the two flagella. Not only are the intrinsic beat frequencies distinct, but so too is their response to intracellular calcium levels. This has been investigated in great detail using so-called cell models, which are cells that have been demembranated yet still function. Without the membrane, it is possible for the experimentalist to alter the ambient concentration of calcium ions experienced by the flagella. The two flagella respond differently to calcium, so that the cis flagellum is the dominant one at low calcium, and trans dominates at high levels. This property is known as flagellar dominance (Kamiya and Witman, 1984). In vivo, flagellar dominance is crucial, for when light falls on the eyespot, there is a transient change in the calcium levels within the cell (owing to the opening of membrane-bound calcium channels), leading to transient changes in the frequencies or amplitudes of the beating of the two flagella. The flagella transiently fall out of precise synchrony and produce a turn. Chlamydomonas swims in helical trajectories with its eyespot facing outwards, and there must be very precise tuning of the transient asymmetries to enable phototaxis (Schaller et al., 1997). Indeed, Yoshimura and Kamiya (2001) found a tuning of the flagellar response dynamics to the spinning frequency of the colony, a feature detailed below for Volvox.
In the case of a multicellular organism such Volvox, the problem is even more interesting. First, as the two flagella on the somatic cells beat in the same direction, as opposed to the breaststroke geometry of Chlamydomonas, steering of the colony as a whole cannot in any obvious way arise from differential flagella beating (Hoops et al., 1999). Second, as demonstrated long ago (Hiatt and Hand, 1972), there is no difference in phototactic ability between species of Volvox that have cytoplasmic connections between somatic cells in the adult and those that do not. Hence, there is no need for cytoplasmic cell-cell communication for phototaxis to operate. As there is no central nervous system in Volvox it is apparent that if the organism can steer to light, then it must be because each somatic cell responds appropriately by itself. The appearance of coordination in the response is illusory! The question is thus: What is the right program of response to a periodic light signal?
Ever since the work of Holmes (1903), it has been clear that some sort of asymmetry in the flagellar beating between the light and dark sides of a colony is necessary for phototactic turning, but only recently has a quantitative theory been proposed and validated by two groups, independently and nearly simultaneously (Drescher et al., 2010b; Ueki et al., 2010). Many issues arising in these studies also appear in an important earlier work on the mechanism of phototaxis of a marine zooplankton (Jékely et al., 2008). Although ultimately it is desirable to understand the phototactic response at the level of the individual somatic cells and their flagella, a useful coarse-grained approach builds on the important work of Stone and Samuel (1996), in which the angular velocity Ω of a spherical swimmer at low Reynolds numbers is expressed in terms of the fluid velocity field u on its surface:
| (9) |
where is the local normal to the sphere. The need for non-uniformity in u for turning of the colony axis is readily apparent from this relationship.
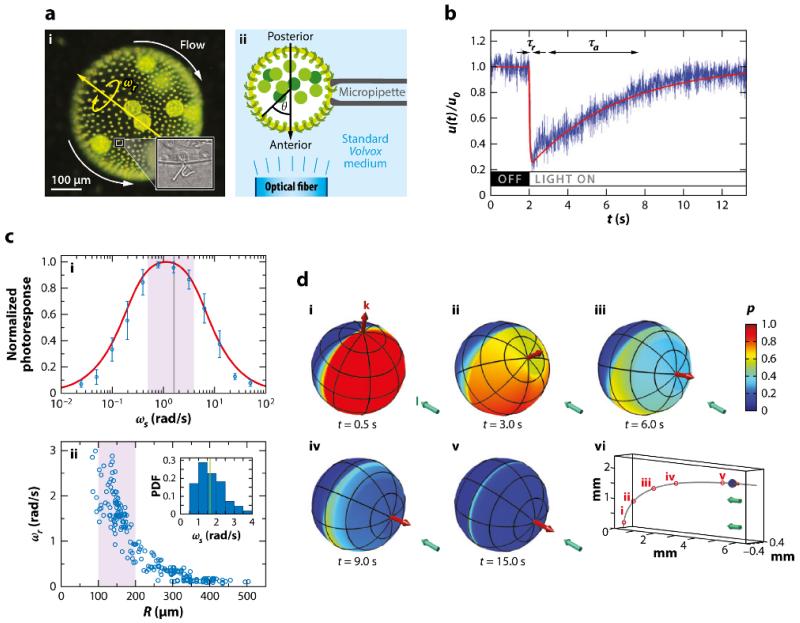
Adopting this coarse-grained approach, one can utilize time-resolved PIV to measure the response of a carpet of flagella on the Volvox surface to changing light conditions. Rather than dealing with freely swimming colonies, it is far simpler to hold them on micropipettes and mimic the effects of colony rotation by turning on and off illumination light at particular frequencies. For confirmation of the directionality, such light is sent through a fiber-optic light guide held within a micropipette near the colony surface (Figure 8a). The essential result of this investigation is shown in Figure 8b, which displays the transient response of the local fluid flow to a sudden illumination of a patch on the surface, mimicking the effects of colony rotation in bringing that patch into the light. There is a rapid (~ 50 ms) decrease in the fluid flow, followed by a much slower recovery back to the original level. This is an adaptive response in the same sense that our eyes or olfactory system adjusts to the sudden onset of a strong signal. If u0 is the local fluid speed before such perturbations, then we find u(t)/u0 = 1 − βp(t), where p(t) is a dimensionless photoresponse variable. A dynamical model for p(t) that captures the experimental behavior invokes the existence of a second, hidden variable h(t), which represents the internal biochemical mechanism of adaptation. These are coupled together in a manner already known from work on bacterial chemotaxis, in which adaptation is well understood:
| (10) |
| (11) |
where s(t) measures the light stimulus; τr and τa are the response and adaptation timescales, respectively; and the Heaviside function ensures that a step down in light stimulus cannot increase u above u0. This pair of ODEs has a stable fixed point at a constant stimulus, h, and p = 0, and will display precisely the biphasic response seen in Figure 8b under step changes in s.
FIG. 8.
Phototaxis in Volvox carteri. (a) Experimental setup. (i) Flows around the colony. (ii) Optical fiber illumination setup. (b) Local flagella-generated fluid speed u(t) (blue), measured with particle image velocimetry just above the flagella during a step-up in light intensity, normalized by the flow speed in the dark. Two timescales are evident: a short response time, τr, and a longer adaptation time, τa. The fitted theoretical curve (red) is from the solution of Equations 10 and 11. (c) Photoresponse frequency dependence and colony rotation. (i) Normalized flagellar photoresponse versus frequencies of sinusoidal stimulation (blue circles). The theoretical response function (red line; Equation 12) shows quantitative agreement. (ii) Colony rotation frequency ωr of V. carteri as a function of radius R. Highly phototactic organisms within the range indicated by the purple shaded region, corresponding to the purple shaded region in part i, demonstrate that response timescales and the colony rotation frequency are mutually optimized to maximize the photoresponse. (d) Colony behavior during a phototurn. (i–v) The colony axis (red arrow) tipping toward the light direction I (aqua arrow). Colors represent the amplitude p(t) of the downregulation of flagellar beating in a model of phototaxis. (vi) The swimming trajectory. Abbreviation: PDF, probability distribution function. Figure adapted with permission from Drescher et al. (2010b). Copyright 2010 by the National Academy of Sciences.
The key implication of this model is that the frequency response of the coupled system exhibits a resonance, a feature also known from studies of Chlamydomonas (Yoshimura and Kamiya, 2001). This can be seen by Fourier transforming Equation 11 (neglecting the Heaviside function for simplicity), yielding
| (12) |
This demonstrates immediately that if the frequency of the stimulus is either too large or too small the response is small. Most interestingly, the peak of the response (Figure 8c) occurs for 0.4 < ω < 4 rad/s, which match the orbital frequencies of those colonies that have the strongest phototactic response. The effect of this tuning is clear: If a patch on the surface rotates into the light, its flagellar beating is downregulated, and if the recovery from that state takes a time on the order of a rotation period, the net effect is that the illuminated side of the colony has weaker beating and the dark side has stronger beating. This is the asymmetry needed. It follows that if one can artificially slow down colony rotation while keeping the adaptive response unchanged, then the phototactic ability should decrease. Experiments verify this directly (Drescher et al., 2010b). The analysis is completed by solving for the trajectories of swimming colonies using the adaptive model over the entire surface. The result clearly illustrates how the initial asymmetries from misalignment with the light are diminished as the colony turns toward the light, with a stable fixed point at perfect alignment (Figure 8d).
VII. TRACER STATISTICS IN SUSPENSIONS
Interest in the properties of concentrated suspensions of microorganisms has expanded greatly since early suggestions (Toner and Tu, 1975; Vicsek et al., 1995) of the possibility that self-propelled organisms could display a transition to long-range order. Although subsequent experimental work showed that such hypothesized order does not occur (Dombrowski et al., 2004; Wu and Libchaber, 2000), the observed dynamics is in many ways more interesting. It takes the form of transient, recurring vortices and jets of coherent swimming with characteristic length scales reaching 100 μm and beyond, far larger than the individual swimmers. There is a continuing debate in the literature regarding the mechanism underlying this behavior - whether it arises purely from steric effects or requires long-range hydrodynamic interactions. This is reviewed in detail elsewhere. Here, the focus is on the issue of how these turbulent flows (Dunkel et al., 2013) impact the transport of suspended tracer particles. From the pioneering work of Wu and Libchaber (2000) and later work by others (Angelani et al., 2009) swimming bacteria can be viewed as analogous to molecules in a conventional fluid whose collisions with tracers, such as the pollen grains of Brown (1828), produce Brownian motion. Whereas in conventional Brownian motion with a molecular bath and micrometer-sized particles there is an enormous separation of timescales between the picoseconds of molecular collisions and the perhaps milliseconds on which we resolve the tracer displacements, no such separation exists in microorganism suspensions. Instead, we are able to resolve the collisions of the swimmers with the tracers.
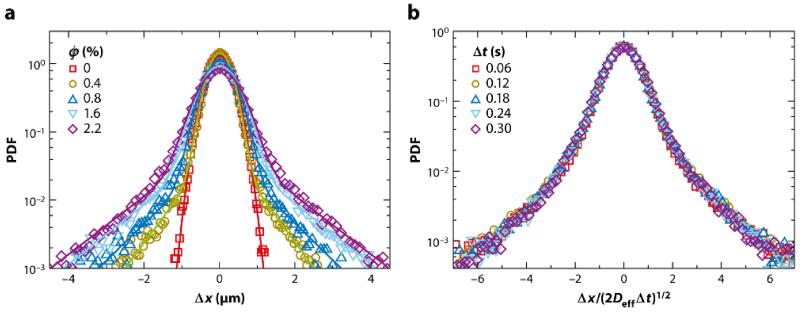
The first and most basic observation from studies of bacterial suspensions is that the tracer particles exhibit enhanced diffusion with increasing swimmer concentration, with diffusivities reaching ~ 10−6 cm2/s at cell concentrations of n ~ 5 × 1010/cm3, orders of magnitude larger than the purely thermal values of D. These measurements were obtained by tracking of the trajectories of individual tracers and calculating the mean-square displacement ⟨Δr2⟩ versus time (t). Such analyses show at short times a scaling ⟨Δr2⟩ ≃ tα with 1.5 < α < 2, not quite the ballistic scaling α = 2 one might expect, but definitely superdiffusive. At larger times (t ≳ 3 s) there is a clear crossover to diffusive behavior, with α = 1 holding beyond. Of course, the mean-square displacement is only one moment of a distribution of particle displacements observable over some time interval t, and more details are available in the full PDF. In this case, Chlamydomonas has a number of advantages over the use of bacteria. First, its mean swimming speed is considerably larger than that of typical bacteria, so one would anticipate stronger effects on the tracer particles. Second, the organism is larger than easily observed tracer particles, and is therefore likely to be unaffected by their presence. Moreover, it is possible to visualize the tracers’ encounters with the swimmers in detail. This is then not unlike the situation considered by Darwin (1953) in his analysis of the trajectories of particles in an inviscid fluid as a body is moved through the fluid, giving rise to the so-called Darwin drift.
Figure 9a shows the results from the study of tracer particles in Chlamydomonas suspensions (Leptos et al., 2009) as a semilogarithmic graph of the PDF of particle displacements Δx along one axis of observation, at a fixed time interval Δt for various volume fractions ϕ of swimmers. For ϕ = 0, we see an inverted parabola, signifying a familiar Gaussian PDF, P(Δx) ~ exp(−Δx2/2DΔt), where D is the Stokes-Einstein diffusivity of the tracers. At higher volume fractions, the distribution develops a heavy tail, consistent with an exponential form. One infers that the core of each of these distributions continues to arise from the thermal Brownian motion of the tracers, whereas the tails result from the fluid flows created by the swimmers. Strikingly, as shown in Figure 9b, a diffusive rescaling collapses all the data at various Δt at a given ϕ. At almost exactly the same time as this discovery, Granik and collaborators found analogous behavior in two completely different systems, and dubbed it ‘anomalous but Brownian’(Wang et al., 2009). Their systems were (a) colloidal microspheres that diffuse along phospholipid bilayer tubes of the same radius and (b) microspheres diffusing through networks of filamentous actin, in which the mesh size is considerably larger than the spheres. Although the mean-square displacement of the spheres in both cases grew linearly with time, the PDFs were decidedly non-Gaussian. Later work (Kurtuldu et al., 2011) on tracer dynamics in Chlamydomonas suspensions confined to thin films revealed even stronger deviations from Gaussianity than in three dimensions (Leptos et al., 2009). In the three-dimensional case, an examination of the trajectories of particles near the alga reveals complex loops qualitatively similar to those of the Darwin problem, consistent with recent calculations of tracer paths at zero Reynolds number (Dunkel et al., 2010; Pushkin et al., 2013; Zaid et al., 2011).
FIG. 9.
Probability distribution functions (PDFs) for tracer displacements in suspensions of Chlamydomonas. (a) PDFs at a fixed time interval Δt = 0.12 s, at various volume fractions ϕ. The Gaussian develops apparently exponential tails as ϕ increases. (b) Diffusive rescaling of PDFs at ϕ = 2.2% for several time intervals (Δt), leading to data collapse to a non-Gaussian function. Figure adapted with permission from Leptos et al. (2009). Copyright 2009 by the American Physical Society.
The notion that these non-Gaussian distributions are anomalous arises from the expectation that the random encounters between swimmers and tracers would satisfy the conditions of the central limit theorem (bounded second moment of the distribution). But things are not so simple because of the long-range flow fields around the swimmers (Rushkin et al., 2010). If we have a suspension of N swimmers, each of radius R, in a box of linear dimension L, and consider a volume fraction ϕ = 4πR3N/3L3 that is sufficiently small, the PDF of velocities arises from a random superposition of the flow fields around each swimmer. Averaging over their positions is equivalent to integrating over space when the distribution is uniform. Let us suppose that the velocity around a swimmer decays as |v(r)| ~ A(Ω)/rn, with Ω an angular factor. Then the probability distribution P(v) of velocities is
| (13) |
A simple scaling argument shows that the tail of P has the form
| (14) |
The second moment of P(v) is finite only if n < 3/2, the case of a Stokeslet (n = 1). This is the condition for the validity of the central limit theorem; the velocity field from a large number of independently placed Stokeslets is Gaussian. It will not be so for any higher integer singularity, such as stresslets (n = 2) or source doublets (n = 3) (Blake and Chwang, 1974). If the decay law deviates from v ∝ r−n below a certain radius, the PDF shape (Equation 14) will break down above the corresponding value of v. Hence, deviations from Gaussianity provide a direct probe of the near-field velocity around the swimmers. Experiments on velocity fluctuations in suspensions of Volvox explicitly demonstrated that the presence or absence of the Stokeslet contribution has a strong effect on the fluctuation spectrum (Rushkin et al., 2010).
Several explicit models have been proposed to connect the near-field behavior to the non-Gaussian statistics. Lin et al. (2011) used a squirmer calculation to examine the displacements of tracers in the path of a swimmer and were able to find non-Gaussian statistics arising from the proximity to a stagnation point on the squirmer surface, although the non-Gaussianity had different scaling properties from those seen in experiment. In related work, Eckhardt and Zammert (2012) examined the implications of power-law distributions of trapping times and step lengths in a continuous-time random walk (Zaid et al., 2011) and found conditions that gave good agreement with experiment. It was suggested that these distributions could arise from the existence of stagnation points in the flow. These are promising developments in understanding the non-Gaussianity seen in experiments. Future experiments that can visualize which tracer displacements give rise to the heavy tails can provide tests of these theories.
VIII. SUMMARY POINTS
The average and time-resolved flow fields around individual freely swimming microorganisms have been measured and interpreted in terms of elementary force singularities. Attention should now focus on connecting those velocity fields to the detailed action of the underlying flagella.
Interactions of microswimmers with boundaries can induce striking dynamics. Some can be explained by purely hydrodynamics mechanisms, but others require explicit consideration of the contact interactions between the flagella and the surface.
There is strong evidence that the synchronization of eukaryotic flagella can occur through hydrodynamic interactions, but the particular mechanism is still under investigation. The synchronization dynamics is intrinsically stochastic and subject to intracellular biochemical changes on intermediate timescales. Mutants have revealed unusual modes of synchronization that provide a challenge to current theories.
The mechanism of phototaxis in multicellular green algae has been shown to involve a tuning between the adaptive response time of the flagellar apparatus to changing light levels and the orbital period of the spinning organisms. This mechanism does not require any explicit communication between cells in the colony.
Suspensions of swimming algae can exhibit non-Gaussian yet Brownian statistics of tracer particle displacements. These are thought to arise from the detailed form of the flow field around the swimmers.
IX. FUTURE ISSUES
The demonstration of the in vitro evolution of multicellularity, first with yeast (Ratcliff et al., 2012) and then with Chlamydomonas (Ratcliff et al., 2013), has shown that selection based on simple hydrodynamic properties (e.g., gravitational settling speed) can induce multicellularity from organisms previously thought of as strictly unicellular. What would happen with other selective pressures? What can theory say about these results?
The recent discovery (Croft et al., 2005) of a symbiotic relationship between bacteria and algae, in which bacteria provide needed vitamin B12 to the algae, raises a host of fascinating questions in physical ecology. How do these organisms find each other in the vastness of the oceans? How does the symbiosis persist in the presence of turbulence? More generally, what are the spatiotemporal dynamics of such symbioses?
A quantitative theory for phototaxis in Chlamydomonas is still lacking, as are tests of the tuning mechanism for species intermediate between Chlamydomonas and Volvox. The origin of the slow timescale in the adaptive phototactic response of Volvox is unclear from a biochemical perspective, yet it is crucial for the tuning mechanism.
The existence of both in-phase and antiphase synchronization in the ptx1 mutant of Chlamydomonas remains unexplained at a mechanistic level. Similarly, a test of the hypothesis that these are two among many possible discrete undulation modes of the eukaryotic flagellum is needed.
A detailed understanding of metachronal waves is still lacking, as are quantifications of the stochastic dynamics of ciliary carpets on large length scales and timescales. Volvox may be the ideal organism for such studies.
Acknowledgments
I am deeply indebted to Cristian Solari, John Kessler, and Rick Michod for first interesting me in the evolution of multicellularity and the Volvocales, and I thank them and D. Brumley, K. Drescher, J. Dunkel, S. Ganguly, J.S. Guasto, J.P. Gollub, M. Herron, V. Kantsler, K.C. Leptos, T.J. Pedley, A.I. Pesci, M. Polin, M.B. Short, I. Tuval, and K. Wan for collaborations. This work was supported by NSF grant PHY-0551742, BB-SRC grant BB/F021844/1, ERC Advanced Investigator Grant 247333, the Leverhulme Trust, the Schlumberger Chair Fund, and a Wellcome Trust Senior Investigator Award.
Footnotes
Annual Review of Fluid Mechanics 47, in press (2015)
Disclosure statement
The author is not aware of any biases that might be perceived as affecting the objectivity of this review.
REFERENCES
- Acrivos A, Taylor TD. Phys. Fluids. 1962;5:387. [Google Scholar]
- Adler R. Proc. I. R. E. 1946;34:351. [Google Scholar]
- Adrian RJ. Annu. Rev. Fluid Mech. 1991;23:261. [Google Scholar]
- Angelani L, Leonardo RD, Ruocco G. Phys. Rev. Lett. 2009;102:048104. doi: 10.1103/PhysRevLett.102.048104. [DOI] [PubMed] [Google Scholar]
- Bell G, Mooers A. Biol. J. Linn. Soc. 1997;60:345. [Google Scholar]
- Bennett M, Schatz MF, Rockwood H, Wiesenfeld K. Proc. R. Soc. Lond. A. 2002;458:563. [Google Scholar]
- Bennett RR, Golestanian R. Phys. Rev. Lett. 2013;110:148102. doi: 10.1103/PhysRevLett.110.148102. [DOI] [PubMed] [Google Scholar]
- Berg HC, Brown DA. Nature. 1972;239:500. doi: 10.1038/239500a0. [DOI] [PubMed] [Google Scholar]
- Berg HC, Purcell EM. Biophys. J. 1977;20:193. doi: 10.1016/S0006-3495(77)85544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berke AP, Turner L, Berg HC, Lauga E. Phys. Rev. Lett. 2008;101:038102. doi: 10.1103/PhysRevLett.101.038102. [DOI] [PubMed] [Google Scholar]
- Blake JR. Proc. Camb. Phil. Soc. 1971a;70:303. [Google Scholar]
- Blake JR. J. Fluid Mech. 1971b;46:199. [Google Scholar]
- Blake JR, Chwang AT. J. Eng. Math. 1974;8:23. [Google Scholar]
- Bonner J. Integr. Biol. 1998;1:27. [Google Scholar]
- Bonner JT. Evolution. 2004;58:1883. doi: 10.1111/j.0014-3820.2004.tb00476.x. [DOI] [PubMed] [Google Scholar]
- Brennen C. J. Fluid Mech. 1974;65:799. [Google Scholar]
- Brennen C, Winet H. Annu. Rev. Fluid Mech. 1977;9:339. [Google Scholar]
- Brokaw CJ. Proc. Natl. Acad. Sci. UA. 1975;72:3102. doi: 10.1073/pnas.72.8.3102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown R. Phil. Mag. 1828;4:161. [Google Scholar]
- Brumley DR, Polin M, Pedley TJ, Goldstein RE. Phys. Rev. Lett. 2012;109:268102. doi: 10.1103/PhysRevLett.109.268102. [DOI] [PubMed] [Google Scholar]
- Brumley DR, Wan KY, Polin M, Goldstein RE. eLife. 2014;3:e02750. doi: 10.7554/eLife.02750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruot N, Kotar J, de Lillo F, Lagomarsino MC, Cicuta P. Phys. Rev. Lett. 2012;109:164103. doi: 10.1103/PhysRevLett.109.164103. [DOI] [PubMed] [Google Scholar]
- Camalet S, Jülicher F, Prost J. Phys. Rev. Lett. 1999;82:1590. [Google Scholar]
- Catton KB, Webster DR, Brown J, Yen J. J. Exp. Biol. 2007;210:299. doi: 10.1242/jeb.02633. [DOI] [PubMed] [Google Scholar]
- Croft MT, Lawrence AD, Raux-Deery E, Warren MJ, Smith AG. Nature. 2005;438:90. doi: 10.1038/nature04056. [DOI] [PubMed] [Google Scholar]
- Crowdy DG, Samson O. J. Fluid Mech. 2011;667:309. [Google Scholar]
- Darwin C. Math. Proc. Camb. Phil. Soc. 1953;49:342. [Google Scholar]
- Dombrowski C, Cisneros L, Chatkaew S, Goldstein RE, Kessler JO. Phys. Rev. Lett. 2004;93:098103. doi: 10.1103/PhysRevLett.93.098103. [DOI] [PubMed] [Google Scholar]
- Drescher K, Dunkel J, Cisneros LH, Ganguly S, Goldstein RE. Proc. Natl. Acad. Sci. USA. 2011;108:10940. doi: 10.1073/pnas.1019079108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drescher K, Goldstein RE, Michel N, Polin M, Tuval I. Phys. Rev. Lett. 2010a;105:168101. doi: 10.1103/PhysRevLett.105.168101. [DOI] [PubMed] [Google Scholar]
- Drescher K, Goldstein RE, Tuval I. Proc. Natl. Acad. Sci. USA. 2010b;107:11171. doi: 10.1073/pnas.1000901107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drescher K, Leptos K, Goldstein RE. Rev. Sci. Instrum. 2009;80:014301. doi: 10.1063/1.3053242. [DOI] [PubMed] [Google Scholar]
- Dunkel J, Heidenreich S, Drescher K, Wensink HH, Bar M, Goldstein RE. Phys. Rev. Lett. 2013;110:228102. doi: 10.1103/PhysRevLett.110.228102. [DOI] [PubMed] [Google Scholar]
- Dunkel J, Putz VB, Zaid IM, Yeomans JM. Soft Matter. 2010;6:4268. [Google Scholar]
- Eckhardt B, Zammert S. Eur. Phys. J. E. 2012;35:96. doi: 10.1140/epje/i2012-12096-7. [DOI] [PubMed] [Google Scholar]
- Elfring GJ, Lauga E. J. Fluid Mech. 2011;674:163. [Google Scholar]
- Evans E, Rawicz W. Phys. Rev. Lett. 1990;64:2094. doi: 10.1103/PhysRevLett.64.2094. [DOI] [PubMed] [Google Scholar]
- Fauci LJ. J. Comp. Phys. 1990;86:294. [Google Scholar]
- Foster KW, Smyth RD. Microbiol. Rev. 1980;44:572. doi: 10.1128/mr.44.4.572-630.1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedrich BM, Jülicher F. Proc. Natl. Acad. Sci. USA. 2007;104:13256. doi: 10.1073/pnas.0703530104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedrich BM, Jülicher F. Phys. Rev. Lett. 2012;109:138102. doi: 10.1103/PhysRevLett.109.138102. [DOI] [PubMed] [Google Scholar]
- Geyer VF, Jülicher F, Howard J, Friedrich BM. Proc. Natl. Acad. Sci. USA. 2013;110:18058. doi: 10.1073/pnas.1300895110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghose S, Adhikari R. Phys. Rev. Lett. 2014;112:118102. doi: 10.1103/PhysRevLett.112.118102. [DOI] [PubMed] [Google Scholar]
- Goldstein RE, Polin M, Tuval I. Phys. Rev. Lett. 2009;103:168103. doi: 10.1103/PhysRevLett.103.168103. [DOI] [PubMed] [Google Scholar]
- Goldstein RE, Polin M, Tuval I. Phys. Rev. Lett. 2011;107:148103. doi: 10.1103/PhysRevLett.107.148103. [DOI] [PubMed] [Google Scholar]
- Gray J. Ciliary movement. Cambridge University Press; Cambridge: 1928. [Google Scholar]
- Guasto JS, Johnson KA, Gollub JP. Phys. Rev. Lett. 2010;105:168102. doi: 10.1103/PhysRevLett.105.168102. [DOI] [PubMed] [Google Scholar]
- Guasto JS, Rusconi R, Stocker R. Annu. Rev. Fluid Mech. 2012;44:373. [Google Scholar]
- Guirao B, Joanny J-F. Biophys. J. 2007;92:1900. doi: 10.1529/biophysj.106.084897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guirao B, Meunier A, Mortaud S, Aguilar A, Corsi JM. Nature Cell Biol. 2010;12:341. doi: 10.1038/ncb2040. [DOI] [PubMed] [Google Scholar]
- Hand WG, Haupt W. J. Protozool. 1971;18:361. [Google Scholar]
- Harris EH. The Chlamydomonas Sourcebook: Introduction to Chlamydomonas and Its Laboratory Use. Academic Press; Oxford: 2009. [Google Scholar]
- Hiatt JDF, Hand WG. J. Protozool. 1972;19:488. [Google Scholar]
- Higdon JJL. J. Fluid Mech. 1979;94:305. [Google Scholar]
- Hirokawa N, Okada Y, Tanaka Y. Annu. Rev. Fluid Mech. 2009;41:53. [Google Scholar]
- Holmes SJ. Biol. Bull. 1903;4:319. [Google Scholar]
- Hoops HJ, Brighton MC, Stickles SM, Clement PR. J. Phycol. 1999;35:539. [Google Scholar]
- Horst CJ, Witman GB. J. Cell Biol. 1993;120:733. doi: 10.1083/jcb.120.3.733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huygens C. Oeuvres complétes de Christiaan Huygens. Martinus Nijhoff; The Hague: 1893. [Google Scholar]
- Ibañez-Tallon I, Heintz H, Omran H. Hum. Mol. Gen. 2003;12:R27. doi: 10.1093/hmg/ddg061. [DOI] [PubMed] [Google Scholar]
- Ishikawa T, Pedley TJ. Phys. Rev. Lett. 2008;100:088103. doi: 10.1103/PhysRevLett.100.088103. [DOI] [PubMed] [Google Scholar]
- Jékely G. Philos. Trans. R. Soc. B. 2009;364:2795. doi: 10.1098/rstb.2009.0072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jékely G, Columbelli J, Hausen H, Guy K, Stelzer E, Nédélec F, Arendt D. Nature. 2008;456:395. doi: 10.1038/nature07590. [DOI] [PubMed] [Google Scholar]
- Jennings HS. Am. Nat. 1901;35:369. [Google Scholar]
- Kamiya R, Witman GB. J. Cell Biol. 1984;98:97. doi: 10.1083/jcb.98.1.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kantsler V, Dunkel J, Polin M, Goldstein RE. Proc. Natl. Acad. Sci. USA. 2013;110:1187. doi: 10.1073/pnas.1210548110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MJ, Bird JC, Parys AJV, Breuer KS, Powers TR. Proc. Natl. Acad. Sci. USA. 2003;100:15481. doi: 10.1073/pnas.2633596100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King N. Dev. Cell. 2004;7:313. doi: 10.1016/j.devcel.2004.08.010. [DOI] [PubMed] [Google Scholar]
- Kirk D. Volvox: Molecular-genetic origins of multicellularity and cellular differentiation. Cambridge University Press; Cambridge: 1998. [Google Scholar]
- Knight-Jones EW. Q. J. Microsc. Sci. 1954;95:503. [Google Scholar]
- Kotar J, Debono L, Bruot N, Box S, Phillips D, Simpson S, Hanna S, Cicuta P. Phys. Rev. Lett. 2013;111:228103. doi: 10.1103/PhysRevLett.111.228103. [DOI] [PubMed] [Google Scholar]
- Koufopanou V, Bell G. Proc. Roy. Soc. B. 1993;254:107. [Google Scholar]
- Kurtuldu H, Guasto JS, Johnson KA, Gollub JP. Proc. Natl. Acad. Sci. USA. 2011;108:10391. doi: 10.1073/pnas.1107046108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauga E, Goldstein RE. Physics Today. 2012;65:30. [Google Scholar]
- Lauga E, Powers TR. Rep. Prog. Phys. 2009;72:096601. [Google Scholar]
- Lechtreck K-F, Melkonian M. Protoplasma. 1991;164:38. [Google Scholar]
- van Leeuwenhoek A. Phil. Trans. Roy. Soc. 1700;22:509. [Google Scholar]
- Leoni M, Liverpool TB. Phys. Rev. E. 2012;85:040901. doi: 10.1103/PhysRevE.85.040901. [DOI] [PubMed] [Google Scholar]
- Leptos KC, Guasto JS, Gollub JP, Pesci AI, Goldstein RE. Phys. Rev. Lett. 2009;103:198103. doi: 10.1103/PhysRevLett.103.198103. [DOI] [PubMed] [Google Scholar]
- Leptos KC, Wan KY, Polin M, Tuval I, Pesci AI, Goldstein RE. Phys. Rev. Lett. 2013;111:158101. doi: 10.1103/PhysRevLett.111.158101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Tang JX. Phys. Rev. Lett. 2009;103:078101. doi: 10.1103/PhysRevLett.103.078101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lighthill MJ. Commun. Pure Appl. Math. 1952;5:109. [Google Scholar]
- Lin Z, Thiffeault J-L, Childress S. J. Fluid Mech. 2011;669:167. [Google Scholar]
- Linneaus C. Systema Naturae. Impensis Laurentii Salvii; Holmiae: 1758. [Google Scholar]
- Magar V, Goto G, Pedley TJ. Q. J. Mech. App. Math. 2003;56:65. [Google Scholar]
- Magar V, Pedley TJ. J. Fluid Mech. 2005;539:93. [Google Scholar]
- Michelin S, Lauga E. Phys. Fluids. 2010;22:111901. [Google Scholar]
- Michelin S, Lauga E. Phys. Fluids. 2011;23:101901. [Google Scholar]
- Mitchison TJ, Mitchison HM. Nature. 2010;463:308. doi: 10.1038/463308a. [DOI] [PubMed] [Google Scholar]
- Müller UK, van den Heuvel BLE, Stamhuis EJ, Videler JJ. J. Exp. Biol. 1997;200:2893. [Google Scholar]
- Niedermayer T, Eckhardt B, Lenz P. Chaos. 2008;18:037128. doi: 10.1063/1.2956984. [DOI] [PubMed] [Google Scholar]
- Orme BAA, Blake JR, Otto SR. J. Fluid Mech. 2003;475:333. [Google Scholar]
- Pazour GJ, Agrin N, Leszyk J, Witman GB. J. Cell. Biol. 2005;170:103. doi: 10.1083/jcb.200504008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedley TJ, Kessler JO. Annu. Rev. Fluid Mech. 1992;24:313. [Google Scholar]
- Pepper RE, Roper M, Ryu S, Matsudaira P, Stone HA. J. Roy. Soc. Interface. 2010;7:851. doi: 10.1098/rsif.2009.0419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettitt ME, Orme BAA, Blake JR, Leadbeater BSC. Europ. J. Protistol. 2002;38:313. [Google Scholar]
- Polin M, Tuval I, Drescher K, Gollub JP, Goldstein RE. Science. 2009;325:487. doi: 10.1126/science.1172667. [DOI] [PubMed] [Google Scholar]
- Prochnik SE, Umen J, Nedelcu AM, Hallmann A, Miller SM, et al. Science. 2010;329:223. doi: 10.1126/science.1188800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pushkin DO, Shum H, Yeomans JM. J. Fluid Mech. 2013;726:5. [Google Scholar]
- Rafai S, Jibuti L, Peyla P. Phys. Rev. Lett. 2010;104:098102. doi: 10.1103/PhysRevLett.104.098102. [DOI] [PubMed] [Google Scholar]
- Ratcliff WC, Denison RF, Borrello M, Travisano M. Proc. Natl. Acad. Sci. USA. 2012;109:1595. doi: 10.1073/pnas.1115323109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff WC, Herron MD, Howell K, Pentz JT, Rosenzweig F, Travisano M. Nature Comm. 2013;4:2742. doi: 10.1038/ncomms3742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riedel-Kruse IH, Hilfinger A, Howard J, Jülicher F. HFSP J. 2007;1:192. doi: 10.2976/1.2773861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roper M, Dayel MJ, Pepper RE, Koehl MAR. Phys. Rev. Lett. 2013;110:228104. doi: 10.1103/PhysRevLett.110.228104. [DOI] [PubMed] [Google Scholar]
- Rothschild L. Nature. 1949;163:358. doi: 10.1038/163358a0. [DOI] [PubMed] [Google Scholar]
- Rüffer U, Nultsch W. Cell Motil. Cytoskeleton. 1985;5:251. doi: 10.1002/(SICI)1097-0169(1998)41:4<297::AID-CM3>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- Rüffer U, Nultsch W. Cell Motil. Cytoskeleton. 1987;7:87. doi: 10.1002/(SICI)1097-0169(1998)41:4<297::AID-CM3>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- Rüffer U, Nultsch W. Cell Motil. Cytoskeleton. 1997a;41:297. doi: 10.1002/(SICI)1097-0169(1998)41:4<297::AID-CM3>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- Rüffer U, Nultsch W. Cell Motil. Cytoskeleton. 1997b;37:111. doi: 10.1002/(SICI)1097-0169(1997)37:2<111::AID-CM3>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- Rushkin I, Kantsler V, Goldstein R. Phys. Rev. Lett. 2010;105:188101. doi: 10.1103/PhysRevLett.105.188101. [DOI] [PubMed] [Google Scholar]
- Schaller K, David R, Uhl R. Biophys. J. 1997;73:1562. doi: 10.1016/S0006-3495(97)78188-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt JA, Eckert R. Nature. 1976;262:713. doi: 10.1038/262713a0. [DOI] [PubMed] [Google Scholar]
- Short MB, Solari CA, Ganguly S, Powers TR, Kessler JO, Goldstein RE. Proc. Natl. Acad. Sci. USA. 2006;103:8315. doi: 10.1073/pnas.0600566103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JM, Szathmáry E. The Major Transitions in Evolution. Freeman; San Francisco: 1995. [Google Scholar]
- Solari CA, Drescher K, Ganguly S, Kessler JO, Michod RE, Goldstein RE. J. R. Soc. Int. 2011;8:1409. doi: 10.1098/rsif.2011.0023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solari CA, Ganguly S, Kessler JO, Michod RE, Goldstein RE. Proc. Natl. Acad. Sci. USA. 2006a;103:1353. doi: 10.1073/pnas.0503810103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solari CA, Kessler JO, Goldstein RE. Gen. Prog. Evol. Mach. 2007;8:115. [Google Scholar]
- Solari CA, Kessler JO, Michod RE. Am. Nat. 2006b;167:537. doi: 10.1086/501031. [DOI] [PubMed] [Google Scholar]
- Squires TM. J. Fluid Mech. 2001;443:403. doi: 10.1017/jfm.2020.170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Squires TM, Brenner MP. Phys. Rev. Lett. 2000;85:4976. doi: 10.1103/PhysRevLett.85.4976. [DOI] [PubMed] [Google Scholar]
- Stone HA, Samuel ADT. Phys. Rev. Lett. 1996;77:4102. doi: 10.1103/PhysRevLett.77.4102. [DOI] [PubMed] [Google Scholar]
- Szathmáry E, Smith JM. Nature. 1995;374:227. doi: 10.1038/374227a0. [DOI] [PubMed] [Google Scholar]
- Tam D, Hosoi AE. Proc. Natl. Acad. Sci. USA. 2011;108:1001. doi: 10.1073/pnas.1011185108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor GI. Proc. R. Soc. Lond. A. 1951;209:447. [Google Scholar]
- Toner J, Tu Y. Phys. Rev. Lett. 1975;75:4326. doi: 10.1103/PhysRevLett.75.4326. [DOI] [PubMed] [Google Scholar]
- Turner L, Ryu WS, Berg HC. J. Bacter. 2000;182:2793. doi: 10.1128/jb.182.10.2793-2801.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uchida N, Golestanian R. Phys. Rev. Lett. 2011;106:058104. doi: 10.1103/PhysRevLett.106.058104. [DOI] [PubMed] [Google Scholar]
- Uchida N, Golestanian R. Eur. Phys. J. E. 2012;35:135. doi: 10.1140/epje/i2012-12135-5. [DOI] [PubMed] [Google Scholar]
- Ueki N, Matsunaga S, Inouye I, Hallmann A. BMC Biol. 2010;8:103. doi: 10.1186/1741-7007-8-103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vicsek T, Czirok A, Jacob EB, Cohen I, Shochet O. Phys. Rev. Lett. 1995;75:1226. doi: 10.1103/PhysRevLett.75.1226. [DOI] [PubMed] [Google Scholar]
- Vilfan A, Jülicher F. Phys. Rev. Lett. 2006;96:058102. doi: 10.1103/PhysRevLett.96.058102. [DOI] [PubMed] [Google Scholar]
- Wan KY, Leptos KC, Goldstein RE. J. R. Soc. Int. 2014;11:20131160. doi: 10.1098/rsif.2013.1160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B, Anthony SM, Bae SC, Granik S. Proc. Natl. Acad. Sci. USA. 2009;106:15160. doi: 10.1073/pnas.0903554106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weismann A. Essays on Heredity and Kindred Biological Problems. Clarendon Press; Oxford: 1892. [Google Scholar]
- Wu X-L, Libchaber A. Phys. Rev. Lett. 2000;84:3017. doi: 10.1103/PhysRevLett.84.3017. [DOI] [PubMed] [Google Scholar]
- Yoshimura K, Kamiya R. Plant Cell Physiol. 2001;42:665. doi: 10.1093/pcp/pce084. [DOI] [PubMed] [Google Scholar]
- Zaid IM, Dunkel J, Yeomans JM. J. Roy. Soc. Int. 2011;8:1314. doi: 10.1098/rsif.2010.0545. [DOI] [PMC free article] [PubMed] [Google Scholar]