Skip to main content
NCBI home page
Scientific Reports logoLink to Scientific Reports
. 2015 May 13;5:10136. doi: 10.1038/srep10136

Conductivity-limiting bipolar thermal conductivity in semiconductors

Shanyu Wang 1,*, Jiong Yang 1,*, Trevor Toll 1, Jihui Yang 1,a, Wenqing Zhang 2,b, Xinfeng Tang 3,c
PMCID: PMC4650813  PMID: 25970560

Abstract

Intriguing experimental results raised the question about the fundamental mechanisms governing the electron-hole coupling induced bipolar thermal conduction in semiconductors. Our combined theoretical analysis and experimental measurements show that in semiconductors bipolar thermal transport is in general a “conductivity-limiting” phenomenon, and it is thus controlled by the carrier mobility ratio and by the minority carrier partial electrical conductivity for the intrinsic and extrinsic cases, respectively. Our numerical method quantifies the role of electronic band structure and carrier scattering mechanisms. We have successfully demonstrated bipolar thermal conductivity reduction in doped semiconductors via electronic band structure modulation and/or preferential minority carrier scatterings. We expect this study to be beneficial to the current interests in optimizing thermoelectric properties of narrow gap semiconductors.

Thermal conduction in solids is one of the most fundamental physical processes. It reveals the nature of lattice dynamics as well as phonon scattering mechanisms. Thermal conductivity of solids also influences many technologically important topics including thermal insulation and management of energy storage and conversion systems, microelectronics, data storage devices; efficiency of thermoelectric materials; and stability of sensors and actuators. For semiconductors the low temperature thermal conductivity is not substantially distinct from those of insulators; at elevated temperatures, however, it becomes interesting and yet intriguing due to the vital roles of charge carriers and their interactions. A signature of electron-hole coupling in semiconductors is the bipolar thermal conduction at elevated temperatures, when the calculated lattice thermal conductivity (κ-LσΤ, where κ is the total thermal conductivity, L the Lorenz number, σ the electrical conductivity, and T the absolute temperature) is significantly higher than the T−1 temperature dependence expected for phonon-phonon interaction dominated thermal conductivity1,2,3,4,5,6,7. Similar effect has also been found in semimetals8,9,10. For intrinsic semiconductors, it is well recognized that the mobility ratio between electrons and holes (Inline graphic) determines the bipolar thermal conductivity (κb), which maximizes when b = 111,12. Consequently, κb is insignificant for InSb, primarily due to its very large mobility ratio (b > 100)13. In the case of heavily doped semiconductors, the mobility ratio however is no longer a valid guide for understanding or predicting κb, due to the substantially different majority and minority carrier concentrations. For example, recent experiments showed significant κb in p-type heavily-doped skutterudites despite of the mobility ratio between two carriers being greater than 10 (hole mobility ~1–5 cm2/V-s with a concentration of ~1021 cm−3 and electron mobility ~30–50 cm2/V-s with a concentration of ~1018–1019 cm−3 at 800 K, according to our numerical analyses which are presented below)14,15,16,17,18, while the n-type skutterudites do not show appreciable κb, consistent with the rather small b value (~1/50)19,20,21,22,23,24,25,26,27,28,29. Similar observations have been reported for many other semiconductors30,31,32,33,34,35,36,37,38,39. These intriguing results necessitate comprehensive understanding of κb in semiconductors. A recent report attempted to model κb in doped Bi2(Te0.85Se0.15)3 crystals but was unable to capture the specific roles of electronic band structure and carrier scattering mechanisms on κb35.

In this study we report a combined experimental and computational effort that focused on unraveling the general behavior of κb in semiconductors. A numerical method for modeling the temperature dependence of κb for intrinsic as well as extrinsic (heavily doped) semiconductors encompassing a wide range of band gap and electronic band structure has been developed. We find that κb in semiconductors is in general “conductivity-limiting”. In analogous to the bipolar ionic conduction and multiple-step diffusion processes, in which the overall kinetics are determined (limited) by the lower rate species or processes, the bipolar thermal conduction is limited by the charge carrier with lower partial electrical conductivity40,41. Therefore, it is determined by the minority carrier partial electrical conductivity and by the mobility ratio (“mobility-limiting”) in extrinsic and intrinsic semiconductors, respectively. In order to validate these findings, we experimentally demonstrated κb reduction based on electronic band structure modulation and preferential minority carrier scattering. These results largely broaden our understanding of thermal conduction in semiconductors as well as offer insights for optimizing thermoelectric properties of narrow gap semiconductors.

Results and Discussion

Bipolar thermal conductivity in semiconductors can be expressed as1,2,3,4

graphic file with name srep10136-m2.jpg

where σi and αi (subscript i = n, p) are the partial electrical conductivity and Seebeck coefficient for electrons and holes, respectively. For a single parabolic band, the Seebeck coefficient of each carrier can be written as42

graphic file with name srep10136-m3.jpg

where kB is the Boltzmann constant, e the free electron charge, ξ the reduce Fermi energy, λ the carrier scattering parameter, Fx the Fermi integral of the order of x. Therefore Inline graphic, where Eg is the band gap4. For acoustic phonon scattering (λ  = −1/2), the term Inline graphic can be written as Inline graphic which is associated with the total energy carried by electron-hole pairs (band gap energy and kinetic energies). The electrical conductivity of each carrier is

graphic file with name srep10136-m7.jpg

where i = n, p designates the carrier concentrations of electron and hole, respectively.

“Conductivity-Limiting” Bipolar Thermal Conductivity

To elucidate the bipolar thermal conduction behavior in semiconductors, we may rearrange Eq. (1) into (assuming acoustic phonon scattering λ = −1/2, which is valid for most thermoelectric materials)

graphic file with name srep10136-m8.jpg

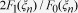For a given material at a fixed T, the variation of Inline graphic as a function of ξp or ξn is rather negligible, while the carrier concentrations and the partial electrical conductivity σi (right side of Eq. (4)) could change by several orders of magnitude because of the activation behavior of the charge carriers. Here Inline graphic and Inline graphic are the reduced kinetic energies of holes (Inline graphic) and electrons (Inline graphic), respectively, which only slightly change their numerical values when varying the Fermi level43. To verify these analyses, numerical data for p-type skutterudites (RxFe3NiSb12) with Eg = 0.2 eV, mp* = 5 m0, mn* = 2 m0, at 800 K are plotted in fig. 1, where mp*, mn*, and m0 are the effective mass of holes, effective mass of electrons, and free electron mass, respectively. The details of the calculations will be discussed below. As shown in fig. 1(a), with increasing ξp from –1 (weakly-degenerate) to 2 (degenerate), Inline graphic only increases from 4.2 to 5.3, ~25% increases; whereas p increases by a factor of ~10 and the minority carrier partial conductivity σn decreases by a factor of ~20. These suggest that for semiconductors in general, Eq. (1) or (4) can be approximated as Inline graphic, therefore κb in semiconductors is actually “conductivity-limiting”, analogous to the rate-limiting phenomena in kinetic diffusion processes41. For intrinsic semiconductors, since n = p, Eq. (4) can be further approximated to be Inline graphic, consistent with the large body of literature already developed. In the case of extrinsic semiconductors (n ≫p or p ≫n) κb is primarily determined by the partial electrical conductivity of the minority carriers, not by the mobility ratio. A linear dependence of κb vs. σn at 800 K for p-type doped skutterudites, as shown in fig. 1(b), further substantiates our proposed “conductivity-limiting” concept for bipolar thermal conduction in semiconductors.

Figure 1.

Figure 1

Open in a new tab

(a) Numerically calculated total reduced kinetic energy Inline graphic for holes and electrons, hole (majority carrier) concentration, and electron (minority carrier) partial electrical conductivity as a function of the reduced Fermi level (ξp); (b) calculated κb as a function of minority carrier partial electrical conductivity σn. The dashed line is a guide for eye. The calculations were carried out for p-type skutterudites (RxFe3NiSb12) with Eg = 0.2 eV, mp* = 5m0, mn* = 2m0, at 800 K.

Numerical Modeling

Data presented in fig. 1 were calculated by our numerical method for modeling the temperature dependence of κb in semiconductors. Our numerical method aimed at discerning the underlying physics that controls κb, including the electronic band structure features and carrier scattering mechanisms. We use the experimental carrier concentration values as those of the majority carriers. Based on the majority carrier concentration and Seebeck coefficient at room temperature, and the maximum Seebeck coefficient value at elevated temperatures, we can determine the Fermi level, the majority carrier effective mass and Eg44,45. The minority carrier effective mass is used as an adjustable parameter. The majority and minority carrier concentrations and their temperature dependences are calculated based on semiconductor statistics46. In order to obtain the T dependence of mobility, we first modeled its carrier concentration dependence at room temperature. We then assumed that the carriers are predominantly scattered by the acoustic phonons, therefore Inline graphic and Inline graphic. For example, the room temperature carrier mobility of n-type and p-type 3d transition metal-based skutterudite antimonides Rx(Fe,Co,Ni)4Sb12 as a function of carrier concentration is shown in fig. 2, where R represents fillers and x the filling fraction. The data were taken from the literatures14,15,16,17,18,19,20,21,22,23,24,25,26,27,47,48,49,50,51,52,53,54,55,56,57,58,59 and were well represented by an empirical expression (the solid lines in fig. 2)60

Figure 2.

Figure 2

Open in a new tab

Room temperature carrier mobility as a function of carrier concentration for (a) p-type and (b) n-type Rx(Fe,Co,Ni)4Sb12 skutterudites. The solid lines are least squares fits to the data using Eq. (5). Data used here are taken from Refs. 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 and 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59.

graphic file with name srep10136-m19.jpg

where iRef is the reference carrier concentration, approximately where degeneracy sets in, a is a fitting parameter, and Inline graphic and Inline graphic are the minimum and maximum possible mobility, respectively. In general, the carrier concentration dependence of mobility for all semiconductors studied in this work can be well accounted by this phenomenological formula and the fitting parameters are summarized in the Table S1 (Supporting Information, SI).

Based on Eqs. (1)–(3) and (5) and the aforementioned method, we were able to numerically fit the temperature dependence of κb in intrinsic and extrinsic semiconductors with a large variation of band gap, the Fermi level, and effective mass values. Figure 3(a) shows the excellent agreement between the experimental data (symbols) for intrinsic Si single crystal7 and degenerate polycrystalline skutterudite Yb0.7Fe3NiSb12 in a wide temperature range. Figure 3(b) shows the calculated (Inline graphic) and experimental (Inline graphic) values of κb for a variety of materials at various temperatures, including (Bi,Sb)2(Te,Se)337,61, skutterudites, Si, and Ge6,7. The dashed line in fig. 3(b) represents Inline graphic. These results suggest that our method well accounts for the temperature dependence of κb in semiconductors (all relevant parameters used in our calculations are summarized in Table S2, SI). Since κb is determined by the minority carrier partial electrical conductivity in doped semiconductors, the minority carrier effective mass and its mobility, as well as Eg will have strong influence. The extent to which these parameters affect κb is illustrated in Fig. S1 (SI). This also suggests that κb modification can be achieved by manipulating these parameters.

Figure 3.

Figure 3

Open in a new tab

(a) Experimental (symbols) and fitted (solid lines) bipolar thermal conductivity of intrinsic Si single crystal and degenerate Yb0.7Fe3NiSb12 vs. T. (b) Experimental (κbExp) and calculated (κbCal) bipolar thermal conductivity for intrinsic Si and Ge single crystals, and degenerate Bi2Te3-based zone melted (ZM) compounds and p-type skutterudites at various temperatures. The dashed line represents κbCal = κbExp.

Bipolar Thermal Conductivity Reduction

In order to examine the validity of the minority carrier dominated bipolar thermal conduction in heavily doped semiconductors, and to utilize the concept of modifying κb presented, we investigated ways of κb reduction motivated by the recent quest for high efficiency thermoelectric materials that necessitate low thermal conductivity62,63,64,65. It is well known that in filled skutterudites66, the triple degenerate conduction band minimum (CBM) is primarily composed of d-orbitals from the transition metals (TMs), with some contribution from Sb p-states (p-d hybridization). Thus the density of states (DOS) at the CBM can be effectively adjusted by varying the TMs. Our first principles calculations reveal that in the p-type Ba-filled skutterudites, DOS at the CBM decreases significantly with decreasing Fe/Co ratio on the TM sites from 2:2 to 1:3, as shown in fig. 4(a), mainly due to the higher energy and thus more contribution of 3d orbitals of Fe as compared with those of Co. The distinct DOS of minority carrier band further suggests that κb for p-type Ba0.5Co3FeSb12 should be smaller than BaCo2Fe2Sb12 due to the minority carrier partial conductivity reduction. Data for 800 K κb vs. the majority carrier (hole) concentration for a series of BaxCo3FeSb12 and BayCo2Fe2Sb12 samples are plotted in fig. 4(b), and the lines represent fitting to the data using the minority carrier effective masses Inline graphic and Inline graphic, respectively. This electronic band modulation induced κb reduction substantiates the dominant role of the minority carriers. Because of the commonly triple-degenerate and 3d-orbital-dominated nature of the CBM, the minority carrier effective masses of the p-type skutterudites are usually much higher than those of the n-type, in which the minority carrier band is mainly composed of single-degenerate Sb p-orbital-featured light bands67. Therefore, the predominant underlying reason for large differences in κb between the n- and p-type skutterudites is actually due to the effective mass differences between the corresponding conduction and valence (minority) bands.

Figure 4.

Figure 4

Open in a new tab

(a) The density of states around the CBM for BaCo2Fe2Sb12 and BaCo3FeSb12. (b) Bipolar thermal conductivity at 800 K as a function of hole (majority carrier) concentration for BaxCo2Fe2Sb12 and BayCo3FeSb12. The lines in (b) are fits to the data using different minority carrier effective mass values.

Our second example of κb reduction takes the advantage of preferential scattering of the minority carriers. Normally in heavily doped semiconductors, the minority carriers are non-degenerate. Given the electronic band structure of a material and the Fermi level (determined by the majority carrier concentration), one can calculate the range of minority carrier wavelength46. For example, the electron wavelength in a heavily-doped p-type Bi2Te3 (p = 3.5 × 1019 cm−3) is approximately between 10 nm and 50 nm, as shown in fig. 5(a). We compare κb of p-type zone melted (ZM) and nanostructured (Nano) Bi0.5Sb1.5Te3 prepared by the melt spinning combined with subsequent spark plasma sintering (MS-SPS) technique61. Figure 5(b) shows, at comparable majority carrier concentrations between the ZM and Nano samples, a significant κb reduction is achieved when nanoprecipitates are introduced into the sample. The minority carrier partial electrical conductivity is determined by Eg, minority effective mass and mobility. The estimated small Eg variation between ZM and Nano is only responsible for 20% of the κb reduction. For a large system like nanostructured Bi0.5Sb1.5Te3, a full electronic band structure calculation is computationally unfeasible. It is difficult to directly determine mn* (minority carrier) at the CBM. The estimated mn* values of n-type doped ZM and Nano Bi2Te2.7Se0.3 are 1.0 m0 and 1.1 m0, respectively38,68. If we assume comparable mn* at CBM between the ZM and Nano samples, the major part of κb reduction between the p-type ZM and Nano Bi0.5Sb1.5Te3 with comparable majority hole concentrations could be attributed to the reduction of minority carrier mobility (μn) corroborated by our κb fittings, where μn = 4095 cm2/V-s for the ZM and 1115 cm2/V-s for the Nano. The TEM image (inset of fig. 5(b)) shows that the sizes of nanoprecipitates closely match those of the minority electron wavelengths. Given the majority hole wavelength is estimated to be ~2 nm, we postulate a strong preferential minority carrier scattering by the nanoprecipitates in the Nano Bi0.5Sb1.5Te3. Similar κb reduction can also be observed in nanostructured n-type Bi2(Te,Se)3 compounds38,69,70. Extensive recent studies have established the role of nanostructure on lattice thermal conductivity reduction63,65, we propose an “preferential minority carrier scatterings” for κb reduction, which is partially responsible for the thermoelectric performance gains reported, especially at elevated temperatures61,71. Recent theoretical work has also demonstrated that similar κb reduction via heterostructure barriers scattering is possible72. Finally we caution that nanostructure induced band structure modulation reported in AgPbmSbTe2-m might be possible for Bi0.5Sb1.5Te373, which could be responsible for part of the κb reduction.

Figure 5.

Figure 5

Open in a new tab

(a) The calculated electron wavelength, and the product of the Fermi-Dirac distribution function and electronic density of states f(E) g(E) vs. energy with the zero point corresponding to the conduction band minimum (Ec). (b) The experimental and modeled bipolar thermal conductivity vs. temperature, for p-type zone melted (ZM) and nanostructured (MS-SPS) Bi0.5Sb1.5Te3. The inset is a TEM picture of the MS-SPS bulk sample which shows 10–50 nm nanoprecipitates. (The room temperature minority carrier mobilities of ZM and Nano samples are μn = 4095 and 1115 cm2/V-s, respectively).

Summary

To conclude, our combined theoretical analysis and experimental measurements have established that in semiconductors bipolar thermal transport is in general a “conductivity-limiting” phenomenon, which is controlled by the carrier mobility ratio and the minority carrier partial electrical conductivity for the intrinsic and extrinsic cases, respectively. The numerical method we developed quantifies the role of electronic band structure and carrier scattering mechanisms. We have also demonstrated feasible strategies for manipulating the bipolar thermal conductivity in doped semiconductors via electronic band structure modulation and/or preferential minority carrier scatterings. We expect our study to be beneficial to the current interests in optimizing thermoelectric properties of narrow gap semiconductors.

Methods

Samples in this study were synthesized by a combination of induction melting and long-term high-temperature annealing, by zone melting, or by MS-SPS, and the details of which were documented elsewhere19,61. High-resolution transmission electron microscopy (TEM) images were collected using a JEM-2100F TEM. Electrical conductivity (σ) and Seebeck coefficient (α) were simultaneously measured by an Ulvac ZEM-3 under a low-pressure helium atmosphere. Thermal conductivity was calculated from the measured thermal diffusivity (D), specific heat (Cp), and density (d) using the relationship κ = DCpd. Thermal diffusivity D was tested by laser flash diffusivity method using a Netzsch LFA-457 system, and Cp was measured by a Netzsch DSC 404F1 using sapphire as the reference. The accuracy of the κ measurements is estimated to be ~10% and the precision <5%. κb were extrapolated from κb + κL = κ-LσT by assuming lattice thermal conductivity κL is inversely proportional to T. Hall measurements were performed on a Janis cryostat equipped with a 9 Tesla superconducting magnet. The carrier concentration of electron (n) or hole (p) and the corresponding Hall mobility μn or μp (subscript n represents the electron and p the hole) were estimated from the measured Hall coefficient (RH) and electrical conductivity by the relation Inline graphic and Inline graphic, respectively.

The first-principles electronic band structure calculations were performed with the generalized gradient approximation functional of Perdew, Burke, and Ernzerhof74, with projected augmented wave method75,76, as implemented in Vienna ab initio simulation package (VASP)77. The computational techniques are similar to those published previously66,78. The de Broglie wavelengths (λ) is defined as, λ = h/m*v, where h, m*, and v are the Planck constant, carrier effective mass, and drift velocity, respectively. m*, v and λ of degenerate majority carriers are almost energy independent (kBT within the Fermi level), while for non-degenerate minority carriers these values are energy dependent, which are derived from band structure. The detailed calculation method is shown in Supporting Information, and the calculated density of state, mn* and vn of electrons for p-type Bi2Te3 (ξp = 0.25, mp* = 1.3 m0) are shown in figure S2 (SI).

Additional Information

How to cite this article: Wang, S. et al. Conductivity-limiting bipolar thermal conductivity in semiconductors. Sci. Rep. 5, 10136; doi: 10.1038/srep10136 (2015).

Supplementary Material

Supplementary Information
srep10136-s1.docx (3.1MB, docx)

Acknowledgments

This work was supported by US Department of Energy under corporate agreement DE-FC26-04NT42278, by GM, and by National Science Foundation under award number 1235535.

Footnotes

Author Contributions Jihui Yang designed research; S.W., Jiong Yang, and T.T. performed research; Jihui Yang, W.Z. and X.T. analyzed data; and Jihui Yang, S.W., and Jiong Yang wrote the paper. All authors reviewed the manuscript.

References

  1. Price P. Ambipolar thermodiffusion of electrons and holes in semiconductors. Philos. Mag. 46, 1252–1260 (1955). [Google Scholar]
  2. Davydov B. & Shmushkewitch J. Electrical conductivity of semi-conductors with an ionic lattice in strong fields. J. Phys. 3, 359 (1940). [Google Scholar]
  3. Goldsmid H. The thermal conductivity of bismuth telluride. Proceed. Phys. Soc. Sec. B 69, 203 (1956). [Google Scholar]
  4. Drabble J. R. & Goldsmid H. J. Thermal Conduction in Semiconductors Pergamon Press: Oxford, 1961). [Google Scholar]
  5. Berman R. Thermal Conduction in Solids. Clarendon Press: Oxford, 1976). [Google Scholar]
  6. Slack G. A. & Glassbrenner C. Thermal conductivity of germanium from 3 °K to 1020 °K. Phys. Rev. 120, 782 (1960). [Google Scholar]
  7. Glassbrenner C. & Slack G. A. Thermal conductivity of silicon and germanium from 3 K to the melting point. Phys. Rev. 134, A1058 (1964). [Google Scholar]
  8. Gallo C., Miller R., Sutter P. & Ure R. Jr Bipolar Electronic Thermal Conductivity in Semimetals. J. Appl. Phys. 33, 3144–3145 (1962). [Google Scholar]
  9. Uher C. & Goldsmid H. Separation of the electronic and lattice thermal conductivities in bismuth crystals. phys. stat. solid. (b) 65, 765–772 (1974). [Google Scholar]
  10. Magomedov A.-M. & Pashaev B. Thermal conductivity of alloys of the bismuth-antimony system in solid and liquid states. Sov. Phys. J. 15, 287–290 (1972). [Google Scholar]
  11. Abeles B. Thermal conductivity of germanium in the temperature range 300–1080 K. J. Phys. Chem. Solids 8, 340–343 (1959). [Google Scholar]
  12. Kettel F. Die Wärmeleitfähigkeit von Germanium bei hohen temperaturen. J. Phys. Chem. Solids 10, 52–58 (1959). [Google Scholar]
  13. Bowers R., Ure R. Jr, Bauerle J. & Cornish A. InAs and InSb as thermoelectric materials. J. Appl. Phys. 30, 930–934 (1959). [Google Scholar]
  14. Liu R. et al. p-Type skutterudites RxMyFe3CoSb12 (R, M = Ba, Ce, Nd, and Yb): Effectiveness of double-filling for the lattice thermal conductivity reduction. Intermetallics 19, 1747–1751 (2011). [Google Scholar]
  15. Cho J. Y. et al. Thermoelectric properties of p-type skutterudites YbxFe3.5Ni0.5Sb12 (0.8 < x < 1). Acta Mater. 60, 2104–2110 (2012). [Google Scholar]
  16. Rogl G. et al. Thermoelectric properties of p-type didymium (DD) based skutterudites DDy(Fe1-xNix)4Sb12 (0.13 < x < 0.25, 0.46 < y < 0.68). J. Alloy. Compd. 537, 242–249 (2012). [Google Scholar]
  17. Liu R., Qiu P., Chen X., Huang X. & Chen L. Composition optimization of p-type skutterudites CeyFexCo4−xSb12 and YbyFexCo4−xSb12. J. Mater. Res. 26, 1813–1819 (2011). [Google Scholar]
  18. Qiu P. et al. Effects of Sn-doping on the electrical and thermal transport properties of p-type Cerium filled skutterudites. J. Alloy. Compd. 509, 1101–1105 (2011). [Google Scholar]
  19. Shi X. et al. Multiple-filled skutterudites: high thermoelectric figure of merit through separately optimizing electrical and thermal transports. J. Am. Chem. Soc. 133, 7837–7846 (2011). [DOI] [PubMed] [Google Scholar]
  20. Ballikaya S., Uzar N., Yildirim S., Salvador J. R. & Uher C. High thermoelectric performance of In, Yb, Ce multiple filled CoSb3 based skutterudite compounds. J. Solid State Chem. 193, 31–35 (2012). [Google Scholar]
  21. Xiong Z., Chen X., Huang X., Bai S. & Chen L. High thermoelectric performance of Yb0.26Co4Sb12/yGaSb nanocomposites originating from scattering electrons of low energy. Acta. Mater. 58, 3995–4002 (2010). [Google Scholar]
  22. Bai S. et al. Enhanced thermoelectric performance of dual-element-filled skutterudites BaxCeyCo4Sb12. Acta. Mater. 57, 3135–3139 (2009). [Google Scholar]
  23. Zhao X. et al. Synthesis and thermoelectric properties of Sr-filled skutterudite SryCo4Sb12. J. Appl. Phys. 99, 053711-053711-053714 (2006). [Google Scholar]
  24. Chen L. et al. Anomalous barium filling fraction and n-type thermoelectric performance of BayCo4Sb12. J. Appl. Phys. 90, 1864–1868 (2001). [Google Scholar]
  25. Li H., Tang X., Zhang Q. & Uher C. High performance InxCeyCo4Sb12 thermoelectric materials with in situ forming nanostructured InSb phase. Appl. Phys. Lett. 94, 102114 (2009). [Google Scholar]
  26. Shi X. et al. Low thermal conductivity and high thermoelectric figure of merit in n-type BaxYbyCo4Sb12 double-filled skutterudites. Appl. Phys. Lett. 92, 182101 (2008). [Google Scholar]
  27. Dyck J. S. et al. Thermoelectric properties of the n-type filled skutterudite Ba0.3Co4Sb12 doped with Ni. J. Appl. Phys. 91, 3698–3705 (2002). [Google Scholar]
  28. Singh D. J. & Du M.-H. Properties of alkaline-earth-filled skutterudite antimonides: A(FeNi)4Sb12 (A= Ca, Sr, and Ba). Phys. Rev. B 82, 075115 (2010). [Google Scholar]
  29. Yang J., Wang S., Yang J., Zhang W. & Chen L. Electron and Phonon Transport in n-and p-type Skutterudites. in MRS Proceed. 1490, 9–18 (Cambridge Univ Press).(2013). [Google Scholar]
  30. Joffe A. Heat transfer in semiconductors. Can. J. Phys. 34, 1342–1355 (1956). [Google Scholar]
  31. Shanks H., Maycock P., Sidles P. & Danielson G. Thermal conductivity of silicon from 300 to 1400 K. Phys. Rev. 130, 1743 (1963). [Google Scholar]
  32. Dismukes J., Ekstrom L., Steigmeier E., Kudman I. & Beers D. Thermal and Electrical Properties of Heavily Doped Ge-Si Alloys up to 1300 °K. J. Appl. Phys. 35, 2899–2907 (1964). [Google Scholar]
  33. Nikitin E., Tamarin P. & Tarasov V. Thermal and electrical properties of cobalt monosilicide between 4.2 and 1600 K. Sov. Phys. Solid. Stat. 11, 2002–2004 (1970). [Google Scholar]
  34. Martin J. Thermal conductivity of Mg2Si, Mg2Ge and Mg2Sn. J. Phys. Chem. Solids 33, 1139–1148 (1972). [Google Scholar]
  35. Yelgel Ö. C. & Srivastava G. Thermoelectric properties of n-type Bi2(Te0.85Se0.15)3 single crystals doped with CuBr and SbI3. Phys. Rev. B 85, 125207 (2012). [Google Scholar]
  36. Jiang J., Chen L., Bai S., Yao Q. & Wang Q. Thermoelectric properties of textured p-type (Bi,Sb)2Te3 fabricated by spark plasma sintering. Scrip. Mater. 52, 347–351 (2005). [Google Scholar]
  37. Wang S. et al. Enhanced thermoelectric properties of Bi2(Te1−xSex)3-based compounds as n-type legs for low-temperature power generation. J. Mater. Chem. 22, 20943–20951 (2012). [Google Scholar]
  38. Puneet P. et al. Preferential Scattering by Interfacial Charged Defects for Enhanced Thermoelectric Performance in Few-layered n-type Bi2Te3. Sci. Rep. 3, 3212; 10.1038/srep03212 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Wang S. et al. Anisotropic multicenter bonding and high thermoelectric performance in electron-poor CdSb. Chem. Mater. 27, 1071–1081 (2015). [Google Scholar]
  40. Kingery W. D. Introduction To Ceramics. John Wiley & Sons: New York, 1960). [Google Scholar]
  41. Crank J. The Mathematics of Diffusion. Clarendon Press: Oxford, 1975). [Google Scholar]
  42. Fistul V. I. Heavily doped semiconductors. Plenum Press: New York, 1969). [Google Scholar]
  43. Ioffe A. F. Physics of Semiconductors Academic Press: New York, 1960). [Google Scholar]
  44. Goldsmid H. J. Electronic Refrigeration. Pion Limited: London, 1986). [Google Scholar]
  45. Goldsmid H. & Sharp J. Estimation of the thermal band gap of a semiconductor from Seebeck measurements. J. Electron. Mater. 28, 869–872 (1999). [Google Scholar]
  46. Blakemore J. S. Semiconductor Statistics. (New York: Courier Dover Publications, 2002). [Google Scholar]
  47. Caillat T., Borshchevsky A. & Fleurial J. P. Properties of single crystalline semiconducting CoSb3. J. Appl. Phys. 80, 4442–4449 (1996). [Google Scholar]
  48. Yang J., Meisner G., Morelli D. & Uher C. Iron valence in skutterudites: Transport and magnetic properties of Co1-xFexSb3. Phys. Rev. B 63, 014410 (2000). [Google Scholar]
  49. Zhou C., Morelli D., Zhou X., Wang G. & Uher C. Thermoelectric properties of P-type Yb-filled skutterudite YbxFeyCo4−ySb12. Intermetallics 19, 1390–1393 (2011). [Google Scholar]
  50. Yang K. et al. Synthesis and thermoelectric properties of double-filled skutterudites CeyYb0.5-yFe1.5Co2.5Sb12. J. Alloy. Compd. 467, 528–532 (2009). [Google Scholar]
  51. Leszczynski J. et al. Electronic band structure, magnetic, transport and thermodynamic properties of In-filled skutterudites InxCo4Sb12. J. Phys. D Appl. Phys. 46, 495106 (2013). [Google Scholar]
  52. Salvador J., Yang J., Wang H. & Shi X. Double-filled skutterudites of the type YbxCayCo4Sb12: Synthesis and properties. J. Appl. Phys. 107, 043705 (2010). [Google Scholar]
  53. Pei Y. et al. Improving thermoelectric performance of caged compounds through light-element filling. Appl. Phys. Lett. 95, 042101 (2009). [Google Scholar]
  54. Pei Y., Chen L., Bai S., Zhao X. & Li X. Effect of Pd substitution on thermoelectric properties of Ba0.3PdxCo4-xSb12. Script. Mater. 56, 621–624 (2007). [Google Scholar]
  55. Zhao W. et al. Enhanced thermoelectric performance in barium and indium double-filled skutterudite bulk materials via orbital hybridization induced by indium filler. J. Am. Chem. Soc. 131, 3713–3720 (2009). [DOI] [PubMed] [Google Scholar]
  56. Yang J. et al. Low temperature transport and structural properties of misch-metal-filled skutterudites. J. Appl. Phys. 102, 083702 (2007). [Google Scholar]
  57. Kuznetsov V., Kuznetsova L. & Rowe D. Effect of partial void filling on the transport properties of NdxCo4Sb12 skutterudites. J. Phys. Condens. Mat. 15, 5035–5048 (2003). [Google Scholar]
  58. Nolas G., Cohn J. & Slack G. Effect of partial void filling on the lattice thermal conductivity of skutterudites. Phys. Rev. B 58, 164 (1998). [Google Scholar]
  59. Morelli D. T., Meisner G. P., Chen B., Hu S. & Uher C. Cerium filling and doping of cobalt triantimonide. Phys. Rev. B 56, 7376 (1997). [Google Scholar]
  60. Slack G. A. & Hussain M. A. The maximum possible conversion efficiency of silicon-germanium thermoelectric generators. J. Appl. Phys. 70, 2694–2718 (1991). [Google Scholar]
  61. Xie W. et al. Identifying the specific nanostructures responsible for the high thermoelectric performance of (Bi,Sb)2Te3 nanocomposites. Nano Lett. 10, 3283–3289 (2010). [DOI] [PubMed] [Google Scholar]
  62. Snyder G. J. & Toberer E. S. Complex thermoelectric materials. Nat. Mater. 7, 105–114 (2008). [DOI] [PubMed] [Google Scholar]
  63. Dresselhaus M. S. et al. New Directions for Low-Dimensional Thermoelectric Materials. Adv. Mater. 19, 1043–1053 (2007). [Google Scholar]
  64. Yang J., Yip H. L. & Jen A. K. Y. Rational design of advanced thermoelectric materials. Adv. Energy Mater. 3, 549–565 (2013). [Google Scholar]
  65. Minnich A., Dresselhaus M., Ren Z. & Chen G. Bulk nanostructured thermoelectric materials: current research and future prospects. Energy Environ. Sci. 2, 466–479 (2009). [Google Scholar]
  66. Yang J. et al. Trends in electrical transport of p-type skutterudites RFe4Sb12 (R= Na, K, Ca, Sr, Ba, La, Ce, Pr, Yb) from first-principles calculations and Boltzmann transport theory. Phys. Rev. B 84, 235205 (2011). [Google Scholar]
  67. Sofo J. & Mahan G. Electronic structure of CoSb3: A narrow-band-gap semiconductor. Phys. Rev. B 58, 15620 (1998). [Google Scholar]
  68. Wang S., Li H., Lu R., Zheng G. & Tang X. Metal nanoparticle decorated n-type Bi2Te3-based materials with enhanced thermoelectric performances. Nanotechnology 24, 285702 (2013). [DOI] [PubMed] [Google Scholar]
  69. Wang S., Xie W., Li H. & Tang X. Enhanced performances of melt spun Bi2(Te,Se)3 for n-type thermoelectric legs. Intermetallics 19, 1024–1031 (2011). [Google Scholar]
  70. Wang S., Xie W., Li H. & Tang X. High performance n-type (Bi,Sb)2(Te,Se)3 for low temperature thermoelectric generator. J. Phys. D Appl. Phys. 43, 335404 (2010). [Google Scholar]
  71. Poudel B. et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 320, 634–638 (2008). [DOI] [PubMed] [Google Scholar]
  72. Bahk J.-H. & Shakouri A. Enhancing the thermoelectric figure of merit through the reduction of bipolar thermal conductivity with heterostructure barriers. Appl. Phys. Lett. 105, 052106 (2014). [Google Scholar]
  73. Zhang Y., Ke X., Chen C., Yang J. & Kent P. R. Nanodopant-induced band modulation in AgPbmSbTe2+m-type thermoelectrics. Phys. Rev. Lett. 106, 206601 (2011). [DOI] [PubMed] [Google Scholar]
  74. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
  75. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994). [DOI] [PubMed] [Google Scholar]
  76. Kresse G. & Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999). [Google Scholar]
  77. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996). [DOI] [PubMed] [Google Scholar]
  78. Yang J. et al. Evaluation of Half-Heusler Compounds as Thermoelectric Materials Based on the Calculated Electrical Transport Properties. Adv. Funct. Mater. 18, 2880–2888 (2008). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep10136-s1.docx (3.1MB, docx)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES