N-acetyl-aspartate levels correlate with intra-axonal compartment parameters from diffusion MRI

Abstract

Diffusion MRI combined with biophysical modeling allows for the description of a white matter (WM) fiber bundle in terms of compartment specific white matter tract integrity (WMTI) metrics, which include intra-axonal diffusivity (D_axon), extra-axonal axial diffusivity (D_e∥), extra-axonal radial diffusivity (D_e⊥), axonal water fraction (AWF), and tortuosity (α) of extra-axonal space. Here we derive these parameters from diffusion kurtosis imaging to examine their relationship to concentrations of global WM N-acetyl-aspartate (NAA), creatine (Cr), choline (Cho) and myo-Inositol (mI), as measured with proton MR spectroscopy (¹H-MRS), in a cohort of 25 patients with mild traumatic brain injury (MTBI). We found statistically significant (p<0.05) positive correlations between NAA and D_axon, AWF, α, and fractional anisotropy; negative correlations between NAA and D_e,⊥ and the overall radial diffusivity (D_⊥). These correlations were supported by similar findings in regional analysis of the genu and splenium of the corpus callosum. Furthermore, a positive correlation in global WM was noted between D_axon and Cr, as well as a positive correlation between D_e∥ and Cho, and a positive trend between D_e∥ and mI. The specific correlations between NAA, an endogenous probe of the neuronal intracellular space, and WMTI metrics related to the intra-axonal space, combined with the specific correlations of D_e∥ with mI and Cho, both predominantly present extra-axonally, corroborate the overarching assumption of many advanced modeling approaches that diffusion imaging can disentangle between the intra- and extra-axonal compartments in WM fiber bundles. Our findings are also generally consistent with what is known about the pathophysiology of MTBI, which appears to involve both intra-axonal injury (as reflected by a positive trend between NAA and D_axon) as well as axonal shrinkage, demyelination, degeneration, and/or loss (as reflected by correlations between NAA and D_e⊥, AWF, and α).

1. INTRODUCTION

Diffusion MRI (dMRI) is the imaging method of choice to probe white matter (WM) microstructure. To date, diffusion tensor imaging (DTI) has been the primary dMRI technique used to conduct in vivo investigations of WM microstructural integrity (Basser, 1995; Jones, 2010). DTI quantifies the Gaussian part of the probability distribution of molecular displacement in terms of the overall diffusion tensor from which derived metrics such as the mean, radial, and axial diffusivities (MD, D_∥, and D_⊥), and fractional anisotropy (FA) are derived. DTI metrics have been shown to be significantly altered in multiple pathologies (Horsfield and Jones, 2002; Jones, 2010). In addition, over the past decade several techniques have been proposed to assess the non-Gaussian part of the diffusion displacement distribution (Alexander et al., 2002; Jensen and Helpern, 2010; Liu et al., 2004; Maier et al., 2004; Özarslan et al., 2013; Tuch, 2004; Wedeen et al., 2005). In particular, diffusion kurtosis imaging (DKI), a clinically feasible non-Gaussian method (Jensen and Helpern, 2010; Jensen et al., 2005; Lu et al., 2006), has shown promise in several brain pathologies. (Jensen and Helpern, 2010; Steven et al., 2014)

The growing list of clinical studies using both DTI and DKI demonstrates the high sensitivity of their empirical diffusion parameters to microstructural changes in WM integrity. However, such empirical measures only provide an indirect characterization of microstructure. Their physical meaning in terms of specific tissue properties still remains uncertain. Indeed, it is imperative to distinguish between mathematical models representing the diffusion signal (e.g., the cumulant expansion (Kiselev, 2010), mono-, bi-, and stretched exponential models (Assaf and Cohen, 1998; Bennett et al., 2003; Niendorf et al., 1996), and mean apparent propagator (Özarslan et al., 2013)) and true biophysical models taking into account actual neuronal structure as described below for WM. The former (e.g., DTI and DKI) are applicable in all brain voxels and do not make assumptions about the underlying microstructure, whereas the latter are specifically tailored to model the effects of microstructure on diffusion in certain regions of the brain. Hence, such biophysical models are especially useful to gain insight into the underlying pathological processes and to increase the pathophysiological specificity.

In modeling WM diffusion, the common practice has been to model axons as zero radius, infinitely long, impermeable tubes and cylinders (Assaf and Basser, 2005; Assaf et al., 2004; Kroenke et al., 2004) or sticks (Behrens et al., 2003). Another common assumption is to neglect the water exchange through the myelin sheath surrounding axons. As a result, the diffusion signal in the WM contains at least two components, which correspond to the intra- and extra-axonal spaces. While these assumptions seem plausible and form the basis for most current diffusion models of WM in the brain (Alexander et al., 2010; Assaf and Basser, 2005; Assaf et al., 2004; Basser et al., 2007; Jespersen et al., 2007; Nilsson et al., 2013; Panagiotaki et al., 2009; Panagiotaki et al., 2012; Wang et al., 2011; Zhang et al., 2012), further validation remains warranted.

Based on the assumptions of a two non-exchanging compartments model, we recently showed that for a single WM fiber bundle, a minimum set of two shells in q-space (i.e., two nonzero b-values in each direction) together with b = 0 are sufficient to discern between intra- and extra-axonal water, and allow for the description of compartment specific white matter tract integrity (WMTI) metrics from the diffusion and kurtosis tensor (Fieremans et al., 2011; Fieremans et al., 2010). Specifically, as shown in Fig. 1, these include intra-axonal diffusivity (D_axon), extra-axonal axial and radial diffusivities (D_e∥ and D_e⊥), axonal water fraction (AWF), and tortuosity (α) of extra-axonal space (Sen and Basser, 2005). To date, WMTI metrics have been preliminarily applied to several brain conditions and shown to provide useful information about plausible biophysical mechanisms. (Benitez et al., 2014; Fieremans et al., 2013; Hui et al., 2012; Lazar et al., 2014)

Fig. 1.

The WMTI model for compartment specific cellular diffusivity: (a) a white matter fiber bundle is composed of cylindrical axons surrounded by a myelin sheath; (b) the diffusion signal reflects restricted water molecule movement in both intra-axonal (red) and extra-axonal (cyan) space; (c) transverse and (d) parallel cross-sections illustrate the metrics used to estimate this activity which are summarized by the model parameters legend.

The purpose of the current study is to examine the in vivo relationship between these WMTI parameters and concentrations of the metabolites N-acetylaspartate (NAA), creatine (Cr), choline (Cho), and myo-Inositol (mI) measured using ¹H-MRS. Our results could help clarify their meaning and shed light on the validity of the assumptions typically made when modeling the diffusion signal in WM. In particular, we hypothesized that NAA, as an endogenous probe of the neuronal intracellular space (Kroenke et al., 2004), would correlate specifically with the WMTI parameters related to axonal density and diffusion inside the axons.

The relationship between FA and NAA, Cr, and Cho has been evaluated in the WM of healthy adults in a previous study which showed that NAA concentrations explained most of the variance in FA (Wijtenburg et al., 2012). Here, we evaluate the relationship between DTI, DKI, model-specific WMTI parameters, and ¹H-MRS metabolites (NAA, Cr, Cho, and mI absolute concentrations) in a cohort of patients with mild traumatic brain injury (MTBI). This cohort has already been compared to age-matched controls using DTI (Grossman et al., 2013), DKI (Grossman et al., 2013), and ¹H-MRS (Kirov et al., 2013a; Kirov et al., 2013b). By combining the results from both diffusion and spectroscopy measurements in MTBI, we aim (i) to investigate the specificity of diffusion parameters for ¹H-MRS-detectable metabolites; and (ii) to elucidate specific biophysical mechanisms that influence structural and metabolic changes following MTBI.

2. METHODS

2.1. Subjects

Approval for the study was obtained from the Institutional Review Board of the New York University School of Medicine and all participants provided informed written consent. Twenty-five adult patients with MTBI (20 male, 5 female; mean age = 33.6 years ± 11.2) prospectively recruited in our previous studies (Grossman et al., 2013; Kirov et al., 2013a) were examined retrospectively. Patients had been included if they were within 1 month following injury (mean interval = 21.2 days ± 14.3) and classified with MTBI using diagnostic criteria developed by the Mild Traumatic Brain Injury Interdisciplinary Special Interest Group of the American Congress of Rehabilitation Medicine (Esselman and Uomoto, 1995). Enrollment was permitted only in cases in which there existed no other history of brain damage or disorders of the central nervous system, no history of systemic illness, and no history of alcoholism or drug dependency. Patient demographics and clinical data are summarized in Table 1. Nineteen patients had an emergency room Glasgow Coma Scale score of 15, five had a score of 14, and one had a score of 13. Conventional MRI scans showed in each of four patients the separate presence of a right frontal convexity arachnoid cyst, a nonspecific focus of T2 hyperintense signal in the left frontal lobe white matter, a stable right cerebellopontine angle arachnoid cyst, and left temporal lobe encephalomalacia.

Table 1.

Patient demographics.

Patient	Age/sex	Cause of injury	GCS score	Days since injury	T2W MRI findings
1	41/M	Fall	15	3	Normal
2	41/M	Fall	15	5	Normal
3	42/M	Fall	14	5	Normal
4	23/M	Assault	13	6	Normal
5	18/M	Assault	15	10	Normal
6	25/M	Assault	15	10	Right frontal convexity arachnoid cyst
7	28/M	Fall	15	12	Normal
8	29/M	Fall	15	13	Normal
9	25/F	Ped/auto	15	14	Normal
10	32/M	Assault	15	17	Normal
11	25/M	Assault	15	17/18	Normal
12	23/M	Assault	14	18	Nonspecific left frontal lobe white matter foci
13	23/M	Assault	15	18	Normal
14	19/M	Ped/auto	15	19	Normal
15	20/M	Assault	14	19	Normal
16	51/F	Fall	14	20/21	Stable right cerebellopontine arachnoid cyst
17	51/M	MVA	14	19	Nonspecific frontal and parietal lobe white matter foci. Left temporal lobe encephalomalacia
18	36/M	Sports	15	23	Normal
19	36/M	Sports	15	24	Normal
20	29/F	Cyclist/auto	15	29	Normal
21	39/M	Fall	15	31	Normal
22	57/M	Assault	15	40	Normal
23	33/F	Fall	15	44	Normal
25	50/M	Fall	15	54	Normal
24	45/F	Ped/auto	15	55	Normal

GCS: Glasgow Coma Scale, T2W MRI: T2 weighted magnetic resonance imaging, Ped/auto: pedestrian struck by an automobile, MVA: motor vehicle accident, Cyclist/auto: cyclist struck by an automobile.

2.2. Data Acquisition

DKI and ¹H-MRS were performed on a 3T Magnetom Tim Trio whole-body scanner (Siemens, Erlangen, Germany) as previously described (Grossman et al., 2013; Kirov et al., 2013a) within the same or next day of each other. The DKI-protocol included a 2D T2-weighted image double-echo turbo spin-echo, which was applied to 50 axial sections that were 3-mm-thick and contiguous, with repetition time (TR) = 4330 ms, echo time 1 (TE1) = 11 ms, TE2 = 91 ms, flip angle = 120°, field of view (FOV) = 220 × 190 mm², and image matrix 448 × 358. DKI was applied to 28 axial sections that were 2.7-mm-thick and contiguous, with TR = 3700 ms, TE = 96 ms, FOV = 222 × 222 mm², image matrix = 82 × 82, and voxel size = 2.7 × 2.7 × 2.7 mm³, using a twice-refocused spin-echo diffusion technique with 30 different gradient-encoding directions and 3 b-values (0, 1000, and 2000 s/mm²).

The ¹H-MRS protocol included a sagittal 3D Magnetization Prepared RApid Gradient Echo (MP-RAGE) with TR = 1360 ms, TE = 2.6 ms, inversion time = 800 ms, FOV 256×256×160 mm³, and image matrix = 256 × 256 × 160 for guidance of the ¹H-MRS volume-of-interest (VOI) and for tissue segmentation. Our chemical-shift imaging (CSI) based automatic shim procedure adjusted the scanner’s first and second order currents in under 5 minutes (Hu et al., 1995). A 10 × 8 × 4.5 = 360 cm^{3 1}H-MRS imaging VOI was then image-guided over the corpus callosum, angled along the genu-splenium line, as shown in Fig. 3a–b. The VOI was excited with point resolved spectroscopy using TR = 1800 ms and TE = 35 ms in three 1.5 cm thick, second-order Hadamard-encoded slabs (6 slices) interleaved every TR along the inferior-superior direction, as shown in Fig. 3a, for minimal chemical shift displacement error (Goelman et al., 2007) and optimal signal-to-noise and spatial coverage (Goelman et al., 2006). The axial slabs were encoded with 2D 16×16 CSI over a 16 × 16 cm² FOV and an 8 × 10 cm VOI defined in their planes with two 11.2 ms long numerically optimized 180° radio frequency pulses (4.5 kHz bandwidths) under 1.34 and 1.1 mT/m gradients, yielding 480 voxels 0.75 cm³ each in the VOI, as shown in Figs. 2c and d. The MR signal was acquired for 256 ms at ±1 kHz bandwidth. At two averages, the ¹H-MRS imaging took 34 minutes.

Fig. 3.

Sagittal (a), coronal (b), and axial (c) T1-weighted MRI of patient #12 in Table 1, with the 8 × 10 × 4.5 (left-right × anterior-posterior × inferior-superior) VOI (thick white frame) and 16 × 16 × 6 FOV (thin white grid) superimposed. The three second-order Hadamard Spectroscopic Imaging slabs are indicated with yellow and orange outline, the orange arrow marks the ¹H-MRS slice shown in c and d. The genu and the splenium of the corpus callosum outlined in red on c fall within a number of voxels, but only those satisfying the thresholding criteria are used for the quantification: they are shown in red on the corresponding 8 × 10 spectral matrix from slice c in d and in detail in e (thin black lines) superimposed with their fitted functions (thick gray lines).

Fig. 2.

DTI, DKI, and WMTI parametric maps of patient #12 in Table 1: top row: DTI parametric maps (i.e., MD, D_∥, D_⊥, and FA); center row: kurtosis parametric maps (i.e., MK, K_∥, and K_⊥); and bottom row: WMTI parametric maps (i.e., D_axon, D_e∥, D_e⊥, AWF, and α) as overlays on the FA map.

2.3 White matter tract integrity parameters derived from DKI

DKI extends conventional DTI by estimating the kurtosis of the water diffusion displacement probability function (Jensen and Helpern, 2010; Jensen et al., 2005; Lu et al., 2006). The kurtosis is a general dimensionless statistic for quantifying the non-Gaussianity of any distribution (DeCarlo, 1997) and, in the case of diffusion in biological tissue, is an indicator of diffusional heterogeneity and microstructural complexity. Because diffusion in the brain is anisotropic, DKI requires the introduction of a fourth order diffusion kurtosis tensor in addition to the second order diffusion tensor used in DTI. Hence, DKI differs from DTI in that it requires at least 3 b-values, compared to only two for DTI, and 15 independent diffusion gradient directions, compared to 6 for DTI. DKI thus provides both the diffusion and kurtosis tensors, from which Gaussian and non-Gaussian diffusion metrics such as MD, D_∥, D_⊥, FA, and mean, radial and axial kurtoses (MK, K_∥, and K_⊥) are derived. Both DTI and DKI metrics are model-independent diffusion measures, and their physical meaning for microscopic tissue properties needs to be further established with respect to tissue type and brain region.

We recently introduced a WM model that relates DKI metrics directly to WM microstructure (Fieremans et al., 2011; Fieremans et al., 2010). In this model we characterize WM microstructure that consists of aligned fiber bundles by assuming that the tissue is composed of cylindrical axons, each surrounded by a myelin sheath (illustrated in Fig. 1). The relative volume of water within the collective intra-axonal space (IAS) represents the AWF. The remainder of the WM is modeled as the extra-axonal space (Fieremans et al., 2010). Water inside the myelin is not included in the model since its diffusion MRI signal decays too rapidly to be detected with the imaging parameters of this study. For a sufficiently coherent single fiber bundle, the WM model metrics (i.e., AWF and the individual compartmental diffusion tensors for the IAS and for the EAS) can be calculated from the diffusion and kurtosis tensors:

$$\mathit{\text{AWF}}=\frac{K_{\mathit{\text{max}}}}{K_{\mathit{\text{max}}}+3},D_{e,n}=D_n[1+\sqrt{\frac{K_n\mathit{\text{AWF}}}{3(1-\mathit{\text{AWF}})}}],D_{a,n}=D_n[1-\sqrt{\frac{K_n(1-\mathit{\text{AWF}})}{3(1-\mathit{\text{AWF}})}}],$$ (1)

where K_max is the maximum kurtosis over all possible directions, and D_e,n, D_a,n, D_n, K_n are, respectively, the extra-axonal diffusivity, axonal diffusivity, total diffusivity, and total kurtosis in a given diffusion direction n. Equations in (1) are valid in any direction, so by choosing 6 or more independent directions we can then reconstruct (using the standard DTI method) the compartmental diffusion tensors, D_e and D_a This model is valid only for single fiber bundles and is therefore assumed to be applicable in major WM tracts including, for example, the corpus callosum (Fieremans et al., 2011). In this study, we focus on the following WMTI metrics, illustrated in Fig. 1:

• D_a = tr(D_a), the intra-axonal diffusivity (along the axons), a potential marker for axonal injury.

• D_e∥ and D_e⊥, the axial and radial diffusivities in the EAS, potential markers for extra-axonal changes including extracellular inflammation, gliosis, and demyelination.

• f = V_IAS / (V_IAS + V_EAS), where f is AWF, a potential marker for axonal loss, and V_IAS and V_EAS are the water volumes of the IAS and the EAS, excluding the myelin.

• α= D_e∥ / D_e⊥, the tortuosity of the EAS, a potential marker for demyelination.

Fig. 2. shows representative parametric maps of all these metrics for patient #12 in Table 1.

2.4. Data Processing and Analysis

The global ¹H-MRS data were processed as previously described (Kirov et al., 2013a); the MP-RAGE images were segmented into GM, WM, and cerebral spinal fluid (CSF) by Statistical Parametric Mapping 8 software (Wellcome Trust Centre for Neuroimaging, 2010), and the resultant masks were co-registered with the ¹H-MRS grid using in-house software (Tal et al., 2012). Metabolite levels in each ¹H-MRS voxel were estimated by the SITools-FITT spectral modeling software (Soher et al., 1998), as shown in Fig. 3e. Global GM and WM metabolite levels were calculated using linear regression (Tal et al., 2012). These were converted to absolute concentrations using phantom replacement with correction for T₁ and T₂ relaxation time differences (Ethofer et al., 2003; Kirov et al., 2008) between the in vitro and in vivo experiments. For NAA, Cr, Cho, and mI the in vivo T₁ s used were 1360, 1300, 1145, and 1170 ms, and the in vivo T₂ s used were 400, 185, 258, and 200 ms. The corresponding values measured in the reference phantom were T₁ = 605, 336, 235, and 280 ms and T₂ = 483, 288, 200, and 233 ms. Spectral quality control was comprised to exclude any voxels with lipid contamination, Cramer-Rao lower bounds over 15%, and linewidths under 4 or over 13 Hz.

Regional ¹H-MRS data was obtained as follows; the genu and splenium of the corpus callosum were manually outlined on each patient’s axial MP-RAGE images based on DTI atlas parcellations (Mori et al., 2005) as shown in Fig. 3. The resulting binary masks were co-registered with the ¹H-MRS matrix and the GM, WM, and CSF masks. Only voxels containing more than 50% of the genu and splenium were retained for analysis. The remaining partial volumes were carefully controlled; since the corpus callosum is adjacent to the lateral ventricles, any voxels with more than 30% CSF were excluded, and since GM concentrations differ from those in WM (Tal et al., 2012), only 30% GM partial volume was allowed. Moreover, the values were corrected for any remaining CSF content and amount of corpus callosum mask inside the selected voxels. Absolute quantification and spectral quality control were identical to those employed in calculating the global values.

DKI images were processed and WMTI parametric maps were derived as described in Fieremans et al., 2011. In-house image processing software written in Matlab R2014a (The Mathworks, Natick, MA, USA) was used for checking image quality, motion, and eddy current correction, and estimating the DKI tensor elements. After selective smoothing of the DKI images with an isotropic, two-dimensional Gaussian kernel (full width at half maximum = 1.25 × voxel size) to reduce the Gibbs ringing artifact, a constrained weighted linear least squares estimator was used to compute the DKI tensors, including both the diffusion and kurtosis tensors (Veraart et al., 2013). Selectivity within the smoothing procedure is based on the exclusion of the CSF voxels in order to avoid a quantitative bias due to CSF contamination (Jelescu et al., 2015). The estimated diffusion and kurtosis tensors in each voxel were then used to derive (a) parametric diffusivity maps (i.e., MD, D_∥, D_⊥, and FA), (b) the additional kurtosis metric maps (i.e., MK, K_∥, and K_⊥), and (c) WM parametric maps (i.e., D_axon, D_e∥, D_e⊥, AWF, and α). An example of all these parametric maps for patient #12 in Table 1 are shown in Fig. 2.

FA maps were nonlinearly coregistered to the Montreal Neurological Institute (MNI) 152 standard brain and the transformations applied to WMTI parametric maps using the Functional MRI of the Brain Software Library (FSL) (FMRIB Analysis Group, Oxford University, Oxford, UK) (Smith et al., 2006; Smith et al., 2004). A rectangular shaped global WM region of interest (ROI) was defined on the MNI 152 FA template in 45 contiguous oblique slices oriented along the anterior commissure-posterior commissure line that corresponded with the VOI specified in our previous ¹H-MRS investigations (Kirov et al., 2013a) using MRIcron software (Chris Rorden, University of South Carolina, South Carolina, USA). The mean value for each WMTI metric was calculated by employing a threshold of FA > 0.4 to select out all voxels containing single white matter fiber bundles (Fieremans et al., 2011) using an in-house MATLAB script. Examples of slices from the MNI 152 standard brain displaying voxels containing single white matter fiber bundles that were used to calculate the mean value for WMTI, DTI, and DKI metrics are shown in Fig. 4. The global WM ROI covered the internal capsule, corona radiata, and centrum semiovale, as well as the genu, body, and splenium of the corpus callosum. In addition, regional mean values for the same parameters were also extracted over the genu and splenium of the corpus callosum, as drawn on the FA template available within FSL on the basis of the John Hopkins University WM label atlas (Mori et al., 2005), to correlate specifically with the ¹H-MRS metabolite concentrations derived in these regions.

Fig. 4.

Representative slices from the MNI 152 standard brain displaying voxels (blue: global WM with FA > 0.4, red: splenium corpus callosum, yellow: genu corpus callosum) of white matter contained in the ¹H-MRS VOI (green) that were selected to calculate the mean value for WMTI, diffusivity, and kurtosis metrics.

2.5. Statistical Analysis

Correlations between mean WMTI (D_axon, D_e∥, D_e⊥, AWF, and α), DTI (MD, D_∥, and D_⊥, and FA), and DKI (MK, K_∥, and K_⊥) metrics and mean ¹H-MRS (NAA, Cr, Cho, and mI) metabolite concentrations were tested with partial Pearson coefficients adjusted with age as a controlling variable, and assessed for corresponding p values using an in-house MATLAB script. All p values reported were two-sided and declared statistically significant when p < 0.05. In addition, trends towards statistical significance associated with a p-value < 0.1 were reported if they supported expectations and/or provided meaningful insight into the employed biophysical model underlying WMTI metrics.

3. RESULTS

With respect to the diffusivity metrics, significant positive correlation was found in the global WM for NAA with FA (ρ = 0.69, p < 0.001), and significant negative correlation with D_⊥ (ρ = −0.45, p = 0.024), as shown in Fig. 5. Similarly for the corpus callosum ROIs, positive correlation was found with FA (ρ = 0.48, p = 0.028) and a negative trend with D_⊥ (ρ = −0.38, p = 0.081) in the splenium, and a positive trend between FA and NAA (ρ = 0.38, p = 0.073). In addition, no correlations were found between DTI metrics and concentrations of Cho, Cr, and mI in any ROI.

Fig. 5.

Scatter plots between NAA levels and FA and D± in global WM of MTBI patients showing best fit lines and partial Pearson coefficients (ρ) and p-values: triangles represent females, circles represent males.

With respect to the kurtosis metrics, no correlations were found in global WM for any ¹H-MRS metabolite concentrations. However, in the genu and splenium, positive correlations were found between NAA and K_⊥ (ρ = 0.47, p = 0.032 and ρ = 0.44, p = 0.037, respectively) (Fig. 6). Also, a positive correlation was found in the genu between K∥ and Cr (ρ = 0.52, p = 0.029) and a positive correlation in the splenium between K_∥ and Cho (ρ = 0.47, p = 0.024).

Fig. 6.

Scatter plots between NAA levels and K_⊥ in the genu (left) and splenium (right) of the corpus callosum of MTBI patients showing best fit lines and partial Pearson coefficients (ρ) and p-values: triangles represent females, circles represent males.

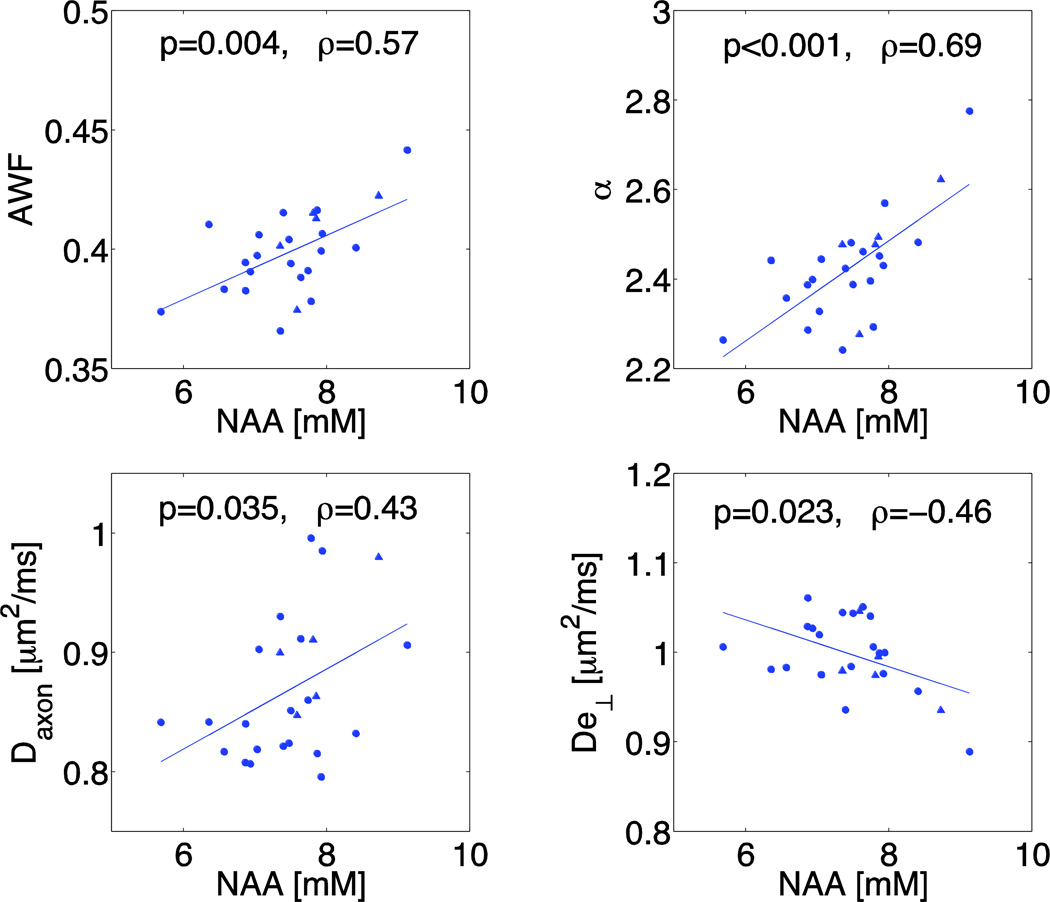
Plots of the WMTI metrics versus NAA concentrations in global WM are shown in Fig. 7, demonstrating positive correlations between NAA and AWF (ρ = 0.57, p = 0.004) and α (ρ = 0.69, p < 0.001), and a negative correlation between NAA and D_e⊥ (ρ = −0.46, p = 0.023). Similar positive correlations are observed in the genu and splenium between NAA and AWF (ρ = 0.45, p = 0.040 in genu and ρ = 0.49, p = 0.017 in splenium), and between NAA and α (ρ = 0.52, p = 0.017 in genu and ρ = 0.40, p = 0.055 in splenium), as well as a negative trend between NAA and D_e⊥ in the genu (ρ = −0.37, p = 0.1).

Fig. 7.

Scatter plots between NAA levels and WMTI (D_axon, D_e⊥, AWF, and α) in global WM of MTBI patients showing best fit lines and metrics and partial Pearson coefficients (ρ) and p-values: triangles represent females, circles represent males.

With respect to the axial compartment diffusivities, in global WM (Fig. 7), positive correlations are noted between NAA and D_axon (ρ = 0.43, p = 0.035). Additional correlations were found between Cr and D_axon (ρ = 0.44, p = 0.032), shown in Fig. S1, as well as a positive correlation between D_e∥ and Cho (ρ = 0.48, p = 0.019) and a positive trend between D_e∥ and mI (ρ = 0.38, p = 0.064), both shown in Fig. S2.

4. DISCUSSION

While the diffusion signal is very sensitive to changes in microstructural WM integrity, empirical dMRI measures lack specificity. Here we have shown that biophysical modeling of the diffusion signal in the WM provides insight into microstructural changes and underlying pathological processes. Using the common WM modeling assumption that myelinated axons can be represented as impermeable cylinders, we were recently able to separate between intra- and extra-axonal diffusion in terms of compartment specific WMTI parameters in DKI (Fieremans et al., 2011; Fieremans et al., 2010). When applied to stroke (Fieremans et al., 2012; Hui et al., 2012), for example, we provided direct evidence for reduction in D_axon, which can be interpreted in terms of axonal beading (Budde and Frank, 2010; Li and Murphy, 2008) or any other increase in structural disorder along effectively one-dimensional neurites (Novikov et al., 2014) related to primary mechanisms that underlie a drop in diffusion associated with ischemia. Furthermore, when WM microstructure in patients with mild cognitive impairment and Alzheimer’s disease were compared with age-matched normal controls, WMTI metrics supported the hypothesis that demyelination and axonal loss are key neurodegenerative processes describing the progression from normal control to mild cognitive impairment, and from mild cognitive impairment to Alzheimer’s disease, respectively (Fieremans et al., 2013).

This study examined the relationship between WMTI metrics and the levels of ¹H-MRS-derived metabolites. Partial volume issues resulting from the different spatial resolutions of the two modalities (0.02 cm³ for DKI vs 0.75 cm³ for ¹H-MRS) were addressed by using a global ¹H-MRS approach which computes the average metabolic concentrations of GM and WM over the entire 360 cm³ VOI (Tal et al., 2012). Regional analysis was performed to validate the global results. The use of absolute metabolic quantification avoided ambiguities inherent in metabolic ratios, in which the contributions of the numerator (often NAA) and denominator (often Cr) cannot be disentangled.

Overall, most correlations and trends observed in the corpus callosum are also present in global WM, except for additional correlations with K_∥ and K_⊥ in both the genu and splenium. Furthermore, extra correlations with respect to the compartment diffusivities are observed in global WM. The observed correlations between NAA and DTI metrics (D_⊥ and FA) in MTBI patients are similar to those found in a previous study in healthy controls (Wijtenburg et al., 2012). We also observed specific correlations between the NAA and K_⊥ in the genu and splenium of corpus callosum, which could potentially be explained by the specific sensitivity of K_⊥ to the presence of myelin and axonal density. These additional correlations further suggest that DKI indeed does provide additional information compared to DTI alone.

These results show that when global WM was examined with respect to WMTI metrics in patients with MTBI, NAA exhibited correlations with D_axon, D_e⊥, AWF, and α but not with D_e∥, and that both Cho and mI exhibited correlations with D_e∥. The finding that NAA exclusively correlates with the intra-axonal compartment parameters as well as with D_e⊥, which is directly sensitive to the myelin surrounding axons, provides insight in the validity of compartment models for diffusion in WM, which is explained in more detail below. We also discuss how these relationships help to elucidate the subtle biophysical mechanisms underlying injury in MTBI, and then, finally, some potential limitations of this study.

4.1 Correlations with NAA support WM modeling assumptions

Since the WMTI diffusion model allows for the separation of the diffusion signal into intra-and extra-axonal contributions (Fieremans et al., 2011), we investigated the specificity of its parameters to neurochemical changes measured for individual metabolites. Interestingly, we found correlations between NAA, a compound which exists predominantly inside neurons (Baslow, 2003), and D_axon, D_e⊥, AWF, and α and no such correlation between NAA and D_e∥. Indeed, the correlation with D_axon was expected as it reflects the diffusivity inside of axons. The correlations with AWF and α were also expected as they are determined by axonal and myelin density, respectively. On the other hand, the correlation with D_e∥ was unexpected since it reflects the diffusivity in the extra-cellular space alongside the axon, which does not depend directly on an endogenous probe like NAA. There was also an interesting trend towards significant correlation between mI, a putative astroglial marker, and D_e∥ exclusively in astrocytes (Brand et al., 1993). The findings that Cr correlated with D_axon and Cho correlated with D_e∥ are not as informative, however, as these two metabolites are found in both neurons and glia (Urenjak et al., 1993). Hence, these results are in overall agreement with the common assumptions used in WM diffusion modeling for non-exchanging compartments and show that for single WM bundles, a minimum set of two shells in q-space (i.e., two nonzero b-values in each direction) together with b = 0 are sufficient to accurately distinguish between the intra- and extra-axonal space using compartment specific WMTI parameters.

We extracted the WMTI metrics from the diffusion and kurtosis tensor (Fieremans et al., 2011), which can be derived using a straightforward linear least-square estimation procedure (Tabesh et al., 2011; Veraart et al., 2013). It should be noted that there are several other modeling approaches which start with the same premise of the axon as a non-exchanging compartment and which also extract compartmental parameters directly from the diffusion signal, but they use non-linear fitting techniques and differ among each other in their underlying assumptions and fitting procedures (Alexander et al., 2010; Assaf and Basser, 2005; Assaf et al., 2004; Basser et al., 2007; Jespersen et al., 2007; Panagiotaki et al., 2009; Panagiotaki et al., 2012; Wang et al., 2011; Zhang et al., 2012).

It is also of interest to note that we found D_e∥, an estimate for the intrinsic extra-axonal diffusion coefficient, to be twice as high as D_axon, a measure for the intrinsic intra-axonal diffusion coefficient. This finding is in distinction to the assumption frequently made during modeling of setting the compartment diffusivities as equal (Alexander, 2008; Alexander et al., 2010; Panagiotaki et al., 2012; Zhang et al., 2012) or being higher inside axons than outside (Assaf and Basser, 2005; Assaf et al., 2004), rather than to obtain their values by fitting data. In fact, when deriving equation (1), the solution where D_e∥ ≤ D_axon (another case for the solutions to quadratic equations (B.3) and (B.4) in (Fieremans et al., 2011)) has been discarded. For this study, we considered both solutions and found specific correlations (NAA and D_axon, mI and D_e∥) for the solution where D_e∥ ≥ D_axon but no correlations or trends in the compartment diffusivities for the solution where D_e∥ ≤ D_axon. Therefore, within the WMTI framework, the choice of D_e∥ ≥ D_axon seems to be the more plausible solution. However, the other solution produces less aligned fiber configurations (the transverse eigenvalues of D_a become on the order of 10% the longitudinal one), which may take us away from the scope of applicability for WMTI. To investigate the role of fiber dispersion, one would need to go beyond the DKI framework and use at least 3 shells in q-space (3 nonzero b-values) (Novikov et al., 2015).

While our results are in overall agreement with the common assumptions used in WM diffusion modeling for non-exchanging, the simple picture of axons as narrow hollow cylinders may need further refinement. In particular, this picture has recently been complemented by investigations of structural disorder to account for the time-dependence of the diffusion coefficient (Burcaw et al., 2014; Novikov et al., 2014). Therefore, the two compartments should perhaps be treated as having effective rather than free-water parameters, with these effective diffusivities incorporating the overall influence of neuronal fibers and their intricate structure on scales below a few micrometers.

4.2 Biophysical mechanisms underlying injury in MTBI

Although there have been few clinical histological studies of MTBI since patients rarely die from such injuries, there is evidence that it can cause microstructural and functional changes like diffuse axonal injury (DAI) and detrimental secondary chemical cascades (Johnson et al., 2013). These arise from impact forces, in which the head strikes or is struck by something, or impulsive forces, in which the head undergoes sudden acceleration or deceleration, resulting in linear, angular, or rotational movement of the brain, or some combination of them, as well as elongation and deformation of brain tissue. Initially, this results in ionic imbalances, which perturb cellular functioning, and misalignment of the cytoskeletal network in axonal membranes, which can be followed by impairment of axoplasmic transport and local accumulation of organelles, causing local swelling and expansion of the axonal cylinder. In DAI, the swollen axon separates into a proximal segment in continuity with the soma and a distal segment which will undergo Wallerian degeneration within weeks (Christman et al., 1994; Inglese et al., 2005; Povlishock and Christman, 1995).

In our previous work we reported that for the same MTBI subjects used in this study NAA was decreased in comparison to age-matched controls (Kirov et al., 2013a). The correlations observed in the current study between NAA and specific WMTI metrics have the potential to provide a more direct link to the disease mechanisms occurring in MTBI. All patients in this study possessed the mildest degree of injury (average Glascow Coma Scale score = 14.7, Table 1) and were within the subacute phase of MTBI (mean time from injury = 21.2 days, Table 1), suggesting that the reduction in intra-axonal diffusivity might be explained not by the presence of axons damaged enough to degenerate, but by the presence of axons that demonstrate some misalignment in their cytoskeletal network resulting in impairment of axonal transport, which is still within the assumptions of our WMTI model. On the other hand, the reduction in NAA and its association with a decrease in AWF and α and an increase in D_e⊥ might also be consistent with changes in axonal integrity, including axonal shrinkage and demyelination as well as some amount of Wallerian and retrograde degeneration in axons. Indeed, based on these findings, we conjecture that diffusion metrics may be more sensitive to subtle axonal demyelination at the subacute or acute stage of MTBI, while this process may be beneath the detection threshold of ¹H-MRS until further out from injury, as previously observed by the positive correlation of Cr and Cho with increasing time since trauma (but not mI, thus excluding gliosis) (Kirov et al., 2013a). In addition, the overall correlations with NAA were not particularly strong, which may reflect the view that there are only subtle pathological changes in this very mildly injured cohort, and that NAA also reflects a range of non-structural pathophysiology, such as mitochondrial impairment, to which diffusion imaging is not sensitive.

4.3 Limitations

A number of potential limitations can be found with this study. Although our findings support the validity of the two compartments non-exchange model, they can only be confirmed when histopathological validation of WMTI metrics finally becomes available. The relationships between ¹H-MRS metabolites and WMTI metrics in WM have been reported here only for a cohort of patients with MTBI. However, while no control data were available for inclusion in this study, the same MTBI cohort was previously evaluated in comparison to age-matched controls with respect to both ¹H-MRS metabolites (Kirov et al., 2013a) and DKI metrics (Grossman et al., 2013). Testing these relationships in MTBI provided a large enough range in both diffusion and ¹H-MRS metrics to allow for the observation of correlations, which were similar to those previously reported for FA in controls (Wijtenburg et al., 2012). Therefore, because all of the patients in this study possessed the mildest degree of injury, we believe our findings might also have the potential to be useful for cases of normal WM.

Furthermore, the cross-sectional design of the study precluded the assessment of dynamic correlations between NAA concentrations and WMTI metrics. Longitudinal investigations will be required to quantify changes in the relationship between NAA and WMTI metrics over short and long time intervals. Our study focused on the cross-validation of WMTI metrics with respect to a well-accepted and pathologically specific marker for axonal injury (NAA) rather than on the investigation of the clinical impact of WMTI metrics. As a next step, we plan to evaluate changes in WMTI metrics over the course of a longitudinal study. Future research will also have to examine the association between WMTI metrics and clinical as well as cognitive impairment and assess its prognostic value for determining clinical outcome.

5. CONCLUSION

The relationship between compartment-specific white matter tract integrity (WMTI) parameters from diffusion MRI and concentrations of ¹H-MRS-detectable metabolites was investigated in vivo in a cohort of patients with mild traumatic brain injury (MTBI). Results demonstrated significant correlations associating NAA with those WMTI parameters that are affected by intra-axonal diffusion and axonal density, providing arguments for the validity of a two-compartment non-exchange model of intra- and extra-axonal diffusion in a single WM fiber bundle. Our results also indicate that NAA may reflect TBI processes related to intra-axonal injury, as well as axonal degeneration in MTBI. This information might be useful to improving understanding of MTBI by providing a method for investigating specific biophysical mechanisms that underlie tissue damage and pathological development.

Highlights.

• -Diffusion MRI is correlated with 1H-MRS in mild traumatic injury (MTBI) subjects
• -Diffusion MRI included kurtosis and white matter tract integrity (WMTI) metrics
• -N-acetyl-aspartate (NAA) correlates with fractional anisotropy and radial kurtosis
• -NAA also correlates with all WMTI metrics related to the intra-axonal space
• -Our findings are discussed in light of the pathophysiology of MTBI

ABBREVIATIONS

α

tortuosity

AWF

axonal water fraction

Cho

choline

Cr

creatine

CSF

cerebral spinal fluid

CSI

chemical shift imaging

DAI

diffuse axonal injury

D_axon

intra-axonal diffusivity

D_e∥

extra-axonal axial diffusivity

D_e⊥

extra-axonal radial diffusivity

DKI

diffusion kurtosis imaging

D_∥

axial diffusivity

D_⊥

radial diffusivity

dMRI

diffusion MRI

DTI

diffusion tensor imaging

EAS

extra-axonal space

FA

fractional anisotropy

FOV

field of view

GM

gray matter

¹H-MRS

proton magnetic resonance spectroscopy

IAS

intra-axonal space

K_∥

axial kurtosis

K_⊥

radial kurtosis

MD

mean diffusivity

mI

myo-inositol

MK

mean kurtosis

MNI

Montreal Neurological Institute

MPRAGE

Magnetization Prepared RApid Gradient Echo

MTBI

mild traumatic brain injury

NAA

N-acetylaspartate

ROI

region of interest

TE

echo time

TR

repetition time

VOI

volume of interest

WM

white matter

WMTI

white matter tract integrity