Use of gEUD for predicting ear and pituitary gland damage following proton and photon radiation therapy

Abstract

Objective:

To determine the relationship between the dose to the inner ear or pituitary gland and radiation-induced late effects of skull base radiation therapy.

Methods:

140 patients treated between 2000 and 2008 were considered for this study. Hearing loss and endocrine dysfunction were retrospectively reviewed on pre- and post-radiation therapy audiometry or endocrine assessments. Two normal tissue complication probability (NTCP) models were considered (Lyman–Kutcher–Burman and log-logistic) whose parameters were fitted to patient data using receiver operating characteristics and maximum likelihood analysis. The method provided an estimation of the parameters of a generalized equivalent uniform dose (gEUD)-based NTCP after conversion of dose–volume histograms to equivalent doses.

Results:

All 140 patients had a minimum follow up of 26 months. 26% and 44% of patients experienced mild hearing loss and endocrine dysfunction, respectively. The fitted values for TD₅₀ and γ₅₀ ranged from 53.6 to 60.7 Gy and from 1.9 to 2.9 for the inner ear and were equal to 60.6 Gy and 4.9 for the pituitary gland, respectively. All models were ranked equal according to Akaike's information criterion.

Conclusion:

Mean dose and gEUD may be used as predictive factors for late ear and pituitary gland late complications after skull base proton and photon radiation therapy.

Advances in knowledge:

In this study, we have reported mean dose effects and dose–response relationship of small organs at risk (partial volumes of the inner ear and pituitary gland), which could be useful to define optimal dose constraints resulting in an improved therapeutic ratio.

Proton beam therapy is a highly conformal technique that can maximize the dose gradient between tumours and the surrounding structures. This technique has been widely used for skull base tumours, in which dose escalation to the target volume without increasing the dose to the adjacent normal tissues is recommended.¹ However, skull base tumours frequently arise adjacent to normal tissues such as the inner ears or the pituitary gland, and it is often impossible to deliver the prescribed dose to the tumour without decreasing constraints to the organs at risk (OARs). Our protocol¹ does not impose specific dose constraints on the pituitary gland or the inner ear, when they are located within the clinical target volume, as one ear or both ears are often included in the radiation field and a substantial number of patients subsequently develop transient serous otitis media or sensorineural hearing loss, owing to the proximity of the middle or inner ear to the irradiation field. Hearing preservation has been reported to be significantly related to the radiation dose to the cochlea^2,3 and is found between 0.5 and 2.0 years after irradiation.³ Similarly, the pituitary gland or the hypothalamus is also generally close to the target volume, and partial pituitary failures are commonly reported during radiation-induced late effects^4–6 with speeds of onset ranging from a few months to several years. As a wide range of doses are delivered to these critical structures, the objective of this study was to determine the dose–response relationship of the inner ear and the pituitary gland for radiation-induced late effects of photon and proton therapy and to show that generalized equivalent uniform dose (gEUD) may be used as a predictive factor for late complications.

METHODS AND MATERIALS

Population and end point definition

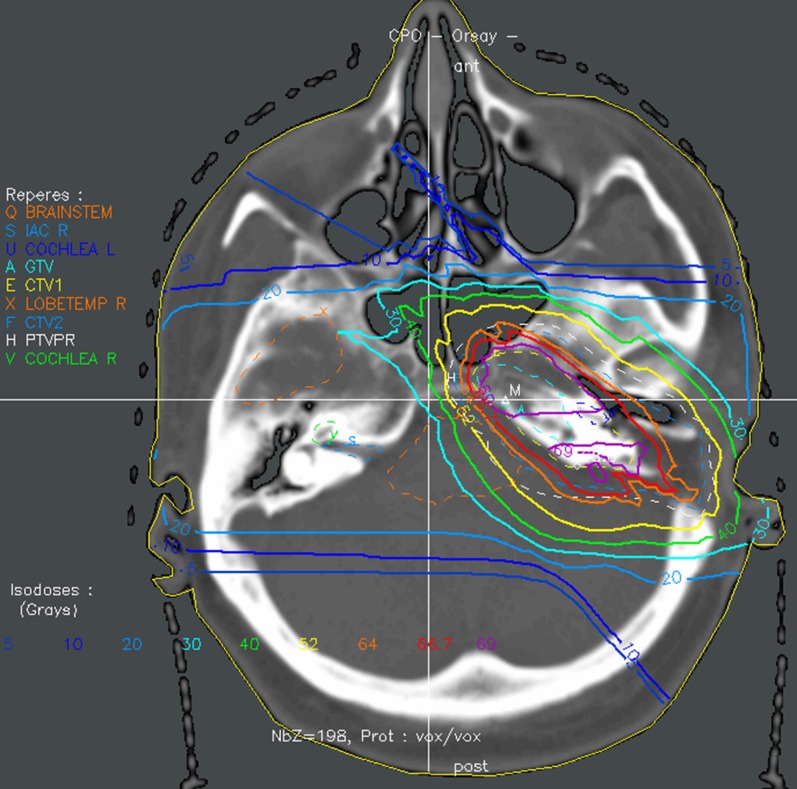
From 2000 to 2008, 140 patients (114 adults and 26 children) with a histologically documented diagnosis of chordoma or chondrosarcoma (116 and 24 patients) of the skull base post-operatively received conventional fractionated radiation therapy; data from all patients with long-term follow up, treated by a combination of three-dimensional (3D) conformal photon and proton therapy (Figure 1 depicts the treatment plan for a patient with chondrosarcoma), were recorded.¹ The photon component was performed at one of the five oncology centres affiliated with Orsay Proton Therapy Center, Orsay, France. 6- to 20-MV photons of a linear accelerator were used. Three to five isocentric coplanar or non-coplanar beams were generally designed. The proton part was performed with the 201-MeV proton beam of the synchrocyclotron and a fixed horizontal beam. Proton beams were delivered using the double scattering technique at the Orsay Proton Therapy Center, and the widely used relative biological effectiveness (RBE) value of 1.1 was used for proton therapy.^1,7 Fiducial markers and custom-made thermoplastic masks were used for positioning and immobilization. The irradiation procedure has also been previously described in more detail.^1,8 Photons represented two-thirds of the total dose and protons represented one-third (for 80% of cases), except for one child and five adults who received proton therapy only. The median doses delivered by photons and by protons were 45 Gy (range, 0–45 Gy) and 26 Gy-RBE (range, 21.6–70.2 Gy-RBE), respectively. The median total dose delivered to the gross tumour volume was 70 Gy-RBE (range, 67–74 Gy-RBE) for adults and 68.7 Gy-RBE (range, 54.4–71.8 Gy-RBE) for children, in fractions of 1.8–2.0 Gy per day for 5 consecutive days per week. No patient included in this study received concurrent chemotherapy.

Figure 1.

Typical treatment plan for a patient with a skull base chondrosarcoma treated up to a total dose of 70.2 Gy-RBE with combined photon–proton therapy (34.2 Gy photons, 36 Gy-RBE protons). ant, anterior; CTV, clinical target volume; IAC, internal auditory canals; L, left; post, posterior; LOBETEMP, temporal lobe; PTV, planning target volume; R, right.

Matched CT scan and MRI (with 2- to 3-mm slice thicknesses) were systematically used to delineate target volumes and OARs, by the same three experienced physicians. The inner ears and the pituitary glands were contoured for all the patients from the initiation of the protocol. The hypothalamus was also contoured for 26 children (mean age, 12.8 years), who were analysed separately. As this study focussed on hearing loss, the cochlea and the internal auditory canals (IACs) were also contoured for 70 patients treated between 2004 and 2008 in order to provide a comparison of organ response sensitivity.

All patients had follow up (every 6 months for at least 2 years and then yearly) and hearing tests (pure-tone average of frequencies audiometry) or neuroendocrine assessments conducted immediately before treatment and at regular time intervals after the completion of therapy. None of the patients enrolled in the study presented any hearing loss or endocrine dysfunction prior to treatment. Minor and mild side effects (≥grade 1–2) were considered and retrospectively scored according to the National Cancer Institute Common Terminology Criteria for Adverse Events (CTCAE v. 4.03). Hearing loss >15 dB at two contiguous test frequencies, tinnitus or endocrine functions outside of the normal reference range (hyperprolactinemia, delayed thyroid-stimulating hormone response to thyroid-releasing hormone, panhypopituitarism) were considered to be late effects.^5,6 Growth hormone deficiency was often the first endocrine deficiency observed in both children and adults but was not followed for adults in this study.

Equivalent uniform dose, normal tissue complication probability models

The concept of equivalent uniform dose (EUD) was originally introduced for tumours^9–11 and was subsequently generalized to both tumours and normal tissues;¹² it represents the uniform dose resulting in the same response probability as a corresponding inhomogeneous dose distribution. The parameter a of the gEUD [Equation (1)] is optimized to give the best fit to patient data; a is organ specific and can be derived from observed dose–response data. gEUD tends towards the maximum dose when a is large (OAR with serial architecture) and towards the mean dose when a approaches one (OAR with parallel architecture), meaning that gEUD and a characterize the dose–response behaviour of the OAR.

$$\text{gEUD}={\left[{\displaystyle \sum _{\mathit{i}}\left({\mathit{v}}_{\mathit{i}}{\mathit{D}}_{\mathit{i}}^{\mathit{a}}\right)}\right]}^{\frac{1}{\mathit{a}}}$$ (1)

where v_i is the volume fraction of the dose bin corresponding to the dose D_i.

In this study, we used the classical Lyman–Kutcher–Burman and log-logistic models both with dose–volume histograms (DVHs) reduced to gEUD, as the actual organ dose is non-uniform. Because of the small volume of the cochlea and the pituitary gland, dose–volume analysis has been rarely performed and only mean dose effects have been mainly reported.^13,14 As steep dose gradients can be achieved with proton beams (and a fortiori with combined photon–proton beams as discussed in Feuvret et al⁸), we considered that non-uniform doses could be delivered within the organ volume and that dose–volume analysis could be evaluated for partial volumes of the OARs.¹⁵

The first step consisted of estimation of the value of parameter a, for which a model can be built with gEUD that best describes the data. We used an optimized method for determination of this parameter, based on receiver operating characteristics (ROC) as described by Boulé et al¹⁶ and Das et al.¹⁷ As a higher area under the ROC curve (AUROC) indicates a more accurate model,¹⁸ we determined the value of a that would maximize this area. The gEUD model is thus used as a discriminant to separate the groups with and without defects. The ROC curve analysis is used for evaluating the link between gEUD and clinical outcomes, and therefore estimating the seriality of the tissue response to radiation.

As the normal tissue complication probability (NTCP) has a sigmoid shape when plotted as a function of gEUD, gEUD can also be used as an input parameter for this probability model. The maximum likelihood method was then used to determine in 3D parameter space the best estimation of all the parameters (a, TD₅₀ and γ₅₀) of the NTCP models for our patient data.

Because of their simplicity or widespread use,^9,19 the Lyman–Kutcher–Burman [Equation (2)] and log-logistic [Equation (3)] formulae, which describe the dose–response relationship for normal tissues^11,20,21 based on TD₅₀ (tolerance uniform dose delivered to the whole organ for 50% complication rate at a specific time) and γ₅₀ (slope of the response curve at TD₅₀), were used to calculate the NTCP with DVH reduced to gEUD.

$$\begin{array}{l}\text{NTCP}=\frac{1}{\sqrt{2\pi }}{\displaystyle \underset{\mathrm{-}\infty }{\overset{\mathit{t}}{\int }}{\mathit{e}}^{\frac{\mathrm{-}{\mathit{x}}^2}{2}}}\mathit{dx}\\ \text{where}\\ \mathit{t}=\frac{\text{gEUD}\mathrm{-}{\text{TD}}_{50}}{\mathit{m}\mathrm{\times }{\text{TD}}_{50}}\\ \text{and}\\ \mathit{m}=\frac{\pi }{8{\gamma }_{50}}\end{array}$$ (2)

$$\text{NTCP}=\frac{1}{1+{\left(\frac{{\text{TD}}_{50}}{\text{gEUD}}\right)}^{4{\gamma }_{50}}}$$ (3)

Treatment planning

Dose calculations were established with dose-scoring grid resolution of 1 × 1 × 1 mm³ by the ISIS 3D treatment planning system (Technologie Diffusion, France), which comprises broad beam and pencil beam algorithms for proton beam calculations^22–24 and dose engine for photons. The photon algorithms are based on a double decomposition algorithm and Clarkson–Cunningham integration, with inhomogeneity corrections based on the 3D subtraction method.²⁵ The DVHs are calculated with a random sampling method. Proton and photon plans were performed on the same CT, with tissue inhomogeneity corrections. Analytical models and optimization of the parameters were performed using the MATLAB^® computing environment v. 7.0.0 (MathWorks^®, Natick, MA).

Statistical analysis

In order to estimate the best parameter a (which would maximize the AUROC), ROC curves were generated by plotting “sensitivity” vs “1-specificity” and by changing the initial a value (between 0.1 and 50.0 with 0.1 steps). We plotted the ROC curve defined by the fraction of cases with complications and gEUD > D₀ vs the fraction of cases without side effects and gEUD > D₀, for all values of D₀. The area under the curve reflects the accuracy of the model; a higher area implies more accurate parameterization. Furthermore, AUROC has the property to be equal to the Mann–Whitney U test (Wilcoxon) statistic, which gives the probability that a positive patient has to have a higher rank than a negative one. The estimation of parametric confidence intervals (CIs) for the AUROC estimates was performed as described by other authors.^16,18

The maximum likelihood method was also used to simultaneously determine the best estimation of a, TD₅₀ and γ₅₀ parameters of NTCP modelling;²⁶ the value of the parameters maximizing the logarithm of the likelihood function L was defined by Equation (4):

$$\text{ln}\left[\mathit{L}\left(\overrightarrow{\mathit{x}}\right)\right]={\displaystyle \sum _{{\mathit{i}}_{\text{notoxicity}}}\text{ln}\left[1\mathrm{-}{\text{NTCP}}_i\left(\overrightarrow{\mathit{x}}\right)\right]}+{\displaystyle \sum _{{\mathit{i}}_{\text{toxicity}}}\text{ln}\left[{\text{NTCP}}_i\left(\overrightarrow{\mathit{x}}\right)\right]}$$ (4)

where the vector $\overrightarrow{\mathit{x}}$ is composed of the model's parameters; NTCP_i is used when the ith patient experiences a side effect; and (1 − NTCP_i) when no side effect is observed. One-dimensional 95% CIs for the maximum likelihood estimates were calculated using the profile log-likelihood method. The two NTCP models were informally compared using the Akaike's information criteria (AIC); a better fit to the data corresponds to smaller values of AIC.²⁷

RESULTS

Inner ear study

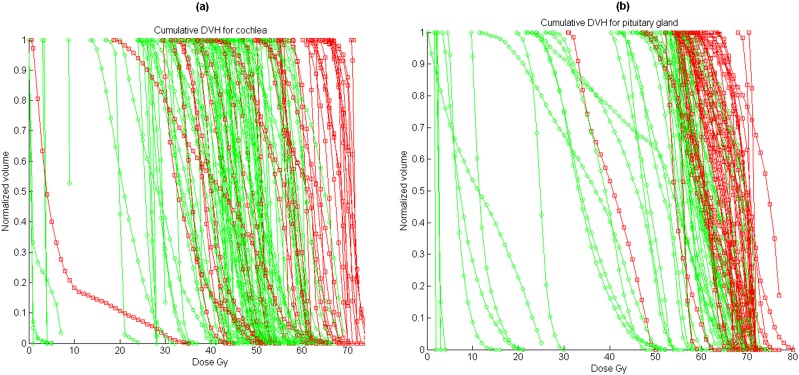
Data from 280 DVHs for ipsilateral and contralateral inner ears were recorded and analysed (only 138 and 133 data sets were available for the cochlea and IAC, as contouring of these structures was only started later). Hearing loss was scored per ear, and we assumed that the two ears of the same patient could be analysed as independent observations (as also suggested in Honoré et al²⁸). During follow-up, 73 cases experienced significant late effects, mainly hearing loss, tinnitus or otitis media, and 207 cases did not experience any complications. The mean volume and radiation dose to the various subvolumes of the ear are shown in Table 1. Figure 2a shows the cumulative DVH for patients with and without late effects. Significant differences in complication rate were observed between low doses and high doses; the mean doses with/without toxicities are shown in Table 1. A mean dose of 54 Gy can be qualitatively associated with auditory toxicity, but a significant cut-off value for tolerable radiation dose cannot be easily deduced, as even very high doses to small volumes did not always induce complications; for example, the toxicity incidence for inner ear is 20% for mean doses <54 Gy and 45% for mean doses >54 Gy. One patient experienced unexplained hearing loss with a mean dose to the cochlea of <10 Gy.

Table 1.

Characteristics of the subvolumes of the ear (140 patients), the pituitary gland and hypothalamus (103 adults + 26 children) with and without complications (73/280 cases with hearing late effects, 10/26 children and 45/103 adults with endocrinopathy)

Organ at risk	Number of structures	Volume (cm3)	Mean dose (Gy-RBE) without toxicity	Mean dose (Gy-RBE) with toxicity (any end point)
Inner ear	280	2.80 ± 1.0 (1.20–5.10)	35.0 ± 14.0 (0.6–61.0)	54.0 ± 11.0 (30.6–73.3)
Cochlea	138	0.11 ± 0.07 (0.03–0.36)	36.8 ± 14.0 (0.5–62.6)	54.6 ± 16.0 (4.7–72.8)
Internal auditory canal	133	0.22 ± 0.07 (0.07–0.35)	42.0 ± 16.0 (0–71.2)	54.0 ± 15.0 (0.3–73.7)
Pituitary gland (adults)	103	0.38 ± 0.20 (0.06–0.90)	46.7 ± 20.0 (1.8–68.3)	63.5 ± 6.8 (34.0–72.8)
Pituitary gland (children)	26	0.30 ± 0.10 (0.10–0.50)	42.9 ± 27.0 (2.0–69.9)	55.6 ± 10.8 (39.7–71.5)
Hypothalamus (children)	22	0.40 ± 0.10 (0.10–0.70)	31.2 ± 21.6 (1.4–64)	39.7 ± 14.0 (13.0–54.8)

Data are expressed as mean ± standard deviation (minimum–maximum).

Figure 2.

Cumulative dose–volume histogram (DVH) for patients with (squares) and without (circles) late effects: (a) cochlea, (b) pituitary gland (adults).

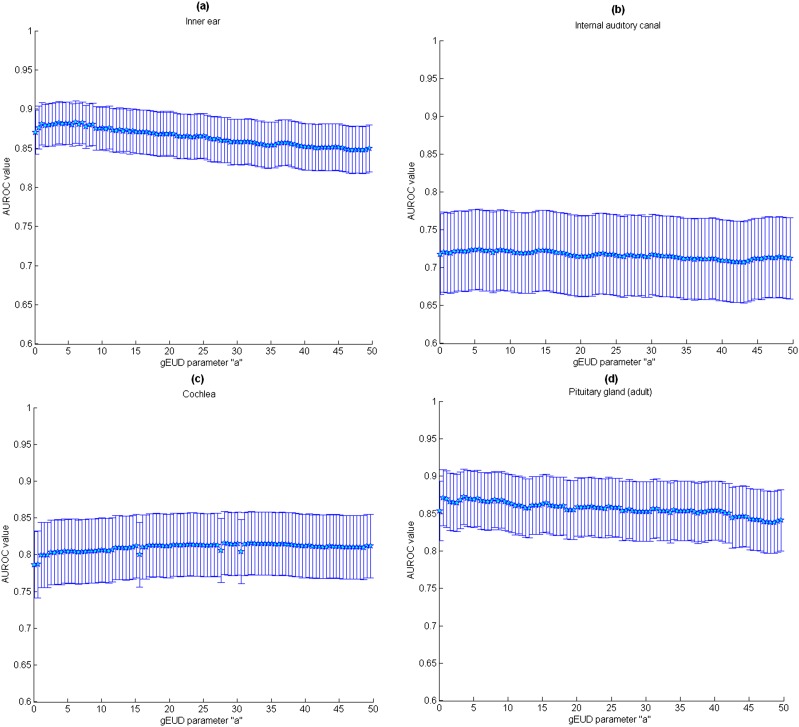
As a cut-off dose has not been determined, ROC analysis was used to select the best a parameter of the gEUD (that maximized AUROC). As shown in Figure 3a and also listed in Table 2, the a values that most clearly distinguished between the groups with and without late effects are different when considering different subvolumes of the ear. The AUROC ± standard deviation (using Wilcoxon statistic) values for these curves are also listed in Table 2. All the models correctly fitted clinical data and presented good performance with maximum AUROC values close to 0.86 for the inner ear, 0.81 for the cochlea and 0.72 for the IAC. However, the standard deviations were quite wide, and no significant differences in relative importance of dose levels were found in the AUROC values obtained by using the gEUD model. Parameters a, TD₅₀ and γ₅₀ were then estimated from the logistic and Lyman–Kutcher–Burman regression model and are listed in Table 3. The fitted (gEUD) dose–response curves for the inner ear, IAC and cochlea together with the experimental data are shown in Figure 4a–c. For all the organs, the best a values were <1.2, and the gEUD tended towards the mean dose. For patients with no complications, the mean gEUD calculated with the previous best a value for the inner ear was 37  ± 14 Gy. For patients who experienced hearing loss (73/280 patients—26%), the mean gEUD was 56  ± 10 Gy.

Figure 3.

Variation of the area under the receiver operating characteristics (AUROC) curve with standard error for several subvolumes of the ear: (a) inner ear, (b) internal auditory canal, (c) cochlea and (d) pituitary gland (adults). gEUD, generalized equivalent uniform dose.

Table 2.

Best estimates of Lyman–Kutcher–Burman (LKM) and log-logistic model parameters with 95% confidence interval (CI), log-likelihood (LL), Akaike's information criteria (AIC) and mean area under the ROC curve (AUROC)

Organ at risk	Model	a (95% CI)	TD50 (95% CI)	γ50 (95% CI)	LL	AIC	Mean AUROC ± standard error
Inner ear	Log-logistic	0.1 (0.1–0.6)	53.6 (51.8–55.4)	2.9 (2–3.8)	−74.4	154.8	0.86 ± 0.03
	LKM	0.1 (0.1–0.6)	53.7 (51.9–55.3)	2.8 (2.1–3.7)	−74.2	154.3
Cochlea	Log-logistic	1.2 (0.1–3.6)	56.0 (53.6–58.8)	2.9 (1.8–4.3)	−36.1	78.1	0.81 ± 0.04
	LKM	1.2 (0.1–3.6)	56.0 (53.6–58.5)	2.8 (1.9–4.2)	−35.8	77.5
Internal auditory canal	Log-logistic	0.1 (0.1–4.5)	60.7 (56.8–65.0)	1.9 (1–3)	−42.5	90.9	0.72 ± 0.05
	LKM	0.1 (0.1–4.5)	61.0 (56.8–65.0)	1.9 (1.0–2.9)	−42.5	90.9
Pituitary gland (adults)	Log-logistic	6.4 (0.9–8.2)	60.5 (59.1–62.0)	5.2 (3.1–8.0)	−43.2	92.4	0.86 ± 0.04
	LKM	6.4 (0.9–8.2)	60.6 (59.1–62.0)	4.9 (3.1–8.0)	−43.2	92.3
Pituitary gland (children)	–	–	–	–	–	–	0.59 ± 0.13
	–	–	–	–	–	–
Hypothalamus (children)	–	–	–	–	–	–	0.65 ± 0.11
	–	–	–	–	–	–

TD₅₀ is the tolerance uniform dose delivered to the whole organ for 50% complication rate at a specific time; γ₅₀, slope of the response curve at TD₅₀.

Table 3.

Incidence and mean generalized equivalent uniform dose (gEUD) for the main radiation-induced endocrine dysfunctions (10/26 children, 45/103 adults)

Type of dysfunction	Number of cases	Mean gEUD (Gy-RBE) to pituitary axis	Mean gEUD (Gy-RBE) to hypothalamus
Growth hormone (children)	7/10 (70%)	51 ± 12 (40.0–71.5)	48 ± 12 (23–64)
Hyperprolactinemia (children)	2/10 (20%)	60 ± 5 (56.0–64.8)	57 ± 7 (52–62)
Panhypopituitarism (adults)	17/45 (38%)	66 ± 4 (59–75)
Hyperprolactinemia (adults)	13/45 (29%)	63 ± 9 (34–72)
Hypothyroidism (adults)	5/45 (11%)	60 ± 8 (52–71)
Others (adults)	13/45 (29%)	62 ± 5 (51–73)

The a value for gEUD is 1 and 6.4 for children and adults, respectively.

Data expressed as mean ± standard deviation (minimum–maximum).

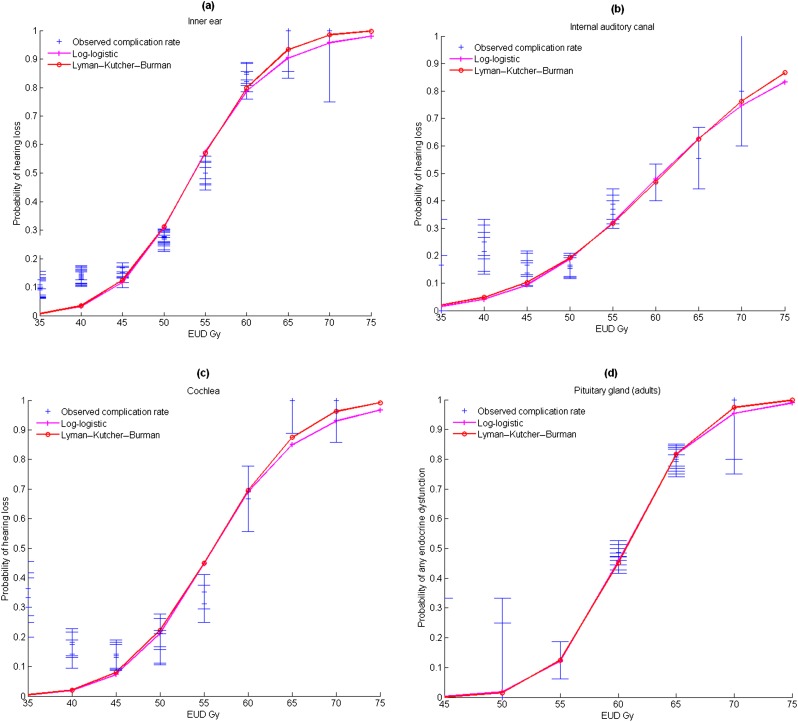
Figure 4.

Normal tissue complication probability for (a) inner ear, (b) internal auditory canal, (c) cochlea and (d) pituitary gland (adults), and best curves (log-logistic/Lyman–Kutcher–Burman equivalent uniform dose models) fitting the clinical data (lines, models; crosses, experimental incidence). EUD, equivalent uniform dose.

Pituitary gland and hypothalamus study

Data from 103 adult patients (subset of previous ear study) were recorded: 45 cases experienced significant late effects, and 58 cases did not experience any complications. Figure 2b shows the cumulative DVH for adult patients with and without pituitary gland late effects. Characteristics such as mean volume and mean radiation doses to the various structures are shown in Table 1. High radiation doses appeared to be correlated with the rate of pituitary deficiency, but a specific cut-off for tolerable radiation dose cannot be qualitatively determined. The method appeared to have a good performance for adults with AUROC values close to 0.86. For adult patients who had no complications, the mean gEUD (a = 6.4) to the pituitary gland was 50.5  ± 19 Gy and 65  ± 5 Gy for those with any endocrine dysfunction (45/103 adults—44%).

The same analysis was also applied to 26 children with skull base tumours for whom the pituitary gland and hypothalamus DVHs were available: 10 cases experienced minor or mild late effects and 16 cases did not experience any complications. The mean dose ± standard deviation to the pituitary and hypothalamus were 45  ± 25 Gy and 35  ± 22 Gy, respectively, for children with no complications and 58  ± 8 Gy and 44  ± 13 Gy, respectively, for children with any endocrine dysfunction (10/26 children—38%). AUROC values for the hypothalamus (0.65) were slightly higher than those for the pituitary gland (0.59) but proved to be relatively flat as a function of the parameter a. In addition, the AUROC for the paediatric cohort was much smaller than that obtained for adults (0.59–0.65 vs 0.86).

Table 3 lists data for children and adults for specific outcomes; incidences and mean doses are shown for the main radiation-induced endocrine dysfunctions, showing that the relationship between dose or gEUD and outcome may depend on the type of effect. The fitted (gEUD) dose–response curve for adult pituitary glands together with the experimental data is plotted on Figure 4b but was not applied to children data, owing to the small sample size. Optimum values for the parameters are shown in Table 2.

DISCUSSION

Inner ear analysis

A review of the literature conducted by Bhandare et al¹⁴ as part of the Quantitative Analysis of Normal Tissue Effects in the Clinic (QUANTEC^®) reported significant hearing loss with increasing doses to the cochlea, but no specific dose cut-off was defined. In their review, the initial recommendations of TD5/5 = 60 Gy, TD50/5 = 70 Gy suggested by Emami et al¹³ to minimize the risk for hearing loss were updated to a mean dose to the cochlea ≤45 Gy. Owing to the small volume of the ear (especially the cochlea) and to the limited importance of dose gradients in previous studies, dose–volume or functional organization analysis of the subunits of the ear have never been performed to the best of our knowledge. Previously published data on ear complications suggested that the ear is a parallel organ.¹⁴ Our data confirm this trend for the cochlea, in which the best a value is close to 1, as well as for the inner ear and IAC, which seem to present a more parallel architecture. As reported by some authors,^14,28,29 an initial γ₅₀ value of four could be a reasonable estimate for an OAR. γ₅₀ values of 2.75 and 3.40 have been reported for the mean dose to the inner ear, and γ₅₀ values between 0.7 and 3.4 have also been reported depending on adjustments for risk factors. We determined this parameter and found values between 1.9 and 2.9 depending on the subvolume (Table 2). The log-logistic model for the probability of hearing loss was also used by Honoré et al,²⁸ who reported a TD₅₀ value of 48 Gy. In this study, all models were ranked equal according to AIC. We found a slightly higher TD₅₀ (53.6 Gy) using the gEUD as dose end point in the probability model with fairly small values for a (between 0.1 and 1.2).

Our results indicate that mean dose and gEUD with small a values (≤1.2) to the cochlea or inner ear accurately predict the risk of late hearing effects. Indeed the mean dose model corresponds to the best criterion for small OARs where the dose gradients are of minor importance. As the ear may be composed of subvolumes that respond to irradiation independently of each other, a more detailed study would be required to assess the mechanisms of hearing loss, contouring of several other subvolumes of the inner ear, such as the vestibule or semicircular canals, or even the middle ear in order to determine whether maximum doses reach any critical structures.

Pituitary gland and hypothalamus analysis

Darzy³⁰ published an overview of radiation-induced hypopituitarism. The incidence of endocrine dysfunction mainly depends on dose, age at irradiation, fractionation and gender, and can occur after doses as low as 18 Gy. In adults, one team demonstrated a dose–effect relationship with DVH analysis.⁶ They reported that a minimum and maximum dose of 50 and 70 Gy for the pituitary gland were predictive of endocrinopathy. A maximum dose of 50 Gy to the hypothalamus was also predictive of higher rates of endocrine dysfunction. In our study, we found that a mean gEUD (a = 6.4) value >65 Gy to the pituitary gland was a significant risk factor for endocrine dysfunction.

There is no consensus in the literature concerning the predominant site of radiation damage in children, as both the pituitary and the hypothalamus appear to be involved. In our study, we were not able to estimate the best a values in the paediatric cohort because the AUROC and the range of variation for a parameter for the paediatric cohort were much smaller than those obtained for adults, indicating that the model is not as accurate for prediction of events in children as in adults, probably owing to the insufficient number of data for children. In accordance with previous studies,^6,30 the structures for these organs could be consistent with parallel and serial architectures, respectively. However, our data for children show that the hypothalamus has a higher AUROC than does the pituitary gland and could be a more predictive organ for endocrine dysfunction. The mean gEUD (a = 1) value for the hypothalamus of children experiencing complications (48  ± 12 Gy and 57 ± 12 Gy for hyperprolactinemia or growth hormone deficiency) is also consistent with the hypothalamus cut-off reported by Pai et al⁶ for adults.

Limitations of predictive model and uncertainties

Clinical studies are essential to confirm the ability of the NTCP model to predict toxicity. Literature describing the dose–volume relationship for normal tissues has become more abundant, as reviewed by the QUANTEC (the recent report by Marks et al³¹). Although our individual organ-specific study followed some of the recommendations for coding toxicity, inherent limitations and uncertainties restrict the usefulness of our work, and further investigations in a larger population study will be needed to confirm our preliminary results. Owing to the small number of patients and late effects observed in children, the power of our analysis is limited and major uncertainties persist in the ROC method and for determination of fitted parameters. There is also a high degree of uncertainty concerning α/β values; the robustness of EUD and NTCP concepts has not yet been thoroughly evaluated for normal tissues.¹⁴ To account for variations in dose per fraction in different subvolumes of an OAR,^19,32 total physical dose corresponding to each DVH bin can be converted into isoeffective dose EQD2 for 2-Gy fractions. This correction (which has not been carried out in this study) was extended to take into account dose per fraction effect that can be appropriate especially for the low α/β ratio usually observed in normal tissues. Moreover, healthy organs are usually irradiated heterogeneously at lower doses or different doses per fraction than are tumours, and this increases the uncertainty of the effect.

The use of several analytic functions, for example, logit or probit functions, to obtain an appropriate NTCP fit to clinical data has been investigated by several authors since the differences between functions, particularly their asymmetry to model the sigmoid shape of normal tissue complication probabilities, could be significant.^21,33 However, accurate modelling of the dose–volume effect is complex owing to the difficulty of collecting a sufficiently large volume of data with no restriction in incidence range, and no consensus has been reached concerning the optimal model to be used. For the purposes of this study, we quantitatively compared two classical models (Lyman–Kutcher–Burman and log-logistic) with DVHs reduced to gEUD to determine whether the difference between the two models could be significant. The gEUD with tissue-specific parameter a was introduced into the NTCP modelling to account for dose heterogeneity. In our study, the difference between the AUROC values for different a values was never statistically significant, indicating a possible weak dependence of the best gEUD parameter with OAR dose heterogeneity and little impact on clinical NTCP modelling, or uncertainties in clinical data.

Modelling the RBE of proton beams may also be important for accurate risk assessment. Despite abundant evidence indicating that RBE varies with many factors (for example, our team reported on the variation of the RBE with depth in the spread-out Bragg peak of the 76 and 201 MeV proton beams used for treatment in Calugaru et al⁷), the use of a generic RBE of 1.1 at 2 Gy in routine clinical practice seems reasonable in view of the lack of experimental data to define accurate RBE models³⁴ and the lack of clear clinical evidence for RBE variations. In practice, the gradient at the distal end of proton dose distributions is also rarely used (or used for a small fraction of the total dose) to spare critical normal tissues owing to uncertainties about its exact position in the patient. In the near future, new Monte Carlo-based treatment planning, providing the computation of linear energy transfers and variable RBE, may help to reduce these uncertainties.

CONCLUSION

This study was designed to determine the dose–response relationships using equivalent uniform doses for certain OARs that often receive high doses during skull base irradiation and which may therefore present high complication probabilities. We used a method based on clinical data and ROC to determine the phenomenological parameter a and studied its relevance to explain a specific organ's response to radiation. As expected, our study demonstrated significant correlations between certain normal tissue toxicities and high-dose 3D conformational radiation therapy, allowing estimation of cut-off values. The relationships that have been determined could be useful to define optimal dose constraints resulting in an improved therapeutic ratio that are not too conservative and that take individual heterogeneous dose distributions into account.