Abstract
Mathematical and numerical competence is a critical foundation for individual success in modern society yet the neurobiological sources of individual differences in math competence are poorly understood. Neuroimaging research over the last decade suggests that neural mechanisms in the parietal lobe, particularly the intraparietal sulcus (IPS) are structurally aberrant in individuals with mathematical learning disabilities. However, whether those same brain regions underlie individual differences in math performance across the full range of math abilities is unknown. Furthermore, previous studies have been exclusively cross-sectional, making it unclear whether variations in the structure of the IPS are caused by or consequences of the development of math skills. The present study investigates the relation between grey matter volume across the whole brain and math competence longitudinally in a representative sample of 50 elementary school children. Results show that grey matter volume in the left IPS at the end of 1st grade relates to math competence a year later at the end of 2nd grade. Grey matter volume in this region did not change over that year, and was still correlated with math competence at the end of 2nd grade. These findings support the hypothesis that the IPS and its associated functions represent a critical foundation for the acquisition of mathematical competence.
Keywords: Voxel-based morphometry, mathematical competence, intraparietal sulcus, educational neuroscience, grey matter volume
Introduction
Mathematical and numerical competence is a critical foundation for individual success in modern society. Poor numeracy predicts higher rates of unemployment, physical and mental illness, and even arrest and incarceration (Bynner & Parsons, 1997; Parsons & Bynner, 2005), and yet, as many as one in four economically active individuals fail to develop appropriate skills and are ‘functionally innumerate’ (Gross, Hudson, & Price, 2009). Furthermore, the United States lags behinds its economic peers in terms of math skills development, ranked 21st of 23 countries in a recent report by the Institute of Education Sciences (Goodman, M., Finnegan, R., Mohadjer, L., Krenzke, T., & Hogan, 2014). In order to address this burgeoning problem, a deeper understanding of the developmental mechanisms underlying math skills acquisition is needed. Characterization of the neural mechanisms underlying this process can contribute significantly to this understanding, and help to identify potential avenues for educational interventions and improved pedagogical methods.
Recent years have seen a growth in the number of neuroimaging studies investigating the development of math skills, yet in comparison to reading research for example, there remains a severe paucity of information. Consequently, knowledge regarding the neurocognitive factors underlying individual differences in math competence remains limited. Nonetheless, a growing number of behavioral studies indicate that the ability to represent and process nonsymbolic numerical magnitude is a key cognitive foundation of math development. That cognitive mechanism is often referred to as the ‘approximate number system’ (ANS), and is typically measured via performance on nonsymbolic numerical comparison tasks (i.e. selecting which of two sets of dots is more numerous). Performance on this task has been shown to correlate with math ability in typically developing children (Halberda, Mazzocco, & Feigenson, 2008; Mazzocco, Feigenson, & Halberda, 2011) and adults (Halberda, Ly, Wilmer, Naiman, & Germine, 2012), as well as being impaired in children with dyscalculia, a specific mathematical learning disability (Mazzocco, Feigenson, & Halberda, 2011; Piazza et al., 2010). Neuroimaging studies in typically developing populations have shown that the ANS is subserved by cortical mechanisms in the parietal lobe, in particular, the intraparietal sulcus (IPS). This region is reliably activated during nonsymbolic numerical comparison tasks in children and adults (Ansari, Dhital, & Siong, 2006; Ansari & Dhital, 2006; Cantlon, Brannon, Carter, & Pelphrey, 2006), and shows atypical activation in children with mathematical learning disabilities (Price, Holloway, Räsänen, Vesterinen, & Ansari, 2007). The IPS has also been shown to be actively involved in the processing of symbolic numerical magnitude (i.e. selecting which of two Arabic digits is numerically larger) in typically developing children and adults (Ansari, Garcia, Lucas, Hamon, & Dhital, 2005; Pinel, Dehaene, Rivière, LeBihan, & Riviere, 2001). Parietal brain activation during symbolic magnitude processing has been related to math competence in typically developing children (Bugden, Price, McLean, & Ansari, 2012) and is atypical in children with mathematical learning disabilities (Mussolin et al., 2009).Taken together, these findings suggest that the ability of IPS to process numerical magnitude is a key foundation in the development of mathematical skills.
This critical role for the IPS in supporting the acquisition of math skills is supported by structural as well as functional neuroimaging data. In line with the functional results reported above, several studies have identified structural abnormalities, such as reduced grey matter volume and abnormal sulcal geometry, in the IPS in children with mathematical learning difficulties (Cappelletti & Price, 2014; Han et al., 2008; Isaacs, Edmonds, Lucas, & Gadian, 2001; Lubin et al., 2013; Molko et al., 2003; Rotzer et al., 2007; Rykhlevskaia, Uddin, Kondos, & Menon, 2009; Starke et al., 2013). These studies show that a failure to acquire age-appropriate math skills is associated with atypical structural integrity of the IPS, suggesting again that this region is a key mechanism in the development of math competence. However, there is a limit to the extent that evidence from atypically developing population can be extrapolated to typically developing populations. While the structure of the IPS may be atypical in children with mathematical learning disabilities, it does not necessarily follow that individual differences in the math skills of typically developing children derive from the same source, as dyscalculia may represent a qualitatively distinct disorder rather than an extreme on a spectrum (Mazzocco et al., 2011a). Furthermore, many of the studies listed above reported data from populations with genetic syndromes such as Turner Syndrome (Molko et al., 2003) or atypical developmental environments such as prematurity/low birth-weight (Isaacs et al., 2001; Starke et al., 2013), and thus it is difficult to know whether the mathematical difficulties present in those populations mirror those in children with ‘pure’ math learning disabilities in their neurocognitive origins. Therefore it is imperative that the role of the structure of the IPS in typical math development be established in a representative sample without mathematical learning disabilities.
Only one study to date has assessed the association between individual differences in neuroanatomical structure and math competence in a typically developing sample (Li, Hu, Wang, Weng, & Chen, 2013). That study reported that math scores were positively correlated with grey matter volume in the left intraparietal sulcus, suggesting that the IPS is critical for typical as well as atypical math development. However, that study employed a region of interest (ROI) analysis approach whereby their analyses were restricted solely to the IPS regions. Therefore it remains unknown whether other regions of the brain may show equally strong or even stronger, and by extension, more important relationships with individual differences in math skills.
The present study addresses this open question by assessing the relation between grey matter volume across the whole brain and math performance in a representative sample of 50 children without diagnosis of dyscalculia. In addition, the present study is the first to address this issue with longitudinal data. Previous studies have all been cross-sectional, leaving open the question of whether individual differences in IPS structure are the cause or consequence of differences in math competence. The present study relates grey matter volume at the end of 1st grade to math competence at the end of 2nd grade, as well as grey matter volume at the end of 2nd grade to math competence at the same time point, thereby examining both longitudinal and concurrent relations. In so doing this study is, to the best of our knowledge, the first to ask (a) whether grey matter volume across the whole brain relates to math ability in a representative sample of children, and (b) whether any such relations are persistent over time.
Materials and methods
Participants
The present data were collected as part of a larger scale longitudinal study investigating reading development. The current study comprises those participants for whom standardized math scores were available. The following exclusion criteria were applied during the initial recruitment phase: 1) previous diagnosis of intellectual disability; 2) known, uncorrectable visual impairment; 3) documented hearing impairment greater than or equal to 25 dB loss in either ear; 4) history of known neurological disorders including epilepsy, spina bifida, cerebral palsy, traumatic brain injury; 5) current or past diagnosis of an autism spectrum disorder; 6) treatment with any psychotropic medication - with the exception of stimulant medications for ADHD; 7) parental report of significant symptoms of a severe psychiatric diagnosis including major depression, bipolar disorders, or conduct disorder of note. Individuals meeting criteria for ADHD, Oppositional Defiant Disorder, adjustment disorder, and mild depression were not necessarily excluded from participation.
The final sample for the current study comprised 50 students who met the above inclusion criteria and completed standardized measures of math achievement. Using the Edinburgh Handedness Inventory (Oldfied, 1971), 33 students were classified as right-handed, 12 as ambidextrious, and 5 as left-handed. Scanning sessions took place during the summers following 1st grade and 2nd grade, 1 year apart (M = 0.98, SD = 0.07). Two participants were missing WASI scores, but all other measures for those participants were within 1 standard deviation of the standardized test score means (M = 100, SD = 15). No participants were excluded based on IQ or reading achievement. Descriptive and cognitive data for the sample are presented in Table 1. It should be noted that participants in the current sample demonstrated a large range in math scores. However, the mean scores were at or above average in for Calculation, Applied Problems, and the composite measure. In addition, Kolgorov-Smirnoff tests show that for each of the measures performance was normally distributed (p > .05 for each measure), suggesting that the present sample comprised a representative range of math performance levels.
Table 1.
| Measure | 1st Grade (N = 50) | 2nd Grade (N=50) | ||
|---|---|---|---|---|
| M | SD | M | SD | |
| Males/Females | 19/31 | 19/31 | ||
| Age | 7.44 | 0.34 | 8.41 | 0.35 |
|
| ||||
| WCJ-III Calculation | 102.92 (66 - 125) | 13.01 | ||
| WCJ-III Applied Problems | 108.74 (72 - 132) | 13.74 | ||
| WCJ-III Math Composite | 105.83 (72 - 125.5) | 12.37 | ||
| WCJ-III Basic Reading | 111.16 (71 - 131) | 13.05 | ||
|
| ||||
| WASI (abbreviated IQ) | 113.50 (78 - 147)* | 17.09 | ||
| PPVT-4 (verbal IQ) | 112.46 (74 - 143) | 15.35 | ||
WASI-IQ was unavailable for 2 participants, but all other measures were within 1SD of mean.
Standardized cognitive measures used for Analyses
Verbal Ability
Due to the fact that in our sample WCJ-III Basic Reading was not normally distributed (Kolmogorov-Smirnov = .143, p = .012), the Peabody Picture Vocabulary Test IV, fourth edition (PPVT-4) was used as a measure of Verbal IQ to control for the influence of language ability on math scores. In the PPVT, participants are asked to identify a picture that corresponds to words of increasing difficulty. An abbreviated version of the Wechsler Abbreviated Scale of Intelligence (WASI), including the vocabulary and matrix reasoning subtests, was administered during first grade as a metric of global IQ.
Mathematical Competence
Age normed standard scores from the Woodcock-Johnson III Tests of Achievement Calculation and Applied Problems subtests were averaged to create a composite measure of math ability (WCJ-III Math Composite). The Calculation subtest is an untimed, paper-and-pencil test that includes age appropriate content beginning with basic number knowledge and digit-based arithmetic. Applied Problems is an untimed verbal, picture-based test that includes basic number knowledge, counting, and arithmetic. Math competence scores were only available for 2nd grade as they were not collected during the first year of the ongoing longitudinal study. Correlations between the above cognitive variables are reported in Table 2.
Table 2.
| 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|
| 1. |
WCJ-III
Composite |
||||
|
|
|||||
| 2. |
WCJ-III
Calculation |
.921** | |||
|
|
|||||
| 3. |
WCJ-III Applied
Problems |
.929** | .712** | ||
|
|
|||||
| 4. | PPVT-4 | .576** | .456** | .607** | |
| 5. |
WCJ-III Basic
Reading |
.645** | .475** | .712.** | .617** |
indicates p <.001
Neuroanatomical Data Acquisition and Preprocessing
Image Acquisition
T1-weighted MRI was performed on a Philips Achieve 3T scanner with a 32-channel head coil. Magnetization Prepared Rapid Gradient Recalled Echo (MP-RAGE; (Mugler and Brookeman, 1990) anatomical scans were acquired according to the following parameters: 256×256 scan resolution; 170 slices; 1mm slice thickness; 9.051s TR; 4.61s TE; Flip Angle=8°; voxel size 1mm isotropic; acquisition time 274s. Scans were oriented AC-PC.
Voxel-Based Morphometry
Images were analyzed using SPM8 (Wellcome Trust Centre for Neuroimaging, http://www.fil.ion.ucl.ac.uk), on a MATLAB platform (version 7.11, Mathworks, Natick, MA). Anatomical images for all analyses were processed according to the VBM protocol described by Ashburner (2010) with the following specifications. T1-weighted structural scans were first segmented to obtain separate grey matter (GM), white matter WM), and cerebral spinal fluid (CSF) images (Ashburner and Friston, 2005). Second, a population-specific template was created using Diffeomorphic Anatomical Registration Through Exponentiated Lie Algebra (DARTEL) (Ashburner, 2007). Third, each subject’s GM map was transformed to customized template space based on the sample of 50 participants and then normalized into MNI space by coregistering with the Montreal Neurological Institute (MNI152) brain template. The warped images were modulated by the Jacobian determinants derived from DARTEL to obtain maps of GM volume maintaining an isotropic voxel resolution of 1.0 × 1.0 × 1.0 mm3. Two options exist in SPM8 for handling the effects of warping of GM that affect subsequent interpretation (Mechelli et al., 2005). One option is to leave voxel intensities “unmodulated” thereby preserving the concentration of GM in each voxel and changing the total amount of GM. Analyses on unmodulated images should be interpreted as findings related to GM concentration or density. The second option is to scale the intensity of GM by the Jacobian determinants derived from spatial normalization at each voxel, “modulated” normalization. This procedure results in preserved volumetric data (Ashburner and Friston, 2005). All subsequent analyses were performed on “modulated” data utilizing the second option of normalization and thus the present results are interpreted in terms of regional GM volume. In the final stage of preprocessing, the GM volume maps were smoothed with a full-width at half-maximum Gaussian kernel of 10mm to normalize the data and accommodate minor variations in individual’s anatomy.
Analyses
Math Competence and Whole Brain Grey Matter Volume
To investigate whether regional grey matter volume across the whole brain at the end of 1st grade and 2nd grade relate to individual differences in math achievement scores at the end of 2nd grade, we used two multiple linear regression models relating WCJ-III Math Composite scores to VBM derived grey matter volume maps at 1st and 2nd grade respectively. Age at time of scan, sex, global brain volume (WM + GM + CSF), and PPVT-4 (2nd grade) were included as covariates in the model to control for anatomical differences related to age, sex, overall brain volume, and verbal ability. The regression analysis was run on the whole brain with an absolute threshold mask of 0.01. A cluster level correction threshold of p < 0.05 was applied using the REST AlphaSim correction (uncorrected p < .0005, minimum cluster threshold : 680 voxels 1st grade, 587 voxels 2nd grade). AlphaSim is a non-parametric and non-isotropic, simulation-based method for determining the family-wise error threshold (http://restfmri.net/forum/REST).
Math Competence and Changes in Whole Brain Grey Matter Volume
In addition to testing whether grey matter volume in year 1 or year 2 relates to math ability in year 2, we tested whether change in grey matter volume between years 1 and 2 relates to math performance at year 2. To this end, voxel-wise change in the grey matter volume for each participant was measured by subtracting the grey matter volume image at 1st grade from that at 2nd grade using the ImCalc utility (http://robjellis.net/tools.html) in SPM8. The correlation between this change metric and grey matter volume at 1st grade was non-significant (r = −.05, p −.73), indicating that variance in change scores was not driven by values at baseline. The resulting individual subject maps detailing the voxel-wise change in grey matter volume were then subjected to the same regression analysis as described in the above analyses, with standardized math performance as the covariate of interest, and age, sex, and PPVT-4 as covariates of non-interest.
Region-of-Interest (ROI) analysis
To eliminate the possibility that different individuals account for the results at 1st grade and 2nd grade, and to establish the stability of grey matter volume within the left IPS, a correlation between the mean regional grey matter volumes per voxel across both years was performed. ROIs were defined based on the clusters identified in the primary VBM analyses (1st grade’s ROI peak voxel coordinates: x = −33, y = −60, z = 50, cluster size: 1041 voxels; 2nd grade’s ROI peak voxel coordinates: x = −33, y = −61, z = 50, cluster size: 675 voxels). For each ROI, the mean grey matter volume per voxel was extracted from all participants using the MarsBaR region of interest toolbox (version 0.44; http://marsbar.sourceforge.net/), with proportional scaling applied.
Results
Math Competence and Whole Brain Grey Matter Volume
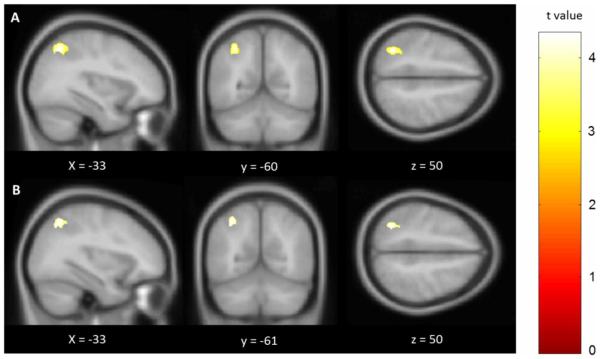
The multiple regression analysis predicting 2nd grade math scores from grey matter volume in 1st grade identified one cluster in the Left IPS after controlling for age at time of scan, sex, and verbal IQ (peak MNI coordinate: × = −33, y = −60, z = 50, t = 4.80, 1041 voxels, p < .05 cluster corrected) (Figure 1a) . The regression analysis predicting 2nd grade math scores from 2nd grade grey matter volume identified an almost identical cluster in the Left IPS with the same control variables (peak MNI coordinate: × = −33, y = −61, z = 50, t = 4.33, 675 voxels, p < .05 cluster corrected) (Figure 1b). The majority of each cluster was identified as hIP3 within the IPS using the SPM8 Anatomy Toolbox v2.15 (Eickhoff et al. 2005) with the cluster extending into nearby parietal regions (Table 3). To ensure that the results above were not driven by the inclusion of PPVT as a covariate, we conducted the analysis with math competence as the sole cognitive predictor. The relation between grey matter volume in left IPS region and math competence remained significant (p = .0005 uncorrected, p < .05 cluster level corrected). The same was true of grey matter at 2nd grade, albeit at a slightly lower (but widely used) uncorrected threshold (p = .005 uncorrected, p < .05 cluster level corrected).
Figure 1.
Significant clusters of grey matter related to math in 1st grade (A) and 2nd grade (B) after controlling for age at time of scan, sex, and PPVT-4.
Table 3.
VBM Results for 1st and 2nd grade
| Grade (at scan) |
Hemisphere | Peak MNI (x y z) |
Cluster Size |
T | Z | P corrected | BA | Anatomical Description |
|---|---|---|---|---|---|---|---|---|
| 1st | Left | (−33 −60 50) | 1041 | 4.80 | 4.29 | < 0.05 | 7 | IPS |
| 2nd | Left | (−33 −61 50) | 675 | 4.33 | 3.94 | <0.05 | 7 | IPS |
IPS (intraparietal sulcus)
Our main analysis used a composite measure of math competence to capture mathematical/computational processes over and above those specific to a single subtest (e.g. digit processing for calculation vs verbal processing for applied problems). However, we were additionally interested in whether the two subtests were associated differentially with grey matter volume across the whole brain. Therefore, we conducted two additional analysis using Woodcock-Johnson Calculation and Applied Problems as the dependent variables respectively. These separate analyses revealed that when age at time of scan, sex, global brain volume (WM + GM + CSF), and PPVT-4 (2nd grade) were included as covariates in the model, WCJ-Calculation was related to increased grey matter in region in the Superior Temporal/Angular (−47, −54, 9) gyrus for both 1st and 2nd grade (1st grade = 555 voxels, 2nd grade = 503 voxels. p = .0005 uncorrected, p < .05 cluster level corrected). The left IPS region reported in the main analysis was present but only survived cluster-level (p <.05) correction at a lower uncorrected threshold of p = .005 for year 1, and did not survive correction for year 2. The same analysis using Applied Problems revealed an association with the same left IPS region reported in the main analysis for both 1st and 2nd grade (1st grade = 922 voxels, 2nd grade = 921 voxels. p = .0005 uncorrected, p < .5 cluster level corrected).
Math Competence and Changes in Whole Brain Grey Matter Volume
No suprathreshold clusters were found at a threshold of p < .0005 (uncorrected), or at a more liberal uncorrected threshold of p < .005. Therefore cluster level correction was not applied. In other words, individual differences in math performance at 2nd grade were not predicted by changes in grey matter volume in the preceding year in any brain region.
ROI Analysis
Mean grey matter volume in the left IPS regions identified in the 1st and 2nd grade analyses showed a strong positive correlation with each other (r = .955, p < .001). This suggests that the mean grey matter volume within these regions remained relatively stable within a one-year period. More importantly, it indicates that the results of 1st grade and 2nd grade analyses were likely to be accounted for by the same individuals.
Discussion
The current study is the first to investigate the longitudinal relationship between grey matter volume across the whole brain and math competence in children without mathematical learning difficulties. Testing for a relation between math competence at the end of 2nd grade and grey matter volume at the end of 1st grade, we show that across the whole brain, only left intraparietal sulcus (IPS) grey matter volume relates to math competence at the end of 2nd grade. Grey matter volume in the same region at the end of 2nd grade related to concurrent math competence, and no region of the brain showed a relation between change in grey matter volume from year 1 to year 2 and math competence. These results indicate a significant and stable role for the left IPS in the development of individual differences in math competence.
The present results compliment a growing body of literature suggesting that the IPS is a critical neural foundation for the development of math competence. Previous studies have shown that the IPS has atypical structural properties in children with mathematical learning disabilities (Starke et al., 2013; Lubin et al, 2013; Rykhlevskaia et al., 2009, Isaacs et al., 2001; Molko et al., 2003). Furthermore, the activation of this region during numerical processing tasks is atypical in children with dyscalculia (Price et al., 2007; Mussolin et al., 2010). However, it cannot be assumed that neuroanatomical mechanisms that distinguish children with math learning disabilities from their typically developing peers are the same mechanisms that underlie individual differences in typically developing math competence. To the best of our knowledge, only one study to date has investigated the relation between grey matter volume and math competence in typically developing children (Li et al., 2013), showing that math competence correlated with grey matter volume in the left IPS. However, that study employed a region of interest analysis, excluding regions outside the bilateral IPS from analysis, leaving open the question of whether grey matter volume in the IPS is in fact the most significant neuroanatomical predictor of math competence. Indeed, several functional imaging studies have shown that while functional activation of the IPS during numerical magnitude processing predicts math ability (Bugden et al., 2012), activation of other frontal and parietal regions during arithmetic tasks, in particular the left angular and supramarginal gyri, correlate with math ability (Ansari, Grabner, Koschutnig, Reishofer, & Ebner, 2011; Price, Mazzocco, & Ansari, 2013). This distinction further highlights the need to explore the whole brain as opposed to a priori restricted regions when investigating the relation between brain structure and math competence.
The present results suggest that in terms of structural neuroanatomy, when considering math competence broadly across multiple subtests, the IPS demonstrates the most significant association with math competence. Structural properties of the left superior temporal/angular gyrus, on the other hand, appear to have an association with calculation specifically.
The left IPS region identified in this study has previously been associated at the cognitive level with numerical magnitude processing. Activation in this region is often observed during numerical comparison tasks using both Arabic digits (Bugden et al., 2012; Mussolin, Mejias, Noël, & Noel, 2010; Pinel et al., 1999) and nonsymbolic quantities (Ansari & Dhital, 2006; Cantlon et al., 2006; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004). Therefore, at a basic level the current findings could be seen to lend support to the hypothesis that numerical magnitude system or ‘approximate number system’ (ANS) is a critical foundation for the development of math competence. However, more recent evidence suggests that some degree of hemispheric lateralization may be at play in the intraparietal sulcus, whereby the left IPS is engaged by symbolic magnitude processing while the right IPS is more engaged by nonsymbolic magnitude processing (Ansari, 2008; Holloway, Battista, Vogel, & Ansari, 2013; Vogel, Celia, & Ansari, 2015). In addition, a number of recent studies have suggested that symbolic magnitude processing is a stronger predictor of math skills than nonsymbolic magnitude processing (De Smedt, Noël, Gilmore, & Ansari, 2013). Therefore, the current findings suggest that the neural mechanisms underlying the processing of symbolic numerical magnitude in particular are the critical foundation for the development of math competence. Whether this symbolic magnitude processing represents an interaction between the ANS and symbolic systems, or whether it is fully abstracted from the ANS remains an open empirical question. The left angular gyrus, on the other hand, has previously been more typically associated with calculation fluency (Delazer, 2003; Grabner, Ansari, et al., 2009; Grabner, Ischebeck, et al., 2009). The present results provide further evidence for the role of this region in calculation as a specific sub-domain of mathematical competence.
Findings relating basic numerical magnitude processing to math development has led some researchers to conclude that improving basic magnitude processing ability may have beneficial implications for math competence (Lindskog, Winman, & Juslin, 2013; Park & Brannon, 2013). The current data suggests that this approach may be productive, as the structural integrity of the IPS appears to be a key foundation for math competence. However, the lack of change in grey matter volume in that region over a year of schooling suggests that interventions targeting that system may need to be enacted early in development, at least prior to 1st grade, as by the end of 1st grade this neural system may no longer be malleable. Furthermore, it should also be noted that changes in functional activation over development are not always mirrored by concomitant changes in grey matter structure (Rivera, Reiss, Eckert, & Menon, 2005) and so the extent to which the neural systems underlying numerical magnitude processing are subject to sensitive periods remains an open empirical question. It should also be noted as a limitation of the present study that math competence measures were only available for 2nd grade as they were not collected during the first year of the longitudinal study. This fact restricts our ability to draw causal inferences from the current data as a true bidirectional relationship could not be established. Future research comprising both neuroanatomical and math competence data from two time points is needed to further elucidate the question of causality.
In summary, the present results show that grey matter volume in the left IPS at the end of 1st grade is related to math competence a year later at the end of 2nd grade. Grey matter volume in this region did not change over that year, and was still correlated with math competence at the end of 2nd grade. These findings support the hypothesis that the IPS and its associated functions represent a critical foundation for the acquisition of mathematical competence.
Highlights.
1st grade grey matter volume in Intraparietal sulcus predicts 2nd grade math competence
Grey matter volume in same region correlates with math competence at end of 2nd grade
Change in grey matter volume does not predict 2nd grade math competence
Table 4.
Cluster details for 1st and 2nd grade
| Number of Voxels |
% of voxels in cluster |
Anatomical Description |
% Coverage of Anatomical Description Area |
|
|---|---|---|---|---|
|
Cluster at 1st grade
(1041 voxels) |
695 | 66.8 | Left hIP3 (IPS) | 20.3 |
| 264 | 25.4 | Left 7A | 2.6 | |
| 39 | 3.7 | Left hIP1 (IPS) | 2.0 | |
| 39 | 3.7 | Left PGa (IPL) | 0.8 | |
|
|
||||
| total | 1037 | 99.6 | ||
|
| ||||
| Cluster at 2nd grade
(675 voxels) |
503 | 74.5 | Left hIP3 (IPS) | 14.7 |
| 138 | 20.4 | Left 7A (SPL) | 1.4 | |
| 20 | 3.0 | hIP1 (IPS) | 1.0 | |
| 12 | 1.8 | PGa (IPL) | 0.2 | |
|
|
||||
| total | 673 | 99.7 | ||
(IPS) intraparietal sulcus, (hIP3) subregion of IPS, (7A) Brodmann area 7A, (hIP1) subregion of the IPS, (PGa) subregion of the superior parietal lobule
Acknowledgments
This work was supported by NICHD/NIH R01 HD044073, NICHD/NIH R01 HD046130, NICHD/NIH P30 P30HD015052, and NCATS/NIH UL1 TR000445.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ansari D. Effects of development and enculturation on number representation in the brain. Nature Reviews. Neuroscience. 2008;9(4):278–91. doi: 10.1038/nrn2334. doi:10.1038/nrn2334. [DOI] [PubMed] [Google Scholar]
- Ansari D, Dhital B. Age-related changes in the activation of the intraparietal sulcus during nonsymbolic magnitude processing: an event-related functional magnetic resonance imaging study. Journal of Cognitive Neuroscience. 2006;18(11):1820–8. doi: 10.1162/jocn.2006.18.11.1820. doi:10.1162/jocn.2006.18.11.1820. [DOI] [PubMed] [Google Scholar]
- Ansari D, Dhital B, Siong SC. Parametric effects of numerical distance on the intraparietal sulcus during passive viewing of rapid numerosity changes. Brain Research. 2006;1067(1):181–8. doi: 10.1016/j.brainres.2005.10.083. doi:10.1016/j.brainres.2005.10.083. [DOI] [PubMed] [Google Scholar]
- Ansari D, Garcia N, Lucas E, Hamon K, Dhital B. Neural correlates of symbolic number processing in children and adults. Neuroreport. 2005;16(16):1769–73. doi: 10.1097/01.wnr.0000183905.23396.f1. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/16237324. [DOI] [PubMed] [Google Scholar]
- Ansari D, Grabner RH, Koschutnig K, Reishofer G, Ebner F. Individual differences in mathematical competence modulate brain responses to arithmetic errors: An fMRI study. Learning and Individual Differences. 2011;21(6):636–643. doi:10.1016/j.lindif.2011.07.013. [Google Scholar]
- Bugden S, Price GR, McLean DA, Ansari D. The role of the left intraparietal sulcus in the relationship between symbolic number processing and children’s arithmetic competence. Developmental Cognitive Neuroscience. 2012;2(4):448–57. doi: 10.1016/j.dcn.2012.04.001. doi:10.1016/j.dcn.2012.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bynner J, Parsons S. Does Numeracy Matter? The Basic Skills Agency; London: 1997. [Google Scholar]
- Cantlon JF, Brannon EM, Carter EJ, Pelphrey KA. Functional imaging of numerical processing in adults and 4-y-old children. PLoS Biology. 2006;4(5):e125. doi: 10.1371/journal.pbio.0040125. doi:10.1371/journal.pbio.0040125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cappelletti M, Price CJ. Residual number processing in dyscalculia. NeuroImage: Clinical. 2014;4:18–28. doi: 10.1016/j.nicl.2013.10.004. doi:10.1016/j.nicl.2013.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Smedt B, Noël M-P, Gilmore C, Ansari D. How do symbolic and non-symbolic numerical magnitude processing skills relate to individual differences in children’s mathematical skills? A review of evidence from brain and behavior. Trends in Neuroscience and Education. 2013;2(2):48–55. doi:10.1016/j.tine.2013.06.001. [Google Scholar]
- Delazer M. Learning complex arithmetic—an fMRI study. Cognitive Brain Research. 2003;18(1):76–88. doi: 10.1016/j.cogbrainres.2003.09.005. doi:10.1016/j.cogbrainres.2003.09.005. [DOI] [PubMed] [Google Scholar]
- Goodman M, Finnegan R, Mohadjer L, Krenzke T, Hogan J. Problem Solving in Technology-Rich Environments Among U. S. Adults. 2014 Retrieved from http://nces.ed.gov/pubs2014/2014008.pdf.
- Grabner RH, Ansari D, Koschutnig K, Reishofer G, Ebner F, Neuper C. Mapping arithmetic problem solving strategies in the brain: The role of the left angular gyrus in arithmetic fact retrieval. Neuroimage. 2009;47:S111. doi: 10.1016/j.neuropsychologia.2008.10.013. [DOI] [PubMed] [Google Scholar]
- Grabner RH, Ischebeck A, Reishofer G, Koschutnig K, Delazer M, Ebner F, Neuper C. The interplay of arithmetic fact training and mathematical competence on parietal brain activation during mental calculation. Neuroimage. 2009;47:S88. [Google Scholar]
- Gross J, Hudson C, Price D. The Long Term Costs of Numeracy Difficulties. 2009 [Google Scholar]
- Halberda J, Ly R, Wilmer JB, Naiman DQ, Germine L. Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(28):11116–20. doi: 10.1073/pnas.1200196109. doi:10.1073/pnas.1200196109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MMM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455(7213):665–8. doi: 10.1038/nature07246. doi:10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Han Z, Fuchs L, Davis N, Cannistraci CJ, Anderson AW, Gore JC, Dawant BM. Analysis of anatomic variability in children with low mathematical skills. Proceedings of SPIE. 2008;6916 69160S–69160S–8. doi:10.1117/12.771214. [Google Scholar]
- Holloway ID, Battista C, Vogel SE, Ansari D. Semantic and perceptual processing of number symbols: evidence from a cross-linguistic fMRI adaptation study. Journal of Cognitive Neuroscience. 2013;25(3):388–400. doi: 10.1162/jocn_a_00323. doi:10.1162/jocn_a_00323. [DOI] [PubMed] [Google Scholar]
- Isaacs EB, Edmonds CJ, Lucas A, Gadian DG. Calculation difficulties in children of very low birthweight: a neural correlate. Brain. 2001;124:1701–1707. doi: 10.1093/brain/124.9.1701. Pt 9. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/11522573. [DOI] [PubMed] [Google Scholar]
- Li Y, Hu Y, Wang Y, Weng J, Chen F. Individual structural differences in left inferior parietal area are associated with schoolchildrens’ arithmetic scores. Frontiers in Human Neuroscience. 2013 Dec;7:844. doi: 10.3389/fnhum.2013.00844. doi:10.3389/fnhum.2013.00844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindskog M, Winman A, Juslin P. Are there rapid feedback effects on Approximate Number System acuity? Frontiers in Human Neuroscience. 2013 Jun;7:270. doi: 10.3389/fnhum.2013.00270. doi:10.3389/fnhum.2013.00270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubin A, Rossi S, Simon G, Lanoë C, Leroux G, Poirel N, Houdé O. Numerical Transcoding Proficiency in 10-Year-Old Schoolchildren is Associated with Gray Matter Inter-Individual Differences: A Voxel-Based Morphometry Study. Frontiers in Psychology. 2013 Apr;4:197. doi: 10.3389/fpsyg.2013.00197. doi:10.3389/fpsyg.2013.00197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MMM, Feigenson L, Halberda J. Impaired acuity of the approximate number system underlies mathematical learning disability (dyscalculia) Child Development. 2011a;82(4):1224–37. doi: 10.1111/j.1467-8624.2011.01608.x. doi:10.1111/j.1467-8624.2011.01608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MMM, Feigenson L, Halberda J. Preschoolers’ Precision of the Approximate Number System Predicts Later School Mathematics Performance. PLoS ONE. 2011b;6(9):e23749. doi: 10.1371/journal.pone.0023749. doi:10.1371/journal.pone.0023749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molko N, Cachia A, Riviere D, Mangin JF, Bruandet M, Le Bihan D, Rivière D. Functional and structural alterations of the intraparietal sulcus in a developmental dyscalculia of genetic origin. Neuron. 2003;40(4):847–858. doi: 10.1016/s0896-6273(03)00670-6. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/14622587. [DOI] [PubMed] [Google Scholar]
- Mussolin C, De Volder A, Grandin C, Schlogel X, Nassogne MC, Noel MP. Neural Correlates of Symbolic Number Comparison in Developmental Dyscalculia. Journal of Cognitive Neuroscience. 2009:1–15. doi: 10.1162/jocn.2009.21237. Early Access. [DOI] [PubMed] [Google Scholar]
- Mussolin C, Mejias S, Noël M-P, Noel MP. Symbolic and nonsymbolic number comparison in children with and without dyscalculia. Cognition. 2010;115(1):10–25. doi: 10.1016/j.cognition.2009.10.006. doi:10.1016/j.cognition.2009.10.006. [DOI] [PubMed] [Google Scholar]
- Park J, Brannon EM. Training the Approximate Number System Improves Math Proficiency. Psychological Science. 2013 doi: 10.1177/0956797613482944. August. doi:10.1177/0956797613482944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsons S, Bynner J. Does numeracy matter more. NRDC (National Research and Development Centre for Adult Literacy and numeracy).[aRCK] 2005 [Google Scholar]
- Piazza M, Facoetti A, Trussardi AN, Berteletti I, Conte S, Lucangeli D, Zorzi M. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition. 2010 doi: 10.1016/j.cognition.2010.03.012. [DOI] [PubMed] [Google Scholar]
- Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S. Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron. 2004;44(3):547–555. doi: 10.1016/j.neuron.2004.10.014. doi:10.1016/j.neuron.2004.10.014. [DOI] [PubMed] [Google Scholar]
- Pinel P, Dehaene S, Rivière D, LeBihan D, Riviere D. Modulation of parietal activation by semantic distance in a number comparison task. Neuroimage. 2001;14(5):1013–1026. doi: 10.1006/nimg.2001.0913. doi:10.1006/nimg.2001.0913. [DOI] [PubMed] [Google Scholar]
- Pinel P, Le Clec’H G, van de Moortele PF, Naccache L, Le Bihan D, Dehaene S, Le Clec HG. Event-related fMRI analysis of the cerebral circuit for number comparison. Neuroreport. 1999;10(7):1473–9. doi: 10.1097/00001756-199905140-00015. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/10380965. [DOI] [PubMed] [Google Scholar]
- Price GR, Holloway ID, Räsänen P, Vesterinen M, Ansari D. Impaired parietal magnitude processing in developmental dyscalculia. Current Biology. 2007;17(24):1042–1043. doi: 10.1016/j.cub.2007.10.013. doi:10.1016/j.cub.2007.10.013. [DOI] [PubMed] [Google Scholar]
- Price GR, Mazzocco MMM, Ansari D. Why Mental Arithmetic Counts: Brain Activation during Single Digit Arithmetic Predicts High School Math Scores. Journal of Neuroscience. 2013;33(1):156–163. doi: 10.1523/JNEUROSCI.2936-12.2013. doi:10.1523/JNEUROSCI.2936-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera SM, Reiss AL, Eckert MA, Menon V. Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb Cortex. 2005;15(11):1779–1790. doi: 10.1093/cercor/bhi055. Retrieved from http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=15716474. [DOI] [PubMed] [Google Scholar]
- Rotzer S, Kucian K, Martin E, von Aster M, Klaver P, Loenneker T. Optimized voxel-based morphometry in children with developmental dyscalculia. Neuroimage. 2007;39(1):417–422. doi: 10.1016/j.neuroimage.2007.08.045. doi:10.1016/j.neuroimage.2007.08.045. [DOI] [PubMed] [Google Scholar]
- Rykhlevskaia E, Uddin LQ, Kondos L, Menon V. Neuroanatomical correlates of developmental dyscalculia: combined evidence from morphometry and tractography. Frontiers in Human Neuroscience. 2009 Nov;3:51. doi: 10.3389/neuro.09.051.2009. doi:10.3389/neuro.09.051.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogel SE, Celia G, Ansari D. Developmental specialization of the left parietal cortex for the semantic representation of Arabic numerals: An fMR-Adaptaton study. Accident Analysis and Prevention. 2015;12:61–73. doi: 10.1016/j.dcn.2014.12.001. doi:10.1016/j.dcn.2014.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]