A Nested Phosphorus and Proton Coil Array for Brain Magnetic Resonance Imaging and Spectroscopy

Abstract

A dual-nuclei radiofrequency coil array was constructed for phosphorus and proton magnetic resonance imaging and spectroscopy of the human brain at 7 Tesla. An eight-channel transceive degenerate birdcage phosphorus module was implemented to provide whole-brain coverage and significant sensitivity improvement over a standard dual-tuned loop coil. A nested eight-channel proton module provided adequate sensitivity for anatomical localization without substantially sacrificing performance on the phosphorus module. The developed array enabled phosphorus spectroscopy, a saturation transfer technique to calculate the global creatine kinase forward reaction rate, and single-metabolite whole-brain imaging with 1.4 cm nominal isotropic resolution in 15 min (2.3 cm actual resolution), while additionally enabling 1 mm isotropic proton imaging. This study demonstrates that a multi-channel array can be utilized for phosphorus and proton applications with improved coverage and/or sensitivity over traditional single-channel coils. The efficient multi-channel coil array, time-efficient pulse sequences, and the enhanced signal strength available at ultra-high fields can be combined to allow volumetric assessment of the brain and could provide new insights into the underlying energy metabolism impairment in several neurodegenerative conditions, such as Alzheimer’s and Parkinson’s diseases, as well as mental disorders such as schizophrenia.

1. Introduction

Phosphorus (³¹P) magnetic resonance spectroscopy (MRS) is a unique tool for evaluating cerebral metabolism in vivo (Shulman et al., 2004). It allows direct detection and quantification of cerebral phospholipids, high-energy phosphates such as phosphocreatine (PCr) and adenosine triphosphate (ATP) (Ackerman et al., 1980), intracellular pH, and the rate constants of important reactions such as the creatine kinase (CK), and the ATP synthesis hydrolysis cycle (ATPase) (Alger and Shulman, 1984). ³¹P-MRS has provided new evidence of underlying bioenergetic abnormalities in many conditions including Alzheimer’s disease (Mandal et al., 2012), Parkinson’s disease (Hattingen et al., 2009; Hu et al., 2000), bipolar disorder (Sikoglu et al., 2013; Yuksel et al., 2015), schizophrenia (Smesny et al., 2007), and epilepsy (Hetherington et al., 2002). Unlike other techniques that measure cerebral metabolism such as positron emission tomography (PET) or carbon (¹³C) MRS, ³¹P-MRS does not require the injection of labeled precursors and is completely noninvasive (Chaumeil et al., 2009).

It is well established that energy demand in the brain is not uniform (Dudley et al., 2014; Zhu et al., 2012) and distribution of ³¹P containing metabolites varies in white and gray matter (Hetherington et al., 2001). Therefore, it is important to develop techniques able to resolve this spatial variation in health and disease. ³¹P-MRS data typically suffer from low signal-to-noise ratio (SNR) due to the low concentration of ³¹P containing metabolites in the brain and the low MR sensitivity associated with the ³¹P nucleus. As a result, ³¹P MR signal in the brain is about four orders of magnitude lower than ¹H signal. As a result, undesirable compromises in spatial resolution and coverage have been required to perform ³¹P-MRS in reasonable acquisition times in standard magnets (< 3 Tesla). High-field magnets (≥ 3 Tesla) provide increased chemical shift dispersion, improved SNR per unit acquisition time through greater bulk magnetization, as well as shorter longitudinal relaxation time (T₁), which have been parlayed into improved resolution and coverage (Lei et al., 2003b; Lu et al., 2013; Twieg et al., 1994). These benefits can be naturally extended to ultra-high field devices (≥ 7 Tesla) where ³¹P SNR efficiency is more than double that at 3 Tesla.

Significant SNR enhancement can also be achieved with improved radiofrequency (RF) coil detectors, which have transitioned from preceding single channel and volume coils to multi-element phased arrays. Owing to their dominant relevance in clinical MRI, proton (¹H) arrays were the first to be developed during the previous two decades (Roemer et al., 1990; Wright and Wald, 1997). The advantages of phased arrays have been well documented and include extended coverage over an individual surface coil, SNR improvement over a volume coil, and the ability to perform accelerated imaging through parallel reception techniques (Griswold et al., 2002; Pruessmann et al., 1999; Sodickson and Manning, 1997).

More recently, phased arrays have been established for non-proton nuclei to benefit SNR starved ³¹P and ²³Na applications (Avdievich and Hetherington, 2007; Brown et al., 2014; Brown et al., 2013; Kaggie et al., 2014; Lakshmanan et al., 2014; Moon et al., 2013; Shajan et al., 2015; van der Velden et al., 2014). Paradoxically, one of the main difficulties associated with dual-nuclei phased array development is that the ensemble detector is required to allow ¹H imaging. The ¹H module is essential for anatomical localization and is particularly useful for B0 shimming in high field MRI where reduced B0 uniformity can be unfavorable in ³¹P applications that demand differentiation of the multi-peak spectra. A dual-nuclei ³¹P/¹H coil typically requires performance tradeoffs on one or both modules (Schnall et al., 1985). Various methods have been utilized in dual-nuclei volume or surface coils to minimize loss on the ³¹P module, while tolerating greater ¹H loss due to its overwhelming baseline SNR advantage (Adriany and Gruetter, 1997; Alecci et al., 2006; Bottomley et al., 1989; Fitzsimmons et al., 1993; Lanz et al., 1997; Murphy-Boesch et al., 1994; Shen et al., 1997; Xie et al., 2007).

In this work, we expand on previous methods to develop a ³¹P/¹H array for brain imaging at 7 T. The array consists of an eight-channel ³¹P module and separate eight-channel ¹H module that embodied the underlying strategy to enhance ³¹P performance through a multi-channel phased array free of extraneous elements such as detuning circuits, fuses, inductors, and trap circuits. This strategy led to a ³¹P transmit/receive degenerate birdcage (DBC) structure that was paired with a “nested” eight-channel module to provide ¹H imaging capability without significantly conceding ³¹P performance. We outline the dual-nuclei nested design strategy and provide benchmark measurements along with in vivo data collected using both standard and non-Cartesian pulse sequences.

2. Methods

2.1. Coil Design Strategy

The main objective for the ³¹P/¹H head coil was to provide high ³¹P SNR, while secondary objectives included the generation of a uniform ³¹P transmit magnetic field (B₁⁺) and a ¹H module for anatomical localization and B₀ shimming. Several strategies were utilized to accomplish these objectives. First, a ³¹P multi-coil array configuration was preferred over a volume coil because of well-known SNR advantages (Roemer et al., 1990; Wright and Wald, 1997). Second, it was sought to eliminate lossy elements such as detuning circuits, fuses and extraneous inductors from the ³¹P receive coils. Finally, the introduction of ¹H coils was to be done in such a way that ³¹P coil efficiency was not conceded.

A transmit/receive array was pursued in order to satisfy the multi-coil array criteria while simultaneously eliminating lossy elements such as detuning circuits and fuses that are required in receive-only arrays. Further, a fully surrounding transmit/receive array with radial symmetry enables a circularly polarized B₁⁺ field to be generated in the center of the object in a straightforward manner. One topology that matches these criteria is a degenerate birdcage, where modes collapse at the transition point between the high pass and low pass configurations (Cheng et al., 2003; Leussler et al., 1997; Lin et al., 2003; Nistler et al., 2006; Taracila et al., 2006; Tropp, 1992; Wong and Luh, 1999). A key benefit of the DBC is its ability to function as both a multi-coil array with a SNR advantage during signal reception and as a traditional birdcage with uniform B₁⁺ during spin excitation. To eliminate inline high impedance “trap” circuits or diodes that have been utilized to achieve dual-resonance (Schnall et al., 1985), the DBC was designed to resonate at the ³¹P frequency only. To simultaneously provide ¹H imaging capability, a “nested” strategy was utilized in which separate ¹H coils were inserted concentric to the ³¹P coils (Brown et al., 2013; Fitzsimmons et al., 1987; Mispelter et al., 1989). The ³¹P and ¹H coils are described in more detail in subsequent sections.

Meanwhile, the following analysis is provided to demonstrate the efficacy of the dual nuclei nested coil strategy. Coil impedance is given by Z = jωL+(jωC)⁻¹, where j is the imaginary unit, ω is radial frequency, L is coil inductance, C is coil capacitance and the resistance is ignored. Consider a coil tuned to the proton frequency:Z(ω= ω_1H)=0. When viewed at the lower x-nucleus frequency, its impedance is dominated by the large capacitive reactance and therefore approximates an open circuit:Z(ω= ω_low)∼(jω_lowC)⁻¹→∞. Of course, the degree to which the open circuit condition is approached is proportional to the ratio between the resonant frequencies of interest. For ³¹P applications,$\frac{{\omega }_{1\mathrm{H}}}{{\omega }_{\mathit{low}}}\sim 2.5$ and the resulting impedance is in the 500 Ω range, which is sufficient to predominately disallow co-rotating (in-phase) current flow. Therefore, the performance of a neighboring ³¹P coil is principally preserved. Consider next a coil tuned to the x-nuclei frequency Z′(ω=ω_low)=0. When viewed at the proton frequency, its impedance is dominated by its inductive reactance and therefore can be thought of as a shield:Z′(ω=ω_1H)∼jω_1HL. This combination of behaviors can be leveraged in a concentric nested dual nuclei strategy; 1) the outer low frequency coil is not affected by the inner high frequency coil, while 2) the low frequency coil shields the high frequency coil to reduce its radiation loss and neighbor coupling (Lanz and Griswold, 2006), albeit at the expense of coverage and penetration due to counter-rotating (out-of-phase) current induced in the low frequency coil shield (Mispelter et al., 1989).

To evaluate the nested strategy in practice, several circular coils with 8 cm or 6 cm diameter were etched on 0.8 mm thick FR4 copper clad (1 oz/ft2) circuit boards. The coils were tuned to 297.2 MHz (¹H resonant frequency at 7 Tesla) or 120.3 MHz (³¹P) using four (¹H) or two (³¹P) distributed capacitors (series 5, Voltronics Corp., Salisbury MD). A ³¹P/¹H dual-tuned “trap” coil was also realized using three distributed capacitors and one capacitor/inductor parallel circuit. The inductor was hand wound (air core) using 20 AWG wire a nd its in ductance was approximately 5 times less than that of the coil to achieve a desirable tradeoff between ³¹P and ¹H performance (Schnall et al., 1985). Quality factor (Q) measurements were performed in the following baseline isolated as well as dual-nuclei configurations (see Figure 1): 1) isolated ³¹P coil, 2) isolated ¹H coil, 3) “offset” ³¹P/¹H coil pair; 4) concentric nested ³¹P/¹H coil pair, and 5) trap circuit coil. The Q was measured with a network analyzer connected to a shielded double probe that was coupled lightly to the coil. Measurements were made with the coil in free space and loaded with a water phantom doped with 3.75g NiSO₄ and 5g NaCl per 1000g dH₂O.

Figure 1.

Illustration of various single and dual tuned coil arrangements. The corresponding Q values are listed in Table 2.

2.2. ³¹P Degenerate Birdcage

The nested dual nuclei strategy was initially put into practice using an eight leg DBC with 20 cm length and 28 cm diameter that was constructed on FR4 circuit boards with 12 mm conductor width (see Figure 2). One difficulty associated with a DBC is that inductive coupling between segments prevents complete degeneracy that could undermine transmit efficiency (Cheng et al., 2003) (note that coupling can be mitigated during signal reception using preamplifier decoupling). Tapered legs were implemented to effectively reduce the size of the individual segments and hence the means for inductive coupling, albeit at the expense of coverage in the z-direction.

Figure 2.

Photograph of the ³¹P/¹H 16-channel array and interface with the protective cover removed. Overlays outline the cable trap and interface boards that accommodate the power dividers, transmit/receive switches, and preamplifiers.

The means for achieving degeneracy wherein the modes of the birdcage collapse at the desired frequency was achieved through an iterative process (Alagappan et al., 2007). Briefly, 1) individual coil segments were tuned to the Larmor frequency (120.3 MHz for ³¹P at 7 Tesla) while the other segments were disabled, 2) two neighboring coil segments were tuned and isolated by adjusting the ratio between the end ring and leg capacitors while the other segments were disabled, and 3) step two was repeated for all segment pairs (typically it is necessary to iterate this step at least twice to compensate for perturbations caused by adjustments to the system). DBC segments were capacitively matched to 50 Ω (see the electrical schematic in Figure 3) while loaded with a water based gel phantom (Duan et al., 2014) whose anatomical structure and dielectric properties (Gabriel et al., 1996) were designed to mimic those of the human head.

Figure 3.

Flattened two-dimensional schematic diagram of the ³¹P/¹H coil array and interface. For simplicity one ³¹P and one ¹H coil of the 16-channel nested array are highlighted in black while neighboring elements are displayed in light gray. The status of the DC bias is forward in transmit mode and reverse in receive mode. In receive mode, components D₁ and iso provide isolation between the RF amplifier and preamplifiers in receive mode, while the iso’ components minimize insertion loss between the coils and preamplifiers. The λ/4, 50Ω circuit help balance the transmit path and improve isolation. Typical component values are; C₁ = 40 pF, C₂ = 56 pF, C₃ = 27 pF, C₄ = 75 pF, C₅ = 5.3 pF, C₆ = 30 pF, C₇ = 36 pF, L₁ = 24 nH, RFC: radiofrequency choke (1 to 10 uH), and RFS: radiofrequency short (330 to 1000 pF).

To generate a circularly polarized B₁⁺ field, the DBC was driven through an eight-way power splitter consisting of three stages of Wilkinson power dividers and quadrature hybrids arranged to provide outputs with 45° phase offsets that corresponded to the azimuthal angle of the eight birdcage segments. Individual power splitter outputs were connected to transmit/receive switches to protect the preamplifiers during ³¹P transmission. The transmit/receive switches utilized a quarter-wavelength-based design similar to that previously outlined in (Shajan et al., 2011). The interface electronics shared a common ground that was broken by individual cable traps that were connected to each DBC port; the cable traps were tuned to block common mode current at both ³¹P and ¹H (297.2 MHz) frequencies on the coaxial cable shield. Preamplifier decoupling was accomplished by selecting the coaxial cable length such that the low input impedance of the preamplifier was translated into an inductance that formed a parallel resonant circuit with the DBC match capacitor (Roemer et al., 1990).

The dual frequency cable traps were formed by bridging two individual inductors with distinct capacitors; 3 turns of semi-rigid coaxial cable with 6 mm diameter bridged by a 27 pF capacitor for the ³¹P trap and a 2-turn inductor bridged by a 3.3 pF capacitor for the ¹H trap. Note that cable traps were included at both frequencies to counteract ground loops that may form in the complex system consisting of a multitude of coils and coaxial cables. The operating frequencies of the back-to-back ³¹P and ¹H cable traps were sufficiently separated to avoid resonant frequency splitting. Each trap was surrounded on three sides with copper “fences” that formed a partial shield to reduce interaction between neighboring traps tuned to the same frequency.

2.3. ¹H Eight Channel Array

We begin by reiterating that a coil tuned to the ¹H frequency has a large negative reactance at the ³¹P frequency. This characteristic is harmonious with the nested design approach because the ¹H coils are expected to have minimal impact on the ³¹P DBC. To simultaneously achieve ¹H B₀ shimming and anatomical localization, an array of eight ¹H transmit/receive coils was constructed. It should be noted that the ¹H coils were tuned subsequent to the ³¹P DBC, which is important because the ³¹P coil is perceived as a shield at the ¹H frequency and has a significant impact on the ¹H coil resonance. To utilize the shielding effect, the ¹H coils were inserted concentric to the ³¹P DBC segments, which can reduce radiation loss and coupling between neighboring coils (Lanz and Griswold, 2006), albeit at the possible expense of coverage and B₁ penetration due to counter-rotating currents induced in the ³¹P DBC.

The ¹H coils were octagonal in shape with an arc length of 7.7 cm and head/foot length of 15 cm at their widest points. To reduce eddy currents induced by the ³¹P DBC, the ¹H coils were constructed using 12 AWG copper wire, which can be advantageous compared to etched copper traces (Kumar et al., 2009; Wiggins et al., 2009). The coils were tuned and matched while loaded with the head phantom described above, and neighboring coils were inductively decoupled. The ¹H array was interfaced through an eight-way power splitter and transmit/receive switch apparatus in an analogous manner to that described for the ³¹P DBC (see Figure 3).

Unloaded and loaded Q values were measured on all 16 ³¹P/¹H coil elements in situ in the developed array. To evaluate the impact of module interaction, separate sets of measurements were performed on one module (³¹P or ¹H) while the other was resonant or open-circuited. Additionally, the scattering parameter (S) matrix was measured by directly coupling to a given pair of coil elements while all other elements were resonant and terminated with 50 Ω.

2.4. Coil performance

3D electromagnetic models of the ³¹P and ¹H arrays were constructed in CST Microwave Studio (Framingham, MA) to numerically analyze the coil. The coil models included realistic geometric representations of the actual copper conductors, while cable traps, coaxial cables, and other interface electronics were excluded. Coupling between the ³¹P and ¹H arrays were accounted for by performing simulations at either the ³¹P or ¹H frequency while the other array was resonant. The maximum specific absorption rate averaged over 10 g of tissue (SAR10g) was calculated in a multi-structure virtual family “Duke” body model (Christ et al., 2010) to establish a safe operating regime below the local limit of 10 W/kg set by the International Electrotechnical Commission (IEC document 60601-2–33 2010). To accelerate the simulation process a co-simulation framework was implemented (Kozlov and Turner, 2009) and the Duke model was truncated in a transverse plane below the lungs.

All imaging experiments were performed on a whole-body 7 Tesla scanner (MAGNETOM, Siemens Medical Solutions, Erlangen, Germany). An anatomically realistic head phantom filled with distilled water and doped with 42 mM Pi was used to characterize coil performance. In order to provide improved SNR for coil performance measurements, the phantom was prepared with roughly 10-times greater ³¹P concentration compared to that in the brain. The phantom’s electrical properties (conductivity = 0.58 S/m and relative permittivity = 80) were similar to those in the brain (Gabriel et al., 1996) and therefore provided a realistic representation of in vivo magnetic field patterns, though the phantom’s higher permittivity and lack of tissue boundaries are expected to accentuate interference patterns.

The B1⁺ field generated by the ³¹P/¹H array was measured using the method described in (Breton et al., 2010). Because the pulse sequence was not available for ³¹P B₁⁺ mapping, the measurement was performed by scaling the period of a sine curve fitted to the pixel-wise signal intensities of a series of gradient echo images that were collected with a range of imaging pulse amplitudes (parameters are listed in Table 1). For comparison, benchmark measurements were provided by a variety of commercial coils available at our Center (see Figure 4): 1) conventional single-nuclei ¹H birdcage head coil (∼27 cm diameter, “Siemens 7.0T Tim Head Coil”, Invivo Corp., Gainesville, FL), 2) state-of-the-art single-nuclei ¹H head array (“24 Channel Duyn Array”, Nova Medical, Wilmington, MA), 3) dual-tuned single-channel surface coil (∼12 cm diameter, “¹H/³¹P TxRx Loop Coil”, Quality Electrodynamics, Mayfield, OH), and 4) dual-tuned ³¹P/¹H knee birdcage (∼19 cm diameter, “³¹P/¹H Knee Coil 7T”, Rapid Biomedical, Rimpar, Germany). Knee coil measurements were performed with a cylindrical phantom (14.5 cm diameter, 42 mM Pi) due to its inability to accommodate the head phantom.

Table 1.

Pulse sequence parameters.

Description	B1+ mapping		SNR measurement		Anatomical	Metabolic Imaging	Spectroscopy
Pulse sequence	2D GRE		2D GRE		T1w MP-RAGE	FLORET*	3D CSI
Nucleus or metabolite	31P	1H	31P	1H	1H	PCr γ- ATP	31P
Acquired voxel size (mm2)	7.8×7.8	2.0×2.0	7.8×7.8	2.0×2.0	1.0×1.0	14.0×14.0	16.7×16.7
Slice thickness (mm)	50.0	5.0	50.0	5.0	1.0	14.0	16.7
TE (ms)	6.4	1.2	6.4	3.5	2.2	0.2	-
TI (ms)	-	-	-	-	1100	-	-
TR (ms)	10000	15000	10000	3500	2250	5000 2000	1500
Nominal flip angle (°)	-	-	50	10	9	75 75	35
Number of slices	1	1	1	1	176	32	16
Field-of-view (mm2)	500×500	256×256	500×500	256×256	216×256	445×445	200×200
Number of signal averages	1	1	1	1	1	6 15	10
Acquisition time (s)	632	15	632	338	486	900 900	2124

^*Other FLORET parameters were: 3 hubs at 45°, 10 interleaves per hub, ADC duration = 12 ms, and dwell time = 10 µs.

Figure 4.

Photographs of the five coils examined in this study: (a) the developed ³¹P/¹H 16-channel array, (b) ³¹P/¹H knee birdcage coil manufactured by Rapid Biomedical, (c) ¹H 24-channel Duyn array by Nova Medical, (d) ¹H head birdcage coil by Invivo Corp, and (e) ³¹P/¹H single-channel loop by Quality Electrodynamics.

To determine the receive sensitivity, signal maps were acquired with a gradient echo pulse sequence, and noise data were acquired with the same sequence and the RF pulse amplitude set to zero. Raw SNR maps were calculated from the signal and noise measurements using the optimal array combination method (Kellman and McVeigh, 2005; Roemer et al., 1990). To account for the spatially dependent B₁⁺ and finite repetition time (TR), the raw SNR maps were scaled according to $\mathit{\text{SNR}}=SN{R}_{\mathit{\text{raw}}}\frac{(1-\text{cos}\alpha )e^{-TR/T_1}}{(1-e^{-TR/T_1})\text{sin}\alpha },$ where α is the flip angle and T₁ is the predetermined relaxation time (¹H T₁ = 2.4 s and ³¹P T₁ = 5.8 s).

2.5. In vivo spectroscopy and imaging

The study was approved by our internal review board and human subjects were scanned after providing informed written consent. The efficacy of the array was investigated in vivo using several techniques. On the proton module, acquisitions were performed using a magnetization prepared rapid acquisition gradient echo (MP-RAGE) pulse sequence (Table 1). Prior to ³¹P experiments, the free induction decay signal was measured over a range of pulse amplitudes and fit to a sine curve to determine the nominal flip angle. Performance of the ³¹P module was displayed using three methods: 1) a product 3D chemical shift imaging (CSI) sequence that utilized elliptical k-space sampling. Post acquisition processing included zero-filling the free induction decay data from 1024 to 8192 points and applying a 30-Hz exponential line broadening filter. 2) Spectra were also acquired using a previously developed unlocalized progressive saturation transfer (ST) sequence (Parasoglou et al., 2014a) in order to evaluate volumetric suppression of γ-ATP using non-adiabatic saturation pulses and estimate the global CK forward exchange rate in the head (Horska and Spencer, 1997; Spencer et al., 1988). Saturation time (t_sat) was incremented by varying the number of Gaussian pulses (each 50 ms duration and 60 Hz bandwidth) irradiated at the γ-ATP frequency. Spoiler gradients (magnitude 20 mT/m and duration 5 ms) were inserted during the 7 ms delay between two consecutive pulses to destroy remaining transverse magnetization. The number of Gaussian pulses defined t_sat in each experiment (eight experiments total, t_sat min = 0, and t_sat max = 6.8s). 3) Images of single metabolites (PCr and γ-ATP) were acquired using a spectrally selective 3D non-Cartesian fermat looped, orthogonally encoded trajectories (FLORET) pulse sequence with 1.4 cm isotropic resolution (Madelin et al., 2014; Pipe et al., 2011).

3. Results

3.1. Coil Benchmark Measurements

Q measurements for a variety of single and dual-nuclei coil configurations are given in Table 2. Importantly, the Q of the ³¹P coil was practically unaffected (< 5%) by the presence of the ¹H coil in the offset and concentric dual-nuclei arrangements. Conversely, the offset ³¹P coil shielded the ¹H coil, resulting in a slightly higher unloaded Q value (likely due to reduced radiation loss) but also a 10-fold increase in loaded Q due to shielding from the sample and thus a significantly reduced Q ratio. The concentric arrangement partially restored the Q ratio of the ¹H coil, although counter-rotating currents generated in the ³¹P coil prevented optimal performance. Finally, the trap method results in loss at both frequencies.

Table 2.

Qvalues at the ³¹P and ¹H resonant frequencies for a variety of demonstrational single and dual tuned coil configurations as illustrated in Figure 1. Values are listed as Q_u:Q_L.

	31P Isolated	1H Isolated	31P/1H Offset	31P/1H Concentric	31P/1H Trap*
31P	440:34	-	447:33	418:31	346:35
1H	-	245:9	270:105	315:47	190:67

^*The ratio of the trap inductance to coil inductance was approximately 1:5.

Similar to the demonstrational results above, Q measurements on the in situ ³¹P array suggested that the ¹H array had little impact on ³¹P performance; Q_u : Q_L = 301±25 : 66±2 with the ¹H coils open-circuited and 274±10 : 62±3 with the ¹H coils resonant. For the ¹H array, the unloaded Q was higher in the presence of the 31P array but the Q ratio was lower; 139±16 : 46±4 with the ³¹P coils open-circuited and 287±11 : 202±10 with the ³¹P coils resonant. The Q ratio of the ¹H coils were reduced when the ³¹P coils were introduced due to counter-rotating (out-of-phase) currents induced in the shield-like ³¹P elements (Dabirzadeh and McDougall, 2009). Shielding had the advantage of reducing radiation loss as evidenced by the higher unloaded Q value. This, however, comes at the expense of shielding the ¹H coils’ magnetic field from the loading tissue, which reduced the Q ratio compared to an isolated ¹H coil.

The S-parameter and noise correlation matrices are summarized in Table 3. The ³¹P DBC elements were well matched to 50Ω (≤ −16 dB), while decoupling was marginally adequate (< −9 dB) between both nearest and next-nearest neighbors. Coupling between ¹H coils was easily controlled (< −18 dB) due in part to the shielding effect of the ³¹P elements. Noise correlation values for both ³¹P and ¹H modules were in the expected range (Roemer et al., 1990), suggesting that common mode currents on the coaxial cables were suppressed and preamplifier feedback loops were absent.

Table 3.

Scattering (S) and noise correlation measurements for the developed array. The measurements were performed while the array was loaded with a tissue equivalent gel phantom. Values are listed as mean ± standard deviation with the worst case or maximum value in parentheses.

	S (dB)	Noise correlation
	31P Channel
Diagonal elements	−17.2 ± 2.5 (−16.0)	1
Adjacent neighbors	−12.3 ±6.9 (−9.7)	0.18 ±0.11 (0.39)
Next nearest neighbors	−12.9 ±9.1 (−9.1)	0.09± 0.10 (0.29)
Distant neighbors	−18.0 ±4.1 (−13.6)	0.16 ±0.08 (0.30)
	1H Channel
Diagonal elements	−20.3 ±3.2 (−16.3)	1
Adjacent neighbors	−21.6 ±2.3 (−18.8)	0.06 ±0.05 (0.14)
Next nearest neighbors	−25.7 ±7.6 (−20.2)	0.05 ±0.10 (0.29)
Distant neighbors	−33.3 ±6.0 (−22.3)	0.07 ±0.05 (0.16)

Loss through the receive paths between the coil ports to preamplifier inputs (including coaxial cables, cable traps and transmit/receive switch) were less than 0.55 dB on the ³¹P channels and 0.75 dB on the ¹H channels. Loss through the transmit paths including the power dividers, transmit/receive switches, cable traps, and coaxial cables was approximately 10.0 dB on the ³¹P channels and 10.4 dB on the ¹H channels (compared to 9 dB for an ideal system with eight-way power division). Preamplifier protection in transmit mode was greater than 35 dB on both ³¹P and ¹H channels. For 1 W input power the calculated maximum SAR_10g in the Duke head model was 0.47 W/kg for the ³¹P array and 0.37 W/kg for the ¹H array. In practice, the transmit power was restricted according to the simulated values with a two-fold safety buffer below the 10 W/kg limit set by the IEC.

3.2. Phantom Measurements

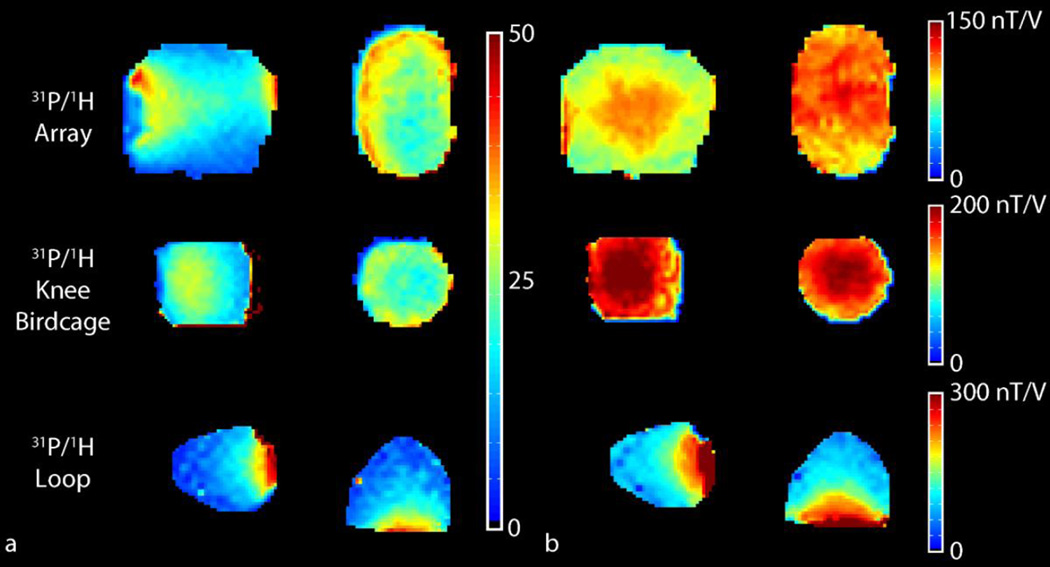
B₁⁺ and SNR maps measured in the 42 mM Pi phantom using the ³¹P modules of the developed array and single channel reference coil are shown in Figure 5 and are summarized in Table 4. The central and peripheral SNR provided by the ³¹P/¹H head array was 22 and 42, respectively. Owing to its smaller diameter and volume receive configuration, the ³¹P/¹H knee birdcage provided higher central SNR (29) but did not provide an advantage in the periphery. In comparison, the central and peripheral SNR for the ³¹P/¹H loop coil was 12 and 63, respectively. Central transmit efficiency for the developed ³¹P/¹H head array and ³¹P/¹H knee birdcage were 123.1 and 215.6 nT/V, respectively. The developed array provided better than 80% transmit uniformity in the masked regions in Figure 5b (defined as 1 minus the standard deviation divided by the mean B₁⁺).

Figure 5.

³¹P SNR (a) and B₁⁺ maps (b) in the 42mM Pi head and knee phantoms in the central sagittal (left column) and transverse planes (right column) for the developed array (top row) and two commercially available coils. B₁⁺ maps were smoothed using a two dimensional median filter with a 3×3 kernel. The results are summarized in Table 4. The maps were masked to remove regions with low SNR or B₁⁺.

Table 4.

Summary of B₁⁺ and SNR measurements in the 42 mM Pi head phantom.

							SNR
	Center (nT/V)		B1+ Sagittal uniformity		Transverse uniformity		Center		Maximum
Nucleus	31P	1H	31P	1H	31P	1H	31P	1H (×103)	31P	1H (× 103)
31P/1H Array	123.1	65.5	0.81	0.48	0.87	0.64	22	4.2	42	9.5
31P/1H Knee
Birdcage	215.6	144.6	0.90	0.51	0.86	0.50	29	5.1	29	5.3
31P/1H Loop	72.6	40.4	-	-	-	-	12	2.6	63	13.4
1H 24-ch Duyn									-	18.5
Array	-	89.6	-	0.66	-	0.68	-	6.9
1H Head Birdcage	-	93.1	-	0.72	-	0.59	-	3.8	-	3.8

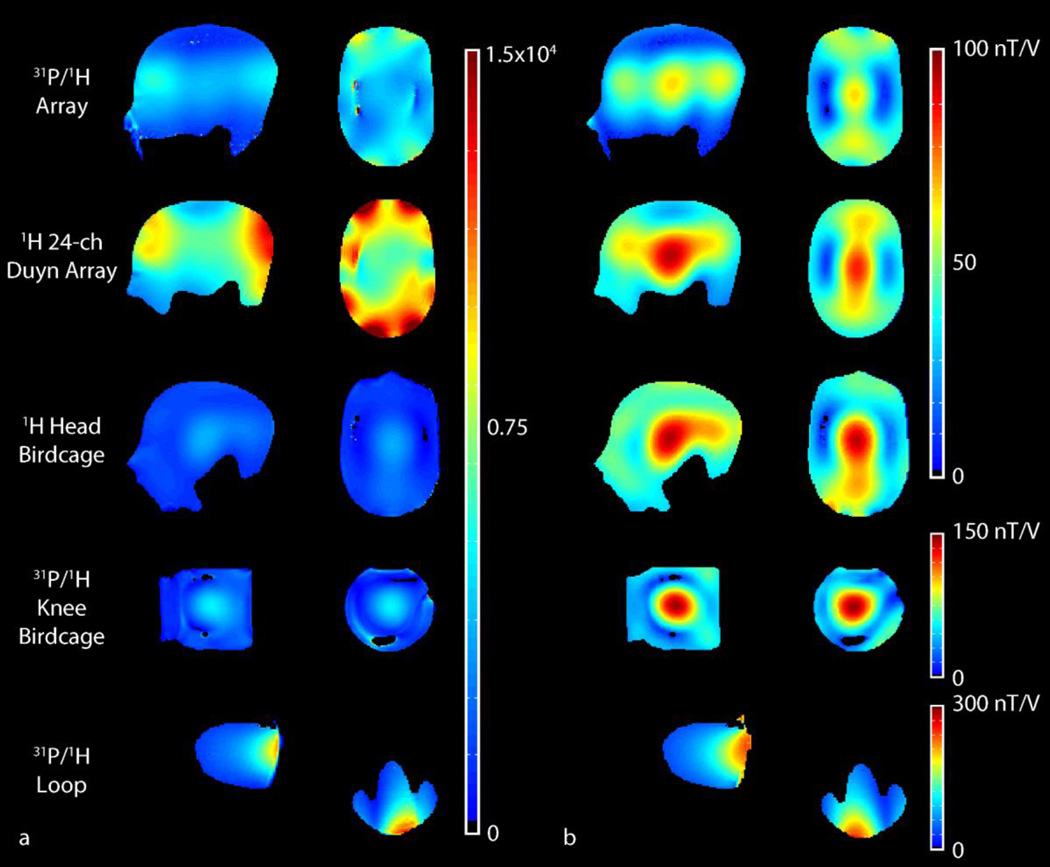
The transmit efficiency and SNR of the ¹H module of the developed array was 65.5 nT/V and 4.2×10³ in the center of the phantom, respectively (Figure 6). Out-of-phase currents generated in the shield-like ³¹P array likely contributed to a reduction in ¹H transmit efficiency compared to the single-nuclei 24-channel Duyn array, which delivered 89.6 nT/V and a central SNR of 6.9×10³. Nonetheless, the developed array achieved superior ¹H SNR in both the center and periphery compared to the conventional ¹H head birdcage.

Figure 6.

¹H SNR (a) and B₁⁺ maps (b) in the 42mM Pi head and knee phantoms in the central sagittal (left column) and transverse planes (right column) for the developed array (top row) and four commercially available coils. The results are summarized in Table 4. The maps were masked to remove regions with low SNR or B₁⁺.

3.3. In Vivo Measurements

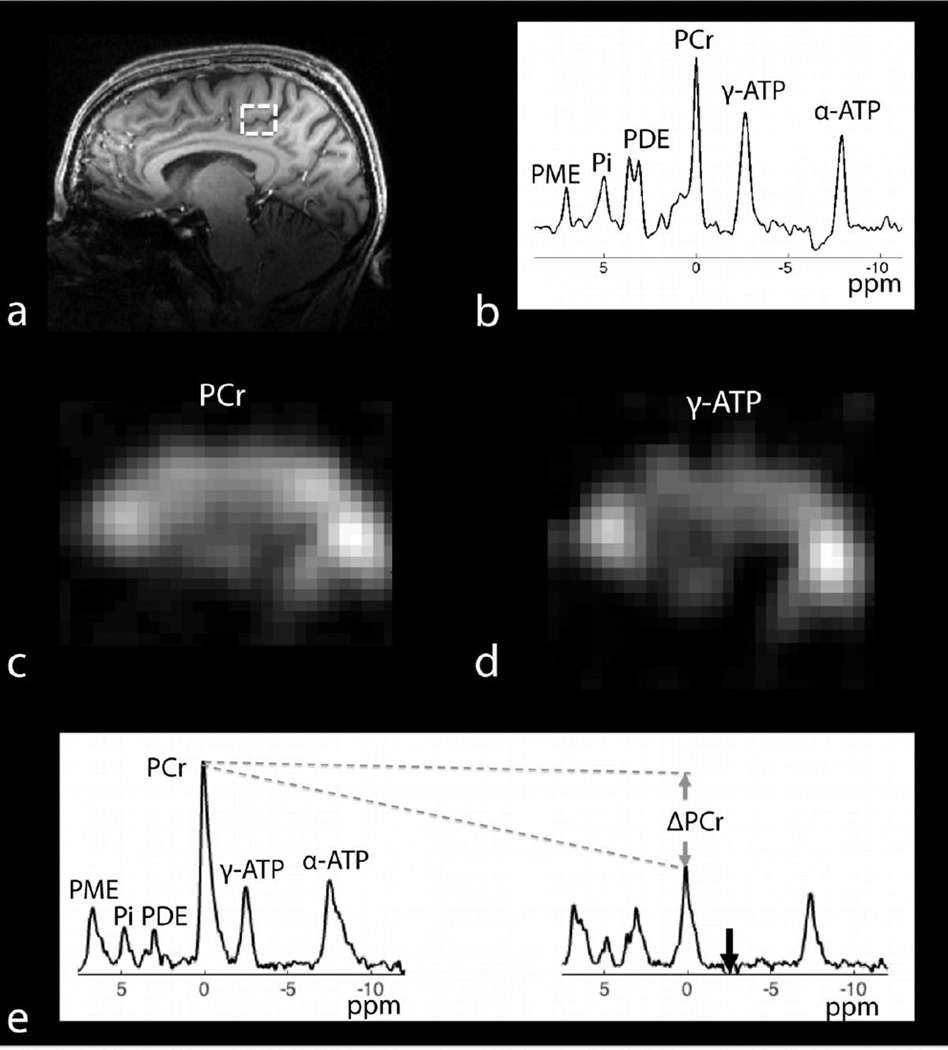
³¹P spectra acquired with a product 3D–CSI sequence and isotropic resolution of 16.7 mm is shown in Figure 7b. The SNR of PCr across all voxels was 30.5 ± 7.5 (mean ± standard deviation). Ratios of PCr to γ-ATP after correcting for T₁ relaxation (Lei et al., 2003b) ranged from 1.4 ± 0.1 in central regions of the brain to approximately 5 in voxels with muscle tissue. Intracellular pH was estimated to be 7.0 ± 0.1 using the chemical shift of Pi (Petroff et al., 1985). Spectroscopic images of PCr and γ-ATP derived from the 3D–CSI dataset are shown in Figure 7c,d.

Figure 7.

³¹P/¹H data set: a) anatomical ¹H MP-RAGE in the sagittal plane, b) typical ³¹P-CSI spectrum from a 4.66 mL voxel whose location is outlined in (a), spectroscopic images of (c) PCr and (d) γ-ATP in the sagittal plane derived from the 3D–CSI data, e) global ³¹P spectra (4-averages, TR = 12 s) acquired in the absence (t_sat = 0, left) and presence (t_sat = 6.8 s, right) of γ-ATP saturation. Complete saturation of γ-ATP is observed despite the use of non-adiabatic saturation pulses. Eight spectra were acquired by varying t_sat in order to estimate the global CK forward reaction rate.

Global ³¹P spectra acquired in the absence (t_sat = 0 s) and presence (t_sat = 6.8 s) of saturation of γ-ATP are shown in Figure 7e. Complete saturation of γ-ATP is observed despite the use of non-adiabatic saturation pulses. By acquiring a series of spectra at different t_sat the global pseudo first-order forward rate constant of the CK reaction was estimated to be 0.22 s-1 by fitting the PCr signal to a Bloch equation modified to account for chemical exchange in a two-pool PCr and γ-ATP system (Horska and Spencer, 1997).

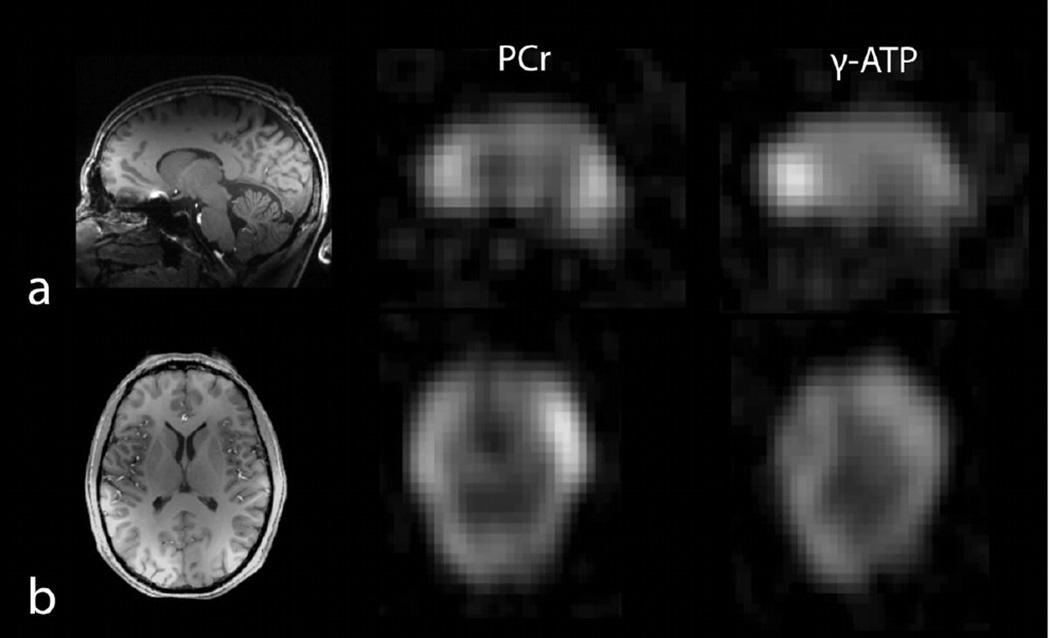
Single metabolite images acquired using a spectrally selective 3D–FLORET sequence are shown in Figure 8. The pseudo-SNR of the PCr image was 20.1 ± 4.5, which was calculated as the mean signal divided by the standard deviation of the noise background. The ratio of PCr-to-γ-ATP was 1.5 ± 0.1, which was in good agreement with that derived from the CSI measurement.

Figure 8.

¹H MP-RAGE and single metabolite ³¹P images (2.74 mL voxel, 15 min acquisition per metabolite) using a spectrally selective 3D–non uniform FLORET sequence: a) sagittal ¹H MP-RAGE (left) and coregistered images of PCr (middle), and γ-ATP (right). b) axial ¹H MP-RAGE and co-registered PCr and γ-ATP images.

¹H MP-RAGE images acquired with the developed array enable straightforward co-registration with ³¹P data. The sagittal image in Figure 7a shows excellent grey/white matter contrast in the frontal, parietal, and occipital lobes, while the transverse image in Figure 8b illustrates good coverage and uniformity.

4. Discussion and Conclusion

In this work we have demonstrated that a ³¹P transmit/receive DBC structure paired with a “nested” 8-channel 1H array can provide high quality ³¹P and ¹H spectroscopy and imaging data with volumetric coverage at 7 Tesla. This new coil design was combined with efficient pulse sequences, such as FLORET, to demonstrate mapping of important ³¹P containing metabolites in the brain at relatively high spatial resolution. We were able to map PCr and γ-ΑTP at 1.4 cm isotropic nominal voxel size. The point spread function of the sampling scheme was estimated to be 1.6 voxels, resulting in an actual resolution of 2.3 cm. To the best of our knowledge, such resolution has only been reported previously at 9.4 Tesla using a mono-tuned volume coil (Lu et al., 2013).

In several previous brain studies, exchange rates and metabolic fluxes of important reactions such as CK and ATPase have been mapped using surface coils that have limited coverage and require power-demanding adiabatic preparation pulses (Lei et al., 2003a). Zhu et al. (Zhu et al., 2012), were the first to acquire high-resolution metabolic fluxes using a ³¹P-MT approach, which employed 3D–CSI and a dual-tuned volume coil. The ³¹P DBC coil described here provided whole-brain coverage that was combined with a spectrally selective pulse sequence to study the CK reaction in a manner similar to that described previously by our group in the skeletal muscle (Parasoglou et al., 2013a, b; Parasoglou et al., 2014b). Despite the use of non-adiabatic saturation pulses, γ -ATP was completely saturated (Figure 7) throughout the head due to the relatively homogenous B₁⁺ generated by the DBC.

The essential goal of the developed coil was to enable ³¹P MR imaging and spectroscopy of the brain with good resolution in a reasonable acquisition time. The first stage of the design utilized a ³¹P transmit/receive DBC to satisfy several requirements. In receive mode, the DBC was configured as an eight-channel phased array to provide full coverage and SNR advantages over a surface or volume coil. In transmit mode, a fixed RF shim was applied to the DBC to produce a circularly polarized field similar to that of a standard birdcage. Combining the transmit and receive functionalities eliminated a separate transmit structure, as well as lossy components such as fuses and detuning circuits that are required in receive-only coils. For example, popular fuses rated from 315 to 800 mA have resistances of about 0.2 to 1.6 Ω at 120 MHz (395 series; Littelfuse; Chicago, IL). However, we point out that advantages associated with the transceive configuration are tempered by losses associated with transmit/receive switches and distant preamplifiers (∼0.55 dB loss on the ³¹P receive path). Further, while preamplifier decoupling was utilized to counteract residual coupling between ³¹P DBC segments in receive mode, coupling likely reduced DBC transmit efficiency compared to a standard birdcage.

Another challenge in dual-nuclei coil design is to provide ¹H imaging capability. Of course, an ideal dual-nuclei coil matches the performance on both the low and high frequency modules to that of two independent single-nuclei coils. The co-planar design utilized in this work, where ¹H coils are nested within ³¹P elements, provided improved ¹H SNR over a traditional birdcage coil without sacrificing ³¹P performance. The ¹H module provided adequate SNR for 1 mm isotropic MP-RAGE imaging while its B₀ shimming capability preserved the excellent spectral resolution available at 7 Tesla as evident in the dual-peak PDE spectra (Figure 8). Going forward, advanced B₀ correction techniques are expected to be useful for ³¹P quantification at ultra-high fields (Mirkes et al., 2014).

Furthermore, although a multi-channel array substantially improves SNR over a volume coil, its spatially varying B₁− field (and to a lesser extent B₁⁺) can make 3¹P quantification less straightforward. Because of the low SNR associated with 3¹P applications, subject-specific B1 maps are generally not a viable option and may not be necessary given the relatively small variation of head sizes compared to the wavelength associated with the ³¹P operating frequency at 7 Tesla. An alternative that overcomes this complexity in vivo is to assume a constant γ-ATP level, which allows PCr quantification by calculating the ratio of the two metabolites. However, it is unknown if γ-ATP is constant in certain pathological states. The phantom replacement method may also be pursued (Atkinson et al., 2011; Jansen et al., 2006), in which pre-scans are performed on a variety of phantoms in order to relate the spatially dependent signal intensity to concentration.

We point out that the ³¹P DBC structure was implemented with eight channels on a cylindrical former, whereas substantial sensitivity gains have been previously demonstrated with 32 and 96 channel ¹H head arrays at 3 Tesla using tight-fitting domed structures (de Zwart et al., 2002; de Zwart et al., 2004; Wiggins et al., 2009; Wiggins et al., 2006) (which can be expected to perform similar to 7 Tesla ³¹P arrays due to their comparable operating frequencies). These designs are appealing for future implementation, although an irregular domed coil structure in a dual-nuclei array may necessitate the abandonment of the DBC transceive arrangement, as it would be difficult to find azimuthal symmetries that are preferred for its operation.

On the ¹H module, the nested approach gave rise to counter-rotating ¹H currents on the ³¹P element While this shielding reduced radiation loss, it also contributed to reduced transmit efficiency (about 70% that of the 1H Duyn array and standard 1H head birdcage). A potential improvement could include ¹H current “blocking” trap circuits in the ³¹P DBC, an approach that has been shown to reduce counter-rotating currents with minimal loss of performance on the x-nuclei channel (Dabirzadeh and McDougall, 2009; Klomp et al., 2006). (Note that blocking traps serve a different function than the “intermediate” trap circuits introduced to provide dual-resonance on a single coil element (Schnall et al., 1985).) Additionally, the elements’ tapered geometry combined with the shielding effect of the ³¹P elements led to compromised coverage in the head/foot direction. This was evident in sagittal views of the B1⁺, SNR, and MP-RAGE acquisitions, in which either inferior regions such as the cerebellum or superior regions such as the central sulcus were difficult to visualize depending on subject positioning (Figure 7 and Figure 8). Coverage is a common problem for coils operating at high frequency due to the conflicting desires to reduce parasitic and radiation loss. Alternative solutions include dual-row coils (Kozlov and Turner, 2011; Shajan et al., 2013) and half-wavelength electric dipoles (Raaijmakers et al., 2011; Shajan et al., 2015; Wiggins et al., 2012), both of which could conceivably provide extended coverage in a dual-nuclei array.

³¹P-MR has provided evidence of underlying energy metabolism impairment in several neurodegenerative conditions, such as Alzheimer’s (Brown et al., 1989) and Parkinson’s (Hoang et al., 1998) diseases, as well as mental disorders such as schizophrenia (Smesny et al., 2007). Relatively high-resolution ³¹P-MR with complete brain coverage can be achieved with an efficient multi-channel coil array, time-efficient pulse sequences, and the enhanced signal strength at ultra-high fields. This combination of hardware and software improvements will allow simultaneous assessment of a variety of brain regions and could provide new insights into the patterns of disease progression.

Highlights.

• A degenerate birdcage array provided high SNR and a uniform B₁⁺ field for ³¹P MRI.

• Single metabolite imaging was demonstrated with a 3D non-Cartesian acquisition.

• γ-ATP was saturated with non-adiabatic pulses to estimate the CK forward reaction rate.

• A nested ¹H array enabled straightforward image co-registration.