Abstract
By modeling axons as thin cylinders, it is shown that the inverse Funk transform of the diffusion MRI (dMRI) signal intensity obtained on a spherical shell in q-space gives an estimate for a fiber orientation density function (fODF), where the accuracy improves with increasing b-value provided the signal-to-noise ratio is sufficient. The method is similar to q-ball imaging, except that the Funk transform of q-ball imaging is replaced by its inverse. We call this new approach fiber ball imaging. The fiber ball method is demonstrated for healthy human brain, and fODF estimates are compared to diffusion orientation distribution function (dODF) approximations obtained with q-ball imaging. The fODFs are seen to have sharper features than the dODFs, reflecting an enhancement of the higher degree angular frequencies. The inverse Funk transform of the dMRI signal intensity data provides a simple and direct method of estimating a fODF. In addition, fiber ball imaging leads to an estimate for the ratio of the fraction of MRI visible water confined to the intra-axonal space divided by the square root of the intra-axonal diffusivity. This technique may be useful for white matter fiber tractography, as well as other types of microstructural modeling of brain tissue.
Keywords: fiber orientation density function, Funk transform, q-ball imaging, high-angular-resolution diffusion imaging, brain, diffusion MRI
Introduction
For strong diffusion weightings (i.e., high b-values), the angular dependence of the diffusion MRI (dMRI) signal intensity in white matter is sensitive to the complex geometries associated with intersecting axonal fiber bundles (Tuch et al., 2002). High-angular-resolution diffusion imaging (HARDI) methods exploit this property to estimate either a diffusion orientation distribution function (dODF) or a fiber orientation density (or distribution) function (fODF) that can be used, for example, as the basis for white matter fiber tractography (Lazar, 2010; Tournier et al., 2011). Q-ball imaging is a particularly elegant HARDI method in which a dODF is derived by taking a Funk transform of the dMRI signal intensity on a spherical shell in q-space (Descoteaux et al., 2007; Hess et al., 2006; Tuch, 2004; Tuch et al., 2003). The Funk transform (Bailey et al., 2003) is a straightforward linear operation that avoids the need for detailed modeling of the microstructure or for nonlinear numerical fitting procedures.
In this paper, we show that the inverse Funk transform of the dMRI signal provides an estimate of a fODF. The difference between a dODF and a fODF is that a dODF reflects the angular dependence of the water diffusion dynamics, while a fODF is meant to describe the angular dependence of the axonal fiber bundles. Typically, fODFs are based on a detailed tissue model for white matter microstructure, with the modeling parameters being determined by fitting to dMRI data (Anderson, 2005; Tournier et al., 2004, 2007). Such approaches have been highly successful (Wilkins et al., 2015), although the necessary calculations can be challenging (Parker et al., 2013). The fiber ball method described here may offer advantages in terms of simplicity and in being based on relatively mild assumptions.
The physical picture underlying fiber ball imaging is that the MRI visible water in white matter can be divided into two non-exchanging pools, one corresponding to water inside the axons and one to water outside the axons. This idealization has been widely used with dMRI for tissue modeling (Assaf et al., 2004; Fieremans et al., 2011; Jespersen et al., 2007; Panagiotaki et al., 2009, 2012; Zhang et al., 2012) and is supported by q-space imaging experiments (Assaf and Cohen, 2000). The extra-axonal water is assumed to be relatively mobile so that the dMRI signal from this pool decreases exponentially with increasing b-value. However, the signal from the intra-axonal water pool has a slower drop-off due to its diffusion being strongly restricted by the axon cell membranes. For this reason, the intra-axonal water becomes the dominant source of signal for large b-values, which enables properties of the intra-axonal space to be more easily calculated.
The primary purpose of this article is to describe the theory for fiber ball imaging and to contrast it with the closely related q-ball imaging method. In particular, we derive the inverse Funk transform relationship between the fODF and the dMRI signal intensity in the large b-value limit. We also consider a correction method that may improve the accuracy of the fODF for finite b-values. Finally, we present preliminary results for human brain obtained at 3T with a bvalue of 4000 s/mm2.
Theory
Assumptions
Fiber ball imaging is based on several general assumptions about water diffusion and white matter microstructure. These are very similar to ones that have been used in prior studies and are commonly considered to be plausible idealizations, although definitive validation has so far not been fully achieved. Our key assumptions are:
The water that contributes substantially to the dMRI signal can be divided into two pools, corresponding to intra-axonal and extra-axonal water. This excludes the water within myelin, which makes a relatively small contribution to the signal because of its short T2 relaxation time (Stanisz et al., 1999).
The exchange time between the two water pools is large in comparison to the diffusion time of the dMRI sequence so that water exchange can be neglected. Water exchange times in white matter have been measured to be about 1 s (Nilsson et al., 2013) which is indeed long compared to the typical dMRI diffusion times. This assumption substantially simplifies the diffusion dynamics (Fieremans et al., 2010).
The diffusivities of the extra-axonal water compartments exceed some minimum value, De,min, for all diffusion directions. This is what we mean by the extra-axonal water being relatively mobile.
The axons can be regarded as thin, straight cylinders. This requires that the q-vector be sufficiently small so that the dMRI signal is not sensitive to the internal geometry of the axons. More specifically, we must have qa << 1, where q is the magnitude of the q-vector and a is a typical axon radius. In terms of the b-value, this condition can be written as ba2 << Δ, where b is the b-value and Δ is the diffusion time. For a diffusion time of 50 ms and an axon radius of 2 µm (Aboitiz et al., 1992), this gives the condition b << 12,500 s/mm2. In addition, the radius of curvature of the axons should be less than the typical diffusion length along the axis of the cylinders so that the straight cylinder approximation is justified. If the radius of curvature is rc and the intrinsic intra-axonal diffusivity is Da, this means that ; for Δ = 50 ms and Da = 1.0 µm2/ms (Fieremans et al., 2011), one then has 10µm << rc.
The b-value is sufficiently large so that bDe,min >> 1. When this is true, the contribution of the extra-axonal water to the dMRI signal can be neglected due to its exponential decrease with increasing b-value. The prior study of Fieremans and coworkers (Fieremans et al., 2011) found that the extra-axonal diffusivity was typically greater than 0.5 µm2/ms, which suggests that we need b >> 2000 s/mm2.
All the axons within any given voxel have the same intrinsic intra-axonal diffusivity, Da, although this may vary between voxels, and bDa >> 1. This assumption also sets a lower limit on the required b-value, which will depend on Da. For Da = 1.0 µm2/ms, we must then have b >> 1000 s/mm2.
Inverse Funk Transform Expression for fODF
With the above assumptions, the dMRI signal intensity in white matter takes the form
| (1) |
where S0 is the signal without diffusion weighting, n is the diffusion-encoding direction (with |n| =1), δ is the Dirac delta function, and f is the fODF. The fODF is assumed to be independent of the magnitude of u and is normalized so that
| (2) |
where fa is the fraction of dMRI visible water for the axonal compartment. Without loss of generality, we can also assume, the reflection symmetry property
| (3) |
This follows from the fact that our postulated cylindrical geometry for the axons is invariant with respect to a point reflection through the origin.
The Dirac delta function has the representation
| (4) |
This allows us to write
| (5) |
in the limit that bDa >>1 which holds according to Assumption 6. The integral in Eq. (5) is precisely the Funk transform of the fODF (Tuch, 2004). Thus we have
| (6) |
with TF indicating the Funk transform. Note that the signal decreases as , which is much slower than the exponential decrease assumed for the extra-axonal water pool.
The signal calculated from Eq. (6) is automatically invariant under the reflection symmetry S(n)= S(−n), which is indeed a generic property of the dMRI signal for an ideal experiment (e.g., if background gradients are negligible). Since the Funk transform is invertible for functions with reflection symmetry (Bailey et al., 2003), the fODF can be estimated by using the formula
| (7) |
where signifies the inverse Funk transform.
The Funk transform and its inverse are most conveniently calculated by using spherical harmonic representations for S and f. This is because the spherical harmonics, , are the eigenfunctions of the Funk transform (Descoteaux et al., 2007; Hess et al., 2006). Specifically,
| (8) |
where (θ,ϕ) are the spherical angles for n and Pl is the Legendre polynomial. This result allows Eq. (7) to be recast as
| (9) |
Here the parameters are the spherical harmonic expansion coefficients for S / S0 so that
| (10) |
Because of reflection symmetry for S, the coefficients vanish whenever the degree l is an odd integer, and the sum in Eq. (9) is therefore only taken over even degrees of . The result of Eq. (9) is the key expression that can be used in practice to calculate the fiber ball approximation for the fODF.
It is of interest to contrast Eq. (9) with the Funk transform of the dMRI signal utilized in q-ball imaging to approximate the dODF (Descoteaux et al., 2007; Hess et al., 2006; Tuch, 2004; Tuch et al., 2003). From Eqs. (8) and (10), this is seen to be
| (11) |
where ψ represents the dODF. If we neglect the overall scaling, the spherical expansion coefficients for the fODF differ from those of dODF by factors of [P2l (0)]−2. Since
| (12) |
the fODF has a greater relative weight for higher degree harmonics than does the dODF, which thereby leads to sharper angular profiles. The asymptotic limit in Eq. (12) follows directly from Sterling’s formula for factorials (Abramowitz & Stegun, 1972).
From Eqs. (2) and (9), one sees that the total water fraction for the intra-axonal space is given by
| (13) |
where q0 is the q-vector magnitude corresponding to b. In deriving Eq. (13), we have used the facts that P0(0) = 1 and that . From Eq. (13), one also has
| (14) |
Hence the quantity ζ can be obtained from the lowest degree harmonic of the dMRI signal. Moreover, if an estimate for fa is available, then Da can be calculated from ζ. These results may be useful in constraining models of white matter microstructure.
Corrections for Finite b-values
The accuracy of Eq. (9) depends on bDa being large. To better understand the deviations from Eq. (9) that occur for finite b-values, we consider the spherical harmonic expansion of Eq. (1). To do this, we first introduce spherical harmonic coefficients, , for the fODF so that
| (15) |
The result of Eq. (9) can then be expressed as
| (16) |
A direct calculation of the spherical harmonic expansion for the signal of Eq. (1) yields
| (17) |
where
| (18) |
with 1F1 indicating the confluent hypergeometric function of the first kind and Γ indicating the gamma function. There are close connections between Eq. (17) and prior work of Özarslan and coworkers (Özarslan et al., 2006) and of Jespersen and coworkers (Jespersen et al., 2007), as suggested by the appearance in these studies of the same confluent hypergeometric function as occurs here in the definition of g2l.
For large values of bDa, we have the approximation
| (19) |
so that g2l approaches one as bDa is increased and Eq. (17) becomes equivalent to Eq. (16) in the limit bDa → ∞. Notice that g2l decreases rapidly with increasing l, which implies that the accuracy of Eq. (16) is highest for the low degree harmonics. For the special case of l = 0, we have
| (20) |
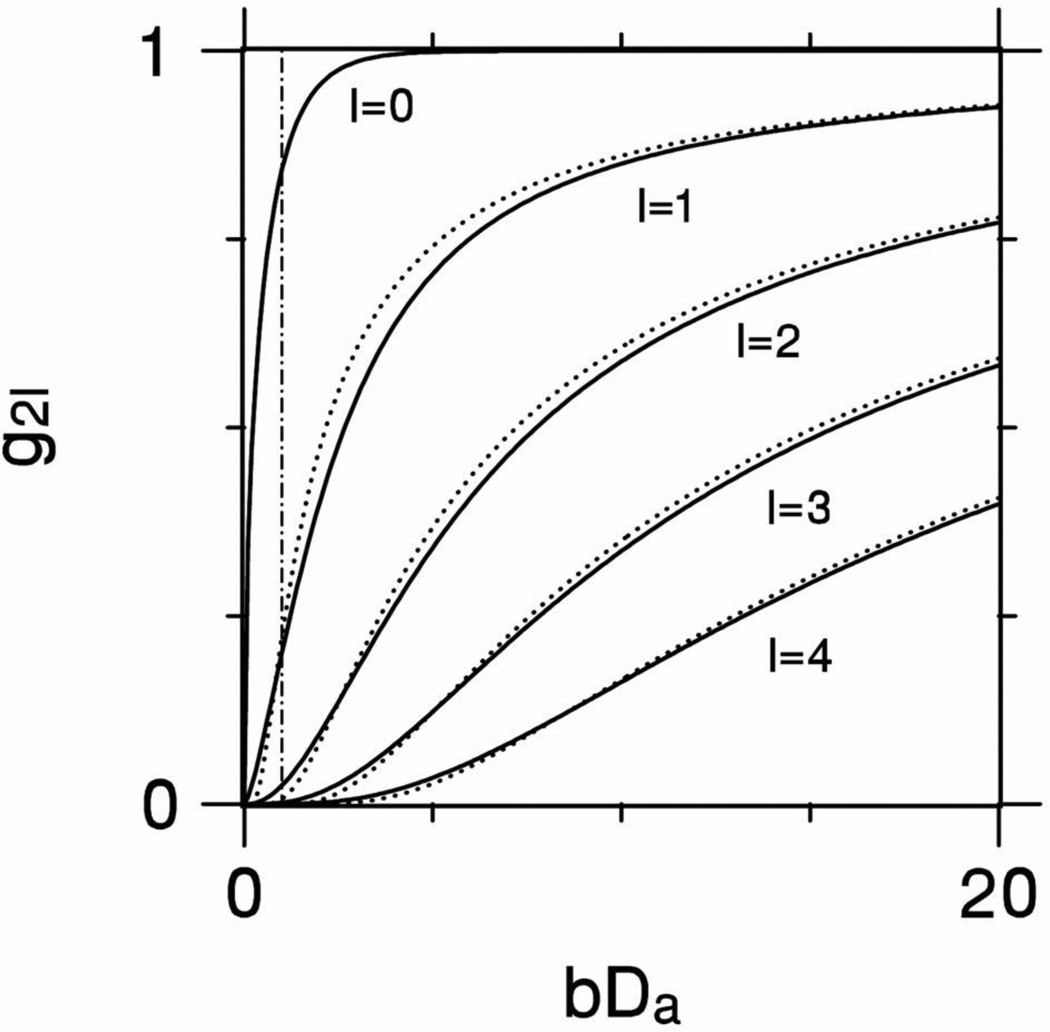
where erf represents the error function. Plots of g2l(bDa) for l = 0, 1, 2, 3 and 4 are shown in Fig. 1 together with the approximation of Eq. (19). This approximation is reasonably accurate for bDa ≥ 1, with maximum absolute errors of 0.157, 0.073, 0.028, 0.014, and 0.008 for l = 0, 1, 2, 3 and 4, respectively. The derivations of Eqs. (17), (19), and (20) are discussed in Appendix A.
Figure 1.
The function g2l(bDa) defined by Eq. (18). The solid lines show the exact results for l = 0, 1, 2, 3, and 4, while the dotted lines show approximations derived from Eq. (19). For large bDa, g2l approaches unity, but the drop off as bDa is reduced is more rapid as l is increased. The approximation of Eq. (19) is quite accurate for bDa ≥ 1. For l = 0, this approximation is simply g0 = 1 and so coincides with the top of the plotting frame. The broken vertical line shows bDa =1.
We can use Eq. (17) to calculate the fODF harmonic coefficients as
| (21) |
which may improve the accuracy of the fODF estimation relative to Eq. (16). However, this requires an a priori value for Da and could be problematic for the higher degree harmonics as g2l(bDa) becomes small for large l, leading to an amplification of noise effects in the fODF, as discussed further in Appendix B. Nonetheless, conservative, partial correction factors can be obtained by noting that Da should not exceed the diffusivity of free water, D0, which is about 3.0 µm2/ms at 37 °C (Holz et al., 2000). Since g2l(bDa) is a monotonically increasing function, we then have
| (22) |
Thus the approximation
| (23) |
can improve upon Eq. (16) without exceeding the true value of . For a b-value of 4000 s/mm2, bD0 is about 12. This gives g2l(bD0) equal to 1.000, 0.875, 0.644, 0.403, and 0.217 for l = 0, 1, 2, 3 and 4, respectively. The intra-axonal diffusivity Da still enters into Eq. (23), but only as an overall scaling that does not affect the angular dependence of the fODF.
If HARDI data were obtained for two or more b-value shells, it may be possible to estimate Da by fitting Eq. (17) to this data. One could then determine improved correction factors for the fODF harmonic coefficients by calculating g2l(bDa) rather than g2l(bD0).
Methods
Numerical Simulations
In order to illustrate the fiber ball approximations given by Eqs. (9) and (23) for the fODF, numerical calculations of four different examples were performed. In each case, a set of nonzero spherical harmonic coefficients were selected, and the exact fODF was calculated from Eq. (15). The spherical harmonic coefficients for the dMRI signal were then obtained from Eq. (17) with bDa = 5. The fiber ball profiles were found from the inverse Funk transform of Eq. (9), while the corrected fiber ball profiles were calculated from Eqs. (23) and (15) with bD0 = 12. As references for comparison, the corresponding q-balls were also calculated by using the Funk transform of Eq. (11).
For the first example, the only nonzero spherical harmonic coefficients for the fODF were chosen to be and , which models a single fiber bundle with fanning of the axon directions. The second example had nonzero fODF harmonic coefficients of and , which models an intersection of two fiber bundles, where the crossing angle is 90° between the directions of the fODF peaks. For the third example, the selected harmonic coefficients were , and , corresponding to a fiber crossing angle of about 67°. The final example had , and , which models a triple fiber crossing with angles of 82.4° and 48.8°. As with the first example, the fiber bundles for the three examples with crossings all had some degree of angular dispersion.
Data Acquisition
To demonstrate fiber ball imaging, HARDI data were acquired for one healthy volunteer on a Siemens 3T TIM Trio MRI scanner (Siemens Healthcare, Erlangen, Germany) using a 32 channel head coil in adaptive combine mode, 256 diffusion-encoding directions, a b-value of 4000 s/mm2, and 45 contiguous axial slices under a protocol approved by the institutional review board of the Medical University of South Carolina. A twice-refocused diffusion-weighted sequence was used to minimize eddy current distortion (Reese et. al, 2003). The slice thickness was 2.7 mm, the field of view was 222×222 mm2, and the acquisition matrix was 82×82, yielding an in-plane resolution of 2.7×2.7 mm2. The echo time was TE = 131 ms, and the repetition time was TR = 7500 ms. Other imaging parameters were bandwidth = 1356 Hz/px, echo spacing = 0.82 ms, and parallel imaging factor = 2. A single image with the same parameters, but without diffusion weighting was also acquired to estimate S0. The total scan time was 32 min and 32 s.
To aid in the analysis of the fiber ball results, standard diffusional kurtosis imaging (DKI) data were also acquired in the same scan session (Jensen and Helpern, 2010). The image acquisition parameters were the same as for the HARDI dataset, except the number of diffusion-encoding directions was 64, the nonzero b-values were 1000 and 2000 s/mm2, the echo time was TE = 102 ms, the repetition time was TR = 6100 ms, and 20 additional images without diffusion weighting were acquired. The total scan time for the DKI acquisition was 15 min 43 s.
Finally, for qualitative anatomical reference, magnetization-prepared rapid gradient echo (MPRAGE) images were acquired with 192 sagittal slices, TE = 2.26 ms, TR = 1900 ms, and an inversion time of TI = 900 ms. The slice thickness was 1.0 mm, the field of view was 256×256 mm2, the in-plane resolution was 1.0×1.0 mm2, and the total scan time was 4 min 26 s.
Image Analysis
The HARDI and DKI images were co-registered by using Statistical Parametric Mapping software (ver. SPM12, Wellcome Trust Center for Neuroimaging, London, UK), with the images without diffusion weighting being chosen as references. Following co-registration, all images were smoothed with a Gaussian kernel of 1.25 times the voxel dimensions in order to reduce the effects of signal noise and Gibbs ringing (Tabesh et al., 2011).
From the HARDI images, the spherical harmonic coefficients of the signal within each voxel were calculated using a linear least squares formulation (Descoteaux et al., 2007; Hess et al., 2006). Only harmonics of degree 6 or less were used for the analysis, since the higher degree harmonics were typically smaller in magnitude and thus more susceptible to noise effects. Fiber balls were then calculated, up to an overall scaling factor, by applying the inverse Funk transform according to Eq. (9). In addition, corrected fiber balls were obtained by using Eqs. (15) and (23) with bD0 = 12, and q-balls were estimated from the Funk transform of Eq. (11). Maps of ζ were determined from Eq. (14).
The DKI data were post-processed with Diffusional Kurtosis Estimator (DKE) (http://www.nitrc.org/projects/dke/, Center for Biomedical Imaging, Medical University of South Carolina) to obtain standard diffusion metrics maps (Tabesh et al., 2011), including the mean diffusivity (MD), the fractional anisotropy (FA), and the mean kurtosis (MK). Voxels with MD > 1.5 µm2/ms were excluded from all region of interest (ROI) analyses, as these voxels were regarded as having a substantial amount of cerebrospinal fluid. Two ROIs were considered: 1) whole brain, which included both gray and white matter, and 2) white matter, defined as MK > 1 and FA > 0.15. The basis of these conditions for defining white matter is discussed by Yang and coworkers (Yang et al., 2013).
The signal-to-noise ratio (SNR) in white matter for the diffusion-weighted images was estimated to be 6.3. The signal noise was determined by fitting the signal in two ROIs of similar size to a Rician distribution, with one ROI being chosen in the background and one within the ventricles, where negligible tissue signal is expected. Two ROIs were selected since noise can be spatially varying for parallel acquisitions. A mean noise level was then obtained by averaging the noise for the ROIs. The white matter signal was obtained by averaging over all white matter voxels and diffusion-encoding directions, and the SNR was calculated by dividing this mean signal by the mean noise.
For the white matter ROI, the distribution function for ζ was found by using bins of size 0.05 ms1/2/µm. For the whole brain ROI, ζ was determined as a function of FA, with FA intervals of 0.05 as bins. We also calculated the distribution function in white matter for the quantity
| (24) |
where Kmax is the maximum of the diffusional kurtosis over all possible directions for each voxel. In prior work, it has been argued that the quantity Kmax/(Kmax + 3) is an estimate for fa in white matter (Fieremans et al., 2011; Hui et al., 2015). Thus as follows from Eq. (14), η should be approximately equal to and can be used to estimate Da. For the η distribution, we used a bin size of 0.1 ms1/2/µm. Kmax was determined from the diffusion and kurtosis tensors generated by the DKE post-processing of the DKI data.
Results
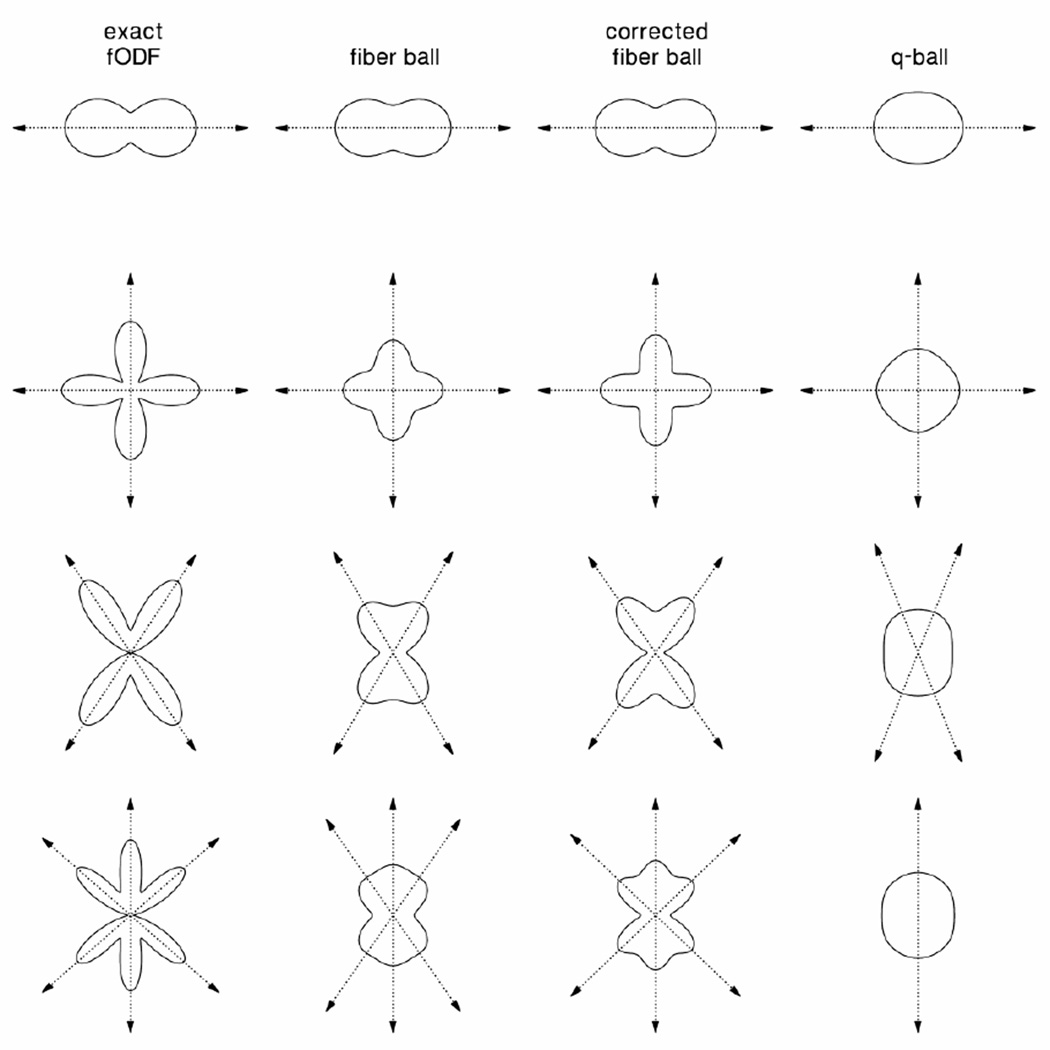
Numerical comparisons of exact fODFs with the corresponding fiber balls, corrected fiber balls, and q-balls are given by Fig. 2. The plots are cross sections of the exact and approximate fODFs/dODF in the θ =π / 2 plane. The three types of approximate fODFs correspond to smoothed versions of the exact fODF. The corrected fiber ball is the sharpest of the approximate fODFs, while the q-ball (dODF) is the smoothest. The fact that the q-ball is less sharp than the fiber balls is due to the fact that the Funk transform suppresses the higher degree harmonics of the dMRI signal while the inverse Funk transform, as discussed under Theory, actually enhances them.
Figure 2.
Numerical simulations of exact fODFs, for four different examples, together with the corresponding fiber ball, corrected fiber ball, and q-ball approximations, all shown with solid curves. The dotted arrows indicate the directions of the peaks (local maxima) for each of the angular profiles. The fiber balls and q-balls all give smoothed approximations of the fODFs. The fiber balls were obtained from the inverse Funk transform of the dMRI signal, which was calculated from the exact fODF by using Eq. (17) with bDa = 5. The q-ball was found by applying a Funk transform to the same signal and is necessarily smoother than the fiber ball because of the intrinsic properties of the Funk transform. The corrected fiber ball was derived by using Eq. (23) with bD0 = 12 to partially compensate for the smoothing effects of a finite b-value. For the last example (bottom row), the q-ball only detects one of the three peak directions.
In Fig. 2, the arrows indicate the directions of the fODF/dODF peaks (i.e., local maxima). For the second example (second row), the crossing angle is 90° for all four profiles. For the third example (third row), the exact crossing angle is 67.0°, while the fiber ball, corrected fiber ball, and q-ball yield crossing angles of 61.0°, 65.2°, and 43.2°, respectively. For the final example of a triple crossing shown in the fourth row, the exact crossing angles are 82.4° and 48.8°, the fiber ball crossing angles are 110.2° and 34.9°, and the corrected fiber ball crossing angles are 87.4° and 46.3°. In this case, the q-ball failed to detect the crossing, yielding just a single fiber bundle direction. Notice that the corrected fiber balls provide the most accurate estimates for the exact crossing angles.
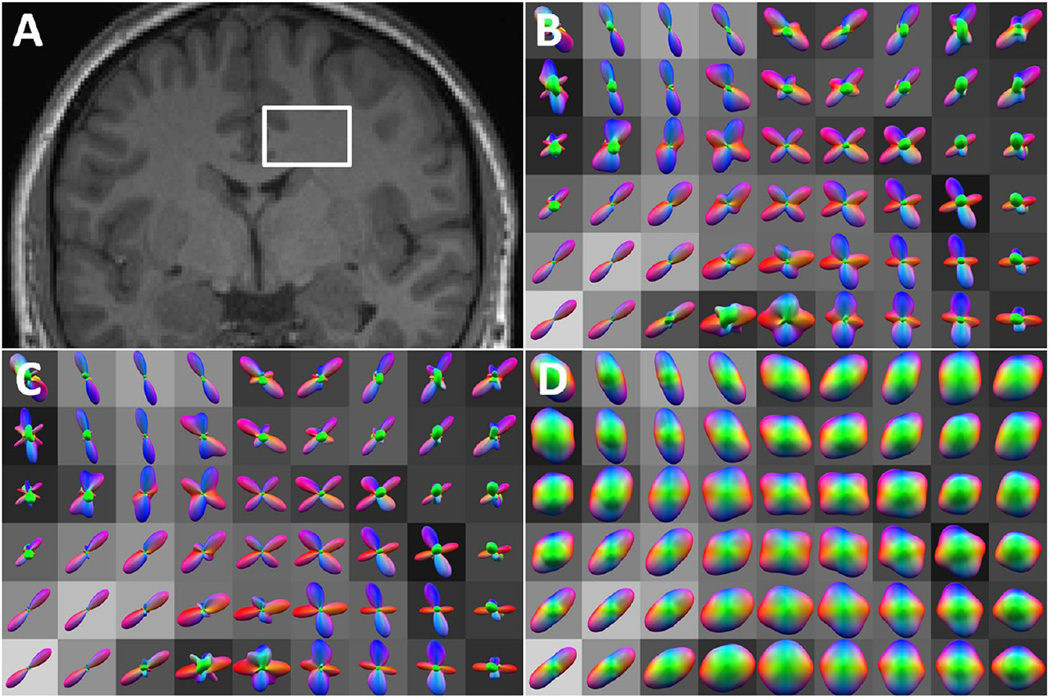
Examples of fiber balls and q-balls obtained with our in vivo data are shown in Fig. 3 for a brain region with known fiber crossings (centrum semiovale). These were co-registered to an MPRAGE image for anatomical reference. The fiber balls have sharper angular profiles than the q-balls, reflecting the relative enhancement of the higher degree harmonics. One may also appreciate that the corrected fiber balls have a stronger angular variation than the uncorrected fiber balls. The commonly employed min-max normalization (Tuch 2004; Hess et al., 2006) is not utilized in Fig. 3, so as to better highlight the differences between the three methods.
Figure 3.
In vivo fiber balls and q-balls for a white matter region (centrum semiovale) with crossing fibers. A: selected region on anatomical MPRAGE image. B: fiber balls calculated with the inverse Funk transform of Eq. (9). C: corrected fiber balls calculated from Eqs. (15) and (23) with bD0 = 12. Note that the corrected fiber balls have somewhat sharper profiles than the uncorrected fiber balls. D: q-balls calculated with the Funk transform of Eq. (11). Fiber balls and q-balls were overlaid on the corresponding FA image, and the overall scalings were adjusted for visual clarity.
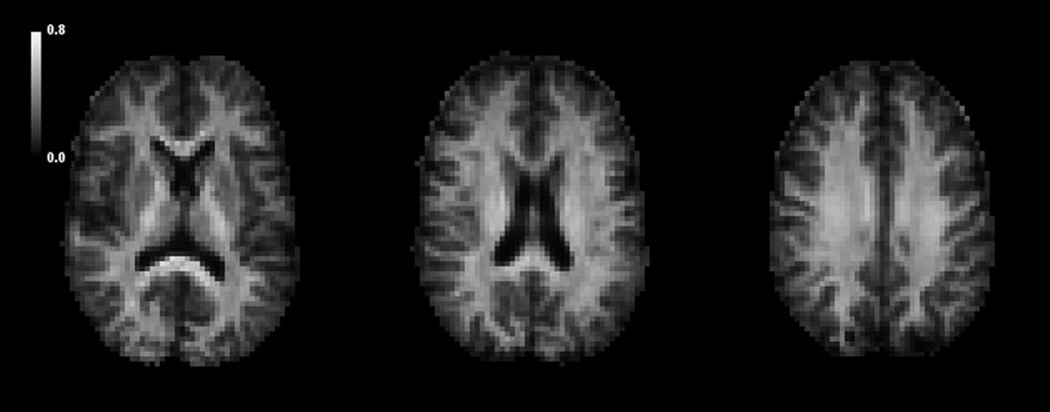
Maps of the parameter ζ for three nonconsecutive axial slices are shown in Fig. 4 as calculated from Eq. (14). While our theory gives a biophysical interpretation for the measured values of ζ in white matter, their meaning in gray matter is less clear. However, the gray matter values are seen to be substantially lower than those in white matter.
Figure 4.
Axial maps of for a single human subject as estimated with Eq. (14). White matter regions, in which fiber ball theory is expected to apply, have elevated values in comparison to gray matter regions. Gray matter also contains a substantial fiber component in the form of axons and dendrites, but it is less clear whether the assumptions underlying fiber ball imaging are accurately fulfilled. The scale bar is in units of ms1/2/µm.
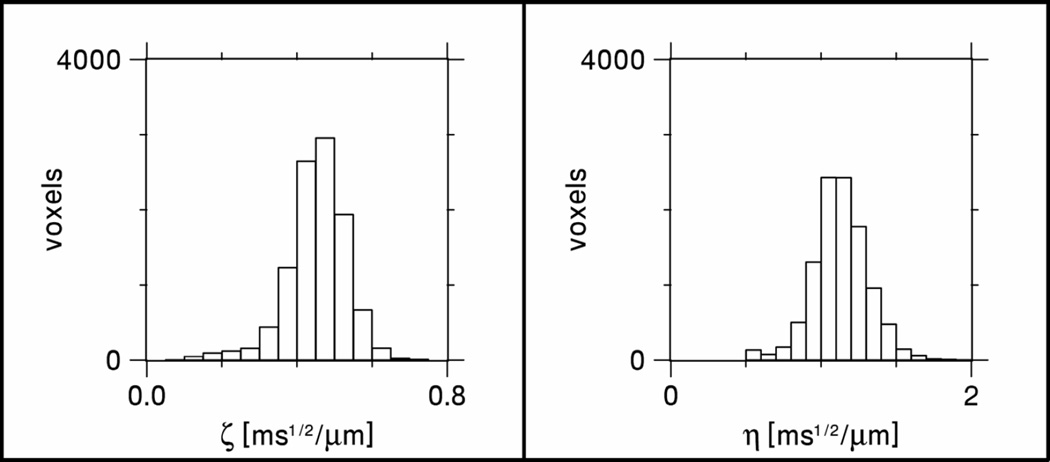
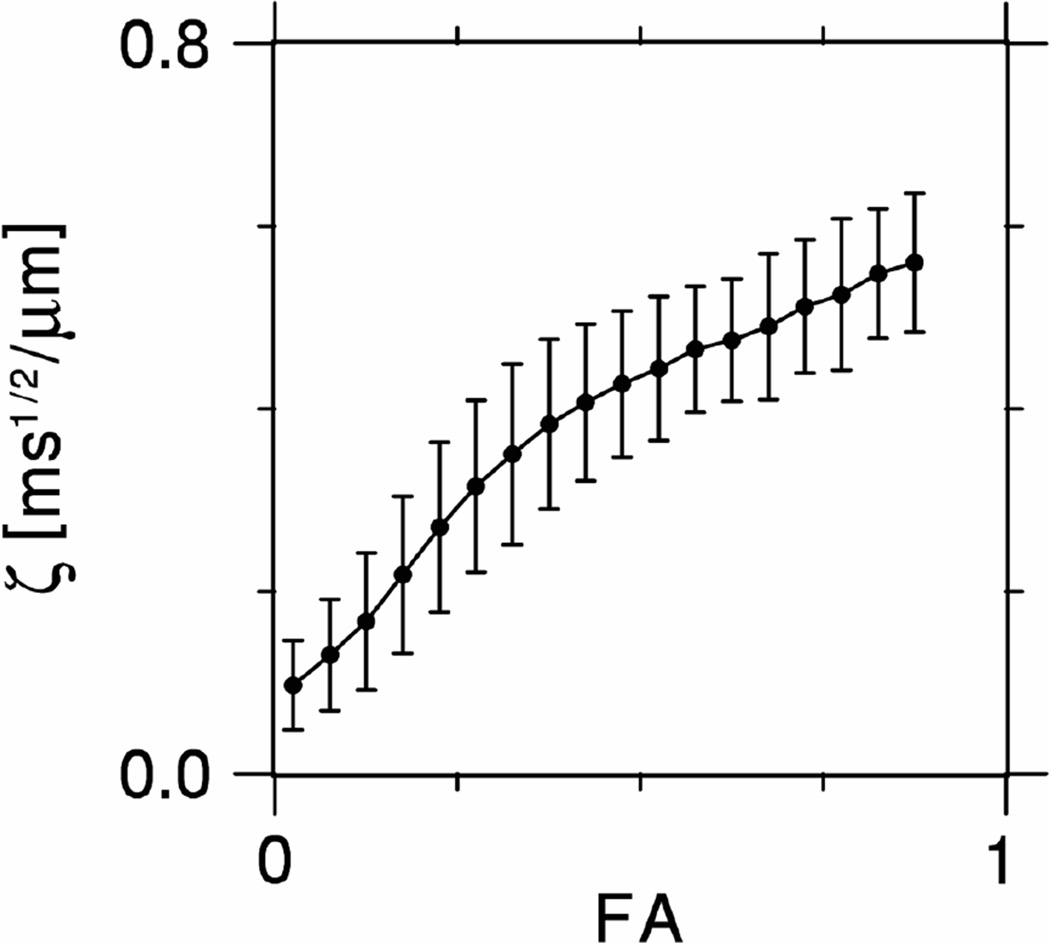
Histograms for ζ and η in white matter are plotted in Fig. 5. The corresponding mean values are ζ = 0.453 ± 0.081 ms1/2/µm and η = 1.129 ± 0.185 ms1/2/µm, where the uncertainties indicate the standard deviations. If we assume , as suggested under Methods, then our results lead to the estimate Da ≈ 0.785 ± 0.257 µm2/ms. Figure 6 shows ζ as a function of FA for the whole brain. One sees that ζ tends to grow with increasing FA. In the regions with FA > 0.6, ζ is typically in the range from 0.4 to 0.6 ms1/2/µm.
Figure 5.
Histograms for ζ and η in white matter. These distributions give mean values of ζ = 0.453 ± 0.081 ms1/2/µm and η = 1.129 ± 0.185 ms1/2/µm.
Figure 6.
Plot of ζ as a function of FA for the whole brain, showing a monotonic increase. The error bars indicate standard deviations.
Discussion
The main observation of this paper is that the inverse Funk transform of the HARDI signal intensity provides an estimate for the fODF in white matter. Given our assumptions, this estimate becomes more accurate as the b-value is increased, although the q-vector magnitude should not be so large that the signal becomes sensitive to the internal geometry of the axons. In addition, the SNR should be sufficient so that any bias due to the rectified noise floor is minimal (Glenn et al., 2015; Gudbjartsson & Patz, 1995; Henkelman, 1985). We have called this method fiber ball imaging to acknowledge its close connection with q-ball imaging. The key difference is that the Funk transform of q-ball imaging is replaced by the inverse Funk transform. The practical effect of this change is to enhance the higher degree harmonics and thereby sharpen the angular profile, as illustrated in Fig. 2. It should be emphasized, however, that there is also an important conceptual distinction between fiber ball and q-ball imaging in that q-ball imaging is intended to provide an approximation for the dODF rather than the fODF, and for this reason it is not surprising that the two methods yield significantly different results.
As with q-ball imaging, fiber ball imaging can form the basis of white matter fiber tractography, and this is one possible application. Because of the enhancement of the higher degree harmonics, fiber ball imaging may have a greater sensitivity for the detection of intra-voxel fiber crossings in comparison to q-ball imaging. In addition, fiber ball imaging leads to an estimate for the quantity . As Eq. (14) indicates, it can be simply determined from the lowest degree harmonic of the HARDI data, without requiring any detailed modeling or numerical fitting. This parameter may be directly relevant to characterizing white matter microstructure, and it can be used to constrain more explicit modeling approaches, such as neurite orientation dispersion and density imaging (Zhang et al., 2012) and kurtosis analysis of neural diffusion organization (Hui et al., 2015). Such methods typically require the nonlinear optimization of several model parameters and can often be simplified if additional information is available to reduce the dimensions of the parameter space.
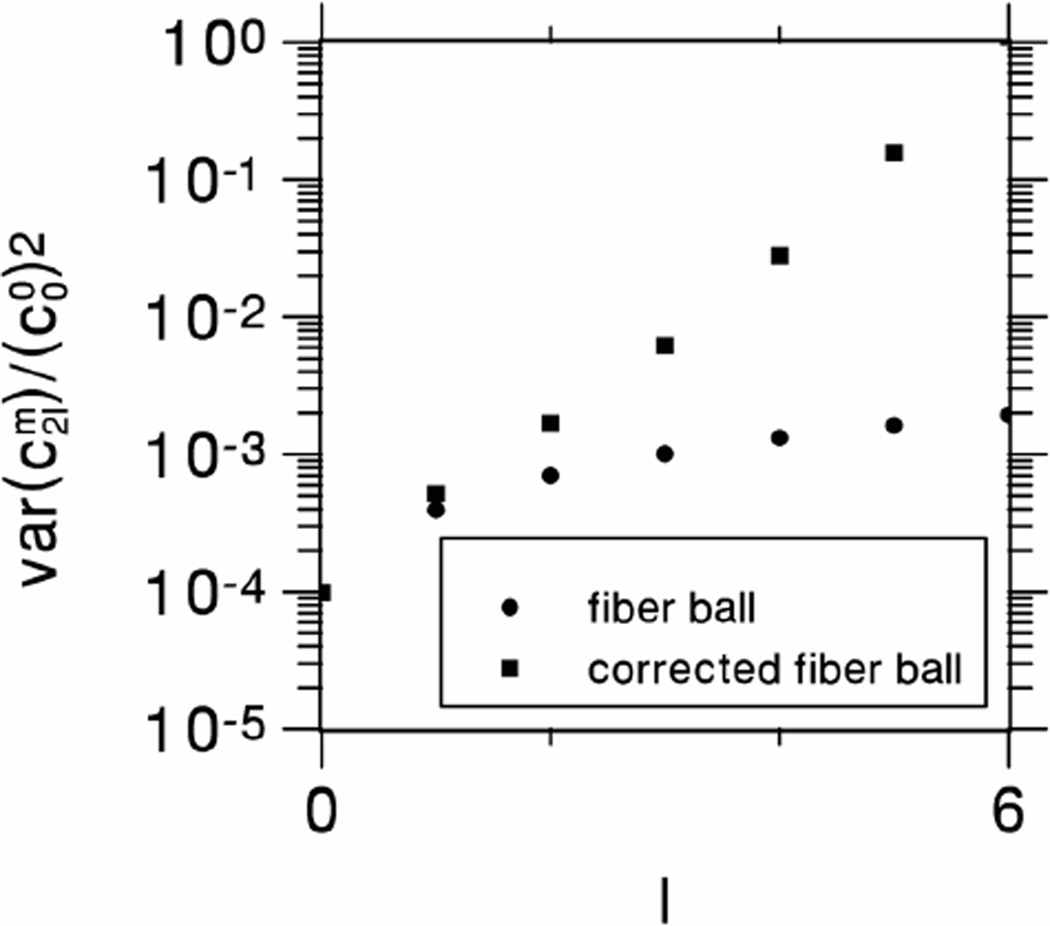
For finite b-values, it is important to appreciate that the accuracies of the estimated harmonic coefficients for the fODF decrease rather rapidly with increasing degree, as follows from Eq. (17), with the higher degree harmonics being strongly suppressed relative to their true values. For this reason, we have described a possible correction scheme that can partially compensate for this. As shown in Fig. 2, this may significantly improve the accuracy of the estimated peak directions. However, in applying the correction, the effects of signal noise are also amplified, and so it should be used with caution (See Appendix B and Fig. 7).
Figure 7.
Relative variances of Eqs. (B.10) and (B.11) for the uncertainties in the fiber ball spherical harmonic coefficients due to signal noise as a function of the degree l. The plots are for parameter choices that match those of the experiment performed in this study (N = 256, SNR = 6.3, bD0 = 12). Notice the rapid increase for large l in the variance for the corrected fiber ball coefficients. For this reason, the estimates of the higher degree coefficients may be substantially less precise than for the lower degree coefficients.
In order to demonstrate the feasibility of fiber ball imaging, we have obtained preliminary human data for a b-value of 4000 s/mm2. This b-value was chosen as a compromise between maximizing the accuracy of the fODF estimates and maintaining an adequate SNR. Exemplary fiber balls are shown in Fig. 3, together with the corresponding q-balls. These are qualitatively similar to the numerical results of Fig. 2, and they clearly demonstrate the sharper variation with angle for the fiber balls relative to the q-balls. In Figs. 4–7, we also give preliminary results for ζ. We find a mean value of ζ = 0.453 ± 0.081 ms−1/2/µm in white matter, and a general increase in ζ with higher FA is observed throughout the brain (Fig. 6).
While fiber ball imaging is primarily intended for white matter, it is of interest to briefly consider the values for ζ measured in gray matter. In Fig. 6, it is seen that ζ drops off substantially in the low FA regions, which are primarily gray matter for FA < 0.15. Relatively low gray matter values are also apparent in the maps of Fig. 4. Naively, this may be surprising, as a substantial portion of gray matter is composed of axons and dendrites (i.e., neurites), for which the thin cylinder approximation seems plausible. Indeed, models of this type have been applied to gray matter in several prior studies (Hui et al., 2015; Jespersen et al., 2007; Zhang et al., 2012). In this context, fa would be regarded as the water fraction for neurites, and Da would be regarded as the intra-neurite intrinsic diffusivity. While it is possible that the “true” ζ (i.e., ) is actually smaller in gray matter, this seems unlikely to be a full explanation for our results given the histological evidence that the neurite volume fraction in gray matter is about 0.6 (Chklovskii, et al., 2002). To obtain gray matter values of 0.2 to 0.3 ms1/2/µm for ζ, which is typical of our data, would then require Da to be about 4.0 µm2/ms or more, which is higher than the diffusivity of free water and therefore unphysical. As a consequence, it is probable that one or more of the assumptions that underlie fiber ball imaging are not valid for gray matter. One possibility is that the exchange time for neurite water in gray matter may be comparable to or less than the diffusion time (~50 ms) of our experiment.
In Figure 5, we show the white matter histogram for the parameter η defined by Eq. (24). Since in prior work it was proposed that Kmax /(Kmax + 3) is an estimate for fa in white matter (Fieremans et al. 2011; Hui et al., 2015), η should be approximately equal to . Our results then imply that Da ≈ 0.785 ± 0.257 µm2/ms. This value for the intrinsic intra-axonal diffusivity in white matter is roughly similar to some estimates previously obtained for particular models of white matter microarchitecture (Fieremans et al. 2011; Hui et al., 2015). However, other experiments suggest a somewhat larger value. For example, Kroenke and coworkers (Kroenke et al., 2004) found a ratio of 0.46 for the intra-neurite diffusivity of N-acetyl-L-aspartate relative to its free aqueous diffusivity. If it is assumed that the diffusivity ratio for intra-axonal and free water is similar, one obtains Da ≈ 1.38 µm2/ms. More recently, an even higher estimate for Da has been given (Dhital et al., 2015). Our values for Da might be systematically low both because of contributions to the measured η from the extra-axonal water signal (that have been neglected) and because our estimate for fa is formally a lower bound when the axons are not perfectly aligned (Fieremans et al. 2011). In any case, the value for Da obtained from the combination fiber ball imaging and DKI is at least in a plausible range, although further work is required to better evaluate its accuracy.
Besides q-ball imaging, there are a number of related methods for quantifying diffusional anisotropy and estimating axonal fiber bundle orientations (Daducci et al., 2014; Wilkins et al., 2015). Among these are variations on the original q-ball of Tuch and coworkers (Tuch et al., 2003; Tuch, 2004), such as those proposed by Aganj and coworkers (Aganj et al., 2010), by Tristán-Vega and coworkers (Tristán-Vega et al., 2009, 2010), and by Haldar and Leahy (Haldar and Leahy, 2013). These methods share the qualitative feature with fiber ball imaging in that they tend to give sharper angular profiles than the original q-ball, but none has a direct connection to the fODF of the type described by Eq. (9). On the other hand, alternative methods have been developed for estimating the fODF that are based on more detailed microstructural models for white matter than is fiber ball imaging and involve substantially more complicated mathematical computations (Anderson, 2005; Parker et al., 2013; Tournier et al., 2004, 2007; Wilkins et al., 2015). Fiber ball imaging may offer potential advantages both in terms of being based on relatively mild assumptions and in terms of calculational simplicity. Nonetheless, additional investigations would be needed to fully assess the comparative utility of fiber ball imaging with respect to these alternatives.
As previously mentioned, there are close connections between our method of correcting for the effect of a finite b-value and the prior work of Özarslan and coworkers (Özarslan et al., 2006) and of Jespersen and coworkers (Jespersen et al., 2007), as signaled by the appearance of the confluent hypergeometric function in Eq. (18). The paper of Jespersen and coworkers is particular relevant, and in Appendix A we have applied mathematical results from this study in the derivation of Eq. (17).
A possible extension of the fiber ball imaging approach described here would be to fit Eq. (17) to multi-shell HARDI data in order to directly estimate Da together with the spherical harmonic coefficients for the fODF. In this way, improved accuracy may be achieved. However, this would require nonlinear numerical optimization and forgoing the simplicity of the inverse Funk transform.
Finally, it should be emphasized that, although we regard the assumptions needed for the validity of fiber ball imaging to be quite plausible in healthy brain with typical HARDI protocols used for human imaging, this may not be true in some other cases. In stroke, for example, there is evidence that the intra-axonal diffusivity drops substantially (Budde and Frank, 2010; Hui et al., 2012). As a consequence, the condition bDa >> 1 is less well satisfied, and the accuracy of fiber ball imaging is thereby reduced. One should also be cautious about applying fiber ball imaging to fixed brain, as the diffusivities may be quite different than for in vivo brain (D'Arceuil et al., 2007).
Conclusions
Fiber ball imaging uses the inverse Funk transform of the dMRI signal on a spherical shell in q-space to find an approximation for the fODF in white matter. The accuracy of the fODF improves with increasing b-value and is highest for the lower degree spherical harmonics. Compared to the dODF estimated with q-ball imaging, the fiber ball fODF has sharper features which may help to improve white matter fiber tractography. In addition, fiber ball imaging provides maps for the ratio of the axonal water fraction to the square root of the intrinsic intra-axonal diffusivity. This quantity can be useful in characterizing brain microstructure and could be applied to constrain dMRI tissue modeling calculations.
Highlights.
A method of estimating the fiber orientation density function in brain is proposed.
The method is based on the inverse Funk transform of the diffusion MRI signal.
It generates sharper angular profiles than the related q-ball imaging method.
Possible applications include fiber tractography and microstructure modeling.
Acknowledgements
This work was supported in part by National Institutes of Health research grant T32GM008716 (to P. Halushka) and by the Litwin Foundation (to J.A.H.).
Appendix A
Here we outline the derivations for Eqs. (17), (19), and (20). From Jespersen and coworkers (Jespersen et al., 2007), one has (see their equations 10 and 14)
| (A.1) |
where we have applied our thin cylinder assumption to set the transverse intra-axonal diffusivity to zero. Combining Eq. (A.1) with the definition of Eq. (18) then gives
| (A.2) |
With the help of Eq. (12), this may be rewritten as
| (A.3) |
The duplication formula for the Gamma function (Abramowitz & Stegun, 1972) implies that
| (A.4) |
which together with Eq. (A.3) leads to
| (A.5) |
By recalling that Γ(l +1)= l!, one then sees Eq. (A.5) can be simplified to yield Eq. (17). The approximation of Eq. (19) may be obtained from the leading term in an asymptotic expansion of ln[g2l(bDa)] for large values of bDa, while Eq. (20) follows from Eq. (17) and the mathematical identity (Abramowitz & Stegun, 1972)
| (A.6) |
Appendix B
In this appendix, we discuss the effects of signal noise on the estimates of the spherical harmonic coefficients for the fODF. The spherical harmonic coefficients for the dMRI signal may be calculated from the expression
| (B.1) |
where Sn is the signal for the nth diffusion-encoding direction, (θn,ϕn) are the spherical angles for the nth diffusion-encoding direction, and N is the total number of diffusion-encoding directions. The directions are assumed to be uniformly distributed so that the sum in Eq. (B.1) approximates an integral over all angles. The variances for these harmonic coefficients are then
| (B.2) |
with the angle brackets indicating an averaging over the signal noise distribution. Well above the Rician noise floor, we have the approximation
| (B.3) |
where σ2 is the signal noise variance and δnn′ is the Kronecker delta. Typically, an SNR greater than about 3 is adequate for the validity of Eq. (B.3) (Glenn et al., 2015; Gudbjartsson & Patz, 1995; Henkelman, 1985). Combining Eqs. (B.2) and (B.3) yields
| (B.4) |
Since
| (B.5) |
Eq. (B.4) simplifies to
| (B.6) |
Note that all the have the same variance. From Eqs. (16) and (B.6), we find the variances for the fODF spherical harmonic coefficients, as computed with the inverse Funk transform, to be
| (B.7) |
It is convenient to normalize this with respect to , which gives the relative variance:
| (B.8) |
From Eq. (13), it is apparent that
| (B.9) |
Thus we finally obtain
| (B.10) |
As follows from Eq. (12), this relative variance increases linearly with l for large degrees. For the corrected fiber ball, the relative variance takes the form
| (B.11) |
as may be seen with the help of Eq. (23). The approximation of Eq. (19) then indicates that, in this case, the relative variance increases exponentially with the degree. In practice, this relative variance will be excessive whenever l is large in comparison to (bD0)1/2. Plots for the relative variances of Eqs. (B.10) and (B.11) are given in Fig. 7 as a function of l for the parameters used in this experiment.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res. 1992 Dec 11;598(1–2):143–153. doi: 10.1016/0006-8993(92)90178-c. [DOI] [PubMed] [Google Scholar]
- Abramowitz M, Stegun IA. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables. Dover, New York: 1972. [Google Scholar]
- Aganj I, Lenglet C, Sapiro G, Yacoub E, Ugurbil K, Harel N. Reconstruction of the orientation distribution function in single- and multiple-shell q-ball imaging within constant solid angle. Magn. Reson. Med. 2010 Aug;64(2):554–566. doi: 10.1002/mrm.22365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson AW. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magn. Reson. Med. 2005 Nov;54(5):1194–1206. doi: 10.1002/mrm.20667. [DOI] [PubMed] [Google Scholar]
- Assaf Y, Cohen Y. Assignment of the water slow-diffusing component in the central nervous system using q-space diffusion MRS: implications for fiber tract imaging. Magn Reson Med. 2000 Feb;43(2):191–199. doi: 10.1002/(sici)1522-2594(200002)43:2<191::aid-mrm5>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- Assaf Y, Freidlin RZ, Rohde GK, Basser PJ. New modeling and experimental framework to characterize hindered and restricted water diffusion in brain whitematter. Magn. Reson. Med. 2004 Nov;52(5):965–978. doi: 10.1002/mrm.20274. [DOI] [PubMed] [Google Scholar]
- Bailey TN, Eastwood MG, Gover R, Mason LJ. Complex analysis and the Funk transform. J. Korean Math. Soc. 2003;40(4):577–593. [Google Scholar]
- Budde MD, Frank JA. Neurite beading is sufficient to decrease the apparent diffusion coefficient after ischemic stroke. Proc Natl Acad Sci USA. 2010 Aug;107(32):14472–14477. doi: 10.1073/pnas.1004841107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chklovskii DB, Schikorski T, Stevens CF. Wiring optimization in cortical circuits. Neuron. 2002 Apr;34(3):341–347. doi: 10.1016/s0896-6273(02)00679-7. [DOI] [PubMed] [Google Scholar]
- Daducci A, Canales-Rodríguez EJ, Descoteaux M, Garyfallidis E, Gur Y, Lin YC, Mani M, Merlet S, Paquette M, Ramirez-Manzanares A, Reisert M, Rodrigues PR, Sepehrband F, Caruyer E, Choupan J, Deriche R, Jacob M, Menegaz G, Prčkovska V, Rivera M, Wiaux Y, Thiran JP. Quantitative comparison of reconstruction methods for intra-voxel fiber recovery from diffusion MRI. IEEE Trans. Med. Imaging. 2014 Feb;33(2):384–399. doi: 10.1109/TMI.2013.2285500. [DOI] [PubMed] [Google Scholar]
- D'Arceuil HE, Westmoreland S, de Crespigny AJ. An approach to high resolution diffusion tensor imaging in fixed primate brain. Neuroimage. 2007 Apr;35(2):553–565. doi: 10.1016/j.neuroimage.2006.12.028. [DOI] [PubMed] [Google Scholar]
- Descoteaux M, Angelino E, Fitzgibbons S, Deriche R. Regularized, fast, and robust analytical Q-ball imaging. Magn. Reson. Med. 2007 Sep;58(3):497–510. doi: 10.1002/mrm.21277. [DOI] [PubMed] [Google Scholar]
- Dhital B, Kellner E, Reisert M, Kiselev VG. Isotropic diffusion weighting provides insight on diffusion compartments in human brain white matter in vivo. Proc. Intl. Soc. Mag. Reson. Med. 2015;23:2788. [Google Scholar]
- Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage. 2011 Sep 1;58(1):177–188. doi: 10.1016/j.neuroimage.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fieremans E, Novikov DS, Jensen JH, Helpern JA. Monte Carlo study of a two-compartment exchange model of diffusion. NMR Biomed. 2010 Aug;23(7):711–724. doi: 10.1002/nbm.1577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glenn GR, Tabesh A, Jensen JH. A simple noise correction scheme for diffusional kurtosis imaging. Magn. Reson. Imaging. 2015 Jan;33(1):124–133. doi: 10.1016/j.mri.2014.08.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gudbjartsson H, Patz S. The Rician distribution of noisy MRI data. Magn. Reson. Med. 1995 Dec;34(6):910–914. doi: 10.1002/mrm.1910340618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldar JP, Leahy RM. Linear transforms for Fourier data on the sphere: application to high angular resolution diffusion MRI of the brain. Neuroimage. 2013 May;71:233–247. doi: 10.1016/j.neuroimage.2013.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henkelman RM. Measurement of signal intensities in the presence of noise in MR images. Med. Phys. 1985 Mar-Apr;12(2):232–233. doi: 10.1118/1.595711. [DOI] [PubMed] [Google Scholar]
- Hess CP, Mukherjee P, Han ET, Xu D, Vigneron DB. Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis. Magn. Reson. Med. 2006 Jul;56(1):104–117. doi: 10.1002/mrm.20931. [DOI] [PubMed] [Google Scholar]
- Holz M, Heil SR, Sacco A. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements. Phys. Chem. Chem. Phys. 2000;2(20):4740–4742. [Google Scholar]
- Hui ES, Fieremans E, Jensen JH, Tabesh A, Feng W, Bonilha L, Spampinato MV, Adams R, Helpern JA. Stroke assessment with diffusional kurtosis imaging. Stroke. 2012 Nov;43(11):2968–2973. doi: 10.1161/STROKEAHA.112.657742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hui ES, Glenn GR, Helpern JA, Jensen JH. Kurtosis analysis of neural diffusion organization. Neuroimage. 2015 Feb;106:391–403. doi: 10.1016/j.neuroimage.2014.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010 Aug;23(7):698–710. doi: 10.1002/nbm.1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jespersen SN, Kroenke CD, Østergaard L, Ackerman JJ, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. Neuroimage. 2007 Feb 15;34(4):1473–1486. doi: 10.1016/j.neuroimage.2006.10.037. [DOI] [PubMed] [Google Scholar]
- Kroenke CD, Ackerman JJ, Yablonskiy DA. On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn. Reson. Med. 2004 Nov;52(5):1052–1059. doi: 10.1002/mrm.20260. [DOI] [PubMed] [Google Scholar]
- Lazar M. Mapping brain anatomical connectivity using white matter tractography. NMR Biomed. 2010 Aug;23(7):821–835. doi: 10.1002/nbm.1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson M, Lätt J, van Westen D, Brockstedt S, Lasič S, Ståhlberg F, Topgaard D. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magn. Reson. Med. 2013 Jun;69(6):1573–1581. doi: 10.1002/mrm.24395. [DOI] [PubMed] [Google Scholar]
- Özarslan E, Shepherd TM, Vemuri BC, Blackband SJ, Mareci TH. Resolution of complex tissue microarchitecture using the diffusion orientation transform (DOT) Neuroimage. 2006 Jul 1;31(3):1086–1103. doi: 10.1016/j.neuroimage.2006.01.024. [DOI] [PubMed] [Google Scholar]
- Panagiotaki E, Fonteijn H, Siow B, Hall MG, Price A, Lythgoe MF, Alexander DC. Two-compartment models of the diffusion MR signal in brain white matter. Med. Image Comput. Comput. Assist Interv. 2009;12(Pt 1):329–336. doi: 10.1007/978-3-642-04268-3_41. [DOI] [PubMed] [Google Scholar]
- Panagiotaki E, Schneider T, Siow B, Hall MG, Lythgoe MF, Alexander DC. Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison. Neuroimage. 2012 Feb 1;59(3):2241–2254. doi: 10.1016/j.neuroimage.2011.09.081. [DOI] [PubMed] [Google Scholar]
- Parker GD, Marshall D, Rosin PL, Drage N, Richmond S, Jones DK. A pitfall in the reconstruction of fibre ODFs using spherical deconvolution of diffusion MRI data. Neuroimage. 2013 Jan;65:433–448. doi: 10.1016/j.neuroimage.2012.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-currentinduced distortion in diffusion MRI using a twice-refocused spin echo. Magn. Reson. Med. 2003 Jan;49(1):177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- Stanisz GJ, Kecojevic A, Bronskill MJ, Henkelman RM. Characterizing white matter with magnetization transfer and T2. Magn. Reson. Med. 1999 Dec;42(6):1128–1136. doi: 10.1002/(sici)1522-2594(199912)42:6<1128::aid-mrm18>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- Tabesh A, Jensen JH, Ardekani BA, Helpern JA. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn. Reson. Med. 2011 Mar;65(3):823–836. doi: 10.1002/mrm.22655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage. 2007 May;35(4):1459–1472. doi: 10.1016/j.neuroimage.2007.02.016. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Gadian DG, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage. 2004 Nov;23(3):1176–1185. doi: 10.1016/j.neuroimage.2004.07.037. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Mori S, Leemans A. Diffusion tensor imaging and beyond. Magn. Reson. Med. 2011 Jun;65(6):1532–1556. doi: 10.1002/mrm.22924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tristán-Vega A, Westin C-F, Aja-Fernández S. Estimation of fiber orientation probability density functions in high angular resolution diffusion imaging. Neuroimage. 2009 Aug 15;47(2):638–650. doi: 10.1016/j.neuroimage.2009.04.049. [DOI] [PubMed] [Google Scholar]
- Tristán-Vega A, Westin C-F, Aja-Fernández S. A new methodology for the estimation of fiber populations in the white matter of the brain with the Funk-Radon transform. Neuroimage. 2010 Jan 15;49(2):1301–1315. doi: 10.1016/j.neuroimage.2009.09.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuch DS. Q-ball imaging. Magn. Reson. Med. 2004 Dec;52(6):1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn. Reson. Med. 2002 Oct;48(4):577–582. doi: 10.1002/mrm.10268. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Wedeen VJ. Diffusion MRI of complex neural architecture. Neuron. 2003 Dec;40(5):885–895. doi: 10.1016/s0896-6273(03)00758-x. [DOI] [PubMed] [Google Scholar]
- Wilkins B, Lee N, Gajawelli N, Law M, Leporé N. Fiber estimation and tractography in diffusion MRI: development of simulated brain images and comparison of multi-fiber analysis methods at clinical b-values. Neuroimage. 2015 Apr;109:341–356. doi: 10.1016/j.neuroimage.2014.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang AW, Jensen JH, Hu CC, Tabesh A, Falangola MF, Helpern JA. Effect of cerebral spinal fluid suppression for diffusional kurtosis imaging. J. Magn. Reson. Imaging. 2013 Feb;37(2):365–371. doi: 10.1002/jmri.23840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012 Jul 16;61(4):1000–1016. doi: 10.1016/j.neuroimage.2012.03.072. [DOI] [PubMed] [Google Scholar]