Abstract
The blood oxygen level dependent (BOLD) signal evoked by brief neural stimulation, the hemodynamic response function (HRF), is a critical feature of neurovascular coupling. The HRF is directly related to local transient changes in oxygen supplied by cerebral blood flow (CBF) and oxygen demand, the cerebral metabolic rate of oxygen (CMRO2). Previous efforts to explain the HRF have relied upon the hypothesis that CBF produces a non-linear venous dilation within the cortical parenchyma. Instead, the observed dynamics correspond to prompt arterial dilation without venous volume change. This work develops an alternative biomechanical model for the BOLD response based on the hypothesis that prompt upstream dilation creates an arterial flow impulse amenable to linear description. This flow model is coupled to a continuum description of oxygen transport. Measurements using high-resolution fMRI demonstrate the efficacy of the model. The model predicts substantial spatial variations of the oxygen saturation along the length of capillaries and veins, and fits the varied gamut of measured HRFs by the combined effects of corresponding CBF and CMRO2 responses. Three interesting relationships among the hemodynamic parameters are predicted. First, there is an offset linear correlation with approximately unity slope between CBF and CMRO2 responses. Second, the HRF undershoot is strongly correlated to the corresponding CBF undershoot. Third, late-time-CMRO2 response can contribute to a slow recovery to baseline, lengthening the HRF undershoot. The model provides a powerful mathematical framework to understand the dynamics of neurovascular and neurometabolic responses that form the BOLD HRF.
Keywords: Cerebral hemodynamics, Cerebral blood flow, Functional MRI (fMRI), Computational model, Neurophysiology, Neurovascular coupling, Neurovascular unit
Introduction
Neural activity leads to an increase in local cerebral blood flow (CBF) to compensate for the energy demands of the corresponding brain region. This local functional hyperemia, called neurovascular coupling, provides a means to infer brain activity. Various imaging modalities, such as functional magnetic resonance imaging (fMRI), optical imaging, and positron emission tomography (PET), use neurovascular coupling responses to identify and quantify local neural activation.
FMRI is widely used for human brain research because it is safe and non-invasive, yet provides good spatiotemporal resolution. Most fMRI relies on the blood-oxygen-level dependent (BOLD) signal: local microvascular hyperemia leads to less paramagnetic deoxyhemoglobin, thus reducing magnetic field distortion and increasing the MR signal observed during a gradient-recalled echo sequence (Buxton, 2013). The BOLD signal is, therefore, directly related to local transient changes in the oxygen supplied by CBF. In addition, the BOLD signal is affected by oxygen demand, the cerebral metabolic rate of oxygen (CMRO2), because oxygen diffuses from the blood as it passes through the activated brain region. However, the quantitative relationship between the BOLD response, CBF, and CMRO2 remains unclear. In fact, it has long been known that the observed increase in CBF evoked by neural activity is substantially larger than the corresponding increase in CMRO2; this has been termed “neurovascular uncoupling” (Fox and Raichle, 1986). This apparent physiological mismatch has complicated attempts to understand the underlying mechanism of the BOLD response.
The response evoked by brief neural activity is called the hemodynamic response function (HRF). Analysis of event-related fMRI, which relies on sequences of episodic neural activations, is particularly dependent on a complete understanding of the HRF. The HRF typically includes three stereotypical temporal phases: initial dip or delay (Frostig et al., 1990; Hu and Yacoub, 2012; Menon et al., 1995), then a hyperoxic peak, followed by an undershoot (Buxton, 2012; Kruger et al., 1996; van Zijl et al., 2012) with possible oscillatory ringing (Ress et al., 2009; Thompson et al., 2003). The time scale of the HRF is ~20–30 s when evoked by <5-s stimulation.
Most attempts to explain and model the BOLD response also assume that neural activity results in changes in cerebral blood volume (CBV), as well as changes in CBF and CMRO2. The volume changes have generally been associated with venous vasodilation, motivated by a host of steady-state, slow time-scale measurements showing a nonlinear relationship between CBV and CBF (Buxton et al., 1998; Grubb et al., 1974; Kety and Schmidt, 1948; Zheng et al., 2005; Zheng et al., 2002). Based on this assumption, the calibrated-BOLD approach was introduced to estimate CMRO2 and CBV from measurements of BOLD signal and CBF (Davis et al., 1998). The model used two non-linear relationships to describe the BOLD signal, one giving venous blood-oxygen changes, and the other giving venous CBV changes driven by a CBF response. This mathematical framework has been a basis of most biophysical models to describe the BOLD signal with the underlying dynamics of CBF, CMRO2 and CBV changes. The “balloon model” has been the most popular, postulating that brain activation causes increased CBF leading to non-linear venous dilation (Buxton et al., 1998). It considered both intra- and extra-vascular compartments as sources of the BOLD signal. Mandeville et al. (1999) measured CBF using laser-Doppler flowmetry and inferred CBV using fMRI, and introduced a similar model based upon delayed compliance to fit the experimental data. Recently, many non-linear models have been introduced with greater elaboration and sophistication (Buxton et al., 2004; Griffeth and Buxton, 2011; Kong et al., 2004; Obata et al., 2004; Zheng et al., 2002; Zheng and Mayhew, 2009). Some balloon models also include convection–diffusion oxygen transport (Huppert et al., 2007). Very recently, a convection–diffusion transport model (Fang et al., 2008) was applied to two-photon measurements of the vascular network to permit detailed evaluation of BOLD responses from extravascular compartments (Gagnon et al., 2015).
However, the underlying assumption of the non-linear CBV to CBF relationship for the comparatively fast time scale of the HRF remained untested until recently. Various forms of in vivo optical imaging of individual blood vessels have demonstrated that there are no significant venous volume changes caused by brief brain activation (Drew et al., 2011; Fernandez-Klett et al., 2010; Hillman et al., 2007; Vazquez et al., 2010). These experimental findings consistently indicate that venous volume changes are not a source of the BOLD signal for brief neural activation, and support the hypothesis that upstream pial artery dilation generates a transient CBF response to compensate the local oxygen demand in parenchyma. Such arterial vasodilation can create an underdamped flow response because it involves larger vessel diameters (e.g., >200 μm) and flow speeds (>5 mm/s). In previous work, we used a model that combined underdamped flow and convection–diffusion oxygen transport to successfully explain a host of tissue-oxygen measurements (Kim et al., 2013; Ress et al., 2009).
Here, we extend our mathematical framework to interpret the BOLD signal for short stimulation, the HRF. The new “arterial impulse” model includes only CBF and CMRO2 responses as drivers of the BOLD HRF; it excludes venous CBV changes based on the plethora of recent experimental findings.
We utilize a linear-network model to model the underdamped CBF response created by the prompt arterial vasodilation in terms of energy exchange between the kinetic energy of flow and the stored energy of downstream venous compliance. Although venous CBV changes in the cortical parenchyma have not been observed following short periods of activation, the compliance, which has been well documented experimentally (Binzoni et al., 2000; Romney and Lewanczuk, 2001), could be manifest downstream in larger venous vessels such as the sinuses. A stereotypical parametric temporal form is assumed for the CMRO2 response.
The CBF and CMRO2 are coupled to a spatiotemporal oxygen-transport model that include the mechanisms of blood flow, hemoglobin dissociation, and transmural oxygen diffusion to produce longitudinal profiles of oxygen concentration in capillaries. Because the BOLD signal is dominantly driven by venous-compartment oxygen-concentration changes, we also include flow and hemoglobin-dissociation effects in the venous compartment. Thus, we predict the longitudinal profiles of oxygen concentration in both capillary and venous compartments, which are then related to the HRF, including both intravascular and extravascular BOLD effects.
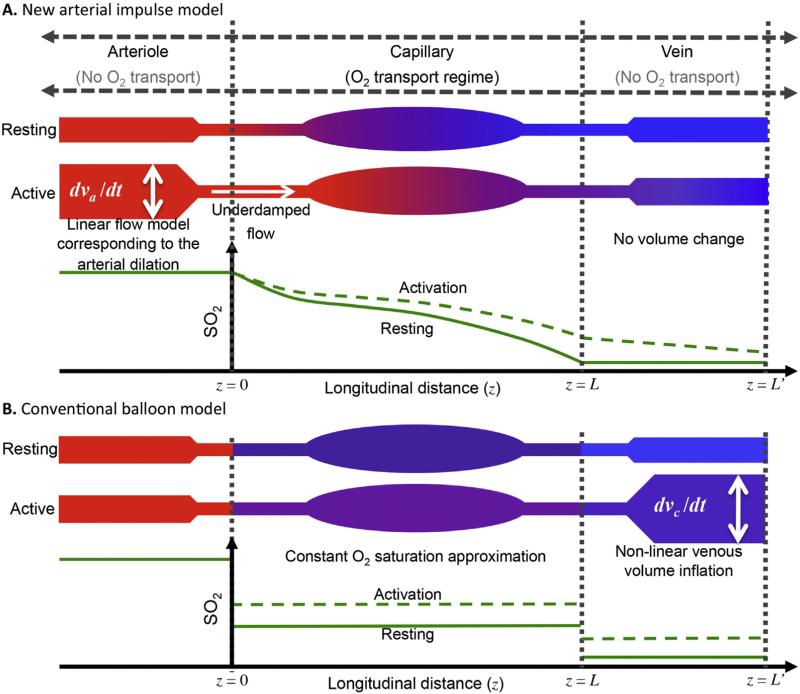
The arterial impulse model is distinguished from the balloon models (Buxton and Frank, 1997; Buxton et al., 2004; Buxton et al., 1998; Griffeth and Buxton, 2011; Zheng et al., 2005; Zheng et al., 2002) in multiple ways. First, it describes the short-stimulation HRF with experimentally observed (Drew et al., 2011; Fernandez-Klett et al., 2010; Hillman et al., 2007; Itoh and Suzuki, 2012; Vazquez et al., 2010) dynamics: prompt arterial dilation without venous volume change. In contrast, the balloon model's venous vasodilation is only observed in consequence to very long stimulation periods. Second, our model utilizes 1-D continuum dynamics for oxygen dissociation, diffusion, and flow in capillary and vein, thus providing details of the longitudinal profiles (Fig. 1A); the balloon model uses a compartmental, spatially constant oxygen saturation (SO2) approximation for capillary and vein (Fig. 1B). Third, our model provides a simpler and more linear interpretation of the HRF than balloon models, in which most non-linearity comes from non-linear venous inflation (Buxton et al., 2004; Buxton et al., 1998; Griffeth and Buxton, 2011). The absence of the putative venous inflation in the arterial impulse model results in an offset-linear relationship between CBF and CMRO2 responses that is consistent with the observed non-linearity between the BOLD response and neural activity (Pfeuffer et al., 2003; Vazquez and Noll, 1998). Fourth, our model postulates independent CBF and CMRO2 response kernels driven by the neural response. Most previous models assume a fixed ratio of CBF to CMRO2 response. Finally, the modified balloon model assumes a temporal delay between CBF and CMRO2 responses to obtain the observed initial delay in the HRF (Buxton et al., 2004); no physiological mechanism is provided for this delay. In our model, mass balance of the longitudinally resolves system links these responses without further assumption.
Fig. 1.
Schematic of longitudinal SO2 changes for activation and resting states with corresponding longitudinal SO2 profiles for (A) arterial model, (B) balloon model; solid green line for resting, dotted green line for activation.
We test the arterial impulse model against measurements of the BOLD HRF in human visual cortex evoked by brief stimulation; these measurements use high-resolution fMRI to avoid contamination from large pial blood vessels. The model provides excellent fits to the measured HRFs, and quantifies how fMRI measurements correspond to competition between CBF and CMRO2 for brief neural activation, offering a simpler, more linear theoretical interpretation for the BOLD HRF.
Materials and methods
BOLD signal
The basis of BOLD contrast is the transient phase dispersion of water proton spins by distortion of the local magnetic field (Ogawa et al., 1993). This distortion is mainly produced by the dominant concentration of deoxygenated hemoglobin (Hb) in parenchymal brain tissues such as cortical gray matter. In the absence of experimental neural activation, this distortion creates a relatively smaller MR signal. Contrast is primarily driven by transient CBF changes that have two effects. First, inflowing arterial blood replaces deoxygenated Hb with oxygenated Hb, reducing phase dispersion and thereby increasing the MR signal. Second, the increase in blood volume displaces extravascular fluid, causing a net decrease in MR signal. Griffeth and Buxton (2011) recently developed a BOLD signal equation based on magnetization components from three intravascular compartments (artery, capillary, and vein) and their associated extravascular compartments. The BOLD signal thereby depended on changes in SO2 and CBV in each intravascular compartment. For the short-stimulation regime, we simplified their results, based on recent experimental findings, by neglecting volume changes in capillaries and veins. BOLD contrast evoked by arterial changes in oxygen concentration and volume can also be neglected for two reasons. First, arterial blood will have little direct effect on BOLD contrast because its SO2 is relatively high (⪆ 90%) (Vovenko, 1999), and its magnetic susceptibility is similar to that of extravascular tissue. Second, arterial CBV increases promptly when neural activity occurs. For short stimulation experiments, these prompt CBV effects may lead to a small increase in MR signal because highly saturated arterial blood generates slightly more signal than the extravascular fluid (Griffeth and Buxton, 2011; Spees et al., 2001). However, such prompt effects will have little impact on the full time-scale of the HRF. Moreover, it has been reported that arterial contribution to the BOLD signal is minimal at 3 T (Uludag et al., 2009). Altogether, we conclude that arterial CBV effects will be brief and small, and can therefore be neglected.
Under these assumptions, the BOLD contrast, the relative change in MR signal, δS, is now only a function of the SO2 change in the capillary and venous compartments, and each compartment has intravascular and extravascular components:
| (1) |
where ε is the ratio of resting intravascular signal to extravascular signal, v is blood volume fraction, and subscripts I, and E represent intravascular and extravascular. (See Table 1 for parameter values used and their references, and Appendix A for details of the derivation.)
Table 1.
Steady-state and BOLD signal parameters.
| Description | Values | Reference |
|---|---|---|
| Oxygen extraction fraction at steady state | 0.428 | Ito et al. (2004) and Vovenko (1999) |
| Initial erythrocyte concentration in steady state, Qh0 (mmol/L) | 8.56 | Vovenko (1999) |
| Diffusivity (mm2/s) | 1.6E–5 | Clark et al. (1978) |
| Diffusion rate constant | 80 | Clark et al. (1978), Tsai et al. (2003) and Vovenko (1999) |
| Steady-state CMRO2, Γ0 (mmol/L/s) | 0.081 | Kim et al. (2013) and Lenigerfollert (1977) |
| Steady-state CBF, U0 (mm/s) | 0.7 | Kim et al. (2013) and Nguyen et al. (2011) |
| Initial transmural gradient, σ | 0.1 | Kim et al. (2013) and Vovenko (1999) |
| Capillary volume fraction | 0.4 | Weber et al. (2008) |
| Vein volume fraction | 0.4 | Weber et al. (2008) |
| Effective CBV fraction | 0.014 | Cassot et al. (2006) and Vovenko (1999) |
| Hematocrit (capillary), Htc | 0.2 | Lecoq et al. (2011) |
| Hematocrit (vein), Htv | 0.44 | Gustard et al. (2003) |
| Resting extravascular rate of signal decay, R*2E (s–1) | 25.1 | Perthen et al. (2008) |
| Susceptibility of fully deoxygenated blood, Δχ | 2.64E–7 | Spees et al. (2001) |
| Blood saturation for equal tissue-blood susceptibility, SO2,ref | 0.95 | Spees et al. (2001) |
| Constant term for vein, Cv* (s–1) | 174.7 | Zhao et al. (2007) |
| Constant term for vein, Av* (s–1) | 21.2 | Zhao et al. (2007) |
| Constant term for capillary, Cc* (s–1) | 142.7 | Zhao et al. (2007) |
| Constant term for capillary, Ac* (s–1) | 19.7 | Zhao et al. (2007) |
Our oxygen transport model is spatially resolved, so we need to make assumptions about the gross distribution of oxygen transport within the vasculature. For simplicity, we assume that transport occurs only in capillaries, so oxygen saturation is constant in all of the arterial vasculature, then decreases through the capillaries by oxygen transport into tissue (Fig. 1A). We assume that there is no transmural oxygen transport in the veins (Tsai et al., 2003; Vovenko, 1999), so the baseline venous oxygen saturation is constant.
We assume a uniform cylindrical geometry for the capillary and vein, and finely grid their lengths. In the capillary, we use differential mass balance, including the processes of blood flow, hemoglobin oxygen dissociation, and oxygen diffusion into extravascular tissue, to obtain a continuous SO2 spatial profile using a finite-difference method (FDM, details below). The longitudinal profile in the venous compartment is calculated in a similar fashion, but neglecting diffusive transport of oxygen.
Previous models have neglected the longitudinal profile of oxygen concentration within the microvasculature (Buxton et al., 2004; Griffeth and Buxton, 2011). To deal with the spatially dependent oxygen saturation, the BOLD signal equation can be written as the sum of spatial averages (Kim and Ogawa, 2012) over four compartments:
| (2) |
where subscripts c and v represent capillary and vein.
The first term on the right side of the equation represents the intravascular signal change in capillaries:
| (3) |
Here, the intravascular capillary transverse relaxation rate is:
| (4) |
where C* is an empirical constant (Griffeth and Buxton, 2011; Zhao et al., 2007). Subscripts 0 and 1 denote resting and activation, respectively. The term εc(z) is the ratio of resting intravascular to extravascular signals in capillaries as a function of the longitudinal direction:
| (5) |
The second term in Eq. (2) is the intravascular signal change in veins with spatial averaging given by the quantity:
| (6) |
where
| (7) |
We assume that the resting venous oxygen saturation is spatially constant at its value at the distal end of the capillary, SO2,v0 (z) = SO2,c0 (z = L), so the ratio of resting intravascular to extravascular signals in the vein, εv is also spatially constant.
The third and forth terms in Eq. (2) are the extravascular signal changes in capillaries and veins, which have forms similar to the intravascular terms:
| (8) |
| (9) |
Here,
| (10) |
| (11) |
where Δχ is the susceptibility of fully deoxygenated blood, Ht is the hematocrit, γ is the gyromagnetic ratio of protons, B0 is the magnetic field strength, SO2,ref is the oxygen saturation for equal blood-tissue susceptibility.
CBF response
Recent experiments indicate that brief brain activation produces a rapid wave of vasodilation starting from the activated brain region and extending to the superficial pial arteries (Devor et al., 2011; Itoh and Suzuki, 2012; Tian et al., 2010). Therefore, the flow response spans two fluid-behavior regimes: upstream transient CBF in arteries and corresponding downstream CBF in the microvasculature. In pial arteries, relatively larger vessel diameters (>200 μm) and high flow speeds (>20 mm/s) make inertial effects significant (Kim et al., 2013; Ress et al., 2009). So, we model the upstream flow response using a lumped linear network that includes inertial effects. Prompt arterial vasodilation creates an impulsive resistance decrease, yielding the flow impulse-response:
| (12) |
with frequency f, damping time τ, and amplitude U1. The underdamped oscillatory response corresponds to exchange between kinetic (inertial) energy and compliant energy distributed through the downstream venous vasculature, resulting in an oscillatory flow response. This linear model provides a biomechanical basis for a damped sinusoidal flow response.
Because of the small vessel diameters and slow flow speeds, the CBF in capillaries should exhibit “creeping” flow that is driven linearly by the upstream CBF response (UFEW), modulated by a viscous friction. Therefore, the CBF response in the capillaries should have the same underdamped form as in the upstream vasculature.
CMRO2 response
We assume an analytic form for the CMRO2 as an input to our convection–diffusion transport model. The CMRO2 response shows how much oxygen diffuses into surrounding tissues evoked by neural activity. We assume spatially uniform oxygen uptake to avoid complexity. Prompt increases and relatively slow decays in the CMRO2 temporal response were observed in previous experiments (Masamoto and Tanishita, 2009; Vazquez et al., 2010), with substantial variability among the observed responses. So, we use a gamma-variate function to characterize various CMRO2 responses:
| (13) |
where N is a normalization constant, damping time is η, shape coefficient ξ, and amplitude Γ1. The damping time mostly characterizes the decay of the transient CMRO2 change, while the shape coefficient principally affects its rise time.
Relating CBF and CMRO2 to the HRF
We estimate neural activity as a rectangular pulse inducing transient responses in both CBF and CMRO2. Accordingly, convolution with the rectangular pulse models the full CBF and CMRO2 responses corresponding to the neural activity.
Capillary oxygen transport
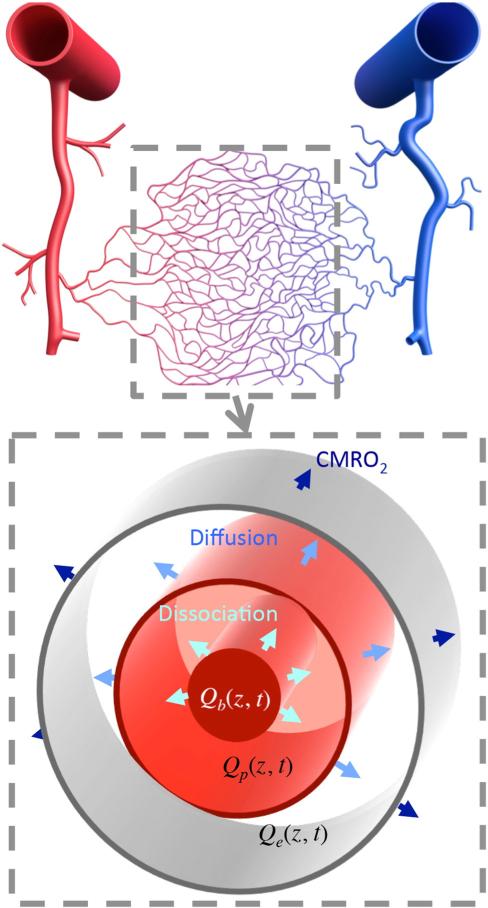
We model the aggregate behavior of capillary transport using a single cylinder consisting of three radial compartments (erythrocyte, plasma and extravascular tissue, see Fig. 2). Mass balance includes four components: convection, dissociation, diffusion, and CMRO2. First, convection corresponds to the blood flow along the vessel (z-axis), and this occurs in both erythrocyte and plasma compartments. Second, hemoglobin-bound oxygen in the erythrocyte compartment dissociates into the plasma compartment, which is calculated using a quadratic fit to the Hill equation (Sharan et al., 1989). Third, oxygen diffuses from the plasma to the extravascular tissue. Fourth, the CMRO2 response is modeled as spatially uniform oxygen uptake from the extravascular compartment. The combination of these dynamics produces a set of three partial-differential equations, one for each radial compartment, which can be solved numerically; see Appendix B for details. Resting flow speed in the capillary was assumed to be 0.7 mm/s; cylinder length was determined from resting oxygen mass balance to be 842 μm (Appendix B).
Fig. 2.
(Upper) Schematic of a cortical vascular network; the gray dotted line shows the capillary bed when oxygen transport mainly occurs. (Lower) Schematic of the cylindrical geometry for the oxygen transport model with three radial compartments (erythrocyte, plasma and extravascular tissue) that is used to model oxygen dissociation, diffusion, and oxygen demands in capillaries.
Venous oxygen transport
The venous geometry is modeled as a second cylinder extending beyond the capillary. Because we assume no venous oxygen diffusion, mass balance includes only two components: convection and dissociation. Venous flow speed is assumed to be 2.5 mm/s (Santisakultarm et al., 2012). Cylinder length was approximated on order of the gray-matter thickness (Fischl and Dale, 2000; Ress et al., 2007), ~2 mm.
Measurement of the BOLD HRF
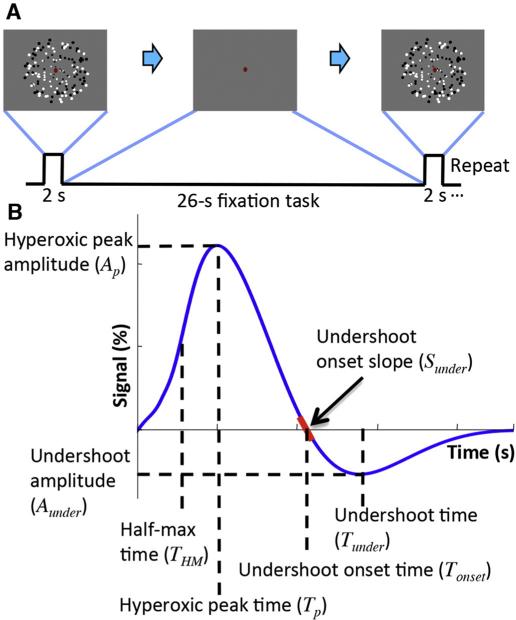
The BOLD HRF is evoked in 7 subjects and 9 sessions using 2-s presentations of 4-Hz flickering dots covering the full visual field, followed by 26-s inter-stimulus intervals (Fig. 3A). Subjects perform a fixation-dot task throughout to encourage stable fixation and visual attention. High-resolution (0.9-mm voxels) fMRI data are obtained using a 3T GE Signa scanner. Acquisition (1.5 s/volume) uses a 2-shot spiral trajectory on 8 slices (90-mm FOV, 25-ms TE, 750-ms TR) oriented normally to the calcarine sulcus in posterior occipital cortex, to cover portions of visual areas V1—3. We average the time series from a set of strongly responding voxels (top 50% of contrast-to-noise-ratio), to obtain the averaged HRF for two regions-of-interest (ROIs): striate visual cortex (V1) and extrastriate cortex (V2 and V3 combined, termed V23). We separate these ROIs because substantial differences in their cytoarchitecture could potentially lead to different HRFs. Each session produces 72–85 HRF measurements, depending on the number of runs collected. Our high spatial resolution allows us to use only fMRI voxels that are fully embedded in the gray matter to minimize contamination from large pial vessels.
Fig. 3.
(A) Visual stimulus for BOLD HRF measurement in cerebral cortex. (B) Temporal and amplitude parameters used to characterize the HRF and corresponding CBF and CMRO2 responses.
Fitting model to measurements
The transient mass balance equations for the cylindrical geometries in both capillary and vein are solved using a FDM. We finely grid the length of the cylinders, and approximate derivatives as centered differences. The resulting gridded system of algebraic equations is then solved for each time step to obtain the temporal evolution of the longitudinal oxygen spatial profile in all compartments. To obtain an initial set of longitudinal profiles for the capillary compartment, we use the analytical solutions for steady-state mass balance (Appendix B).
These spatial profiles are then longitudinally integrated, Eqs. (3)–(11), and fit to measurements of the BOLD response by adjusting the six CBF and CMRO2 parameters in Eqs. (12)–(13). The six parameters are initially adjusted manually to approximately match each measured HRF. From these initial parameters, we use non-linear optimization to adjust these parameters to minimize the RMS deviation between the theoretical fit and the measured HRF. Fits are deemed successful when the ratio of mean deviation of the fit to the experimental standard error is <1.
This procedure is subject to ambiguity because of local minima within the highly complex six-parameter feature space, but the initial manual adjustment helped substantially by providing a physically reasonable starting point. We also found similar results using a “default” set of initial parameters. Although there may be a plethora of possible good fits, we believe that this procedure provides parameters that well describe the HRF within the framework of our model.
Quasi-steady-state solution
To understand relationships between CBF and CMRO2 responses, we derived a quasi-steady-state mathematical form at the peak HRF where the temporal derivatives are all approximately zero (Appendix B). At the HRF peak, the CBF and CMRO2 response can be expressed as sums of resting and activation response: Uact = U0 + ΔU, Γact = Γ0 + ΔΓ. The result yields an offset linear relationship form between changes in transient CBF (ΔU) and CMRO2 (ΔΓ) responses:
| (14) |
where S is a complex parameter that depends on transient OEF, as well as many of the fixed resting-state parameters of flow, hemoglobin oxygen dissociation, and diffusion. We also obtain a reciprocal relationship between the CBF-to-CMRO2 response amplitude ratio, n = ΔU / ΔΓ, and the CMRO2 response:
| (15) |
Analysis of the model HRF
We investigate correlations between parameters of the HRF, and corresponding CBF and CMRO2 responses. We define seven parameters for HRF, CBF and CMRO2 responses (Fig. 3B). For the initial delay, a temporal parameter (THM) is obtained at the half-max of the peak. For the peak of the initial hyperoxic response, we obtain amplitude (Ap) and time (Tp) parameters. For the undershoot, we obtain amplitude (Aunder) and time (Tunder) parameters corresponding to the maximum negative response following the hyperoxic peak. Undershoot-onset-slope (Sonset) and time (Tonset) are obtained at the zero crossing of the response after the hyperoxic peak. For successful fits, we examine correlations between parameters and evaluate variance explained by linear relationships, R2.
Results
Characteristics of the arterial impulse model
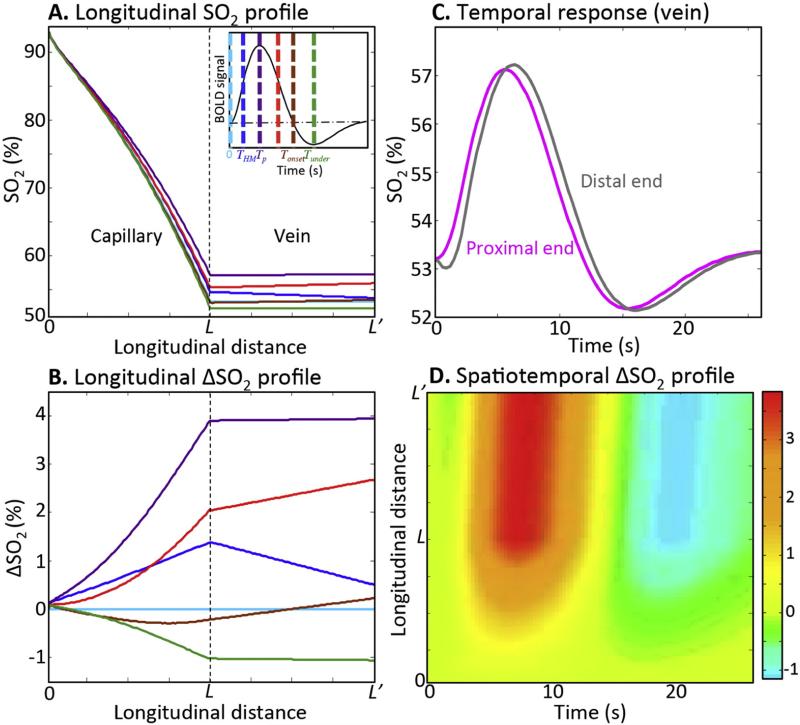
Starting from analytic resting solutions, the spatiotemporal evolution of the oxygen responses are calculated in capillary and vein. The largest variation of the oxygen saturation (~10% of oxygen extraction fraction) is predicted at the distal end of the capillary. This change in oxygen extraction fraction (OEF) by activation agrees with previous reports (Buxton, 2013; Griffeth and Buxton, 2011; He and Yablonskiy, 2007). The SO2 and ΔSO2 vary non-linearly from the proximal end of the capillary to distal end of the vein. In absolute terms, activation creates fairly small changes in oxygen saturation (Fig. 4A), but the relative changes are substantial (Fig. 4B). Profiles are shown at six different time points, which are keyed to colored vertical lines along the corresponding volume integrated BOLD response (Fig. 4A, inset). The capillary dynamics are fairly complex. As flow rises initially, relative oxygen saturation rises and develops curvature, then sags downward before inverting to become the undershoot with reversed curvature. In the venous compartment, longitudinal profiles are more linear with strong correlations between temporal and spatial gradients. At onset, peak, and undershoot times, the spatial gradients are relatively flat, while at times of strong temporal change, the gradients are relatively large; this is a manifestation of transient convective transport through this compartment. Accordingly, there is a temporal lag between the proximal and distal ends of the SO2 response in the vein (Fig. 4C). The substantial ΔSO2 variation along the vessel length in both capillary and vein is summarized throughout time course of the HRF (Fig. 4D).
Fig. 4.
Characteristics of the arterial impulse model. Examples of longitudinal (A) SO2 and (B) ΔSO2, profiles for six time points in capillary and vein: resting (light blue), initial half-maximum (blue), HRF peak (purple), trailing half-maximum (red), undershoot-onset (brown), undershoot peak (green). Inset shows these time points on a stereotypical HRF. (C) Examples of SO2 time course for distal (gray) and proximal (magenta) ends of the vein. (D) An example of spatiotemporal color contour map for ΔSO2 in capillary and vein.
Model fits to the measurements
We aimed to obtain 18 HRF measurements from two ROIs in nine sessions (from seven subjects), but one ROI in one session did not yield useful information because of the orientation of the slice prescription, so we present results for 17 HRF measurements. Analysis of BOLD HRF parameters shows no significant differences between V1 and V23, and between V2 and V3, and their corresponding CBF and CMRO2 response predictions.
The model estimates the contribution to the BOLD signal for four compartments: intra- and extravascular vein and capillary. There is little temporal variation in the relative contributions of these compartments, but the effects are clearest at the hyperoxic peak and the undershoot. The largest contribution (75.8 ± 1.1%) is from the extravascular venous compartment, followed by intravascular vein (16 ± 0.3%), intravascular capillary (5.1 ± 0.9%), and extravascular capillary (3.1 ± 0.3%).
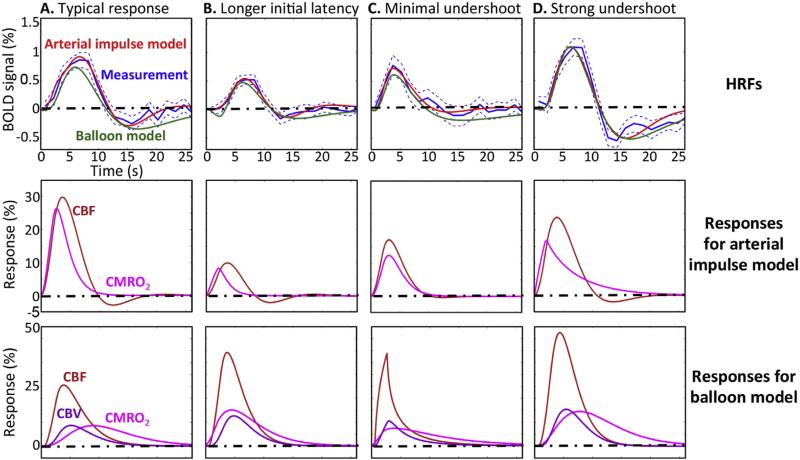
Most of the measured BOLD HRFs show stereotypical temporal response patterns consisting of initial latency, hyperoxic peak, and undershoot (Fig. 5A). Overall, the arterial impulse model (Fig. 5, red) successfully fit the measurements (blue), but the fit quality is highest during the hyperoxic peak, and tends to deteriorate somewhat during the undershoot.
Fig. 5.
(Upper) Examples of fits from arterial impulse model (red), and balloon model (green) to measured BOLD responses (blue); dotted blue lines show 68% confidence intervals. (Middle) The CBF (orange) and CMRO2 (magenta) responses predicted by the arterial impulse model. (Lower) CBF, CMRO2, and CBV (purple) responses predicted by the balloon model.
The model explains the HRF as competition between CBF (orange) and CMRO2 (magenta), shown in the middle panels of Fig. 5. At the onset of the HRF, CMRO2 immediately increases followed by the CBF; this competition creates the initial latency. Then, the HRF starts increasing as the CBF-driven oxygenation exceeds the diffusion-mediated CMRO2 demand; this is the transient “neurovascular uncoupling.” Differences in the timing and magnitude of the uncoupling create the variability in the initial latency. For example, one HRF exhibiting long initial latency (THM = 4.1 s, Fig. 5B) is predicted to correspond to a relatively prompt increase in CMRO2 compared with the CBF response. In contrast, an HRF with short initial latency (THM = 2.1 s, Fig. 5C) is predicted to correspond to slower CMRO2 responses. Generally, the CBF response continues to increase after the CMRO2 peak, but the HRF peaks significantly later than the CBF peak (mean delay 2.1 s, p < 0.01). This delay corresponds to the longitudinal transport of oxygen along the length of the vessels, driven by the corresponding CBF and CMRO2 responses.
We observe significant undershoot amplitudes (Aunder) in all of the HRFs (mean amplitude 0.24 ± 0.13%; p < 0.01). However, there are substantial session-to-session variations of the undershoot amplitude. The model fits these variations well with combinations of CBF oscillation and slow CMRO2 recovery. In the typical HRF (Fig. 5A), the BOLD undershoot is largely driven by CBF undershoot, while HRFs with small undershoot (e.g., Fig. 5C) are predicted to correspond to small CBF undershoot. On the other hand, a combination of CBF undershoot and slow CMRO2 decay can form HRFs exhibiting strong undershoot with slow recovery to baseline (Fig. 5D).
We also fit the measured HRFs using the balloon model (Fig. 5, upper panels, green curves; see Appendix C for details). The corresponding CBF, CMRO2 and CBV (lower panels) show the reliance of this model on venous dilation effects to match both early- and late-time dynamics of the HRF. Overall, the balloon model did not perform as well as the new arterial impulse model; successful fits were obtained for only 10 of the 17 measured HRFs. We consistently observe that the balloon model fails to fit the varied late-time behaviors of the measurements.
Fit parameters are summarized in Table 2. There are substantial session-to-session variations for both CBF and CMRO2 peak amplitudes (Ap), but the variability is within the range of previous measurements (Feng et al., 2004; Griffeth and Buxton, 2011; Huo et al., 2014; Ito et al., 2005). The predicted oscillation frequency of the HRF is fairly stable among the measurements (0.052 ± 0.009 Hz), consistent with previous extravascular oxygen measurements and modeling (Kim et al., 2013; Thompson et al., 2003) (0.064 ± 0.016 Hz). Damping times of the model fits were somewhat more variable (3.7 ± 0.8 s), and are substantially shorter and less variable than those observed for the tissue oxygen data (11 ± 11 s), which exhibited much more undershoot and oscillation.
Table 2.
Mean and standard deviations of fit parameters.
| τ (S) | f (Hz) | η (s) | ξ | Tp (s) | Ap (%) | Tunder (s) | Aunder (%) | |
|---|---|---|---|---|---|---|---|---|
| HRF | 3.7 ± 0.8 | 0.052 ± 0.009 | 2.4 ± 1.2 | 1.8 ± 0.5 | 5.9 ± 1.0 | 0.93 ± 0.22 | 15.5 ± 1.7 | 0.24 ± 0.13 |
| CBF | 3.7 ± 0.3 | 21.6 ± 10.5 | 13.7 ± 1.9 | 1.6 ± 0.9 | ||||
| CMRO2 | 3.0 ± 0.8 | 15.8 ± 10.8 |
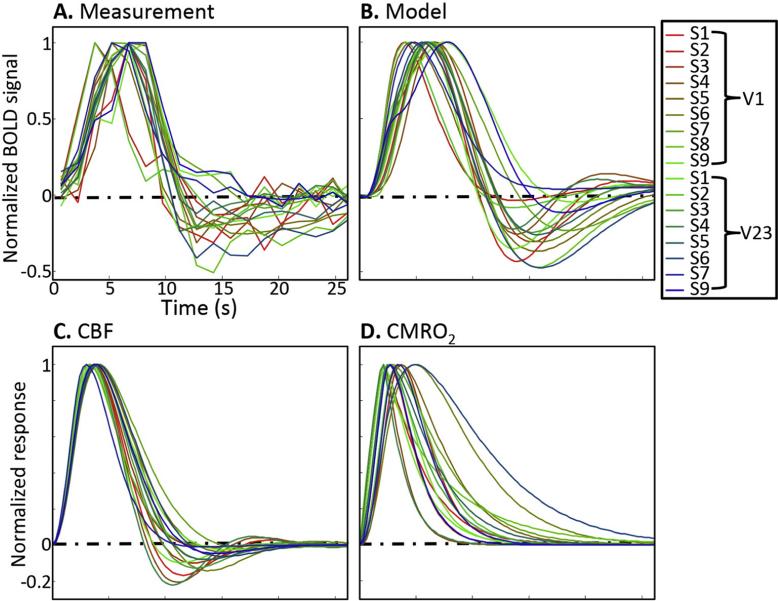
We normalize all measurement time series, their model fits, and corresponding CBF and CMRO2 by their maximum values to compare response waveforms across sessions (Fig. 6). Experimentally, we observe substantial session-to-session variations among the HRF time courses. In general, variability is relatively small at early times, and grows larger after the hyperoxic peak. The normalized-model HRFs again show good correspondence to the measurements (Fig. 6B). Normalized CBF responses (Fig. 6C) follow a similar pattern as the HRFs: similar shapes before the hyperoxic peak, and much larger session-to-session variations after the peak. These features correspond to the stability of the oscillation frequency, and the session-to-session variability of the flow damping parameter. Normalized CMRO2 responses (Fig. 6D) generally exhibit a prompt increase to their peak, followed by slow decay back to baseline, but show much greater variability throughout their time courses than the predicted CBF responses.
Fig. 6.
Time series of (A) BOLD measurements, (B) models, with corresponding (C) CBF and (D) CMRO2, all normalized by their maximum values. Each colored line corresponds to a different HRF measurement. The comparison highlights the periods of temporal stability and variability among the HRFs.
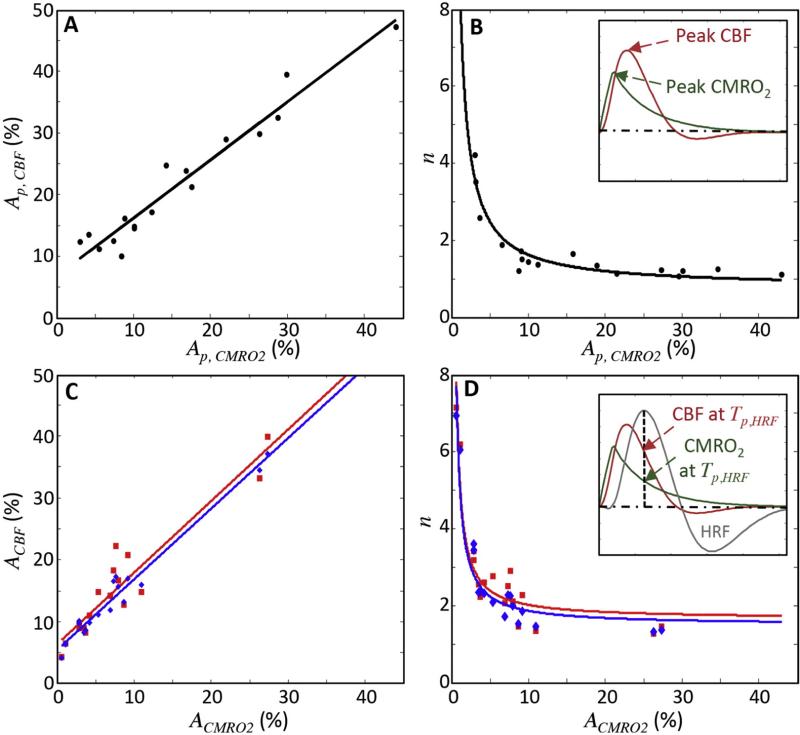
The consistent early-time behavior of the HRF is manifest in several ways. First, the time-to-peak (Tp,HRF) of the HRFs is relatively stable at 5.9 ± 1.0 s. The model predicts that the early time behavior of both CBF and CMRO2 responses are correspondingly consistent across HRFs (Figs. 6C, D). Moreover, the model shows strong and significant relationships between the peak amplitudes. There is a positive relationship between the CBF and CMRO2 peak amplitudes (R2 = 0.94, slope = 0.95, p < 0.01; Fig. 7A). This offset linear relationship is consistent with a strongly nonlinear relationship between the CBF-to-CMRO2 amplitude ratio (n) and the CMRO2 amplitude (Ap,CMRO2); the range of n in our data is 1–4 (Fig. 7B). Using the predicted peak CBF and CMRO2 amplitudes, this nonlinear relationship can be very well fit by a simple reciprocal relationship; n = a / Ap,CMRO2 + b (black line; R2 = 0.9; Fig. 7B).
Fig. 7.
(A-B) Correlations between peak CBF and peak CMRO2 responses for the 17 HRFs; inset in (B) shows example of peak CBF and peak CMRO2 corresponding to one data point. (C–D) Comparison of correlations between full model (blue) and quasi-steady-state approximation (red) at peak HRF; inset in (D) shows an example of the CBF and CMRO2 responses at HRF peak for one data point.
Both of these relationships are well explained by the quasi-steady-state limit of our model (Eqs. (14)–(15); Figs. 7C–D). The quasi-steady-state assumption only holds at the HRF peak (Fig. 7D inset). So, we use the full model to obtain corresponding CBF and CMRO2 responses at the HRF peaks for all sessions (Figs. 7C–D, blue points), and compare them with CBF and CMRO2 responses analytically obtained from the quasi-steady-state assumption (red points). Both of them show strong linear correlations between CBF and CMRO2 responses (blue line: R2 = 0.93, slope = 1.17, p < 0.01; red line: R2 = 0.82, slope = 1.18, p < 0.01; Fig. 7C). For a set of the predicted CMRO2 responses, the calculated CBF responses from Eq. (14) are similar to those from the full model, demonstrating the accuracy of quasi-steady-state approximation (R2 = 0.98, root-mean-square error = 2.2%). Examining the dependence of response ratio n vs. CMRO2 at the HRF peak, the full model (Fig. 7D, red points) and quasi-steady-state approximation (blue points) again show good agreement (R2 = 0.98, RMSE = 0.32). Accordingly, the data thus confirm the reciprocal relationship between n and the CMRO2 response from the full model (Fig. 7D, red line), which is very similar (RMSE = 0.15) to the quasi-steady state prediction (Eq. (15); Fig. 7D, blue line).
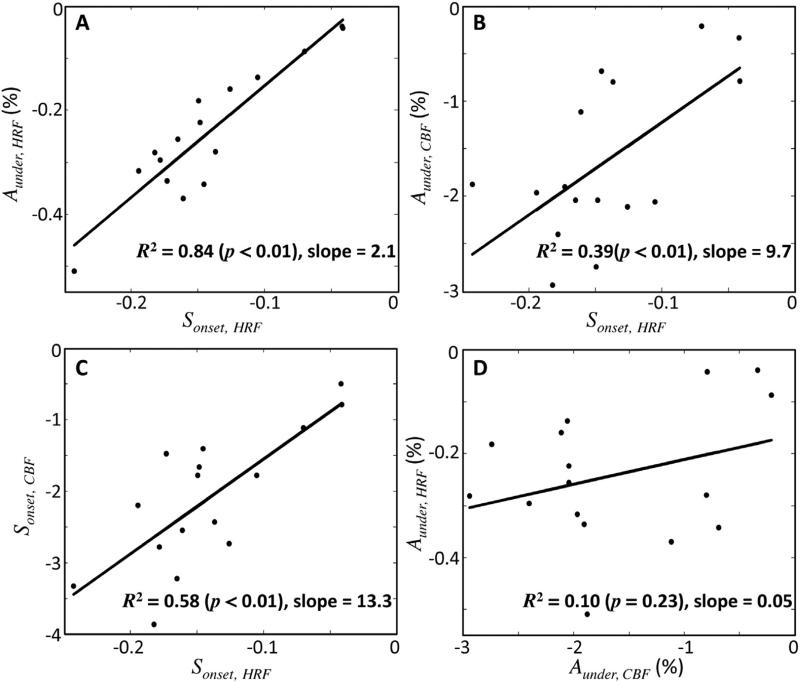
In contrast to the generally stereotypical early-time behavior, the HRF undershoot varies substantially among measurements. Despite this variability, there is a strong correlation between the HRF slope at undershoot onset (Sonset,HRF) and the corresponding undershoot amplitude (R2 = 0.84, p < 0.01, slope = 2.1; Fig. 8A). In other words, the faster the decay of the hyperoxic peak, the greater the subsequent undershoot. Our model explains this behavior with the underdamped CBF response: both the predicted CBF undershoot amplitude (Aunder,CBF) and its slope at undershoot onset (Sonset,CBF) show significant correlations with Sonset,HRF (CBF undershoot amplitude: p < 0.01, R2 = 0.39, slope = 9.7, Fig. 8B; CBF undershoot slope: p < 0.01, R2 = 0.58, slope = 13.3, Fig. 8C). However, there is no significant correlation between HRF-undershoot amplitude and CBF-undershoot amplitude (p = 0.23; R2 = 0.10; slope = 0.05, Fig. 8D).
Fig. 8.
Correlations among the undershoot parameters. (A) Strong linear correlation between measured HRF undershoot amplitude and HRF slope at undershoot onset. (B) Correlation between predicted CBF amplitude and HRF slope at undershoot onset. (C) Correlation of predicted CBF slope at undershoot onset with HRF slope at undershoot onset. (D) No significant correlation between HRF undershoot amplitude and CBF undershoot amplitude is observed.
Discussion
For over a decade, volume change in the venous compartment was considered a key feature for the BOLD HRF (Buxton et al., 2004; Buxton et al., 1998; Griffeth and Buxton, 2011; Mandeville et al., 1999; Obata et al., 2004). However, recent experiments using optical imaging techniques reported no significant change in venous CBV for brief neural activation. In fact, they observed strong and prompt volume changes in the arterial side. For example, Hillman et al. characterized the depth-resolved hemodynamic responses in individual arterioles and veins evoked by 4-s somatosensory stimulus using two-photon laser microscopy in rat gray matter. They found significant capillary hyperemia in the activated region, as well as prompt upstream arterial vasodilation. However, there was no significant volume change in the venous vasculature during neural activation (Hillman et al., 2007). Another two-photon imaging study produced hemodynamic responses by inducing brief seizure activity using pharmaceutical manipulation, and measured volume changes in corresponding pial arteries, penetrating arterioles, precapillary arterioles, and capillaries during neural activation (Fernandez-Klett et al., 2010). Both transient flow speed and volume changes were observed in all upstream arterial vessels, but there was no dilation in capillaries, which implied active flow control by upstream pial arteries and penetrating/precapillary arterioles. Pial arteries and veins also showed similar dynamics in optical measurements of vessel-diameter changes evoked by 20-s somatosensory stimulation in anesthetized rats (Vazquez et al., 2010). No dilation was seen in veins with ~150–350 μm diameter, while significant volume changes were found in arterioles (~80–130 μm diameter). Drew et al. measured arteriolar and venular diameters for three different vibrissa stimulation durations in mice with 20-ms puffs of air (single puff, 10-s stimulation train with 50% duty cycle, and 30-s stimulation train) using two-photon laser microscopy. They found that brief stimulation led only to arterial dilation, while long stimulation periods produced large prompt arterial dilation followed by smaller gradual venous dilation (Drew et al., 2011). Recently, they also measured vessel dilations and corresponding CBF responses in awake, behaving rats, and reported fast arterial (5.5 ± 5.1 s) and slow venous (25.1 ± 17.9 s) time constants. These results also showed that the pial artery dilation evoked by locomotion had a linear relationship with the corresponding CBF response (Huo et al., 2014).
Here, we establish a biomechanical model that includes the hypothesis that prompt upstream arterial dilation is a key physiological mechanism for the HRF, and link this description to the BOLD signal to formulate a new arterial impulse model. Measurements using high-resolution fMRI demonstrate the efficacy of the model.
The arterial impulse model has three longitudinal compartments (artery, capillary, and vein) to describe the physiology of the HRF. In the arterial compartment, the prompt dilation corresponding to neural activation generates an underdamped flow response that propagates to the downstream capillary and vein. In the capillary, we obtain longitudinal oxygen-saturation profiles by solving differential equations (with dissociation, convection, and diffusion dynamics) within three radial divisions (erythrocyte, plasma, and extravascular) driven by the upstream CBF response and local CMRO2 demand. In the vein, there is no radial oxygen diffusion, but blood flow and oxygen dissociation combine to give longitudinal oxygen transport. The model links the arterial dilation and flow dynamics to oxygen transport within capillary and venous compartments, and thereby obtains the venous compartment oxygen saturation that has the greatest contribution (~90%) to the BOLD signal.
In this model, we considered both intravascular and extravascular contributions to the BOLD signal. Although intravascular venous and capillary volume fraction is small (~3.6%) (Ladurner et al., 1976; Phelps et al., 1979), the model shows a substantial intravascular contribution (~20% of total BOLD response). This result is consistent with previous reports that intravascular signal change in blood, per unit volume, is more than an order of magnitude higher than that in extravascular tissue (Boxerman et al., 1995).
By appropriately neglecting venous volume effects, our model greatly simplifies the interpretation of BOLD HRF as a competition between oxygen supply (delivered by CBF) and demand (CMRO2). Notably, there is an initial brief decoupling of CBF from CMRO2. The CMRO2 response is always predicted to come first, which corresponds to oxygen demand from neural activity, followed by the CBF response that supplies oxygen and other metabolic substrates. For the first few seconds, the CMRO2 responses are predicted in most measurements to be higher than the CBF responses, and the degree of this local decoupling determines the duration of the initial latency of the HRF. For example, there is a long initial latency in Fig. 5B, which the model explains as CMRO2 demand increasing faster than the CBF, while there is a minimal initial latency in Fig. 5C, which the model explains as greater temporal synchrony between the CMRO2 and CBF responses.
After the CMRO2 peak, the CBF response continues to increase, reaching its peak at ~3.8 s. Remarkably, the HRF peak, the most prominent feature of the BOLD HRF, occurs substantially later at 5.9 s. Our model explains this decoupling of BOLD response from metabolism as a convective response delay. Although arterial vasodilation follows the local transient neural activity, the consequent blood flow has momentum that will continue to provide more blood and oxygen in the microvascular network, producing the delayed CBF. Moreover, these blood-flow effects introduce different convective delays in the different compartments. In particular, the flow effect occurs latest in the venous compartment, thus producing the late peak of the HRF. As the blood flows through the compartments, it produces longitudinal gradients in oxygen saturation that must propagate fully to establish peak oxygen saturation at the HRF peak. The linear convective gradients are most clearly evident in the venous compartment because of the absence of transmural oxygen diffusion (Fig. 4A). The corresponding temporal decoupling is then evident in the time delay between the oxygen saturation peaks at the proximal and distal ends of the vein (Fig. 4B).
The conventional balloon model was also able to fit the measured HRFs, but its performance was inferior, particular for the late-time dynamics of the HRF. The balloon model also relied on venous CBV changes to obtain detailed fits, but these changes have not been observed experimentally. Moreover, balloon models generally fix the CBF/CMRO2 response ratio n, and utilize an unexplained temporal delay between these response components. By contrast, the arterial impulse model allows the CBF and CMRO2 responses to vary appropriately based on oxygen mass balance within the dynamic constraints of our convention–diffusion transport model. Thus, the new model provides a more detailed, physiologically complete description of the BOLD HRF.
A number of previous models have included convection–diffusion transport. Huppert et al. (2007) combined convection–diffusion transport with a delayed-compliance Windkessel model to obtain excellent fits to experimental optical imaging data. However, this model was extremely complex, including many parameters that necessitated a much more intricate fitting procedure; moreover, this model still relied on a venous dilation effects. Also, a 3D convection–diffusion model was developed for direct application to the complex measured topology of the vascular network (Fang et al., 2008). This model was then applied and expanded with multiple imaging techniques (two-photon microscopy, confocal microscopy, and fMRI) to consider the effect of individual vascular compartments on the BOLD signal (Gagnon et al., 2015). The model predicted the precise dynamics of SO2 profiles of the actual vascular network, providing detailed understanding of microvascular responses that compose the BOLD signal. While the detail and scope of this model is admirable, our approach has two substantial advantages. First, our model is much simpler. We used a cylindrical vascular unit with weighted volume fractions for capillary and venous compartments. Thus, we aimed to capture the dominant features of the oxygen transport in the simplest possible geometry. Accordingly, our model requires only two partial differential equations with six independent parameters for CBF and CMRO2 responses. This simple model successfully fit the variable dynamics of BOLD HRF measurements across subjects and sessions, providing physiologically reasonable estimates of corresponding CBF and CMRO2 responses. Second, we do not assume a fixed ratio of CBF-to-CMRO2 response; this ratio varies as needed to fit the measurements.
Various relationships between model parameters and the HRF measurements buttress our interpretation of neurovascular and neurometabolic coupling consequent to brief neural stimulation. The model fits to the measured HRFs show an offset linear relationship (approximately unity slope) between CBF and CMRO2 peak amplitudes (Fig. 7A). Thus, averaged over each gray-matter ROI, CBF and CMRO2 responses are predicted to vary together linearly, although CBF always exceeds CMRO2.
This offset in the linearity between CBF and CMRO2 is consistent with non-linearities in the BOLD response that have been observed and characterized in a number of reports (Friston et al., 2000; Pfeuffer et al., 2003; Vazquez and Noll, 1998). Largest non-linearities were generally observed for very short stimulation durations, in response to which we expect very low metabolic demand and very small CMRO2 response. In these circumstances, our model predicts a breakdown in linearity because small increases CMRO2 will create relatively large changes in CBF (see Eq. (14)).
The quasi-steady state approximation at the HRF peak explicitly describes this offset linear relationship (Fig. 7C). Consider the offset in this relationship, the second and third terms on the right side of Eq. (14). The offset corresponds to the disparity between oxygen supply and demand, because blood flow transports oxygen longitudinally far more effectively than the combination of dissociation and diffusion across the blood vessel walls (Buxton and Frank, 1997; Uludag et al., 2004). At rest, the excess longitudinal transport maintains the requisite transmural gradient so that diffusion can supply the steady metabolic demand. During activation, this equilibrium is disturbed, resulting in the linear deviation from the resting state. The increase in metabolic demand requires a disproportionate increase in longitudinal oxygen supply. At the peak of the HRF, the quasi-steady-state relationship approximates this disparity by the slope term L/S, explicitly describing how the transient decoupling of supply and demand is simply a manifestation of the relative effectiveness of convection over dissociation and diffusion.
Moreover, there is an interesting non-linear relationship between the ratio of CBF-to-CMRO2 amplitudes (n) and CMRO2 amplitude (Fig. 7B). For over a decade, this ratio has been investigated to quantify the degree of the neurovascular decoupling, and a wide range of values have been reported; n = 1.3–5 using fMRI (Davis et al., 1998; Griffeth and Buxton, 2011; Kastrup et al., 2002; Uludag et al., 2004), and n = 6–10 for earlier studies using PET (Fox and Raichle, 1986; Fox et al., 1988). The arterial impulse model predicts that n is within the fMRI range. More importantly, the model shows that n is not a fixed value, but decreases with increasing CMRO2 peak amplitude in a simple reciprocal relationship. A small metabolic demand increase requires a large relative boost in flow, but for large metabolic demand, n becomes approximately constant at its resting value. The volume-averaged CBF and CMRO2 responses are more closely coupled to one other as metabolic demand increases. This closer coupling for strong-activation regimes is consistent with the several studies that show a near-linear relationship between the BOLD response and simultaneous measurements of electrophysiology (Goense and Logothetis, 2008; Logothetis, 2003; Logothetis et al., 2001).
At the HRF peak, the quasi-steady-state solution also provides a reciprocal relationship, and the calculated n is nearly identical to that predicted from the full model (Fig. 7D). The quasi-steady-state solution explicitly quantifies how the reciprocal relationship (Eq. (15)) is a consequence of the offset-linear relationship (Eq. (14)). The quasi-steady state at the HRF peak is an approximation because the oxygen concentrations in the radial compartments (erythrocyte, plasma and extravascular) do not reach their peak values at the same time as the HRF. So, the temporal gradient for each compartment will not be precisely zero at the HRF peak. However, we find that the predicted blood flow amplitudes from the quasi-steady state analytic solutions (Figs. 7C–D, blue) are very similar to those from our full model (red).
The arterial impulse model thus quantifies the competition between convection and diffusion precisely, and this results in the variable n. The simple offset linear relationship between CBF and CMRO2 emerges naturally from the mass balance (Eqs. (B.6)–(B.7)). In fact, this relationship is confirmed explicitly by the quasi-steady-state approximation to the dynamics despite the intricacies of the coupled systems of partial differential equations. Thus, the new model provides an extremely compact and logical description of BOLD response physiology.
The measured HRF undershoot amplitudes are very strongly correlated with their corresponding HRF undershoot-onset-slopes (Sonset,HRF), Fig. 8A. Strong undershoot is observed following fast decreases in the BOLD signal after the hyperoxic peak, while minimal undershoot is observed following slow decreases in the signal. This suggests a causal relationship between the dynamics driving the oxygen-concentration decrease and its subsequent minimum that is very similar to the underdamped behavior of the CBF. In fact, we also see strong linear correlations between the measured HRF undershoot-onset slope and both the CBF undershoot amplitude (Aunder,CBF, Fig. 8B) and the corresponding CBF undershoot-onset slope (Sonset,CBF, Fig. 8C). These observations bolster the notion that the CBF response strongly affects the late-time dynamics of the HRF. Strong HRF undershoots are tightly coupled to the underdamped upstream arterial flow response.
However, the undershoot is not driven entirely by flow. In fact, the HRF undershoot amplitude is not strongly correlated with the corresponding CBF undershoot (Fig. 8D). Our model explains this as a variable contribution of late-time CMRO2 to the HRF undershoot. The model predicts relatively fast increases and slow decays to baseline, consistent with previous CMRO2 measurements (Masamoto and Tanishita, 2009; Vazquez et al., 2010). For example, we observe that some of the HRFs exhibit a slow return to baseline after undershoot, and the model explains this behavior as slow CMRO2 decay to baseline (Fig. 5D). More experiments, perhaps using arterial spin labeling MRI to obtain simultaneous BOLD and flow measurements (Huppert et al., 2006; Liu and Brown, 2007; Liu and Wong, 2005; Liu et al., 2002), are needed to confirm our prediction of underdamped flow behavior.
The inclusion of inertia may also help to explain previously observed time-scale changes in the HRF produced by baseline CBF changes. For example, hyperemia induced by hypercapnia results in a slower CBF response to transient vasodilation and a slower HRF (Ances et al., 2001; Bakalova et al., 2001; Liu et al., 2004; Matsuura et al., 2000). Our model can explain this effect as an increase in baseline blood flow that increases the kinetic energy stored in blood flow, which thereby increases the inertial “stiffness” of the system, decreasing the CBF response frequency and slowing the CBF and HRF. However, these effects depend upon both the initial conditions and detailed topology of the vascular network, so further elaborations upon our model will be necessary to confirm such explanations.
The arterial impulse model requires solution of a system of partial differential equations. It is useful to have a simple analytic form for the BOLD HRF to enable analysis. The difference of two gamma-variate functions is a popular heuristic form for the HRF. Motivated by the CBF and CMRO2 responses in our model, we suggest an alternative form consisting of the difference between a damped sinusoid and a gamma-variate function, e.g.,: F(t) = As exp (−t / τs) sin(fs t) − Ag tεg − 1exp (−t / τg). This expression is closer to the predicted dynamics of the BOLD response, and will better match measured HRFs that exhibit oscillatory late-time behavior.
We emphasize that the arterial impulse model is only appropriate for the BOLD response evoked by brief neural activation. For longer periods of activation, there is substantial evidence that sluggish venous volume effects become significant, and it is likely that these effects can be modeled using the well-investigated balloon models. A full model of the BOLD response must include prompt arterial dilation and the slow venous dilation effects that have been well documented experimentally (Drew et al., 2011; Fernandez-Klett et al., 2010; Hillman et al., 2007; Huo et al., 2014).
Acknowledgments
We thank Michael Beauchamp, and Jeffrey Yau for providing thoughtful comments and advice. Rez Khan, Sucharit Katyal, Clint Greene, Elizabeth Halfen, and Evan Luther assisted with gathering the experimental data. This work was supported by NIH R21HL108143.
Appendix A
We derive the equations for the arterial impulse model of the BOLD signal. Total signal consists of two compartments: intravascular (subscript I) and extravascular tissue (subscript E):
| (A.1) |
where v is blood volume fraction. We ignore the signal change by arterial dilation, so the volume fraction of the each compartment is:
| (A.2) |
| (A.3) |
where subscript c and v represent capillary and vein respectively. We assume no volume change in both capillary and vein (Drew et al., 2011; Fernandez-Klett et al., 2010; Hillman et al., 2007; Vazquez et al., 2010). Therefore, the volume is constant for both resting (subscript 0), and activation (subscript 1). Resting signal is:
| (A.4) |
During activation, the signal is:
| (A5) |
where TE is echo time, is the change in the MR signal relaxation rate during activation. The BOLD signal is fractional change in the MR signal:
| (A.6) |
Substituting ε, the ratio of intrinsic intravascular signal to extravascular signal, into Eq. (A.6):
| (A.7) |
Appendix B
B.1. Full solutions
We derive partial differential equations for mass balance between three compartments (erythrocyte, plasma, and extravascular tissue) in the capillary:
| (B.1) |
| (B.2) |
| (B.3) |
where Q is concentration, F is the oxygen dissociation flux, U is flow speed, A is a diffusion rate constant, c is volume per length, and subscript h, p, and e represent erythrocyte, plasma, and extravascular tissue respectively. A weighted sum of Eqs. (B.1) and (B.2) eliminates the oxygen-dissociation flux term, F(z,t):
| (B.4) |
To deal with the non-linear character of oxygen dissociation, we can approximate the Hill equation using a quadratic fit to describe oxygen dissociation within a limited range of oxygen saturation, 50–93% O2 saturation, so:
| (B.5) |
where k1 = −1043, k2 = 197.74 and k3 = −0.82. We substitute this approximation into Eq. (B.4) to describe oxygen mass balance for the plasma compartment including oxygen dissociation:
| (B.6) |
We also can rewrite Eq. (B.3) for the extravascular compartment using volume ratio α = (Ch + Cp)/Ce, and hematocrit, Ht:
| (B.7) |
Eqs. (B.6) and (B.7) are our chosen form for numerical solution of the transient oxygen mass-balance equations.
For the vein, there are only the flow and dissociation terms in the mass balance, because we assume no oxygen transport to the tissue:
| (B.8) |
| (B.9) |
Use Eq. (B.6) to include oxygen dissociation, and form the weighted sum of Eqs. (B.8) and (B.9) to eliminate F:
| (B.10) |
Thus, venous mass balance equation is simply:
| (B.11) |
This, together with Eq. (B.6), defines oxygen transport in the vein.
B.2. Steady-state solutions
At rest, we can approximate the dynamics by setting all time derivatives to zero. In the vein, this simply forces all oxygen concentrations to be spatially constant. In the capillary, the dynamics are more complex. Combining Eqs. (B.6) and (B.7) in the steady state yields:
| (B.12) |
Applying the boundary condition, Qp = Qp,s, at the proximal end (z = 0):
| (B.13) |
Therefore, the analytic steady-state solution of the system is:
| (B.14) |
We can obtain the capillary length (L) by applying the distal boundary condition, Qp = Qp,L, at z = L:
| (B.15) |
At the peak of the HRF, we can assume an approximate steady state because the temporal gradient is nearly zero, a similar relationship to Eq. (B.15) can be held between flow speed, Uact = U0 + ΔU, and CMRO2, Γact = Γ0 + ΔΓ at HRF peak:
| (B.16) |
Let
| (B.17) |
in Eq. (B.16), and one obtains manuscript Eq. (14).
Appendix C
We reconstruct a balloon model for comparison purpose. We use the modified balloon model (Buxton et al., 2004). The basic BOLD equation is:
| (C.1) |
where vv is venous volume fraction, q is normalized total deoxyhemoglobin, x is the normalized volume of the venous balloon, and a1 and a2 are dimensionless parameters. The mass balance of the balloon model for blood and deoxyhemoglobin is:
| (C.2) |
| (C.3) |
| (C.4) |
where m is normalized CMRO2, f is normalized CBF, fout is normalized outflow from the balloon, τMTT is mean transit time through the balloon at rest, α is flow-volume coefficient at rest, and τ is a time constant. The forms of the CBF and CMRO2 responses are postulated as a gamma-variate function h(t). We assume that these two transient impulse responses in CBF and CMRO2 are driven by neural activity, which we model as a 2-second duration rectangular pulse N(t). Then, the CBF and CMRO2 responses for activation are obtained by convolution with N(t):
| (C.5) |
| (C.6) |
where f1 and m1 are scaling amplitude parameters, δtf and δtm are delay time of CBF and CMRO2 responses. The ratio of CBF to CMRO2 responses, n = (f1 − 1) / (m1 − 1) is fixed (n = 2). Time delay of CBF relative to CMRO2 responses (δt = δtf − δtm) is assumed for initial delay of the HRF.
To fit the balloon model to our measured HRFs, we performed non-linear optimization with six parameters: damping time and shape coefficient of the gamma-variate function for each response, scaling amplitude parameter (f1) and relative time delay (δt).
References
- Ances BM, Greenberg JH, Detre JA. The effects of graded hypercapnia on the activation flow coupling response due to forepaw stimulation in a-chloralose anesthetized rats. Brain Res. 2001;911:82–88. doi: 10.1016/s0006-8993(01)02721-4. [DOI] [PubMed] [Google Scholar]
- Bakalova R, Matsuura T, Kanno I. Frequency dependence of local cerebral blood flow induced by somatosensory hind paw stimulation in rat under normo-and hyper-capnia. Jap. J. Physiol. 2001;51:201–208. doi: 10.2170/jjphysiol.51.201. [DOI] [PubMed] [Google Scholar]
- Binzoni T, Quaresima V, Ferrari M, Hiltbrand E, Cerretelli P. Human calf micro-vascular compliance measured by near-infrared spectroscopy. J. Appl. Physiol. 2000;88:369–372. doi: 10.1152/jappl.2000.88.2.369. [DOI] [PubMed] [Google Scholar]
- Boxerman JL, Bandettini PA, Kwong KK, Baker JR, Davis TL, Rosen BR, Weisskoff RM. The intravascular contribution to fMRI signal change: Monte Carlo modeling and diffusion-weighted studies in vivo. Magn. Reson. Med. 1995;34:4–10. doi: 10.1002/mrm.1910340103. [DOI] [PubMed] [Google Scholar]
- Buxton RB. Dynamic models of BOLD contrast. Neuroimage. 2012;62:953–961. doi: 10.1016/j.neuroimage.2012.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton RB. The physics of functional magnetic resonance imaging (fMRI). Rep. Prog. Phys. 2013;76:096601. doi: 10.1088/0034-4885/76/9/096601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton RB, Frank LR. A model for the coupling between cerebral blood flow and oxygen metabolism during neural stimulation. J. Cereb. Blood Flow Metab. 1997;17:64–72. doi: 10.1097/00004647-199701000-00009. [DOI] [PubMed] [Google Scholar]
- Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magn. Reson. Med. 1998;39:855–864. doi: 10.1002/mrm.1910390602. [DOI] [PubMed] [Google Scholar]
- Buxton RB, Uludag K, Dubowitz DJ, Liu TT. Modeling the hemodynamic response to brain activation. Neuroimage. 2004;23:S220–S233. doi: 10.1016/j.neuroimage.2004.07.013. [DOI] [PubMed] [Google Scholar]
- Cassot F, Lauwers F, Fouard C, Prohaska S, Lauwers-Cances V. A novel three-dimensional computer-assisted method for a quantitative study of microvascular networks of the human cerebral cortex. Microcirculation. 2006;13:1–18. doi: 10.1080/10739680500383407. [DOI] [PubMed] [Google Scholar]
- Clark D, Erdmann W, Halsey J, Strong E. Oxygen diffusion, conductivity and solubility coefficients in the microarea of the brain. Oxygen Transport to Tissue—IIISpringer. 1978:697–704. doi: 10.1007/978-1-4684-8890-6_96. [DOI] [PubMed] [Google Scholar]
- Davis TL, Kwong KK, Weisskoff RM, Rosen BR. Calibrated functional MRI: mapping the dynamics of oxidative metabolism. Proc. Natl. Acad. Sci. U. S. A. 1998;95:1834–1839. doi: 10.1073/pnas.95.4.1834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devor A, Sakadzic S, Saisan PA, Yaseen MA, Roussakis E, Srinivasan VJ, Vinogradov SA, Rosen BR, Buxton RB, Dale AM. “Overshoot” of O2 is required to maintain baseline tissue oxygenation at locations distal to blood vessels. J. Neurosci. 2011;31:13676–13681. doi: 10.1523/JNEUROSCI.1968-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew PJ, Shih AY, Kleinfeld D. Fluctuating and sensory-induced vasodynamics in rodent cortex extend arteriole capacity. Proc. Natl. Acad. Sci. U. S. A. 2011;108:8473–8478. doi: 10.1073/pnas.1100428108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Q, Sakadzic S, Ruvinskaya L, Devor A, Dale AM, Boas DA. Oxygen advection and diffusion in a three-dimensional vascular anatomical network. Opt. Express. 2008;16:17530–17541. doi: 10.1364/oe.16.17530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng C-M, Narayana S, Lancaster JL, Jerabek PA, Arnow TL, Zhu F, Tan LH, Fox PT, Gao J. CBF changes during brain activation: fMRI vs. PET. Neuroimage. 2004;22:443–446. doi: 10.1016/j.neuroimage.2004.01.017. [DOI] [PubMed] [Google Scholar]
- Fernandez-Klett F, Offenhauser N, Dirnagl U, Priller J, Lindauer U. Pericytes in capillaries are contractile in vivo, but arterioles mediate functional hyperemia in the mouse brain. Proc. Natl. Acad. Sci. U. S. A. 2010;107:22290–22295. doi: 10.1073/pnas.1011321108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc. Natl. Acad. Sci. U. S. A. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox PT, Raichle ME. Focal physiological uncoupling of cerebral blood flow and oxidative metabolism during somatosensory stimulation in human subjects. Proc. Natl. Acad. Sci. U. S. A. 1986;83:1140–1144. doi: 10.1073/pnas.83.4.1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox PT, Raichle ME, Mintun MA, Dence C. Nonoxidative glucose consumption during focal physiologic neural activity. Science. 1988;241:462–464. doi: 10.1126/science.3260686. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Mechelli A, Turner R, Price CJ. Nonlinear responses in fMRI: the balloon model, Volterra kernels, and other hemodynamics. Neuroimage. 2000;12:466–477. doi: 10.1006/nimg.2000.0630. [DOI] [PubMed] [Google Scholar]
- Frostig RD, Lieke EE, Ts'o DY, Grinvald A. Cortical functional architecture and local coupling between neuronal activity and the microcirculation revealed by in vivo high-resolution optical imaging of intrinsic signals. Proc. Natl. Acad. Sci. U. S. A. 1990;87:6082–6086. doi: 10.1073/pnas.87.16.6082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gagnon L, Sakadzic S, Lesage F, Musacchia JJ, Lefebvre J, Fang Q, Yucel MA, Evans KC, Mandeville ET, Cohen-Adad J, Polimeni JR, Yaseen MA, Lo EH, Greve DN, Buxton RB, Dale AM, Devor A, Boas DA. Quantifying the microvascular origin of BOLD-fMRI from first principles with two-photon microscopy and an oxygen-sensitive nanoprobe. J. Neurosci. 2015;35:3663–3675. doi: 10.1523/JNEUROSCI.3555-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goense JB, Logothetis NK. Neurophysiology of the BOLD fMRI signal in awake monkeys. Curr. Biol. 2008;18:631–640. doi: 10.1016/j.cub.2008.03.054. [DOI] [PubMed] [Google Scholar]
- Griffeth VE, Buxton RB. A theoretical framework for estimating cerebral oxygen metabolism changes using the calibrated-BOLD method: modeling the effects of blood volume distribution, hematocrit, oxygen extraction fraction, and tissue signal properties on the BOLD signal. Neuroimage. 2011;58:198–212. doi: 10.1016/j.neuroimage.2011.05.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grubb RL, Raichle ME, Eichling JO, Ter-Pogossian MM. The effects of changes in PaCO2 cerebral blood volume, blood flow, and vascular mean transit time. Stroke. 1974;5:630–639. doi: 10.1161/01.str.5.5.630. [DOI] [PubMed] [Google Scholar]
- Gustard S, Williams E, Hall L, Pickard J, Carpenter T. Influence of baseline hematocrit on between-subject BOLD signal change using gradient echo and asymmetric spin echo EPI. Magn. Reson. Imaging. 2003;21:599–607. doi: 10.1016/s0730-725x(03)00083-3. [DOI] [PubMed] [Google Scholar]
- He X, Yablonskiy DA. Quantitative BOLD: mapping of human cerebral deoxygenated blood volume and oxygen extraction fraction: default state. Magn. Reson. Med. 2007;57:115–126. doi: 10.1002/mrm.21108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillman E, Devor A, Bouchard MB, Dunn AK, Krauss G, Skoch J, Bacskai BJ, Dale AM, Boas DA. Depth-resolved optical imaging and microscopy of vascular compartment dynamics during somatosensory stimulation. Neuroimage. 2007;35:89–104. doi: 10.1016/j.neuroimage.2006.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu X, Yacoub E. The story of the initial dip in fMRI. Neuroimage. 2012;62:1103–1108. doi: 10.1016/j.neuroimage.2012.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huo B-X, Smith JB, Drew PJ. Neurovascular coupling and decoupling in the cortex during voluntary locomotion. J. Neurosci. 2014;34:10975–10981. doi: 10.1523/JNEUROSCI.1369-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huppert T, Hoge R, Diamond S, Franceschini MA, Boas DA. A temporal comparison of BOLD, ASL, and NIRS hemodynamic responses to motor stimuli in adult humans. Neuroimage. 2006;29:368–382. doi: 10.1016/j.neuroimage.2005.08.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huppert TJ, Allen MS, Benav H, Jones PB, Boas DA. A multicompartment vascular model for inferring baseline and functional changes in cerebral oxygen metabolism and arterial dilation. J. Cereb. Blood Flow Metab. 2007;27:1262–1279. doi: 10.1038/sj.jcbfm.9600435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito H, Kanno I, Kato C, Sasaki T, Ishii K, Ouchi Y, Iida A, Okazawa H, Hayashida K, Tsuyuguchi N. Database of normal human cerebral blood flow, cerebral blood volume, cerebral oxygen extraction fraction and cerebral metabolic rate of oxygen measured by positron emission tomography with 15O-labelled carbon dioxide or water, carbon monoxide and oxygen: a multicentre study in Japan. Eur. J. Nucl. Med. Mol. Imag. 2004;31:635–643. doi: 10.1007/s00259-003-1430-8. [DOI] [PubMed] [Google Scholar]
- Ito H, Ibaraki M, Kanno I, Fukuda H, Miura S. Changes in cerebral blood flow and cerebral oxygen metabolism during neural activation measured by positron emission tomography: comparison with blood oxygenation level-dependent contrast measured by functional magnetic resonance imaging. J. Cereb. Blood Flow Metab. 2005;25:371–377. doi: 10.1038/sj.jcbfm.9600030. [DOI] [PubMed] [Google Scholar]
- Itoh Y, Suzuki N. Control of brain capillary blood flow. J. Cereb. Blood Flow Metab. 2012;32:1167–1176. doi: 10.1038/jcbfm.2012.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastrup A, Kruger G, Neumann-Haefelin T, Glover GH, Moseley ME. Changes of cerebral blood flow, oxygenation, and oxidative metabolism during graded motor activation. Neuroimage. 2002;15:74–82. doi: 10.1006/nimg.2001.0916. [DOI] [PubMed] [Google Scholar]
- Kety SS, Schmidt CF. The nitrous oxide method for the quantitative determination of cerebral blood flow in man: theory, procedure and normal values. J. Clin. Invest. 1948;27:476. doi: 10.1172/JCI101994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S-G, Ogawa S. Biophysical and physiological origins of blood oxygenation level-dependent fMRI signals. J. Cereb. Blood Flow Metab. 2012;32:1188–1206. doi: 10.1038/jcbfm.2012.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JH, Khan R, Thompson JK, Ress D. Model of the transient neurovascular response based on prompt arterial dilation. J. Cereb. Blood Flow Metab. 2013;33:1429–1439. doi: 10.1038/jcbfm.2013.90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong Y, Zheng Y, Johnston D, Martindale J, Jones M, Billings S, Mayhew J. A model of the dynamic relationship between blood flow and volume changes during brain activation. J. Cereb. Blood Flow Metab. 2004;24:1382–1392. doi: 10.1097/01.WCB.0000141500.74439.53. [DOI] [PubMed] [Google Scholar]
- Kruger G, Kleinschmidt A, Frahm J. Dynamic MRI sensitized to cerebral blood oxygenation and flow during sustained activation of human visual cortex. Magn. Reson. Med. 1996;35:797–800. doi: 10.1002/mrm.1910350602. [DOI] [PubMed] [Google Scholar]
- Ladurner G, Zilkha E, Iliff D, Du Boulay G, Marshall J. Measurement of regional cerebral blood volume by computerized axial tomography. J. Neurol. Neurosurg. Psychiatry. 1976;39:152–158. doi: 10.1136/jnnp.39.2.152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lecoq J, Parpaleix A, Roussakis E, Ducros M, Houssen YG, Vinogradov SA, Charpak S. Simultaneous two-photon imaging of oxygen and blood flow in deep cerebral vessels. Nat. Med. 2011;17:893–898. doi: 10.1038/nm.2394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenigerfollert E. Direct determination of local oxygen-consumption of brain cortex in vivo. Pflug. Arch. Eur. J. Phy. 1977;372:175–179. doi: 10.1007/BF00585333. [DOI] [PubMed] [Google Scholar]
- Liu TT, Brown GG. Measurement of cerebral perfusion with arterial spin labeling: part 1. Methods. J. Int. Neuropsychol. Soc. 2007;13:517–525. doi: 10.1017/S1355617707070646. [DOI] [PubMed] [Google Scholar]
- Liu TT, Wong EC. A signal processing model for arterial spin labeling functional MRI. Neuroimage. 2005;24:207–215. doi: 10.1016/j.neuroimage.2004.09.047. [DOI] [PubMed] [Google Scholar]
- Liu TT, Wong EC, Frank LR, Buxton RB. Analysis and design of perfusion-based event-related fMRI experiments. Neuroimage. 2002;16:269–282. doi: 10.1006/nimg.2001.1038. [DOI] [PubMed] [Google Scholar]
- Liu TT, Behzadi Y, Restom K, Uludag K, Lu K, Buracas GT, Dubowitz DJ, Buxton RB. Caffeine alters the temporal dynamics of the visual BOLD response. Neuroimage. 2004;23:1402–1413. doi: 10.1016/j.neuroimage.2004.07.061. [DOI] [PubMed] [Google Scholar]
- Logothetis NK. The underpinnings of the BOLD functional magnetic resonance imaging signal. J. Neurosci. 2003;23:3963–3971. doi: 10.1523/JNEUROSCI.23-10-03963.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001;412:150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- Mandeville JB, Marota JJA, Ayata C, Zaharchuk G, Moskowitz MA, Rosen BR, Weisskoff RM. Evidence of a cerebrovascular postarteriole Windkessel with delayed compliance. J. Cereb. Blood Flow Metab. 1999;19:679–689. doi: 10.1097/00004647-199906000-00012. [DOI] [PubMed] [Google Scholar]
- Masamoto K, Tanishita K. Oxygen transport in brain tissue. J. Biomech. Eng. 131. 2009 doi: 10.1115/1.3184694. [DOI] [PubMed] [Google Scholar]
- Matsuura T, Fujita H, Kashikura K, Kanno I. Modulation of evoked cerebral blood flow under excessive blood supply and hyperoxic conditions. Jap. J. Physiol. 2000;50:115–123. doi: 10.2170/jjphysiol.50.115. [DOI] [PubMed] [Google Scholar]
- Menon RS, Ogawa S, Hu X, Strupp JP, Anderson P, Ugurbil K. BOLD based functional MRI at 4 Tesla includes a capillary bed contribution: echo-planar imaging correlates with previous optical imaging using intrinsic signals. Magn. Reson. Med. 1995;33:453–459. doi: 10.1002/mrm.1910330323. [DOI] [PubMed] [Google Scholar]
- Nguyen J, Nishimura N, Fetcho RN, Iadecola C, Schaffer CB. Occlusion of cortical ascending venules causes blood flow decreases, reversals in flow direction, and vessel dilation in upstream capillaries. J. Cereb. Blood Flow Metab. 2011;31:2243–2254. doi: 10.1038/jcbfm.2011.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obata T, Liu TT, Miller KL, Luh W-M, Wong EC, Frank LR, Buxton RB. Discrepancies between BOLD and flow dynamics in primary and supplementary motor areas: application of the balloon model to the interpretation of BOLD transients. Neuroimage. 2004;21:144–153. doi: 10.1016/j.neuroimage.2003.08.040. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Menon R, Tank D, Kim S, Merkle H, Ellermann J, Ugurbil K. Functional brain mapping by blood oxygenation level-dependent contrast magnetic resonance imaging. A comparison of signal characteristics with a biophysical model. Biophys. J. 1993;64:803. doi: 10.1016/S0006-3495(93)81441-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perthen JE, Lansing AE, Liau J, Liu TT, Buxton RB. Caffeine-induced uncoupling of cerebral blood flow and oxygen metabolism: a calibrated BOLD fMRI study. Neuroimage. 2008;40:237–247. doi: 10.1016/j.neuroimage.2007.10.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeuffer J, McCullough JC, Van de Moortele P-F, Ugurbil K, Hu X. Spatial dependence of the nonlinear BOLD response at short stimulus duration. Neuroimage. 2003;18:990–1000. doi: 10.1016/s1053-8119(03)00035-1. [DOI] [PubMed] [Google Scholar]
- Phelps ME, Huang SC, Hoffman EJ, Kuhl DE. Validation of tomographic measurement of cerebral blood volume with C-11-labeled carboxyhemoglobin. J. Nucl. Med. 1979;20:328–334. [PubMed] [Google Scholar]
- Ress D, Glover GH, Liu J, Wandell B. Laminar profiles of functional activity in the human brain. Neuroimage. 2007;34:74–84. doi: 10.1016/j.neuroimage.2006.08.020. [DOI] [PubMed] [Google Scholar]
- Ress D, Thompson JK, Rokers B, Khan R, Huk AC. A model for transient oxygen delivery in cerebral cortex. Front. Neuroenergetics. 2009;1:3. doi: 10.3389/neuro.14.003.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romney JS, Lewanczuk RZ. Vascular compliance is reduced in the early stages of type 1 diabetes. Diabetes Care. 2001;24:2102–2106. doi: 10.2337/diacare.24.12.2102. [DOI] [PubMed] [Google Scholar]
- Santisakultarm TP, Cornelius NR, Nishimura N, Schafer AI, Silver RT, Doerschuk PC, Olbricht WL, Schaffer CB. In vivo two-photon excited fluorescence microscopy reveals cardiac-and respiration-dependent pulsatile blood flow in cortical blood vessels in mice. Am. J. Physiol. Heart Circ. Physiol. 2012;302:H1367–H1377. doi: 10.1152/ajpheart.00417.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharan M, Singh M, Aminataei A. A mathematical model for the computation of the oxygen dissociation curve in human blood. BioSyst. 1989;22:249–260. doi: 10.1016/0303-2647(89)90066-x. [DOI] [PubMed] [Google Scholar]
- Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJ. Water proton MR properties of human blood at 1.5 Tesla: magnetic susceptibility, T1, T2, T*2, and non-Lorentzian signal behavior. Magn. Reson. Med. 2001;45:533–542. doi: 10.1002/mrm.1072. [DOI] [PubMed] [Google Scholar]
- Thompson JK, Peterson MR, Freeman RD. Single-neuron activity and tissue oxygenation in the cerebral cortex. Science. 2003;299:1070–1072. doi: 10.1126/science.1079220. [DOI] [PubMed] [Google Scholar]
- Tian P, Teng IC, May LD, Kurz R, Lu K, Scadeng M, Hillman EM, De Crespigny AJ, D'Arceuil HE, Mandeville JB, Marota JJ, Rosen BR, Liu TT, Boas DA, Buxton RB, Dale AM, Devor A. Cortical depth-specific microvascular dilation underlies laminar differences in blood oxygenation level-dependent functional MRI signal. Proc. Natl. Acad. Sci. U. S. A. 2010;107:15246–15251. doi: 10.1073/pnas.1006735107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai AG, Johnson PC, Intaglietta M. Oxygen gradients in the microcirculation. Physiol. Rev. 2003;83:933–963. doi: 10.1152/physrev.00034.2002. [DOI] [PubMed] [Google Scholar]
- Uludag K, Dubowitz DJ, Yoder EJ, Restom K, Liu TT, Buxton RB. Coupling of cerebral blood flow and oxygen consumption during physiological activation and deactivation measured with fMRI. Neuroimage. 2004;23:148–155. doi: 10.1016/j.neuroimage.2004.05.013. [DOI] [PubMed] [Google Scholar]
- Uludag K, Muller-Bierl B, Ugurbil K. An integrative model for neuronal activity-induced signal changes for gradient and spin echo functional imaging. Neuroimage. 2009;48:150–165. doi: 10.1016/j.neuroimage.2009.05.051. [DOI] [PubMed] [Google Scholar]
- van Zijl PC, Hua J, Lu H. The BOLD post-stimulus undershoot, one of the most debated issues in fMRI. Neuroimage. 2012;62:1092–1102. doi: 10.1016/j.neuroimage.2012.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazquez AL, Noll DC. Nonlinear aspects of the BOLD response in functional MRI. Neuroimage. 1998;7:108–118. doi: 10.1006/nimg.1997.0316. [DOI] [PubMed] [Google Scholar]
- Vazquez AL, Fukuda M, Tasker ML, Masamoto K, Kim SG. Changes in cerebral arterial, tissue and venous oxygenation with evoked neural stimulation: implications for hemoglobin-based functional neuroimaging. J. Cereb. Blood Flow Metab. 2010;30:428–439. doi: 10.1038/jcbfm.2009.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vovenko E. Distribution of oxygen tension on the surface of arterioles, capillaries and venules of brain cortex and in tissue in normoxia: an experimental study on rats. Pflug. Arch. Eur. J. Phy. 1999;437:617–623. doi: 10.1007/s004240050825. [DOI] [PubMed] [Google Scholar]
- Weber B, Keller AL, Reichold J, Logothetis NK. The microvascular system of the striate and extrastriate visual cortex of the macaque. Cereb. Cortex. 2008;18:2318–2330. doi: 10.1093/cercor/bhm259. [DOI] [PubMed] [Google Scholar]
- Zhao JM, Clingman CS, Narvainen MJ, Kauppinen RA, van Zijl P. Oxygenation and hematocrit dependence of transverse relaxation rates of blood at 3 T. Magn. Reson. Med. 2007;58:592–597. doi: 10.1002/mrm.21342. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Mayhew J. A time-invariant visco-elastic Windkessel model relating blood flow and blood volume. Neuroimage. 2009;47:1371–1380. doi: 10.1016/j.neuroimage.2009.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Martindale J, Johnston D, Jones M, Berwick J, Mayhew J. A model of the hemodynamic response and oxygen delivery to brain. Neuroimage. 2002;16:617–637. doi: 10.1006/nimg.2002.1078. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Johnston D, Berwick J, Chen D, Billings S, Mayhew J. A three-compartment model of the hemodynamic response and oxygen delivery to brain. Neuroimage. 2005;28:925–939. doi: 10.1016/j.neuroimage.2005.06.042. [DOI] [PubMed] [Google Scholar]