Assessment of glaucoma using extreme learning machine and fractal feature analysis

Dear Sir,

I am Dr. Kavitha S, from the Department of Electronics and Communication Engineering, Nandha Engineering College, Erode, Tamil Nadu, India. I write to present the detection of glaucoma using extreme learning machine (ELM) and fractal feature analysis. Glaucoma is the second most frequent cause of permanent blindness in industrial developed countries and its detection is essential to prevent visual damage^[1]. Development of modern digital imaging systems offered very high resolution in optic fundus imaging and applies extensively fractal geometries in order to detect and diagnose the pathologies^[2]. In the screening and monitoring, the health status of human eye, fractal analysis (FA) plays a vital role in the retinal images^[3]. FA can characterize complex geometric objects and has proved effective in various applications including detecting brain tumors and distinguishing glaucomatous from normal eyes^[4]. Bock et al^[5] proposed an automated glaucoma detection system where different generic features are compressed by an appearance based dimension reduction technique. These features types are combined by two stage classification to extract glaucoma risk index.

Energy distribution over wavelet sub bands was analyzed by Dua et al^[6] to find texture features obtained by using 2D Discrete Wavelet Transform (DWT). Wavelet features achieved an accuracy of 93%. Glaucoma evaluation based on differential entropy was performed in^[7]. An automated identification of normal and an abnormal class was discussed using Higher Order Spectra (HOS), Trace Transform (TT) and DWT features^[8]. Extracted features when fed to Support Vector Machine (SVM) classifier provided an accuracy of 91.67%, sensitivity of 90% and specificity of 93.33%. A system was discussed for the automated identification of normal and glaucoma classes using HOS and wavelet energy features in^[9]. The extracted features when fed to SVM classifier provided an accuracy of 95%, sensitivity of 93.33% and specificity of 96.67%.

A glaucoma detection system was reported by Acharya et al^[10] using a combination of texture and HOS features from fundus images. Then features after Z-score normalization when combined with random forest classifier provided an accuracy of more than 91%. Uses of FA were investigated as a basis of a system for multiclass prediction of glaucoma progression^[11]. Fractal geometry and multifractals were described by Reljin and Reljin^[12] that can be used for describing, modeling, analyzing and programming different complex shapes and signals. An effective method is proposed to characterize the spatial distribution of image patterns in fundus images using fractal features and evaluated on real time images. A novel automated glaucoma detection system using fractal features is shown in Figure 1.

Figure 1. Flow diagram of the proposed glaucoma detection system.

During preprocessing, the retinal color fundus images are converted to gray scale images and the image contrast is increased with histogram equalization. After preprocessing, the acquired images are skeletonized using mathematical morphology and different types of fractal features are analyzed that are intended to capture glaucomatous structures. Extracted fractal based features are subjected to feature selection process using Sequential Forward Floating Selection (SFFS). Subsequently, these selected features are fed to ELM for classification. Further, a comparison on the influence of different features in the accuracy of glaucoma assessment is performed. Fractal and multifractals analyses have been widely used in the medical assessment of the optical fundus^[13]. These mathematical analyses offer a natural description of the retinal vessel and morphology and are very useful in the detection, and diagnosis of pathological symptoms^[14]. FA of fundus photographs allows a quantitative measure of the morphological changes that occur around the optic disc. Fractal Dimension (FD) calculated using box-counting method^[15] is estimated by the slope of points (log N versus log 1/r), using the least square method. Lacunarity is based on the pixel distribution for an image obtained from scans at different box sizes at different grid orientations. Skeletonized digital images measure certain characteristics such as the presence of gaps and detection of branching points more effectively than the binary version and skeletonized images are used for further analysis. SFFS algorithm experimented by Jain and Zongker^[16] was used to find the best feature set for classification. SFFS algorithm employs a “plus 1, take away r” to find nested groups of good features. Selected optimized features namely FD, correlation coefficient, lacunarity with respect to foreground pixels, background pixels, and variation in count are shown in Table 1.

Table 1. Optimized fractal features for 50 real time images.

Features	Normal image		Abnormal image
	Binary	Skeleton	Binary	Skeleton
Fractal dimension (FD)	1.66±0.043	1.69±0.032	1.51±0.019	1.62±0.084
Correlation coefficient (r2)	0.96±0.004	0.96±0.007	0.93±0.172	0.95±0.001
Lacunarity using Fλ	0.26±0.022	0.21±0.041	0.29±0.078	0.28±0.045
Variation in count(σ/µ)	0.63±0.050	0.67±0.061	0.52±0.038	0.57±0.099
Lacunarity using Eλ	0.59±0.028	0.49±0.085	0.27±0.075	0.46±0.047

Optimized feature are then fed to ELM classifier to discriminate normal and abnormal images. As the learning rate of feed forward neural networks is time consuming, ELM algorithm that makes use of Single Hidden Layer Feed forward Network (SLFN) is used. ELM randomly selects the input weights and analytically determines the output weights of SLFN and generates the neuron parameters before seeing the training data. ELM algorithm is summarized as follows.

Given a training set , N=(xi, ti), xi ∈ Rn, ti ∈ Rm, i={1, ...N}, activation function g(x), number of hidden nodes M.

1. Randomly assign input weight w_i and bias b_i, i ∈ [1…M];

2. Calculate the hidden layer output matrix H;

3. Calculate output weights matrix β = H^†T.

where T= [t₁,….t_n], H^† is the Moore–Penrose generalized inverse of hidden layer output. Radial basis activation function is used in this work. Fractal features when fed into ELM classifier, the training time, testing time, training accuracy and testing accuracy were observed as shown in Table 2.

Table 2. Training, testing accuracy using ELM.

No. of features	Training time (ms)	Testing time (ms)	Training accuracy (%)	Testing accuracy (%)
5	0.0815	0.0174	94.98	86.51
4	0.0788	0.0217	98.1	95.4
3	0.0732	0.0227	89.1	65.9
2	0.0521	0.0129	68.7	72.1
1	0.0427	0.0206	48.9	56.1

Input data was normalized between the values 0 and 1. In the design of ELM, experiments were carried out by varying the hidden nodes from 3 to 75 with different training and test data set. Approximation of ELM was performed with additive neurons for SLFN. Mean square error was 0.937. Performance of each classifier measured in terms of sensitivity, specificity and accuracy is shown in Figure 2.

Figure 2. Performance analysis of fractal features.

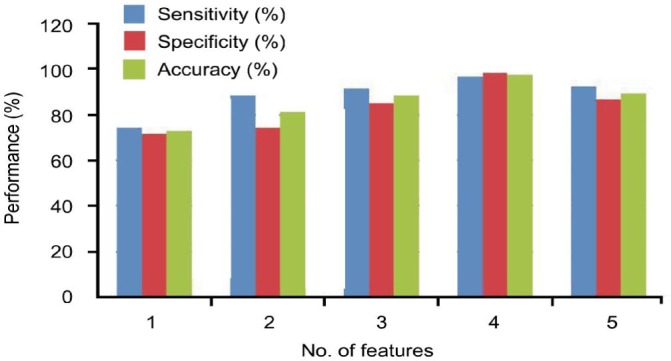
FD alone provided 74.16 % sensitivity and 71.6 % specificity. Correlation coefficient and FD provided 88.3% sensitivity, 84.16% specificity and 81.23% accuracy. These features when combined with lacunarity with respect to foreground pixels provided 91.6% sensitivity, 85% specificity and 88.3% accuracy. For four features, 58 images out of 60 mild stage images, 118 images in normal stages and 116 images in abnormal groups were properly classified contributing to 96.6% sensitivity and 98.3% specificity. Accuracy increased to 97.15% when lacunarity with respect to background pixels were also included. Accuracy reduced to 89.5% when the variation in count feature was included. Out of 120 abnormal images used in this study, 50 images include early stages and 70 images with moderate and severe stages. In the early stage detection, two misclassifications were found for five features contributing to 96% accuracy and one misclassification for four features providing 98% accuracy. Ground truth images based on the progressive structural optic nerve damage from stereo photography provided by ophthalmologists were taken as the gold standard for this work. FD and lacunarity represent the most suitable tool to characterize glaucoma texture as it is able to describe discontinuity of the optic disc and optic cup, changes of which are index of increased glaucoma risk. The novelty of this technique lies in the use of fractal application dimension on fundus images and does not require image segmentation and there is no global threshold. Further this technique is insensitive to the choice of optic disc centre. Feature set is better than the features extracted from gray level co-occurrence matrix and provides more discriminating capability in the diagnosis. ELM outperforms the existing neural network approaches in terms of minimum square error. ELM offers significant advantages such as fast learning speed, ease of implementation, and minimal human intervention. Fractal geometry provides a good discrimination of glaucomatous eyes from the normal images than the euclidean geometry and can be used as a part of a screening tool for early detection of retinal diseases and in mass screening. Classification accuracy can be further improved by using more number of diverse training images. Multifractal approaches can also be explored in order to quantify the morphological changes that occur around the optic disc.