Real Diffusion-Weighted MRI Enabling True Signal Averaging and Increased Diffusion Contrast

Abstract

This project aims to characterize the impact of underlying noise distributions on diffusion-weighted imaging. The noise floor is a well-known problem for traditional magnitude-based diffusion-weighted MRI (dMRI) data, leading to biased diffusion model fits and inaccurate signal averaging. Here, we introduce a total-variation-based algorithm to eliminate shot-to-shot phase variations of complex-valued diffusion data with the intention to extract real-valued dMRI datasets. The obtained real-valued diffusion data are no longer superimposed by a noise floor but instead by a zero-mean Gaussian noise distribution, yielding dMRI data without signal bias. We acquired high-resolution dMRI data with strong diffusion weighting and, thus, low signal-to-noise ratio. Both the extracted real-valued and traditional magnitude data were compared regarding signal averaging, diffusion model fitting and accuracy in resolving crossing fibers. Our results clearly indicate that real-valued diffusion data enables idealized conditions for signal averaging. Furthermore, the proposed method enables unbiased use of widely employed linear least squares estimators for model fitting and demonstrates an increased sensitivity to detect secondary fiber directions with reduced angular error. The use of phase-corrected, real-valued data for dMRI will therefore help to clear the way for more detailed and accurate studies of white matter microstructure and structural connectivity on a fine scale.

Introduction

Diffusion-weighted MRI (dMRI) has long been employed to provide neuroscientific and clinical imaging data by sensitizing MRI signals to anisotropic water diffusion (Stejskal and Tanner, 1965; Turner et al., 1990). In order to achieve this contrast, the MR signal is attenuated by application of magnetic field gradients along a specific direction, depending on the direction in which diffusion is to be measured. This results in an image with useful contrast but reduced signal-to-noise ratio (SNR). Diffusion MRI models such as Diffusion Tensor Imaging (DTI) (Basser et al., 1994), Q-ball (Descoteaux et al., 2007; Tuch et al., 2002), Diffusion Spectrum Imaging (DSI) (Wedeen et al., 2005) or AxCaliber (Assaf et al., 2008) employ such diffusion-weighed signals to gain microstructural tissue information.

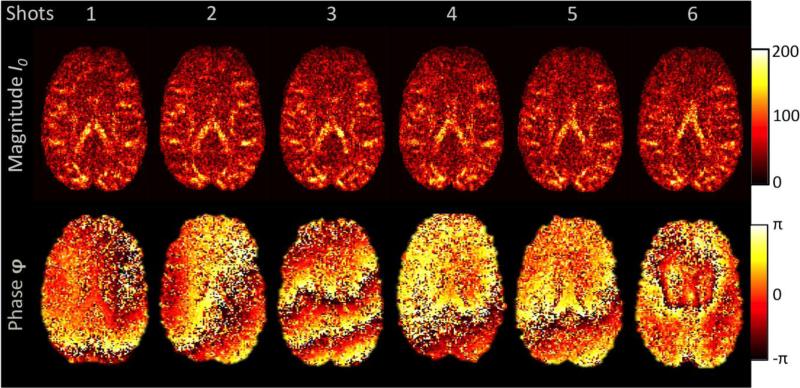
An MRI signal is inherently complex-valued, having both magnitude and phase components. During the diffusion-encoding process, physiological effects such as brain motion, cardiac pulsation, perfusion and respiration cause background phase variations, φ_BG, across the acquired complex image. Even though the background phase strongly varies for each imaging slice and repetition, it generally follows a spatially smooth distribution (Bammer et al., 2010). These background fields do not have an impact on the commonly used magnitude of the data. Phase data are generally not included in diffusion analyses since they are overlaid by φ_BG, which varies considerably for each imaging slice and repetition (see Figure 1).

Figure 1.

Complex Diffusion-Weighted MRI Signal. The figure shows six repetitions of one specific diffusion direction. The magnitude image (top row) remains constant, whilst the phase image (bottom row) shows different patterns for each shot. Such shot-to-shot phase variations can arise from subject movement (e.g., shot 3), cardiac pulsation (e.g., shot 6), blood circulation or field inhomogeneities when diffusion gradients are employed.

When the SNR of magnitude data is low, the distribution of image noise can have an impact on the diffusion data. A complex MRI signal, S, generally consists of positive signal intensity, I₀, with phase information, φ_BG, and uncorrelated complex Gaussian noise, S_E. For visualization purposes, complex MRI data, S, are generally split into magnitude, I, and phase, φ.

$$S=I{e}^{i\phi }=S_0\pm S_E=I_0{e}^{i{\phi }_{BG}}\pm I_E{e}^{i{\phi }_E}$$ (1)

In this equation, both the signal and the noise distribution of the magnitude, I, are not Gaussian. Signal and noise rather resemble a non-zero-mean Rician distribution - more specifically, for multi-channel data and parallel imaging, a non-central χ² distribution (Aja-Fernández et al., 2011; Gudbjartsson and Patz, 1995). This is generally not an issue if the SNR is high, because the distribution of noise approximates a Gaussian in such cases. In dMRI and other low SNR acquisitions, however, signal averaging unfortunately “piles up” the non-Gaussian noise. This results in biased data points at low signal intensities - the so-called “noise floor”. Please note that the Gaussian nature of thermal noise entails both positive and negative signal fluctuations. However, the magnitude representation of noise can be best described by means of a non-central χ² distribution. As a result, fitting low SNR data to a model of diffusion-related attenuation becomes challenging when only its magnitude is used.

The noise induced bias on the diffusion signal is a well-known issue in dMRI, especially when signal averaging is employed to increase SNR (Jones et al., 2013). The individual dMRI data often have low contrast, which leads to inaccurate diffusion measures such as fractional anisotropy (FA) and increased angular error in fiber tracking (Jones and Basser, 2004). The problem becomes more severe as SNR drops, for example with strong diffusion weighting or high spatial resolution. However, such data promise to provide the most detailed information about anatomical microstructure (Cohen-Adad et al., 2012; Descoteaux et al., 2011; Heidemann et al., 2012; Setsompop et al., 2013; Wedeen et al., 2012). The noise floor induces a signal bias and, therefore, prevents such data from being used to their full benefit.

When optimized coil combinations are used to obtain magnitude data, the impact of non-Gaussian noise distributions for multi-channel data can be reduced (Setsompop et al., 2012a; Sotiropoulos et al., 2013). However, this strategy only ameliorates the noise floor problem associated with combining coil-elements, and does not solve it for the analysis of the diffusion-direction data.

For complex-valued data with low SNR, signal averaging and model fitting are only valid if the data are overlaid by an uncorrelated Gaussian noise distribution. This condition is fulfilled if the real part, $\mathfrak{R}$, and the imaginary part, $\mathfrak{J}$, of the complex signal, S, are considered separately.

$$S=\mathfrak{R}+i\mathfrak{J}=S_0\pm S_E=({\mathfrak{R}}_0\pm {\mathfrak{R}}_E)+i({\mathfrak{J}}_0\pm {\mathfrak{J}}_E)$$ (2)

In this equation, $\mathfrak{R}$ and ${\mathfrak{J}}_0$ denote the real and imaginary part of the complex MR signal, whilst ${\mathfrak{R}}_E$ and ${\mathfrak{J}}_E$ denote uncorrelated real and imaginary complex noise. If averaging is carried out in such a complex-valued domain without noise bias, it is possible to significantly increase the spatial resolution for structural imaging (Bernstein et al., 1989; Oros-Peusquens et al., 2010; Turner et al., 2008).

Unfortunately, it is not beneficial to directly average complex dMRI data, since the shot-to-shot variability in background phase contamination, φ_BG, diminishes signal coherence in both the real and imaginary components. This causes unwanted elimination in the signal due to averaging. This effect does not occur when the magnitude, I, is taken. If the time- and spatially-dependent phase variation could be eliminated, a coherent complex signal with constant background phase could be reconstructed. Removing φ_BG would enable to coherently average the real part of the signal, $\mathfrak{R}$, without an undesirable noise bias.

Because of these significant gains from complex averaging in dMRI, several attempts have been made to resolve this issue. For instance, the background phase has been estimated by means of extensive spatial smoothing (Holdsworth et al., 2012; Pipe, 1999). In another study, the removal of φ_BG is performed with the help of various polynomial and linear fits to the signal in image and diffusion space (q-space) (Sperl et al., 2013).

Background phase contamination is also an important issue for multi-shot dMRI measurements, where varying background phase terms prevent accurate combinations of multiple imaging shots. One way of estimating the smooth background phase is by acquiring low resolution two-dimensional navigators and performing phase correction before multiple shots are combined (McNab et al., 2010; Miller and Pauly, 2003; Porter and Heidemann, 2009). In a more recent implementation, multi-shot dMRI data acquired without additional navigator application were reconstructed using total variation (TV) for background phase estimation (Chang et al., 2014; Chen et al., 2013). However, it needs to be noted that even in the advance of methods to remove background phase contamination, it is still a common, yet suboptimal practice to use magnitude images for dMRI.

In this work, characterization of background phase elimination was performed for dMRI, specifically for high spatial resolutions and strong diffusion weightings. A TV smoothing algorithm was used to estimate and remove φ_BG, in order to gain real-valued data with significantly reduced noise bias.

DMRI data were acquired with strong diffusion and high resolution as well as with conventional clinical acquisition parameters. Real and Magnitude data were extracted from these datasets to perform a qualitative and quantitative comparison of both data types. The presented reconstruction method achieved idealized conditions for signal averaging without noise bias and allows higher contrast in diffusion model reconstructions with reduced magnitude bias as well as more accurate fiber tracking results.

Theory

Background Phase Correction

An accurate estimation of φ_BG is the first necessary step for an effective background phase removal. The image phase term, φ, can be regarded as a superposition of background phase contamination, φ_BG, tissue phase, φ_Tissue, coil phase, φ_Coil, and phase noise, φ_E.

$$\phi ={\phi }_{BG}+{\phi }_{Tissue}+{\phi }_{Coil}\pm {\phi }_E$$ (3)

It is not directly obvious from Equation (1) that the total phase can be derived from the uncorrelated superposition of φ_BG and φ_E. However, it has been shown that signals with noisy phase are closely approximated by Gaussian distributions even for low SNR values (Gudbjartsson and Patz, 1995). Additionally, if the coil-element data are combined with an optimized complex weighting, as in Sotiropoulos et al. (Sotiropoulos et al., 2013), the noisy phase signal retains its Gaussian character. Therefore the phase noise, φ_E, can be viewed as superimposed on the other phase contributions.

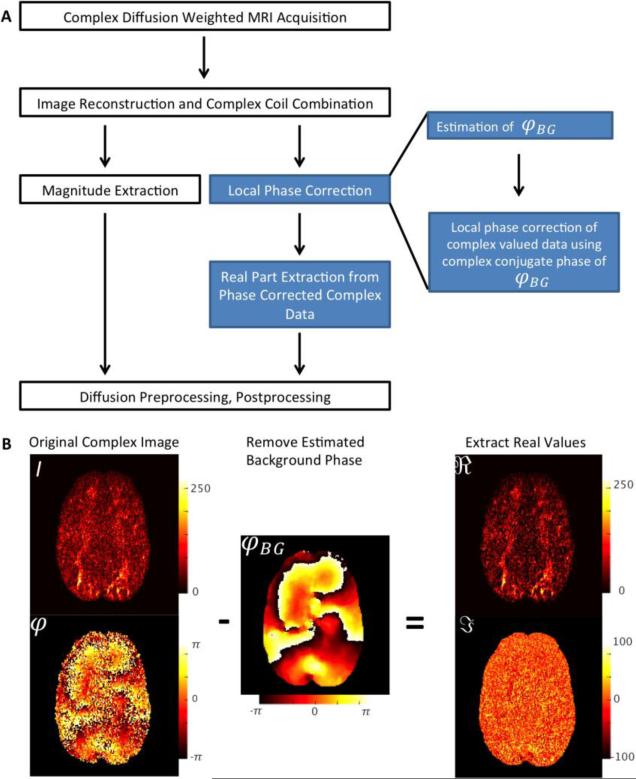
Figure 2A shows the image reconstruction process as a flowchart. It is crucial to use a complex coil combination method, which flattens out coil phase information and thereby yielding a smooth phase image (Hammond et al., 2008; Pruessmann et al., 1999). For the sake of brevity, coil and tissue phase information can be disregarded since they will be removed with φ_BG.

$$\phi ={\phi }_{BG}\pm {\phi }_E$$ (4)

Figure 2.

Workflow for Extracting Real-Valued Diffusion Data. A Flow chart for creating real-valued dMRI data. The standard reconstruction steps are displayed in white. The additional steps for extracting real-valued data are indicated in blue. B Depiction of the phase correction process. The complex-valued dMRI signal is used for the estimation of the smooth background phase, φ_BG, without noise contamination. The background phase is subtracted, creating a complex image without background phase contamination. The real part, including diffusion-contrast and Gaussian noise are extracted. The imaginary part contains only imaginary part of the complex Gaussian noise and can therefore be discarded.

As can be seen in the flowchart (see Figure 2A), the real diffusion image reconstruction method differs from the standard magnitude reconstruction strategy only after the multi-channel coil combination. The real valued diffusion data reconstruction requires two additional steps of local phase correction and real-part extraction.

The local phase correction itself can also be subdivided into two sub steps: i.) an accurate estimation of the background phase contamination and ii.) a subsequent removal of φ_BG (see Figure 2B). The result of this operation is a diffusion-weighted dataset, S_corr, without background phase contaminations.

$$S_{corr}=S{e}^{-i{\phi }_{BG}}=I{e}^{i(\phi -{\phi }_{BG})}\underset{\text{with eq.}4}{\underbrace{\cong }}I{e}^{i{\phi }_E}$$ (5)

The new dataset, S_corr, contains no further phase information apart from the uncorrelated phase error and can, therefore, be directly viewed as real and imaginary part (see equation 2). Once the data have been accurately rephased, it is no longer necessary to use the magnitude of the data. In this way, a complex valued dMRI dataset is obtained, containing no undesired noise bias.

Regarding the background phase estimation, it is crucial to adequately separate actual background phase information, φ_BG, from the phase noise, φ_E, which is part of the complex Gaussian noise and should, therefore, not be rephased. In practice, an elimination of the phase noise, φ_E, would result in transforming the real part of S_corr into its magnitude, I. This would reintroduce the undesired noise bias to the data and thus make the whole process redundant (Holdsworth et al., 2012).

If phase estimation and correction are performed correctly, the actual signal will be repositioned in the real part of S_corr. Therefore, S_corr is a superposition of the original signal, I₀, and the real and imaginary parts of the complex Gaussian noise, S_E (see equation 1).

$$S_{corr}={\mathfrak{R}}_{corr}+i{\mathfrak{J}}_{corr}=I_0+{\mathfrak{R}}_E+i{\mathfrak{J}}_E$$ (6)

In this case, the imaginary part of the signal contains only Gaussian noise and can, therefore, be discarded from further processing. At this step, the real part of the data, which is overlaid by Gaussian noise, can be extracted for further analyses.

$$S_{corr}={\mathfrak{R}}_{corr}=I_0+{\mathfrak{R}}_E$$ (7)

Please note that the different notations of S_corr in the previous equations (see equations 5, 6 & 7) do not introduce the same quantity multiple times. In contrast, they show different representations of the same complex-valued dataset.

Implementation of Background Phase Estimation

A precise estimation of φ_BG is the key step in removing background phase. As already stated in the Introduction, there are different methods for background phase estimation in dMRI.

Spatial smoothing operations such as triangular filtering of k-space has been shown to be fast and suitable for background phase removal in clinical dMRI, even on a large scale (Holdsworth et al., 2012; Pipe, 1999). However, the optimal smoothing kernel size depends on image SNR and resolution and is, therefore, hard to configure. Problems can also arise when strong diffusion weighting is used. In such cases, background phase contaminations can take convoluted shapes (see Figure 2B) that might be unresolved in the smoothed image. A similar problem arises when using low-order polynomial fitting for estimation of φ_BG (Sperl et al., 2013). Polynomial functions may be inappropriate to properly estimate higher-order phase terms and, therefore, be unsuitable at strong diffusion weighting. The polynomial method is furthermore restricted to high-density q-space sampling for DSI, and involves additional processing steps (i.e., phase unwrapping and brain masking), making an implementation for online reconstruction difficult.

Navigator-based phase removal strategies for multi-shot dMRI were shown to be stable and reliable (McNab et al., 2010; Miller and Pauly, 2003; Porter and Heidemann, 2009). However, reacquiring data at the k-space center is time consuming, making this method less desirable for fast EPI acquisitions.

In this work, a total variation (TV) denoising algorithm was employed for background phase estimation. TV has already been successfully used for combining multi-shot dMRI data without additional navigation (Chen et al., 2013).

The TV denoising algorithm assumes a piecewise smooth distribution of an n-dimensional noisy signal, y, to estimate the underlying denoised signal, x. Similarity of the original and denoised signals is measured by the sum of squares error, $\frac{1}{2}\sum {(y-x)}^2={\Vert y-x\Vert }_2^2$. To enforce the degree of smoothness, a regularization term, λ, of the l₁ norm of the signal gradient, ▽x, is introduced:

$$\arg \underset{\mathrm{x}\in {\mathbb{C}}^{\mathrm{n}}}{\min }\left\{\frac{1}{2}{\Vert y-x\Vert }_2^2+\lambda {\Vert \nabla x\Vert }_1\right\}$$ (8)

The TV algorithm was selected due to its edge-preserving denoising characteristics (Rudin et al., 1992). TV can be used on complex-valued datasets, $\mathbb{C}$, yielding an image intensity weighted estimation of background phase contamination. Furthermore, no additional preprocessing steps, such as masking or phase unwrapping are required, providing a future option for online real-valued dMRI reconstruction.

It must be noted, however, that even though real-valued dMRI extraction employs TV, it is not a denoising strategy for dMRI. It rather employs knowledge about smoothness of the background field to correct for phase contamination and, thus, for creating an image with a Gaussian noise distribution. In this context, equation 8 was only employed to extract the smooth phase term of the denoised signal, x, to subsequently rephase the original noisy non-smoothed dataset, y.

Methods

High-resolution dMRI Data Acquisition

Diffusion MRI data of one healthy adult were acquired. Written informed consent was obtained before the experiment. Imaging was performed on the MGH-UCLA Skyra Connectom Scanner (Siemens Healthcare Sector, Erlangen) using a maximum gradient strength of G_Max=300mT/m with a slew rate of 200T/m/s. A custom-built 64 channel phased-array coil was employed for signal reception (Keil et al., 2013). Six repetitions of one dMRI dataset were acquired using a single-refocused spin-echo Stejskal Tanner sequence (Stejskal and Tanner, 1965) with an EPI readout.

The acquisition parameters were repetition time (TR)=4600ms, echo time (TE)=54ms, Field of View (FoV)= 210×210mm², Matrix size = 176×176, 98 slices, in plane GRAPPA acceleration (R)=2 (Griswold et al., 2002), Partial Fourier (PF)=6/8, Simultaneous Multi Slice (SMS) acceleration factor SMS=2, blipped-CAIPI PE-Shift=3 (Setsompop et al., 2012a, 2012b) and Bandwidth=1578 Hz/Px. MRI data with diffusion weighting of b=5000s/mm² and 128 diffusion directions were acquired with 10 interspersed b=0 images in a total acquisition time of 10:35 for each repetition. SMS was performed using a dedicated online reconstruction software with low inter-slice leakage (Cauley et al., 2014a).

To create complex-valued multi-channel dMRI data, the reconstruction of magnitude and phase images was performed separately. The reconstructed magnitude data for each channel were combined using a vendor-provided adaptive coil combination (Walsh et al., 2000). Phase data of individual coil-elements were combined using an optimized method for high field strength (Hammond et al., 2008). This method provides a good approximation to the SENSE coil combine described by Pruessmann et al. (1999) for field strengths of up to 3T. For higher field strength, it might be necessary to acquire coil sensitivity maps to employ SENSE coil combination, or to use local phase offset corrections (Robinson et al., 2011). The magnitude and phase data were combined into complex-valued datasets using Mathworks Matlab 8.3.

Conventional dMRI Data Acquisition

In addition to high-resolution dMRI, diffusion data with conventional acquisition parameter settings were recorded from one healthy adult. Written informed consent was obtained before the experiment. Imaging was performed on a MAGNETOM Verio MRI system (Siemens Healthcare Sector, Erlangen) using a maximum gradient strength of G_Max=40mT/m with a slew rate of Slew=200T/m/s. A 12-element head matrix coil (Siemens Healthcare Sector, Erlangen) was employed for signal reception. A dMRI dataset was acquired using a twice-refocused spin-echo sequence with EPI readout (Reese et al. 2003).

The acquisition parameters were TR=13800ms, TE=100ms, FoV= 218×218mm², Matrix size = 128×128, 72 slices, R=2 and b = 1000s/mm² with 60 diffusion directions and 7 interspersed b=0 images. This dMRI dataset was recorded in a total acquisition time of 15:24 min. The data were reconstructed offline using Matlab. The individual coil-elements were combined using root sum of squares for magnitude and an optimized method (Hammond et al., 2008) for phase data. The magnitude and phase data were combined into complex-valued datasets.

Real Value Extraction of Acquired dMRI Data

The background phase has a distinct shape for each EPI shot. Real value extraction was performed as depicted in Figure 2B, using TV with Matlab 8.3. The l₁ regularized TV formulation was solved through a fast iterative Split-Bregman method, using a preconditioned hierarchically semi separable (HSS) solver (Cauley et al., 2014b; Goldstein and Osher, 2009; Xia et al., 2010). The algorithm was run using a soft threshold of β=30% of the total variation and a TV regularization of λ = 6. These parameters were chosen based on experience and resulted in stable phase correction for both the high-resolution and conventional dMRI dataset. As can be seen from Figure 2A, the real-valued data are a direct output of our suggested phase correction algorithm. For comparison, the identical dMRI dataset was reconstructed as standard magnitude images.

Diffusion Data Processing

Diffusion MRI magnitude as well as real data were preprocessed using the standard FMRIB Software Library (FSL) diffusion tensor imaging (DTI) preprocessing pipeline¹. In a nutshell, both real and magnitude data were concatenated and corrected for motion and eddy currents using the function eddy as implemented in FSL. Next, a DTI fit of the corrected real and magnitude data was conducted using the FSL function dtifit.

Additionally, both real and magnitude data of the high-resolution dataset were averaged over the number of repetitions to enable a qualitative evaluation of signal averaging ability. To demonstrate the impact of noise bias in dMRI data on the DTI fit, the six-fold averaged high-resolution dataset was increasingly contaminated with χ² -distributed noise with five degrees of freedom. The noise was distributed homogenously throughout the image (i.e. no parallel noise amplification was taken into account). DTI fits of the noise-contaminated datasets were realized using FSL dtifit.

An evaluation of “diffusion contrast” within fiber structures with homogenous orientation was performed for real and magnitude dMRI data. This contrast was defined as the difference between the maximum and the minimum image intensity, over the complete range of diffusion gradient directions, for a given b-factor and region of interest (i.e., diffusion perpendicular vs. along the fiber direction). Using the averaged dMRI datasets, a region of interest (ROI) with homogeneous fiber direction was selected within the corpus callosum. The diffusion-contrast was calculated within this ROI.

High SNR Human Connectome Project dMRI Dataset

The openly available Human Connectome Project (HCP) dataset was employed to compare the results of the DTI fits for the acquired real/magnitude dMRI data with randomly selected high SNR dMRI data. An MGH HCP dataset of five subjects with 1.5 mm isotropic resolution was obtained from the HCP database². The MGH HCP data were acquired using the same pulse sequence and system hardware as the data acquired for this study. The acquisition parameters were TR=8800ms, TE= 57ms, FoV= 210 × 210 mm², Matrix size = 140 × 140, 96 slices and b-values = [1000,3000,5000,10.000] s/mm² with [64,64,128,256] diffusion directions respectively. The downloaded dataset was already preprocessed, including corrections for gradient non-linearity, motion-correction and eddy-currents. A DTI fit of the MGH HCP dataset was conducted using FSL dtifit. The mean distribution and standard deviation of FA values was calculated and normalized to the number of image voxels using Matlab.

Quality Assessment of Non-averaged Real and Magnitude Q-ball Reconstructions Using Regular Bootstrap

The quality and variability of the magnitude and real data based Q-ball reconstruction were assessed using a regular bootstrapping method of the six acquired repetitions with high resolution (Cohen-Adad et al., 2011).

The preprocessed dMRI data were re-shuffled with regular bootstrapping using jackknife sampling to synthesize 500 bootstrapped repetitions. For each synthetic dataset, the diffusion orientation distribution function (ODF) was estimated voxel-by-voxel, using Q-ball reconstruction based on spherical harmonics functions (Descoteaux et al., 2007). To assess stability of the estimated fiber directions, the angular confidence intervals were derived for the first (CI1) and the second ODF maxima (CI2) as a measure of angular uncertainty.

Quality Assessment of Averaged Real and Magnitude Q-ball Reconstructions Using Residual Bootstrap

Regular bootstrapping can provide valuable information about uncertainties in ODF reconstruction. However, multiple repetitions of datasets are required to resample a high number of synthetic bootstraps. An alternative approach to assess Q-ball reconstruction quality of dMRI data, which does not require multiple repetitions, is residual bootstrapping (Sotiropoulos et al., 2011). Residual bootstrapping was employed on both the averaged magnitude and real diffusion high-resolution datasets to evaluate the effect of noise floor on the ODF reconstructions. This was done using the FSL function qboot with the default settings: Constant Solid Angle (CSA) ODF (Aganj et al., 2010), l_max=4, number of peaks = 2, threshold for ODF peak = 0.4.

Results

Magnitude vs. Real Averaging

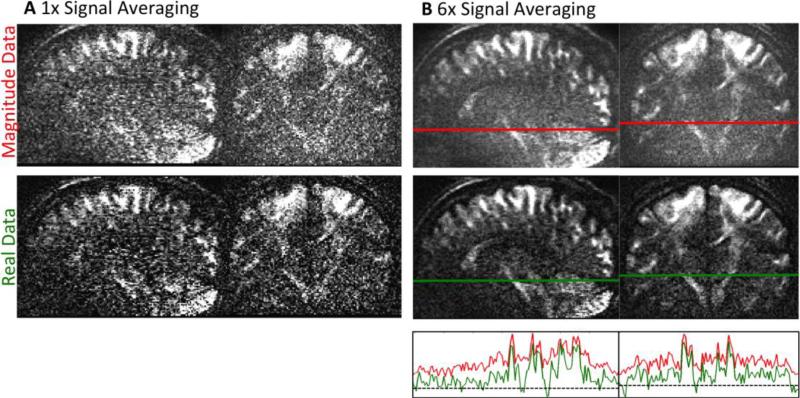
Figure 3 shows the results of signal averaging six acquisitions for real and magnitude data. The non-averaged real and magnitude data quality is displayed in Figure 3A, and the six-times averaged data are shown in Figure 3B. All images are displayed on the same scale.

Figure 3.

A Single repletion of dMRI data with low SNR for magnitude (top) and phase corrected real-valued data (bottom). B Results of signal averaging for both data types. After six averages, the magnitude data show accumulated noise - visible as a “mist” overlaying the image. The phase corrected real-valued dMRI data are not affected by noise bias. Therefore, averaging visibly increases SNR for real diffusion data. The bottom graph of Figure B shows the signal course of real and magnitude data alongside the lines in the averaged data. The dashed line marks a signal intensity of zero. The diminished noise floor of real-valued data allows identifying smaller intensity differences. All images in this figure are displayed on the same scale.

The very low SNR is clearly noticeable in both non-averaged images (see Figure 3A). However, it can be seen that the Gaussian noise of the real data already results in higher contrast than in the magnitude counterpart.

The difference in the underlying noise distribution becomes even more evident in the averaged data in Figure 3B. The averaged magnitude data clearly show the effect of accumulated noise, resulting in a mist of uniform noise overlaying the image, even if a high number of averages is employed. In contrast, the real data after phase correction show a different behavior after signal averaging. There is no accumulation of noise floor, allowing for small-scale signal changes to become clearly visible (see Figure 3B, bottom). Furthermore, employing real-valued data prevents magnitude related upward bias – especially in the center of the image, where parallel g-factor noise amplification is the strongest.

The evaluation of diffusion contrast for the high-resolution real-valued dMRI dataset showed an increase of approximately 75% compared with the corresponding magnitude dataset. With conventional acquisition parameters, the real-valued data dMRI gave an increase of diffusion contrast by ~20%.

Diffusion Tensor Imaging for Real and Magnitude High-Resolution Data

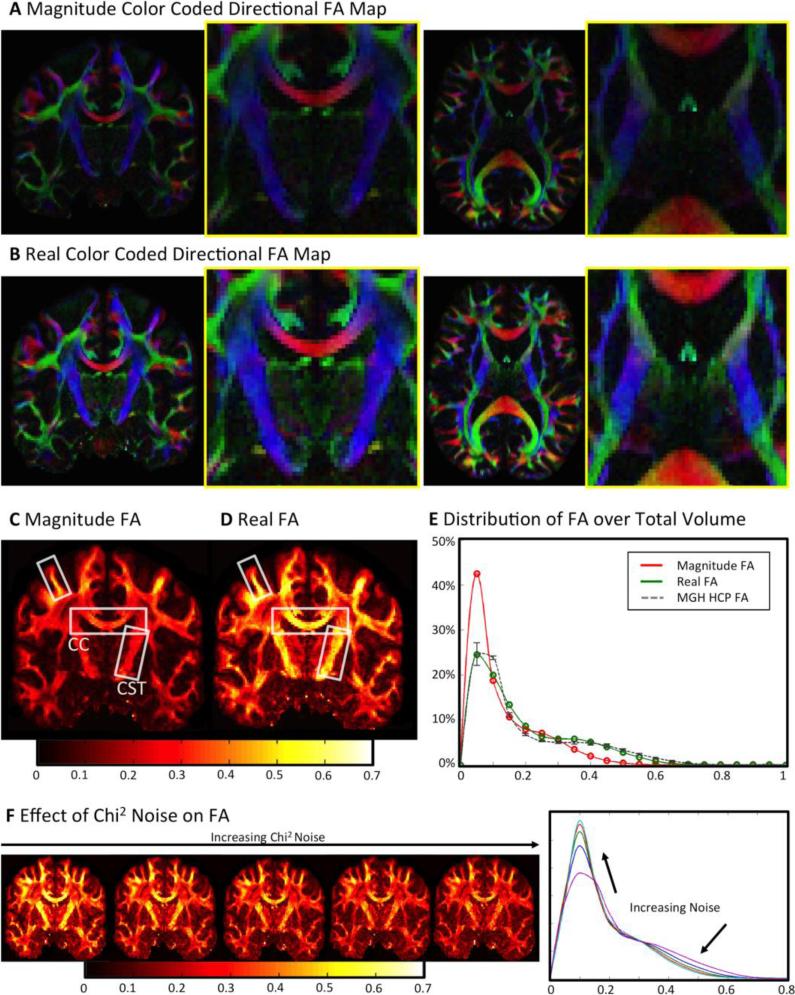
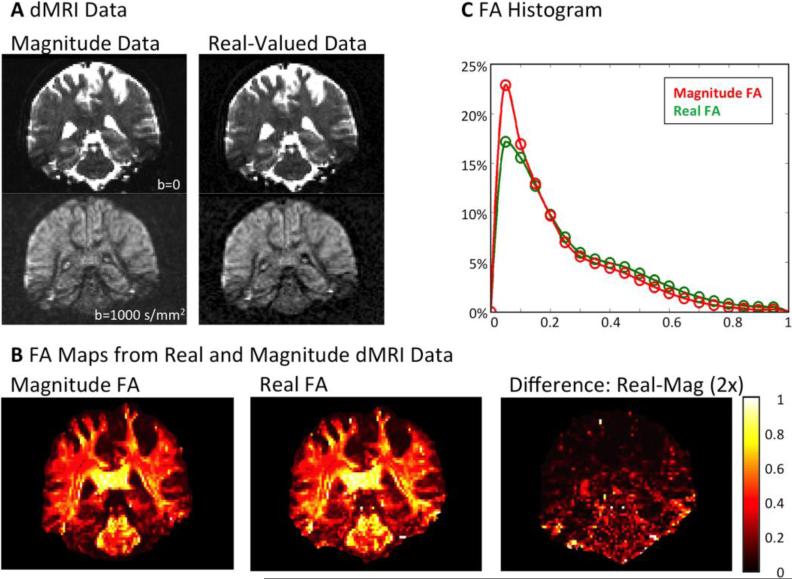
The results of the DTI fits for the acquired high-resolution dMRI data are summarized in Figure 4. A direct comparison between color-coded directional fractional anisotropy (FA) values for both real-valued and magnitude data is shown in Figure 4A (magnitude data) and Figure 4B (real data). The effect of noise bias becomes visible, as FA values based on magnitude data are in average smaller than FA data based on real-valued data. This is the result of diffusion attenuation being damped by the noise floor in highly attenuated regions, leading to a reduction of measured diffusion fractional anisotropy. This effect is not present for real dMRI data, leading to a more accurate representation of the diffusion propagator (i.e., less “blobby”). Therefore, real-valued dMRI data generally create an FA map with higher contrast (see Figure 4B). This effect is especially severe in the central brain regions (magnified), where the intrinsic SNR of the receiver array is reduced. In addition, the coil profiles are less orthogonal in these regions, leading to higher g-factor noise amplification, which further reduces SNR when parallel imaging is employed (Keil and Wald, 2013; Pruessmann et al., 1999; Wiesinger et al., 2004).

Figure 4.

A, B DTI fit results for standard magnitude and real-valued dMRI data. Real diffusion DTI results are significantly brighter - especially in central magnified low SNR regions of the brain, where additional anatomical structures become visible. C, D For standard magnitude data, large FA values are only visible in high SNR areas (close to receive coil-elements). In the center, the noise bias of magnitude data greatly reduces FA, even in highly anisotropic fiber structures (such as the corticospinal tract). Real diffusion is not influenced by noise bias, thereby creating more anatomically correct FA maps, even in low SNR regimes. E A shift to higher FA contrast over a larger range can be observed for real diffusion data. The distribution of FA based on real-valued data rather resembles the FA distribution resulting from high quality HCP datasets. The error bars on the HCP histogram denote biological variability of FA across the five observed HCP subjects. F Left: An artificial increase of χ² noise level results in a total reduction of DTI FA values. Right: datasets with artificial strong χ² noise contamination yield FA histograms that resemble the magnitude FA in histogram E.

The effect of noise on magnitude-based FA is also illustrated in Figure 4C. The FA calculated from low SNR magnitude data is reduced in highly anisotropic regions, such as in the corpus callosum (CC, reduced by ~40%) and the corticospinal tracts (CST, reduced by ~50%)³. High magnitude-based FA values in Figure 4C are only visible in areas adjacent to the reception coil, where SNR is generally higher (Keil et al., 2013) (difference highlighted by white boxes). In contrast to the magnitude-based FA dataset, the results of the FA calculation based on real-valued data correctly identify highly anisotropic areas as such (see Figure 4D). The calculated real FA values are distributed evenly throughout the brain, with no bias towards high SNR areas.

The distribution of FA values over the whole brain volume can be seen in the histograms in Figure 4E. Both real-based and magnitude-based FA histograms show two peaks for gray and white matter. Comparing both histograms, it is visible that the real-based FA values cover a wider dynamic range of values, resulting in increased contrast. The magnitude-based FA distribution shows a clear trend to smaller values, which can also be observed in the respective FA images (Figure 4A-D).

In contrast to low SNR magnitude data, the distribution of real FA values shows large agreement with the FA distribution of the HCP dataset. Both, the dynamic range and intensity distribution of FA values of the two datasets are very similar. Figure 4F displays the effect of an increasing level of artificial χ² noise on FA values. A homogenous increase of the χ² noise level visibly reduces the FA contrast throughout the image. The histogram in Figure 4F confirms this observation, as an increasing noise level reduces the dynamic range of FA values and shifts higher amounts of image voxels to small values.

The DTI results of a conventional dMRI dataset (1.7mm isotropic, b=1000s/mm²) are summarized in Figure 5. Figure 5A shows preprocessed dMRI data quality prior to the DTI fit. The real-valued dataset displays visibly higher image contrast at b=1000s/mm² compared to the magnitude dataset. The DTI FA values of this dataset show differences in FA contrast. This is especially evident in inferior parts of the brain, where non-uniform noise amplification induces a bias in the DTI fit (see Figure 5B, difference image). The distribution of FA values across the brain shows that conventional dMRI datasets are not as strongly influenced by noise as the high-resolution datasets with strong diffusion weighting. However, a similar trend is observable, as the real-valued data result in higher dynamic range and a reduced amount of low FA values.

Figure 5.

DTI Results for conventional dMRI dataset. A preprocessed real-valued and magnitude dMRI data prior to the DTI fit (corresponding images displayed on same scale). B Coronal FA maps, resulting from DTI fit. The real-valued dataset results in higher FA contrast in the inferior parts of the brain (right). C FA distribution for real and magnitude dMRI dataset with conventional acquisition parameters. The FA distribution of real-valued data shows an attenuated, yet generally similar behavior as for the high-resolution dMRI dataset.

Regular Bootstrapping Results

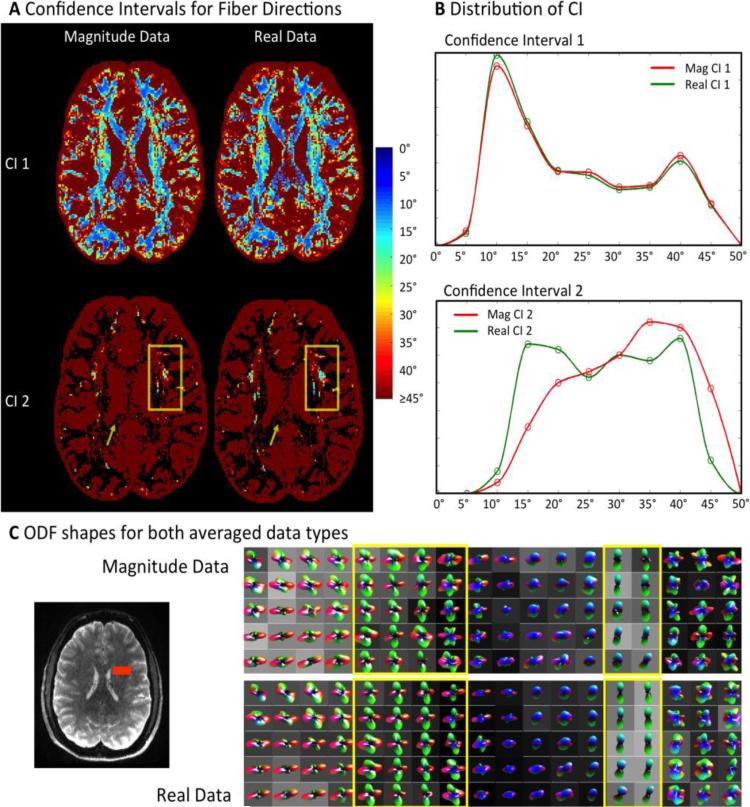
The regular bootstrapping results are summarized in Figure 6. The angular uncertainty of the primary (CI1) and secondary maximum (CI2) are shown for one axial brain slice in Figure 6A. The distributions of CI1 and CI2 values within this slice are displayed in histograms in Figure 6B. Note that the angular uncertainty of fiber directions is shown only up to CI<45°. No visible difference between the angular uncertainties of the first maximum (CI1) can be observed (see Figure 6A). The top histogram in Figure 6B confirms this observation. Real dMRI data provide a slight shift to smaller angular error, CI1, compared to magnitude data. Both CI1 histograms have the same basic shape, with one distinct peak at approximately 10° angular uncertainty.

Figure 6. Regular Bootstrapping Results from Six Repetitions.

A Angular Confidence Intervals for the primary and secondary fiber direction (CI1, CI2). Angular error of CI 1 is similar for magnitude and real data. Real diffusion data show more secondary fiber directions with CI2<45° (box). Magnitude data result in more secondary fiber reconstructions with high CI2>45° - even in single fiber structures such as the corpus callosum (arrow). B Voxel histograms of CI1 and CI2: Real diffusion data show increased sensitivity to secondary fiber crossings with low angular error. The histograms were masked to show the distribution of voxel locations, where directions were detected for both data types. C Calculated ODF shapes within fiber crossing area marked (red) in b0 image. ODFs based on real-valued dMRI data are more accurately defined in crossing fiber areas (left yellow box). In areas without fiber crossings, real diffusion ODFs yield less secondary fiber directions and appear sharper than magnitude ODFs (right yellow box).

A greater impact of dMRI data type on angular uncertainty can be seen with regard to the second ODF maximum (CI2). The arrows in the bottom row of Figure 6A indicate that for magnitude data a much larger number of spurious secondary fiber directions with an angular uncertainty CI2>45° appear in the corpus callosum. In fiber crossing areas, more secondary fiber directions with low angular error (CI2) appear in the real-based data (Figure 6A, bottom, boxes). In total, 25% more crossing fibers with an angular uncertainty of CI2<45° can be found using real dMRI data. At locations, where both real and magnitude data were able to resolve fiber crossings, a shift to lower uncertainty is observed for real dMRI data (Figure 6B). The magnitude-based CI2 histogram is clearly shifted to higher errors, due to the lower contrast these data provide.

ODF Shapes for both Data Types

Averaged ODFs were calculated using Matlab during regular bootstrapping. For visual comparison, averaged ODFs are displayed for one region of interest (ROI) with fiber crossings in Figure 6C. The selected ROI is displayed as an orange box within the brain on the left side of Figure 6C. Visual inspection of both ODF types shows that ODFs based on real data are sharper and more uniform within one tissue type (see yellow boxes in Figure 6C). Fiber crossings are resolved more clearly (left box) and single fiber directions show no small secondary maxima (right box).

Residual Bootstrapping Results

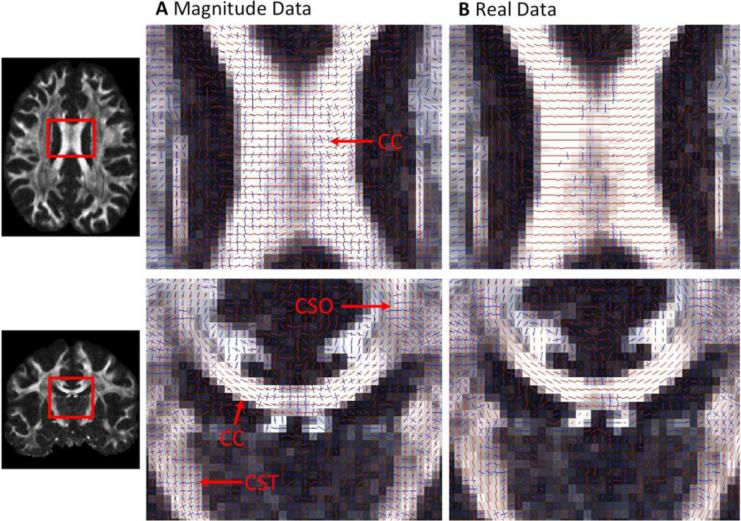
The results of residual bootstrapping for CSA ODF reconstruction are displayed in Figure 7. Axial and coronal views are shown with the estimated fiber orientations for six-times averaged magnitude and real dMRI data (see Figure 7). The real and magnitude reconstructions were both able to resolve crossing fibers (i.e. in the crossing region between corpus callosum, CC, and corticospinal tracts, CST, also known as centrum semiovale, CSO). However, the magnitude reconstructions identified a high number of non-existing fiber crossings, perpendicular to the true fiber orientation in the corpus callosum - even after low SNR magnitude dMRI data had been averaged extensively (Figure 7A). When averaged real dMRI data was used, the number of incorrectly estimated fiber crossings was visibly reduced in the CC (see Figure 7B).

Figure 7.

Residual-Bootstrapping Results for Six-Fold Averaged Data of A Magnitude and B Real Diffusion data. Many anatomically implausible orthogonal fiber crossings are detected in the Corpus Callosum for magnitude data (A). These are almost completely eliminated for real diffusion data

Adjustment of the threshold for finding fiber directions for the calculated magnitude-based dyads made it possible to suppress the spurious fiber crossings in the corpus callosum. However, this procedure also eradicated the anatomically plausible fiber crossings in the centrum semiovale.

Discussion and Conclusion

This study illustrates the substantial benefit of using real-valued data for diffusion MRI. Advances in both imaging methods and hardware allow previous limits of dMRI data acquisitions to be surpassed for contemporary neuroscientific and clinical applications. However, this striving for higher resolution and stronger diffusion weighting will reduce the SNR. Especially with low SNR acquisitions, a non-Gaussian noise distribution has a severe impact on diffusion reconstruction, resulting in reduced diffusion-contrast and biased model fits.

We introduced a total-variation based method for background phase correction of complex-valued dMRI data with high resolutions and strong diffusion weighting. The employed rephrasing algorithm uses TV to estimate the smooth background phase of dMRI data, which is then subtracted from the whole complex dataset. This results in a complete rotation of the complex dMRI signal into the real part. The complex image noise does not follow a smooth variation and is, therefore, unaffected by the TV algorithm. After rephasing, the real part, $\mathfrak{R}$, of the complex data contains all of the actual image information and can be extracted for further analysis. In contrast to magnitude data, the image noise of real data does not follow a non-central χ² distribution but rather a Gaussian distribution with a zero mean. The use of real dMRI data thus significantly reduces the bias of image noise on low SNR images. The employed Matlab Code for background phase correction is available upon request.

In this work, we acquired six repetitions of a high-resolution dMRI data set with a strong diffusion weighting of b=5000s/mm². We chose a combination of both high resolution and strong diffusion weighting to acquire a dataset with very low SNR to help illustrating the effect of noise distributions. Real data extraction was performed using the introduced TV based method (see Figure 2). The presented results indicate that real diffusion data enable true signal averaging without an accumulation of noise as opposed to traditional magnitude MRI (see Figure 3).

Furthermore, we compared the results of fitting a diffusion tensor model to the extracted real as well as the traditional magnitude data. The results for magnitude data are largely in agreement with previously published studies showing a damping of FA contrast if magnitude data are employed (Jones and Basser, 2004). After real-part extraction, the DTI fit showed visibly increased FA contrast, especially in central brain regions where noise amplification from parallel imaging noticeably reduces SNR. The FA distribution over the whole brain volume (Figure 4E) shows that the dynamic range of FA across the brain was increased when real dMRI data were employed. After real-value extraction, the FA distribution of the acquired data resembled the FA distribution of high quality dMRI data from the Human Connectome Project. This suggests that an elimination of noise bias in dMRI can dramatically increase the quality of diffusion model fits of low SNR data. In this work, we employed a strong diffusion weighting of b=5000s/mm² to emphasize the effect of χ² noise on low SNR data. Please note that the DTI model is generally not valid for such high b-values due to non-Gaussian diffusion contributions (Kiselev and Il'yasov, 2007). Therefore, it is advisable to employ lower b-values up to b=3000s/mm² for accurate DTI results.

Even though, dMRI datasets with high resolutions and strong diffusion weightings provide large amounts of information, they are generally not employed in clinical and neuroscientific practice. To estimate the influence of non-Gaussian noise bias on conventional dMRI acquisitions, we acquired a dataset with 1.7mm isotropic resolution and b=1000s/mm². As expected, the DTI FA results of this dataset are not as susceptible to real value extraction as high-resolution datasets. However, a similar trend showing a larger dynamic range and fewer low FA values can also be observed for this dataset - especially in inferior brain regions. Even though the direct impact of real-valued data on dMRI acquisitions with conventional parameters is not drastic, the introduced method will help to maintain sufficient FA contrasts, when higher resolutions or diffusion weightings are desired. In this context, slice-accelerated acquisition methods (Setsompop et al., 2012b) will help to generate sufficient amounts of data to increase SNR by averaging.

Real valued data follow a Gaussian intensity value distribution. Therefore, heavy noise might result in negative intensity values at low signal. This might engender issues when using a log transformation to linearize the diffusion decay. In such cases, it might be beneficial to either exclude the data from the fit or to replace negative intensity values with a small value greater than zero.

Advanced dMRI models using non-linear least squares and weighted least squares algorithms employ knowledge about the noise floor to minimize its impact on diffusion model fits (Veraart, Sijbers, et al. 2013). Such advanced diffusion models will show less benefit from real valued dMRI data than general linear least squares approaches.

Unfortunately, parallel imaging methods induce spatially varying noise levels in the data, thereby complicating proper estimations of noise levels. Additionally, diffusion data processing steps (such as eddy correction & registration) transform the underlying non-Gaussian noise distributions from known χ² distributions to unknown distributions (Veraart, Rajan, et al. 2013). These effects hamper the use of advanced data fitting strategies to reduce bias in model fitting.

The log transformation, which is often applied to dMRI data during model fitting, induces heteroscedasticity on the data. This is a general problem of diffusion model fits and also occurs when using real valued dMRI data. Hence, for optimal DTI fitting results of real valued dMRI data, it is also recommended to employ non-linear or weighted fitting procedures (Jones and Cercignani, 2010; Jones et al., 2013; Veraart et al., 2013b).

We would like to emphasize that the noise floor of magnitude dMRI data introduces severe signal bias not only for DTI, but also generally for every diffusion MRI experiment. For example, model-free (Lätt et al., 2008; Ong et al., 2008) or model-based (Assaf and Basser, 2005; Assaf et al., 2008) q-space methods aiming at estimating axon diameter strongly suffer from this magnitude bias, because the estimated parameters become incorrect (Alexander, 2008). Utilization of real instead of magnitude data thus has the potential to significantly increase the performance of diffusion MRI models in general. Future work will aim to investigate the impact of real-valued dMRI data on higher order diffusion models. Some of these models already account for a noise bias (Assaf and Basser, 2005) and might therefore show less benefit from removing it.

For both real and magnitude data, a regular bootstrap comparison was performed to evaluate the angular error of primary and secondary fiber direction estimations. During this process, six repetitions of the acquired high resolution dMRI data were resampled to create 500 synthetic bootstraps. Orientation density functions were calculated for all synthesized datasets. Subsequently, the angular uncertainties of primary and secondary (crossing) fiber orientations were estimated from the distribution of ODFs. For this consideration, we employed a Q-ball reconstruction based on Descoteaux et al. (2007), which is known to create smooth ODFs and can therefore result in an underestimation of fiber directions (Aganj et al., 2010). However, for comparing very noisy data, as in the current work, it can be beneficial to use conservative reconstruction methods, since more recent strategies tend to show increased susceptibility to noise and might, therefore, detect a higher number of non-existent fiber crossings for both data types. The results of the employed bootstrapping methods show that the use of real diffusion data for Q-ball reconstruction detected 25% more existing fiber crossings with an angular uncertainty of less than 45°, compared to magnitude data. When only fiber crossings detected by both data types were compared, real dMRI data Q-ball reconstruction created ODFs with strongly reduced angular error of the secondary fiber direction (see Figure 6). Furthermore, regular bootstrapping revealed that a greater number of incorrectly estimated fiber crossings with high angular error greater than 45° was found when using magnitude data. The angular uncertainty of the first fiber direction for Q-ball reconstructions did also improve slightly for real compared to magnitude dMRI data.

To evaluate the effect of signal averaging on CSA Q-ball reconstruction, we conducted a residual bootstrapping analysis. For magnitude data, the accumulation of noise as a result of averaging (see Figure 3) prevented an accurate ODF reconstruction. Even though anatomically plausible fiber crossings were correctly identified, the magnitude reconstruction also identified spurious fiber crossings in almost every voxel within the highly anisotropic corpus callosum – even after extensive signal averaging. Changing the threshold for ODF maxima recognition resulted in a failure to identify existing fiber crossings for magnitude data. Again, real dMRI data did not show this behavior and was able to show anisotropic diffusion within the corpus callosum whilst resolving existing fiber crossings.

Our analyses show that using real-value dMRI data is advantageous over magnitude data both for increased diffusion and image contrast and data fitting. Please note that the major benefits of our presented strategy are partially due to the fact that very low SNR data were acquired. Magnitude dMRI data with low resolution and weak diffusion weighting, as still often employed in clinical and neuroscientific practice, are influenced to a lesser extent from magnitude-induced noise bias, due to their higher SNR. In such low-resolution cases, real-valued dMRI only achieved an ~20% increase of diffusion contrast. However, SNR has a strict trade-off with spatial resolution and diffusion weighting. Recently-developed MRI systems with stronger gradients and a higher number of parallel imaging channels allow to acquire data with significantly higher diffusion-weightings and spatial resolutions (but still, unavoidably, with low SNR) (Keil et al., 2013; Setsompop et al., 2013). For such high-resolution data, the use of real dMRI data resulted in a direct increase of diffusion contrast by ~75%.

Importantly, current advances in SMS for diffusion enable faster acquisitions than traditional MRI, allowing a higher number of averages to be acquired (Eichner et al., 2014a; Feinberg et al., 2010; Setsompop et al., 2012a, 2012b). Slice-acceleration has only recently been developed and further improvements can be expected using specialized technologies for slice excitation and reconstruction (Bilgic et al., 2014; Eichner et al., 2014b; Norris et al., 2011).

For these reasons, real-valued dMRI will fully reveal its potential as it deals with highly accelerated data, with high spatial resolution and/or strong diffusion weighting. The possibility of acquiring high numbers of averages will enable true signal averaging with significantly reduced noise bias, leading to higher resolutions and deeper insight into tissue microstructure.

Highlights.

• We implemented a method to overcome the noise bias in dMRI

• Real-valued dMRI data are overlaid with Gaussian noise

• Real dMRI enables unbiased signal averaging and linear least squares model fits

• Increased diffusion-contrast and sensitivity to crossing fibers

• More accurate fiber tracking results with reduced angular error