Abstract
Introduction
When measured using the computer-assisted method CUMULUS, mammographic density adjusted for age and body mass index predicts breast cancer risk. We asked if new mammographic density measures defined by higher brightness thresholds gave better risk predictions.
Methods
The Korean Breast Cancer Study included 213 women diagnosed with invasive breast cancer and 630 controls matched for age at full-field digital mammogram and menopausal status. Mammographic density was measured using CUMULUS at the conventional threshold (Cumulus), and in effect at two increasingly higher thresholds, which we call Altocumulus and Cirrocumulus, respectively. All measures were Box-Cox transformed and adjusted for age, body mass index, menopausal status and machine. We used conditional logistic regression to estimate the change in Odds PER standard deviation of transformed and Adjusted density measures (OPERA). The area under the receiver operating characteristic curve (AUC) was estimated.
Results
Corresponding Altocumulus and Cirrocumulus density measures were correlated with Cumulus measures (r approximately 0.8 and 0.6, respectively). Altocumulus and Cirrocumulus measures were on average 25 % and 80 % less, respectively, than the Cumulus measure. For dense area, the OPERA was 1.18 (95 % confidence interval: 1.01−1.39, P = 0.03) for Cumulus; 1.36 (1.15−1.62, P < 0.001) for Altocumulus; and 1.23 (1.04−1.45, P = 0.01) for Cirrocumulus. After fitting the Altocumulus measure, the Cumulus measure was no longer associated with risk. After fitting the Cumulus measure, the Altocumulus measure was still associated with risk (P = 0.001). The AUCs for dense area was 0.59 for the Altocumulus measure, greater than 0.55 and 0.57 for the Cumulus and Cirrocumulus measures, respectively (P = 0.001). Similar results were found for percentage dense area measures.
Conclusions
Altocumulus measures perform better than Cumulus measures in predicting breast cancer risk, and Cumulus measures are confounded by Altocumulus measures. The mammographically bright regions might be more aetiologically important for breast cancer, with implications for biological, molecular, genetic and epidemiological research and clinical translation.
Introduction
Historically, the incidence and prevalence of breast cancer has been lower in Asian countries than Western countries [1, 2]. However, this is changing rapidly with economic development over the past few decades and is expected to increase over the next 20 years [3, 4]. Identification of predictors of risk for Asian women could be an important tool in breast cancer control, especially if they can be readily measured.
Mammographic density is one of strongest risk factors for breast cancer [5, 6]. Conventionally, it has been defined by the white or bright, as distinct from dark, areas on a mammogram. A well-established measurement uses the computer-assisted thresholding method CUMULUS, in which the observer visually selects a pixel threshold to define the dense areas for each particular mammogram [7–9].
In establishing the evidence for mammographic density as a predictor of disease [5, 10], considerable and warranted attention has been made to having observers ‘see’ density in a similar and repeatable way. New observers have been trained to ensure comparability and repeatability with previous observers to measure what has conventionally been referred to as the ‘mammographically dense’ regions of the breast.
Multiple studies of Western women, and a few of Asian women, have shown that, after adjusting for age and body mass index (BMI), the standard measure of mammographic density above predicts breast cancer risk [11–16]. It is important to adjust for age and BMI because these mammographic density measures decrease with increasing age, and with increasing BMI, yet breast cancer risk increases with these factors [17, 18].
We used a Korean case-control study to assess if using in effect a higher than conventional pixel threshold to define density better discriminates cases from controls, i.e. better predicts risk of breast cancer. We assessed the relative discrimination by fitting the density measures based on different degrees of brightness both independently, and together.
We also represented the strength of association for each measure by a new approach, Odds PER Adjusted standard deviation (OPERA), which considers risk gradients for measured variables as a function not of the standard deviation of the unadjusted risk factor, as has been conventional practice, but of the standard deviation of that factor after adjusting for all other factors taken into consideration, either by design or analysis, in the case-control comparison [6]. The reason for this is that the correct interpretation of a risk estimate is the change per unit of that factor holding all other factors constant. Therefore it is obvious that the risk per unadjusted standard deviation is not the appropriate scale, which should be based on the distribution of that risk factor once it has been adjusted for all relevant covariates.
Methods
Subjects
As previously described [19], cases and controls were selected from women who underwent a periodic health checkup at the Health Promotion Center in the Samsung Medical Center, Korea, between February 2006 and December 2011. Breast cancer cases were selected based on a medical record review after breast cancer screening with a mammogram. For each breast cancer case, we chose approximately three controls matched for age (within 1 year), menopausal status, and date of health examination (within 1 month) randomly selected from women who had undergone the same routine health checkup. All controls had no evidence of malignant disease for at least 1 year after the routine health checkup. This study involved 213 breast cancer cases and 630 matched controls. The median age at mammography was 51.5 years and 45 % were under the age of 50 years. This study was approved by the Institutional Review Board of Samsung Medical Center (2011-0013545 and 2014R1A2A2A01002705) [19]. All women gave written consent [19].
Mammographic density measurements
Mammographic images were obtained using the processed full-field digital mammography system (Senograph 2000D/DMR/DS, General Electric Company, Milwaukee, WI, USA or Selenia, Hologic Inc., Marlborough, MA, USA) in the same institution. We used the cranio-caudal (CC) view of the breast, and for cases, the breast contralateral to that involved in the cancer diagnosis. All measures were conducted in sets of 100, plus a 10 % random repeat sample from within the set (to estimate the intra-class correlation within a set), and in every fifth set, plus the 10 % random sample from the first set (to estimate the intra-class correlation between sets). All measurements were blinded to case-control status as in [19] and blinded to the previous measures.
Mammographic density was measured first using the conventional approach for defining dense areas, and we call those measures Cumulus, and they were conducted by TLN, YKA, and CEF. The black or dark areas are not included. TLN’s measures were used in our previous publication [19].
Two of the same observers, TLN and YKA, re-measured all mammograms. This time the observers chose the bright, as distinct from white, areas to be ‘dense’ and therefore in effect defined mammographic density at a higher threshold. The grayish areas that are usually selected when measuring Cumulus were not included. We call these latter measures Altocumulus. TLN then measured all mammograms using in effect an even higher level of pixel intensity based on what were considered to be only the brightest regions. We call this measure Cirrocumulus. The intra-class correlation coefficients for the Altocumulus and Cirrocumulus measures of dense area were 0.93 and 0.80 cf. 0.98 for the Cumulus measure [19]. Figure 1 shows an example of Cumulus, Altocumulus and Cirrocumulus measures from the same mammogram.
Fig. 1.
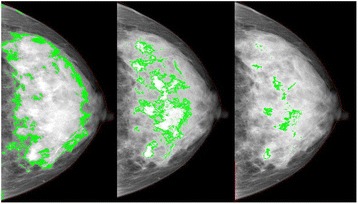
Example of Cumulus (left), Altocumulus (middle) Cirrocumulus (right) measurements from the same image using the CUMULUS software package. For Cumulus, Altocumulus and Cirrocumulus measures, respectively, the dense area (percentage dense area) was: 716,702 pixels (58 %); 268,374 pixels (22 %); and 51,475 pixels (4 %)
Other measurements
Height and weight, and hence BMI, as well as family history of breast cancer among first-degree relatives, menstrual and reproductive history, and health-related behaviours were measured as described previously [19].
Statistical analysis
We used the Box-Cox power function to transform the mammographic density measures so that their residuals after adjusting for age and menopausal status (due to the design), BMI (due to negative confounding), and machine (due to technological differences) were approximately normally distributed. We found that the cube root transformation was appropriate for the Cumulus and Altocumulus dense area measures and a logarithmic transformation was appropriate for the Cirrocumulus measure. A cube root transformation was appropriate for their respective percentage dense areas.
We evaluated the association between mammographic density and breast cancer risk by fitting conditional logistic regression models, adjusting for machine (due to different sampling ratios of cases and controls), with the mammographic density measures as both continuous and categorical variables. For the latter, we categorized the transformed mammographic measures, adjusted for age, menopausal status, BMI and machine, into four levels based on the quartile distribution of subjects in the control group, so as to be consistent with the OPERA concept; see below.
We estimated the mammographic density risk associations as the change in log odds per standard deviation of the age, menopausal status, BMI and machine adjusted measures so as to produce values of OPERA [6, 20]. Therefore the risk estimates refer to change in odds per standard deviation of mammographic density adjusted for age, BMI, menopausal status and machine, not of cross-sectional unadjusted mammographic density as is conventionally done, so we derived the former measures, standardized them, and fitted them in our models. Let r be the correlation between two mammographic density measures, Y1 and Y2. Since the standard deviation of Yj adjusted for Yk is SDj||k = [(1 – r2)]0.5, j,k = 1,2, when Yj is fitted with Yk we multiplied the log(OR) estimate from fitting Yj by SDj|k and then exponentiated to obtain the appropriate OPERA (see Appendix).
Statistical analyses, including generation of the receiver operating curves and estimates of and tests of the differences between areas under the receiver operating curves (AUCs) using the DeLong test, and use of the likelihood ratio criterion to test the relative goodness-of-fit of nested models, were performed using the STATA software package [21]. Nominal statistical significance was, by convention, taken to be P = 0.05.
Results
Table 1 shows that the mean age at breast cancer diagnosis for the cases was 51.6 years and 45 % were diagnosed before the age of 50 years, and that 63 % of cases and controls were premenopausal.
Table 1.
Characteristics of the case and control samples
| Cases (n = 213) mean (SD) | Controls (n = 630) mean (SD) | P a | |
|---|---|---|---|
| Age at mammogram (years) | 51.6 (7.6) | 51.5 (7.4) | 0.9 |
| Body mass index (kg/m2) | 22.5 (2.7) | 22.6 (2.8) | 0.8 |
| Age at menarche (years) | 14.6 (1.6) | 14.6 (1.6) | 0.9 |
| Number of live birth (per child) | 2.11 (0.75) | 2.27 (0.91) | 0.02 |
| Menopausal status (n, %) | 0.9 | ||
| Premenopausal | 134 (62.9) | 395 (62.7) | |
| Postmenopausal | 79 (37.1) | 235 (37.3) | |
| Benign breast lump (n, %) | <0.0001 | ||
| Yes | 34 (16.0) | 36 (5.6) | |
| No | 179 (84.0) | 594 (94.4) | |
| Ever smoking (n, %) | 0.08 | ||
| Yes | 17 (8.0) | 30 (4.8) | |
| Never | 196 (92.0) | 600 (95.2) | |
| Ever alcohol consumption (n, %) | 0.04 | ||
| Yes | 95 (44.6) | 232 (36.8) | |
| Never | 118 (55.4) | 398 (63.2) | |
| Physical exercise (n, %) | 0.2 | ||
| More and equal 90 mins per week | 85 (39.9) | 223 (35.4) | |
| Less than 90 mins per week | 128 (60.1) | 407 (64.6) | |
| Ever use of hormonal therapy (n, %) | 0.3 | ||
| Yes | 33 (15.5) | 82 (13.0) | |
| Never | 180 (84.5) | 548 (87.0) | |
| Mammographic measurements | |||
| Cumulus | |||
| Dense area (cm2) | 18.1 (14.9) | 15.6 (11.7) | 0.01 |
| Non-dense area (cm2) | 84.3 (36.0) | 85.3 (34.2) | 0.7 |
| Percentage dense area | 18.6 (12.3) | 16.2 (10.3) | 0.006 |
| Total area (cm2) | 102.3 (37.3) | 100.9 (35.0) | 0.6 |
| Density thresholds (0 to 4095) | 2174 (355) | 2142 (343) | 0.2 |
| Altocumulus | |||
| Dense area (cm2) | 14.3 (11.6) | 11.4 (8.4) | 0.0002 |
| Non-dense area (cm2) | 85.0 (35.3) | 87.5 (34.7) | 0.4 |
| Percentage dense area | 15.3 (10.8) | 12.4 (8.5) | 0.0001 |
| Total area (cm2) | 99.2 (36.2) | 99.0 (34.8) | 0.9 |
| Density thresholds (0 to 4095) | 2247 (301) | 2252 (300) | 0.8 |
| Cirrocumulus | |||
| Dense area (cm2) | 3.5 (3.4) | 3.0 (2.3) | 0.03 |
| Non-dense area (cm2) | 98.1 (41.0) | 97.7 (38.8) | 0.9 |
| Percentage dense area | 3.8 (2.8) | 3.3 (2.4) | 0.03 |
| Total area (cm2) | 101.6 (41.4) | 100.8 (39.0) | 0.8 |
| Density thresholds (0 to 4095) | 2559 (205) | 2574 (226) | 0.4 |
SD standard deviation
a P refers to statistical significance for the discrimination between cases and controls
For both cases and controls, the Altocumulus measures for dense and percentage dense area were 20–25 % less than the corresponding Cumulus measures (all P < 0.001); see Table 1. For dense area (percentage dense area), the differences were 4.1 cm2 (3.7 %) between Cumulus and Altocumulus measures, and 13.1 cm2 (13.4 %) between Cumulus and Cirrocumulus measures, respectively. The correlations were 0.84 and 0.79 for Cumulus and Altocumulus, 0.63 and 0.56 for Cumulus and Cirrocumulus, and 0.59 and 0.54 for Altocumulus and Cirrocumulus, respectively.
Table 1 shows that, for Cumulus, Altocumulus and Cirrocumulus, the mean of the dense and percentage dense areas differed between cases and controls (all P < 0.05). The statistical significance was greater for the Altocumulus measures (all P < 0.001).
Table 2 shows there were significant risk gradients for dense and percentage dense areas after adjusting for covariates (all P < 0.05). The OPERA estimates and the AUCs were highest for Altocumulus: 1.36 (95 % confidence interval (CI): 1.15–1.62, P < 0.001) for dense area and 1.41 (1.19–1.68, P < 0.001) for percentage dense area, respectively. The corresponding OPERA estimates for Cumulus were 1.18 (1.01–1.39, P = 0.03) for dense area and 1.23 (1.05– 1.44, P = 0.01) for percentage dense area, respectively. For Cirrocumulus they were 1.23 (1.04–1.45, P = 0.01) for dense area and 1.21 (1.03–1.42, P = 0.02) for percentage dense area, respectively.
Table 2.
Breast cancer risk association (OPERA) for the mammographic measurements after adjusted for age, body mass index, menopausal status and machine (Hologic and General Electric)
| Cases | ORa | 95 % CIb | P c | AUCd (95 % CI) | LL | |
|---|---|---|---|---|---|---|
| Cumulus | ||||||
| Dense area | ||||||
| Q1e (n = 211) | 47 | 1.00 | − | − | ||
| Q2e (n = 211) | 54 | 1.18 | 0.76−1.84 | 0.5 | ||
| Q3e (n = 211) | 53 | 1.17 | 0.74−1.84 | 0.5 | ||
| Q4e (n = 210) | 59 | 1.37 | 0.88−2.14 | 0.2 | ||
| OPERA | 213 | 1.18 | 1.01−1.39 | 0.03 | 0.55 (0.51−0.59) | -290.1865 |
| Percent density | ||||||
| Q1 | 49 | 1.00 | − | − | ||
| Q2 | 49 | 0.98 | 0.63−1.54 | 0.9 | ||
| Q3 | 53 | 1.09 | 0.70−1.71 | 0.7 | ||
| Q4 | 62 | 1.4 | 0.90−2.17 | 0.1 | ||
| OPERA | 213 | 1.23 | 1.05−1.44 | 0.01 | 0.56 (0.52−0.61) | -289.0511 |
| Altocumulus | ||||||
| Dense area | ||||||
| Q1 | 43 | 1.00 | − | − | ||
| Q2 | 55 | 1.46 | 0.91−2.34 | 0.1 | ||
| Q3 | 52 | 1.38 | 0.85−2.22 | 0.2 | ||
| Q4 | 63 | 1.84 | 1.13−2.99 | 0.01 | ||
| OPERA | 1.36 | 1.15−1.62 | <0.001 | 0.59 (0.55−0.63) | -285.9140 | |
| Percentage density | ||||||
| Q1 | 42 | 1.00 | − | − | ||
| Q2 | 54 | 1.49 | 0.92−2.39 | 0.1 | ||
| Q3 | 44 | 1.16 | 0.70−1.92 | 0.6 | ||
| Q4 | 73 | 2.49 | 1.52−4.09 | <0.001 | ||
| OPERA | 213 | 1.41 | 1.19−1.68 | <0.001 | 0.60 (0.56−0.65) | -284.7104 |
| Cirrocumulus | ||||||
| Dense area | ||||||
| Q1 | 41 | 1.00 | − | − | ||
| Q2 | 58 | 1.61 | 1.01−2.58 | 0.05 | ||
| Q3 | 53 | 1.42 | 0.89−2.26 | 0.1 | ||
| Q4 | 61 | 1.78 | 1.11−2.86 | 0.02 | ||
| OPERA | 213 | 1.23 | 1.04−1.45 | 0.01 | 0.57 (0.52−0.61) | -289.3243 |
| Percentage density | ||||||
| Q1 | 49 | 1.00 | − | − | ||
| Q2 | 51 | 1.06 | 0.67−1.67 | 0.8 | ||
| Q3 | 52 | 1.09 | 0.70−1.69 | 0.7 | ||
| Q4 | 61 | 1.40 | 0.89−2.22 | 0.1 | ||
| OPERA | 213 | 1.21 | 1.03−1.42 | 0.02 | 0.56 (0.52−0.61) | -289.6855 |
OPERA Odds PER Adjusted standard deviation, LL log likelihood
aOdds ratio per standard deviation of the risk factors adjusted for age, body mass index (BMI), menopausal status and machine (Hologic and General Electric)
bCI = confidence interval
c P refers to statistical significance of the odds ratio (OR) estimate
dAUCs refer to the area under the receiver operating characteristic curves for mammographic measurements after adjusted for age, body mass index, menopausal status and machine (Hologic and General Electric)
eQuartiles (Q1-Q4) defined by distribution of the measure adjusted for age, body mass index, menopausal status and machine (Hologic and General Electric)
Table 3 shows the results from fitting the corresponding Altocumulus, Cirrocumulus and Cumulus measures together. From the OPERA estimates and standard errors, and from examining the change in log likelihood (LL) and AUCs, it was apparent that after fitting the Altocumulus measure the addition of the Cumulus or Altocumulus measures did not improve the fit (P > 0.05). On the other hand, from Tables 2 and 3 it can be seen that addition of the Altocumulus measure gave a better fit than the Cumulus or Altocumulus measures alone (P = 0.001).
Table 3.
Estimates of OPERA, 95 % confidence intervals (95 % CI) from fitting multiple mammographic density measures together, correlation between estimates (R) and log likelihood (LL) for dense area and percentage dense area
| OPERA (95 % CI) | P | R | LL | |
|---|---|---|---|---|
| Dense area | ||||
| Cumulus a | 0.73 (0.53−1.00) | 0.05 | -0.87 | -280.34 |
| Altocumulus a | 1.83 (1.30−2.57) | 0.001 | ||
| Cumulus b | 1.07 (0.88−1.30) | 0.5 | -0.6 | -285.22 |
| Cirrocumulus b | 1.19 (0.97−1.47) | 0.1 | ||
| Altocumulus c | 1.32 (1.07−1.65) | 0.01 | -0.62 | -282.17 |
| Cirrocumulus c | 1.04 (0.85−1.29) | 0.7 | ||
| Cumulus d | 0.71 (0.52−0.98) | 0.04 | -0.79 | -279.97 |
| Altocumulus d | 1.77 (1.24−2.51) | 0.002 | -0.19 | |
| Cirrocumulus d | 1.10 (0.89−1.36) | 0.4 | -0.22 | |
| Percentage dense area | ||||
| Cumulus a | 0.87 (0.66−1.14) | 0.3 | -0.81 | -280.79 |
| Altocumulus a | 1.59 (1.18−2.14) | 0.002 | ||
| Cumulus b | 1.15 (0.96−1.38) | 0.1 | -0.50 | -284.74 |
| Cirrocumulus b | 1.14 (0.94−1.37) | 0.2 | ||
| Altocumulus c | 1.39 (1.13−1.70) | 0.002 | -0.51 | -284.65 |
| Cirrocumulus c | 1.03 (0.86−1.25) | 0.7 | ||
| Cumulus d | 0.87 (0.66−1.15) | 0.3 | -0.74 | -284.165 |
| Altocumulus d | 1.55 (1.14−2.10) | 0.005 | -0.15 | |
| Cirrocumulus d | 1.05 (0.87−1.27) | 0.6 | -0.23 | |
OPERA Odds PER Adjusted standard deviation
a Cumulus and Altocumulus measures fitted together
b Cumulus and Cirrocumulus measures fitted together
c Altocumulus and Cirrocumulus measures fitted together
d Cumulus, Altocumulus and Cirrocumulus measures fitted together
Figure 2 shows that, for dense area, the AUCs were: 0.55 (95 % CI 0.51–0.59); 0.59 (0.55–0.63); 0.57 (0.52–0.61) for the Cumulus, Altocumulus and Cirrocumulus measures, respectively. The AUCs for the Altocumulus measures were highly significantly greater than for the corresponding Cumulus measures (P = 0.001). For dense area, the change in AUC from 0.55 for the Cumulus measure to 0.59 for the Altocumulus measure is 80 % when compared with the baseline AUC of 0.5 corresponding to no association, and this is reflected in a similar change in the log (OPERA) estimates. Similar AUCs applied to the percentage dense area measurements.
Fig. 2.
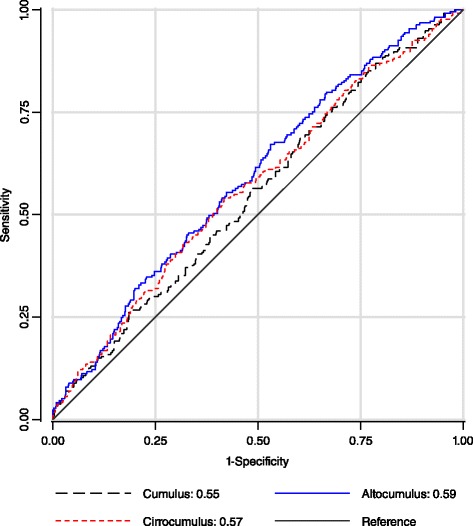
Receiver operating characteristic curve plot of sensitivity against 1-specificty for breast cancer risk, and area under the curve (AUC), for the various dense area measures from full-field digital mammograms in terms of breast cancer risk: Health Promotion Center in the Samsung Medical Center, Korea
Discussion
We have introduced two new measures of mammographic density, Altocumulus and Cirrocumulus (Nguyen et al: Mammographic density defined by higher than conventional pixel brightness thresholds better predicts breast cancer risk, submitted), based on defining the mammographically ‘dense’ regions by being successively brighter, and therefore in effect at higher pixel brightness thresholds, than has been convention, which we call Cumulus. All density measures discriminated between cases and controls. The risk gradients and AUCs for the dense area and percentage dense area measurements were the same as well as their AUC.
Even though these density measures were correlated, the Altocumulus measure performed better than the Cumulus and Cirrocumulus measures. Moreover, when measures were fitted together, the risk gradient for the Altocumulus measure remained statistically significant, while the risk gradient for the Cumulus and Cirrocumulus measures were reduced and no longer statistically significant. This implies that the apparent risk relationship from traditional Cumulus measures has been confounded by the true causes being in breast tissue seen at higher thresholds of pixel intensity, so that the white but not bright areas on a mammogram do not appear to be associated with risk.
Therefore, measuring density at a higher pixel threshold appears to capture more risk-predicting information than measuring at the usual threshold. This is important for several reasons. First, in terms of clinical relevance, we studied digital images, so our findings are relevant to mammography as it is now and will be conducted across most of the world. Digital mammography makes possible automated measures that can be used to provide information in real time. While different measures of ‘breast density’ from digital mammograms are being developed and applied (e.g. [22]), at the moment their only clinical use is to identify women most prone to have a breast cancer missed due to ‘masking’, rather than those at increased risk of a future breast cancer. Our findings inform future developments of automated measures. They also highlight that the two issues – masking and risk prediction – need to be considered separately. While the Altocumulus measures of dense area appear to be better predictors of risk, the Cumulus measures of percent dense area might be better predictors of masking.
Second, these findings suggest that the mammographically denser regions might be more aetiologically important for breast cancer. The relevant tissues and biological processes involved in explaining why ‘mammographic density’ is a risk factor for breast cancer are more likely to be in the higher density areas of the breast. If confirmed, this is a critical observation for molecular, genetic and other studies trying to determine the underlying biological processes behind this phenomenon [23]. It is also important for research and translation on the prospect of using ‘mammographic density’ to better predict women for interventions or targeted screening.
Third, Altocumulus is one of the strongest yet known risk factors for breast cancer when viewed on a population, as distinct from individual, perspective. OPERA is an omnibus measure for discrimination between cases and controls similar to the area under the receiver operator curve, but has the advantage of explicitly taking into account other risk factors. The OPERA we estimated here of 1.4–1.5 for Altocumulus is comparable to that for a risk score based on the current common genetic markers (SNPs) recently found to be associated with risk [24]. In comparison, the OPERA for rare mutations in BRCA1 and BRCA2, combined, is only about 1.2, while the OPERA for number of live births is close to 1.1 in a Western population [6].
Obviously there must be an optimal threshold, at least for a given population measured on a given machine by the same observer. This study suggests that it is at a higher pixel level than has been convention, at least for digital mammograms and Korean women. While we are not claiming that Altocumulus, as we have measured it, is necessarily the optimal measure, we have shown that the current threshold is not optimal. More research is needed to clarify the situation, especially if automated measures can be developed that allow for changing the threshold. We are currently measuring mammographic density across different thresholds in different populations, and using multiple observers, to try to obtain better mammographic predictors of risk. We encourage others to try varying thresholds to help clarify this important issue.
We are also measuring the familial aggregation of Altocumulus and Cirrocumulus using twin and family studies, we have done for Cumulus [17, 25, 26]. We aim to study the associations of genetic variants known to be associated with breast cancer risk with the Altocumulus and Cirrocumulus measures, and compare these findings to those for Cumulus measures (e.g. [27]).
There are several limitations to this study. The Cumulus, Altocumulus and Cirrocumulus measures depend on the observers. However, given that measurements are performed blind to case-control status, the main issue is repeatability, and all were highly repeatable, the most for Cumulus measures. Also, the concepts of “bright” and brightest” regions is somewhat subjective, and can vary across observers. But we have tried to see if and how risk prediction depends on the threshold, so the key issue was to have measurements in effect at different thresholds (and of course conducted blind to case-control status) and then use OPERA, log likelihoods and AUC to assess the relative goodness of fits.
Conclusions
This case-control study found that better discrimination between women with and without breast cancer can be achieved by defining mammographic density at a higher pixel brightness threshold than conventional, at least for Asian women. A new measure, Altocumulus, performed better than the conventional measure, Cumulus, in predicting breast cancer risk from digital mammography images. This suggests that the mammographically denser (bright) regions might be more aetiologically important for breast cancer, with implications for biological, molecular, genetic and epidemiological research and clinical translation. More research is required to work out which threshold is optimal and we encourage other researchers to work on this question.
Acknowledgements
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (number 2011-0013545 and 2010-0029113) and the Ministry of Science, ICT and Future Planning (2014R1A2A2A01002705). The funding sources had no involvement in conducting this study. TLN is supported by a Postgraduate Scholarship from the National Health and Medical Research Council (NHMRC) and The Richard Lowell Travelling Scholarship, The University of Melbourne. YKA was supported by the Australian Agency for International Development (AusAID). JLH is a NHMRC Senior Principal Research Fellow and a Distinguished Visiting Professor at Seoul National University.
Abbreviations
- AUC
area under the receiver operating curve
- BMI
body mass index
- CI
confidence interval
- LL
log likelihood
- OPERA
Odds PER Adjusted standard deviation
- P
refers to statistical significance of the odds ratio estimate
- R
correlation between estimates
- r
correlation
- SDj|k
standard deviation of Yj adjusted for Yk
Appendix
For each transformed density measure, Y, we fitted a regression for the mean as a linear function of age and BMI and the other fitted covariates. For individual i, E[Yi] = b0 + bage.agei + bBMI. BMIi + b1X1i + … + bnXni, where Yi is their observed value; E[.] represents the expected value; and agei, BMIi, X1i, …, Xni are their age, BMIi, and other fitted covariates; and b0, …, bn are the corresponding regression coefficients. We then divided the residuals, Ri = Yi – E[Yi], by the standard deviation of the residuals, SD(Ri), to give Y’ = Ri/SD(Ri).
The different density measures, Y’, were fitted independently and then together; the improvement in fit was assessed using the likelihood ratio test. When we fitted two density measures, Y1’ and Y2’, into the same model, we presented the risk estimates in terms of the change in the standard deviation after adjusting also for the other measure, to be consistent with the OPERA concept. Let r be the correlation between Y1’ and Y2’. Because the standard deviation of Yj’ adjusted for Yk’ is SD’ = [(1 – r2)]0.5, for j,k = 1,2, when Yj’ is fitted with Yk’ we multiplied the log(OR) estimate from fitting Yj’ by SD’ and then exponentiated it to obtain the appropriate OPERA. [For r = 0.6, 0.7, and 0.8, SD’ approximately 0.8, 0.7, and 0.6, respectively].
Footnotes
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
TLN conceived the concepts of Altocumulus and Cirrocumulus, performed mammographic density measurements, trained CEF and YKA, conducted the statistical analysis and wrote the first draft of the manuscript. CEF and YKA performed the mammographic density measurements. Y-MS, CY-H and JS designed the study and recruited the participants. JLH advised on statistical analyses, in particular with the use of OPERA, and contributed to interpretation and revising the draft manuscript. MAJ and JS supervised and advised TLN, and contributed to the methodology, statistical analyses, manuscript drafting and interpretation. All authors contributed to the interpretation of the results, providing critical advice on the draft manuscript for important intellectual content, and read and approved the final version of the manuscript.
Authors’ information
This manuscript is from PhD research being conducted by TLN (the first and corresponding author), exploring the possibilities of producing better predictors of risk from mammographic images by changing the threshold at which the image is presumed to represent ‘dense’ (i.e. aetiologically relevant) tissue. YKA has a MD (Myanmar) and a Master of Public Health (Melbourne). He was trained by TLN to measure mammographic density. JLH is a Senior Principal Research Fellow of the National Health and Medical Research Council (NHMRC) and has been leading Australian mammographic density research for more than 15 years, having established the first twin study and the Australian Mammographic Density Research Facility. MAJ is the principal supervisor of TLN’s PhD. JS is a co-supervisor and works with Y-MS, who led the Korean Healthy Twin Study and Korean Breast Cancer Study.
Contributor Information
Tuong Linh Nguyen, Phone: +61-3-9035-8200, Email: nguk@unimelb.edu.au.
Ye Kyaw Aung, Email: ye.aung@unimelb.edu.au.
Christopher Francis Evans, Email: cfevans@unimelb.edu.au.
Choi Yoon-Ho, Email: choismc@skku.edu.
Mark Anthony Jenkins, Email: m.jenkins@unimelb.edu.au.
Joohon Sung, Email: jsung@snu.ac.kr.
John Llewelyn Hopper, Email: j.hopper@unimelb.edu.au.
Yun-Mi Song, Email: yunmisong@skku.edu.
References
- 1.Weir HK, Thun MJ, Hankey BF, Ries LA, Howe HL, Wingo PA, et al. Annual report to the nation on the status of cancer, 1975-2000, featuring the uses of surveillance data for cancer prevention and control. J Natl Cancer Inst. 2003;95:1276–1299. doi: 10.1093/jnci/djg040. [DOI] [PubMed] [Google Scholar]
- 2.Kohler BA, Sherman RL, Howlader N, Jemal A, Ryerson AB, Henry KA, et al. Annual report to the nation on the status of cancer, 1975-2011, featuring incidence of breast cancer subtypes by race/ethnicity, poverty, and state. J Natl Cancer Inst. 2015;107:djv048. doi: 10.1093/jnci/djv048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Park SK, Kang D, Kim Y, Yoo KY. Epidemiologic characteristics of the breast cancer in Korea. J Korean Med Assoc. 2009;52:937–945. doi: 10.5124/jkma.2009.52.10.937. [DOI] [Google Scholar]
- 4.Sung H, Rosenberg PS, Chen WQ, Hartman M, Lim WY, Chia KS, et al. Female breast cancer incidence among Asian and Western populations: more similar than expected. J Natl Cancer Inst. 2015;107. doi:10.1093/jnci/djv107. [DOI] [PMC free article] [PubMed]
- 5.Boyd NF, Rommens JM, Vogt K, Lee V, Hopper JL, Yaffe MJ, et al. Mammographic breast density as an intermediate phenotype for breast cancer. Lancet Oncol. 2005;6:798–808. doi: 10.1016/S1470-2045(05)70390-9. [DOI] [PubMed] [Google Scholar]
- 6.Hopper JL, Odds PER. Adjusted standard deviation (OPERA): comparing strengths of associations for risk factors measured on different scales, and across diseases and populations. Am J Epidemiol. 2015;182:863–867. doi: 10.1093/aje/kwv193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Byng JW, Boyd NF, Fishell E, Jong RA, Yaffe MJ. The quantitative analysis of mammographic densities. Phys Med Biol. 1994;39:1629–1638. doi: 10.1088/0031-9155/39/10/008. [DOI] [PubMed] [Google Scholar]
- 8.Byng JW, Boyd NF, Fishell E, Jong RA, Yaffe MJ. Automated analysis of mammographic densities. Phys Med Biol. 1996;41:909–923. doi: 10.1088/0031-9155/41/5/007. [DOI] [PubMed] [Google Scholar]
- 9.Byng JW, Yaffe MJ, Jong RA, Shumak RS, Lockwood GA, Tritchler DL, et al. Analysis of mammographic density and breast cancer risk from digitized mammograms. Radiographics. 1998;18:1587–1598. doi: 10.1148/radiographics.18.6.9821201. [DOI] [PubMed] [Google Scholar]
- 10.Boyd NF, Guo H, Martin LJ, Sun L, Stone J, Fishell E, et al. Mammographic density and the risk and detection of breast cancer. N Engl J Med. 2007;356:227–236. doi: 10.1056/NEJMoa062790. [DOI] [PubMed] [Google Scholar]
- 11.Ursin G, Ma H, Wu AH, Bernstein L, Salane M, Parisky YR, et al. Mammographic density and breast cancer in three ethnic groups. Cancer Epidemiol Biomarkers Prev. 2003;12:332–338. [PubMed] [Google Scholar]
- 12.Buck E, Eyzaguirre A, Brown E, Petti F, McCormack S, Haley JD, et al. Rapamycin synergizes with the epidermal growth factor receptor inhibitor erlotinib in non-small-cell lung, pancreatic, colon, and breast tumors. Mol Cancer Ther. 2006;5:2676–2684. doi: 10.1158/1535-7163.MCT-06-0166. [DOI] [PubMed] [Google Scholar]
- 13.Vachon CM, Brandt KR, Ghosh K, Scott CG, Maloney SD, Carston MJ, et al. Mammographic breast density as a general marker of breast cancer risk. Cancer Epidemiol Biomarkers Prev. 2007;16:43–49. doi: 10.1158/1055-9965.EPI-06-0738. [DOI] [PubMed] [Google Scholar]
- 14.Kotsuma M, Tokui T, Freudenthaler S, Nishimura K. Effect of CYP2D6 polymorphism on pharmacokinetics of a novel ACAT inhibitor, pactimibe and its unique metabolite, R-125528. Int J Clin Pharmacol Ther. 2008;46:545–555. doi: 10.5414/CPP46545. [DOI] [PubMed] [Google Scholar]
- 15.Heusinger K, Loehberg CR, Haeberle L, Jud SM, Klingsiek P, Hein A, et al. Mammographic density as a risk factor for breast cancer in a German case-control study. Eur J Cancer Prev. 2011;20:1–8. doi: 10.1097/CEJ.0b013e328341e2ce. [DOI] [PubMed] [Google Scholar]
- 16.Razzaghi H, Troester MA, Gierach GL, Olshan AF, Yankaskas BC, Millikan RC. Mammographic density and breast cancer risk in White and African American Women. Breast Cancer Res Treat. 2012;135:571–580. doi: 10.1007/s10549-012-2185-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Boyd NF, Dite GS, Stone J, Gunasekara A, English DR, McCredie MR, et al. Heritability of mammographic density, a risk factor for breast cancer. N Engl J Med. 2002;347:886–894. doi: 10.1056/NEJMoa013390. [DOI] [PubMed] [Google Scholar]
- 18.McCormack VA, dos Santos SI. Breast density and parenchymal patterns as markers of breast cancer risk: a meta-analysis. Cancer Epidemiol Biomarkers Prev. 2006;15:1159–1169. doi: 10.1158/1055-9965.EPI-06-0034. [DOI] [PubMed] [Google Scholar]
- 19.Kim BK, Choi YH, Nguyen TL, Nam SJ, Lee JE, Hopper JL, et al. Mammographic density and risk of breast cancer in Korean women. Eur J Cancer Prev. 2015;24:422–429. doi: 10.1097/CEJ.0000000000000099. [DOI] [PubMed] [Google Scholar]
- 20.Kim BK, Choi YH, Song YM, Park JH, Noh HM, Nguyen TL, et al. Bone mineral density and the risk of breast cancer: a case-control study of Korean women. Ann Epidemiol. 2014;24:222–227. doi: 10.1016/j.annepidem.2013.11.009. [DOI] [PubMed] [Google Scholar]
- 21.StataCorp. Stata Statistical Software. Release 12. College Station, TX: StataCorp LP; 2009.
- 22.Eng A, Gallant Z, Shepherd J, McCormack V, Li J, Dowsett M, et al. Digital mammographic density and breast cancer risk: a case inverted question mark control study of six alternative density assessment methods. Breast Cancer Res. 2014;16:439. doi: 10.1186/s13058-014-0439-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Martin LJ, Boyd NF. Mammographic density. Potential mechanisms of breast cancer risk associated with mammographic density: hypotheses based on epidemiological evidence. Breast Cancer Res. 2008;10:201. doi: 10.1186/bcr1831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mavaddat N, Pharoah PD, Michailidou K, Tyrer J, Brook MN, Bolla MK, et al. Prediction of breast cancer risk based on profiling with common genetic variants. J Natl Cancer Inst. 2015;107. doi:10.1093/jnci/djv036. [DOI] [PMC free article] [PubMed]
- 25.Stone J, Dite GS, Gunasekara A, English DR, McCredie MR, Giles GG, et al. The heritability of mammographically dense and nondense breast tissue. Cancer Epidemiol Biomarkers Prev. 2006;15:612–617. doi: 10.1158/1055-9965.EPI-05-0127. [DOI] [PubMed] [Google Scholar]
- 26.Nguyen TL, Schmidt DF, Makalic E, Dite GS, Stone J, Apicella C, et al. Explaining variance in the cumulus mammographic measures that predict breast cancer risk: a twins and sisters study. Cancer Epidemiol Biomarkers Prev. 2013;22:2395–2403. doi: 10.1158/1055-9965.EPI-13-0481. [DOI] [PubMed] [Google Scholar]
- 27.Odefrey F, Stone J, Gurrin LC, Byrnes GB, Apicella C, Dite GS, et al. Common genetic variants associated with breast cancer and mammographic density measures that predict disease. Cancer Res. 2010;70:1449–1458. doi: 10.1158/0008-5472.CAN-09-3495. [DOI] [PubMed] [Google Scholar]


