Sensitivity of Tumor Motion Simulation Accuracy to Lung Biomechanical Modeling Approaches and Parameters

Abstract

Finite element analysis (FEA)-based biomechanical modeling can be used to predict lung respiratory motion. In this technique, elastic models and biomechanical parameters are two important factors that determine modeling accuracy. We systematically evaluated the effects of lung and lung tumor biomechanical modeling approaches and related parameters to improve the accuracy of motion simulation of lung tumor center of mass (TCM) displacements. Experiments were conducted with four-dimensional computed tomography (4D-CT). A Quasi-Newton FEA was performed to simulate lung and related tumor displacements between end-expiration (phase 50%) and other respiration phases (0%, 10%, 20%, 30%, and 40%). Both linear isotropic and non-linear hyperelastic materials, including the Neo-Hookean compressible and uncoupled Mooney-Rivlin models, were used to create a finite element model (FEM) of lung and tumors. Lung surface displacement vector fields (SDVFs) were obtained by registering the 50% phase CT to other respiration phases, using the non-rigid demons registration algorithm. The obtained SDVFs were used as lung surface displacement boundary conditions in FEM. The sensitivity of TCM displacement to lung and tumor biomechanical parameters was assessed in eight patients for all three models. Patient-specific optimal parameters were estimated by minimizing the TCM motion simulation errors between phase 50% and phase 0%. The uncoupled Mooney-Rivlin material model showed the highest TCM motion simulation accuracy. The average TCM motion simulation absolute errors for the Mooney-Rivlin material model along left-right (LR), anterior-posterior (AP), and superior-inferior (SI) directions were 0.80 mm, 0.86 mm, and 1.51 mm, respectively. The proposed strategy provides a reliable method to estimate patient-specific biomechanical parameters in FEM for lung tumor motion simulation.

1. Introduction

Tumor motion management strategies are important in both planning and delivery stages of radiation therapy (Zhuang et al., 2014; Cole et al., 2014; Cervino et al., 2011; Lewis et al., 2010; Keall et al., 2006; Papiez, 2004; Papiez et al., 2005). Since the introduction of four-dimensional (4D) imaging techniques, including 4D-CT, significant efforts have been undertaken to manage lung and upper abdominal tumor motion(Keall et al., 2006; Lu et al., 2005; Sonke et al., 2005). Accurate motion tracking based on 4D-CT is divided into three main techniques: 1) image registration, 2) biomechanical modeling, and 3) a combination of image registration and biomechanical modeling (Zhong et al., 2012). Deformable image registration algorithms provide an estimation of motion by matching image intensities or features in 4D-CT image sequences (Gu et al., 2010; Xie et al., 2009). Respiratory mechanics and physiology are often ignored in these registration strategies, which could lead to unrealistic deformation (Brock et al., 2005). In biomechanical modeling, lung deformation is simulated according to more realistic causes such as tissue properties, passive and active interaction forces between organs, gravity and boundary conditions (Mead et al., 1970). In recent years, studies have been conducted to incorporate the biomechanical properties of organs into deformable image registration by using finite element analysis (FEA), with promising results (Brock et al., 2005; Zhang et al., 2004; Li et al., 2013; Chhatkuli et al., 2009; Al-Mayah et al., 2009; Fuerst et al., 2012).

FEA is a numerical method that provides a framework for dividing a complex problem into small elements. Each element contains the material and structural properties that define how the structure will react to certain external conditions such as boundary contacts or forces. Thus, in FEA-based modeling, accuracy is influenced by the elastic properties assigned to each element. In conventional lung finite element modeling (FEM), lung tissue is typically assumed to be isotropic, homogeneous and linearly elastic. Brock et al., for instance, developed a finite element model-based platform called MORFEUS (Brock et al., 2005) and considered homogeneous lung materials with Poisson’s ratio (v) equal to 0.450 and Young’s modulus (E) equal to 5.0 KPa. Eom et al. developed a hyperelastic lung model and studied the mechanics of pleural sliding and intra-pleural pressure within the ribcage (Eom et al., 2010). Lung mechanical characteristics were simulated as a homogeneous, isotropic, hyperelastic model with E equal to 6.0 kPa and v equal to 0.4, with a large simulation error at the tumor region. Werner et al. proposed an FEM approach to model 12 lung cancer patients (Werner et al., 2009). In their study, tumor and lung tissue were assumed to be homogeneous. They reported that lung tumor size and location influenced the simulation results, and that accuracy decreased in the region surrounding the tumor. These results suggest that appropriate modeling of lung and tumor biomechanical properties in FEA is critical for accurate simulation of the tumor motion.

In this study, we considered the lung and the tumor as distinct soft tissues, and studied the interaction between lung surface deformation and tumor center of mass (TCM) displacement. We investigated the influence of biomechanical modeling approaches and tissue parameters on the accuracy of tumor motion estimation in FEA simulation. Three different linear and nonlinear hyperelastic models were explored, including a linear isotropic elastic model, the Neo-Hookean compressible material model, and the uncoupled Mooney-Rivlin material model. Surface displacement vector fields (SDVFs) were used as boundary conditions for nonlinear modeling of lung motion in the FEA modeling among different respiratory phases. Sensitive biomechanical parameters to the TCM motion simulation error were first identified and then on a patient-specific level optimized (within the range of current literature values) to minimize the TCM motion simulation error.

2. Materials and Methods

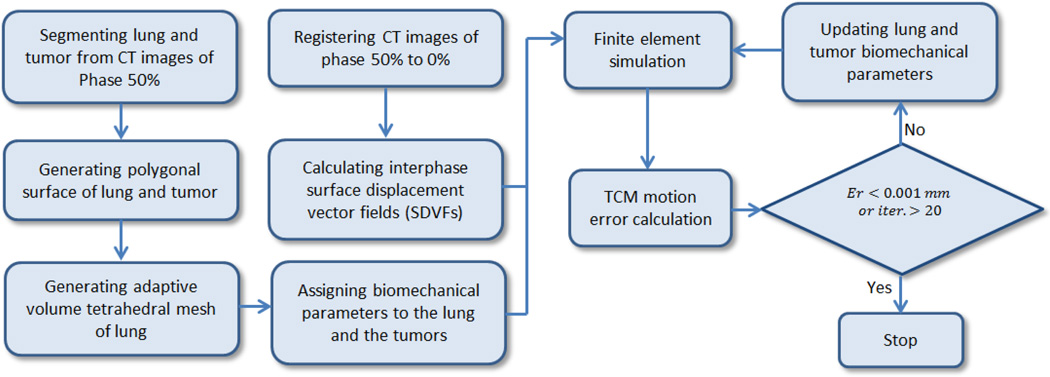
Figure 1 shows the strategy to estimate the optimal biomechanical parameters of lung and tumor to minimize the TCM motion simulation error. First, the CT images of phase 50% (end-expiration) were segmented, and the tetrahedral mesh volumes of lung and tumor were generated from the polygonal surface. The CT images of phase 0% (end-inspiration) were registered to phase 50% and the surface displacement vector fields (SDVFs) were extracted. Using SDVFs as the boundary condition, the finite element solver determined the TCM motion simulation error with the initial biomechanical parameters. These parameters were updated to minimize the TCM motion simulation error iteratively. The algorithm stopped when the TCM motion simulation error was less than 0.001 mm or when the number of iteration reached 20. In the following sections, the strategy is described in detail.

Figure 1.

Flowchart of the strategy to estimate the optimal biomechanical parameters of lung and tumor.

2.1 Building 3D Geometries

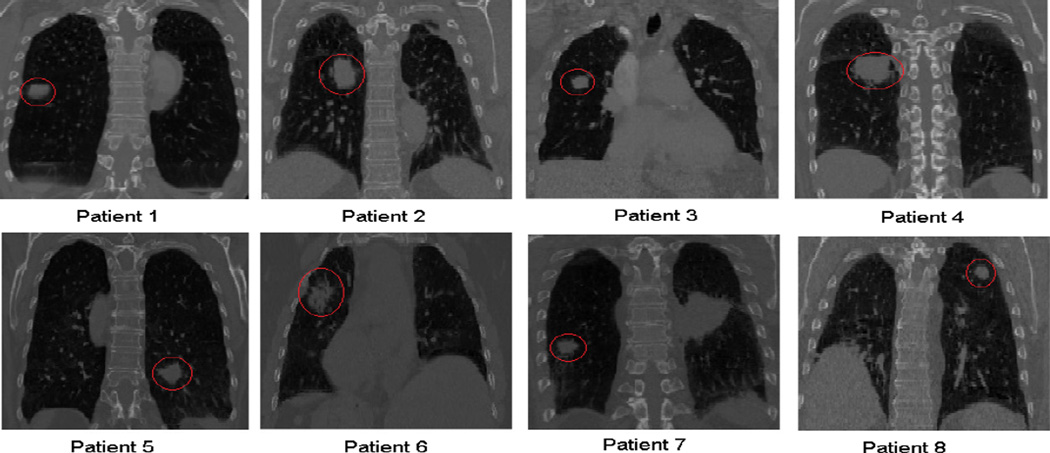
In this study, CT images from eight lung cancer patients were used. The phase 50% images are shown in Figure 2, with red circles indicating tumors. The images were acquired by a Philips Brilliance Big Bore CT-simulator (Phillips Healthcare, Cleveland, OH). The resolution of CT images varied from 0.937mm × 0.937mm × 1.5mm to 1.178mm × 1.178mm × 2.5mm.

Figure 2.

End-expiration CT images (coronal plane) of the eight lung cancer patients used in this study. The red circles indicate tumor regions.

For each patient, these images were used to construct a 3D geometric model for the FEA model. Therefore, a 3D triangular surface mesh of the tumor and lung region was obtained by thresholding-based segmentation using ITK-SNAP (Yushkevich et al., 2006). The level of thresholding was selected manually and set to −300 HU. Morphologic operations were applied to smooth irregular boundaries of the mediastinum, using a MeshLab open source code (Cignoni et al., 2008). Adaptive volume meshes were automatically created by the CUBIT v11.1 Geometry and Mesh Generation Toolkit (Sandia National Laboratory) (Blacker et al., 1994), based on the geometric properties of the volumes. For example, the tetrahedron inside the tumor and the surface area around the diaphragm were denser than other regions. The minimum and maximum edge lengths of tetrahedral elements were set between 0.7 mm and 4.0 mm in the created adaptive meshes (Lober et al., 1992).

The characteristics of the finite element models, as well as lung and tumor volumes, are summarized in Table 1 for each patient. Average numbers of tetrahedral elements and vertices for the lung were calculated as 53003 and 13626, respectively, and as 2989 and 745 for the tumor, respectively. The minimum change in lung volume between 0% and 50% phases was determined at 8% in patient 3, while patient 6 exhibited the greatest volume difference at 19%.

Table 1.

Characteristics of the finite-element model in each patient. Lung ΔV refers to the change in lung volume between 0% and 50% phase.

Patient #	#vertices/ #elements lung	#vertices/ #elements tumor	#surface vertices	Lung volume V (mm3)	Lung ΔV %	Tumor volume (mm3)
1	12505/48241	499/2114	15873	2987422	10	3404
2	9880/37547	702/2702	12345	2190196	13	15810
3	21013/85495	487/2101	24557	1507066	8	1795
4	11109/40729	1294/5041	14127	1909109	10	25699
5	14180/54945	1117/4625	8587	1166465	16	3775
6	18394/73506	2319/10429	10288	717546	19	4499
7	25500/115126	901/3919	11589	1484455	16	2121
8	12644/47837	1205/4833	11357	1610346	10	1768

2.2 Lung surface displacement estimation

The non-rigid demons registration algorithm (Kroon and Slump, 2009; Thirion, 1998) was used to calculate the voxel DVFs between CT images in two different respiration phases. The demons algorithm was previously shown to achieve accurately lung motion estimation from 4D-CT (Gu et al., 2010). The algorithm was implemented in Matlab (Matlab 2014) and run on a personal computer (CPU: Intel Core i7, 2.4 GHz; 16 GB DDR3 RAM). The standard deviation of the Gaussian regularization kernel of the algorithm was set to 1 voxel. Nearest neighbor interpolation was used to extract surface vertices DVFs from the voxel DVFs.

2.3 Elasticity Models

The elastic properties of lung tissue have often been modeled with linear Hooke’s law (Werner et al., 2009; Carter et al., 2005), which describes a simple linear relation between the force (stress) and the deflection (strain). However, a study by Pinart et al. (Pinart et al., 2011) demonstrated that rat lungs exhibit a non-linear behavior under certain physiological conditions, such as lung fibrosis. Freed et al. (Freed et al., 2012) recently reported that the Mooney-Rivlin (Mooney, 1940) model is appropriate to describe the viscoelasticity for the lung. In this study, we systematically investigated the influence of the elasticity model for lung and lung tumor tissue on the accuracy of tumor motion in lungs of cancer patients. Specifically, we used the following three models to describe lung deformation: 1) the linear isotropic elastic model, 2) the Neo-Hookean (Bonet and Wood, 1997) compressible model, and 3) the uncoupled Mooney-Rivlin model. The strain-energy functions for these models and their corresponding parameters are summarized in Table 2. The detailed description of these functions can be found in the FEbio theory manual (Maas et al., 2014).

Table 2.

Strain-energy functions of three elastic models (Maas et al., 2014).

Elastic model	Strain-energy function	Parameter description
Linear isotropic elastic	$W=\frac{1}{2}\lambda {(\mathit{\text{tr}}E)}^2+\mu \mathit{\text{tr}}(E^2)$	E: Euler-Lagrange strain tensor λ and μ: Lamé parameters J: determinant of the deformation gradient tensor Ĩ1 and Ĩ2: first and second invariants of the deviatoric right Cauchy-Green deformation tensor c1 and c2: material parameters K: bulk modulus
Neo-Hookean compressible Material	$W=\frac{\mu }{2}({Ĩ}_1-3)-\mu \text{ln}J+\frac{\lambda }{2}{(\text{ln}J)}^2$
Uncoupled Mooney-Rivlin material	$W=c_1({Ĩ}_1-3)+c_2({Ĩ}_2-3)+\frac{1}{2}K{(\mathit{\text{ln}}J)}^2$

In the linear isotropic elastic and Neo-Hookean compressible material models, Lamé parameters λ and μ were related to the Young’s modulus E and Poisson’s ratio v as follows:

$$\lambda =\frac{\upsilon \mathrm{E}}{(1+v)(1-2v)},\hspace{1em}\mu =\frac{\mathrm{E}}{2(1+v)}.$$ (1)

Both parameter sets – (λ, μ) and (E, v) – are commonly used in current literature on lung motion modeling; here, we focus on E and v. In the Mooney-Rivlin model, we evaluated the TCM motion simulation accuracy with condition c₁ = c₂ to simplify the problem. The strain energy function of the Mooney-Rivlin model is a 2–parameter model based on c_1,2 as material constants for deviatoric deformations and K as the bulk modulus for volumetric deformations. The deviatoric deformation describes pure shape change without volume change, while the volumetric deformation describes pure volume change without shape change. In the Mooney-Rivlin model, the commonly used incompressibility of materials (k − factor) is defined as (K/c_1,2). Parameters c₁, c₂ and K are related to the Young’s modulus E and Poisson’s ratio v as follows (Maas et al., 2014):

$$c_1+c_2=\frac{E}{4(1+v)}$$ (2)

$$K=\frac{4(c_1+c_2)(1+v)}{3(1-2v)}.$$ (3)

2.4 Minimizing TCM motion simulation error

The TCM motion simulation error was defined as the Euclidean distance between TCM positions as observed in the 4D-CT data and the predicted location of the TCM based on the finite element (FE) solver simulation. Initially, we had four parameters (two for the tumor and two for the lung) to minimize the TCM motion simulation error. The parameters for the isotropic elastic and Neo-Hookean models were set as Young’s Modulus and Poisson’s ratio of lung and tumor (E^lung, v^lung, E^tumor, and v^tumor), while for the Mooney-Rivlin model they were set as ${\mathrm{c}}_{1,2}^{\text{tumor}},{\mathrm{c}}_{1,2}^{\text{lung}}$, k − factor^lung, and k − factor^tumor. We modified and applied the open source FE solver FEBio (Maas et al., 2012; Moerman et al., 2013) to investigate the sensitivity of lung and tumor biomechanical parameters by sweeping parameters on the full four-dimensional (4D) space, including E^lung, v^lung, E^tumor, and v^tumor for the isotropic elastic model and Neo-Hookean model, and k − factor^tumor, k − factor^lung, $c_{1,2}^{\mathit{\text{tumor}}}$, and $c_{1,2}^{\mathit{\text{lung}}}$ for the Mooney-Rivlin model. As currently no consensus exists regarding the choice of optimal parameter values for the different material models (Werner, 2013), we selected lower and upper bounds for the biomechanical parameter sensitivity analysis and optimization based on previous studies. Table 3 summarizes the biomechanical parameters used in previous studies for lung modeling (Brock et al., 2005; Lai-Fook and Hyatt, 2000; Matthews and West, 1972; Zhang et al., 2004; Sundaram and Feng, 1977; Villard et al., 2005; De Wilde et al., 1981; Eom et al., 2010). The lower and upper bounds for Poisson’s ratio of lung were set at 0.1 and 0.49 during the parameter optimization in our study. These bounds encompassed the values used in previous studies. For Young’s modulus of lung, the lower and upper bounds in our study were 0.25 kPa and 7.0 kPa, respectively. In the Mooney-Rivlin model, the range of ${\mathrm{c}}_{1,2}^{\text{tumor}},{\mathrm{c}}_{1,2}^{\text{lung}}$ was set to 0 and 40 kPa during the parameter sweeping. Using the selected range of Poisson’s ratio (0.1–0.49), the range of the k − factor^lung calculated by equation (3) was between 3.6 and 198.6. The range of k − factor for both lung and tumor was initially set to 0.5 to 200 during parameter sweeping in the sensitivity analysis. However, k − factor^lung was less than 40 to achieve the minimum TCM motion simulation error for all eight patients in this study. Therefore, the final search range for k − factor^lung was set to 0.5 to 40 during the parameter optimization.

Table3.

Biomechanical parameter values used in previous studies for lung modeling.

Previous research	Biomechanical parameters
	Poisson’s ratio	Young’s Modulus
	(West and Matthews, 1972)	0.2 to 0.48	0.25 kPa
(Sundaram and Feng, 1977)	0.45	0.25 kPa
(De Wilde et al., 1981)	0.3, 0.4, and 0.45	0.73 kPa
(Zhang et al., 2004)	0.35	4.0 kPa
(Brock et al., 2005)	0.45	5.0 kPa
(Villard et al., 2005)	0.25, 0.3, and 0.35	0.25 to 7.0 kPa
(Eom et al., 2010)	0.4	6.0 kPa

During the initial parameter sweeping, parameters were considered to be sensitive when they affected the TCM motion simulation error by at least 0.1 mm. Our results (see Section 3) showed that sensitive parameters for the isotropic linear elastic and the Neo-Hookean models were Young’s Modulus and Poisson’s ratio for lung (E^lung, ν^lung). In the Mooney-Rivlin model, the sensitive parameter was the k − factor^lung. The optimal values of these sensitive parameters were then obtained for each patient through the optimization strategy described below: The Matlab function ‘fmincon’ (as part of the Matlab optimization toolbox) was used to minimize the TCM motion simulation error. For the isotropic elastic and Neo-Hookean material models, the objective function was the Euclidean distance between TCM in breathing phase 0% (target) and the predicted TCM, based on the FE solver simulation as follows:

$$\underset{E^{\mathit{\text{lung}}},v^{\mathit{\text{lung}}}}{\text{min}}(\Vert TCM\mathit{\text{in}}FE\mathit{\text{solver}}(E^{\mathit{\text{lung}}},v^{\mathit{\text{lung}}})-TCM\mathit{\text{in phase}}0\%\Vert ),$$ (4)

where ‖·‖ is the Euclidean distance. Inputs to the FE solver were the interphase SDVFs, the tetrahedral mesh of lung in phase 50% and the biomechanical parameters for lung and tumor. Initial values of Young’s Modulus and Poisson’s ratio were the same as those previously used by Li et al. (Li et al., 2013) as follows: E^lung=1.5 kPa, v^lung =0.38. To obtain the minimal TCM motion simulation error in the Mooney-Rivlin material model, the corresponding objective function was calculated as:

$$\underset{k-{\mathit{\text{factor}}}^{\mathit{\text{lung}}}}{\text{min}}(\Vert TCM\mathit{\text{in}}FE\mathit{\text{solver}}(k-{\mathit{\text{factor}}}^{\mathit{\text{lung}}})-TCM\mathit{\text{in phase}}0\%\Vert ),$$ (5)

The value of $c_{1,2}^{\mathit{\text{tumor}}}$ and $c_{1,2}^{\mathit{\text{lung}}}$ was set at 0.135 kPa and k − factor^tumor was set at 15.42. The initial value for lung k − factor^lung was also set 15.42, which was calculated from equations (2) and (3) with E=1.5 kPa and v = 0.38. We assigned a large value to the tumor incompressibility ratio (k − factor^tumor = 15) to minimize the tumor volume change during respiration.

3. Results

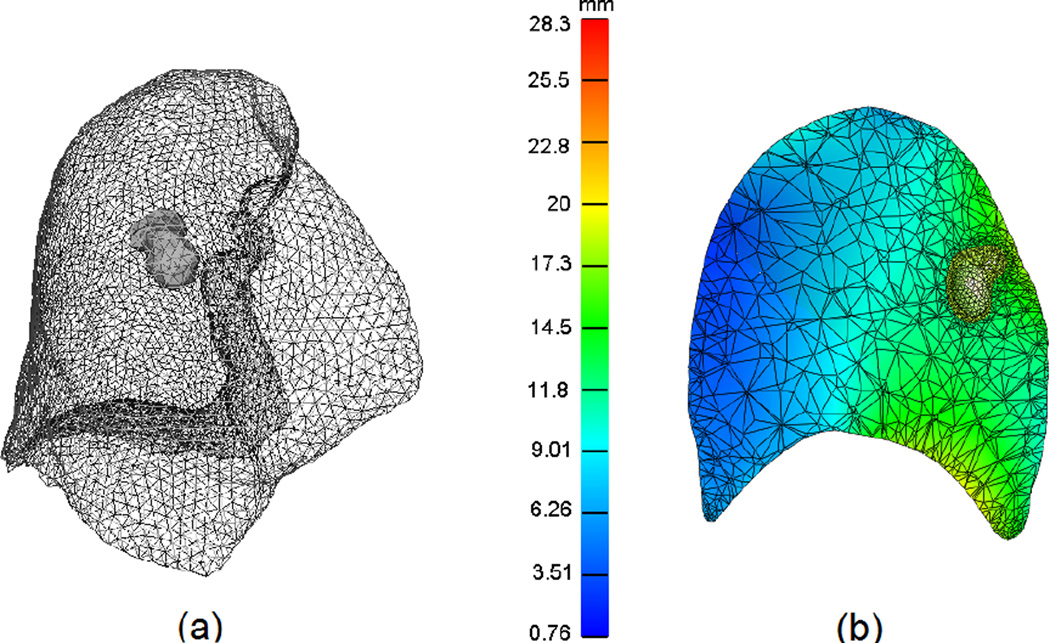
Unless indicated otherwise, we report representative results from patient 2 as the largest TCM distance between the 0% and 50% respiratory phases was observed in this case. Similar trends were observed for other patients. Figure 3(a) illustrates a sample of the surface triangle mesh, while figure 3(b) shows the total nodal displacement amplitude in a cutting-plane of volumetric mesh after lung motion simulation, using the Mooney-Rivlin material model. The color bar indicates the magnitude of nodal displacement (in mm), with minimum displacement depicted in blue and maximum displacement indicated in red.

Figure 3.

(a) 3D surface mesh of the lung and tumor reconstructed from the end-inspiration CT from patient 2. (b) the cutting plane through the lung and tumor motion simulation in the Mooney-Rivlin material model. The color bar illustrates the magnitude of displacement in millimeters.

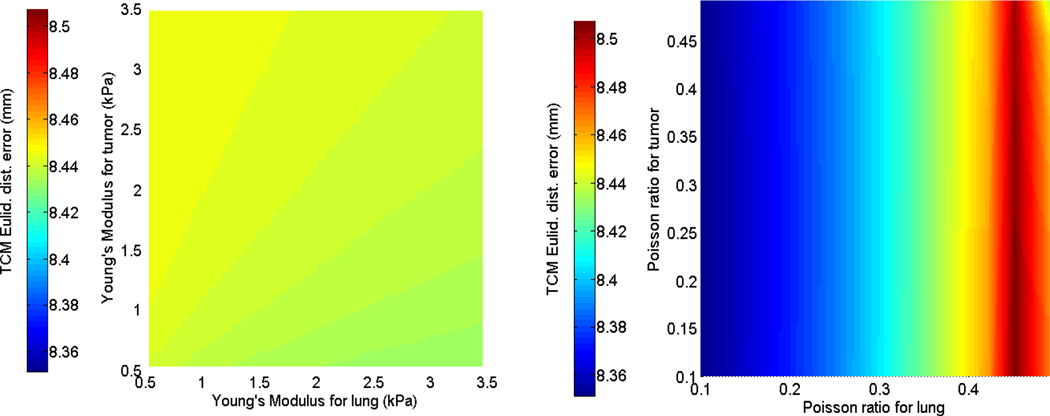
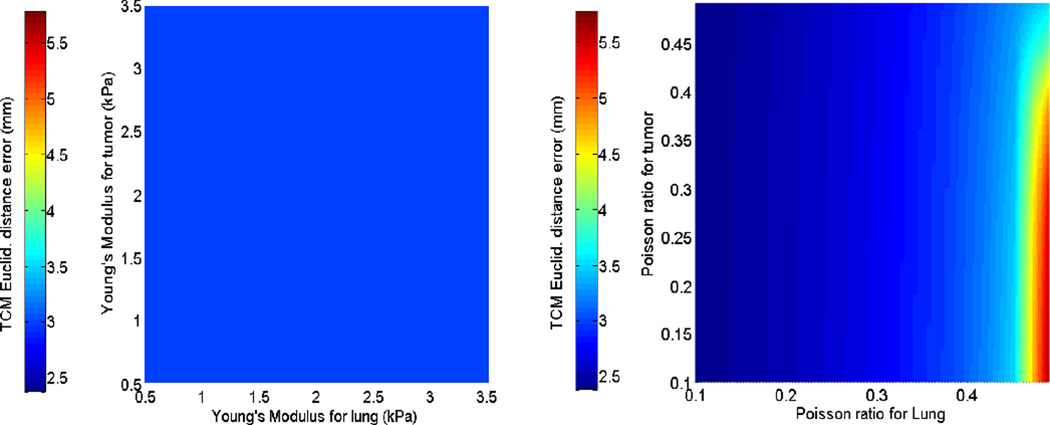
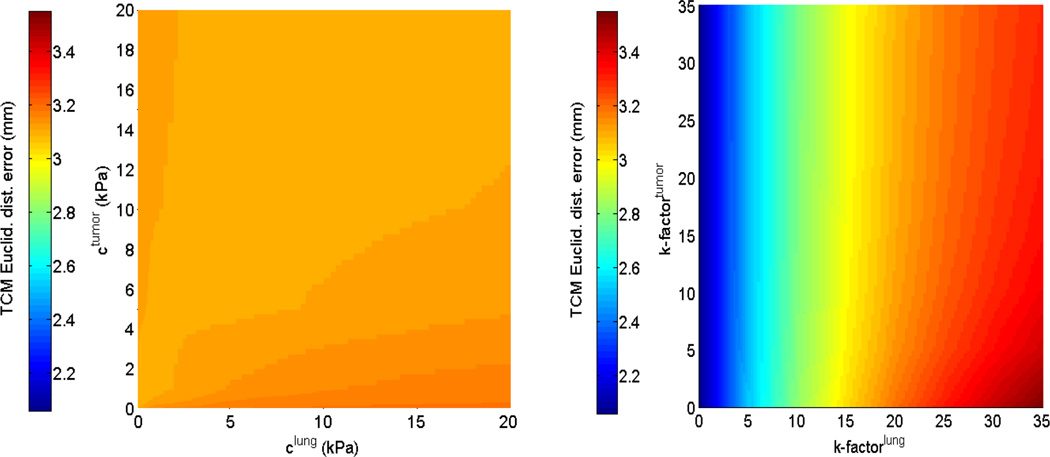
The first and second rows of figure 4 display the sensitivity of the TCM simulation error to biomechanical parameters in the isotropic elastic and Neo-Hookean material models for patient 2. While parameter sweeping was performed in the full 4D parameter space with the specified bounds (as extracted from current literature), these illustrations were displayed in the 2-parameter plane, e.g., Young’s modulus for tumor and lung. Figure 5 shows the sensitivity of TCM simulation error to biomechanical parameters in the Mooney-Rivlin model. These results indicate that the TCM motion simulation error is less sensitive to the tumor biomechanical parameters in both isotropic elastic and Neo-Hookean material models. In the Mooney-Rivlin model, parameters $c_{1,2}^{\mathit{\text{tumor}}}$ and $c_{1,2}^{\mathit{\text{lung}}}$ changed the TCM motion simulation error to less than 0.1 mm. Similar results were found for the other patients. These results are as expected as c values were related to the deviatoric deformation, while most of the lung deformation was volumetric.

Figure 4.

Sensitivity of the TCM motion simulation error to biomechanical parameters for patient 2. The first row shows the results of the isotropic elasticity model by varying Young’s Modulus and Poisson’s ratio for both lung and tumor. The second row shows corresponding results of the Neo-Hookean model.

Figure 5.

TCM motion simulation error sensitivity in the Mooney-Rivlin model for patient 2: (Left side) to the deviatoric deformation c_1,2 (tumor and lung); and (Right side) to the volumetric change k − factor of lung and tumor.

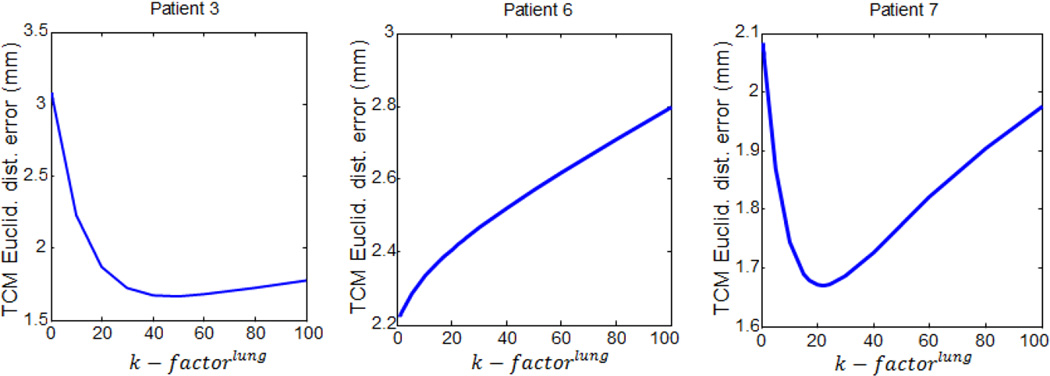
Table 4 lists the optimal biomechanical parameters and the minimized TCM Euclidean distance errors in the three biomechanical models for each patient. The optimal biomechanical parameters were patient-specific to achieve minimal TCM simulation error. The average incompressibility ratio for the lung in eight patients was approximately 17, with the highest k-factor observed in patient 3. Increasing the k − factor^lung increases lung stiffness and decreases the degree of freedom of tumor motion within the lung. Figure 6 illustrates three representative trends of TCM motion simulation error variation on k − factor^lung for patients 3, 6, and 7. These results indicate a need to select different values of k − factor^lung to reach the minimum TCM motion simulation error.

Table 4.

Optimal biomechanical parameters and the Euclidean TCM simulation errors between phase 0% and phase 50% for eight patients.

	Isotropic Elastic			Neo-Hookean			Mooney-Rivlin
Patient #	Young’s Modulus of lung (kPa)	Poisson’s ratio of lung	Euclid. TCM error (mm)	Young’s Modulus of lung (kPa)	Poisson’s ratio of lung	Euclid. TCM Error (mm)	k − factorlung	Euclid. TCM error (mm)
1	0.633	0.10	2.44	0.846	0.10	1.36	3.70	1.28
2	3.229	0.10	8.34	1.815	0.10	2.37	4.14	2.15
3	2.925	0.48	2.01	1.616	0.45	1.75	38.96	1.67
4	1.906	0.10	4.35	1.500	0.30	2.63	9.70	2.64
5	1.658	0.48	4.22	1.900	0.44	3.43	32.00	3.43
6	0.823	0.11	2.21	0.603	0.10	2.30	3.55	2.21
7	1.500	0.38	4.20	0.794	0.40	1.59	18.59	1.66
8	1.782	0.41	4.46	1.700	0.37	3.07	12.81	3.06
Mean	1.807	0.27	4.03	1.346	0.28	2.31	15.43	2.26

Figure 6.

Three representative patterns of TCM motion simulation error variations over the k − factor^lung in the Mooney-Rivlin modeling, for patients 3, 6 and 7.

Table 5 shows the TCM motion simulation error for left-right (LR), anterior-posterior (AP) and superior-inferior (SI) directions, separately. The isotropic elastic model showed a larger TCM motion simulation error than the other two models. The mean Euclidean TCM motion simulation error remained at 4.03 mm, even using optimal biomechanical parameters. By considering the nonlinear stress-strain behavior in the lung, the mean Euclidean TCM motion simulation error was reduced to 2.31 mm in the Neo-Hookean model. The mean Euclidean TCM motion simulation error was further reduced to 2.26 mm when the uncoupled Mooney-Rivlin compressible model was used. Noticeably, by using the Mooney-Rivlin model with optimal biomechanical parameters, the maximum TCM motion simulation errors among eight patients in LR, AP, and SI directions were determined as 1.30 mm (patient 5), 2.76 mm (patient 5), and 2.99 mm (patient 8), respectively. These values were greatly reduced from the errors in the isotropic elastic model, where the maximum TCM motion simulation errors along LR, AP, and SI directions were 2.16 mm (patient 2), 3.41 mm (patient 5), and 7.79 mm (patient 2), respectively. To further illustrate the modeling capabilities, the DICE overlap coefficients (Crum et al., 2006) between the modeled tumors and their target at phase 0% are summarized in table 6. The mean DICE coefficients for both Neo-Hookean and Mooney-Rivlin models were increased (0.90) as compared with the isotropic elastic model (0.84).

Table 5.

Values of TCM motion simulation error along left-right (LR), anterior-posterior (AP) and superior-inferior (SI) directions in phase 0%.

Patient #	Tumor motion range between phase 0% and phase 50% (mm)			TCM error in isotropic elastic model (mm) phase 0%			TCM error in Neo- Hookean model (mm) phase 0%			TCM error in Mooney- Rivlin model (mm) phase 0%
Direction	LR	AP	SI	LR	AP	SI	LR	AP	SI	LR	AP	SI
1	0.5	2.07	6.07	−0.84	−1.14	−1.99	−1.05	−0.48	0.73	−1.10	−0.24	0.61
2	2.63	3.56	14.22	−2.16	−2.07	−7.79	−1.91	−0.63	−1.63	−1.29	−0.35	−1.69
3	1.70	5.44	1.55	0.23	−1.86	−0.73	0.05	−1.74	−0.24	−0.01	−1.66	−0.18
4	0.96	0.18	6.98	−0.26	0.12	−4.35	−0.18	0.15	−2.63	−0.20	−0.19	−2.63
5	0.82	1.11	7.96	−1.83	−3.41	1.69	−1.33	−2.93	1.24	−1.30	−2.76	1.10
6	1.58	6.41	1.43	1.00	−0.10	1.97	0.93	−0.4	2.07	0.92	−0.53	1.94
7	0.98	0.63	12.46	0.98	−0.02	−4.09	0.89	−1.00	0.95	1.08	−0.75	1.01
8	1.01	0.14	7.02	−1.50	0.8	−4.13	−0.51	−0.42	−3.00	−0.50	−0.40	−2.99
Mean	1.27	2.44	7.21	−0.54	−0.96	−2.42	−0.38	−0.93	−0.31	0.30	−0.86	−0.35

Table 6.

DICE overlap coefficients between the modeled tumor and target in phase 0%.

Patient #	Isotropic Elastic	Neo-Hookean	Mooney-Rivlin
1	0.89	0.93	0.93
2	0.78	0.93	0.93
3	0.89	0.90	0.91
4	0.90	0.93	0.93
5	0.82	0.86	0.86
6	0.91	0.90	0.91
7	0.8	0.91	0.91
8	0.78	0.84	0.84
Mean	0.84	0.90	0.90

Using the optimal biomechanical parameters determined from the 0% and 50% phases, we also simulated lung deformation in other respiration phases, including 10%, 20%, 30% and 40%. Table 7 summarizes the TCM simulation error for the Mooney-Rivlin model based on the optimal parameters listed in Table 4 for the intermediate phases. Table 7 shows that the phase closer to the reference phase (50%) generally has a lower TCM simulation error as the TCM distance of this phase is shorter to the reference phase.

Table 7.

TCM simulation error (mm) of additional 4D-CT phases in Mooney-Rivlin modeling with the optimal biomechanical parameters from table 4.

Patient #	Phase 10%			Phase 20%			Phase 30%			Phase 40%
Direction	LR	AP	SI	LR	AP	SI	LR	AP	SI	LR	AP	SI
1	−0.45	0.32	0.53	−0.42	−0.41	−0.22	−0.52	−0.23	−0.19	−0.03	−0.57	−0.10
2	−1.53	0.21	−2.20	−0.79	−0.97	−1.80	−0.17	−2.28	−1.64	−0.04	−0.88	−0.33
3	0.12	−1.32	−0.32	0.08	−0.82	0.12	−0.11	−0.61	0.05	−0.15	−0.52	0.09
4	−0.32	−0.23	−1.78	−0.40	−0.12	−1.51	−0.12	0.23	−1.02	−0.19	−0.11	−0.91
5	−1.08	−1.76	−0.49	−0.42	−1.74	0.21	−0.11	−1.81	0.48	−0.22	−2.01	1.07
6	1.32	−0.97	1.80	0.32	−0.04	0.75	0.61	−0.33	0.51	0.24	−0.86	0.19
7	0.55	−0.64	1.60	1.02	−0.58	1.20	0.90	−0.88	0.28	0.52	−0.64	0.30
8	−0.51	−0.64	−2.81	−0.32	−0.38	−2.63	−0.36	−0.22	−1.54	−0.12	−0.51	−1.01
Mean	−0.23	−0.62	−0.45	−0.11	−0.63	−0.48	0.01	−0.76	−0.38	0.0	−0.76	−0.08

To evaluate the influence of uncertainty in the demons-based deformable image registration, a normally distributed random noise was added to the calculated surface DVFs with a signal to noise ratio equal to 25dB. Table 8 shows the Euclidean TCM simulation error of Mooney-Rivlin modeling with noisy boundary conditions in the eight patients. The corresponding error without noise is reported in the last column of table 4. The mean TCM simulation error change is 0.4 mm for the eight patients. The maximum difference between the results in table 4 and 8 was related to patient 3 with 1.2 mm difference. The difference was less than 0.75 mm for other patients. These results suggest that the pre-registration accuracy has small impact on the TCM motion simulation accuracy.

Table 8.

TCM simulation error in the Mooney-Rivlin model with 25dB normal random noise added to SDVFs.

Patient #	1	2	3	4	5	6	7	8	Mean
Euclidean TCM error (mm)	1.18	2.08	2.87	2.65	2.69	1.85	2.12	3.32	2.35

4. Discussion and Conclusions

In this study, we systematically investigated the sensitivity of the TCM motion simulation error in three elasticity models, and analyzed the biomechanical parameters of lung and lung-related tumors in eight lung cancer patients. We selected lung voxels as uniform material as previous studies showed that the homogeneous model was sufficient to model large scale lung deformation (Al-Mayah et al., 2010; Lai-Fook, 1981). The range of tumor motion magnitude and lung volume change (between end-inspiration and end-expiration) varied among the 8 different patients selected for the study. The maximum tumor motion distance was calculated as 14.2 mm in patient 2, while the minimum tumor motion distance was 5.9 mm in patient 3. Patient 6 exhibited a maximum volume change of 19%, while patient 3 had a minimum lung volume change of 8%. Despite these variations, accurate tumor motion simulations were achieved for all patients in non-linear elastic models (uncoupled Mooney-Rivlin model and Neo-Hookean compressible model).

TCM motion simulation errors along LR, AP, and SI directions were less than 3 mm with the Mooney-Rivlin model; the maximum error along the SI direction was 2.99 mm in patient 8. In the isotropic elastic model, the TCM motion simulation error was much higher than in the non-linear models; the maximum error along the SI direction was as high as 7.79 mm for patient 3. Figure 5 further shows that the TCM motion simulation error for the isotropic elastic model is large even when a broad range of biomechanical parameters are used in the simulation. Thus, our results suggest that nonlinear elastic models are to be preferred for tumor motion FEM simulation. TCM motion simulation error in the Mooney-Rivlin model was only slightly decreased when compared to the Neo-Hookean compressible model; the two models share similar hyperelastic strain-energy functions which could explain this similarity. In practice, the uncoupled Mooney-Rivlin model could be converted to an uncoupled version of the neo-Hookean model by selecting c₂ = 0.

In FEM modeling, different biomechanical parameters affect the TCM motion simulation error differently. The 4D sensitivity analysis of biomechanical parameters showed that in the Mooney-Rivlin model the k − factor^lung was effective in determining TCM motion simulation error variation, while the lung deviatoric deformation parameter $(c_{1,2}^{\mathit{\text{tumor}}},c_{1,2}^{\mathit{\text{lung}}})$ played a less important role. For example, Figure 5 shows that the TCM motion simulation error only varied by 0.2 mm upon extensively changing the lung deviatoric deformation parameter $(c_{1,2}^{\mathit{\text{tumor}}},c_{1,2}^{\mathit{\text{lung}}})$. This result was not surprising considering that deformation of the lung is related to volumetric changes. In the isotropic elastic and Neo-Hookean models, the TCM motion simulation error was more sensitive to Poisson’s ratio than Young’s Modulus, as shown in Figure 4. Sensitivity analysis also showed that the TCM motion simulation errors were less sensitive to the biomechanical parameters of tumors, and the minimum TCM motion simulation error could be achieved by adjusting the biomechanical parameters of lung only. This behavior could be caused by that the tumor motion is mainly driven by lung motion.

Referring to Table 4, it can be seen that the patient-specific “optimal” Poisson’s ratio of lung hits the upper or lower bound of the literature-based selected limitations for half of the cases in both linear isotropic and Neo-Hookean models. The solution hitting the bound can be partially explained by the TCM motion simulation error trend within the pre-set bounds of these parameters. For example, in the sensitivity analysis shown in Figure 4, the TCM error increases with Poisson’s ratio. Therefore, the solution reaches the lower bound for this patient. When the solution reaches the upper bound, it indicates opposite trend between the TCM motion simulation error and Poisson’s ratio. In both cases, the chosen parameter ranges could be considered as being too restrictively chosen. On the other hand, the objective function defined in this work is the TCM motion simulation error of lung tumor only. While the obtained “optimal” Poisson’s ratio leads to the minimal TCM motion simulation error, it is not necessarily the “optimal” parameter regarding accuracy and/or physical plausibility of lung motion estimation. This could be another reason that the optimizer finds the “optimal” value at the bound of defined range in these patients. Nevertheless, the number of patients used in this study is relatively small. A study using more patients is warranted to further evaluate the findings of this work.

It should also be noted that the optimal biomechanical parameters were estimated by minimizing the TCM motion simulation error between phase 0% and phase 50%. These two phases were chosen because the tumor exhibits largest motion from phase 0% to phase 50%. The obtained optimal parameters were then used to simulate the lung deformation in other respiration phases in this study. The TCM motion simulation error for all phases can also be used as the objective function to obtain the optimal parameters. This could improve the overall simulation accuracy and we will investigate its potential gain in a future study.

Other strategies have previously been explored to improve the biomechanical parameter estimation. Li et al. (Li et al., 2013) combined a varying intensity flow (VF) block-matching algorithm with FEM for lung deformation, from end-expiration phase to end-inspiration phase. Young’s modulus distributions were estimated by solving an optimization problem with a quasi-Newton method. However, this approach involved extra optimization (nearly 10 hours on an NVIDIA Tesla 2070 GPU) to estimate Young’s modulus of the lung. Different from this optimization based strategy, our proposed parameter estimation took less than 30 minutes to perform the parameter estimation. It should also be noted that once the optimal biomechanical parameters were obtained, and the adaptive meshes of lung and the tumor were created, the FEM computation was fast. The maximum FEM computation time was no longer than 20 seconds with about eighty thousand elements (patient 3).

In summary, we assessed the influence of lung and tumor elasticity models and biomechanical parameters on tumor motion simulation accuracy. Our results showed that optimal biomechanical parameters achieving the minimum TCM simulation error are patient-specific. The non-linear Mooney-Rivlin model offers the best simulation accuracy on tumor motion among the three elasticity models investigated in this work. The simulation of lung and tumor motion based on different biomechanical parameters also allows a better understanding of the biomechanical motion behavior in the lung. Our proposed optimal estimation strategy represents a practical way to select patient-specific optimal biomechanical parameters. With improved simulation accuracy, the FEM-based simulation could be a useful tool to estimate tumor position during radiation therapy.