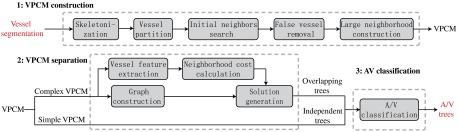
Abstract.
While many approaches exist to segment retinal vessels in fundus photographs, only a limited number focus on the construction and disambiguation of arterial and venous trees. Previous approaches are local and/or greedy in nature, making them susceptible to errors or limiting their applicability to large vessels. We propose a more global framework to generate arteriovenous trees in retinal images, given a vessel segmentation. In particular, our approach consists of three stages. The first stage is to generate an overconnected vessel network, named the vessel potential connectivity map (VPCM), consisting of vessel segments and the potential connectivity between them. The second stage is to disambiguate the VPCM into multiple anatomical trees, using a graph-based metaheuristic algorithm. The third stage is to classify these trees into arterial or venous (A/V) trees. We evaluated our approach with a ground truth built based on a public database, showing a pixel-wise classification accuracy of 88.15% using a manual vessel segmentation as input, and 86.11% using an automatic vessel segmentation as input.
Keywords: fundus, retinal vasculature, tree construction, graph, optimization
1. Introduction
A retinal fundus image is a two-dimensional (2-D) color photograph of the retina at the back of the eye and is used by clinicians to diagnose and manage ophthalmic diseases. The retinal vasculature is clinically important, because in addition to showing the typical changes in eye diseases, its properties can also be used as biomarkers for systemic diseases and the general state of health.
For example, in diabetic retinopathy, which is a complication of diabetes mellitus, the vascular vessels show abnormalities including caliber changes1 and widening of veins.2 Similarly, cardiovascular disease3 such as hypertension and atherosclerosis are also associated with such changes like the narrowing of arterioles and the widening of venules. One method of quantifying these changes is the arteriolar-to-venular diameter ratio (AVR).4 Specifically, a decrease in the AVR, i.e., thinning of the arteries and/or widening of the veins, is associated with an increased risk of stroke and myocardial infarction.5,6 In addition, a smaller AVR is associated with smoking, hyperglycemia, obesity, and dyslipidemia.7
In addition to measures like AVR and the widths of arteries and veins, other clinically relevant features are junctional exponents,8 vascular bifurcation angles,9 vascular tortuosity,10 length-to-diameter ratios,11 and the detection of arteriovenous crossing phenomenon.12 To facilitate these measurements and collect data on a large-scale number of images, a solid automated method is required to analyze arterial and venous (AV) vasculatures.
However, this requires an automated method to determine which vessel segments are arterial and which are venous. Unfortunately, the disambiguation and the construction of AV vasculatures is a complex problem, because the images provide flat superpositions of multiple trees in the plane of the retina, where the three-dimensional structure of the trees is not very helpful. It also requires to determine the anatomical connectivity between arteries and veins; in other words, to recognize all landmarks such as bifurcations and crossing points.
Classical approaches for constructing arterial and venous trees are the tracking-based methods.13–20 The common strategy is to first detect vessels as separated segments usually in terms of centerlines, and then to detect all different types of landmarks including bifurcations, crossing points and/or vessel end points. The vascular trees are built by iterating through the vessel segments and their connected landmarks. For example, an early semiautomatic method to build the retinal vascular trees based on the vessel segmentation image was developed by Martinez-Perez et al.18 They first skeletonized the segmentation image and then identified three types of significant points: bifurcations, crossing points, and terminal points. They tracked vessels from every manually-indicated root segment to iteratively construct the trees. Tsai et al.19 proposed a model-based method using the tracking-based strategy that iteratively traces the vessel centerline pixels using local neighborhood information, and then distinguishes bifurcations using a mathematical model with angle information. Lin et al.20 developed a tracing algorithm combining a grouping method to build the vascular tree. They first obtained a set of disconnected vessel segments by using a tracing algorithm. Then, a grouping algorithm was applied to reconnect these segments to form trees. The grouping algorithm iteratively connected ungrouped segments to grouped ones by maximizing the continuity of the vessel using an extended Kalman filter.
One main drawback of these types of methods is they recognize the landmarks with local information, thus correspondingly are susceptible to local errors. These errors might be generated due to the imperfect image itself, or during any image preprocessing like vessel segmentation, skeletonization, and others. Some typical mistakes due to these errors are: (a) the misclassification of a crossing point as a bifurcation when one vessel is missing or disconnected; (b) the disconnection of the tree due to a missing part of vessels; and (c) the identification of false bifurcations and crossings due to spurious vessels. In addition, some complex landmarks are difficult to recognize with local knowledge, e.g., overlapping landmarks.
Our group recently tried to construct A/V trees using graph-based methods. Joshi et al.21 used morphological information and a graph search method based on vessel probability maps. Vessels were initially separated into centerline segments, and then a vessel network was constructed by recognizing every landmark. Then, using graph search, the network was separated into arteries and veins. Other groups have followed similar approaches: Dashtbozorg et al.22 also extract vessel centerlines and partitions them into segments first. In a graph where each node represents an intersection point and each edge represents a segment, the vascular trees were built by determining the node types and vessel types together. However, these two graph-based methods use a graph with static structure and the nodes representing landmarks are determined using local information in advance; thus their solutions are locally optimal.
Rothaus et al.23 proposed to solve the problem in a more global way. Based on a presegmentation image, they obtained the skeletonized vessel segments and identified bifurcations and crossing points. Then, they modeled the problem of labeling vessel segments as arteries or veins as a satisfiability problem and propagate the labels of vessels from some initial labels. Although they incorporated some global information into the satisfiability problem, the model was still relatively local, and the algorithm to solve the problem was greedy in nature. Furthermore, manual inputs were required to determine the initial labels and more manual inputs were required if there were conflicts that could not be resolved by the algorithm. In addition, a very recent technique proposed by Estrada et al.24 used a semiautomatic graph-based method to construct A/V trees. They first semiautomatically extract a graph representing the vasculature from a fundus image, then separate it into A/V trees by maximizing the likelihood of A/V trees. The drawback of their method is that the graph is semiautomatically constructed and thus requires human effort.
Therefore, in the present study, we propose an automated, novel and global framework to build the A/V vascular tree from a vessel segmentation. By taking advantage of properties of the retinal vasculature, we combine global and local information to recognize landmarks. Instead of recognizing each landmark independently, we consider landmark relationships, thus recognize them simultaneously and globally. By doing so, local noise in the images and local errors during preprocessing are corrected to some degree, and small vessels that are difficult to classify locally can also be recognized. The strategy of the proposed method is to build an overconnected vessel network, separate it into vascular trees, and then classify them into A/V trees. With a special graph design, we are able to give each landmark multiple possible configurations and corresponding costs, and the optimal solution follows from the global property of the whole vascular network. With each landmark recognized, the A/V trees are easily inferred. The preliminary work was presented at MICCAI.25 In this paper, the complete method is presented with updated cost functions, which incorporates vessel intensity, width, and orientation information. Also, an A/V classification method is included. In addition, a publicly available ground truth is generated based on a public dataset for the evaluation.
2. Methods
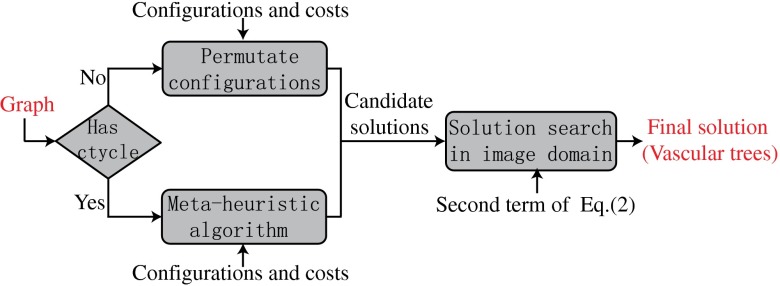
Our approach to build A/V trees is based on a property of the retinal vasculature that arteries only cross with veins, but never with themselves. Using this constraint, labeling vessels into A/V vessels and determining vessel connectivity is the same problem under some assumptions. In general, the method consists of three stages, summarized in Fig. 1. Taking a vessel segmentation as the input, in the first stage it generates a vessel potential connectivity map (VPCM). A VPCM is an overconnected vessel network consisting of vessel segments and the potential connectivity between them. In the second stage, the VPCM is disambiguated into multiple anatomical trees with two labels. The tree disambiguation problem is modeled as a constrained optimization problem, and solved by using a special graph with a metaheuristic optimization algorithm. To separate the VPCM, both local and global costs are calculated on the VPCM for the optimization problem. Finally, at the third stage, these separated anatomical trees, as well as independent trees, are classified into A/V trees using a machine-learning method. Because our approach incorporates some well-known techniques, in this paper we only describe the new techniques in detail, and refer to the Appendices for implementation details of the other techniques.
Fig. 1.
The flowchart of the proposed framework.
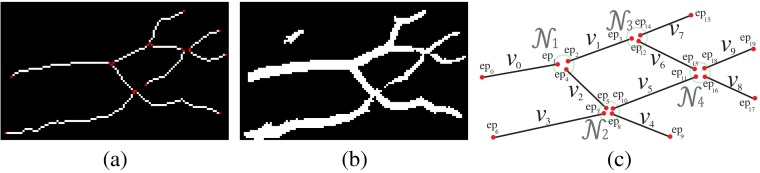
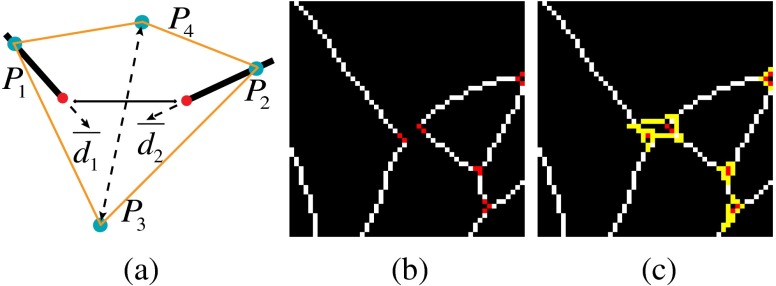
First, we introduce the VPCM, which is a vessel network consisting of partitioned vessel segments in terms of centerlines and their potential anatomical neighbors. In a VPCM, each segment has two ends and , which are connected to the ends of neighboring segments. (While use of to represent segments may seem counterintuitive at this stage because the segments do not yet reflect vertices of a graph, this notation was chosen because each segment will eventually have a one-to-one correspondence with a vertex of a graph, as discussed in Sec. 2.2.2.) A neighborhood, denoted as , is a set of end points whose segments are connected on the VPCM. If end points , then they are neighbors and segments that they belong to, and , are also neighbors. The size of a neighborhood, denoted as , is the number of segment ends within , or the number of segments connected within. An example is shown in Fig. 2. Figure 2(b) shows a set of vessel segments, and Fig. 2(c) shows the corresponding VPCM virtually. In this example, segment has two indexed ends and , and has two neighbors and . Altogether they form a neighborhood , and therefore segments , , and are neighbors as well.
Fig. 2.
A vessel potential connectivity map (VPCM) example (only a portion of the image is shown). (a) The vessel segmentation, (b) vessel segments (end points in red), and (c) the virtual VPCM.
Here, two assumptions about the VPCM are introduced as the prerequisite of the proposed method. The first is based on the property of the vasculature in 2-D retinal images that arteries do not cross arteries and veins do not cross veins. With this property, we assume that within each neighborhood, segments of the same type are connected anatomically and segments of different types are not anatomically connected. In other words, if two segments are of the same type in a neighborhood, we assume that they are connected. If they are of different types, they are not connected. Because of this constraint, for each neighborhood, determining the anatomical connectivity between segments is equivalent to determine the types (artery or vein) of the segments. The second assumption is that the anatomical connectivity between segments is included within a neighborhood. It means that to determine the anatomical connectivity between segments, we only need to check whether two segments within each neighborhood are anatomically connected or not. In other words, it means that all neighborhoods cover all possible landmarks of the vasculature. With these two assumptions, to build A/V trees, we only need to determine the anatomical connectivities of segments (ends) within every neighborhood, which is equivalent to determining the segment types within every neighborhood. Neighborhoods cannot be too small which will violate the second assumption and pre-exclude the true anatomical neighbors, and cannot be too large which will violate the first assumption, and may cause two segments of the same type not anatomically connected to be included within one neighborhood.
2.1. Construction of Vessel Potential Connectivity Map
Assuming we have a vessel segmentation, either manually or automatically generated, we first extract the vessel centerlines using a general skeletonization algorithm,26 and then we break it into segments by finding two unique end points for each segment. First, we check the neighborhood for all centerline pixels and classify them into normal points and special points. Normal points are centerline pixels which have two neighboring centerline pixels; special points are centerline pixels which have either one or more than two neighboring centerline pixels. Then, we divide the centerlines into segments by finding pairs of special points.
After separating the skeleton into segments, we overconnect them to build the VPCM. This is done in two steps. The first step is to find initial neighbors for both end points of a segment within a close region. The second step is to find additional potential neighbors in a larger region. During the construction of the VPCM, we remove short independent vessels because many of them are false positive vessels or not important for clinical measurements. In addition, we use a method based on the work of Niemeijer et al.27 to approximately mask out the optic disc (OD) due to the ambiguity of vessels within, as well as locate the fovea if there is one. The detail of the VPCM construction is in Appendix A and an example is shown in Fig. 3. Figure 3(d) shows the VPCM and the enlarged red circle shows a neighborhood of size 5, whose boundary is drawn in yellow.
Fig. 3.
The construction of VPCM. (a) A portion of fundus image, (b) the vessel segmentation, (c) the vessel skeleton, (d) the VPCM (the enlarged red circle shows one neighborhood).
2.2. Separation of the Vessel Potential Connectivity Map
2.2.1. Optimization problem
After we obtain the VPCM, the next stage is to disambiguate this overconnected vessel network into multiple trees with binary labels by finding the true anatomical connectivity between segments. As explained in the beginning of Sec. 2.1, with the two properties of the VPCM, determining the anatomical connectivity within each neighborhood is equivalent to determining the segment types. Here, we define a configuration of a neighborhood as a combination of connectivity between segments within the neighborhood, or a combination of segment labels within it, due to the actual equivalence of these two terms. In practice, a neighborhood is a potential landmark, and the configuration is a possible landmark type i.e., a bifurcation, a crossing point, or others.
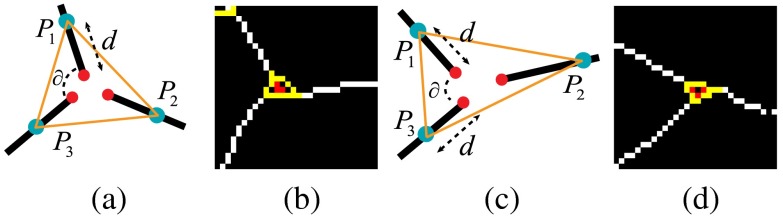
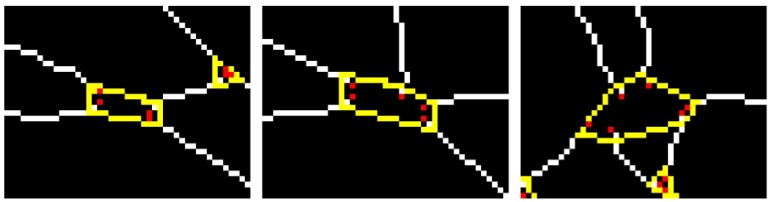
For each neighborhood, we can locally determine their possible configurations but it is difficult to determine exactly which one is the correct one with only local information. Figure 4 shows neighborhoods of size 4 and 5, with some valid potential configurations, and their retinal image equivalents, which show the difficulty of determining the exact types with local information. However, the global property of the retinal vasculature constrains the choices of the potential configurations, thus we determine types of all landmarks simultaneously using both local and global information. Let denotes the labels for all segments in a VPCM. The problem of separating the VPCM is to determine that minimizes Eq. (1) with an additional global constraint that the constructed trees contain no cycles. Here, a cycle is a set of connected segments starting and ending at the same segment, with no repetition of other segments.
| (1) |
where
| (2) |
Fig. 4.
(a) Neighborhoods of size 4 and 5, (b)–(d) possible configurations, and (e) the retinal image parts.
The first term of Eq. (1) represents the configuration cost for all neighborhoods, thus is the local cost. Let reflects the label of segment {, }, then represents the configuration, or the segment labels for the neighborhood . The second term of Eq. (1) is a weighted global term which evaluates the topological properties of constructed trees after segment labels are determined.
For each neighborhood there are multiple possible configurations, and the corresponding cost is computed generally as the reciprocal of its probability, expressed in a general matrix as in Eq. (2). While we keep the general form of the terms here for describing the overall algorithm, we present the details of how to compute and in Sec. 2.3.
The optimization model is designed not only to choose the best configurations from all possible configurations in a local point of view (the first term), but also to obey the global property of the retinal vasculature (the second term and the global constraint). To solve this problem, we divide the VPCM for an image into several independent sub-VPCMs to solve them individually, without loss of generality. Since the OD is masked out, separation into sub-VPCMs is easily done with breadth-first search (BFS). Small sub-VPCMs which are far away from the OD (i.e., trees with fewer than 40 centerline pixels and for which the nearest distance to the OD is larger than twice of the OD radius) are removed from further analysis due to their insignificance in clinics. The difficulty of the optimization problem stems from the global constraint, which is related to the complexity of a VPCM, and thus we categorize VPCMs into three types:
-
•
A simple VPCM: a VPCM which has one segment [see Fig. 5(b)].
-
•
An acyclic VPCM: a VPCM which has more than one segment, but without cycles [see Fig. 5(c)].
-
•
A cyclic VPCM: a VPCM which has one or more cycles [see Fig. 5(d)].
Fig. 5.
(a) Independent VPCMs in different colors, (b) simple VPCMs in different colors, (c) acyclic VPCMs in different colors, and (d) cyclic VPCMs in different colors. (All centerlines are thickened for better visualization.)
The simple VPCM is only a single segment, so we only need to focus on the other two, altogether referred as complex VPCMs. Because of the difficulty of this problem with cyclic VPCMs, we design a graph-based algorithm to approximate an optimal solution. We first transfer a complex VPCM into a special graph which incorporates the global constraint, and we use it to find candidate solutions with low costs of the first term of Eq. (1). These candidate solutions are then evaluated to generate the final solution by combining the global cost , which is the second term of Eq. (1).
2.2.2. Graph model
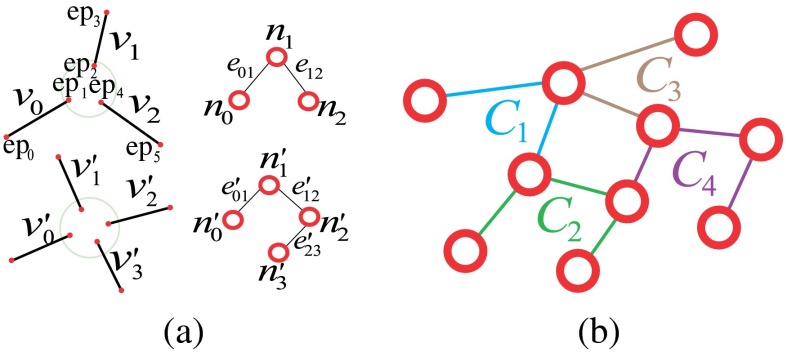
In the proposed graph model, each vertex represents a segment , and each edge represents a relation between segments and within a neighborhood. For each neighborhood, with , edges are built to connect the vertices as a linear tree such that the starting and ending vertices have degree of 1, and other interior vertices have degree of 2. Here, the concept of a cluster is introduced in the graph corresponding to the neighborhood on the VPCM, which is a set of edges generated by the vessel ends within one neighborhood. If in the image domain, , and there is an edge constructed in graph domain, then . Figure 6(a) shows an example of how a 3-p and a 4-p is transformed to clusters in the graph domain, respectively. Using this cluster-based transformation, a VPCM is transferred into a planar graph. Figure 6(b) shows a virtual VPCM with four neighborhoods transferred to a graph. In this example, four neighborhoods in the image domain correspond to the four clusters in the graph, the edges of which are labeled in different colors.
Fig. 6.
(a) Neighborhoods transferred into clusters and (b) a graph transferred from the VPCM in Fig. 2.
In the graph, each vertex needs to be labeled in one of two colors, corresponding to a vessel segment being assigned one of two types; each edge is associated with one of two constraints: equality or inequality, which simulates the connectivity between segments on image domain. The equality constraint dictates the two vertices connected by the edge must be in the same color; the inequality constraint dictates they must be in different colors. Within each cluster, a combination of edge constraints is equivalent to a two-color scheme on vertices, which corresponds to a configuration for the neighborhood. Also, the costs of configurations for each neighborhood are attached to the corresponding combinations of edge constraints for clusters.
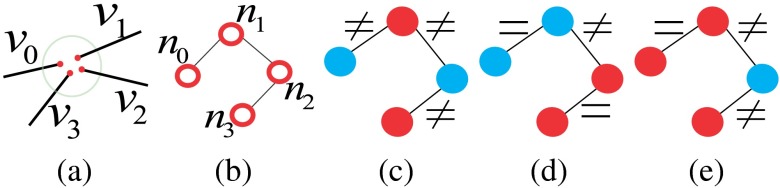
Corresponding to the VPCM, vertex labelings and edge constraints for one cluster are mutually inferable. Figure 7 shows the cluster and its edge constraints and vertex labelings, corresponding to the neighborhood of size 4 in Fig. 4. Specifically, Fig. 7(a) shows the segments with local indexes and Fig. 7(b) shows its corresponding cluster. Figures 7(c)–7(e) show the three configurations in the graph corresponding to those on the VPCM. Figure 7(c) indicates and are the same type and thus connected, and are the other type, meaning the neighborhood represents a crossing point. Figure 7(d) indicates and are the same type thus connected, and are the other type, meaning the neighborhood represents the case of two vessels being close. Figure 7(e) indicates , , and are the same type and connected, is another type and disconnected with them, meaning , , and form a bifurcation, and is falsely connected to it.
Fig. 7.
(a) The neighborhood with local indexes of segments, (b) the cluster, (c)–(e) three configurations corresponding to three landmark types for the neighborhood of size 4 in Fig. 4.
By this transformation, the optimization problem in the VPCM then can be transferred on the graph to the following problem: find a combination of edge constraints for each cluster, which also equals to the vertex color assignment, under three conditions, and meanwhile have the minimal cost in Eq. (1). The three conditions are:
-
1.
The number of inequality edges on a cycle must be even.
-
2.
The number of inequality edges on a cycle must be larger than zero.
-
3.
The inequality edges on a cycle cannot come only from one cluster.
Here, a cycle on the graph is a set of connected vertices starting and ending at the same vertex, and without repetition of other vertices. The first condition guarantees that there is a feasible edge assignment on the graph such that vertices can be colored using two colors. The second and third conditions guarantee that the solution on the graph can be transferred to a feasible solution in the VPCM, which are multiple trees with binary labels.
We define a conflict cycle when the edges on the cycle violate any of the three conditions, and a solution on the graph without a conflict cycle as a feasible solution, and a solution with conflict cycles as an infeasible solution. To find the optimal solution, besides the feasibility, we also need the cost in Eq. (1) to be minimal.
Due to the difficulty of this problem when there are cycles in the graph, we propose a metaheuristic algorithm to find a near-global solution, illustrated in Fig. 8. Metaheuristic algorithms are a type of common algorithms in optimization field which give a near-optimal solution for difficult problems within a reasonable amount of time. The first step of the algorithm is to find a set of feasible candidate solutions with low costs of the first term of Eq. (1). Then, these candidate solutions are evaluated with the second term of Eq. (1) and the one with the minimum cost of Eq. (1) is the final solution. At the first step, we develop different algorithms to generate the candidate solutions depending on whether a graph has cycles or not. If there is no cycle, which only happens when the graph is small, all solutions are feasible; thus we consider all solutions as candidate solutions. If there is at least one cycle, which is the core of the problem, we use a heuristic algorithm to generate feasible solutions with low costs of the first term of Eq. (1), which is explained in detail in the following section.
Fig. 8.
A concise flowchart of the metaheuristic algorithm.
2.2.3. Heuristic algorithm
Here, we denote a solution on the graph domain i.e., the choices of edge constraints, as . As is common in many metaheuristic algorithms, the overall idea is to maintain a candidate solution pool, with candidate solutions generated as in Algorithm 1. If there are conflict cycles, the algorithm permutes the edge constraints to reduce them. The solution pool is updated during every conflict cycle reduction to reduce at least one conflict cycle. The algorithm stops when enough feasible solutions are generated, or the iteration number reaches the maximum limit.
Algorithm 1.
Algorithm for finding candidate solutions, given a graph with cycle basis , (number of feasible solutions required), , initial sol , and iter (maximum iteration number)
| Initialize sol pool with , initialize feasible sol pool |
| whiledo |
| Initialize sol pool |
| for each solution do |
| ← FindConflictCycle(, ) |
| ifthen |
| put into if |
| else |
| sol pool permutateEdgeConstraint (, , ) (see Algorithm 2) |
| for each solution in do |
| put in if it is feasible; otherwise put in if |
| end for |
| end if |
| end for |
| , |
| end while |
| ifthen |
| end if |
| return |
To avoid the trap of local optima, we generate different seed solutions to feed into Algorithm 1. Seed solutions are generated from the solution with the lowest local cost, which might not be feasible in most cases, with random permutation of configurations of random clusters. For each seed solution, Algorithm 1 outputs a pool of candidate solutions, and the final candidates are the union of all pools.
For Algorithm 1, it starts from a seed solution, and checks for conflict cycles first. This is done by detecting a cycle basis first and then checking each cycle of the basis. A cycle basis is a minimal set of cycles that any cycle can be written as a union of the cycles in the basis.28 A cycle basis is found using BFS, and the conflict cycles are detected by checking the three conditions in Sec. 2.2.2 [implemented as FindConflictCycle(, ) in Algorithm 1]. If a solution contains conflict cycles, the algorithm randomly chooses a conflict cycle to resolve. If there are adjacent conflict cycles, they have a higher priority to be chosen.
Within Algorithm 1, permutateEdgeConstraint (, , ) (Algorithm 2) is the component to permute the edge constraints of clusters to remove conflict cycles, and to generate offspring solutions. The algorithm iterates edges on the conflict cycle and finds their corresponding clusters. All the potential configurations of these clusters are sorted based on their costs. A random Gaussian noise is added during the sorting to enlarge the search region and prevent being trapped in local minima. The algorithm starts by changing the configuration based on their costs one at a time, and proceeds to check if the number of conflict cycles are reduced. Here, is the number of offspring required, and controls the relaxation of the cycle reducing criteria. If there are only a couple of solutions with less cycles, this indicates that the algorithm might meet a local minimum. To escape from the local minimum and increase the search space, the algorithm needs to generate offspring that have more cycles than the current solution.
Algorithm 2.
PermutateEdgeConstraint given , ,
| Initialize sol pool , |
| whiledo |
| ← CycleSelection () |
| find clusters on , , |
| for; do |
| select a configuration config based on costs added with random noise |
| ← UpdateSolution (s, config) |
| ← FindConflictCycle(, ) |
| if or then |
| disregard , |
| else |
| put in if |
| , |
| end if |
| ifthen |
| , |
| end if |
| end for |
| end while return |
When Algorithm 1 cannot generate enough feasible solutions, it stops when the iteration number hits the limit. In an extreme case, there might not be feasible solutions. This might happen when there are false vessels in the VPCM that form a false cycle, or when vessels of the same type form a cycle mistakenly in the fundus images. In these cases, the algorithm generates the most favorable infeasible solutions, which are solutions with the least number of cycles and lower costs.
2.3. Cost Function Design
The costs represented by Eq. (1) is essential for the proposed algorithm. The first term is the costs of various possible configurations for each neighborhood, which are calculated by using local vessel features and some global features. The second term is the costs of the constructed trees, which is calculated after the candidate trees are generated.
2.3.1. Feature extraction
First, we introduce the types of vessel features which are used to calculate the costs, which are:
-
•
the vessel end point direction
-
•
the vessel width
-
•
the vessel profile intensities
-
•
the vessel dominant orientation.
The vessel end point direction is a pair of directions along the segment at both end points, with the positive direction being away from the segment, represented as a pair of unit vectors. Principal component analysis is used to calculate the direction with the first pixels starting from each end of the segment.
The feature of vessel width includes the absolute width and the relative width, which are the average vessel width of a segment and its relative average width compared to others. The absolute width is calculated using Xu’s method29 and the relative width is a 4-scale integer representing the vessel width compared with the quartiles of the vessel widths from the whole image.
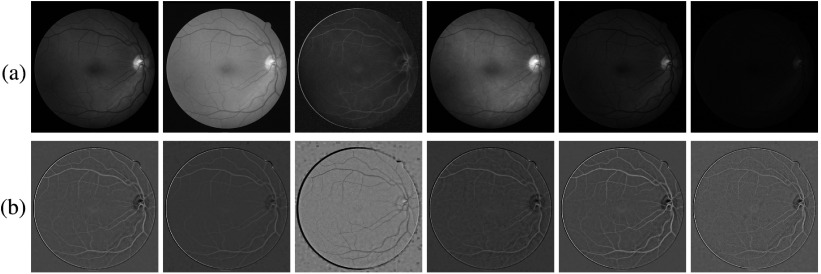
The vessel profile intensities are a set of average intensities along the vessel cross section on a set of color channels. To reduce the effect of potential errors introduced at vessel width measurement, we use the average intensity within the center half of the vessel width. Intensities are collected in six channels, including red, green, and blue in RGB, intensity channel (I) in HSI, and L and b channels in Lab space. Before the calculation, to remove the luminance imbalance, single-channel images are subtracted by their background images and then normalized. The background image is obtained by filtering the original image with a large mean filter. An example of the balanced images is shown in Fig. 9, for the fundus image in Fig. 10.
Fig. 9.
(a) Images in R, G, B, I, L, and b channels. (b) Images after the imbalance removal and intensity normalization.
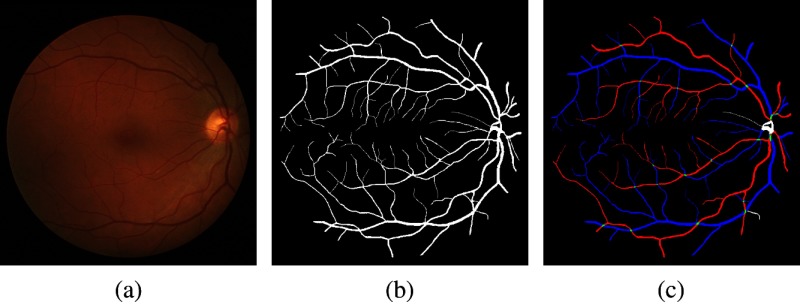
Fig. 10.
(a) A Retinal Images vessel Tree Extraction fundus image, (b) the vessel reference standard of (a), and (c) the A/V reference standard of (a).
The vessel dominant orientation is the expected direction of the blood flowing via a vessel segment, based on its geometric and topological properties. Although the blood flows in reversed directions in arteries and veins, for the purpose of this feature, we define all dominant orientations using an arterial convention where blood flows from the OD to the periphery of an image and the fovea. A binary status is attached to each segment , representing if the dominant orientation is determined for or not. Appendix B contains the details of the computations to determine the vessel dominant orientation. Then, the dominant orientation feature is transferred to the end point level by giving one of three labels to each point: head (), tail () or unknown (). These labels of end points are used to calculate costs for potential configurations of each neighborhood. If the dominant orientation is determined for , its end points are labeled as and , representing the head and the tail of . The head and the tail for a segment are determined in a way that blood flows from the tail to the head. If the dominant orientation cannot be determined, both end points are labeled as , which means end points are unknown. In the following, head, tail, and unknown are indicated by the symbols , , and , respectively. With this rule and the two assumptions about the neighborhood defined at the beginning of Sec. 2, some constraints can be inferred within each neighborhood:
-
•
For any neighborhoods, blood cannot flow from one to another .
-
•
For any neighborhoods larger than 2, there must be at least one and at most 2.
2.3.2. Configurations and costs of local neighborhoods
A configuration for a neighborhood, denoted as , represents the separation of end points within the neighborhood into two categories. Denoting all the possible configurations for a neighborhood as , and the number of neighborhoods in a VPCM as , then the solution space is . It is very expensive to locate the optima in such a big space thus we shrink it by decreasing with retinal vasculature features. Logically, , with the constraint that . However, when , many configurations can be pre-excluded by checking the labels of end points. Specifically, when , we require that there must be two heads and three tails; when , there must be two heads and four tails. With the constraints that heads have to be separated, and one head cannot connect to more than three tails, when , ; and when , . Then, the probabilities or costs of all possible configurations are calculated using different algorithms designed for neighborhoods of different sizes using features explained in Sec. 2.3.1. The details are in Appendix C.
2.3.3. Global cost
The candidate solutions generated by Algorithm 1 might not fit the topology of the retinal vasculature since it only uses the first term of Eq. (1). A set of global costs are thus imposed to select the optimal solution which fit the topology of the vasculature best, which is composed of three components in Eq. (3). For our experiment in Eq. (1) is set as 1.
| (3) |
The first term is the sum of the distances of every constructed tree to the OD in Eq. (4), which is the Euclidean distance from the nearest pixel of a tree to the center of OD.
| (4) |
The second term is the bifurcation evaluator at each bifurcation in Eq. (5). Here, represents each bifurcation; and are the angles between two children vessels and the parent vessel for each bifurcation; and and are the lengths of children vessels.
| (5) |
The third term is the consistency of the vessel dominant orientation. After trees are constructed from the VPCM, the vessel dominant orientations are determined for all segments, and a penalty is imposed for the segments whose dominant orientations are opposite compared with the VPCM. The penalty is the sum of the lengths of these segments.
2.4. A/V Classification
After separation of complex VPCMs into multiple trees of two types, with each separated tree being referred to as an overlapping tree, the next step is to determine which trees (including those from simple VPCMs) are arterial and which are venous. For overlapping trees, the most difficult part was completed as part of the separation of the trees into two types since we now are able to rely on differences between the overlapping trees to help in the final A/V classification. However, for simple VPCMs (each of which is its own tree, by definition), we need to decide on its A/V category independently. Thus, the simple VPCMs are referred to as independent trees. In both cases, we use a pixel-based classification method to help make the arterial/venous determination.
In particular, first, the probability of each centerline pixel being arterial or venous is obtained. The algorithm is similar to the machine-learning method proposed by Niemeijer et al.30 Briefly, 31 features regarding vessel intensity are extracted and 19 features are selected as the final features. The 19 features include the vessel width and 18 intensity-related features on the 6 channels mentioned in Sec. 2.3.1: the average and standard deviation of vessel intensity transectionally, and the ratio of intensities inside and outside of the vessel profile. The intensity inside is the average vessel intensity, and the intensity outside is the average intensity between the vessel boundary and twice the width away from the boundary. Here, a support vector machine (SVM) with the radial basis function kernel is used as the classifier, which is trained on the data of 48 images from our previous work.25 The dataset is evenly separated into two subsets to select these final features.
After each centerline pixel is classified, the probability of a tree being arterial and venous is the normalized summation of all its centerline pixel probabilities. For overlapping trees, which are already separated into two types, the one with higher arterial probability is arterial tree and the other is venous tree. For each independent tree, if the tree probability is larger than 0.5, it is arterial; otherwise it is venous.
3. Experiments and Results
3.1. Image Data
We used two datasets to test the performance for the proposed method. First, we created a publicly available dataset Retinal Images vessel Tree Extraction (RITE) based on a well-known public available dataset DRIVE.31 We had two experts correct the vessel reference standard on nine images, and add arterial and venous labels. The RITE contains 40 sets of images, equally divided into a test subset and a training subset, as the DRIVE does. Each set contains a fundus image, inherited from DRIVE, a vessel reference standard, and a A/V reference standard. For the test subset, the vessel reference standard is the vessel reference standard 2nd_manual in DRIVE. For the training subset, the vessel reference standard is a modified version of the vessel reference standard 1st_manual in DRIVE. The A/V reference standard is generated by labeling each vessel pixel, with one of four labels on the vessel reference standard: artery (A), vein (V), overlap (O), and uncertain (U), encoded by four colors, respectively: red, blue, green, and white. An example of a RITE fundus image, its vessel reference standard and A/V reference standard are shown in Fig. 10. RITE is available at Ref. 32.
Another dataset we used is the same dataset we previously used in our preliminary work.25 It contains 48 low-contrast color mosaiced fundus images [see Fig. 12(a)]; thus we refer to this dataset as the Mosaic dataset in this paper. Since there is no vessel reference for this dataset, the A/V reference is generated by manually labeling the generated VPCM image into an A/V skeleton image [see Fig. 12(d)].
Fig. 12.
An example of result from the Mosaic dataset. (a) A fundus image, (b) the vessel segmentation, (c) the A/V result, (d) the A/V reference. (Skeleton images are thickened for better visualization.)
3.2. Experiments
Two experiments are conducted separately for these two datasets. For the RITE dataset, since the approach is about the disambiguation of arterial and venous trees from a given vessel segmentation, we use two vessel segmentations as the input: the manual ground truth and an automatic vessel segmentation, generated using our well-known method,31 with a hysteresis threshold.
For the manual segmentation, since many very thin vessels are often of little clinical interest, they are removed after we obtain partitioned vessel segments. In our experiment, the segments with width smaller than 1.5 pixels are removed, given the fact the median vessel width is around 4 to 5 pixels and vessels narrower than 1.5 are very difficult to recognize even for humans.
For the Mosaic dataset, we only use the automatic vessel segmentation as the input since there is no manual one. All other parameters and procedures are as the same as those for the RITE with the automatic vessel segmentation as the input.
3.3. Evaluation and Results
The direct output of our algorithm is the labeled A/V vessel centerlines. For the RITE dataset, we evaluate the A/V vessels with respect to the A/V reference standard using the coverage rate and the accuracy. The coverage rate is the ratio of classified vessel pixels over all of the vessel pixels defined in the RITE reference standard, excluding pixels labeled as U or O. The accuracy is the ratio of correctly classified pixels over all classified pixels. Here, both pixel-wise accuracy and centerline accuracy are used.
To calculate the pixel-wise accuracy and the coverage rate, a postprocessing step is conducted to dilate the result of A/V centerlines into A/V vessel images, using the vessel reference standard as a mask. This results in a new image with each vessel pixel in the original vessel reference standard being labeled as A, V, or unclassified, based on the label of the corresponding centerline pixel in the algorithmic result. An unclassified vessel pixel occurs when no corresponding vessel is present in the input vessel segmentation or when the vessel segment has been removed during the VPCM construction. Then, this recovered pixel-based A/V vessel image is compared with the A/V reference standard. To calculate the centerline accuracy, the A/V reference standard is skeletonized first and then is compared with the result. During the measurement of the accuracy, all U is excluded, and all O is considered as correctly classified if classified. The comparison is summarized in the matrix in Table 1 and the measurements are summarized in Eqs. (6) and (7). The test is performed on the whole RITE 40 images and the results on both vessel segmentation inputs are presented in Table 2, with the classification for the overlapping trees, the independent trees and all trees. An example of results for both inputs is shown in Fig. 11.
| (6) |
| (7) |
Table 1.
Evaluation matrix.
| A/V reference | ||||
|---|---|---|---|---|
| A/V algorithm result |
A |
V |
Overlapping |
Uncertain |
| A | TA | FA | / | |
| V | FV | TV | / | |
| Unlabeled | / | |||
Table 2.
A/V classification results for manual and automatic vessel inputs on Retinal Images vessel Tree Extraction.
| Manual | Automatic | |||||
|---|---|---|---|---|---|---|
| Coverage rate (%) | Pixel-wise accuracy (%) | Centerline accuracy (%) | Coverage rate (%) | Pixel-wise accuracy (%) | Centerline accuracy (%) | |
| Overlap. trees | ||||||
| Indep. trees | ||||||
| All trees | ||||||
Fig. 11.
Examples of results from the fundus image in Fig. 10. Row (i): results from the manual input. Row (ii): results from the automatic input. (a) Vessel segmentation, (b) VPCM with neighborhood indicated in yellow boundary, (c) independent VPCMs in different colors (centerlines thickened for better visualization), (d) A/V results overlapped with vessel segmentation ground truth (red for A, blue for V), and (e) A/V results with errors in yellow.
From the table, we see that the results for manual vessel segmentation are better than those for automatic vessel segmentation, which have both higher coverage rate and accuracies. This is reasonable since the manual vessel segmentation has higher quality than the automatic one. However, the difference of accuracies is not large, showing that the proposed method can process vessel segmentations with different qualities. Also, the classification accuracies for overlapping trees are better than those for independent trees, especially the centerline accuracy.
For the Mosaic dataset, we only measure the centerline accuracy. The result is shown in Table 3, along with the result of previous version,25 which only worked on overlapping trees, but ignored independent trees. The higher accuracy of our current approach indicates a cost function combining vessel width, intensity, direction, and dominant orientation is advantageous, since the previous one only used vessel directions. Example results are shown in Fig. 12.
Table 3.
A/V classification results for automatic vessel inputs on Mosaic.
| Overlapping trees | Indep. trees | All trees | Previous method25 | |
|---|---|---|---|---|
| Centerline accuracy (%) |
4. Discussion
A novel method to construct the arterial and venous vasculature from retinal images is proposed in this paper. Using the topological property of the retinal vessels, we are able to use both local and global information to recognize the landmarks of the vessel network thus to construct the anatomical trees. The general strategy is to build an overconnected vessel network first, a VPCM, and then separate it into multiple trees with binary labels. During the construction of the VPCM, neighborhoods are properly constructed to represent potential landmarks. Then, separating the VPCM is modeled as an optimization problem and solved using a special graph-based metaheuristic algorithm. The major merit of the method is that it avoids being trapped at local optima due to local errors (image noise, vessel segmentation, and preprocessing errors), because it utilizes a variety of features both locally and globally. The proposed method also can recognize some small vessels that are difficult to classify using only local knowledge.
To demonstrate its performance, we build a publicly available dataset RITE based on the well-known dataset DRIVE and test on it, as well as another dataset previously used. The result from RITE indicates that our method performs well on both manual and automatic vessel segmentation inputs. Our reported results are also comparable with recent work by Dashtbozorg et al.22 who tested on half of DRIVE (DRIVE test set of 20 images). In particular, using the images from the DRIVE test set with the automatic vessel segmentation as the input (half of the images reported in our results), our method obtains mean and std. of the pixel-wise accuracy as for the overlapping trees, and for all trees. Using a different automated vessel segmentation as input and an A/V reference standard defined by different experts, Dashtbozorg’s algorithm obtained a pixel-wise accuracy of 87.4%. However, Dashtbozorg et al.22 only classified the main vessels (vessels with a width larger than 3 pixels). While they did not provide a reported coverage rate, we assume that since we included classification of smaller vessels that our coverage rate is likely higher. In addition, the accuracy is of course also dependent on the input vessel segmentation as evident by the fact that our accuracy increased when using a manual vessel segmentation as input. For DRIVE test set with manual vessel input, our method achieves mean and std. of pixel-wise accuracy as for the overlapping trees and for all trees. Note that not all methods would necessarily perform better when using a manual vessel segmentation as input, given the additional vessels to classify, as indicated in our pixel-classification-only results in the next paragraph.
It is also interesting to note that the results from both datasets indicate that the core part of the proposed method, which involves the separation and classification of overlapping trees, performs better than the pixel-based classification of independent trees. To further explore the potential advantage of including the tree separation component in final classification results, we computed pixel-based classification results (i.e., determining the label of each vessel segment based only on the majority-vote for all classified centerline pixels within the segment) on all trees for images from RITE. Generating the same coverage rate, the pixel-classification-only approach obtained a mean pixel-wise accuracy and centerline accuracy of and for automatic vessel segmentation as input (which is smaller than the and accuracies obtained by the full approach); for manual vessel segmentation as input, it obtained a mean pixel-wise accuracy and centerline accuracy of and (which, again, is smaller than the and accuracies obtained by the full approach). The fact that using an automatic vessel segmentation as input yields higher accuracy for the pixel-classification-only approach when compared with using a manual vessel segmentation as input is likely because automatic vessel segmentation has fewer thin vessels than the manual vessel segmentation, which are difficult to classify merely using local information.
The algorithm is implemented in C++ and run on a common Linux computer (AMD Opteron Processor 8439 SE). The median of total running time is 175 s, with the maximum case of 573 s. For RITE dataset, the median of the running time for solving the overlapping tree is 26.9 s, with the maximum case of 385 s. Since images in RITE are mostly fovea-centered, most of them contain two major complex VPCMs, with several exceptions containing one, three, or four. A graph transferred by a major complex VPCM normally has around 80 nodes and 100 edges, and 10 cycles. The largest graph contains 248 nodes and 284 edges, with 37 cycles, which corresponds to the image with the maximum running time. It happens for image 13_test in RITE with the manual vessel segmentation as input (Fig. 13). This is the only graph that the heuristic algorithm cannot find a feasible solution and the solution generated contains one cycle.
Fig. 13.
The image with the largest graph. (a) The fundus image, (b) the vessel ground truth, (c) independent VPCMs in different colors, (d) A/V result overlapping with the vessel segmentation, (e) A/V result with errors in yellow.
In future, a smarter method to construct the VPCM could be used for the automatic vessel segmentation so more errors can be rectified. Also, a machine-learning method could be used to classify false vessels and predict missed vessels. In addition, for the independent trees that are difficult to classify with only local intensity information, we plan to include some geometric information to classify them. In summary, we have presented and validated a method for automated disambiguation of retinal arterial and venous trees, and it outperforms the other latest methods tested on the same dataset. Potentially, better separation of arteries and veins will lead to increased accuracy of retinal image analysis, and thereby contribute to preventing visual loss and blindness.
5. Conclusion
In this paper, we present a framework to automatically construct the arterial and venous vascular trees in retinal images given a vessel segmentation. The proposed framework repairs connectivity between vessels by building a strongly connected network and the vessel network is separated into anatomical trees by using a graph-based algorithm, which is further classified into A/V trees. The proposed approach is tested on a public dataset and promising results indicate its reliable performance and potential applicability to large-scale datasets.
Acknowledgments
This work is supported in part by NIH R01 EY018853 and R01 EY023279, and the Department of Veterans Affairs Rehabilitation Research and Development Division (I01 CX000119 and Career Development Award IK2RX000728).
Biographies
Qiao Hu is currently a PhD student in the Department of Electrical and Computer Engineering at the University of Iowa. He received his BE degree in electronics science and technology from Tianjin University, China, in 2009. His current research interests include medical image analysis, image processing, and pattern recognition.
Michael D. Abràmoff is a fellowship-trained retinal specialist with a PhD in image analysis. He received his MD degree from the University of Amsterdam in 1994 and his PhD in 2001 from the University of Utrecht, The Netherlands. He is professor of ophthalmology and visual sciences at the University of Iowa, with joint appointments in electrical and computer engineering and biomedical eEngineering. He has authored over 200 journal papers, 11 patents and patent applications in this field.
Mona K. Garvin is currently an associate professor in the Department of Electrical and Computer Engineering at the University of Iowa and a research health science specialist at the Center for the Prevention and Treatment of Visual Loss in the Iowa City VA Health Care System. She received her PhD in biomedical engineering in 2008, her MS degree in biomedical engineering in 2004, her BSE degree in biomedical engineering in 2003, and her BS degree in computer science in 2003, all from the University of Iowa.
Appendix A.
This appendix describes the steps to construct the VPCM from a set of partitioned vessel segments.
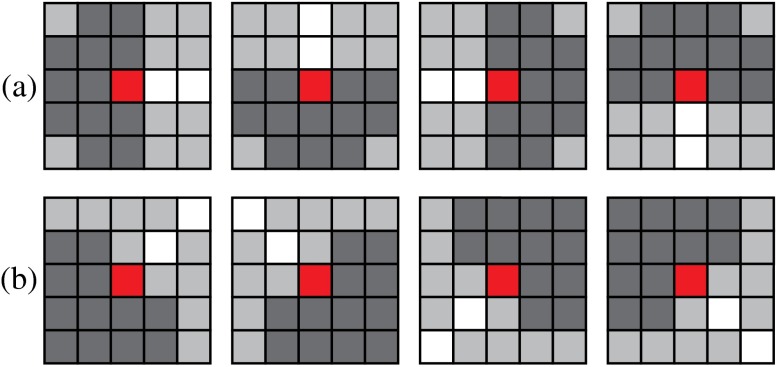
The first step is to initially find neighbors for both end points of each segment in a small region. The shape and direction of the region is defined as shown in Fig. 14. For an end point of from segment (red pixel in Fig. 14), if there is an end point from other segment within its search region (dark gray pixels in Fig. 14), is connected with and is a neighbor of .
Fig. 14.
Two types of search region, which are shown in dark gray and the end point is in red and vessel centerlines in white. (a) The vessel direction is in either horizontal or vertical direction and (b) the vessel direction is in a diagonal direction.
Then, short isolated segments less than 12 pixels are removed because the majority of them are false positives, and the rest are of little clinical significance. In addition, we use a method based on the work of Niemeijer et al.27 (using a SVM classifier rather than a -NN classifier to obtain OD and fovea probability maps) to find the centers of the OD and the fovea. We also estimate the radius of the OD by determining the radius (between 40 and 90 pixels) that maximizes the number of overlapping edge responses from the Gaussian-derivative-filtered OD probability map.
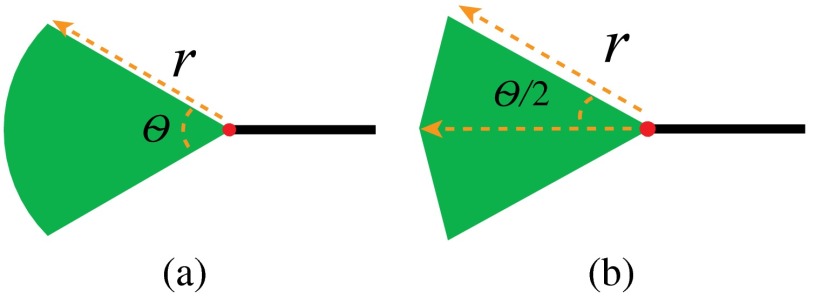
The next step is to find additional potential neighbors for vessel segments in a larger region using a two-step algorithm. The first step is to explore neighbors for segment ends having no neighbors by artificially extending the segment. The extension is defined as a region theoretically similar to a circular sector whose radius is and central angle is . Figure 15(a) shows the shape in the continuous domain, and Fig. 15(b) shows the shape in the digital image domain. The extension region is iteratively grown by increasing until a neighboring segment is found, or reaches a limit . Here, [Eq. (8) is determined by a function of the vessel length , the vessel tortuosity33 , and an arc weight (Eq. (9)]
| (8) |
| (9) |
Fig. 15.
The shape of the extension region.
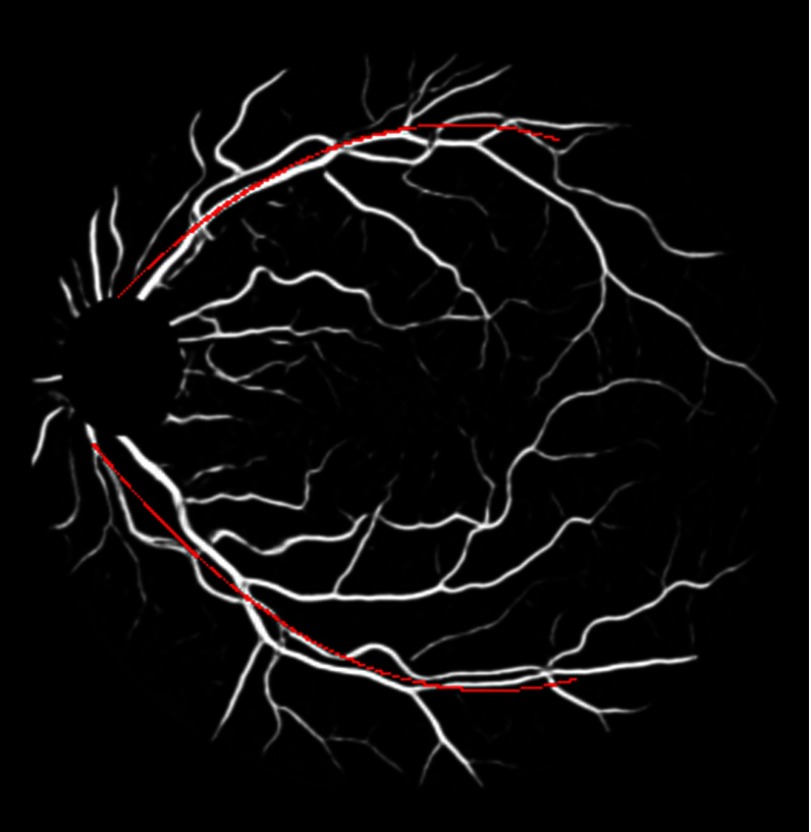
In our experiment, , , , . The arc weight encourages segment ends that are near and aligned with major vessels to have a greater maximum extension. The major vessels are the two largest vessels on a fundus image. They are obtained by downsampling the vessel segmentation, thresholding, and skeletonizing it, and then finding the two largest connected components. Then these two major vessel arcs are represented by 2nd degree curves (Fig. 16). In the arc weight equation given by Eq. (9) above, is the nearest distance between a segment end and an arc and is the angle between the direction of the segment end and the tangent line of the nearest point on the arc.
Fig. 16.
An example of downsampled vessel segmentation with major vessel arcs in red.
The extension region finds a neighbor using Algorithm 3. Examples of the extension region with different connection cases are shown in Fig. 17.
Algorithm 3.
The algorithm to link neighboring segments.
| for each end which has no neighbors do |
| while has no neighbor and do |
| increase and construct the region |
| if meets an end point of another segment then |
| connect to and ’s neighbors if there are any [Fig. 17(a)] |
| else if meet a vessel centerline then |
| break vessel at into two segments, which generates two new end points and , form , and as a neighborhood [Fig. 17(b)] |
| else if meet another extension from end then |
| connect to and ’s neighbors if there are any [Fig. 17(c)] |
| end if |
| end while |
| end for |
Fig. 17.
(a)–(c) Three different cases of finding a neighbor. (d)–(f) After they are connected.
The second step is to merge close neighborhoods. A boundary is defined for each neighborhood , and a neighborhood will merge with others if their boundaries contact. The boundary is a polygon whose shape is defined according to .
When , the boundary is an extending segment of length from the vessel end.
When , the boundary is a quadrangle [see Fig. 18(a)]. Two of the crests and of the quadrangle are on the segments whose distance to their respective end points is , which is controlled by the width of the two segments. Another two crests and are defined using Eq. (10), where is the angle between the directions of the two segments; is a constant, which is set as 7 in our experiment; and are the directions of the two segments. is the centroid of and .
| (10) |
An example of the boundary on the image domain is shown in Figs. 18(b) and 18(c).
Fig. 18.
The boundary illustration for neighborhood with size of 2. (a) The theoretical geometry of the boundary, (b) the vessel segments with two 2-pt neighborhoods in the center, and (c) the corresponding boundaries shown in yellow.
When , the boundary is a triangle. The three crests of the triangle are on the segments whose distances to their respective end points are . Assume , , and are the three angles between directions of segments in a neighborhood. If they are all larger than 110 deg, [see Fig. 19(a)]; Otherwise, for segments whose directions form the smallest angle, and , where is a constant, which is set as 12 in our experiment, and is the smallest angle [see Fig. 19(c)]. An example of each of the cases in actual digital image space is shown in Figs. 19(b) and 19(d).
Fig. 19.
The boundary illustration for neighborhood with size of 3. (a) The first case of boundary construction on theoretical geometric domain, (b) an example of the boundary on image domain for the first case, (c) the second case of boundary construction on theoretical geometric domain, and (d) an example of the boundary on image domain for the second case.
When , the boundary is a polygon whose vertices are the vessel pixels such that , where . An example of the boundaries for neighborhood with different sizes is shown in Fig. 20.
Fig. 20.
Examples of boundary for neighborhood with size of 4, 5, and 6, respectively.
We also limit the size of neighborhoods smaller than 7, based on the observation that the overlapping of three landmarks (bifurcations or crossing points) is extremely rare. Therefore, if a merged neighborhood is larger than 6, we do not merge these neighborhoods. When neighborhoods are merged, if both ends of a segment are within the new neighborhood, the segment is removed.
Appendix B.
This appendix describes the methods to determine the vessel dominant orientations for segments, which are determined using multiple models together.
The first model is to use the root and leaf property. First of all, two special types of segments in a VPCM are introduced, the root segment, from which the trees start; the leaf segment, at which the trees end. There usually are multiple roots and leaves in a complex VPCM. For roots, their tails have no neighbors. For leaves, their heads have no neighbors. Therefore, we first find out all segments that have one end point without neighbors, then we classify them into roots and leaves using their distances to the OD. Roots are the ones closer to the OD, and leaves are the ones farther away from it. After we determine roots and leaves, we extend their labels to other segments using the following method. For a root or leaf, if its end point with neighbors has only one neighbor not already labeled as the same type, then the neighboring segment is also labeled as a root or leaf, respectively. By this rule, we obtain a set of segments labeled as roots and leaves. When a segment is labeled as root or leaf, the dominant orientation is determined simultaneously, so as and for this segment. Figure 21(b) shows root segments in red and leaf segments in yellow, for the fundus in Fig. 21(a). Segments with dominant orientations determined with this model are shown in Fig. 21(c). Segments with dominant orientations determined are in green, and the head part is in red and the tail part is in yellow.
Fig. 21.
An example of determining dominant orientations. (a) A fundus image, (b) vessel roots shown in red, and leaves shown in yellow, (c) dominant orientations determined after using the root and leaf property, (d) dominant orientations determined after using the second model, (e) dominant orientations determined after using the parallel rule, and (f) dominant orientations determined after using the neighborhood connectivity.
The second model is to use the radial distribution of segments with respect to the OD. For a segment , we calculate the displacement of its two end points as a unit vector denoted as . We also calculate the displacement of its center pixel to the OD as a unit vector . If the angle of and is smaller than a degree , then the dominant orientation for is determined and the endpoint near to the OD is , and the other one is . Figure 21(d) shows the segments with dominant orientations determined after using this model.
The third model is the parallel model, which is only applied when there is a fovea in the image. The displacement of the fovea to the OD center is calculated as a unit vector, denoted as . For a segment , if the angle between and is smaller than a degree , the dominant orientation is determined, and the end point near to the OD is , and the other one is . Vessel segments with dominant orientation determined using this model are shown in Fig. 21(e).
The fourth model is the rules of neighborhood connectivity, which are applied on the neighborhood level. Specifically we apply the rules mentioned at the end of Sec. 2.3.1 for neighborhoods with size of 3, 4, 5, and 6. For neighborhoods with size of 3 and 4, there must be at least 1 , or at most 2 . For neighborhoods with size of 5 and 6, there must be 2 and the rest are . With these rules, we could label some as or for some neighborhoods, thus to determine the dominant orientation of the corresponding segments. Also, we could rectify some possible errors made by previous models if there are more in a neighborhood than these rules limit. The basic algorithm to determine a to be a or is based on the direction information. We assume that in a neighborhood all heads are aligned together, and all tails are aligned in the opposite direction. For a , if its associated end point direction is more aligned with other , and more on the opposite direction of other , then it is labeled as ; otherwise it is labeled as . The same rule is applied to choose the extra that should be changed to . When there are three in a neighborhood, one (the that deviates the most with other two and is aligned the most with all other ) is changed to . There are special cases that these rules cannot apply so we design different strategies or just leave them without any process. For example, when all end points are or , we break the neighborhood and disconnect every end point. For neighborhood of size 3, when there is one , one and one , we do nothing. For neighborhood of size 4, when there is one , one and two , we do nothing. Figure 21(f) shows segments with dominant orientation determined after using these rules.
Appendix C.
In this appendix, we describe the algorithms to calculate possible configurations and their costs for neighborhoods with different sizes. First, for better description, we use the labels of end points to denote the members of one neighborhood. For example, a neighborhood with one head, two tails, and one unknown is denoted as . A configuration is denoted as a subset of connected end points. Therefore, in the case of , a configuration of the head being connected with both tails is denoted as . Due to the duality of the connection or the labels, it can also be expressed using the complementary subset, thus .
When , there are two configurations, two end points are either connected, or disconnected. The vessel dominant orientation and the vessel end point direction are used to determine the costs of them. First, if both of end points are heads or tails, there is only one configuration, that they are disconnected, and the cost is set to be an extreme small number, here ; otherwise, end point directions are used to determine the configurations and costs. The cost of them being connected is calculated by Eq. (11) and the cost of them being disconnected is calculated by Eq. (12), where and are the directions of the two end points.
| (11) |
| (12) |
where
| (13) |
When , there are four potential configurations logically. Here, vessel dominant orientations and end point directions are used. Specifically after the determination of vessel dominant orientations, there are only three cases of how many heads, tails or unknowns in the neighborhoods, and different algorithms are designed to generate possible configurations and corresponding costs.
-
1.
For the case of one head and two tails (): we limit the potential configurations to only three cases, , where , and . The costs are calculated using the end point direction vectors. For and , their costs are the cosines of the angles between the direction vectors of two connected end points. For , the cost is the sum of the two cosines of the angles between the direction vectors of the head and two tails.
-
2.
For the case of two heads and one tail (): we limit the potential configurations to only two cases. , where , . The costs for and are the cosines of the angles between the directions of two connected end points.
-
3.
For the case of one head, one tail and one unknown (): four cases are allowed, , where , , and . The costs for , and are the cosines of the angles between the directions of two connected end points. For , the cost is the sum of the two cosines of the angles between the direction vectors of the head and the tail, and the head and the unknown.
We next introduce how to calculate the costs for configurations when (the costs for will be discussed last). When , since there are two heads and the rest are tails, the same strategy is adapted. For all the configurations, three types of costs are calculated independently using the vessel width, profile intensities and end point directions respectively, denoted as , , and . Then they are combined together to obtain the final cost . Specifically, it is the negative of the multiplication of the three costs in Eq. (14). Then configurations with the first 6 lowest costs are preserved for , and configurations with the first eight lowest costs are preserved for .
| (14) |
For , we utilize the fact that the width of parent segment is larger than the width of any children segments. First we use the relative width to eliminate some impossible configurations if , where is the relative width of the parent segment (one providing the head), and is the relative width of the thickest child segment (one providing the tail). Then, we calculate using Eq. (15), where and are the absolute widths of the parent and child segments respectively introduced in Sec. 2.3.1.
| (15) |
For , we evaluate the cost of every child segment being connected to one parent over another parent using intensity information. Specially, for child segment , the cost is calculated using Eq. (16), where is its intensity vector, is the intensity vector of the parent it connects, and is the intensity vector of the parent it disconnects. For a configuration, the is the multiplication of the of three child segments.
| (16) |
For , we make three rules to model the angles between the parent segment and its children segments. If a parent segment has only one child, then the two segments should be as aligned as possible. If a parent segment has two children, then the two children segments should also be connected to the parent in a balanced way. If a parent segment has three children, also the three children segments should be connected to the parent in a balanced way.
When , there are eight potential configurations logically. Since there might be unknowns in this type of neighborhood, three different algorithms are designed for different cases. The first case is when there are two heads and two tails. In this case there are only four possible configurations, and we use the same method for to calculate the costs for them.
The second case is when there is one head and three tails. In this case, three tails are supposed to connect to the head, unless the neighborhood is near the OD. When it is near the OD, we assume one tail should be a root, which should be separated from the head. Thus, there are four configurations: , where , , , and . The cost of is given in Eq. (17), where is a distance factor, is the distance of segment centroid to the OD, and is the radius of the OD. The cost of three other cases is given in Eq. (18), where is the difference of mean intensity between the only separated segment and the three connected segments; and is the difference of mean intensity between the three connected segments.
| (17) |
| (18) |
The third case is when there is only one head, and the number of unknowns is larger than 0. In this case we first determine if there is another head. If there is not, then it belongs to the second case; if there is another head, then it belongs to the first case. Here, end point directions are used to determine if there is another head. Generally, if the direction of the segment with an unknown has a small angle with the direction of the segment of the determined head, and the segment with the unknown aligns well with another segment that is not the head, then this unknown is a head.
References
- 1.Nguyen T. T., Wong T. Y., “Retinal vascular changes and diabetic retinopathy,” Curr. Diabetes Rep. 9(4), 277–283 (2009). 10.1007/s11892-009-0043-4 [DOI] [PubMed] [Google Scholar]
- 2.Guan K., et al. , “Retinal hemodynamics in early diabetic macular edema,” Diabetes 55(3), 813–818 (2006). 10.2337/diabetes.55.03.06.db05-0937 [DOI] [PubMed] [Google Scholar]
- 3.Klein R., Klein B. E., Moss S. E., “The relation of systemic hypertension to changes in the retinal vasculature: the Beaver Dam Eye Study,” Trans. Am. Ophthalmol. Soc. 95, 329–350 (1997). [PMC free article] [PubMed] [Google Scholar]
- 4.Abramoff M. D., Garvin M. K., Sonka M., “Retinal imaging and image analysis,” IEEE Rev. Biomed. Eng. 3, 169–208 (2010). 10.1109/RBME.2010.2084567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wong T. Y., et al. , “Prospective cohort study of retinal vessel diameters and risk of hypertension,” BMJ 329(7457), 79 (2004). 10.1136/bmj.38124.682523.55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hubbard L. D., et al. , “Methods for evaluation of retinal microvascular abnormalities associated with hypertension/sclerosis in the atherosclerosis risk in communities study,” Ophthalmology 106(12), 2269C–2280C (1999). 10.1016/S0161-6420(99)90525-0 [DOI] [PubMed] [Google Scholar]
- 7.Wong T. Y., et al. , “Retinal vascular caliber, cardiovascular risk factors, and inflammation: the multi-ethnic study of atherosclerosis (MESA),” Invest. Ophthalmol. Visual Sci. 47(6), 2341C–2350C (2006). 10.1167/iovs.05-1539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chapman N., et al. , “Peripheral vascular disease is associated with abnormal arteriolar diameter relationships at bifurcations in the human retina,” Clin. Sci. 103(2), 111–116 (2002). 10.1042/cs1030111 [DOI] [PubMed] [Google Scholar]
- 9.Stanton A. V., et al. , “Vascular network changes in the retina with age and hypertension,” J. Hypertens. 13(12), 1724–1728 (1995). [PubMed] [Google Scholar]
- 10.Wolffsohn J. S., et al. , “Improving the description of the retinal vasculature and patient history taking for monitoring systemic hypertension,” Ophthalmic Physiol. Opt. 21(6), 441C–449C (2001). 10.1046/j.1475-1313.2001.00616.x [DOI] [PubMed] [Google Scholar]
- 11.Dhillonb B., et al. , “Retinal image analysis: concepts, applications and potential,” Prog. Retinal Eye Res. 25, 99C–127C (2006). 10.1016/j.preteyeres.2005.07.001 [DOI] [PubMed] [Google Scholar]
- 12.Hatanaka Y., et al. , “Automatic arteriovenous crossing phenomenon detection on retinal fundus images,” Proc. SPIE 7963, 79633V (2011). 10.1117/12.877232 [DOI] [Google Scholar]
- 13.Jung E., Hong K., “Automatic retinal vasculature structure tracing and vascular landmark extraction from human eye image,” in Int. Conf. on Hybrid Information Technology ICHIT’06, Vol. 2, pp. 161–167 (2006). [Google Scholar]
- 14.Bhuiyan A., et al. , “Automatic detection of vascular bifurcations and crossovers from color retinal fundus images,” in Third Int. IEEE Conf. on Signal-Image Technologies and Internet-Based System SITIS’07, pp. 711–718 (2007). [Google Scholar]
- 15.Tramontan L., Grisan E., Ruggeri A., “An improved system for the automatic estimation of the arteriolar-to-venular diameter ratio (AVR) in retinal images,” in 30th Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society EMBS 2008, pp. 3550–3553 (2008). [DOI] [PubMed] [Google Scholar]
- 16.Aibinu A. M., et al. , “Vascular intersection detection in retina fundus images using a new hybrid approach,” Comput. Biol. Med. 40(1), 81–89 (2010). 10.1016/j.compbiomed.2009.11.004 [DOI] [PubMed] [Google Scholar]
- 17.Calvo D., et al. , “Automatic detection and characterisation of retinal vessel tree bifurcations and crossovers in eye fundus images,” Comput. Meth. Prog. Biomed. 103(1), 28–38 (2011). 10.1016/j.cmpb.2010.06.002 [DOI] [PubMed] [Google Scholar]
- 18.Martinez-Perez M. E., et al. , “Retinal vascular tree morphology: a semi-automatic quantification,” IEEE Trans. Biomed. Eng. 49(8), 912–917 (2002). 10.1109/TBME.2002.800789 [DOI] [PubMed] [Google Scholar]
- 19.Tsai C. L., et al. , “Model-based method for improving the accuracy and repeatability of estimating vascular bifurcations and crossovers from retinal fundus images,” IEEE Trans. Inf. Technol. Biomed. 8(2), 122–130 (2004). 10.1109/TITB.2004.826733 [DOI] [PubMed] [Google Scholar]
- 20.Lin K. S., et al. , “Vascular tree construction with anatomical realism for retinal images,” in Ninth IEEE Int. Conf. on Bioinformatics and BioEngineering BIBE’09, pp. 313–318 (2009). [Google Scholar]
- 21.Joshi V. S., et al. , “Automated artery-venous classification of retinal blood vessels based on structural mapping method,” Proc. SPIE 8315, 83151C (2012). 10.1117/12.911490 [DOI] [Google Scholar]
- 22.Dashtbozorg B., Mendonça A. M., Campilho A., “An automatic graph-based approach for artery/vein classification in retinal images,” IEEE Trans Image Process. 23(3), 1073–1083 (2014). 10.1109/TIP.2013.2263809 [DOI] [PubMed] [Google Scholar]
- 23.Rothaus K., Jiang X., Rhiem P., “Separation of the retinal vascular graph in arteries and veins based upon structural knowledge,” Image Vision Comput. 27(7), 864–875 (2009). 10.1016/j.imavis.2008.02.013 [DOI] [Google Scholar]
- 24.Estrada R., et al. , “Retinal artery-vein classification via topology estimation,” IEEE Trans Med. Imaging (2015), [Epub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hu Q., Abràmoff M. D., Garvin M. K., “Automated separation of binary overlapping trees in low-contrast color retinal images,” in Medical Image Computing and Computer-Assisted Intervention–MICCAI 2013, pp. 436–443, Springer; (2013). [DOI] [PubMed] [Google Scholar]
- 26.Lam L., Lee S.-W., Suen C. Y., “Thinning methodologies-a comprehensive survey,” IEEE Trans. Pattern Anal. Mach. Intell. 14(9), 869–885 (1992). 10.1109/34.161346 [DOI] [Google Scholar]
- 27.Niemeijer M., Abramoff M., Van Ginneken B., “Automated localization of the optic disc and the fovea,” in 30th Annual Int. Conf. of the IEEE Eng. in Medicine and Biology Society EMBS 2008, pp. 3538–3541, IEEE; (2008). [DOI] [PubMed] [Google Scholar]
- 28.Kavitha T., et al. , “Cycle bases in graphs characterization, algorithms, complexity, and applications,” Comput. Sci. Rev. 3(4), 199–243 (2009). 10.1016/j.cosrev.2009.08.001 [DOI] [Google Scholar]
- 29.Xu X., et al. , “Vessel boundary delineation on fundus images using graph-based approach,” IEEE Trans. Med. Imaging 30(6), 1184–1191 (2011). 10.1109/TMI.2010.2103566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Niemeijer M., van Ginneken B., Abrmoff M. D., “Automatic determination of the artery vein ratio in retinal images,” Proc. SPIE 7624, 76240I (2010). 10.1117/12.844469 [DOI] [Google Scholar]
- 31.Niemeijer M., et al. , “Comparative study of retinal vessel segmentation methods on a new publicly available database,” Proc. SPIE 5370, 648–656 (2004). 10.1117/12.535349 [DOI] [Google Scholar]
- 32.Hu Q., Garvin M. K., Abràmoff M. D., “RITE dataset,” August 2015, http://www.medicine.uiowa.edu/eye/RITE/
- 33.Joshi V., Reinhardt J. M., Abramoff M. D., “Automated measurement of retinal blood vessel tortuosity,” Proc. SPIE 7624, 76243A (2010). 10.1117/12.844641 [DOI] [Google Scholar]