Abstract
Magnetization transfer (MT) imaging is one way to indirectly assess pools of protons with fast transverse relaxation. However, conventional MT imaging sequences are not applicable to short T2 tissues such as cortical bone. Ultrashort echo time (UTE) sequences with TEs as low as 8 μs can detect signals from different water components in cortical bone. In this study we aim to evaluate two-dimensional (2D) UTE-MT imaging of cortical bone and its application in assessing cortical bone porosity as measured by μCT and biomechanical properties. In total, 38 human cadaveric distal femur and proximal tibia bones were sectioned to produce 122 rectangular pieces of cortical bone for quantitative UTE-MT MR imaging, microcomputed tomography (μCT), and biomechanical testing. Off-resonance saturation ratios (OSR) with a series of MT pulse frequency offsets (Δf) were calculated and compared with porosity assessed with μCT, as well as elastic (modulus, yield stress, and strain) and failure (ultimate stress, failure strain, and energy) properties, using Pearson correlation and linear regression. A moderate strong negative correlation was observed between OSR and μCT porosity (R2 = 0.46–0.51), while a moderate positive correlation was observed between OSR and yield stress (R2 = 0.25–0.30) and failure stress (R2 = 0.31–0.35), and a weak positive correlation (R2 = 0.09–0.12) between OSR and Young’s modulus at all off-resonance saturation frequencies. OSR determined with the UTE-MT sequence provides quantitative information on cortical bone and is sensitive to μCT porosity and biomechanical function.
Keywords: Magnetization transfer, off-resonance saturation ratio, UTE, porosity, cortical bone
Graphical Abstract
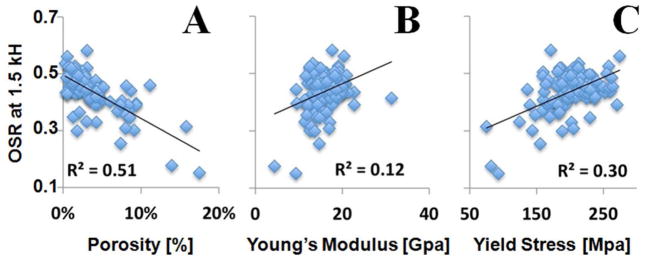
UTE-MT imaging of 122 human cortical bone samples: correlation between OSR (at 1.5 kHz) and μCT cortical porosity (A), Young’s modulus (B) and yield stress (C). OSR is negatively correlated with porosity, and positively correlated with Young’s modulus and yield stress.
INTRODUCTION
Cortical bone is composed of approximately 45% calcium hydroxyapatite, 40% type I collagen, and 15% water [1]. The combination of constituents confers unique biomechanical properties to bone, including the ability to resist compressive forces as well as tensile strength and viscoelasticity [2]. Cortical bone water has been of particular interest in the past several years because it can be detected with 1H magnetic resonance methods and quantification may improve the clinical assessment of fracture risk [3–5].
Cortical bone water exists in various locations as well as in different binding states. It can reside as bulk water in the pores of the Haversian canals and lacunocanalicular system, or be bound to the organic matrix or mineral [4–6]. Bulk water residing in the pores has sufficiently long T2 relaxation times that it can be detected with a number of clinically compatible techniques, including the ubiquitous fast-spin-echo sequences [7]. Imaging of bound water is more challenging due to the rapid decay of transverse magnetization which results in zero or near zero signal levels at the time of encoding. Ultrashort echo time (UTE) sequences can be used to detect signal from species with T2*s of a few hundred microseconds or longer, including water which is loosely bound to the organic matrix and pore water [8, 9]. However, tissues with extremely short T2*s, including tightly bound water and collagen protons, remain “invisible” even with the use of UTE.
Magnetization transfer (MT) imaging is an indirect method that allows for qualitative and quantitative assessment of proton pools with extremely fast transverse relaxation [10]. In a two-pool model, MT contrast is based on interactions between the bound and pore water proton pools. Specifically, off-resonance saturation pulses cause MT effects between bound and pore water protons as well as relaxation time-dependent direct saturation effects on the pore water proton pool. Although detected magnetization decreases from both of these effects, it has been suggested that the precise contribution from each is less relevant in the clinical arena where the main goal is characterization of normal versus pathologic tissue [11]. For the characterization of short T2* tissues, MT has been combined with UTE (UTE-MT) and an off-resonance saturation ratio (OSR) has provided a quantitative measure for the evaluation of tissue [12–14].
However, to the best of our knowledge, the use of UTE-MT on cortical bone has not been validated against established reference standards and biomechanical measures. The aim of this study was to evaluate UTE-MT imaging of cortical bone and its application in assessing cortical bone porosity as measured by μCT and biomechanical properties.
MATERIALS AND METHODS
Sample Preparation
This anonymized cadaveric study was approved by our Institutional Review Board. 122 rectangular pieces of cortical bone were resected from 38 cadaveric femora and tibiae (65.7 ± 16.3 years old, mean ± standard deviation; range 30–94 years). A precision circular diamond-edge saw (ISOMET 1000, Buehler, Lake Bluff, IL) was used to harvest the pieces of bone under saline irrigation and average dimensions of samples were 40 × 4 × 2 mm3 as measured with a digital caliper (± 0.0005″ precision). Samples were individually wrapped in wet saline gauze and frozen at −80 °C (Bio-Freezer; Forma Scientific, Marietta, OH, USA). Samples were thawed for 12 hours at 4 °C prior to MR imaging, μCT, and biomechanical testing. Another three cadaveric human tibial midshaft samples from three donors (57.7 ± 19.8 years old, mean ± standard deviation; age range 36–75 years) were harvested from cadaveric leg specimens, and were cleared of external muscle and soft tissue. Bone marrow was removed with a scalpel. Cross-sectional cortical bone segments with an approximate thickness of 40 mm were prepared. The three bone segments together with a piece of rubber (Pink Eraser, Paper Mate Products Inc) were used for optimization of the imaging protocol.
MR Imaging and Image Analysis
Specimens were imaged on a clinical 3T MR scanner (Signa HDx, GE Healthcare Technologies, Milwaukee, WI), which had gradients capable of a slew rate of 150 T/m/s and amplitude of 40 mT/m on each axis. A home-built birdcage coil (~2.5 cm in diameter) was used for signal excitation and reception. Bone samples were placed in a 20 ml syringe filled with perfluorooctyl bromide (PFOB) during MR imaging to maintain hydration and minimize susceptibility effects at air tissue junctions.
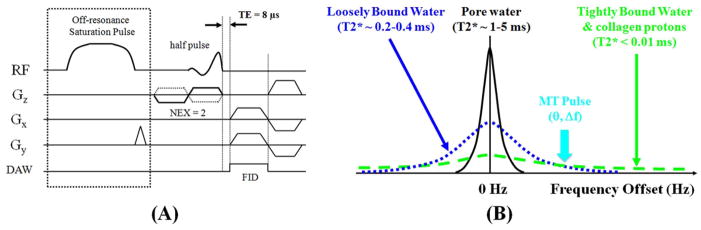
The 2D UTE sequence was performed, which uses a short half pulse excitation (pulse duration = 472 μs, pulse bandwidth = 2.7 kHz) followed by 2D radial ramp sampling (minimal nominal TE of 8 μs) [8]. Immediately following this, a 2D UTE-MT sequence was performed which employs an MT preparation pulse followed by a 2D UTE acquisition (Figure 1). The MT preparation pulse was a Fermi pulse of 8 ms duration (spectral bandwidth = 0.8 kHz), maximal B1 of 24 μT and 1000° maximal saturation flip angle, which provided an improved spectral profile compared with a rectangular pulse and higher efficiency compared with conventional Gaussian or sinc pulses. As a first step, we aimed to establish the 2D UTE-MT protocol by investigating the effects of off-resonance saturation pulse flip angle and off-resonance frequency (Δf) on OSR using three pieces of human cortical bone samples and a rubber eraser (Pink Eraser, Paper Mate Products Inc). T2*s of bone and rubber were measured using a variable TE 2D UTE imaging approach with the following parameters: TR = 100 ms, FOV = 4 cm, flip angle = 60°, slice thickness = 3 mm, bandwidth = 62.5 kHz, 211 projections, reconstruction matrix = 128×128, 19 TEs (0.01, 0.1, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.6, 2, 2.5, 3, 4, 6, 8, 10, 13, 16, 20 ms), 40 sec per image, a total scan time of 12 minutes. A bi-component model was used to fit T2*s of bound and pore water in cortical bone, as well as T2*s of short and long components in rubber using the following equation (15):
| (1) |
where T2B* is the bound water T2*, T2P* is the pore water T2*, SBound and SPore are the signal amplitudes of the bound and pore water components. Apparent bound water fraction was defined as SBound/(SBound+SPore). T2* values were obtained using a Levenberg-Marquardt fitting algorithm developed in-house based on Eq.1.
Figure 1.
(A) Pulse sequence diagram for 2D UTE-MT imaging: UTE acquisition with a minimal nominal TE of 8 μs is preceded by a Fermi (8 ms in duration) saturation pulse centered off the water peak to selectively saturation bound water with a shorter T2* with little effect on pore water with a longer T2*. (B) Diagram showing three pools of protons in cortical bone: tightly bound water and collagen backbone protons are selectively suppressed by the MT pulse with a high MT frequency offset (Δf). Loosely bound water is suppressed with a lower Δf. The efficiency of MTR is related to the MT pulse power (θ).
T1s of cortical bone and rubber eraser were measured using a saturation recovery 2D UTE approach where UTE acquisitions with progressively increasing saturation recovery times (TSRs) were used to detect the recovery of the longitudinal magnetization of cortical bone and rubber eraser, respectively. Imaging parameters were similar to these used for T2* measurements, except a longer constant TR of 1000 ms, a series of TSRs (8, 25, 50, 100, 150, 200, 300, 400, 500, 600, 700 ms), 7 minutes per image, a total scan time of 77 minutes. A single component exponential signal recovery model was used to fit T1s of bone and rubber [16]:
| (2) |
where k accounts for the residual fraction of the longitudinal magnetization of cortical bone and rubber eraser after a nominal 90° pulse. T1 values were obtained using a Levenberg-Marquardt fitting algorithm developed in-house based on Eq.2.
The UTE-MT protocol used imaging parameters similar to these for T2* measurements. However, this protocol used a longer TR of 300 ms, a series of MT pulse power (θ = 1000°, 600°, 300°) and a series of MT frequency offsets including 0.5, 1, 1.5, 3, 5, 7, 10, 15 and 20 kHz, 2.1 minutes per image, and a total scan time of 63 minutes. Regions of interest (ROIs) were carefully placed around each piece of cortical bone and rubber eraser, respectively, on the 2D UTE image and digitally copied to UTE-MT images with various offset saturation frequencies. The off-resonance saturation ratio (OSR) at each frequency was calculated according to the following equation [14]:
| (3) |
where S0 denotes the mean signal intensity acquired without a saturation pulse and SSAT(θ,Δf) denotes the mean signal intensity acquired with the saturation pulse with a flip angle of θ and placed at an off-resonance frequency of Δf. Global ROI OSR was calculated as well as pixel maps. Global ROI OSR was plotted as a function of MT pulse frequency offsets and MT power for the rubber eraser and cortical bone samples.
Based on analysis of OSR vs. θ and Δf, as well as scan time limitations, a simplified UTE-MT protocol was applied to the 122 rectangular pieces of cortical bone samples with a maximal MT pulse power of 1000° and a series of Δf (1.5, 3, 5, 10, 20 kHz). To save scan time, the 122 rectangular pieces of cortical bone samples were divided into 12 groups with about 10 chips per group. The total scan time was about 150 minutes.
Micro Computed Tomography (μCT)
Samples were also imaged on a μCT scanner (Skyscan 1076, Kontich, Belgium) with a 0.5 mm aluminum filter. The imaging parameters were as follows: 72 kV, 140 μA, FOV = 25 mm, 720 views, and 9 μm isotropic voxel size. Imaging time was approximately 3 hours. A previously developed [15] custom MATLAB (The Mathworks Inc., Natick, MA) code was used to import images (12 per sample) which consisted of 2.5 mm steps along the long axis. A global histogram for all images was created and used to determine a local minimum thresholding value. Noise correction was employed through despeckling of binarized images. Bone interfaces were automatically segmented and ROIs of the outer boundaries were automatically generated. Cortical porosity was calculated as one minus the ratio of the area of the bone to that of the outer boundary of the sample.
Biomechanical Testing
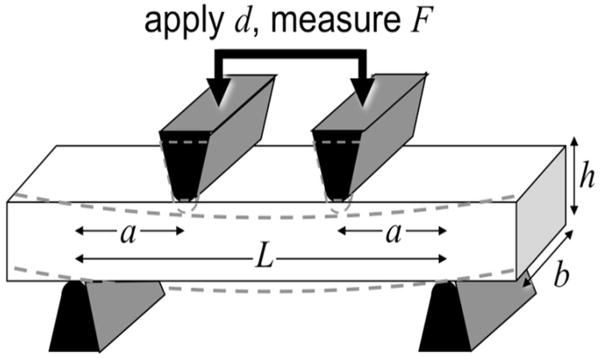
Samples were tested using a materials testing machine (model 8511.20, Instron, Norwood, MA) containing a 100 Newton load cell (Instron 2519-103) with an actuator displacement accuracy of approximately 0.002 mm. A four-point bending-to-failure test was performed as previously described [17] using a set of stainless steel jigs mounted on the mechanical testing system, as shown in Figure 2. The loading protocol consisted of initial contact and subsequent uniaxial compression at 0.1 mm/s until sample failure. Stress-strain relationships were plotted and Young’s modulus of elasticity (E) was determined from the tangent of the initial, linear portion of the curve. Yield stress (σy) and yield strain (εy) were determined by the yield point, defined as the point on the curve where strain deviated by 0.002 from the linear part described by Young’s modulus [18]. The ultimate stress (σult) was defined at the maximum stress and the failure strain (εf) was defined at the point on the curve where the largest drop in stress occurred.
Figure 2.
Experimental set-up for four-point biomechanical testing of a rectangular shaped cortical bone sample with a length of L, a width of b and a height of h. The four-point bending test used two loading jigs with a specific geometry to compress a rectangular sample while recording the force. Biomechanical properties, including Young’s modulus, yield stress and failure stress were derived from the stress-strain curve.
Statistical Analyses
Descriptive statistics were performed. OSRs corresponding to all five off-resonance frequencies were compared to μCT cortical porosity and biomechanical properties using Pearson correlation and linear regression. Data from all 122 cortical bone samples were used for analysis. P value less than 0.05 was considered significant.
RESULTS
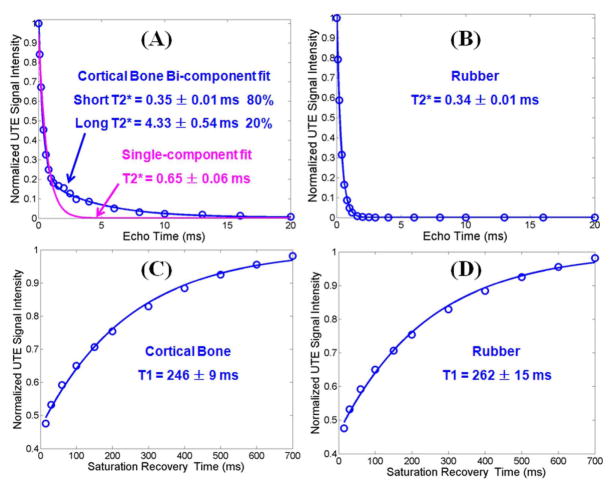
Figure 3 shows single- and bi-component analyses of UTE T2* decays of a piece of cadaveric human cortical bone sample and the eraser, respectively. There is systematic residual signal with single-component fitting for cortical bone, suggesting the existence of another water component. Excellent curve fitting was achieved with a bi-component model which shows two distinct water components: one with a short T2* of 0.35 ms accounting for 80% of the total UTE signal, and the other with a longer T2* of 4.33 ms accounting for the other 20%. The shorter T2* value is consistent with that of collagen bound water, while the longer T2* value is consistent with that of pore water based on recent NMR spectroscopic studies [6]. Together, our results suggest that UTE sequences can assess bound and pore water in cortical bone using a whole-body clinical MR scanner. Meanwhile, the eraser shows a single exponential T2* decay regardless of whether a single- or bi-component model was used. The single short T2* of 0.34 ms is nearly the same as that of bound water in cortical bone. Figure 3 also shows the saturation recovery T1 measurement for the same piece of cortical bone and the same eraser. A short T1 of 246 ± 9 ms was demonstrated for cortical bone, and a short T1 of 262 ± 15 ms was demonstrated for the eraser. Similar results were found between the other two pieces of human cortical bone samples and the eraser. Both T1 and T2* values are highly similar (differences less than 10% for T1s and 5% for T2*s) for the eraser and the bound water component in cortical bone, suggesting that the direct saturation effect for bound water in cortical bone can be evaluated via an OSR measurement of the eraser.
Figure 3.
UTE bi-component analysis of cortical bone (A) and rubber eraser (B), and UTE TSR analysis of cortical bone (C) and eraser (D). Single component fitting of the UTE images of cortical bone shows significant residual signal (> 20%) (A). The fitting residual is reduced to less than 0.6% by bi-component fitting (A), which shows a shorter T2* of 0.35 ± 0.01 ms and a longer T2* of 4.33 ± 0.54 ms with respective fractions of 80% and 20% by volume. The rubber eraser shows a single component decay with a T2* of 0.34 ± 0.01 ms (B). Single-component fitting of saturation recovery UTE imaging shows a T1 of 246 ± 9 ms (C) for cortical bone, and 262 ± 15 ms for the rubber eraser (D).
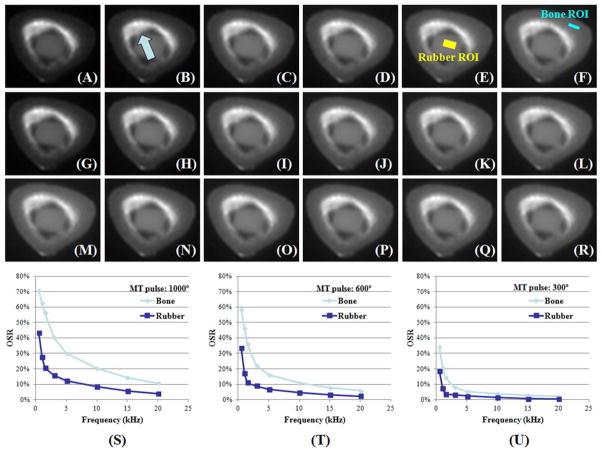
Figure 4 shows representative UTE images and the OSR of the rubber phantom and a cadaveric human cortical bone sample at different frequency offsets and MT pulse powers. Although the eraser and the bound water components in bone samples have similar T1s and T2*s, the OSR versus frequency offset behaviors are very different, reflecting the fact that the eraser only has protons similar to bound water, while cortical bone has both bound and pore water with distinct relaxation times. Pore water accounts for the increased OSR values for cortical bone. There was an inverse relationship observed between OSR of the eraser and Δf. OSR decreased from 40% to less than 20% when Δf was increased from 0.5 kHz to 1.5 kHz or more with a MT power of 1000°. OSR also decreased significantly with the decrease of MT pulse power from 1000° to 600° and then to 300°. As a result, we chose a MT pulse power of 1000° to maximize OSR, and a Δf of 1.5 kHz or higher to minimize direct saturation (to less than 20%) for the subsequent study of 122 cadaveric human cortical bone samples.
Figure 4.
UTE-MT images of a cadaveric human cortical bone sample and a rubber eraser with a MT power of 1000° and Δf of 0.5 (A), 1.5 (B), 5 (C), 10 (D), 20 kHz (E), a MT power of 600° and Δf of 0.5 (G), 1.5 (H), 5 (I), 10 (J), 20 kHz (K), a MT power of 300° and Δf of 0.5 (M), 1.5 (N), 5 (O), 10 (P), 20 kHz (Q), and the corresponding UTE images with MT off (F, L, R). UTE OSR is shown as a function of Δf at three different MT pulse power of 1000° (S), 600° (T) and 300° (U). OSR increases with MT power and decreases with Δf. OSR is consistently lower in rubber than in cortical bone, likely due to the mineral bound water and collagen protons which make a significant contribution to the OSR of cortical bone. These different proton pools are not present in rubber. The bone ROI shown in (F) corresponds to where a rectangular bone chip was sectioned. The bright signal (arrow) near the rubber eraser is from residual bone marrow which was not completely removed with the scapel.
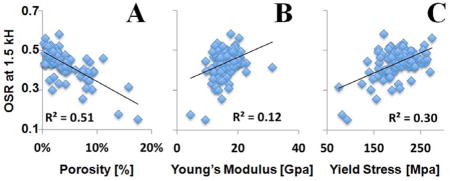
Figure 5 shows the relation between OSR and cortical porosity, the Young’s modulus and yield stress of 122 human bone samples with a Δf of 1.5 kHz. OSR correlated strongly and negatively with porosity (Figure 5A, R2=0.51) and positively with Young’s modulus (Figure 5B, R2=0.12), yield stress (Figure 5C, R2=0.30) and failure stress (R2=0.33).
Figure 5.
UTE-MT imaging of 122 human cortical bone samples: correlation between OSR (at 1.5 kHz) and μCT cortical porosity (A), Young’s modulus (B) and yield stress (C). OSR is negatively correlated with porosity, and positively correlated with Young’s modulus and yield stress.
OSR showed a significant correlation for both cortical porosity and biomechanical properties with all MT pulse frequency offsets (Table 1). Interestingly, the correlations seem to be fairly constant even with an increase in Δf. For example, the correlation between MTR and μCT cortical porosity decreased by less than 10% from 1.5 kHz (R2 = 0.51) to 20 kHz (R2 = 0.46). The correlation between MTR and Young’s modulus remained essentially unchanged from 1.5 kHz (R2 = 0.12) up to 10 kHz (R2 = 0.11), although a 25% reduction was observed at 20 kHz. The correlation between MTR and yield stress reduced by less than 7% from 1.5 kHz (R2 = 0.30) to 10 kHz (R2 = 0.28), although a slightly more reduction of 17% was observed at 20 kHz (R2 = 0.25). The correlation between MTR and failure stress remained nearly unchanged across all Δfs from 1.5 kHz (R2 = 0.33) to 20 kHz (R2 = 0.31). The correlations between MTR and biomechanical properties are comparable with those between μCT porosity and Young’s modulus (R2 = 0.17), yield stress (R2 = 0.35) and failure stress (R2 = 0.36). These results suggest that UTE-MT can potentially evaluate water residing in the microscopic pores of cortical bone, water bound to the organic matrix of cortical bone, and water tightly bound to mineral as well as collagen backbone protons, providing Δf independent information about cortical porosity and biomechanical properties of cortical bone.
Table 1.
Correlation between UTE-MT measured OSR and cortical porosity, Young’s modulus, yield stress and failure stress. OSR is highly negatively correlated with μCT porosity at all Δf, with R2 slightly reduced from 0.51 at 1.5 kHz to 0.46 at 20 kHz. OSR is weakly positively correlated with Young’s modulus at all Δf, with R2 slightly reduced from 0.12 at 1.5 kHz to 0.09 at 20 kHz. OSR is moderately positively correlated with yield stress and failure stress at all Δf, with R2 around 0.3. P values are less than 0.0001 for all the correlations.
| OSR = 1.5 kHz | OSR = 3 kHz | OSR = 5 kHz | OSR = 10 kHz | OSR = 20 kHz | |
|---|---|---|---|---|---|
| Porosity | R2=0.51, P<1e-20 | R2=0.49, P<1e-19 | R2=0.48, P<1e-18 | R2=0.48, P<1e-18 | R2=0.46, P<1e-17 |
| Young’s Modulus | R2=0.12, P<1e-4 | R2=0.11, P<2e-4 | R2=0.11, P<3e-4 | R2=0.11, P<3e-4 | R2=0.09, P<6e-4 |
| Yield Stress | R2=0.30, P<1e-10 | R2=0.28, P<2e-10 | R2=0.28, P<3e-10 | R2=0.28, P<2e-10 | R2=0.25, P<5e-9 |
| Failure Stress | R2=0.33, P<4e-12 | R2=0.34, P<2e-12 | R2=0.34, P<2e-12 | R2=0.35, P<1e-12 | R2=0.31, P<2e-11 |
DISCUSSION
We have demonstrated that off-resonance saturation ratio (OSR) as measured with the UTE-MT sequence provides information on both bound and pore water in cortical bone and is significantly correlated with cortical porosity and the biomechanical properties of cortical bone. In the present study, a rubber eraser was also investigated with the UTE-MT sequence to demonstrate the effect of saturation pulses with varying off-resonance frequencies in a control containing only bound protons, similar to bound water in bone with regards to T2* and T1 relaxation times. Without an MT effect from two pools, the observed OSR differences are expected to be based purely on direct saturation effects on the bound protons. It is notable that direct saturation effects contribute to OSR at all frequencies within the evaluated range with exponentially increasing effects closer to the on-resonance frequency. These findings are in keeping with phantom experiments from previous authors [19, 20]. Furthermore, our results show that the direct saturation contribution to OSR is reduced to less than 20% when the off-resonance frequency is increased to 1.5 kHz or higher, allowing more accurate measurement of true magnetization transfer in cortical bone.
We also demonstrate that OSR shows significant negative correlation with cortical porosity at all off-resonance saturation frequencies. This is an expected finding since increases in cortical porosity correspond to increases in pore water content. Pore water has about 10 times longer T2* than bound water, and thus much narrower spectra profile with little overlap with the off-resonance saturation pulse placed 1.5 kHz or further away. This results in an increased SSAT with the increase of pore water content, leading to an inverse relationship between OSR and cortical porosity. In pathologic bone, however, an increase in cortical porosity (and pore water) is typically accompanied by a decrease in organic matrix (and collagen-bound water) [21, 22]. The decrease in bound water would be expected to have an additive effect on decreasing OSR. This is in contrast to techniques which evaluate bulk water concentration, where the inverse relationships between pore and bound water would be expected to confound results [21].
Numerous studies have shown that increases in cortical porosity have a significant, detrimental impact on the mechanical properties of bone [5, 22–24]. In addition to the negative correlation between OSR and porosity, we found significant positive correlations between OSR and yield stress, and failure stress, suggesting that OSR may be a surrogate marker for biomechanical properties of cortical bone. Of note, in a prior study using UTE with bi-component analysis, Bae et al [5] did not find a significant correlation between Young’s modulus and short T2* fraction or long T2* fraction, likely representing water loosely bound to the organic matrix and pore water, respectively. These results were not surprising since Young’s modulus (stiffness) likely depends on the mineral content which is not detectable with the conventional UTE sequence. Although weak, there was a significant correlation (R2 = 0.09–0.12) between OSR and Young’s modulus at all off-resonance saturation frequencies, which suggests that UTE-MT is more sensitive to the tightly bound proton pool (including tightly bound water and collagen backbone protons) with extremely short T2*s, which are beyond the level of detection with regular UTE sequences on clinical whole-body scanners. UTE-MT is currently the only way to access these proton pools in cortical bone using clinical MR scanners.
Another interesting finding of this study is the little Δf dependence of MTR in correlations with μCT porosity and biomechanical properties, including Young’s modulus, yield stress and failure stress. If only two pools (e.g., pore water and collagen-bound water) were involved, we would expect a significant reduction in the correlation between MTR and pore water (or cortical porosity) at higher Δf, where the longitudinal magnetization of collagen-bound water is less affected by the MT pulse. The near Δf-independent correlation between MTR and μCT porosity suggests that mineral-bound water and collagen backbone protons, although they are not directly detectable with UTE sequences on clinical MR scanners, play a significant role in UTE-MT imaging. At a higher Δf (e.g., > 5 kHz), the longitudinal magnetizations of mineral-bound water and collagen backbone protons with extremely short T2*s are still sensitive to the MT pulse. Their magnetizations can transfer to pore water and thus contribute to OSR at high Δfs. Their involvement in UTE-MT imaging also explains the aforementioned weak but significant correlation (R2 = 0.09–0.12) between OSR and biomechanical properties involving minerals (e.g., Young’s modulus).
Our study also highlights the feasibility of using 2D UTE-MT on a clinical scanner. A major benefit of UTE-MT compared with other methods of bone water quantification such as multi-component T2* analysis and single and double adiabatic inversion techniques is the potential for shorter imaging times [8, 9, 25]. Grosse et al [11, 14] and Syha et al [12] have reported the use of a 3D-UTE technique with MT preparation to calculate OSR in patients using a protocol that is roughly 3.5 minutes. Our 2D UTE-MT scans can be done in 2 minutes. More recently, two other validated UTE-derived indices that can be acquired with short imaging times are the porosity index [26] and suppression ratio [27]. Comparison between the various methods of bone water quantification that show translational potential would be of great interest in future studies.
Although we found a significant positive correlation between MTR and μCT porosity, the correlations between MTR and mechanical properties are relatively weak. Horch et al. reported a high positive correlation (R2 = 0.68) between bound water content and peak stress, and a high negative correlation (R2 = 0.61) between pore water and peak stress [22]. Even the correlation between μCT porosity and yield stress is about 40% lower in our study over the Horch study (R2 = 0.35 vs. 0.58). Multiple factors may contribute to this difference, including sample dimensions, μCT resolution, sample sizes, gender, and donor age.
Recent studies suggest that quantitative UTE-MT can be achieved by acquiring OSR at different MT pulse power and off-resonance frequencies [28–30]. However, most of the quantitative MT models assume only two pools: the free pool which is clinically “visible” and the bound pool which is clinically “invisible”. In UTE-MT imaging of cortical bone, at least three pools, including pore water (T2*~2–5 ms), loosely bound water (T2* ~ 0.3 ms), tightly bound water and collagen backbone protons (T2* ~ 10 μs) contribute to OSR. Therefore, none of the many previously described models can be directly applied to cortical bone, including the classical Henkelman model [28], the simplified Ramani model [29], and the more recently described Hodgson model [30]. More complicated MT modeling (e.g., three-pool system) is required for complete characterization [31], which is beyond the scope of this paper.
There are a number of limitations to this study. First, the precise contribution of direct saturation and magnetization transfer effects were not separated nor were they quantified. The rubber eraser study suggests that direct saturation related OSR should be less than 10% for off-resonance frequency of 1.5 kHz or higher. Accurate measurement of these individual effects would require modeling and lengthy T1 measurements which would not be easily translated in vivo. OSR values are a more semi-quantitative measure, and are influenced by several factors including transmitted B1 field, MT pulse shape, sequence parameters, tissue dependent factors (T1, T2 and relative fractions of different proton pools), magnetization exchange rate, etc. On the other hand, quantitative UTE-MT modeling requires consideration of a three-pool system instead of the standard two-pool system, as described above. Second, actual bone porosity may be underestimated with μCT due to spatial resolution limitations and the inability to detect small pores. Third, biomechanical properties are affected by sample thickness and small local variations in sample thickness may have affected the accuracy of measurements. Fourth, previous authors have suggested that substantial x-ray exposure can degrade the mechanical integrity of bone [32]. By performing lengthy μCT imaging prior to biomechanical testing, an additional source of error may have been introduced. Fourth, UTE-MT imaging of cortical bone in vivo is not investigated in this study. However, it is straightforward to apply our imaging protocol directly to human volunteers and patients with osteoporosis. Finally, UTE-MT can potentially be more sensitive to pore water when a small off-resonance frequency offset is used, or more sensitive to tightly bound water and collagen backbone protons when a far off-resonance frequency offset is used, or more sensitive to loosely bound water when an intermediate off-resonance frequency offset is used. Quantitative assessment of this pool-sensitivity of UTE-MT sequences requires correlation of OSR with pore water, loosely bound water, organic matrix and mineral contents at different frequencies, and will be investigated in future studies.
In summary, OSR determined with the UTE-MT sequence provides quantitative information on cortical bone and is sensitive to μCT porosity and biomechanical function, and these correlations show little dependence on Δf.
Acknowledgments
The authors acknowledge grant support from GE Healthcare, NIH (1R01 AR062581-01A1 and 1R21 AR063894-01A1), and the VA Clinical Science Research and Development Service (Career Development Grant 1IK2CX000749).
Abbreviations used
- 2D
two-dimensional
- FID
free induction decay
- MRI
magnetic resonance imaging
- MT
magnetization transfer
- MTR
magnetization transfer ratio
- NEX
number of excitations
- OSR
off-resonance saturation ratio
- PFOB
perfluorooctyl bromide
- PBS
phosphate buffered saline
- RF
radio frequency
- ROI
region of interest
- SNR
signal to noise ratio
- TE
echo time
- TSR
saturation recovery time
- μCT
micro computed tomography
- UCSD
University of California, San Diego
- UTE
ultrashort echo time
References
- 1.Wehrli FW, Song HK, Saha PK, Wright AC. Quantitative MRI for the assessment of bone structure and function. NMR Biomed. 2006;19:731–64. doi: 10.1002/nbm.1066. [DOI] [PubMed] [Google Scholar]
- 2.Linde F. Elastic and viscoelastic properties of trabecular bone by a compression testing approach. Dan Med Bull. 1994;41:119–38. [PubMed] [Google Scholar]
- 3.Anumula S, Wehrli SL, Magland J, Wright AC, Wehrli FW. Ultra-short echo-time MRI detects changes in bone mineralization and water content in OVX rat bone in response to alendronate treatment. Bone. 2010;46:1391–9. doi: 10.1016/j.bone.2010.01.372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Horch RA, Nyman JS, Gochberg DF, Dortch RD, Does MD. Characterization of 1H NMR signal in human cortical bone for magnetic resonance imaging. Magn Reson Med. 2010;64:680–7. doi: 10.1002/mrm.22459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bae WC, Chen PC, Chung CB, Masuda K, D’Lima D, Du J. Quantitative ultrashort echo time (UTE) MRI of human cortical bone: correlation with porosity and biomechanical properties. J Bone Miner Res. 2012;27:848–57. doi: 10.1002/jbmr.1535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nyman JS, Ni Q, Nicolella DP, Wang X. Measurements of mobile and bound water by nuclear magnetic resonance correlate with mechanical properties of bone. Bone. 2008;42:193–9. doi: 10.1016/j.bone.2007.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Du J, Hermida JC, Diaz E, Corbeil J, Znamirowski R, D’Lima DD, Bydder GM. Assessment of cortical bone with clinical and ultrashort echo time sequences. Magn Reson Med. 2012;70:697–704. doi: 10.1002/mrm.24497. [DOI] [PubMed] [Google Scholar]
- 8.Du J, Carl M, Bydder M, Takahashi A, Chung CB, Bydder GM. Qualitative and quantitative ultrashort echo time (UTE) imaging of cortical bone. J Magn Reson. 2010;207:304–11. doi: 10.1016/j.jmr.2010.09.013. [DOI] [PubMed] [Google Scholar]
- 9.Horch RA, Gochberg DF, Nyman JS, Does MD. Clinically compatible MRI strategies for discriminating bound and pore water in cortical bone. Magn Reson Med. 2012;68:1774–84. doi: 10.1002/mrm.24186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Henkelman RM, Stanisz GJ, Graham SJ. Magnetization transfer in MRI: a review. NMR Biomed. 2001;14:57–64. doi: 10.1002/nbm.683. [DOI] [PubMed] [Google Scholar]
- 11.Grosse U, Syha R, Martirosian P, Wuerslin C, Horger M, Grozinger G, Schick F, Springer F. Ultrashort echo time MR imaging with off-resonance saturation for characterization of pathologically altered Achilles tendons at 3 T. Magn Reson Med. 2013;70:184–92. doi: 10.1002/mrm.24435. [DOI] [PubMed] [Google Scholar]
- 12.Syha R, Martirosian P, Ketelsen D, Grosse U, Claussen CD, Schick F, Springer F. Magnetization transfer in human Achilles tendon assessed by a 3D ultrashort echo time sequence: quantitative examinations in healthy volunteers at 3T. Rofo. 2011;183:1043–50. doi: 10.1055/s-0031-1281742. [DOI] [PubMed] [Google Scholar]
- 13.Hodgson RJ, Evans R, Wright P, Grainger AJ, O’Connor PJ, Helliwell P, McGonagle D, Emery P, Robson MD. Quantitative magnetization transfer ultrashort echo time imaging of the Achilles tendon. Magn Reson Med. 2011;65:1372–6. doi: 10.1002/mrm.22715. [DOI] [PubMed] [Google Scholar]
- 14.Grosse U, Syha R, Hein T, Gatidis S, Grozinger G, Schabel C, Martirosian P, Schick F, Springer F. Diagnostic value of T1 and T2* relaxation times and off-resonance saturation effects in the evaluation of achilles tendinopathy by MRI at 3T. J Magn Reson Imaging. 2014 doi: 10.1002/jmri.24657. in-press. [DOI] [PubMed] [Google Scholar]
- 15.Diaz E, Chung CB, Bae WC, Statum S, Znamirowski R, Bydder GM, Du J. Ultrashort echo time spectroscopic imaging (UTESI): an efficient method for quantifying bound and free water. NMR in Biomed. 2012;25:161–8. doi: 10.1002/nbm.1728. [DOI] [PubMed] [Google Scholar]
- 16.Techawiboonwong A, Song HK, Leonard MB, Wehrli FW. Cortical bone water: in vivo quantification with ultrashort echo-time MR imaging. Radiology. 2008;248:824–833. doi: 10.1148/radiol.2482071995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hammant B. The use of 4-point loading tests to determine mechanical properties. Composites. 1971;2:246–249. [Google Scholar]
- 18.Currey JD. Physical characteristics affecting the tensile failure properties of compact bone. J Biomech. 1990;23:837–44. doi: 10.1016/0021-9290(90)90030-7. [DOI] [PubMed] [Google Scholar]
- 19.Martirosian P, Boss A, Deimling M, Kiefer B, Schraml C, Schwenzer NF, Claussen CD, Schick F. Systematic variation of off-resonance prepulses for clinical magnetization transfer contrast imaging at 0.2, 1.5, and 3. 0 tesla. Invest Radiol. 2008;43:16–26. doi: 10.1097/RLI.0b013e3181559949. [DOI] [PubMed] [Google Scholar]
- 20.Springer F, Martirosian P, Machann J, Schwenzer NF, Claussen CD, Schick F. Magnetization transfer contrast imaging in bovine and human cortical bone applying an ultrashort echo time sequence at 3 Tesla. Magn Reson Med. 2009;61:1040–8. doi: 10.1002/mrm.21866. [DOI] [PubMed] [Google Scholar]
- 21.Ong HH, Wright AC, Wehrli FW. Deuterium nuclear magnetic resonance unambiguously quantifies pore and collagen-bound water in cortical bone. J Bone Miner Res. 2012;27:2573–81. doi: 10.1002/jbmr.1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Horch RA, Gochberg DF, Nyman JS, Does MD. Non-invasive predictors of human cortical bone mechanical properties: T(2)-discriminated H NMR compared with high resolution X-ray. PLoS One. 2011;6:e16359. doi: 10.1371/journal.pone.0016359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McCalden RW, McGeough JA, Barker MB, Court-Brown CM. Age-related changes in the tensile properties of cortical bone. The relative importance of changes in porosity, mineralization, and microstructure. J Bone Joint Surg Am. 1993;75:1193–205. doi: 10.2106/00004623-199308000-00009. [DOI] [PubMed] [Google Scholar]
- 24.Diab T, Vashishth D. Effects of damage morphology on cortical bone fragility. Bone. 2005;37:96–102. doi: 10.1016/j.bone.2005.03.014. [DOI] [PubMed] [Google Scholar]
- 25.Du J, Carl M, Bae WC, Statum S, Chang EY, Bydder GM, Chung CB. Dual inversion recovery ultrashort echo time (DIR-UTE) imaging and quantification of the zone of calcified cartilage (ZCC) Osteoarthritis Cartilage. 2013;21:77–85. doi: 10.1016/j.joca.2012.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bashoor-Zadeh M, Li C, Sun W, Aznarez-Sanado M, Wright AC, Zavaliangos A, Rajapakse CS. Simple ultrashort echo time MRI measure associated with cortical bone porosity. ISMRM 21th Scientific Meeting & Exhibition; Salt Lake City, Utah, USA. 2013; p. 1599. [Google Scholar]
- 27.Li C, Seifert AC, Rad HS, Bhagat Y, Rajapakse CS, Sun W, Benny Lam SC, Wehrli FW. Cortical Bone Water Concentration: Dependence of MR Imaging Measures on Age and Pore Volume Fraction. Radiology. 2014:132585. doi: 10.1148/radiol.14132585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Henkelman RM, Huang X, Xiang Q, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med. 1993;29:759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- 29.Ramani A, Dalton C, Miller DH, Tofts PS, Barker GJ. Precise estimation of fundamental in-vivo MT parameters in human brain in clinically feasible times. Magn Reson Imaging. 2002;20:721–731. doi: 10.1016/s0730-725x(02)00598-2. [DOI] [PubMed] [Google Scholar]
- 30.Hodgson RJ, Evans R, Wright P, Grainger AJ, O’Connor PJ, Helliwell P, McGonagle D, Emery P, Robson MD. Quantitative magnetization transfer ultrashort echo time imaging of the Achilles tendon. Magn Reson Med. 2011;65:1372–6. doi: 10.1002/mrm.22715. [DOI] [PubMed] [Google Scholar]
- 31.Woessner DE, Zhang S, Merritt ME, Sherry AD. Numerical solution of the Bloch equations provides insights into the optimum design of PARACEST agents for MRI. Magn Reson Med. 2005;53:790–799. doi: 10.1002/mrm.20408. [DOI] [PubMed] [Google Scholar]
- 32.Currey JD, Foreman J, Laketic I, Mitchell J, Pegg DE, Reilly GC. Effects of ionizing radiation on the mechanical properties of human bone. J Orthop Res. 1997;15:111–7. doi: 10.1002/jor.1100150116. [DOI] [PubMed] [Google Scholar]