Algorithm for planning a double-jaw orthognathic surgery using a computer-aided surgical simulation (CASS) protocol. Part 2: three-dimensional cephalometry

Abstract

Three-dimensional (3D) cephalometry is not as simple as just adding a ‘third’ dimension to a traditional two-dimensional cephalometric analysis. There are more complex issues in 3D analysis. These include how reference frames are created, how size, position, orientation and shape are measured, and how symmetry is assessed. The main purpose of this article is to present the geometric principles of 3D cephalometry. In addition, the Gateno–Xia cephalometric analysis is presented; this is the first 3D cephalometric analysis to observe these principles.

Introduction

Since 1931, two-dimensional (2D) radiographic cephalometry has been used to measure the shape, size, position, and orientation of the different facial units¹. These measurements have been made on standardized plain radiographs called cephalograms. In these cephalograms, which can be lateral or frontal, all the facial structures are projected onto a single sagittal or coronal plane. There are two fundamental problems associated with traditional 2D cephalometry^2–6. The first is that many important parameters cannot be measured. The second is that most 2D cephalometric measurements are distorted in the presence of facial asymmetry^2,3.

The recent introduction of cone beam computed tomography (CBCT) in an office setting has facilitated the acquisition of three-dimensional (3D) images with lower amounts of radiation. 3D cephalometry can correct the problems associated with its 2D counterpart. However, 3D cephalometry is more complex than just adding a third dimension to a 2D analysis⁴. There are complex issues in 3D cephalometry^2,3. These include how reference systems are created, how size, position, orientation and shape are measured, and how symmetry is assessed. Understanding these basic principles is essential for the correct use of 3D cephalometry. The main purpose of this article is to present the geometric principles of 3D cephalometry. In addition, the Gateno–Xia cephalometric analysis is presented; this is the first 3D cephalometric analysis to observe these principles.

Basic principles of 3D cephalometry

Clinicians use cephalometry to determine the configuration of the face. An ideal cephalometric analysis should measure the five geometric attributes of each facial unit. These include size, position, orientation, shape, and symmetry. Three of these measurements – position, orientation, and symmetry – need a reference frame^2–4,7,8. The reference frames and how the different geometric attributes should be measured are discussed below.

Reference frames

In 3D cephalometry, measuring position, orientation, and symmetry requires several different reference frames. The main reference frame, ‘global’, encompasses the whole head (face and cranium). It can also be called the ‘global coordinate system’. Subordinate reference frames, ‘local’, belong to each facial unit (e.g., maxilla, mandible, and chin). Both reference frames are coordinate systems made up of three mutually perpendicular planes. In cephalometry, there is only one global reference frame and several ‘local coordinate systems’—one for each facial unit. The local coordinate systems can also be called ‘local reference frames’. Although the terms ‘reference frame’ and ‘coordinate system’ can be used interchangeably, in order to avoid confusion for the reader, the term ‘reference frame’ referring to the whole head, and the term ‘coordinate system’ referring to each facial unit, are used in the following text.

A simple way of envisioning the difference between the global and local coordinate system is to imagine a room with a toppled chair. In this scenario, the reference frame of the room is the global coordinate system. It is perfectly aligned to our surroundings: roof is up, floor is down, and walls are east, west, north, and south. The toppled chair, lying in the middle of the room, has its local coordinate system aligned with the top, front, and side of the chair. Only the chair's features define the local coordinate system, which is independent of its spatial position or orientation. The global reference frame and the chair's local coordinate systems were aligned with each other when the chair was standing upright and turned south. However, in this example, when the chair is laid down on its side, the global reference frame and local coordinate system are not aligned. The details of how global and local coordinate systems are used in 3D cephalometry are described below.

Global reference frame for the whole head

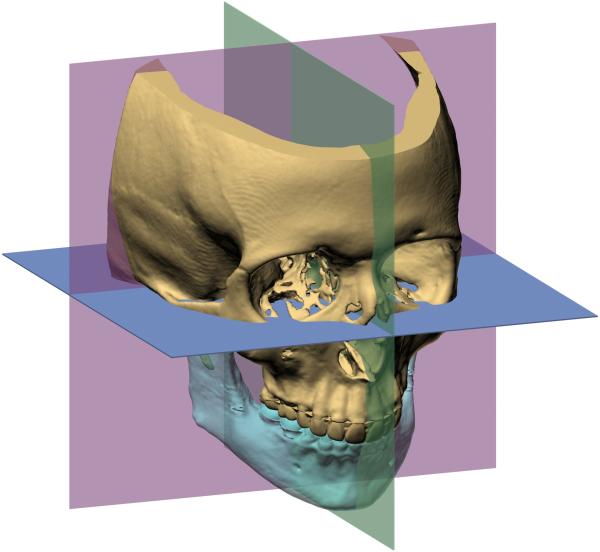
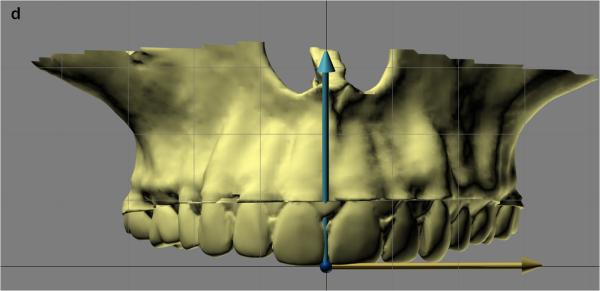
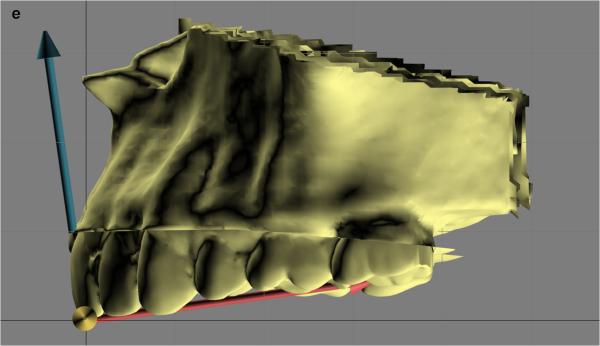
The reference frame for the whole head is composed of the axial, coronal, and sagittal planes. These planes are mutually perpendicular (Fig. 1). The sagittal plane divides the head into right and left halves. The axial plane divides the head into upper and lower halves. The coronal plane divides the head into front and back halves. Traditionally, two methods have been used to define the reference frame for the whole head: anatomical landmark and neutral head posture (NHP).

Fig. 1.

Global reference frame (coordinate system) for the whole head. The reference frame for the whole head includes three orthogonal planes: midsagittal (green), coronal (pink), and axial (blue).

The anatomical landmark method is simple if the face has perfect symmetry. The Frankfort horizontal is constructed using both porions and both orbitales. The sagittal plane is constructed using any three midline landmarks, and the coronal plane, which is made perpendicular to the other planes, is aligned to both porions.

Unfortunately, no human face is perfectly symmetrical. In facial asymmetry, it is complex to use landmarks to construct the reference planes of the face. Let us first consider the Frankfort horizontal. Four points define this plane: right orbitale, left orbitale, right porion, and left porion. However, in facial asymmetry, these points are not coplanar, which creates a dilemma. A plane can be built using any three points. Which three of the four Frankfort points should be used? Each combination results in a different plane. To solve this problem, a best-fitting plane among the four points may be constructed. This is feasible when the head has minor asymmetries. However, in deformities like hemifacial microsomia, this best-fitting method will alter the axial plane by adding a distorted landmark into the equation.

Now let us consider the sagittal plane. This plane can be constructed using three midline landmarks, three pairs of bilateral landmarks, or even just one pair of bilateral landmarks. In the first case, the midline landmarks lie on the sagittal plane. In the second case, the pairs of corresponding bilateral landmarks are used to calculate three midpoints that lie on the sagittal plane. In the last case, a line is drawn between the single pair of bilateral landmarks and the sagittal plane is constructed perpendicular to this line, passing through the midpoint located between the right and left landmarks. In facial asymmetry, any combination of three midline points, any combination of three pairs of bilateral points, or any pair of bilateral points will produce a different sagittal plane. In facial asymmetry, the landmark method may create hundreds of sagittal planes. To solve this problem, a best-fit plane may be used to average all the planes, but the distorted landmarks will skew the plane, making it useless. Besides, in facial asymmetry, a landmark-based sagittal plane will not necessarily be perpendicular to Frankfort horizontal, a fundamental requirement of a Cartesian coordinate system. Finally, there is no point in discussing the coronal plane because if the axial and sagittal planes cannot be constructed accurately, the entire reference frame will be inaccurate.

The NHP method^4,8,9 can solve the problems associated with the anatomical landmark method. This posture is unaltered by most facial deformities and can readily be used to create a reference frame. In NHP, a subject stands upright looking straight forward (visual axis is parallel to the ground). The head is not tilted, flexed, nor rotated. Once in this posture, the reference frame of our surroundings (i.e., our world) is transferred to the patient. A plane that parallels the ground (horizontal) turns into the axial plane. Two orthogonal planes, aligned with gravity, turn into the sagittal and coronal planes. The horizontal plane is moved up and down until it divides the face into the upper and lower halves, becoming the axial plane. The vertical planes are moved right and left, and rotated around their vertical axes until one of them divides the face into right and left halves, becoming the midsagittal plane. The other is moved forward and backward until it divides the face into anterior and posterior halves, becoming the coronal plane.

In 3D cephalometry, there are two ways of orienting a head image to the NHP. The first is to scan the head while in the NHP. The second is to scan the head in an arbitrary orientation, and then reorient the image to the NHP. Spiral computed tomography (CT) scanners require the patient to be in a supine position during image acquisition. Thus, it is impossible to position the patient in the NHP during scanning. CBCT scanners are better, as the patient's head can be upright. Yet chin rests or forehead holders, which are necessary to ensure immobility during scanning, may distort this posture. Therefore, it is more practical to reorient the CT or CBCT model to the NHP after scanning. Currently, three methods are used for this purpose: standardized photographs⁴, laser levels¹⁰, and digital orientation sensors^4,8,9.

In the first method, standardized frontal and lateral facial photographs are taken with the patient standing in the NHP. A plumb line hangs in the background as a true vertical line. A camera is calibrated so its focal plane is perpendicular to the ground. Before the photos can serve as visual guides to manually reorient the 3D-CT models, they are rotated to the true vertical using the plumb line in the background. While this method is subjective, it is valuable for verifying the outcome of the more advanced methods described below.

In the second method, a self-leveling laser is used to simultaneously project horizontal and vertical crosshair lines¹¹. When the patient is in NHP, the horizontal laser is projected onto the malar eminence level, while the vertical laser is simultaneously projected onto the midsagittal plane. Two radiopaque stickers are taped on the skin serving as reference markers along the horizontal laser line, and the other two are taped on the vertical line. The patient then undergoes CBCT along with the reference markers. After the 3D head model is generated, the reference markers are connected to the lines, which are then used to build an anatomical reference frame. A potential disadvantage of this method is that it relies on skin markers that can easily be displaced.

The third method of orienting a head to NHP is to reorient a CT/CBCT model to NHP using a digital orientation sensor^4,8,9. The orientation sensor is attached to a bite-jig. The attachment of the sensor to the bite-jig is designed to ensure that the sensor has the same orientation as the bite-jig frame. While the patient is in NHP with the bite-jig between the teeth and the sensor in front of the face, the pitch, roll, and yaw of the bite-jig frame are recorded. After a CT/CBCT facial model is generated, the recorded sensor orientation is applied to the bite-jig frame, reorienting the head to the recorded NHP. Afterwards, the reference frame can easily be defined. The axial plane is a horizontal plane that passes through the right and left porions, the sagittal plane is the vertical plane that best divides the head into right and left halves, and the coronal plane is a vertical plane that is perpendicular to the other two planes, passing through the right and left porions. The advantage of this method is that it has been validated in vitro^9,12,13 and clinically^8,14,15.

It is important to note that there also are problems with the NHP method. Some patients may have difficulty aligning their heads in the NHP. This is particularly true in young children and in patients who have neuromuscular disorders, torticollis, or eye muscle imbalances. In addition, even within the same patient, there are temporal variations in the NHP. Based on published studies, the intra-class reproducibility error of establishing NHP is less than 2°, an error that is not considered clinically significant^16–18. However, these studies only examined the reproducibility in pitch. The reproducibilities in roll and yaw have not yet been studied formally. If the same is true for roll, a 2° variation may cause significant problems. For example, if a symmetrical patient during NHP recording rolls her head around nasion by 2°, it will cause the upper incisal midpoint and the pogonion to shift 2.8 mm and 4.2 mm, respectively (assuming that the distance between nasion and the upper central incisor is 80 mm, and the distance between nasion and pogonion is 120 mm). Thus one should use the NHP method with caution.

In the authors’ clinical practice, the digital orientation sensor method is used routinely to place the CT head model in the NHP. At the same time, calibrated photographs are also used to cross-validate the correctness of the CT model NHP. Currently, the Surgical Planning Laboratory of the Houston Methodist Research Institute is developing a new method to calculate the reference frame for the face mathematically. The goal is to eliminate the errors caused by the existing methods.

Local coordinate system for each facial unit

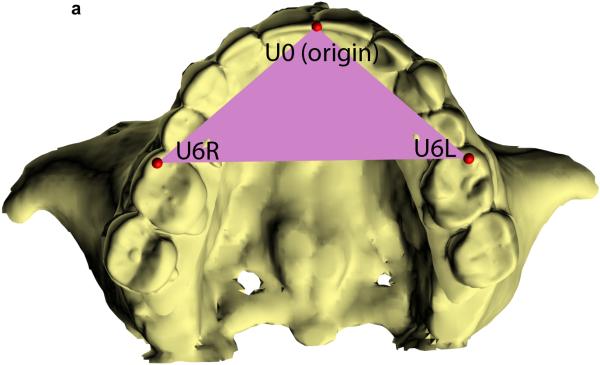
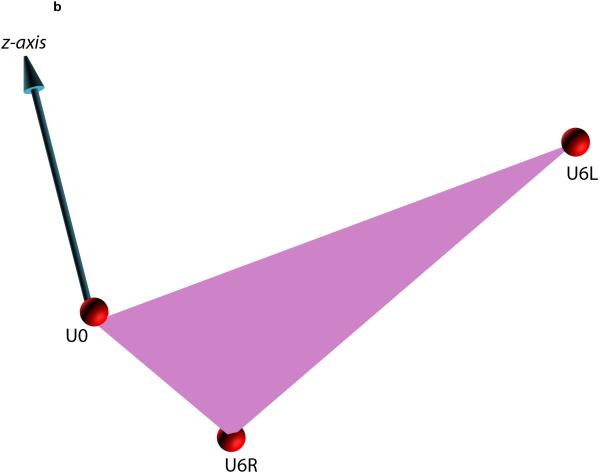
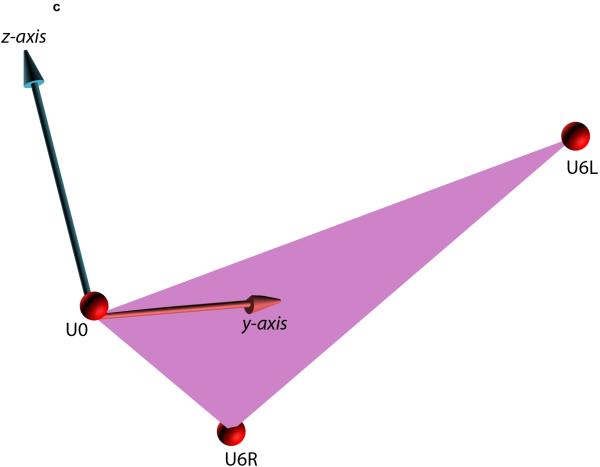
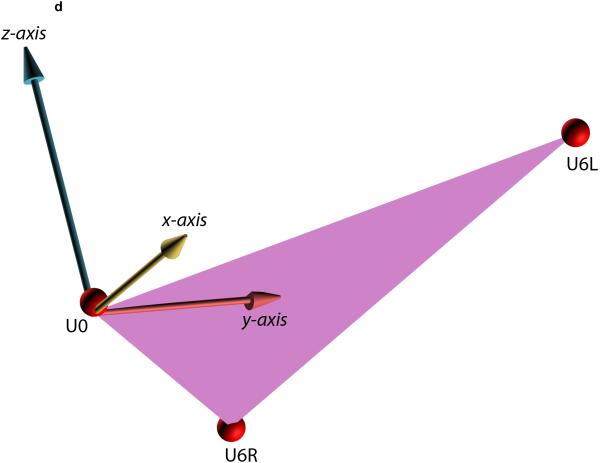
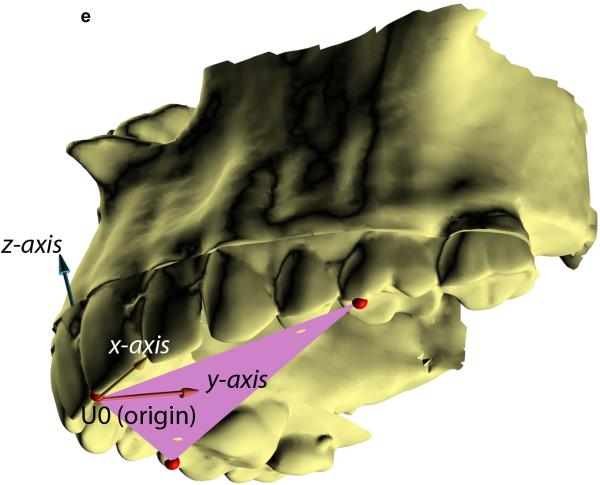
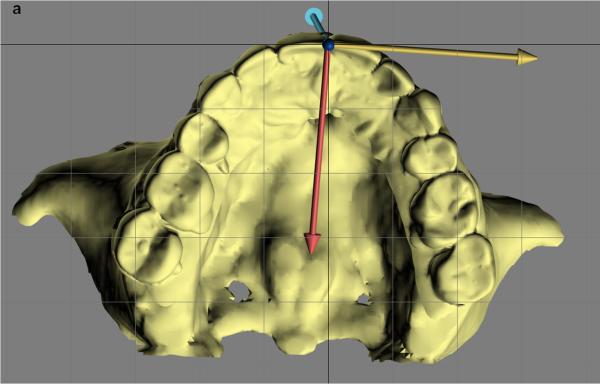
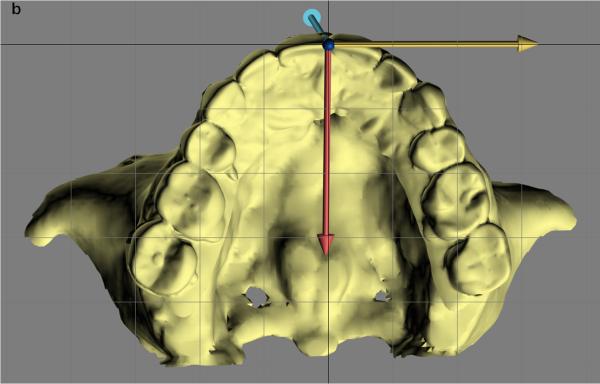
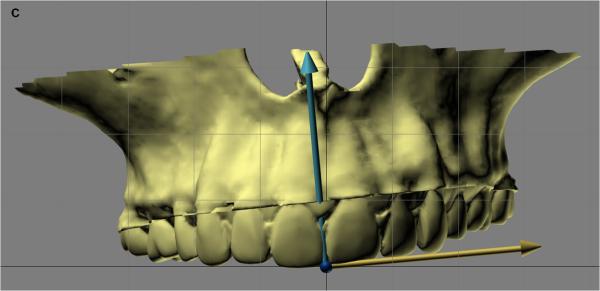
Measuring the orientation of the different facial units (e.g., maxilla, mandible) makes it necessary to build local coordinate systems for each unit. A simple method for building local coordinate systems for the jaws uses an occlusal triangle^2,4. This method is best illustrated using an example (Fig. 2). In this example, a local coordinate system is built for the maxilla. In the first step (Fig. 2A), a triangle is constructed on the maxillary dentition. The vertices of the triangle are the right and the left mesiobuccal cusps of the first molars and the incisal midpoint (the point located on the dental midline at the level of the incisal edges). The incisal midpoint is selected as the origin of the local coordinate system. The computer then calculates a vector that arises from the origin and is perpendicular to the surface of the triangle (occlusal plane, Fig. 2B). This vector becomes the vertical (z) axis of the local coordinate system. The computer next calculates the local anteroposterior (y) axis. This axis originates at the incisal midpoint and bisects the base of the triangle (the line that goes from one first molar to the other) (Fig. 2C). In the final step (Fig. 2D, E), the computer calculates the transverse (x) axis of the local coordinate system. This axis rises from the incisal midpoint pointing perpendicular to z and y axes.

Fig. 2.

Defining the local coordinate system for a facial unit using the triangular method. This example illustrates how the triangular method is completed for the maxilla. (A) In the first step, a maxillary occlusal plane is defined by three points: right mesiobuccal cusp (U6R), left mesiobuccal cusp (U6L), and central dental midline (U0). U0 is used as the origin of the maxillary local coordinate system. (B) In the second step, the computer calculates a normal vector for this plane. This vector represents the vertical (z) axis of the local coordinate system. (C) In the third step, the computer calculates the local anteroposterior (y) axis. This axis passes through U0 and bisects a line that goes from U6R to U6L. (D) In the last step, the computer calculates the transverse (x) axis of the local coordinate system. This axis is perpendicular to z and y axes. (E) 3D view of the maxillary local coordinate system.

Currently, the Surgical Planning Laboratory is investigating an approach that uses a principal component analysis (PCA) to automatically construct local coordinate systems. Unlike the triangle method, which uses only three points, PCA can estimate the x, y, and z coordinate axes using a larger group of points, e.g., all the cusps of the maxillary teeth. Thus, the PCA approach may estimate more accurately the local coordinate systems of the jaws.

Size measurements

Measuring size in 3D cephalometry is straightforward. Size is an intrinsic property of an object that is independent of the space it occupies. We can measure size in 3D space using linear measurements (e.g., length, width, and height), areas, or volumes. In 3D cephalometry, linear measurements of size are calculated as the distance between two points (landmarks) located in 3D space. For example the maxillary width can be measured as the distance between the two first molars.

Position measurements

Position refers to the location of a point in space. Its measurement is always relative and requires a reference frame. In 3D cephalometry, we need to determine the position of the jaws, which are complex 3D objects made up of thousands of points. Each point that makes up a jaw has a different position. In order to measure the position, we must select a point to represent the whole jaw. However, since there is no perfect point, clinicians have had to use several points to represent the jaws. For example, the anteroposterior position of the maxilla has been measured at the anterior nasal spine (ANS), point A, and the upper incisal midpoint.

Measuring position in one, two, and three dimensions requires one, two, and three numbers. Thus, any system that measures jaw position in 3D space must use three numbers. The position of an object can be expressed either by three distances (3D Cartesian coordinate system), or by two distances and one angle (cylindrical coordinate system), or by one distance and two angles (spherical coordinate system). Mathematically, these three coordinate systems are all convertible. Since the spherical coordinate system is more complex than the other two and is seldom used in 3D cephalometry, it is not discussed in this article.

A 3D Cartesian coordinate system consists of three mutually perpendicular axes that cross each other at an origin. The transverse axis is x, the anteroposterior axis is y, and the superoinferior axis is z. Each pair of axes forms a reference plane. The absolute position of any landmark is expressed using three coordinates (x, y, z), which represent the transverse, anteroposterior, and vertical positions, respectively. The relative position between two landmarks can be calculated easily. For example, if the anteroposterior coordinate of pogonion is 62 mm and the anteroposterior coordinate of nasion is 60 mm, pogonion is then 2 mm in front of nasion (62 – 60 = 2 mm). The same is true for relative vertical and transverse positions.

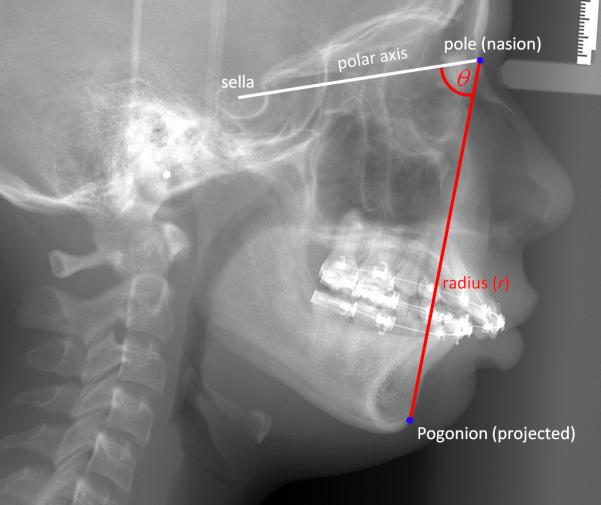
In 2D cephalometry, we often use the combination of one angle and one distance to determine the position of a point. This type of measurement typifies a ‘polar’ coordinate system (Fig. 3). A polar system resides on a plane and consists of a fixed point (the pole) and a ray (the polar axis). From the pole, the polar axis points in a fixed direction. To measure the position of a point in a polar system, a line segment (called the radius, r) is first drawn from the point that we are locating to the pole. The position of the point is then determined by measuring the length of the radius (r) and the angle theta (θ) between the radius and the polar axis. The position of a point in 2D cephalometry is expressed using two coordinates (r, θ).

Fig. 3.

Measuring the 2D position of a point using the polar coordinate system. In this example, the 2D position of pogonion is being measured in relation to sella–nasion. The origin of the coordinate system, the pole, is nasion. The polar axis is the ray that originates on nasion, pointing at sella. The angle θ of sella–nasion–pogonion represents the anteroposterior position of the chin relative to the anterior cranial base (sella–nasion). The radius r is the distance between nasion and pogonion, representing the vertical position of the chin.

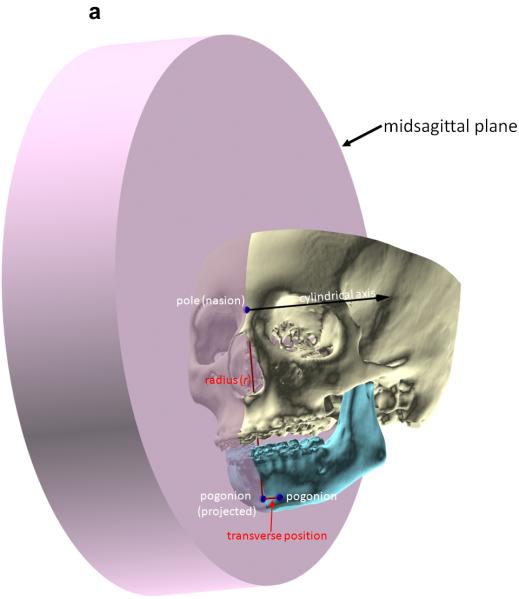
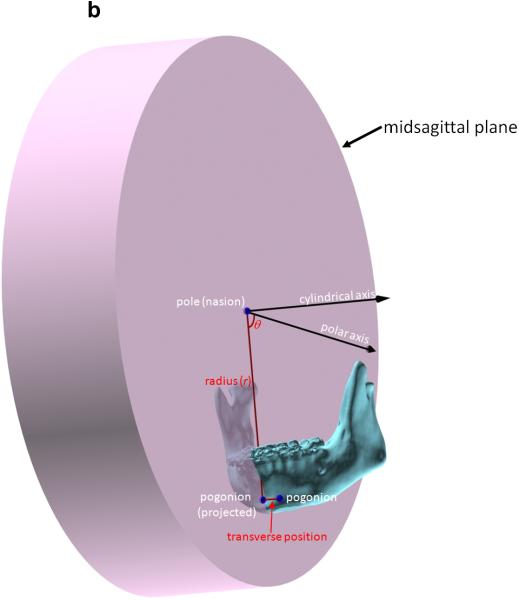
In 3D cephalometry, the same measurements are completed in a cylindrical system by adding a cylindrical axis to the 2D polar system (Fig. 4). The cylindrical axis is perpendicular to the plane of the polar system and passes through the pole. In order to measure the position of a point in a cylindrical system, the point is first projected onto the plane of the polar system, along the cylindrical axis. On this plane, the first two coordinates (r, θ) are expressed in the same fashion as in the polar system. The third coordinate is the distance (z) between the point and its projected point on the plane of the polar system. Thus, the position of a point in 3D cephalometry is expressed using three coordinates (r, θ, z), including two distances and one angle.

Fig. 4.

Measuring the 3D position of a point using the cylindrical coordinate system. The cylindrical system is the 2D polar system with the addition of a cylindrical axis. In this example, the 3D position of pogonion is being measured in relation to sella– nasion. As in the 2D polar system, the origin (pole) of the cylindrical system is nasion. The polar axis is the ray that originates on nasion and points at sella, and the cylindrical axis is perpendicular to the sagittal plane and crosses nasion. The position of pogonion is determined by first projecting it onto the sagittal plane, then by measuring the radius (r) of nasion–pogonion distance and theta (θ) sella–nasion–pogonion on the plane. The third coordinate (z) is the positive or negative transverse distance between pogonion and its projection on the plane of the polar system. (A) The 3D position of pogonion being measured in the cylindrical system. (B) Details of the same cylindrical system by hiding the midface.

Orientation measurements

Orientation is relative. Although there are many different ways to measure the orientation in 3D cephalometry, we usually measure the orientation as three rotations following a specific order. The measurement is done by rotating a facial unit from its reference alignment to its current placement. The reference alignment is the (global) coordinate system of the whole head, while the current placement is the (local) coordinate system of a facial unit. The sequential rotations are yaw, roll, and pitch. In our approach, these rotations occur around the axes of the local coordinate system, which is the one that belongs to the facial unit being measured. Yaw is the rotation around the vertical (z) axis. Roll is the rotation around the anteroposterior (y) axis. Pitch is rotation around the transverse (x) axis.

The order in which one measures pitch, roll, and yaw is important. These rotations are not commutative and the result of following the pitch–roll–yaw order is different from the result of following the yaw–roll–pitch order (Fig. 5)². For 3D cephalometry, we recommend a yaw–roll–pitch sequence. Most facial units (i.e., maxilla and mandible) normally have some degree of pitch, while their ideal roll and yaw is zero. This strategy is helpful in that it minimizes the yaw and roll angles.

Fig. 5.

Measuring the yaw, roll, and pitch of the facial unit. In this example, yaw, roll, and pitch of a maxilla are measured by comparing the orientation of the local coordinate system (colored arrows) with the global coordinate system (black lines). The origin of the local coordinate system is U0. The yellow arrow indicates the x-axis, the red arrow indicates the y-axis, and the blue arrow indicates the z-axis. (A) The first step is to measure the yaw (angle between x-axis of the local coordinate system and x-axis of the global coordinate system as they project on the axial plane, submental vertex view). (B) After yaw has been calculated, the algorithm rotates the local coordinate system around the origin aligning local x-axis to global x-axis (removing yaw, submental vertex view). (C) Frontal view of maxilla at the same orientation as in B. Once yaw is removed, the next step is to measure the roll (angle between local z-axis and global z-axis as they project on the coronal plane). (D) After roll has been calculated, the algorithm rotates the local coordinate system around the origin aligning local z-axis to global z-axis (removing roll, frontal view). (E) The last step is to measure the pitch (angle between local y-axis and global y-axis as they project on the sagittal plane, right view).

Shape measurements

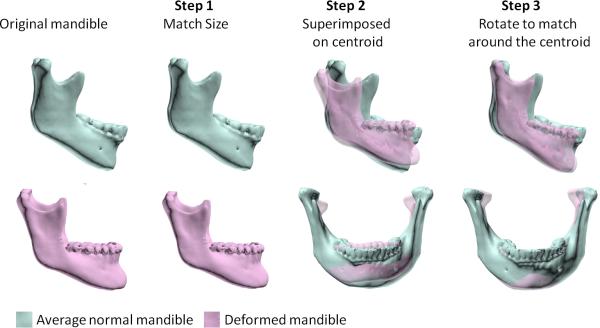
By definition, shape is the geometric attribute of an object that is not size, position, or orientation¹⁹. Thus, the measurement of shape should not be influenced by size, position, or orientation. A method that follows this rule is a Procrustes analysis²⁰. In this analysis, shape is evaluated by comparing two objects after both have been scaled to the same size, placed in the same location, and rotated to the best possible alignment²⁰.

Fig. 6 shows the example of a deformed mandible (pink) that is being compared with an average mandible (blue). Both mandibles differ in size, position, orientation, and shape. To assess shape, a Procrustes superimposition first scales the mandibles to the same size. It then places both mandibles in the same position (both centroids at the origin of the Cartesian coordinate system). Finally, it rotates the deformed mandible until it is best aligned with the normal mandible. After the differences in size, position, and orientation are removed, one can better appreciate the distortion of the deformed mandible. In this example, the deformed mandible has an obtuse gonial angle and a short ramus height.

Fig. 6.

Shape analysis using Procrustes superimposition. Human mandibles always have a different size, position, orientation, and shape from an average normal mandible – the normative data. In this example, the top mandible in blue is an average normal mandible, while the lower one in pink is deformed. Both mandibles differ in size, position, orientation, and shape. In the first step, the subject's mandible is scaled to the same size as the normal mandible. In the second step, the subject's mandible is translated to the normal mandible by perfectly registering the two centroids together. In the third step, the subject's mandible is rotated around its centroid to best fit the normal mandible. After the differences in size, position, and orientation are removed, the remaining component is the shape difference. In this example, the mandible has an obtuse gonial angle and relatively narrow body and ramus.

Symmetry measurements

The two elements that relate to symmetry are ‘object symmetry’ and ‘symmetrical alignment’. Object symmetry refers to the intrinsic – mirror – symmetry that each facial unit should have. Symmetric alignment refers to the alignment of each facial unit with the midsagittal plane of the face.

Object symmetry

The intrinsic symmetry of the dental arches can be assessed using a simple occlusal triangle^2,4,21,22. The triangle is constructed by connecting the incisal midpoint and the mesiobuccal cusps of the first molars. The triangle is isosceles in patients with symmetric dental arches, with two equal lateral sides and two equal base angles. The triangle is scalene in patients with asymmetric dental arches, with three different sides and three different angles. The degree of intrinsic asymmetry of a dental arch is proportional to the difference between the basal angles: the larger the difference, the greater the asymmetry. Alternatively, one can measure the intrinsic asymmetry by comparing the length of the lateral sides of the triangle. The greater the absolute difference between the sides of the triangle, the greater the asymmetry.

One can also measure more elaborately the intrinsic symmetry of any facial unit using a Procrustes analysis of symmetry. It begins by dividing the unit into two half-forms: right and left. In order to divide the form, the landmarks of the facial unit are divided into two groups: the right set contains all the right landmarks as well as all the midline landmarks; the left set contains all the left landmarks and again the midline landmarks. Next, we superimpose the two half-forms using a series of transformations. However, prior to this step, we have to pick one half-form to be the object of the transformations and the other to be the target. Which half-form (right or left) becomes the object is inconsequential. The first transformation reflects (flips) the object half-form around its anteroposterior axis, creating a mirror image. This operation makes the half-forms comparable. The second transformation centers both the half-forms on a Cartesian coordinate system. In order to center the half-forms, we first have to determine their centroids. Then, we translate both forms, so that their centroids are on the origin of the Cartesian system. The third transformation rotates the object half-form around its centroid until the form is aligned to the target. The final alignment is reached when the sum of all the distances between the corresponding landmarks of the right and the left half-forms is minimal. To quantify the degree of asymmetry for each landmark, we measure the distances between analogous right and left landmarks. These distances are (directly) proportional to the degree of asymmetry.

Symmetrical alignment

The other element of the symmetry measurement is the symmetrical alignment. Facial asymmetry can be the result of misalignment of a facial unit about the midsagittal plane. When a unit is not symmetrically aligned, the degree of misalignment (i.e., asymmetry) can be quantified by measuring the transformations (maneuvers) that are necessary to realign it. The three parameters of symmetric alignment are transverse translation, roll, and yaw. Transverse translation places the midpoint on the midsagittal plane. Roll rotates the unit around the midpoint until right and left landmarks are vertically aligned. Yaw rotates the unit around the midpoint, minimizing the distance differences between the corresponding bilateral landmarks and the coronal and midsagittal reference planes. Zero is the ideal value for transverse position, yaw, and roll.

Gateno–Xia cephalometric analysis

In the authors’ 3D cephalometric analysis, the measurements are displayed in a grid (Table 1)². Each row displays a different geometric property: object symmetry, shape, size, position, and orientation. The columns represent the individual facial units: e.g., maxilla, whole mandible, and chin.

Table 1.

Gateno–Xia 3D cephalometric analysis.

			Maxilla	Mandible
				Whole	Chin
Object symmetry
Shape
Size	Length
	Width
	Height
Position	Anteroposterior
	Vertical
	Transverse	Symmetrical alignment
Orientation	Yaw
	Roll
	Pitch

In the first part of the analysis, object symmetry, the intrinsic symmetry of each jaw, is first determined by a Procrustes analysis of symmetry or a triangle. In the second part, shape is measured using a 3D Procrustes analysis. Next, we assess the size by measuring the length, the width, and the height of each jaw. In the fourth part of the analysis, the jaw position is established in all directions: anteroposterior, vertical, and transverse. Depending on the preference of the clinician, the jaw can be measured using the 3D Cartesian system or the cylindrical system. Next, the orientation of the jaws is established by measuring the yaw, roll, and pitch. Finally, the symmetric alignment is determined by a composite of three measurements: transverse position, yaw, and roll.

Table 2 shows an example of the 3D cephalometric measurements that are currently used in our clinical practice. The 3D analysis also incorporates data gathered during the physical examination. The concept behind this analysis is to have all the necessary information needed to plan a surgery in a single report. In addition, this analysis is meant to be modular. The important aspects of the analysis are its concepts and structure. The measurements presented here are the ones that we have found useful. We encourage others to adapt this analysis to their needs by adding, deleting, or replacing measurements (rows) or by adding new elements or units (columns).

Table 2.

An example of 3D cephalometric analysis for orthognathic surgery (a shadowed space indicates input from the clinical examination).

			Maxilla			Mandible
						Whole			Chin
			Parameter	Patient	Norm	Parameter	Patient	Norm	Parameter	Patient	Norm
Object symmetry			Basal angle discrepancy of upper dental arch		0°	Basal angle discrepancy of lower dental arch		0°	Basal angle discrepancy of chin inferior border		0°
						Basal angle discrepancy of mandibular inferior border		0°
Shape			Procrustes analysis			Procrustes analysis
						Right gonial angle (right Co–Go–Me on LMSP)		M 121.4 ± 5.6°a F 123.7 ± 5.0°a
						Left gonial angle (left Co–Go–Me on LMSP)		M 121.4 ± 5.6°a F 123.7 ± 5.0°a
Size	Length		ANS–PNS		M 53.8 ± 3.3 mm F 49.4 ± 2.2 mm	Effective mandibular length (midpoint of right and left Co to Gn)		M 120.0 ± 4.9 mm F 109.9 ± 3.8 mm
	Width		Upper intermolar width (U6R–U6L at central fossae)		M 46.7 ± 2.6 mm F 43.9 ± 4.2 mm	Lower intermolar width (L6R–L6L at centroids)		M 43.0 ± 2.3 mm F 41.7 ± 2.3 mm
						Bicondylar width (right Co–left Co)		M 107.4 ± 4.5 mm F 104.1 ± 3.8 mm
						Bigonial width (right Go–left Go)		M 101.0 ± 6.0 mm F 94.1 ± 4.6 mm
	Height		U1E to nasal floor plane		M 28.2 ± 2.9 mm F 27.3 ± 3.1 mm	L1E to MP		M 40.0 ± 3.3 mm F 37.1 ± 2.9 mm
						Effective mandibular height (distance between midpoints of right and left Co and Go)		M 60.0 ± 4.1 mm F 54.0 ± 3.9 mm
Position	Anteroposterior		Optimal AP position (U1E to para-coronal plane passing through G′)		0 mm	Facial angle (N–Pg to AxP)		M 91.8 ± 4.8°b F 90.5 ± 3.1°b	Holdaway ratio [(L1E – NB)/(P – NB)]		1:1
			Maxillary depth (N–point A to AxP)		M 91.9 ± 3.0°b F 91.6 ± 3.2°b	Posterior airway space		11.0 ± 1.0 mm c
			Maxillomandibular discrepancy
			Parameter			Patient	Norm
			Wits appraisal				M –2.9 ± 3.5 mm F –2.5 ± 3.2 mm
			ANB (A–N–B)				M 2.5 ± 1.6° F 3.0 ± 1.8°
			Convexity of point A (point A to N–Pg)				M 0.3 ± 3.6 mm F 1.2 ± 3.0 mm
			Overjet				M 3.7 ± 2.1 mm F 2.9 ± 0.9 mm
	Vertical		Upper lip length		M 23.4 ± 2.5 mm F 21.2 ± 2.4 mm	Overbite		M 2.5 ± 1.4 mm F 3.2 ± 1.1 mm
			Incisal show at rest		2–5 mm	Lower facial height (ANS–Xi–PM on LMSP)		47 ± 4°d (Ricketts norm)
			Gingival smiling line		M –0.8 ± 2.4 mm F 0.7 ± 2.1 mm
			Incisal attrition		0 mm
			Delayed passive eruption		0 mm
	Transverse	Symmetrical alignment	U1E to MSP		0 mm	L1E to MSP		0 mm	Pg to MSP		0 mm
Orientation	Yaw		Dental arch yaw		0°	Dental arch yaw		0°	Chin yaw		0°
						Basal yaw		0°
	Roll		Dental arch roll		0°	Dental arch roll Basal roll		0° 0°	Chin roll		0°
	Pitch		Dental arch pitch		9.3 ± 3.8°b,e	Dental arch pitch		9.3 ± 3.8°b,e	Pitch of chin inferior border		M 21.6 ± 5.7°b F 23.1 ± 5.0°b
			U1 to AxP		M 117.0 ± 6.9°b F 110.5 ± 9.1°b	Basal mandible pitch		M 21.6 ± 5.7°b F 23.1 ± 5.0°b
						L1 to MP		M 90.6 ± 9.1° F 90.8 ± 6.8°
						Inter-incisal angle (U1–L1)		M 130.8 ± 11.4° F 136.0 ± 11.1°

All the norms were established for Caucasian subjects with normal facial appearance. All the norms for symmetry analyses were based on the authors' opinion. The hard tissue norms were established by Bhatia and Leighton for 20-year-old subjects²³, with the exceptions of the following: the Holdaway ratio was based on Holdaway's opinion^24,25; intercondylar and intergonial distances were established by McNamara for 18-year-old subjects²⁶; maxillary occlusal plane inclination was established by Downs^27,28; the determination of optimal maxillary AP position was inspired by Andrews and based on the authors' clinical observation^29,30; and Ricketts norms were established by Ricketts for 9-year-old subjects^31–33. The soft tissue norms were established by Farkas for 20–26-year-old subjects³⁴, with the exception of the following: incisal show was based on the authors' opinion; lip measurements were established by Peck et al. for 15.5-year-old subjects who were either in orthodontic treatment or post-treatment³⁵; and posterior airway space was established by Riley et al. for male subjects³⁶. The dental arch norms were established by Moyers et al. for 18-year-old subjects³⁷.

^aThe gonial angle is measured by projecting the landmarks articulare, gonion, and menton onto the mandibular local sagittal plane.

^bThe norm is calculated based on the Frankfort horizontal plane. In our 3D cephalometry, this is calculated based on the true horizontal. Please use with caution.

^cPosterior airway space should be measured as the shortest distance between the tongue base and the posterior pharyngeal wall. The norm was established by Riley for measuring the distance between the two landmarks: tongue base (TB, the intersection point of a line from point B through gonion and the base of the tongue), and posterior pharyngeal wall (PPWB, the intersection point of a line from point B through gonion and the base of the posterior pharyngeal wall). Please use with caution.

^dThis is the original Ricketts norm established for 9-year-old subjects. No age adjustment is required.

^eThis is the original Downs norm established for ‘occlusal plane to FH’ (‘cant of occlusal plane’ in Downs's original manuscript²⁷). The occlusal plane was defined as a line bisecting the occluded mesiobuccal cusps of the upper and lowers first molars and the incisal overbite. Please use with caution.

Abbreviations: A: point A (the deepest point on the concave outline of the upper labial alveolar process extending from the anterior nasal spine to prosthion); ANS: anterior nasal spine (the tip of the anterior nasal spine); AP: anteroposterior; AxP: the axial plane; B: point B (the deepest point on the bony curvature between the crest of the alveolus (infradentale) and pogonion); Co: condylion (the most posterosuperior point of the mandibular condyle); F: female; G′: soft tissue glabella (the most prominent or anterior point of the forehead on the midsagittal plane); Go: gonion (the midpoint at the mandibular angle); Gn: gnathion (the midpoint between the soft tissue pogonion and menton); L1: long axis of the mandibular central incisors (a line connecting the lower central incisal embrasure and the midpoint of the right and left lower central incisal apices); L1E: lower central incisal embrasure; L6L: mesiobuccal cusp of the mandibular left first molar; L6R: mesiobuccal cusp of the mandibular right first molar; LMSP: midsagittal plane of the local coordinate system for a given facial unit; M: male; Me: menton (the lowest point on the lower border of the mandibular symphysis); MP: mandibular plane (a plane constructed by the landmarks Me, right Go, and left Go); MSP: midsagittal plane of the reference frame for the whole head; N: nasion (the most anterior point on the frontonasal suture); nasal floor plane: a plane constructed by the landmarks ANS and right and left greater palatine foramen; Pg: pogonion (the most anterior point on the mandibular symphysis); PM: suprapogonion (a point at which the shape of the symphysis mentalis changes from convex to concave – also known as protuberance menti); PNS: posterior nasal spine; S: sella (the center of sella turcica); U1: long axis of maxillary central incisors (a line connecting the upper central incisal embrasure and the midpoint of right and left upper central incisal apices); U1E: upper central incisal embrasure; U6L: mesiobuccal cusp of the maxillary left first molar; U6R: mesiobuccal cusp of the maxillary right first molar; Xi: Ricketts Xi point (the midpoint of the right and left inferior alveolar nerve foramens).