Significance
Direct capture of CO2 from the air and its conversion to fuels using solar energy offers a means for mitigating global warming while also supporting future energy demands. Whereas natural photosynthesis converts CO2 and water to carbohydrates, this process is only 0.5–2.0% efficient and the energy content of the resulting biomass is low. Increasing CO2 levels in the atmosphere combined with rising energy needs motivate the search for an artificial photosynthetic system that is at least 10 times as efficient as that used by nature. Identification of light absorbers that provide a photocurrent density >10 mA cm-2 and a photovoltage >2 V are prerequisites for a >10% efficient artificial photosynthetic system.
Keywords: artificial photosynthesis, electrochemical CO2 reduction, solar-to-fuel efficiency, photoelectrochemical cells, photovoltaic-electrolyzer
Abstract
Thermodynamic, achievable, and realistic efficiency limits of solar-driven electrochemical conversion of water and carbon dioxide to fuels are investigated as functions of light-absorber composition and configuration, and catalyst composition. The maximum thermodynamic efficiency at 1-sun illumination for adiabatic electrochemical synthesis of various solar fuels is in the range of 32–42%. Single-, double-, and triple-junction light absorbers are found to be optimal for electrochemical load ranges of 0–0.9 V, 0.9–1.95 V, and 1.95–3.5 V, respectively. Achievable solar-to-fuel (STF) efficiencies are determined using ideal double- and triple-junction light absorbers and the electrochemical load curves for CO2 reduction on silver and copper cathodes, and water oxidation kinetics over iridium oxide. The maximum achievable STF efficiencies for synthesis gas (H2 and CO) and Hythane (H2 and CH4) are 18.4% and 20.3%, respectively. Whereas the realistic STF efficiency of photoelectrochemical cells (PECs) can be as low as 0.8%, tandem PECs and photovoltaic (PV)-electrolyzers can operate at 7.2% under identical operating conditions. We show that the composition and energy content of solar fuels can also be adjusted by tuning the band-gaps of triple-junction light absorbers and/or the ratio of catalyst-to-PV area, and that the synthesis of liquid products and C2H4 have high profitability indices.
The rapid changes in the global climate during the last century have been widely attributed to the anthropogenic emissions of carbon dioxide produced by combustion of fossil-based fuels (1). Today, the atmospheric concentration of CO2 is increasing at a rate of ∼1.8 ppm/y, and this rate is expected to increase unless efforts are made to reduce the consumption of fossil energy fuels and to develop means for producing carbon-based fuels sustainably (2). One means for achieving the latter goal is artificial photosynthesis––a process in which solar radiation is used to drive the reduction of CO2 to fuels (or fuel precursors) and chemicals (3, 4). In an artificial photosynthetic system one or more light absorbers are used to provide photogenerated electrons and holes for the photo/electrocatalytic reduction of carbon dioxide and water to a fuel, which is physically separated from the oxygen produced as a byproduct of water-splitting using an ion-conducting membrane. The overall efficiency with which such a system produces fuel depends on the identification, evaluation, and optimization of the components and system configuration.
The efficiency of solar-driven, electrochemical reduction of CO2 can be determined from the intersection of the current–voltage characteristics of the light absorber and the electrochemical load curve (5–7). This method has been used previously to calculate experimental and achievable solar-to-hydrogen (STH) efficiencies for water-splitting systems (8–10). The factors affecting the STH efficiency are the activities of the anode and cathode catalysts, the ohmic and Nernstian losses, and the semiconductor current–voltage characteristics (7, 11, 12). By contrast, the factors governing the efficiency of CO2 reduction systems are not well explored and optimized and, therefore, the solar-to-fuel (STF) efficiencies of most systems are typically <7%. For example, the highest reported STF efficiency for formic acid synthesis is 1.8% using a photovoltaic (PV)-electrolyzer (13) and 4.6% using a photoelectrochemical cell (PEC, 14, 15); and the STF efficiency for CO synthesis is 2% using a PV-PEC (16) and 6.5% using PV-electrolyzer (17). The reasons for such low STF efficiencies are (i) higher kinetic overpotential and polarization losses for CO2 reduction, and (ii) improper configuration of light absorbers to provide sufficient photovoltage and photocurrent density to drive CO2 reduction. The factors affecting the STF efficiencies are (i) the catalyst used for the CO2 reduction reaction (CO2RR), (ii) the catalyst used for the oxygen evolution reaction (OER), (iii) the electrolyte composition and concentration, (iv) the membrane or fuel separator, (v) the mechanism of CO2 supply, and (vi) the current–voltage characteristic of the light absorber(s). The properties of each component and the operating conditions affect the cell voltage and the STF efficiency (18).
The objectives of this study were to calculate the thermodynamic, achievable, and realistic STF efficiencies for CO2 reduction to fuels; to determine optimal band-gaps for alternative light-absorber configurations required to achieve efficient CO2 reduction; and to develop strategies for controlling the composition and energy density of solar fuels. The balance of this article is organized as follows. Theory describes the mathematical expressions used to determine the Shockley–Queisser (SQ) limits of multijunction light absorbers, the characteristics of electrochemical load curves for the OER and CO2RR, and how the properties of the light absorber(s) and catalysts are used to define the STF efficiency for CO2 reduction. Results and Discussion presents thermodynamic, achievable, and realistic STF efficiencies for different CO2RR catalysts and device configurations. Conclusions and Perspectives presents conclusions and future directions to overcome present difficulties in making an efficient solar-driven electrochemical device for CO2 reduction.
Theory
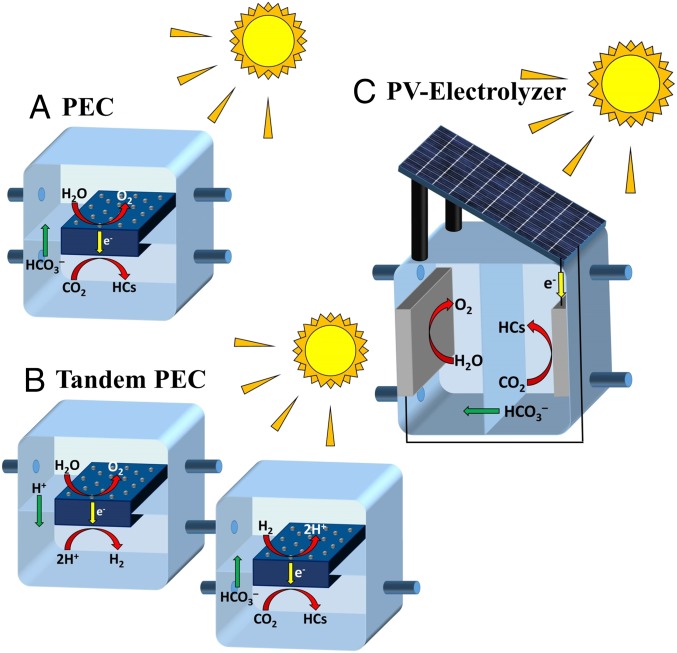
Three different limits of STF efficiencies for CO2 reduction are considered. These are the thermodynamic, achievable, and realistic STF efficiencies. The thermodynamic STF efficiency is defined for a system comprising an ideal light absorber powering an electrochemical reaction under adiabatic conditions. The achievable STF efficiency is defined for a system consisting of an ideal light absorber and real electrocatalysts for the OER and the CO2RR. The realistic STF efficiency is defined for three different configurations of solar-driven electrochemical cells: (i) PECs (multijunction light absorbers with electrocatalysts), (ii) tandem PECs, and (iii) a PV panel connected to an electrochemical cell (also referred to as a PV-electrolyzer). Fig. 1A shows an integrated PEC. In this scenario photogenerated electrons and holes are transported to a cathode and an anode, where they participate in the CO2RR and the OER, respectively. Fig. 1B shows a schematic of two PECs connected by a hydrogen transfer tube, which is referred to as a tandem PEC. Here the first PEC splits water and produces H2, and the second PEC oxidizes the H2 generated in the first PEC and uses the resulting protons to reduce CO2. The architecture of tandem PECs is similar to that of the PEC appearing in Fig. 1A. Fig. 1C shows a PV-electrolyzer scheme, in which a PV panel powers an electrochemical cell used for CO2 reduction.
Fig. 1.
Schematic of three different solar-driven electrochemical cell configurations for the reduction of CO2. (A) PEC, (B) tandem PEC, and (C) PV-electrolyzer. The light absorber is shown in dark blue, the catalysts as gray particles for PECs and as gray plates for the PV-electrolyzer, and the membrane is represented by a light blue sheet passing through the center of the devices.
SQ Limits for Multijunction Light Absorbers and Panels of Light Absorbers.
The current density–voltage (JV) characteristics of light absorbers are governed by extrinsic and intrinsic losses. The extrinsic losses due to light reflection, contact shadowing, series resistance, inefficient collection of electrons and holes, nonradiative recombination, and temperature rise can be minimized or completely eliminated by appropriate material selection and design. However, the intrinsic losses due to mismatch between the energy band-gap and the solar spectrum, and the radiative recombination of the electrons and holes are inherent to the light absorbers chosen and cannot be eliminated. The intrinsic losses and the JV characteristics for an ideal light absorber can be derived from the laws of thermodynamics assuming a terrestrial air mass 1.5 spectrum at 1 sun (19). The generalized expression for the SQ limit for a multijunction absorber is given as (see SI Appendix, section S-1 for the derivation):
| [1] |
where is the bias developed across the multijunction light absorber, is the Boltzmann constant, is the temperature, is the electronic charge, is the number of light absorbers (or junctions) in a multijunction light absorber, is the current density, is the short-circuit density, and is the dark saturation current density of the ith light absorber. Here junction refers to a p–n junction and a multijunction light absorber refers to a material containing such p–n junctions in vertically oriented stacked configuration. For a PV panel of identical light absorbers connected in series, the panel voltage will be increased and the panel current density will be decreased by a factor of . The JV characteristic of a PV panel can be obtained using Eq. 1:
| [2] |
The PV panel refers to a side-by-side serially wired configuration of light absorbers. In this work we only consider PV panels with serially connected light absorbers, as the parallel connection of light absorbers affects neither the cell voltage nor the current density.
Electrochemical Load Curve for CO2 Reduction.
The electrochemical load curve (current density versus cell potential curve) for CO2 reduction depends on (i) physical properties of the catalysts, membrane, and electrolyte; (ii) operating conditions (CO2 flowrate and partial pressure, current density); and (iii) physical dimensions of the cell (18). The cell potential is a sum of the equilibrium potentials and kinetic overpotentials for the OER and CO2RR, the solution losses , and the Nernstian losses , and is given by
| [3] |
Details of how electrochemical load curves are determined for known process conditions and material properties can be found elsewhere (18).
Eq. 3 shows that the required cell potential for an electrochemical reaction can be higher than its equilibrium potential. This potential difference is due to the kinetic overpotentials and polarization losses, which usually cause heat generation. The potential losses and hence heat generation can be reduced by selecting appropriate materials, cell design, and process conditions. The cell potential at which the heat generation is zero is known as the thermoneutral potential, and at this potential the cell operates adiabatically (20). The thermoneutral potential is derived from the enthalpy change of an electrochemical reaction, given as
| [4] |
where is the Faraday constant, is the thermoneutral potential of product , is the standard enthalpy change per mole of product , and is the number of electrons transferred per mole of product .
The value of the thermoneutral potential is always higher than the equilibrium potential. The electrochemical reaction will be exothermic for the cell potentials higher than the thermoneutral potential; the electrochemical reaction will be endothermic for the cell potentials lower than the thermoneutral potential. Therefore, the thermoneutral potential is the lowest feasible cell potential for self-sustained operation (which does not require external heating) of the electrochemical cells. Table 1 shows the equilibrium potentials, thermoneutral potentials, and the lower heating values of different CO2 reduction products at standard conditions.
Table 1.
Number of electrons, equilibrium potential, thermoneutral potential, and lower heating value of various fuels at standard conditions
| Fuel-forming reactions | Number of electrons | Equilibrium potential, V | Thermoneutral potential, V | Lower heating value, kJ mol−1 |
| 2 | 1.229 | 1.481 | 241.81 | |
| 2 | 1.329 | 1.466 | 282.98 | |
| 2 | 1.249 | 1.315 | 209.82 | |
| 6 | 1.199 | 1.255 | 638.73 | |
| 8 | 1.059 | 1.153 | 802.23 | |
| 12 | 1.144 | 1.181 | 1,235.45 | |
| 12 | 1.149 | 1.219 | 1,322.94 |
Electrochemical load curves were computed for three scenarios. The first is for the case in which the OER occurs over an IrO2 anode (21) and the CO2RR over a Ag cathode (22) in a 0.1 M KHCO3 solution at pH 6.8. This arrangement will produce O2 at the anode and H2 and CO at the cathode. The physical cell dimensions and operating conditions are similar to those reported by Hatsukade et al. (22). The electrochemical load curves for this scenario are shown in SI Appendix, Fig. S1A (see SI Appendix, section S-2).
The second scenario is one in which the OER occurs on an IrO2 anode (21) and the CO2RR occurs on a Cu cathode (23) in a 0.1 M KHCO3 solution at pH 6.8. In this case, O2 is produced at the anode and H2, CO, HCOO−, CH4, C2H4, C2H5OH are produced at the cathode. The cell physical dimensions and operating conditions are similar to those reported by Kuhl et al. (23). The electrochemical load curves for this case are shown in SI Appendix, Fig. S1B (see SI Appendix, section S-3).
The third scenario is for the tandem PEC shown in Fig. 1B. The electrochemical load curve for the first PEC (Fig. 1B), which performs water-splitting, using an IrO2 anode and a Pt cathode is shown in SI Appendix, Fig. S2A. The second PEC uses H2 from the first PEC to perform the CO2RR. SI Appendix, Fig. S2B shows the load curve of the second PEC assuming a Pt anode and a Cu cathode. Details concerning the calculation of load curves are discussed in SI Appendix, section S-4.
STF Efficiency.
The power generated by the PEC is the flux of fuel times its lower heating value. The primary source of power to these cells is the solar energy. Therefore, the STF efficiency can be defined as the ratio of power generated as fuel to the incident solar power, and is given by
| [5] |
where is the power generated, is the power consumed; is the operating current density; is the operating cell potential; is the Faradaic efficiency of product , which is a function of the cell potential; is the lower heating value per mole of product ; and is the average power of solar insolation per unit area. The STF efficiency for a given product can be written as
| [6] |
The operating current density and operating cell potential are obtained by finding the intersection of the JV curve for the light absorber given by Eq. 1 (or for a set of m light-absorber panels connected in series given by Eq. 2) and the electrochemical load curve given by Eq. 3. We note that there are other definitions of the STF efficiency that have been proposed that use the equilibrium potential of the fuels instead of the lower heating value (24). Such descriptions of STF efficiency are useful for the fuels (such as hydrogen) that can be used in fuel cells. However, the definition of the STF efficiency based on the lower heating value is better suited for transportation fuels.
The power requirement to concentrate or capture CO2 from a dilute stream (such as air or flue gas) can also be included as an additional term in the denominator of Eqs. 5 and 6. For the case of CO2 recovery from flue gas, the energy required using an monoethanolamine-based system is ∼180 kJ mol−1 of CO2 (25), whereas the consumption of CO2 in solar-fuel generator operating at 10 mA cm−2 is only about mol m−2s−1. Therefore, the power required to concentrate CO2 to the solar-fuel generator is kW m−2, which is less than 10% of incident solar power of 1 kW m−2. If CO2 capture from the atmosphere is considered, then the corresponding energy required will be 3–4 times higher (1). Hence, the energy for carbon capture becomes more significant as the initial concentration decreases. It should be noted that the definition of STF given by Eq. 6 does not account for energy losses associated with the recovery of a fuel from the CO2 stream leaving the electrochemical cell. Taking this energy loss into account would lower the STF efficiency below the values reported in this study.
Results and Discussion
The thermodynamic, achievable, and realistic STF efficiencies for various CO2 reduction products are discussed next. The optimal configuration of light absorbers and PV panels for attaining maximum STF efficiency of CO2 reduction is also examined.
Thermodynamic Limits of STF Efficiency of Fuels.
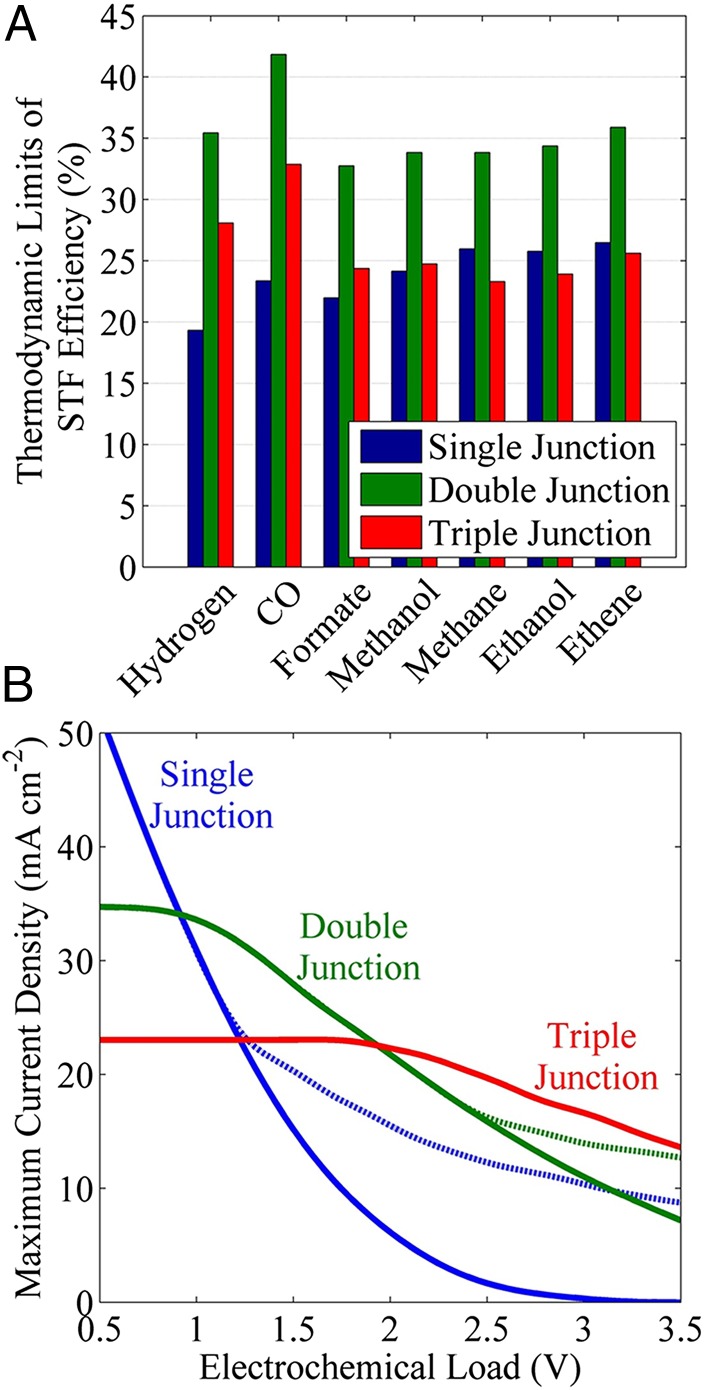
The thermodynamic STF efficiency can be realized for an ideal light absorber powering an electrochemical reaction that is operated adiabatically. The maximum current density in this scenario can be obtained by substituting the thermoneutral potential of an electrochemical reaction (from Table 1) into Eq. 1 for the SQ limit, and subsequent optimization of the band-gaps. The thermodynamic limit for the STF efficiency can be calculated from Eq. 6 using the maximum current density obtained for the optimized band-gaps and the lower heating value of the fuels. Fig. 2A shows the thermodynamic STF efficiencies for H2, CO, HCOOH, CH3OH, CH4, C2H4, and C2H5OH using a single-, double-, or triple-junction light absorber. The maximum efficiencies for different fuels lie between 32% and 42%, and are achieved using a double-junction light absorber. The STF efficiency using single- and triple-junction light absorbers are lower due to insufficient absorption of the solar spectrum and poor matching of current densities between light absorbers, respectively. Our finding shows that double-junction light absorbers are optimal for reactions operating close to thermoneutral potentials. We also note that plant leaves contain two photosystems to use sunlight most efficiently for photosynthesis (26).
Fig. 2.
(A) Thermodynamic limits of STF efficiency of various CO2RR products, and (B) Maximum current density from a single- (blue), double- (green), and triple- (red) junction solar cell and their panels versus electrochemical load. The solid lines correspond to single cell (m = 1) and the dashed lines correspond to multiple cell (m >1) in series connection (PV panel).
The PECs can use waste heat from the unused photons and thereby operate under endothermic condition (27). The thermodynamic limits of STF efficiency for reactions operating at equilibrium potential will be slightly higher than those shown in Fig. 2A. The thermodynamic STF efficiencies of various products under equilibrium condition are 39.5% for H2, 44.4% for CO, 34.0% for HCOOH, 35.2% for CH3OH, 34.5% CH4, 36.9% for C2H4, and 34.6% C2H5OH.
Most electrochemical reactions, including the CO2RR, operate at potentials well above the thermoneutral potential due to various losses in the electrochemical cell (see Eq. 3). Therefore, it is essential to identify the optimal configuration of light absorbers, e.g., the number of junctions , band-gap energies , and number of cells in series connection to obtain the maximum power or maximum current density at a given electrochemical load. Fig. 2B shows the decrease in the maximum current density for single-, double-, and triple-junction solar cells with increasing electrochemical load in the range of 0.5 to 3.5 V. The solid lines [solid lines are obtained by maximizing in Eq. 1 with respect to at a fixed load] correspond to a single cell (m = 1) with optimal band-gap energies, whereas the dashed lines [dashed lines are obtained by maximizing in Eq. 2 with respect to and at a fixed load] correspond to optimally connected cells (m > 1), each containing junctions of optimal band-gap energies. The optimal band-gap energies for single-, double-, and triple-junction light absorbers corresponding to the maximum current density in Fig. 2B are shown in SI Appendix, Fig. S3 (SI Appendix, section S-5).
The decrease in the current density with increasing electrochemical load is due to a decrease in the fraction of the solar spectrum absorbed by the higher band-gap materials. The double- and triple-junction light absorbers show almost constant current densities of 35 and 23 mA cm−2 up to the electrochemical loads of 0.9 and 1.95 V, respectively. The decrease in the maximum current density (plateau at lower loads in Fig. 2B) with increasing junctions of light absorber is due to current matching limitations. It can be seen that the single-, double-, and triple-junction light absorbers provide maximum current density for the load ranges of 0–0.9 V, 0.9–1.95 V, and 1.95–3.5 V, respectively. The double-junction light absorbers are best for water-splitting systems, because typical electrochemical loads are <2 V (SI Appendix, Fig. S2A). However, Fig. 2B shows that a triple-junction light absorber will be efficient for CO2RR systems whose electrochemical loads are in the range from 2 to 3.5 V (SI Appendix, Figs. S1 and S2).
Serially connected light absorbers of relatively lower band-gap materials can absorb a larger portion of the solar spectrum and provide higher current density at higher loads. Fig. 2B shows that the maximum current density from a panel of single-junction light absorbers can be increased by sequentially increasing the number of series connections. In the case of a double-junction light absorber (commonly referred to as tandem light absorbers), a single light absorber is efficient up to a load of 2.45 V and two serially connected light absorbers can be efficient for a load in the range of 2.45–3.5 V. Interestingly, a triple-junction light absorber does not require serial connections to boost its current density for the load range of 0.5–3.5 V.
Achievable STF Efficiency for Synthesis Gas Production over Silver Using a Triple-Junction Light Absorber.
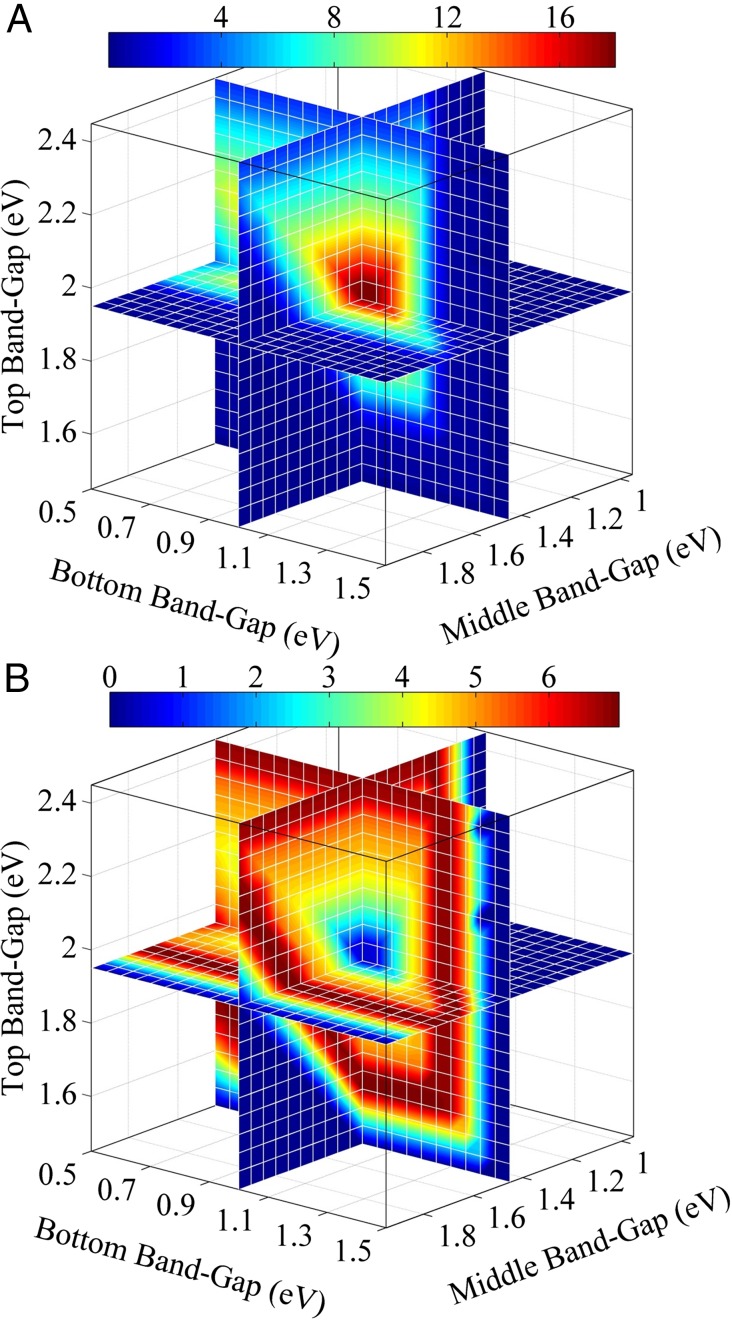
The achievable STF efficiencies for synthesis gas (a mixture of H2 and CO) were determined for a semi-ideal system for which an ideal light absorber powers the load for the electrochemical reactions shown in SI Appendix, Fig. S1A. The electrochemical load for the production of synthesis gas was obtained for the case of an IrO2 anode and a Ag cathode operating under the conditions described in Electrochemical Load Curve for CO2 Reduction. Fig. 3 shows the variation in STF efficiency for (A) H2 and (B) CO as a function of top, middle, and bottom band-gaps of an ideal triple-junction light absorber. The maximum total STF efficiency, 18.4%, is obtained for top, middle, and bottom band-gaps of 1.95 eV, 1.45 eV, and 1 eV, respectively. However, the STF efficiency for CO for this set of band-gaps is only 0.424%. Fig. 3 A and B are complementary, and demonstrate that the band-gap combinations favorable for H2 production are less favorable for CO formation and vice versa. Therefore, the ratio of H2 to CO in the synthesis gas can be set by choosing the band-gaps that are different from those that are optimal for formation of each product. The maximum STF efficiency for CO, 6.95%, can be obtained for various combinations of band-gaps (red contours in Fig. 3B). For example, the band-gap combination of 1.8 eV (top, InGaP), 1.1 eV (middle, Si), and 0.66 eV (bottom, Ge) can give an STF efficiency of 6.95% for CO. Other combinations of semiconductor materials suitable for efficient production of synthesis gas can be found using SI Appendix, Table S1.
Fig. 3.
Achievable STF efficiencies of (A) H2 and (B) CO formation on Ag as a function of band-gaps of an ideal triple-junction light absorber.
The maximum total STF efficiency, 14%, is obtained for an ideal double-junction light absorber with top and bottom band-gaps of 2.15 eV and 1.65 eV, respectively (see SI Appendix, section S-6). Interestingly, the maximum STF efficiency for CO is 6.95%, which is nearly identical to that obtained for a triple-junction light absorber. This similarity is due to the limiting current density for CO characterized by the plateau seen in the load curve (SI Appendix, Fig. S1A). A suitable combination of tandem or double-junction light absorber, e.g., 2.26 eV (top, GaP) and 1.12 eV (bottom, Si), can provide an STF efficiency for CO of 6.95%.
Achievable STF Efficiency of Hythane Production on Copper Using a Triple-Junction Light Absorber.
Hythane (a mixture of H2 and CH4) is an alternative fuel which upon combustion produces significantly lowers emissions of COx, hydrocarbon, and NOx than those obtained from diesel or natural gas operated vehicles (28, 29). SI Appendix, Fig. S1B shows that electrochemical reduction of CO2 on copper can produce Hythane directly together with some minor products, such as C2H4, C2H5OH, HCOO−, and CO. The achievable STF efficiencies for Hythane production are calculated for a semi-ideal system in which an ideal light absorber powers the load for the electrochemical reactions shown in SI Appendix, Fig. S1B. The electrochemical load for Hythane is obtained for an IrO2 anode and a Cu cathode operating under the conditions described in Electrochemical Load Curve for CO2 Reduction. Fig. 4 shows the variation in STF efficiency for (A) H2 and (B) CH4 with top, middle, and bottom band-gaps of an ideal triple-junction light absorber. The maximum STF efficiency for Hythane, 17.7% (out of a total STF efficiency of 20.3%), is obtained for top, middle, and bottom band-gaps of 1.9 eV, 1.35 eV, and 0.9 eV, respectively. The composition of Hythane produced on Cu can be tuned by selecting appropriate band-gaps for the light absorbers. The optimal fraction of H2 in Hythane used in internal combustion engine varies from 0 to 80% depending on the engine load (29). Interestingly, the optimal choice of band-gaps can produce as low as 73% of H2 in Hythane. An ideal triple-junction light absorber, e.g., InGaP (1.8 eV)/GaAs (1.424 eV)/Ge (0.66 eV), with band-gaps close to the optimal values would produce Hythane with an STF efficiency of 4.5%. In the next section we show that the measured JV characteristic of a real InGaP/GaAs/Ge triple-junction light absorber is calculated to have STF efficiency for Hythane of <1% because its fill factor is less than that for an ideal configuration.
Fig. 4.
Achievable STF efficiencies of (A) H2 and (B) CH4 formation over copper as a function of the band-gaps of an ideal triple-junction light absorber.
The maximum STF efficiencies for other products formed on Cu using an ideal triple-junction light absorber are 2.21% for C2H4, 0.91% for C2H5OH, 0.42% for HCOOH, and 0.21% for CO (see SI Appendix, section S-8). The maximum STF efficiency for Hythane, 12.5% (out of a total STF efficiency of 15.4%) is obtained for an ideal double-junction light absorber with top and bottom band-gaps of 2.05 eV and 1.55 eV, respectively (see SI Appendix, section S-7). The maximum STF efficiencies for minor products are similar to those obtained for a triple-junction light absorber.
Comparison of Realistic STF Efficiencies for CO2 Reduction Using a PEC, a Tandem PEC, and a PV-Electrolyzer.
Realistic STF efficiencies are calculated using Spectrolab’s (30) most efficient InGaP/GaAs/Ge triple-junction light absorber (SI Appendix, Fig. S7A) and electrochemical load curve for CO2RR over Cu (SI Appendix, Fig. S1B). As a basis for comparison, we use the same electrochemical load curve (SI Appendix, Fig. S1B) for the PEC and PV-electrolyzer. The electrochemical load curves in SI Appendix, Fig. S2 are used in the case of the tandem PEC. The Spectrolab's triple-junction light absorber was used to estimate STF efficiencies for all three configurations given in Fig. 1, except for the PV-electrolyzer, which has two such light absorbers connected in series, an optimal configuration for that case. The STF efficiencies for a PEC and a PV-electrolyzer are obtained by matching current density and current, respectively.
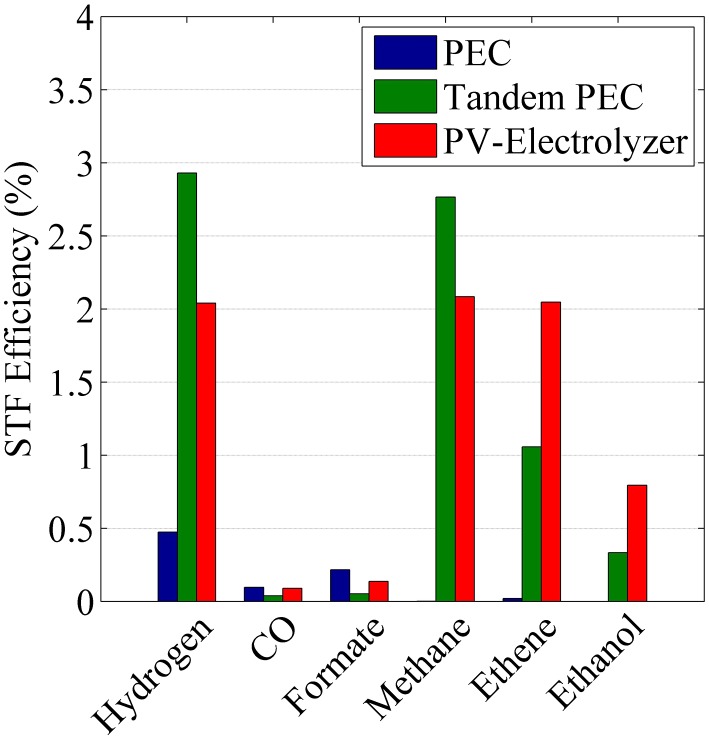
Fig. 5 shows STF efficiencies for CO2 reduction products on Cu using a PEC, a tandem PEC, and a PV-electrolyzer. The total STF efficiencies are 0.8% for the PEC, 7.2% for the tandem PEC, and 7.2% for the PV-electrolyzer. Consistent with what is shown here, the STF efficiencies for most PECs used for CO2 reduction are <1% because the onset potential for the CO2RR is close to the open-circuit voltage of the light absorber. The tandem PEC splits the total electrochemical load for CO2 reduction (SI Appendix, Fig. S1B) into two smaller electrochemical loads (SI Appendix, Fig. S2), and consequently each PEC can operate close to 12.6 mA cm−2, the short-circuit current density of the chosen triple-junction light absorber. Because there are two PECs in the tandem configuration, the total STF efficiency is reduced by half. In the case of the PV-electrolyzer, the two serially connected, triple-junction light absorbers provide twice the open-circuit voltage, 4.58 V, but the short-circuit current density is now half as large. Therefore, the STF efficiency of the PV-electrolyzer is 7.2%, corresponding to an operating current density of 6.3 mA cm−2 (the short-circuit current density of a single panel). Although the STF efficiencies of the tandem PEC and PV-electrolyzer are the same, the product distribution is different due to differences in the operating current densities and overpotential applied to the cathode.
Fig. 5.
STF efficiencies of fuels formed on copper using Spectrolab’s triple-junction light absorber arranged in three different configurations: PEC, tandem PEC, and PV-electrolyzer.
Effect of Polarization Losses and Fill Factor.
The polarization losses in an electrochemical cell depend on various factors such as electrolyte composition, membrane properties, hydrodynamic conditions, CO2 flowrate, and distance between electrodes (18). Increasing the polarization losses not only increases the electrochemical load but also decreases the limiting current density. It is evident from Fig. 2B that the maximum current density and hence the STF efficiency decreases with increasing electrochemical load (or polarization losses).
The fill factor for a light absorber can decrease with increasing extrinsic losses due to light reflection, contact shadowing, series resistance, inefficient collection of electrons and holes, nonradiative recombination, and temperature rise (31). In Achievable STF Efficiency of Hythane Production on Copper Using a Triple-Junction Light Absorber, we showed an STF efficiency of 4.5% using an ideal InGaP/GaAs/Ge triple-junction light absorber with a fill factor of 0.937. The commercial InGaP/GaAs/Ge triple-junction light absorber has a fill factor of 0.756, which significantly reduces the STF efficiency to 0.8% (Comparison of Realistic STF Efficiencies for CO2 Reduction Using a PEC, a Tandem PEC, and a PV-Electrolyzer).
Strategies to Control Quality of Solar Fuels.
The composition and hence the energy content of solar fuels generated in any of the solar-fuel generators shown in Fig. 1 depends on the operating current density and kinetic overpotential of the catalyst. The variation in solar insolation will continuously shift the operating current of the light absorber, and thereby cause a continuous shift in the kinetic overpotential of the catalyst. Wireless PECs and tandem PECs already operate with distributed kinetic overpotentials and current density due to their 2D architecture (32, 33). The band-edge of the semiconductor interface can be tuned such that the catalyst is always operated at a fixed potential even under varying solar insolation. However, the variation in the photocurrent due to varying solar insolation will affect the electrolyte potential (due to solution losses), which in turn affects the kinetic overpotential of CO2RR and selectivity of products. Conversely, the PV-electrolyzers can use dc/dc converters and/or batteries to regulate the operating current and voltage of electrolyzers under varying solar irradiation (34). A dc/dc converter can regulate the varying voltage to a fixed value. However, the current from the dc/dc converter will still change with time. The only way to handle the temporal variation in current for this scenario is to vary the number of active electrolyzers in the array of electrolyzers such that each one operates at close to the designated current density. A more attractive alternative would be to use batteries to operate the electrolyzers and to PV panels to charge the batteries, because batteries can efficiently and precisely control the current density and cell potential of the electrolyzers.
After conditioning of solar power by either power electronics or battery, a specific current and voltage can be applied to an electrolyzer. However, the operating voltage of an electrolyzer for a fixed applied current is dependent on the area of the catalyst or catalyst loading. In such a case, increasing the ratio of specific/geometric area of catalyst to the area of PV can increase the operating current (and STF efficiency) for a fixed kinetic overpotential. The PV-electrolyzer system with an IrO2 anode and a Ag cathode powered by a panel of two InGaP/GaAs/Ge triple-junction light absorbers connected in series can operate at maximum STF efficiency of 8.6% and produce 92.6% pure CO, when the ratio of catalyst to PV area is 1.25 (see SI Appendix, section S-10).
Fuel Selection.
Electrocatalysts exist for producing HCOOH, CO, CH4, and C2H4 selectively (35), and research is ongoing to find electrocatalysts that can produce liquid products such as methanol, ethanol, and propanol selectively. In this section we provide a perspective on the fuel selection based on the electrolysis efficiency, energy density (LHV), and profitability index. The details of these calculations are given in SI Appendix, section S-12.
When comparing potential fuels for use in the transportation sector an important metric is their energy density. Table 2 lists the energy densities for several CO2 reduction products (36). For gaseous products values are given at both ambient and elevated pressures. As can be seen, the liquid-phase products are superior to gaseous products in terms of energy density, even at a pressure 250 times higher than atmospheric for the latter. However, the electrolysis efficiencies of gaseous products, such as CO and H2, are higher by 10% than those of the liquid products.
Table 2.
Electrolysis efficiency, energy density, and profitability index of various CO2RR products
| Product | Electrolysis efficiency, % | Energy density at STP, MJ L−1 | Energy density at elevated pressure, MJ L−1 | Profitability index, ¢ kW-h−1 |
| Hydrogen | 74.1 | 0.010 | 3.74 (at 50 MPa) | 9.95 |
| CO | 73.3 | 0.012 | 2.69 (at 25 MPa) | 1.91 |
| Formic acid | 65.8 | 5.561 | — | 31.56 |
| Methanol | 62.8 | 15.789 | — | 3.77 |
| Methane | 57.7 | 0.033 | 9.68 (at 25 MPa) | 0.99 |
| Ethanol | 59.1 | 21.158 | — | 6.74 |
| Ethene | 61.0 | 0.055 | 20.15 (at 25 MPa) | 6.15 |
| 1-Propanol | 58.2 | 24.636 | — | 14.83 |
Another metric by which potential fuels should be compared is their profitability index, defined as the market value of the fuel obtained for a fixed energy input. The assumption has been made that a solar-fuels generator will operate at a cell voltage of 2 V [which is the required operating voltage to attain the Department of Energy efficiency target of 75% for H2 (37)] and will produce the target fuel with a Faradaic efficiency of 100%. The energy required for product purification and pressurization has been omitted because it will be largely dependent on the architecture of the solar-fuel generator. As shown in Table 2, the profitability indices of gaseous products are generally smaller than the liquid-phase products. Whereas C2H4 and HCOOH are capable of reaching an energy density and profitability index on a par with the liquid-phase products, there is no precedent for using these products in the transportation sector. However, C2H4 can be upgraded to diesel by oligomerization (38) and HCOOH can be used as a fuel for fuel cells (39). The foregoing analysis shows that electrochemical synthesis of liquid products can be profitable; however, including the cost of separating products from the electrolyte could significantly reduce their profitability index. The gaseous products have an advantage, because they can be separated readily from the electrolyte and their profitability index is comparable to that of liquid products.
Conclusions and Perspectives
An analysis of the thermodynamic, achievable, and realistic STF efficiencies for various CO2RR products has been carried out. The thermodynamic STF efficiencies range from 32% to 42%. Forty years of research (40) on solar-driven hydrogen production has led to a device with a record efficiency of 18%, about half of the thermodynamic limit, 35.4% (Fig. 2A). Solar-driven CO2 reduction is considerably less mature than solar-driven hydrogen production. Therefore, the highest reported efficiency for CO formation is only 6.5% (17), but because the thermodynamic limit is 41.8%, this means that there is considerable opportunity for further improvement.
The low STF efficiency for the CO2RR is attributable to inefficient design of the electrochemical cell and/or improper configuration of light absorbers. The effects of cell design, material properties, and operating conditions on the efficiency of CO2R have been discussed in ref. 18. In this article, we have proposed optimal configurations of light absorbers for efficient conversion of sunlight, water, and CO2 to fuels. Fig. 2B shows that the double-junction light absorbers are optimal for the electrochemical loads in the range of 0.9 to 1.95 V, whereas the triple-junction light absorbers are optimal in the load range of 1.95 to 3.5 V, which is the regime for the CO2RR. The achievable STF efficiencies are calculated for the CO2RR occurring on Ag and Cu electrodes, using an ideal triple-junction light absorber. The maximum STF efficiencies obtained with Ag and Cu electrodes are 18.4% and 20.3%, respectively. The maximum achievable STF efficiency of 6.95% for CO in synthesis gas can be obtained using an InGaP/Si/Ge triple-junction light absorber connected to a Ag electrode. Although the maximum achievable STF efficiency for Hythane production on Cu is 17.7%, an ideal triple-junction light absorber of band-gaps close to InGaP/GaAs/Ge can produce Hythane with almost 4.5% efficiency. However, a realistic InGasP/GaAs/Ge triple-junction light absorber with a fill factor of 0.756 significantly reduces the STF efficiency for Hythane formation to 0.8%.
As discussed in Comparison of Realistic STF Efficiencies for CO2 Reduction Using a PEC, a Tandem PEC, and a PV-Electrolyzer, the realistic STF efficiency of a solar-fuels generator depends on how it is configured. We have examined the STF efficiency of a solar-fuels generator consisting of a 28% efficient InGaP/GaAs/Ge triple-junction light absorber, a Cu cathode, and an IrO2 anode in three different configurations (PEC, tandem PECs, and PV-electrolyzer). The tandem PECs and PV-electrolyzers can be six times as efficient as a single PEC. The low efficiency of CO2 reduction in a PEC is primarily due to the open-circuit voltage of the light absorber being very close to the onset potential of the CO2RR. Moreover, the PECs cannot self-regulate the kinetic overpotential and hence the current density of the CO2RR, which can vary due to continuous variation in the solar irradiation. Conversely, a PV-electrolyzer can use either a dc/dc converter or battery to control the output voltage and current of a PV panel under varying solar insolation. Also, the relative areas of the PV and the electrodes can be tuned independently in a PV-electrolyzer to control the kinetic overpotential at fixed current so that the selectivity to the desired products is maximized.
Finally, we note an analysis of product-specific metrics, such as electrolysis efficiency, energy density, and profitability index, demonstrates that liquid products have slightly higher market value per unit energy input and higher energy density than do gaseous products. HCOOH and C2H4 are particularly interesting because of their high profitability index. HCOOH is suitable as a fuel for fuel cells and C2H4 can be converted to diesel by oligomerization.
Supplementary Material
Acknowledgments
We acknowledge Dr. Joel W. Ager III for his valuable suggestions and comments, and thank Karl Walczak for providing current–voltage (JV) characteristics for the InGaP/GaAs/Ge triple-junction light absorber. This material is based on the work performed by the Joint Center for Artificial Photosynthesis, a United States Department of Energy (DOE) Energy Innovation Hub, supported through the Office of Science of the US DOE under Award DE-SC0004993.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1519212112/-/DCSupplemental.
References
- 1.Goeppert A, Czaun M, Prakash GS, Olah GA. Air as the renewable carbon source of the future: an overview of CO 2 capture from the atmosphere. Energy Environ Sci. 2012;5(7):7833–7853. [Google Scholar]
- 2.Carnesale A, Chameides W. America's Climate Choices. NRC/NAS USA Committee on America's Climate Choices, National Academy Press; Washington, DC: 2011. [Google Scholar]
- 3.Graves C, Ebbesen SD, Mogensen M, Lackner KS. Sustainable hydrocarbon fuels by recycling CO2 and H2O with renewable or nuclear energy. Renew Sustain Energy Rev. 2011;15(1):1–23. [Google Scholar]
- 4.Lewis NS, Nocera DG. Powering the planet: Chemical challenges in solar energy utilization. Proc Natl Acad Sci USA. 2006;103(43):15729–15735. doi: 10.1073/pnas.0603395103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bolton JR, Strickler SJ, Connolly JS. Limiting and realizable efficiencies of solar photolysis of water. Nature. 1985;316(6028):495–500. [Google Scholar]
- 6.Winkler MT, Cox CR, Nocera DG, Buonassisi T. Modeling integrated photovoltaic–electrochemical devices using steady-state equivalent circuits. Proc Natl Acad Sci USA. 2013;110(12):E1076–E1082. [Google Scholar]
- 7.Hu S, Xiang C, Haussener S, Berger AD, Lewis NS. An analysis of the optimal band gaps of light absorbers in integrated tandem photoelectrochemical water-splitting systems. Energy Environ Sci. 2013;6(10):2984–2993. [Google Scholar]
- 8.Peharz G, Dimroth F, Wittstadt U. Solar hydrogen production by water splitting with a conversion efficiency of 18% Int J Hydrogen Energy. 2007;32(15):3248–3252. [Google Scholar]
- 9.Rocheleau RE, Miller EL, Misra A. High-efficiency photoelectrochemical hydrogen production using multijunction amorphous silicon photoelectrodes. Energy Fuels. 1998;12(1):3–10. [Google Scholar]
- 10.Surendranath Y, Bediako DK, Nocera DG. Interplay of oxygen-evolution kinetics and photovoltaic power curves on the construction of artificial leaves. Proc Natl Acad Sci USA. 2012;109(39):15617–15621. doi: 10.1073/pnas.1118341109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jin J, et al. An experimental and modeling/simulation-based evaluation of the efficiency and operational performance characteristics of an integrated, membrane-free, neutral pH solar-driven water-splitting system. Energy Environ Sci. 2014;7(10):3371–3380. [Google Scholar]
- 12.Cox CR, Lee JZ, Nocera DG, Buonassisi T. Ten-percent solar-to-fuel conversion with nonprecious materials. Proc Natl Acad Sci USA. 2014;111(39):14057–14061. doi: 10.1073/pnas.1414290111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.White JL, Herb JT, Kaczur JJ, Majsztrik PW, Bocarsly AB. Photons to formate: Efficient electrochemical solar energy conversion via reduction of carbon dioxide. J CO2 Utilization. 2014;7:1–5. [Google Scholar]
- 14.Sekimoto T, et al. Tandem photo-electrode of InGaN with two Si pn junctions for CO2 conversion to HCOOH with the efficiency greater than biological photosynthesis. Appl Phys Lett. 2015;106(7):073902. [Google Scholar]
- 15.Arai T, Sato S, Morikawa T. A monolithic device for CO2 photoreduction to generate liquid organic substances in a single-compartment reactor. Energy Environ Sci. 2015;8(7):1998–2002. [Google Scholar]
- 16.Sugano Y, et al. Crucial role of sustainable liquid junction potential for solar-to-carbon monoxide conversion by a photovoltaic photoelectrochemical system. RSC Advances. 2015;5(67):54246–54252. [Google Scholar]
- 17.Schreier M, et al. Efficient photosynthesis of carbon monoxide from CO2 using perovskite photovoltaics. Nat Commun. 2015;6:7326. doi: 10.1038/ncomms8326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Singh MR, Clark EL, Bell AT. Effects of electrolyte, catalyst, and membrane composition and operating conditions on the performance of solar-driven electrochemical reduction of carbon dioxide. Phys Chem Chem Phys. 2015;17(29):18924–18936. doi: 10.1039/c5cp03283k. [DOI] [PubMed] [Google Scholar]
- 19.Shockley W, Queisser HJ. Detailed balance limit of efficiency of p‐n junction solar cells. J Appl Phys. 1961;32(3):510–519. [Google Scholar]
- 20.Newman J, Thomas-Alyea KE. Electrochemical Systems. John Wiley & Sons; Hoboken, NJ: 2012. [Google Scholar]
- 21.McCrory CC, Jung S, Peters JC, Jaramillo TF. Benchmarking heterogeneous electrocatalysts for the oxygen evolution reaction. J Am Chem Soc. 2013;135(45):16977–16987. doi: 10.1021/ja407115p. [DOI] [PubMed] [Google Scholar]
- 22.Hatsukade T, Kuhl KP, Cave ER, Abram DN, Jaramillo TF. Insights into the electrocatalytic reduction of CO₂ on metallic silver surfaces. Phys Chem Chem Phys. 2014;16(27):13814–13819. doi: 10.1039/c4cp00692e. [DOI] [PubMed] [Google Scholar]
- 23.Kuhl KP, Cave ER, Abram DN, Jaramillo TF. New insights into the electrochemical reduction of carbon dioxide on metallic copper surfaces. Energy Environ Sci. 2012;5(5):7050–7059. [Google Scholar]
- 24.Coridan RH, et al. Methods for comparing the performance of energy-conversion systems for use in solar fuels and solar electricity generation. Energy Environ Sci. 2015;8(10):2886–2901. [Google Scholar]
- 25.Zeman F. Energy and material balance of CO2 capture from ambient air. Environ Sci Technol. 2007;41(21):7558–7563. doi: 10.1021/es070874m. [DOI] [PubMed] [Google Scholar]
- 26.Barber J. Photosynthetic energy conversion: natural and artificial. Chem Soc Rev. 2009;38(1):185–196. doi: 10.1039/b802262n. [DOI] [PubMed] [Google Scholar]
- 27.Khaselev O, Bansal A, Turner J. High-efficiency integrated multijunction photovoltaic/electrolysis systems for hydrogen production. Int J Hydrogen Energy. 2001;26(2):127–132. [Google Scholar]
- 28.Lynch FE, Marmaro RW. 1992. Special Purpose Blends of Hydrogen and Natural Gas; US Patent 5,139,002. [DOI] [PubMed] [Google Scholar]
- 29.Sierens R, Rosseel E. Variable composition hydrogen/natural gas mixtures for increased engine efficiency and decreased emissions. J Eng Gas Turbines Power. 2000;122(1):135–140. [Google Scholar]
- 30.Karam NH, et al. Development and characterization of high-efficiency Ga 0.5 In 0.5 P/GaAs/Ge dual-and triple-junction solar cells. Electron Devices. IEEE Transactions on. 1999;46(10):2116–2125. [Google Scholar]
- 31.Henry CH. Limiting efficiencies of ideal single and multiple energy gap terrestrial solar cells. J Appl Phys. 1980;51(8):4494–4500. [Google Scholar]
- 32.Haussener S, et al. Modeling, simulation, and design criteria for photoelectrochemical water-splitting systems. Energy Environ Sci. 2012;5(12):9922–9935. [Google Scholar]
- 33.Singh MR, Stevens JC, Weber AZ. Design of membrane-encapsulated wireless photoelectrochemical cells for hydrogen production. J Electrochem Soc. 2014;161(8):E3283–E3296. [Google Scholar]
- 34.Coelho RF, Concer F, Martins DC. 2009. A study of the basic DC-DC converters applied in maximum power point tracking. Power Electronics Conference, 2009. COBEP’09. Brazilian, 10.1109/COBEP.2009.5347723.
- 35.Hori Y. Electrochemical CO2 Reduction on Metal Electrodes. Modern Aspects of Electrochemistry. Springer; New York: 2008. pp. 89–189. [Google Scholar]
- 36.Green DW. Perry’s Chemical Engineers’ Handbook. McGraw-Hill; New York: 2008. [Google Scholar]
- 37. Anonymous (2013) Hydrogen Production Technical Team Roadmap (US Drive Partnership, Washington, DC)
- 38.Heveling J, van der Beek A, de Pender M. Oligomerization of ethene over nickel-exchanged zeolite y into a diesel-range product. Appl Catal. 1988;42(2):325–336. [Google Scholar]
- 39.Yu X, Pickup PG. Recent advances in direct formic acid fuel cells (DFAFC) J Power Sources. 2008;182(1):124–132. [Google Scholar]
- 40.Ager JW, III, Shaner M, Walczak K, Sharp ID, Ardo S. Experimental demonstrations of spontaneous, solar-driven photoelectrochemical water splitting. Energy Environ Sci. 2015;8(10):2811–2824. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.