Novel plasticity rule can explain the development of sensorimotor intelligence

Significance

To find how autonomous behavior and its development can be realized by a brain or an artificial neural network is a fundamental challenge for neuroscience and robotics. Commonly, the self-organized unfolding of behavior is explained by postulating special concepts like internal drives, curiosity, specific reward systems, or selective pressures. We propose a simple, local, and biologically plausible synaptic mechanism that enables an embodied agent to self-organize its individual sensorimotor development without recourse to such higher-level constructs. When applied to robotic systems, a rich spectrum of rhythmic behaviors emerges, ranging from locomotion patterns to spontaneous cooperation between partners. A possible utilization of our novel mechanism in nature would lead to a new understanding of the early stages of sensorimotor development and of saltations in evolution.

Abstract

Grounding autonomous behavior in the nervous system is a fundamental challenge for neuroscience. In particular, self-organized behavioral development provides more questions than answers. Are there special functional units for curiosity, motivation, and creativity? This paper argues that these features can be grounded in synaptic plasticity itself, without requiring any higher-level constructs. We propose differential extrinsic plasticity (DEP) as a new synaptic rule for self-learning systems and apply it to a number of complex robotic systems as a test case. Without specifying any purpose or goal, seemingly purposeful and adaptive rhythmic behavior is developed, displaying a certain level of sensorimotor intelligence. These surprising results require no system-specific modifications of the DEP rule. They rather arise from the underlying mechanism of spontaneous symmetry breaking, which is due to the tight brain body environment coupling. The new synaptic rule is biologically plausible and would be an interesting target for neurobiological investigation. We also argue that this neuronal mechanism may have been a catalyst in natural evolution.

Research in neuroscience produces an understanding of the brain on many different levels. At the smallest scale, there is enormous progress in understanding mechanisms of neural signal transmission and processing (1–4). At the other end, neuroimaging and related techniques enable the creation of a global understanding of the brain’s functional organization (5, 6). However, a gap remains in binding these results together, which leaves open the question of how all these complex mechanisms interact (7–9). This paper advocates for the role of self-organization in bridging this gap. We focus on the functionality of neural circuits acquired during individual development by processes of self-organization—making complex global behavior emerge from simple local rules.

Donald Hebb’s formula “cells that fire together wire together” (10) may be seen as an early example of such a simple local rule which has proven successful in building associative memories and perceptual functions (11, 12). However, Hebb’s law and its successors like BCM (13) and STDP (14, 15) are restricted to scenarios where the learning is driven passively by an externally generated data stream. However, from the perspective of an autonomous agent, sensory input is mainly determined by its own actions. The challenge of behavioral self-organization requires a new kind of learning that bootstraps novel behavior out of the self-generated past experiences.

This paper introduces a rule which may be expressed as “chaining together what changes together.” This rule takes into account temporal structure and establishes contact to the external world by directly relating the behavioral level to the synaptic dynamics. These features together provide a mechanism for bootstrapping behavioral patterns from scratch.

This synaptic mechanism is neurobiologically plausible and raises the question of whether it is present in living beings. This paper aims to encourage such initiatives by using bioinspired robots as a methodological tool. Admittedly, there is a large gap between biological beings and such robots. However, in the last decade, robotics has seen a change of paradigm from classical AI thinking to embodied AI (16, 17) which recognizes the role of embedding the specific body in its environment. This has moved robotics closer to biological systems and supports their use as a testbed for neuroscientific hypotheses (18, 19).

We deepen this argument by presenting concrete results showing that the proposed synaptic plasticity rule generates a large number of phenomena which are important for neuroscience. We show that up to the level of sensorimotor contingencies, self-determined behavioral development can be grounded in synaptic dynamics, without having to postulate higher-level constructs such as intrinsic motivation, curiosity, or a specific reward system. This is achieved with a very simple neuronal control structure by outsourcing much of the complexity to the embodiment [the idea of morphological computation (20, 21)].

The paper includes supporting information containing movie clips and technical detail. We recommend starting with Movie S1, which provides a brief overview.

Grounding Behavior in Synaptic Plasticity

We consider generic robotic systems, a humanoid and a hexapod robot, in physically realistic simulations using LpzRobots (22). These robots are mechanical systems of rigid body primitives linked by joints. With each joint i, there is an angular motor for realizing the new joint angles $y_i$ as proposed by the controller network, and there is a sensor measuring the true joint angle $x_i$ (like muscle spindles). The implementation of the motors is similar to muscle/tendon-driven systems by being compliant to external forces.

Controller Network.

One theme of our work is structural simplicity, building on the paradigm that complex behavior may emerge from the interaction of a simple neural circuitry with the complex external world. Specifically, the controller is a network of rate-coded neurons transforming sensor values $x=\left(x_1,x_2,\dots ,x_n\right)$ into motor commands $y=\left(y_1,y_2,\dots ,y_m\right)$. In the application, a one-layer feed-forward network is used, described as

$$y_i=g\left({\displaystyle \sum _{j=1}^n{C}_{ij}{x}_j+h_i}\right)$$ [1]

for neuron i, where C_ij is the synaptic weight for input j, and $h_i$ is the threshold. We use tanh neurons, i.e., the activation function $g\left(z\right)=\text{tanh}\left(z\right)$ to get motor commands between +1 and −1. This type of neuron is chosen for simplicity, but our approach can be translated into a neurobiologically more realistic setting. The setup is displayed in Fig. 1.

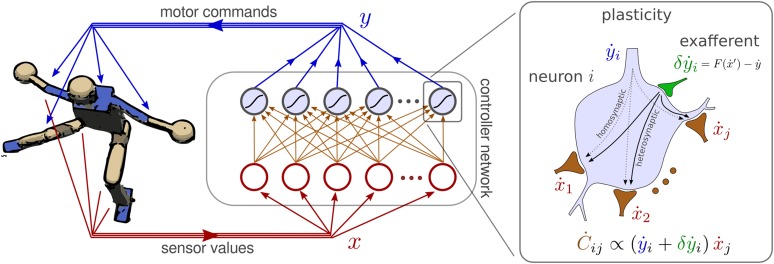
Fig. 1.

(Left) Controller network connected to the humanoid robot. The proposed differential extrinsic plasticity (DEP) rule is illustrated on the Right. In addition to the homosynaptic term $\dot{y}$ of plain differential Hebbian learning, the DEP [3] has the exafferent signal $\delta \dot{y}$ generated by the inverse model F (Eq. 2) that may be integrated by a heterosynaptic mechanism. In the simplest case, e.g., with the humanoid robot, the inverse model F is a one-to-one mapping of sensor to motor values.

This controller network may appear utterly oversimplified. Commonly, and in particular in classical artificial intelligence, a certain behavior is seen as the execution of a plan devised by the brain. This would require a highly organized internal brain dynamics, which could never be realized by the simple one-layer network. However, in this paper, behavior is an emerging mode in the dynamical system formed by brain, body, and environment (16). As we demonstrate here, by the new synaptic rule, the above simple feed-forward network can generate a large variety of motion patterns in complex dynamical systems.

Synaptic Plasticity Rule.

When learning the controller [1] with a Hebbian law, the rate of change ${\dot{C}}_{ij}$ of synapse $C_{ij}$ would be proportional to the input $x_j$ into the synapse of neuron i multiplied by its activation $y_i$, i.e., ${\dot{C}}_{ij}\propto y_i{x}_j$. However, in concrete settings, this rule produces typically fixed-point behaviors. It was suggested earlier (23–25) that time can come into play in a more fundamental way if the so-called differential Hebbian learning (DHL) is used, i.e., replacing the neuronal activities by their rates of change, so that ${\dot{C}}_{ij}\propto {\dot{y}}_i{\dot{x}}_j$ (the derivative of x w.r.t. time is denoted as $\dot{x}$). This rule focuses on the dynamics because there is only a change in behavior if the system is active. As demonstrated in Methods, this may produce interesting behaviors, but in general, it lacks the drive for exploration that is vital for a developing system.

The main reason for the lack in behavioral richness is seen in the product structure of both learning rules which involves the motor commands y generated by the neurons themselves. Trivially, once $y=0$, learning and any change in behavior stop altogether. Now, the idea is to lift this correlative structure entirely to the level of the outside world, enriching learning by the reactions of the physical system to the controls.

Let us assume the robot has a basic understanding of the causal relations between actions and sensor values. In our approach, this is realized by an inverse model which approximately relates the current sensor values $x\prime$ back to its causes, the motor commands y having a certain time lag w.r.t. $x\prime$. The model will reconstruct (the efference copy) y with a certain mismatch $\delta y$. Formulated in terms of the rates of change, we write

$$\dot{y}+\delta \dot{y}=F(\dot{x}\prime ),$$ [2]

with F being the model function and $\delta \dot{y}$ being the modeling error, containing all effects that cannot be captured by the model.

The aim of our approach is to make the system sensitive to these effects. This is achieved by replacing $\dot{y}$ of the DHL rule with $\tilde{\dot{y}}=\dot{y}+\delta \dot{y}$, so that

$$\tau {\dot{C}}_{ij}={\tilde{\dot{y}}}_i{\dot{x}}_j-C_{ij},$$ [3]

where τ is the time scale for this synaptic dynamics and $-C_{ij}$ is a damping term (Fig. 1). Because of the normalization introduced below, we do not need an additional scaling factor for the decay time. In principle, the inverse model F relates the changes in sensor values caused by the robot’s behavior back to the controller output, and the learning rule extends this chain further down to the synaptic weights. This is the decisive step in the “chaining together what changes together” paradigm. The $\delta \dot{y}$ in $\tilde{\dot{y}}$ contains all physical effects that are extrinsic to the system because they are not captured by the model. They are decisive for exploring the behavioral capabilities of the system. This is why we call the new mechanism defined by Eq. 3 differential extrinsic plasticity (DEP).

Optionally, the threshold terms $h_i$ [1] can also be given a dynamics which we simply define as

$${\tau }_h{\dot{h}}_i=-y_i,$$ [4]

where ${\tau }_h$ defines an empirical time scale. The idea is to drive the neurons away from their saturation regions (close to $y=\pm 1$). As the experiments will demonstrate, using the threshold dynamics favors periodic motion patterns. This is because the dynamics of $h_i$ causes a self-switching hysteresis oscillation (26), understood by considering that $y_i=0$ is an unstable fixed point and $h_i$ is driven to the opposite sign of $y_i$ and acting in Eq. 1 to actually invert the sign of $y_i$. So ${\tau }_h$ prescribes the mean frequency of the oscillations without environmental influences; however, the real frequency may be highly different. A precise tuning is not required.

In this framework the task of the inverse model is to root back (mostly small) changes in sensor values, given by $\dot{x}\prime$, to their causes, the changes in motor values given by $\dot{y}$. Thus, a very simple linear model is sufficient, i.e., $F(\dot{x}\prime )=M\dot{x}\prime$, where M is a weight matrix. The robots treated in this paper have only proprioceptive sensors directly reporting the result of the motor action, so each $x_i^{\prime }$ is only effected by $y_i$, such that we can fix $M=\mathbb{I}$ in all experiments of the present paper in the cases of both the humanoid robot and the hexapod robot. The extension of this basic setting to include delay sensors and other sensors will be discussed below. The approach also works with a learned inverse model from a motor babbling step as shown in Methods where we also discuss how it can be learned online.

To make the whole system active and exploratory, we introduce an appropriate normalization of the synaptic weights C and an empirical gain factor $\kappa \sim 1$. The latter regulates the overall feedback strength in the sensorimotor loop. If chosen in the right range, the extrinsic perturbations are amplified, and active behavior can be maintained; see Methods for details. This specific regime, called the edge of chaos, is argued to be a vital characteristic of life and development (27–29). The normalization is supported by neurophysiological findings on synaptic normalization (30) such as homeostatic synaptic plasticity (31) and the balanced state hypothesis (32, 33).

Whereas κ is seen to regulate the overall activity, τ is found to regulate the degree of exploration. As described in Methods, the system realizes a search and converge strategy, wandering between metastable attractors (such as walking patterns) with possibly very long transients. The time spent in an attractor (a certain motion pattern) is regulated by τ. At the behavioral level, this is reflected by the emergence of a great variety of spatiotemporal patterns—the global order obtained from the simple local rules given by Eqs. 3 and 4. The exploration timescale may also be changed online (e.g., interactively or by a higher level of learning) to freeze or tune into a behavior (low values) or to leave the current behavior (high values), but it was kept constant during the experiments reported here.

Behavior as Broken Symmetries.

To understand how very specific behaviors can emerge from the generic synaptic mechanism, we have to consider the role of symmetries. For a discussion, let us consider the system in what we call its least biased initialization, i.e., putting $C_{ij}=0$ and $h_i=0$ so that all actuators are at their central position. In this situation, the agent obeys a maximum number of symmetries. These are the obvious geometric symmetries but also several dynamical ones originating from the invariance of the physical system against certain transformations, like inverting the sign of a joint angle. Technically, the symmetries are seen directly by a linear expansion of the system around the resting situation. As the learning rule does not introduce any symmetry breaking preferences, motion can set in only by a spontaneous breaking of the symmetries. In this picture, behavior corresponds to broken symmetry (in space and time) and development to a sequence of spontaneous symmetry breaking events. This is the very reason for the rich phenomenology observed in the experiments, explaining the emerging dimensionality reduction which makes the approach scalable.

Self-organizing behavior as a result of symmetry breaking was observed before (34, 35) with precursors of the newly proposed learning rule. More specifically, related unsupervised learning rules based on the principle of homeokinesis (26) and the maximization of predictive information (36–39) were studied, which, however, differ in being biologically implausible due to matrix inversions.

Neurobiological Implementation.

To understand how the DEP rule can be implemented neurobiologically, we note first that $x\prime$ is just the reafference caused by y. Commonly, the contribution in $x\prime$ that cannot be accounted for by the (forward) model is called the exafference. Our extrinsic learning signal $\delta y$ is the preimage of this exafference using the forward model. With the inverse models used here, this preimage can be obtained explicitly by a simple neural circuitry calculating the difference between the output of the inverse model $F(x\prime )$ and the efference copy of y (Eq. 2). By feeding this signal back to the neuron by an additional synapse, the output of the neuron is shifted from y to $\tilde{y}$. With the modified output, the new synaptic rule corresponds to classical (differential) Hebbian learning. This procedure, although pointing a way to a concrete neurobiological implementation, is awkward because the additional signal has to be subtracted again from the neuron output before sending the latter to the motors.

Another possibility is the inclusion of the extrinsic term by a heterosynaptic or extrinsic plasticity (40) mechanism as illustrated in Fig. 1. The additional input from $\delta y$ has to simulate the effect of depolarization (firing) for the otherwise unchanged synaptic plasticity. This may by accomplished by G protein (41) signaling or the enhanced/inhibited expression of synapse-associated proteins (42), or via other intracellular mechanism.

The neuron model and synaptic dynamics are formulated in the rate-coding paradigm, abstracting from the details of a spiking neuron implementation. To represent each rate-neuron in our framework, a pool of spiking neurons is potentially required.

Results

Through the following series of experiments, we demonstrate the potential of the new synaptic plasticity for the self-organization of behavior. Even though no specific goal was given, the emerging behaviors seem to be purposeful, as if the learning system develops solutions for different tasks like locomotion, turning a wheel, and so forth. To avoid setting such a task orientation, we always use the same neural network (with the appropriate number of motor neurons and sensor inputs) with the DEP rule of Eq. 3 and start all experiments in its least biased initialization and without added noise. However, the dynamics is robust to large noise.

Early Individual Development.

In a first set of experiments, we study the very early stage of individual development when sensorimotor contingencies are being acquired. The common assumption is that sensorimotor coordination is developed by learning to understand sensor responses caused by spontaneous muscle contractions (called motor babbling in robotics). However, this fails by the abundance of sensorimotor contingencies as may be demonstrated by a coarse assessment for our humanoid robot. If we postulate that each of the m motor neurons has only 5 different output values (rates) we have $5^m$ possible choices. Therefore, with $m=18$ for the humanoid robot and 50 steps per second, a motion primitive of 1 s duration has $5^{{18}^{50}}$ realizations. The number of possible sensor responses is of the same dimension. Therefore, there is no way of probing and storing all sensorimotor contingencies. Alternatively, realizing a search by randomly choosing the synaptic connections ($C_{ij}$ with normalization, gain, and threshold dynamics) yields another tremendous number of possible behaviors, even if we restrict ourselves to the simplified nervous system formulated in Eq. 1.

By contrast, there is no randomness involved in the DEP approach. Both the physical dynamics and the plasticity rule are purely deterministic. Nevertheless, at the behavioral level, the above mentioned “search and converge” strategy creates a large variety of highly active but time-coherent motion patterns, depending on the initial kick, the combination of the parameters τ and κ, and the body–environment coupling.

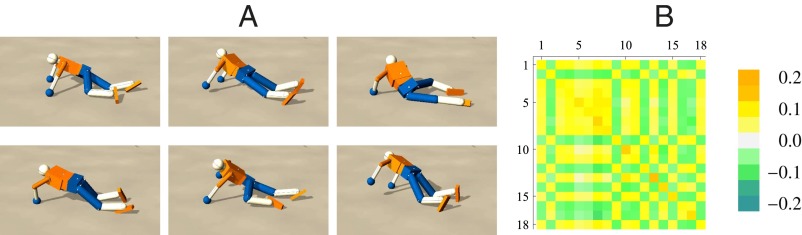
In the following example we consider the humanoid robot on level ground with a certain friction and elasticity. In addition to DEP, in this case, the threshold dynamics [4] was used which supports oscillatory behaviors. The robot starts upright with all joints in their center position ($y_i=0$) slightly above the ground and falls down to its feet and then to its arms, such that the robot is laying face down. The first contact with the ground and the gravitation exert forces on the joints that lead to nonzero sensor readings. This creates a first learning signal and leads to small movements which get more and more amplified and shaped by the body–environment interaction. As a result we observe more and more coordinated movements such as the swaying of the hip to either side. A long transient of different behavioral patterns follows ending up in a self-organized crawling mode (Fig. 2 and Movie S2). This mode is metastable and can be left by perturbations or changes in the parameters. Mainly forward locomotion is emerging, which is due to the specific geometry of the body. For an external observer this looks as if the robot is following a specific purpose, exploring its environment, which is not built in but emerges. When the parameters of the body are changed, e.g., the strength of certain actuators, different behaviors will come out. For instance, a low crawling mode is generated if the arms are weaker.

Fig. 2.

Behavior exploration of the humanoid robot. (A) Crawling-like motion patterns when on the floor. (B) The corresponding controller matrix C reveals a definite structure. Note that the threshold dynamics was included here, which is an important factor for this highly organized behavior.

Hexapod: Emerging Gaits.

In the humanoid robot case, the preference of forward locomotion can be related back to the specific geometry of the body. When the robot is on its hands and knees, the lower legs break the forward–backward symmetry so that backward locomotion is more difficult to achieve. Let us consider now the hexapod robot (Fig. 3), which has an almost perfect forward–backward symmetry, which must be broken for a locomotion pattern. This may happen spontaneously, but in most experiments, motions like swaying or jumping on the spot are observed; see Learning the Model below.

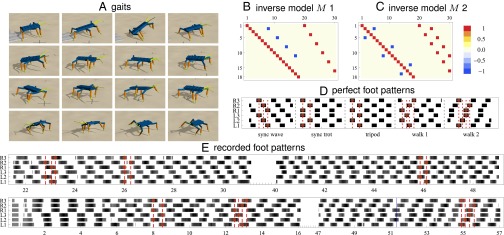
Fig. 3.

Hexapod: emerging gait patterns. The robot is inspired by a stick insect and has 18 actuated DoF. There are $18+12$ sensors (joint angle + delayed ones by 0.2 s). The robot performs different gaits when controlled with DEP: synchronous wave (A, row 1), synchronous trot (A, row 2), tripod (A, row 3), walk 1 (A, row 4), and walk 2 with their corresponding step patterns in D (black means foot is down). The fixed inverse models M in two configurations are displayed in B and C. Recorded foot patterns for model M 1 (E, Top) and model M 2 (E, Bottom) show the transitions between different gaits. Shown is the leg’s vertical position where black means leg is down and white means above center position. These transitions are either spontaneous or induced by interactions with the environment or by changes in the sensor delay. Markers (red dashed lines and points) indicate the gait patterns for synchronous wave, synchronous trot, and tripod (Top) and tripod, walk 1, and walk 2 (Bottom). See also Movie S3A.

Let us now demonstrate how the system can be guided to break its symmetries in a desired way. This method has essentially two elements. On one hand, we have to provide additional sensor information to facilitate circular leg movements. This is done by providing the delayed sensor values of the 12 coxa joint sensors (all sensors could have been used). On the other hand, guidance is implemented by structuring the inverse model M appropriately by hand, which is a new technique for guided self-organization of behavior (43). The rationale is that those connections in the model are added where correlations/anticorrelations in the velocities are desired. For the oscillations of the legs, the delayed forward–backward (anterior/posterior) sensor is linked to the up–down (dorsal/ventral) direction. To excite locomotion behavior, the properties of desired gaits can be specified such as in-phase or antiphase relations of joints. We present here two possibilities where only few such relations are specified to give room for multiple behavioral patterns.

In the first configuration the anterior/posterior direction of subsequent legs should be antiphase, resulting in only four negative entries in M (Fig. 3B). Note that there are no connections between the left and right legs. In the experiment the robot performs the first locomotion pattern already after a few seconds. A sync wave gait emerges where legs on both sides are synchronous and hind, middle, and front leg pairs touch the ground one after another. This transitions into a sync trot gait where hind and front legs are additionally synchronized. After a perturbation (from getting stuck with the front legs) the common tripod (44) (type c) gait emerges (Fig. 3).

The second configuration resembles what is observed in biological hexapods, namely, that subsequent legs on each side have a fixed phase shift (which we achieve by linking in M the delayed sensor and motor of subsequent legs) and that legs on opposite sides are antiphasic. This results in model M 2 (Fig. 3C). In the experimental run the initial resting state develops smoothly to the tripod gait. Decreasing the time delay of the additional sensors leads first to a gait with seemingly inverse stepping order which we call walk 1 and which is also observed in insects (44) (type f). For a smaller delay an inverted ripple gait (45) appears that we call walk 2 (Fig. 3 and Movie S3A).

An important feature of these closed-loop control networks is that they can be used to control nontrivial behavior with fixed synaptic weights, obtained by taking snapshots or from clustering (Fig. S1). Behavior sequences can easily be generated by just switching between these fixed sets of synaptic weights. We demonstrate this using the humanoid robot with different crawling modes in Movie S4A and using the hexapod robot by sequencing all of the emergent gaits in Movie S4B. Notably, the transition between motion patterns is smooth and autonomously performed. In a biological setting different circuits for each behavior have to be used whose outputs can be gated/combined to perform a sequence of behaviors. The learning of these circuits can be performed simultaneously using the same learning rule and stopped as soon as a useful behavior is detected.

Fig. S1.

Clustering of the controller matrices of Movie S2. Displayed are the cluster centers for some of the clusters. The names were given after a visual inspection of their corresponding behavior (Movie S4).

Finding a Task in the World.

Up to now, we have seen how the DEP rule bootstraps specific motion patterns contingent on the physical properties of the body in its interaction with a static environment. A new quality of motion patterns is achieved when the robot interacts with a dynamical, reactive environment. For a demonstration we consider a robot sitting on a stool with its hands attached to the cranks of a massive wheel (Fig. 4). Again, we start with the least biased initialization and with the unit model.

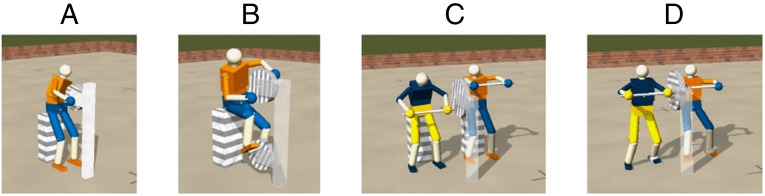
Fig. 4.

Interacting with the environment. The humanoid robot at the wheel with cranks (A); with two wheels (B); and with two robots, each at one of the handles, sitting (C) and standing (D) (Movies S5A and S6A).

Rotating the wheel.

Different from a static environment, the massive wheel exerts reactive forces on the robot depending on its angular velocity, which is a result of the robot’s actions in the recent past. This response and its immediate influence on the learning process initially lead to a fluctuating relation between wheel and robot. This eventually becomes amplified to end up in a metastable periodic motion (Movie S5A). This effect depends on the mass of the wheel. If the inertial mass is too low, it does not provide enough feedback to the robotic system, and the wheel is typically turned back and forth. Once the mass is large enough, continuous turning occurs robustly for a large range of wheel masses (one order of magnitude).

From the point of view of an external observer, one may say that the learning system is keen on finding a task in the world (rotating the wheel) which channels its search into a definite direction. It cannot be stressed enough that the robot has no knowledge whatsoever about the physical properties and/or the position and dynamics of the wheel. All the robot has is the physical answer of the environment (the wheel) by the reactive forces. In this way the robot detects affordances (46) of the environment. An affordance is the opportunity to perform a certain action with an object, like a chair affords sitting and a wheels affords turning.

The constitutive role of the body–environment coupling is also seen if a torque is applied to the axis of the wheel. Through this external force we may give the robot a hint of what to do. When in the fluctuating phase, the torque immediately starts the rotation which is then taken over by the controller. Otherwise, we can also advise the robot to rotate the wheel in the opposite direction (Movie S5A). This can be considered as a kinesthetic training procedure, helping the robot in finding and realizing its task through direct mechanical influences.

Multitasking.

In a variant of this experiment, the feet also get attached to a separate wheel. Because of the simpler physics [fewer degrees of freedom (DoF)], the leg part of the robot requires much less time to find its task than the upper body (Movie S5B). The lack of synchronization between the two subsystems is also noteworthy. At first sight, this is no surprise because the upper and the lower body are completely physically separated (the robot is rigidly fixed on the stool). However, there is an indirect connection given by the fact that each subsystem sees the full set of sensor values. Actually, this might support synchronization given the correlation affinity of the DEP rule. However, due to the largely different physics, synchronization occurs only temporarily, if at all, so that two different subsystems appear, each with their own behavior.

Emerging cooperation.

We have seen above how an exchange of forces with the environment may guide the robot into specific modes. In this paragraph we show how this can be extended to interacting robots by coupling them physically or letting them exchange information. For a demonstration, we extend the wheel experiment by having two robots, each driving one of the cranks (Fig. 4 C and D). In this setting, the robots can communicate with each other through the interaction forces transmitted by the wheel. So, through the induced perturbations of its proprioceptive sensor values, each robot can perceive to some degree what the other one is doing. These extrinsic effects can be amplified through the DEP rule, eventually leading to synchronized motion (Movie S6A). Seen from outside, the robots must cooperate to rotate the wheel, and this high-level effect unexpectedly emerges in a natural way from the local plasticity rule.

Discussion

This paper reports a simple, local, and biologically plausible synaptic mechanism that enables an embodied agent to self-organize its individual sensorimotor development. The reported in silico experiments have shown that at least on the level of sensorimotor contingencies, self-determined development can be grounded in this synaptic dynamics, without having to postulate any higher-level constructs such as intrinsic motivation, curiosity, goal orientation, or a specific reward system. The emerging behaviors—from various locomotion patterns to rotating a wheel and to spontaneous cooperation induced by force exchange with a partner—realize a degree of self-organization unprecedented so far in artificial systems. These do not require modifications of the DEP rule, and for many examples, no task-specific information was provided. To guide symmetry breaking in the space of all possible behaviors, few additional hints can be provided, leading, for instance, to various locomotion gaits in a hexapod robot. The emergent behaviors are all oscillatory. Discrete movements cannot be generated as they end in fixed points of the sensorimotor dynamics which are destabilized by the synaptic rule. Our demonstrations use artificial systems, which is often a problem in computational neuroscience and robotics due to a discrepancy between the behavior of artificial and real systems. In our approach this discrepancy problem is circumvented because the behavior is not the execution of a plan but emerges from scratch in the dynamical symbiosis of brain, body, and environment. Commonly, learning to control an actuated system faces the curse of dimensionality, both in a model and in reality. Without a proper self-organization process or hand-crafted constraints, adding one actuator leads to a multiplicative increase in the time required to find suitable behaviors. We provide evidence for adequate scaling properties of our approach with systems of up to 18 actuators developing, without any prestructuring, useful behaviors within minutes of interaction time. Additionally, we have given arguments on a system theoretical level that by being at the edge of chaos and allowing for spontaneous symmetry breaking, our approach may scale up to systems of biological dimensions, like humans with their hundreds of skeletal muscles.

The presence of the DEP rule in nature may change our understanding of the early stages of sensorimotor development because it introduces an apparent goal orientation and a self-determined restriction of the search space. It still remains an open question whether nature found this creative synaptic dynamics. The simplicity of the neural control structure and the DEP rule, combined with its potential to generate survival-relevant behavior such as locomotion and adaptivity to largely new situations, are good arguments for evolution having discovered it. In addition, the synaptic rule has a simple Hebbian-like structure and may be implemented by combining homosynaptic and heterosynaptic (extrinsic) plasticity mechanisms (40) in real neurons.

The DEP rule may also explain saltations in natural evolution. It is commonly assumed that new traits are the result of a mutation in morphology accompanied by an appropriate mutation of the nervous system, making the likelihood of selection very low because it is the product of two very small probabilities. With DEP, new traits would emerge through mutations of morphology alone. For instance, the fitness of an animal evolving from water to land will be greatly enhanced if it can develop a locomotion pattern on land in its individual lifetime, which could easily be achieved by the DEP rule. Following the argument by Baldwin (47, 48), the self-learning process could be replaced in later generations by a genetically encoded neuronal structure making the new trait more robust.

Adaptability to major changes in morphology may also be necessary for established species during their lifetime. For instance, changes in mass and dimension of body parts due to growth or injuries such as leg impairments or losses have to be accommodated. It has long been known that even small animals such as insects have this capability and substantially reorganize their gait patterns (44). This could be achieved with special mechanisms, but with DEP it comes for free.

Another point concerns the role of spontaneity and volition in nature. Obviously, acting spontaneously is an evolutionary advantage because it makes prey less predictable to predators. Attempts to explain spontaneity and volition range from ignoring it as an illusion to rooting it deep in thermodynamic and even quantum mechanical randomness (49, 50). We cannot give a final explanation, but the DEP rule provides a clear example of how a great variety of behaviors can emerge spontaneously in deterministic systems by a deterministic controller. The new feature is the role of spontaneous symmetry breaking in systems at the edge of chaos. Similarly, there are recent trends in explaining the apparent stochasticity of the nervous system through the complexity of deterministic neural networks (51–53).

This paper studies a neural control unit in close interaction with the physical environment. However, DEP may also be effective in self-organizing the internal brain dynamics by considering feedback loops with other brain regions. This is possible because the DEP approach does not need an accurate model of the rest of the brain—which could never be realized—but requires only a coarse idea of the causal features of the system’s response. In this context our study may provide ingredients required for the big neuroscience initiatives (9) to understand and subsequently realize the functioning brain.

Methods

Normalization.

For controlling the robot we use normalized weight matrices C in Eq. 1. We have the option to perform a global normalization or an individual normalization for each neuron: In global normalization, the entire weight matrix is normalized, $C\leftarrow \kappa C/\left(\Vert C\Vert +\rho \right)$. In individual normalization, each motor neuron is normalized individually, $C_{ij}\leftarrow \kappa C_{ij}/\left(\Vert C_i\Vert +\rho \right)$.

For the global normalization, the Frobenius norm $\Vert C\Vert$ is used, and for the individual normalization, $\Vert C_i\Vert$ denotes the norm of the ith row (length of synaptic vector of neuron i). The regularization term $\rho ={10}^{-12}$ becomes effective near the singularity at $C=0$ or $C_i=0$ and keeps the normalization factor in bounds. Neurobiologically, the normalization can be achieved by a balancing inhibition on a fast timescale accompanied by homeostatic plasticity on a slower timescale.

With κ small (compared with 1), activity breaks down so that the system converges toward the resting state where $\dot{x}=0$. With κ sufficiently large, this global attractor is destabilized so that modes start to self-amplify, ending up in full chaos for large κ. Within an appropriate range of values for κ, the system is led toward an exploratory but still controllable behavior. The parameter could also be adapted autonomously, e.g., to reach a certain mean target amplitude of the motor values.

The type of normalization has a strong effect on the resulting behavior. Individual normalization leads to behaviors that involve all motors because each motor neuron is normalized independently. By contrast, global normalization can restrict the overall activity to a subset of motors. An example for global normalization is the humanoid robot at the wheel (Movie S5A), where the legs are inactive because initially, the arms are moving more strongly, such that only correlations in the velocities of the upper body build up.

How It Works.

Let us start with a fixed point analysis of the Hebbian learning case with M being the unit matrix (as in the humanoid case). Ignoring nonlinearities for this argument (small vectors x and y), the dynamics in the model world is $x\prime =y=\alpha Cx$, where α is the normalizing factor. The system is in a stationary state if $x\prime =x$, which is the case if x is an eigenvector of C with eigenvalue $1/\alpha$. In such a state the learning dynamics ($\tau {\dot{C}}_{ij}=y_i{x}_j-C_{ij}$) converges toward $C=x{x}^{\mathrm{\top }}$, due to the decay term. Using this in the stationary state equation ($x=\alpha Cx$) yields the condition $x=\alpha x{\Vert x\Vert }^2$ such that any vector x with ${\Vert x\Vert }^2=1/\alpha$ can be a stationary state, a Hebb state, of the learning system. This means that the Hebb rule generates a continuum of stationary states instead of an exploratory behavior.

In the plain DHL case a global stationary state exists if the system is at rest so that $C=0$ (recall plasticity rule: $\tau {\dot{C}}_{ij}={\dot{y}}_i{\dot{x}}_j-C_{ij}$). However, if $C\ne 0$, the normalization may counteract the effect of the decay term in the plasticity rule. Thus, Hebb-like states can be stabilized for a while until the regularization term ρ stops this process and C decays to zero. The thereby induced decay $y\to 0$ generates motion in the system, leading to a learning signal. With κ large, this may avoid the convergence altogether so that the system can find another Hebb state and so forth. However, the activities elicited by the interplay between the normalization and the learning dynamics are rather artificial and less rich because they do not incorporate the extrinsic signals given by $\delta y$. In particular, the plain DHL rule has no means of incorporating the extrinsic effects provided by additional sensor information as described in the next section.

The novel feature of the proposed DEP rule (Eq. 3) is the leading role of the extrinsic signal ($\delta y$). For a demonstration, consider the trivial case $\dot{y}=0$, where the body is at rest and will stay there as long as there are no extrinsic perturbations. However, if the body is kicked by some external force, x, $x\prime$ and hence $\tilde{\dot{y}}$ may vary so that C changes and the system is driven out of the global attractor if κ is sufficiently large. In fact, in the experiments we observe how an initial kick acts like a dynamical germ for starting individual behavior development. Moreover, in the behaving system, external influences may change the behavior of the system; see, for instance, the gait switching of the hexapod after being perturbed by obstacles (Movie S3A) or the phenomenon of emerging cooperation of the humanoids (Movie S5A). A quantitative comparison of the learning rules is given in Comparison of Synaptic Rules below.

The next remark concerns the dichotomy between learning as formulated in the velocities and the control of the system based on the (angular) positions, which is vital for the creativity of the DEP rule [3]. This feature can be elucidated by a self-consistency argument, assuming the idealized case where the system is in a harmonic oscillation (e.g., an idealized walking pattern) with period T. By way of example, let us consider the 2D case with a rotation matrix $U\left(s\right)$, generating a periodic motion by rotating a vector $x\left(\alpha \right)={\left(\cos \alpha ,\sin \alpha \right)}^{\mathrm{\top }}$ by an angle s, i.e., $U\left(s\right)x\left(\alpha \right)=x\left(\alpha +s\right)$. We use that $x\prime$ is obtained by the time evolution of x over a finite time step so that $x\prime \left(\alpha \right)=x\left(\alpha +\theta \right)=U\left(\theta \right)x\left(\alpha \right)$ and $\langle \dot{x}\prime {\dot{x}}^{\mathrm{\top }}\rangle =U\left(\theta \right)\langle \dot{x}{\dot{x}}^{\mathrm{\top }}\rangle$. Taking the average over one period we have $\langle \dot{x}{\dot{x}}^{\mathrm{\top }}\rangle \propto \langle x{x}^{\mathrm{\top }}\rangle$ as $\dot{x}$ is a phase shifted copy of x times a factor. For averaging, we consider infinitesimally short time steps so that sums may be replaced with integrals. We obtain $\langle \dot{x}{\dot{x}}^{\mathrm{\top }}\rangle \propto {\displaystyle \int x\left(\alpha \right)x{\left(\alpha \right)}^{\mathrm{\top }}d\alpha \propto I}$, where I is the unit matrix, because ${\displaystyle \int {\text{cos}}^2\left(\alpha \right)d\alpha }={\displaystyle \int {\text{sin}}^2\left(\alpha \right)d\alpha \propto 1}$ and ${\displaystyle \int \text{sin}\left(\alpha \right)\text{cos}\left(\alpha \right)d\alpha =0}$. Neglecting the extrinsic effects, i.e., $\delta y=0$, under these idealized conditions, we may write in the linear regime $Mx\prime =y=Cx$ and with $C=M\langle \dot{x}\prime {\dot{x}}^{\mathrm{\top }}\rangle \propto MU\left(\theta \right)$ we obtain $x\prime =U\left(\theta \right)x$ corroborating that the periodic regime is stationary if the gain factor is chosen appropriately.

In higher dimensions the argument is more involved, but it carries over immediately to the case of rotations about an axis, corresponding to the case that the Jacobian matrix $J=MC$ has just one pair of complex eigenvalues different from zero. This situation is often observed in the experiments, e.g., with the hexapod, even though these experiments are very far from the idealized conditions postulated for the self-consistency argument above.

These patterns are self-consistent solutions of the mentioned dichotomy between control itself and the synaptic dynamics that generates it. As the experiments show, these patterns are metastable attractors of the whole-system dynamics, so that globally, the system realizes a search and converge strategy by switching between metastable attractors via possibly long transients. At the behavioral level, this is reflected by the emergence of a great variety of spatiotemporal patterns—the global order obtained from the simple local rules given by Eqs. 3 and 4. Metastable attractors and near-chaotic dynamics were used for exploration with great success (54, 55) although with central pattern generators as source of oscillatory behavior, whereas here these are generated from the developing sensorimotor coupling.

Parameter Selection: No Fine Tuning Required.

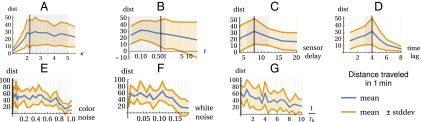
Here we show that the choice of parameters is not critical and works for a wide range of values. The hexapod locomotion experiment allows us to simply quantify success: the distance traveled from the initial position within 1 min after the start. Remember that there is no specific goal for locomotion, just that the guidance restricts the search space such that locomotion behaviors are favored. Fig. 5 shows the result of a parameter scan for all used parameters; additionally, it shows that enabling the threshold dynamics does not degrate performance and that the method is very robust to added noise. The time lag should be chosen to be around the time required for an action to show effect in the sensors. Depending on the update rate of the sensorimotor loop and possible signal delays, a different range may be appropriate.

Fig. 5.

Parameter dependency of the performance of the hexapod robot. Shown are the mean and SD of the traveled distance in 1 min for different parameters. (A–D) Exhaustive parameter scan. For each panel, all other parameters are varied in their gray shaded regions indicated in A–E. (E–G) Single scans for standard parameters (see black lines in A–E and G) with 10 initialization conditions each (random seed for noise and robot’s initial height). (A) Activity parameter (Methods). (B) Time scale for learning dynamics, Eq. 3 in s. Note logarithmic scale. (C) Time delay of delayed sensor values in $1/50$ s. (D) Time lag between y and $x\prime$ in $1/50$ s. (E) Strength v of additive colored sensor noise [Ornstein–Uhlenbeck with $\theta =0.1v,\sigma =\sqrt{0.1}v,\mu =0$ (10 time steps correlation length), and $\sigma =\frac{1}{2}v$]. (F) Strength v of additive white noise uniformly distributed in $\left[-v,v\right]$. (G) Inverse time scale (in 1/s) of threshold learning dynamics (0 means disabled).

Further, we note that the choice of parameters influences which behaviors emerge exactly, in particular for the case without guidance, but the behaviors are qualitatively similar.

Learning the Model.

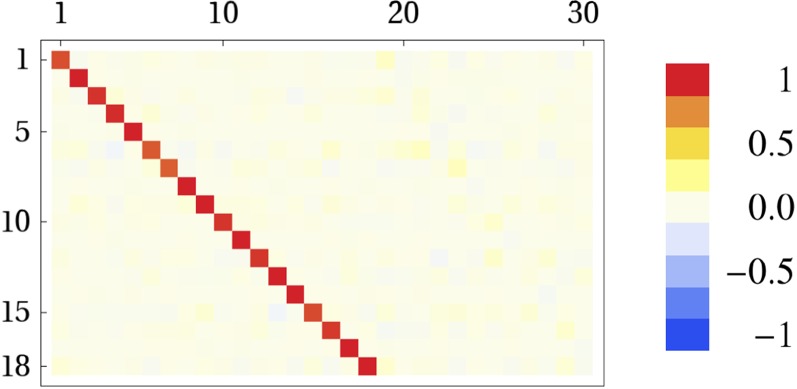
Here we show how to learn the inverse model and remark on its role. Remember that the model’s task is to relate changes in sensor values $\dot{x}\prime$ to their causes $\dot{y}$. Modeling this sensor–motor coordination can be most easily done in a preparatory step using a simple motor babbling in an idealized situation, i.e., by suspending the robot in the air to avoid ground contact and controlling each motor with an independent varying harmonic oscillatory signal. For the robots in this paper, a simple linear model $F\left(u\right)=Mu$ is appropriate with a simple learning procedure like $\mathrm{\Delta }{M}_{ij}={\mathit{ϵ}}_M{e}_i{x}_j$, where $e=\left(y-Mx\prime \right)$ and ${\mathit{ϵ}}_M$ is the learning rate which can be annealed as $1/\sqrt{\left(t\right)}$ (t time steps). As y is the target and $x\prime$ is the measured joint angle, in the idealized situation, one obtains essentially $M=\mathbb{I}$ (unit matrix) with minor deviations which are not decisive for the development of the behaviors. In Movie S7 the learning of the inverse model and the behavior of the robot are shown; see also Fig. 6. The behavior is the same as with the unit model: occasional locomotion patterns are developed, but no stable behavior is found by the dynamics. Adding the additional entries as in M 1 recovers the observed locomotion behavior. Therefore, we use $M=\mathbb{I}$ in all of the other experiments to introduce less bias.

Fig. 6.

Inverse model M obtained from 15-min motor babbling of the hexapod. The rows correspond the weight vectors used to predict each motor value.

Actually, the learning of sensor motor mappings can also be realized concomitantly with the controller’s development. However, this poses a serious difficulty because the model must reflect the causal relationship between sensors and motors. When learning the model F from pairs $\left(\dot{x}\prime ,\dot{y}\right)$ the correlations between ${\dot{x}}_j^{\prime }$ and ${\dot{y}}_i$ for all $i,j$ are learned. In a periodic motion (walking pattern), there are strong correlations for all combinations of sensors and motors. In the case of a linear model, all $M_{ij}$ are roughly of the same size, in striking contrast to $M=\mathbb{I}$ as obtained from the uncorrelated learning above. Thus, naive simultaneous learning produces a wrong result. This is a well-known fact from statistics that correlations do not imply causation; see, for instance, ref. 56. So, extending the model makes sense only with explicitly causal models based on or combined with intervention learning realized by adding uncorrelated perturbations to the controller output y and measuring the correlations of the perturbations with $x\prime$. We refer to the literature on causal Bayesian networks (56, 57).

Note that if the inverse model is perfect, the learning rule [3] becomes the DHL rule. However, if behaviors have been explored to generate enough data to train the model to be perfect, there is no further exploration required.

Comparison of Synaptic Rules.

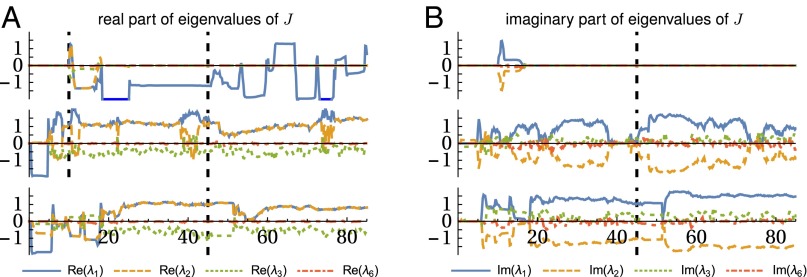
In this section we want to compare the different synaptic rules. We will consider them in their pure form without the threshold dynamics, i.e., $h=0$. Also in experiments we can confirm that plain Hebbian learning produces fixed point behaviors and thus no continuous motion. Therefore, we will only compare DHL with DEP using the hexapod robot as example. To provide a fair comparison the hexapod robot is started in three identical experiments, except for the plasticity rules: DHL, $\tau {\dot{C}}_{ij}={\dot{y}}_i{\dot{x}}_j-C_{ij}$; DEP, $\tau {\dot{C}}_{ij}=\widetilde{{\dot{y}}_i}{\dot{x}}_j-C_{ij}$ [3] (with unit model); and DEP-Guided with model M 1 (Fig. 3B). Note that the same synaptic normalization and decay are used everywhere. Because DHL is not able to depart from the $C=0$ condition, we copy the synaptic weights (C) of the DEP run to the DHL experiment after 10 s. We then consider the eigenvalue spectrum and the corresponding eigenvectors of the Jakobian matrix $J=MC$ of the sensorimotor dynamics (for DHL and DEP $M=\mathbb{I}$). The matrix J captures the linearized mapping from x to $x\prime$—the dynamics of the sensors. For DHL the matrix reduces to have only a single nonzero eigenvalue. This, in turn, means that all future sensor values are projected onto the corresponding eigenvector, and the learning dynamics cannot depart from that. This is demonstrated in Fig. 7 and Movie S8. Under heavy perturbations the robots controlled by DEP change their internal structure and subsequently show a different behavior. For a different initialization, DHL (with normalization) may also produce continuous motion patterns, but it is generally much less sensitive to the embodiment and perturbations and often falls into the $C=0$ state, which it cannot exit anymore.

Fig. 7.

Comparison of plasticity rules: DHL, DEP, and DEP-Guided (with structured model) (from top to bottom). Development of the eigenvalues $\left({\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_6\right)$, real part in A and imaginary in B, of the Jakobian matrix $J=MC$ of the sensorimotor dynamics over time. After 10 s (dashed vertical line) the synaptic weights from DEP were copied to DHL to get some nonzero initialization. The dashed vertical line at 45 s marks a strong physical perturbation which leads to changes in behavior for the DEP rule but not for DHL (Movie S8). Only for DEP do the eigenvectors (Movie S8) and the spectrum change significantly after the perturbations. Parameters are as follows: global normalization, $\kappa =2.2,h=0,\hspace{0.17em}\text{and}\hspace{0.17em}\tau =0.7$ s.

Framework.

The use of artificial creatures has proven a viable method for testing neuroscience hypotheses, providing fresh insights into the function of the nervous system; see, for instance, ref. 19. The benefit of such methods may be debatable on the level of brain processes of higher complexity. So, we focus on lower-level sensorimotor contingencies in settings where the nervous systems cannot be understood in isolation due to a strong brain–body–environment coupling (16, 58). The method works both with hardware robots and with good physical simulations. The inexorable reality gap between simulations and real robotic experiments is a minor methodological problem because the phenomenon of self-organization is largely independent of the particular implementation, as evidenced by the fact that emerging motion patterns are robust against modifications of the physical parameters of both robot and environment.

The control structure in this paper is deliberately chosen to be simple to demonstrate the method’s potential. Although the time lag of sensory feedback is too long for this setting in larger animals, it may still be successful by integrating sensor predictions, a trick the nervous system is using whenever possible (59). In the following we discuss several of the methodological issues in detail.

Initialization.

To have reproducible conditions for our experiments, we always start our system under definite initial conditions. In all our applications we use the same plasticity rule (with appropriately chosen time scale τ and gain factor κ) and, moreover, always start in the same initial conditions for the synaptic dynamics by choosing $C=0$ and $h=0$, meaning that all actuators of the joints are in their central position. In a sense, this is also a state of maximum symmetry because there is (approximately) no difference in moving the joint either forward or backward, so that the observed behaviors are emerging by spontaneous symmetry breaking (34, 35).

Source of variety.

In many robotics approaches to self-exploration and learning of sensorimotor contingencies, innovation is introduced by modifying actions randomly (60, 61), relegating the activities of the agent to the intrinsic laws of a pseudorandom number generator that is entirely external to the system to be controlled. This applies also when the actions are only performed in mental simulation (62). This invokes the curse of dimension as the search is not restricted by the specifics of the brain–body–environment coupling. A more deterministic approach is to use chaos control (55), which, however, requires a specific target signal (e.g., periodicity). In our system, there is only one intrinsic mechanism—the DEP rule—which generates actions deterministically in terms of the sensor values over the recent past (on a timescale given by τ). Variety is produced by the complexity of the physical world in the sense of deterministic chaos. Another approach to obtain informed exploration is to use notions of information gain (63–65) which became recently scalable (66) to the high-dimensional continuous systems.

Simulation.

The experiments are conducted in the physically realistic rigid body simulation tool LpzRobots (22). The tool is open source so that the experiments described in this paper can be reproduced (Simulation Source Code). The humanoid robot (Fig. 2) has the proportions and weight distributions of the human body. The joints are simplified, and only one-axis and two-axis joints are used. The DoF are as follows: 4 per leg (2 hip, knee, and ankle), 3 per arm (2 shoulder and elbow), 1 for the pelvis (tilting the hip), and 3 in the back (torsion and bending front/back and left/right), summing up to 18 DoF.

The hexapod robot (Fig. 3) is inspired by a stick insect and has 18 DoF, 3 in each leg: 2 in the coxa joint and 1 in the femur–tibia joint ($\alpha ,\beta ,\gamma$ in ref. 67). The antennae and tarsi are attached by spring joints and are not actuated.

To implement the actuators we use position-controlled angular motors with strong power constraints around the set point to make small perturbations perceivable in the joint position sensors. Internally, these are torque-limited velocity-controlled motors implemented as physical constraints (implicit look-ahead of acting forces) where the allowed torque f is $f=f_{\text{max}}\text{tanh}\left(0.01+\left|x-x_{\text{target}}\right|\right)$ (26). In this way they perform more like muscles and tendon systems and make the robot compliant to external forces.

Movies of the conducted experiments are presented. Information on the source code is given in Simulation Source Code.

Memorizing and Recalling Behavior

By either taking snapshots of the synaptic weights or, more objectively, using a clustering procedure, a set of fixed control structures can be extracted. Examples of such a clustering are shown in Fig. S1. If these synaptic connections are used in the controller network, the behavior can be reproduced (without synaptic dynamics) in most cases. A demonstration is given in Movie S4A where five clusters from Movie S2 A and B have been selected for demonstration. The switching between behaviors may not be successful if the old behavior does not lie in the basin of attraction of the new one. This happens in particular when starting from inactive behaviors, but this can be helped by a short perturbation. In a second experiment we show how snapshots of the weights taken during Movie S3 A and B can be used to memorize and recall all of the different emergent gaits. The synaptic weights have been copied instantaneously without selecting a precise time point or averaging. In fact, during learning for one particular gait a whole series of weights occurred, but apparently, any of these weight sets is a viable controller.

Simulation Source Code

The experiments can be reproduced by using our simulation software and the following sources. The simulation software can be downloaded from robot.informatik.uni-leipzig.de/software or https://github.com/georgmartius/lpzrobots and has to be compiled on a Linux platform (for some platforms, packages are available). The source code for the experiments of this paper can be downloaded from playfulmachines.com/DEP. Instructions for compilation and execution are included in the bundle.