Extreme electron polaron spatial delocalization in π-conjugated materials

Significance

π-Conjugated organic molecules offer an added dimension to traditional inorganic materials in transistors, solar cells, and light-emitting diodes. The spatial extent over which charges are spread within an organic structure is associated with a material’s suitability for these applications. Here, using two experimental spectroscopic techniques, coupled with computational analysis, we determine the distribution of negative charges within designed organic molecules comprised of multiple π-conjugated repeat units. We find that negative charges in these highly conjugated organic structures are dispersed over greater areas relative to any other organic material that has been studied to date. This discovery is significant, as the design of organic materials that adeptly accommodate and transmit negative charges remains a significant challenge in materials science.

Abstract

The electron polaron, a spin-1/2 excitation, is the fundamental negative charge carrier in π-conjugated organic materials. Large polaron spatial dimensions result from weak electron-lattice coupling and thus identify materials with unusually low barriers for the charge transfer reactions that are central to electronic device applications. Here we demonstrate electron polarons in π-conjugated multiporphyrin arrays that feature vast areal delocalization. This finding is evidenced by concurrent optical and electron spin resonance measurements, coupled with electronic structure calculations that suggest atypically small reorganization energies for one-electron reduction of these materials. Because the electron polaron dimension can be linked to key performance metrics in organic photovoltaics, light-emitting diodes, and a host of other devices, these findings identify conjugated materials with exceptional optical, electronic, and spintronic properties.

Organic π-conjugated materials have found utility in photovoltaic, field-effect transistor, and light-emitting diode devices (1) and are playing a role in spintronics research as well (2). Facilitating this ascendance is the advent of structures that extensively delocalize charges over rigid sp² frameworks. These compositions minimize intramolecular electron-phonon coupling (internal reorganization energy, λ_i) (3, 4), allowing them to accommodate, transmit, and delocalize charges despite intrinsic dielectric constants that are low. Keen interest in organic electron transport media (n-type materials) (5) fuels ongoing exploration into the fundamental properties of the electron polaron, a negatively charged, spin-1/2 excitation, and its associated lattice deformation (6, 7). The polaron is the principal charge carrier in organic electronic media, as observed by electron spin resonance (ESR) measurements on field-effect devices (8, 9) and organic solar cells (10). The inverse relationship between the number of π-conjugated atoms over which a polaron is delocalized and the associated λ_i connects polaron dimension directly with thermal barriers to hopping transport (11), whereas in organic photovoltaic devices, rapid charge delocalization defines an important mechanism that mitigates Coulombic stabilization of photogenerated electron-hole pairs to create separated free charge carriers (12–15).

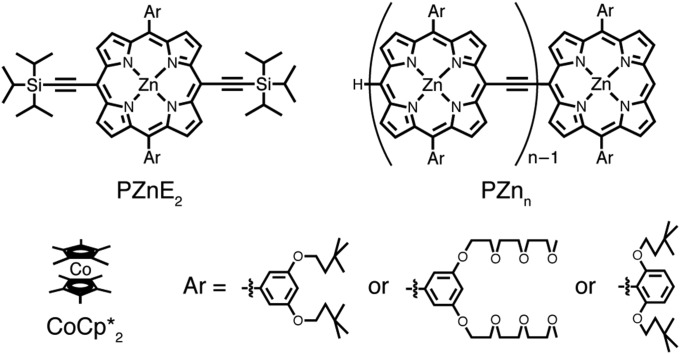
One class of conjugated materials that displays exceptional optical and electronic properties is meso-to-meso ethyne-bridged (porphinato)zinc(II) oligomers (PZn_n; Fig. 1) (16). Break junction single molecule conductance measurements on thiol-terminated PZn_n have demonstrated a distance-dependent junction resistance that followed exponential behavior (R = R₀e^βL, where R₀ is the contact resistance and β is the transmission decay constant across the barrier). A β value of 0.034 Å⁻¹ determined for PZn_n, the lowest yet determined for thiol-terminated single molecules, establishes the potential for charge transfer mediated by these π-conjugated structures at electrode interfaces. Steady-state and time-resolved electronic absorption spectroscopy establishes that PZn_n oligomers evince lowest excited singlet states that are globally delocalized (17, 18). Variable-temperature solution-phase X-band ESR spectroscopic studies of p-doped PZn_n showed that [PZn_n]^+• structures define the longest hole polarons yet measured for a π-conjugated material in solution (∼7.5 nm) (19). Although these previous findings establish exceptional delocalization of ground, photoexcited, and hole polaron states for PZn_n and closely related materials (20), little is known regarding the anion radical (electron polaron) states of such species.

Fig. 1.

Structures of PZnE₂, PZn_n oligomers, and decamethylcobaltocene (CoCp*₂).

Here, we describe solution phase, concurrent visible–near infrared (vis-NIR) optical and ESR spectroscopic measurements, along with electronic structure calculations, of the n-doped (radical anion) states of π-conjugated multiporphyrin arrays to reveal electron polarons having unprecedented, vast spatial delocalization. This discovery signals that electron-lattice couplings are extraordinarily weak in these n-doped porphyrin oligomers; because the extents of these couplings determine, in large part, the magnitudes of interchain charge hopping rate constants and charge mobilities (11), the efficiency at which charge-separated states may be photogenerated (21), and the strength of the hyperfine field (22), these findings identify conjugated materials with exceptional optical, electronic, and spintronic properties.

Results and Discussion

In this study, the electron polaron states of PZn_n oligomers were chemically generated in dilute tetrahydrofuran (THF) solutions using decamethylcobaltocene (CoCp*₂) in a custom-designed air free apparatus that permitted parallel electronic absorption and ESR spectroscopic measurements. For these purposes, CoCp*₂ was found to be an exemplary reagent; it has an oxidation potential (E_1/2^0/+) of −1.86 V vs. ferrocene/ferrocenium in THF solvent, weak and featureless visible-range electronic absorptions (23), and, like cobaltocene (24), evinces no observable ESR spectrum at room temperature. n-Doping of PZnE₂ using the CoCp*₂ reductant (SI Appendix, Fig. S1) gives rise to electronic absorptive spectral features characteristic of a porphyrin radical anion (electron polaron), diminution of the neutral species absorptions, and the emergence of multiple [PZnE₂]^−• electronic transitions in the 600-to-900 nm (2.07–1.38 eV) domain (25). Concomitant with the appearance of these vis-NIR spectral features, ESR measurements reveal a paramagnetic signal at g = 2.0008 ± 0.0002 (SI Appendix, Fig. S2).

The ESR spectra of D_4h porphyrins are broadened by the Jahn-Teller effect into Gaussian envelopes with peak-to-peak linewidths (∆B_pp) ∼2 mT due to the degeneracy of the ²E_g state (26, 27). The ESR spectrum of [PZnE₂]^−•, with ∆B_pp of 0.69 mT and partially resolved hyperfine features, reveals that the two ethyne substituents relieve the orbital degeneracy sufficiently to obliterate this effect (28); microwave power saturation experiments confirm the absence of Jahn-Teller–mediated spin relaxation for this species. For porphyrin anion radicals whose orbital degeneracies are lifted sufficiently to relieve Jahn-Teller broadening, the largest hyperfine interactions are with peripheral protons, principally at the meso positions (28). The [PZnE₂]^−• ESR spectrum displays couplings to the β protons proximal to the ethyne and aryl groups of 0.23 and 0.14 mT, respectively, and density-functional theory (DFT) calculations suggest that significant spin density lies on the ethyne carbons.

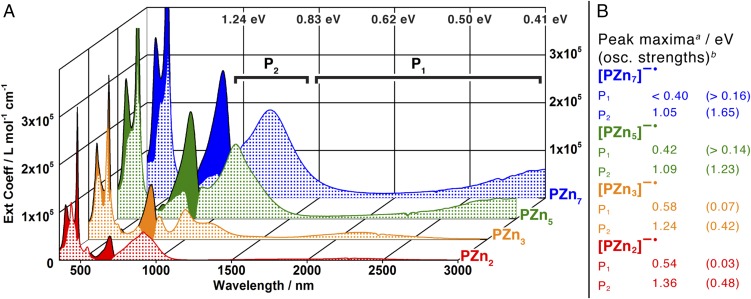
For the highly conjugated PZn_n structures, n-doping via reaction with the CoCp*₂ reductant evokes electronic absorptions between 800 and 3,000 nm (1.55 and 0.41 eV; Figs. 2 and 3) and ESR signals whose intensities peak at a one electron per oligomer stoichiometry. For [PZn₂]^−• and [PZn₃]^−•, further n-doping produces diamagnetic products in which electronic absorptions below 1,200 nm are absent; for [PZn₅]^−• and [PZn₇]^−•, reduced states that feature in excess of one electron per oligomer are characterized by a diminution of ESR signal intensity and spectral broadening, coupled with reduced NIR absorptive oscillator strength. For all PZn_n structures, no further reaction with CoCp*₂ occurs after n-doping exceeds two electrons per oligomer; bubbling air through these solution samples reversibly generates the neutral PZn_n species. These observations are consistent with the formation of electron polarons at low doping levels (no more than one electron per oligomer), with further doping producing spinless bipolaron species on shorter oligomers and side-by-side polaron pairs on longer PZn_n species, as observed previously for oligofluorenes (6). An alternating least squares curve resolution analysis (29) deconvoluted the NIR spectral features associated with [PZn_n]^−•, using the neutral species spectra as constraints and starting with concentration profiles derived from the integrated ESR intensities.

Fig. 2.

n-Doping of PZn₃. Electronic absorption spectra and X-band ESR spectra (Inset) recorded at 298 K in THF solvent; equivalents of CoCp*₂ at each colored trace are provided in the legend to the right.

Fig. 3.

Electronic spectral signatures of the PZn_n electron polarons. (A) Absorption spectra of PZn_n neutral (solid fill) and anion radical states (checked fill) in THF solvent; polaron bands P₁ and P₂ are labeled. (B) Electron polaron P₂ and P₁ transition manifold maxima and associated integrated oscillator strengths. ^aPeak maxima do not reflect [0,0] transition energies due to the vibronic and electronic complexity of the polaron spectra. ^aDetails of oscillator strength determination of various electronic transitions are reported in SI Appendix.

The species-associated spectra for [PZn_2–7]^−• are displayed alongside the electronic absorption data for the neutral oligomers in Fig. 3. Several trends are apparent in these NIR spectroscopic data: (i) the polaron states evince two principal absorption manifolds of lower energy than those of the neutral oligomers, labeled as P₁ and P₂ in Fig. 3, (ii) the transitions in the 1,000- to 3,000-nm (1.24–0.41 eV) spectral window show oscillator strengths that increase with the number of porphyrin repeat units, analogous to the vis-NIR electronic absorptions characteristic of their neutral counterparts, and (iii) the lowest energy transition P₁ for [PZn_2–7]^−• is progressively red-shifted and intensified with increasing oligomer length. In the context of Furukawa’s modification (30) to the one-electron band theory attributed to Fesser, Bishop, and Campbell (FBC model) (31), P₁ and P₂ are assigned as intragap transitions between levels whose energies are associated with the degree of polaronic structural relaxation. In this regard, points ii and iii are especially salient: these polaron bands show dependences of their oscillator strengths and low energy electronic absorption maxima on oligomer length that remain unsaturated for the range of compounds explored here, suggesting that the effective electron polaron delocalization length is not yet reached for [PZn₇]^−• (Fig. 3).

Time-dependent DFT (TD-DFT) calculations using several common range-corrected hybrid functionals (6) show that the absorption spectra of [PZn_n]^−• are only well represented using a model that delocalizes the highest-occupied majority spin orbital (HOMOα) over the entire porphyrin oligomers. Accurate simulations of the experimental NIR spectra used the LC-ωPBE functional (32), with values of the range-separation parameter ω tuned to provide strong agreement between simulated and observed spectra (6). The most intense P₁ region transitions are of HOMOα → LUMOα character, whereas the principal P₂ region transitions are dominated by HOMOβ → LUMOβ configurations (Fig. 4B). The experimental P₁ and P₂ region absorptions observed for these [PZn_n]^−• species derive from these primary HOMOα → LUMOα and HOMOβ → LUMOβ configurations, along with numerous lower oscillator strength transitions (Fig. 4B and SI Appendix).

Fig. 4.

Computational simulations of the PZn_n electron polarons. (A) Comparison of electron polaron spatial delocalization for PZn₇ and conjugated polymers poly(3-decyl)thiophene (P3DT) and poly(9,9’-dioctyl)fluorene (PDOF). For PZn₇, the SOMO is depicted as a 0.007 isodensity surface to illustrate the extent of the anion radical state; the spin density population is broken down into percentages that can be assigned to internal C atoms (no bonds to H), N atoms, and Zn atoms. (B) Energy level diagrams for neutral and n-doped PZn₇, with vertical arrows depicting one-electron configurations that contribute to the principal NIR transitions P₁ (black, alpha spin) and P₂ (blue, beta spin) predicted for [PZn₇]^−• by TDDFT calculations.

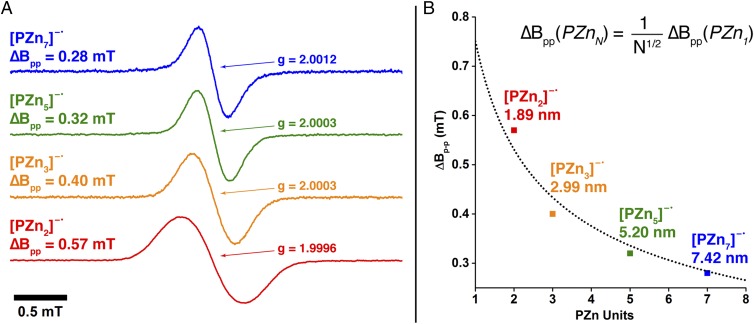
A direct measure of the electron polaron spatial dimension in conjugated materials is provided by ESR measurements through the hyperfine interactions $H_{hf}={\displaystyle \sum }_i{A}_{oi}S\cdot I_i$ (where S and I_i refer to the electron and nuclear spins, respectively, and $A_{oi}$ denotes the isotropic hyperfine coupling constants of spin-carrying nuclei). It is important to note that at the solution concentrations used (50–100 μM), intermolecular spin interactions are minimized and thus the ESR lineshape is governed primarily by isotropic hyperfine interactions. Any anisotropic hyperfine couplings are rotationally averaged to zero at 298 K in THF. The ESR spectra for [PZn_2–7]^−•, displayed in Fig. 5A, show unresolved couplings that manifest approximately Gaussian line shapes; ∆B_pp narrows from 0.57 mT for [PZn₂]^−• to 0.28 mT for [PZn₇]^−•. An important mechanism resulting in linewidth narrowing stems from the decreasing hyperfine field experienced by the spin system as a consequence of either coherent delocalization of the excitation, or incoherent hopping on a time scale more rapid than that associated with the hyperfine interaction (>∼1 MHz). Norris has shown that, in the limit of stochastic, near-barrierless, one-dimensional charge hopping between N equivalent oligomer sites, the theoretical linewidth is given by ∆B_pp(N-mer) = (1/N^1/2)∆B_pp(monomer) (22). The fit to this relationship for the ESR linewidth measurements for [PZn_2–7]^−• determines directly that these spin systems extend over the entire molecular lengths of these oligomers (Fig. 5B).

Fig. 5.

ESR spectral signatures of PZn_n electron polarons. (A) X-band ESR spectra of PZn_n electron polarons recorded at 298 K in THF solvent. (B) (squares) Peak-to-peak line widths ∆B_pp from ESR spectroscopic measurements on [PZn_n]^−• plotted as a function of PZn repeat units, and (dotted line) fit of ∆B_pp to ∆B_pp(N-mer) = (1/N^1/2)∆B_pp(monomer).

Spectroscopic studies of electron polarons generated in conventional polymers via chemical reduction and pulse radiolysis methods have estimated electron polaron lengths of under 5 nm for conventional polymers such as [poly(3-decyl)thiophene]^•– (P3DT, 4.67 nm) (7) and [poly(9,9’-dioctyl)fluorene]^•– (PDOF, 3.55 nm) (6); the values determined for these π-conjugated polymers are approximately half as large as that measured for the [PZn₇]^−• oligomer (7.42 nm). Note that the PZn_n chain width exceeds that of conventional π-conjugated linear polymers; approximating such structures as conjugated 2D ribbons (Fig. 4A), the 5.92-nm² areal delocalization of the [PZn₇]^−• electron polaron dwarfs that for [P3DT]^−• (1.73 nm²) and [PDOF]^−• (1.41 nm²). These data dramatically underscore that the electron-lattice coupling operating in PZn_n oligomers is extraordinarily weak and present the PZn_n motif as a potent alternative to those conventionally used in the design of π-conjugated materials for electron transport (5).

The extent of polaron delocalization, the magnitude of the polaron binding energy, and the degree of nuclear reorganization associated with polaron formation are all closely correlated (11). Congruent with the very small electron-lattice coupling manifest by PZn_n electron polarons, computed internal reorganization energies (λ_i values) for these species are correspondingly low (21, 33). For example, using a four-point method (34), we calculate λ_i = 91.4 meV for [PZn₂]^−•, a value significantly lower than that for C₆₀ (λ_i = 107.0 meV; SI Appendix), the classic electron acceptor having low internal reorganization energy. Such computational data, together with TD-DFT calculations and the optical and ESR data highlighted above, suggest extraordinarily low barriers for self-exchange reactions between PZn_n oligomers and their corresponding electron polaron states. Such modest reorganization energies (weak electron-lattice couplings, low barriers to self exchange) enable, for example, photoinduced electron transfer reactions to achieve maximal rate constants at low thermodynamic driving forces (21, 33) and substantial solid-state charge mobilities (11).

Conclusion

In conclusion, we used vis-NIR optical and ESR spectroscopy along with computational models to discover that electron polarons with extreme spatial dimensions can be generated in PZn_n oligomers. These data reveal that the intrinsic electron-lattice coupling is extraordinarily low in these systems. Because polaron dimensions and electron-lattice couplings are closely associated with properties important to organic photovoltaics, light-emitting diodes, and a host of other devices based on organic semiconductors, these data reveal exceptional electronic, opto-electronic, and spintronic properties in PZn_n molecules.

Materials and Methods

Materials.

All manipulations were carried out under argon previously passed through an O₂ scrubbing tower (Schweitzerhall R3-11G catalyst) and a drying tower (Linde 3-Å molecular sieves) unless otherwise stated. Air-sensitive materials were handled and stored in a Braun 150-M glove box. Standard Schlenk techniques were used to manipulate air-sensitive solutions, using a 10-μm vacuum. THF solvent used for these experiments was freshly distilled from sodium/benzophenone ketyl under argon onto freshly activated molecular sieves and subsequently purged with argon gas for at least 2 min/mL. Permethylcobaltocene was synthesized by sonicating a THF suspension of the bis(pentamethylcycolpentadienyl)cobalt(III) hexafluorophosphate salt (23) over sodium metal for 2 h, followed by air-free filtration through celite and solvent removal under vacuum; CoCp*₂ was sublimed twice before use. The syntheses of PZnE₂, PZn₂, PZn₃, PZn₅, and PZn₇ have been reported previously (17, 19), and all presented pristine characterization data before use in this study. An exemplary synthesis of PZn₇ is outlined in SI Appendix, Fig. S8. The syntheses of synthetic intermediates closely followed the established procedures (17, 35).

Instrumentation.

n-Doping experiments were performed in a custom air-free cell (SI Appendix, Fig. S9) that could be attached to a Schlenk line. Electronic absorption spectra were collected using a Cary 5000 spectrometer. X-band ESR measurements were performed using a Varian E-109 spectrometer; all spectra were collected at 10-mW power, and the magnetic field was referenced to 2,2-diphenyl-1-picrylhydrazyl (dpph) and weak pitch standards. Deconvolution of the electronic spectral data from multistep doping experiments was performed using the MCR-ALS toolbox (29) running in Matlab. All deconvolutions were found to exhibit negligible rotational ambiguity as determined by MCR-BANDS analysis (36). The Origin software package was used for all spectral analysis and display; this was also used for double integrations of ESR spectral data and the fit of peak-to-peak line widths (∆B_pp) for [PZn_2–7]^−• to the Norris expression (22). Oscillator strengths of the NIR bands P1 and P2 were determined as described in Lakowicz (37). The ranges used for P1 and P2 are summarized in SI Appendix, Table S1.

Computational Methods.

All structure optimizations, single-point energy calculations, and TD calculations were performed using DFT in the Gaussian09, Rev D.1 (38) software package. The structures of PZn_n compounds were simplified by modeling the aryl groups as unsubstituted phenyl rings. For all polaron wavefunction models used in the text, as well as for TD-DFT calculations, the structures were further simplified to the D_2h point group by restricting the individual porphyrin rings to lie in a single plane. Optimization of PZn₂ with no symmetry constraint finds an angle between the neighboring N,N,N,N consensus planes of 26.7°, and for [PZn₂]^−•, this angle is calculated to be 16°. These small deviations in interporphyrin dihedral angles have negligible impacts on the PZn_n electronic structures, and the approximation to planarity allows these calculations to serve as useful qualitative models. For the calculations of intramolecular electron-phonon coupling λ_i, models with no symmetry and more realistic interporphyrin plane angles were used (SI Appendix, Fig. S5).

The Becke three-parameter hybrid (39) and the Lee-Yang-Parr correlation functional (40, 41) (B3LYP) were used for initial optimizations of the neutral species. All calculations used tight convergence criteria and the 6–311g basis set (42–50) with two additional d functions [6-311G(2d)] as implemented in Gaussian09. A polarized continuum solvation model (SCRF = IEF-PCM in Gaussian09) with THF as solvent was used for all calculations except for determination of λ_i. TD-DFT calculations were performed using the long-range corrected Perdew–Burke–Ernzerhof (LC-ωPBE) functional (32); ω was optimized to 0.05 by comparison of calculated transitions to experimental spectra. The internal reorganization energies (λ_i) were calculated following an approach attributed to Nelsen et al. (34); in this procedure, the neutral PZn_n and electron polarons [PZn_n]^−• were modeled in the gas phase with no symmetry constraints. Because the LC-ωPBE functional with ω = 0.05 provided an accurate model of [PZn_n]^−•, this was used for all λ_i calculations.