Differential Deformability of the DNA Minor Groove and Altered BI/BII Backbone Conformational Equilibrium by the Monovalent Ions Li⁺, Na⁺, K⁺ and Rb⁺ via Water-Mediated Hydrogen Bonding

Abstract

Recently, we reported the differential impact of the monovalent cations Li⁺, Na⁺, K⁺ and Rb⁺ on DNA conformational properties. These were identified from variations in the calculated solution-state X-ray DNA spectra as a function of the ion type in the solvation buffer in MD simulations using our recently developed polarizable force field based on the classical Drude oscillator. Changes in the DNA structure were found to mainly involve variations in the minor groove width. Because minor groove dimensions vary significantly in protein-DNA complexes and have been shown to play a critical role in both specific and nonspecific DNA readout, understanding the origins of the observed differential DNA modulation by the first-group monovalent ions is of great biological importance. In the present study we show that the primary microscopic mechanism for the phenomenon is the formation of the water-mediated hydrogen bonds between solvated cations located inside the minor groove and simultaneously to two DNA strands, a process whose intensity and impact on DNA structure depends on both the type of the ion and DNA sequence. Additionally, it is shown that formation of such ion-DNA hydrogen bond complexes appreciably modulates the conformation of the backbone by increasing the population of the BII substate. Notably, the differential impact of the ions on DNA conformational behavior is only predicted by the Drude polarizable model for DNA, with virtually no effect observed from MD simulations utilizing the additive CHARMM36 model. Analysis of dipole moments of the water shows the Drude SWM4 model to possess high sensitivity to changes in the local environment, which indicates the important role of electronic polarization in the salt-dependent conformational properties. This also suggests that inclusion of polarization effects is required to model even relatively simple biological systems such as DNA in various ionic solutions.

INTRODUCTION

Conformational preferences of DNA with its ability to adopt certain structures under specific environmental conditions are important prerequisites for many vital biological processes including protein-DNA recognition¹ and chromatin folding.² The abundance of metallic ions in cellular environments are known to significantly contribute to DNA conformational stability and diversity and regulate its functional dynamics.³ Ions modulate DNA structure directly by binding to specific electronegative sites or by perturbing the water hydrogen bond network in the vicinity of DNA leading to local deviations from canonical structures.⁴ Additionally, the layer of condensed counterions (ionic “atmosphere”)^5,6 which neutralizes DNA residual charge, regulates a number of critical physical-mechanical properties such as persistence length and flexibility^3,7-9 and enables such vital biological processes as genomic packaging¹⁰ and RNA folding.¹¹

In a recent experimental study it was demonstrated that establishing a specific minor groove solvation pattern was the key contributor to sequence-specific protein-DNA recognition,⁴ while other numerous NMR,^12-14 X-ray crystallographic^15-18 and computational^19-21 studies indicate the presence of various ionic species inside the DNA grooves. Our recent computational work utilizing a polarizable force field for DNA based on the classical Drude oscillator formalism²² revealed a differential impact of the first-group monovalent ions Li⁺, Na⁺, K⁺ and Rb⁺ on DNA minor groove dimensions.²³ In particular, the width of the minor groove appeared to be strongly correlated with the size of the ion in the solvation buffer according to the following trend, Li⁺ < Na⁺ < K⁺ < Rb⁺,²³ which also indicates that competition may occur among monovalent cations for the DNA minor groove – an important suggestion given the fact that DNA under physiological conditions is exposed to a mixture of several (mono- and divalent) ionic species.^6,24,25 While this phenomena was predicted based on (1) the ability of the Drude polarizable force field to accurately reproduce solution X-ray scattering profiles for a number of B-form DNA sequences in an aqueous NaCl ionic buffer, and (2) an overall DNA structural analysis which identified variations in the dimensions of the minor groove and some other DNA helicoidal parameters as a function of ion type,²³ no further efforts were made towards identifying microscopic mechanisms regulating such conformational changes. Because monovalent ions are abundant in the cellular environment of DNA and the minor groove dimensions of DNA are highly variable in protein-DNA complexes,^1,26,27 understanding the origins of the DNA structural modulation by different monocations at an atomic level of detail is an important issue in structural biology with implications with respect to better understanding DNA readout.

In the present study we focus on details of ionic hydration, steric and electrostatic effects influencing ion penetration into the DNA grooves leading to modulation of the backbone conformation and minor groove dimensions. Additionally, we rationalize the reported earlier qualitatively different outcomes from the CHARMM 36 (C36) additive (non-polarizable) and Drude polarizable models as to the structural changes in DNA induced by different monocations.²³ Our analysis reveals that the primary microscopic mechanism responsible for differential effect of the Li⁺, Na⁺, K⁺ and Rb⁺ monocations on DNA conformational properties is the formation of water mediated hydrogen bonds between ions located in the minor groove and simultaneously two DNA strands, a process whose intensity and the impact on DNA structure depend on the ion type and DNA sequence involved. In terms of the DNA helicoidal and backbone parameters, such hydrogen bond formation appears to appreciably shift BI/BII backbone conformational equilibrium towards the BII population, which, in turn, directly affects DNA minor groove width. Notably, the effect occurs only in the Drude polarizable model. Combined with our earlier studies demonstrating an appreciably closer agreement between the outcomes from the Drude model (versus the C36 model) and predictions from counterion condensation theory,²⁸ experimental results for competitive ionic binding to DNA²⁵ and experimental solution-state DNA X-ray scattering measurements,²³ the present results point to the importance of the inclusion of explicit polarization effects in the force field. The presence of polarization provides a more realistic physical description of the ionic solvation effects and interactions of ions with DNA. Our findings may have important implications for protein-DNA interactions and other salt-mediated biological processes involving DNA.

COMPUTATIONAL AND ANALYSIS METHODS

Additive and Polarizable MD Simulations

The present study is based on detailed analysis of MD simulations for three DNA sequences of different length and content, each independently simulated in four ionic buffers at physiological concentrations (~120 mM): LiCl, NaCl, KCl and RbCl. The DNA systems included the following: (1) and (2) two self-complementary sequences, d(CGCGAATTCGCG)₂ and d(CGCTAGCG)₂, which have been studied experimentally by solution X-ray scattering,²⁹ and (3) an additional sequence, d(CGCATGCTACGC), recently resolved by solution NMR.³⁰ In what follows, we refer to these structures as EcoRI (also known as Drew-Dickerson dodecamer³¹), 1DCV and 2L8Q (based on the corresponding PDB codes for these sequences), respectively.

Simulations were carried out employing the CHARMM C36 additive³² and Drude-2013 polarizable force fields for DNA²² and ions.^25,33 Water was treated with the additive TIP3P³⁴ and polarizable SWM4-NDP³⁵ models. The MD simulation protocols are extensively described elsewhere.^25,28 In short, all DNA molecules were solvated in cubic boxes with water molecules extending at least ~15 Å from the DNA surface, with addition of neutralizing ions (Li⁺, Na⁺, K⁺ or Rb⁺) and an extra ~120 mM of the corresponding chloride salt (LiCl, NaCl, KCl or RbCl). Initial configurations were generated by simulating the analogous additive C36 systems for several nanoseconds according to the protocol described elsewhere,²⁸ taking the last snapshot from these runs as inputs for subsequent Drude simulations. Production runs of all additive C36 MD simulations were continued for another 200 ns. The CHARMM program³⁶ was used for generating the polarizable Drude system, self-consistent relaxation of the Drude particle positions, and short equilibration runs of all systems using the Velocity-Verlet integrator³⁷ in conjunction with the TPCONTROL (Temperature-Pressure Control), as elaborated elsewhere.²² For the production polarizable MD simulations, NAMD³⁸ (v. 2.9) was used whose self-consistent treatment of the Drude model is based on a dual thermostating scheme and Langevin dynamics.³⁹ In particular, real atoms and polarizable degrees of freedom (Drude particles) were coupled to the thermostats at 300 K and 1 K, respectively. Electrostatic interactions were treated using the PME summation⁴⁰ with a coupling parameter of 0.34 and a sixth-order spline for mesh interpolation. Non-bonded pair lists were maintained out to 16 Å, and a real space cutoff of 12 Å was used for the electrostatic and Lennard-Jones (LJ) terms. All covalent bonds involving hydrogen atoms as well as the intramolecular geometries of water molecules were constrained using the SETTLE algorithm.⁴¹ The ‘HARDWALL’ feature enabled the use of a 1 fs time step in the polarizable MD simulations, while a 2 fs time step used in the additive simulations. As previously described,^25,28 the HARDWALL feature is associated with a “hard wall” reflective term in the potential energy function that has been added to resolve potential polarization catastrophe problem in Drude MD simulations. This term was invoked only when Drude particles moved >0.2 Å away from their parent nuclei during MD simulations.

Analysis of the DNA Minor Groove Occupancy by the Counterions

Because the primary DNA conformational mode correlating with the change in the ionic buffer content is the modulation of the minor groove width,²³ we focus on details of ionic structuring inside the minor groove. Our approach is based on decomposition of the overall counterion-DNA radial distribution function (RDF) into contributions from ionic structuring with respect to different DNA segments, particularly, the backbone phosphate and sugar groups and the major and minor grooves. Definitions of the DNA grooves are provided below. Backbone phosphate and sugar groups are defined by the following sets of atoms: P, O1P, O2P, O3’, O5’, C3’ and C1’, C2’, C3’, C4’, O4’, respectively (hydrogen atoms are not listed for brevity). As elaborated previously,^19,25,28 RDFs are computed based on the closest approach, in which ion-DNA separation is defined as the closest distance between the DNA molecule and the particular ion, with the resulting ion-DNA distance histogram, N(r), being normalized by a numerically computed volume Jacobian, J(r). The resulting expression for the RDF has the form,

$$g\left(r\right)=\rho \cdot \frac{N\left(r\right)}{J\left(r\right)}$$ (1)

where ρ is the bulk density of the ions. The Jacobian J(r) is defined as the volume of a shell equidistant from the DNA surface (see Fig. S1, Supporting Information (SI)). As discussed previously,¹⁹ this approach benefits from a more robust measure of the ionic entropy than in commonly used standard procedures relying on cylindrical or spherical symmetries. More importantly, this approach allows for a proper (exact) decomposition of the RDF into individual contributions, as discussed below.

Ion-DNA distance histograms and volume Jacobians were computed over the MD simulations for every snapshot. Three-dimensional (3D) grids with lattice spacings of 0.5 Å were used to calculate both the ion-DNA distance histograms and the volume Jacobian. The biochemical algorithm library (BALL)⁴² was used to implement the computational analysis subroutines. Because DNA strands are treated as independent segments in the course of MD simulations, the strands often appeared to be separated due to unrestricted DNA motions and the periodic boundary conditions imposed. Therefore, prior to computing ionic RDFs (and other overall DNA characteristics such as minor groove width distributions), reimaging/recentering of MD trajectories was performed, with the corresponding computational subroutine for such post-processing written using BALL.

Analysis of the Water Shell around the Counterions

For a quantitative assessment of the ionic hydration in the vicinity of DNA and, particularly, in the minor groove, we analyzed the first solvation shell around the counterions. To determine the radius of the first solvation shell, we used the corresponding counterion-water RDFs, built from independent MD simulations of an electroneutral system consisting of Li⁺, Na⁺, K⁺ or Rb⁺ and Cl⁻ ions at 120 mM in water. For each simulated DNA system we generated a histogram of the average number of water molecules within the counterion’s first solvation shell as a function of the counterion distance from the overall DNA surface, or from the surface of the DNA minor grove.

Analysis of the Residence Times of the Counterions in the DNA Minor Groove

Residence times of the solvated counterions inside the minor groove were estimated to characterize the dynamics of the ionic penetration of the minor groove and to determine if the duration of the MD simulations is satisfactory to obtain the appropriate statistics. We have built distributions for residence times of the Li⁺, Na⁺, K⁺ and Rb⁺ ions from the corresponding MD simulations of the Drude and additive C36 systems. Residence times for each ionic type were estimated from the computed ionic temporal auto-correlation functions.

Definition of the “Strand(1)–Ion–Strand(2) Hydrogen Bond Bridges” (SIS-HBBs)

As elaborated below, differential modulation of DNA minor groove by various counterions is associated with the different extent of hydrogen bond formation between water molecules in the first solvation shell of the ion located inside the minor groove and electronegative atoms of DNA strands. We call such hydrogen-bond formations a “Strand(1)–Ion–Strand(2) Hydrogen Bond Bridge” (SIS-HBB), whose schematic representation is shown in the Fig. 1. We consider a SIS-HBB formed when the distances between hydrogen atoms of the water molecules constituting the cation's first solvation shell and electronegative atoms of DNA are less than a threshold value of 2.0 Å, provided such hydrogen bonds are simultaneously formed with both DNA strands (at least one bond per strand). Simply put, when a SIS-HBB complex is formed, DNA strands are “connected” by the cation located in the minor groove via water-mediated hydrogen bonds.

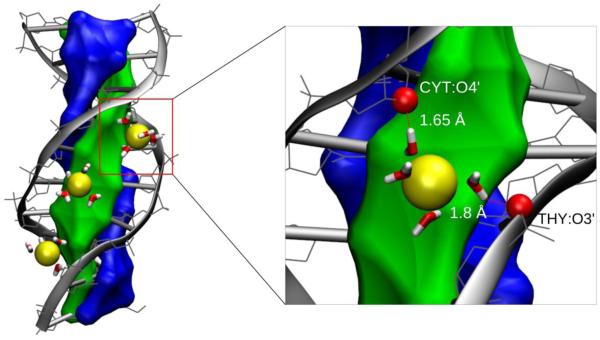
Figure 1.

MD simulation snapshot of the 1DCV sequence demonstrating penetration of three solvated Na⁺ ions into the DNA minor groove (left). One of the ions is shown to form two water-mediated hydrogen bonds with the O4’ and O3’ electronegative DNA atoms of the Cytosine and Thymine, respectively, located on different strands (right). Minor and major grooves are associated with the green and blue virtual surfaces, respectively, whose definitions are used for the proper discrimination between cations located inside the minor and major DNA grooves (see the text). The numbers indicate the distances between hydrogen atoms of the ion’s first solvation shell water molecules and DNA atoms; values of less than 2 Å indicate formation of the hydrogen bonds. When at least one such hydrogen bond is formed per DNA strand, as shown on the right panel, a complex referred to as ‘SIS-HBB’ is formed (see Methods section).

Counterions in the minor groove were identified as follows. First, the DNA interior was considered to be an accessible space for ions within 10 Å from the DNA helical axis (an approximate DNA radius). Next, the cations inside the interior were checked if they reside in the minor or major groove. In so doing, we devised two virtual surfaces on the DNA interior associated with the minor and major grooves which are defined by the following groups of atoms: (1) GUA(N3,N2), CYT (O2), ADE(N3,C2), THY(O2), and (2) GUA(N7,O6), CYT(N4), ADE(N7,N6), THY(O4), respectively. The surfaces are schematically depicted in Fig. 1 in green (minor groove) and blue (major groove). Using these definitions, we considered interior counterions to reside in the minor groove if the closest separation from the minor groove surface was smaller than that from the major groove surface, and vice versa.

Decomposition of MD Trajectories Based on the Number of SIS–HBB Bridges Formed

Analysis included monitoring the changes in the DNA conformational properties as a function of the number of SIS–HBBs formed along the DNA oligomer at a particular instance of time. To facilitate the analysis, the frames of the MD trajectories were grouped into subsets corresponding to different numbers of the SIS–HBB bridges formed, with subsequent structural characterization of the DNA minor groove and key backbone dihedral angles performed on these subsets independently. Fig. 1 clarifies the idea demonstrating the simultaneous formation of three SIS–HBB bridges along the DNA oligomer. We have built minor groove probability distribution functions for all such subsets extracted from the MD simulations of all three DNA systems, in all four ionic buffers, for both the Drude polarizable and C36 additive models.

RESULTS AND DISSCUSSION

In a recent paper we studied the conformational behavior of the 1DCV, EcoRI and 2L8Q DNA sequences simulated in LiCl, NaCl, KCl and RbCl ionic buffers, by computing their solution-state X-ray scattering profiles and comparing to the available experimental scattering measurements.²³ Our calculations revealed variations in the DNA spectra as a function of ion type, indicating a differential impact of the monocations on DNA structure. Further analysis of the overall DNA conformational behavior revealed that the structural changes were mainly reduced to modulations in the minor groove width. Notably, the effect appeared to be sequence dependent and manifested only in the Drude polarizable model, with virtually no spectral or conformational changes observed from the additive C36 simulations. The goal of the present study is to uncover microscopic mechanisms responsible for the structural changes in DNA as a function of both the ion type and oligonucleotide sequence predicted by the Drude polarizable model and to rationalize the qualitatively different outcomes from the Drude polarizable and C36 additive MD simulations.

Analysis of the Ionic Hydration and Structuring in the DNA Minor Groove

We start our analysis by decomposing counterion radial distribution functions (RDF) averaged over the entire DNA structure into contributions from the ions structured with respect to different DNA moieties – minor groove, major groove and backbone phosphate and sugar groups. This is a convenient approach that allows for estimation of the relative extent of the ions penetrating the DNA interior (grooves) and also for qualitative assessment of the ion's hydration state inside the minor groove.

Because of the complex topology of DNA, achieving a proper RDF decomposition is not a straightforward task. For a example, use of the common approach based on computing ionic distribution independently around each DNA atom in a selection of interest (e.g. minor groove), using standard spherical symmetry, with subsequent averaging over all those atoms to get the resulting RDF contribution is not appropriate. Distributions around various DNA moieties computed this way will have significant overlapg because of ion overcounting, and such “non-orthogonality” would render them inappropriate for even qualitative assessment of the relative extent of the ionic structuring with respect to different DNA atomic selections. A proper way of decomposing the structural distribution of ions around DNA (or other topologically complex objects such as proteins) is to adopt a definition of the closest ion-DNA separation which require computation of the numerical Jacobian defined as the volume of a shell equidistant from the DNA surface¹⁹ (see Fig. S1 and the Methods section).

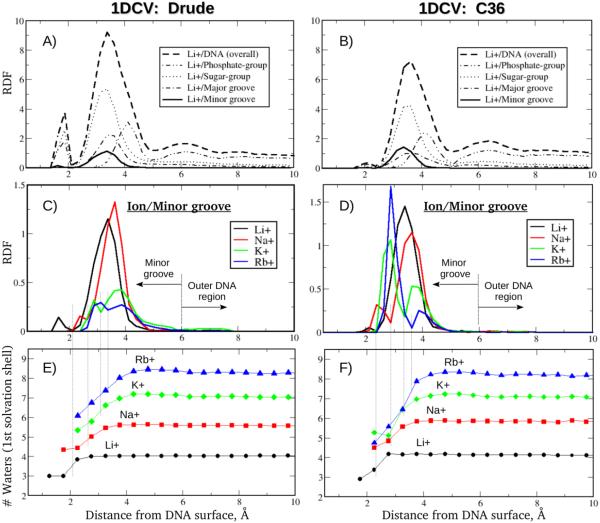
The resulting overall ion-DNA RDFs and their properly dissected (“orthogonal”) contributions for the backbone phosphate and sugar groups and the minor and major grooves are shown in the Figs. 2A, B for the case of the Li⁺ distribution around 1DCV, computed from the Drude and additive C36 MD simulations (analogous plots for two other systems, EcoRI and 2L8Q, are provided in the Figs. S2A, B and S3A, B of SI, respectively). As seen from the graphs, counterions predominantly favor the vicinity of the negatively charged sites of the phosphates and adjacent sugar groups, with significantly smaller contributions arising from the DNA interior and, particularly, from the distribution around the minor groove. A very similar tendency is observed for the other ionic species, Na⁺, K⁺ and Rb⁺. However, it is important to take a closer look at those smaller RDF contributions because changes in the type of ion in the solvation buffer were shown to have the biggest impact on the shape of the DNA minor groove.

Figure 2.

Analysis of the DNA minor groove occupancy by different monovalent ions and the ionic hydration patterns from MD simulations of the Drude polarizable (left) and C36 additive (right) 1DCV system. (A, B) An overall ion-DNA RDF is decomposed into contributions from ionic structuring around different DNA atomic selections; the Li⁺ distributions are shown. (C, D) Ionic structuring of the Li⁺, Na⁺, K⁺ and Rb⁺ ions around the DNA minor groove. (E, F) Number of waters in the first solvation shells of the Li⁺, Na⁺, K⁺ and Rb⁺ ions as functions of the ion’s distance from the DNA surface. Positions separating the first and second minima of the Ion/Minor-groove RDFs are projected (dotted lines) onto the ionic solvation curves.

Figs. 2C and 2D show the ionic distributions around the minor groove for all four types of counterions, Li⁺, Na⁺, K⁺ and Rb⁺, computed from polarizable and additive MD simulations of the 1DCV sequence (results for the other DNA systems are provided in SI, Figs. 2SC, D and 3SC, D). Comparison of the outcomes from the Drude and additive C36 models reveals that ionic hydration patterns differ noticeably, especially for larger size ions. For example, the polarizable model predicts all ionic species to be predominantly fully hydrated as evidenced by the largest peaks occurring beyond 3 Å, with the overall fraction of partially dehydrated ions increasing for K⁺ and Rb⁺, as indicated by the bi-modal shape of their RDFs and the small first peaks (Figs. 2C, S2C and S3C). A quite different picture emerges from the additive C36 model (Figs. 2D, S2D and S2D) predicting an increasingly larger fraction of the partially desolvated Na⁺, K⁺ and Rb⁺ ions interacting directly with the DNA minor groove as evidenced by the large first peaks < 3 Å.

A more quantitative analysis of the ionic hydration state inside the minor groove includes constructing the solvation curves for Li⁺, Na⁺, K⁺ and Rb⁺ ions that indicate the number of water molecules in their first solvation shells as a function of counterion distance from the DNA oligomer surface. As seen in Figs. 2E and 2F counterion solvation shells remain mostly unperturbed except in the immediate vicinity of the DNA molecule (less than ~4 Å from DNA surface), as ions approach DNA from the bulk. Projecting the positions of RDF's minima separating partially desolvated and fully hydrated ionic states in the minor groove (first and second peaks, respectively, in Figs. 2C, D) onto the solvation curves (Figs. 2E, F) reveals that upon desolvation Li⁺, Na⁺, K⁺ and Rb⁺ ions loose on average ~1, ~1, ~1.5 and ~2 water molecules, respectively, in the Drude model, and ~1, ~1, ~1.6 and ~3 water molecules, respectively, in the additive C36 model.

While these results reflect an overall consistency between the models in predicting the state of hydration for counterions located inside the DNA minor groove, the differences in Ion/Minor-groove RDFs point to distinctions in the thermodynamic aspects of the ionic dehydration. A more robust way to characterize the change in the ion solvation shells as the ions approach the minor groove from the bulk is to combine the results from Figs. 2C, D and Figs. 2E, F and calculate an average amount of water molecules the ions lose in the course of this process. This information is presented in the Table 1, with the numbers obtained by integrating the solvation curves weighted by the corresponding Ion/Minor-groove RDFs over two spatial regions, within and beyond ~6 Å from DNA surface, to get an average number of water molecules solvating the ions in the minor groove and in the bulk, respectively. Also shown for comparison are the values computed for ions forming a direct contact with the DNA minor groove (corresponding to the first RDF peaks in Figs. 2C, D). As seen from the results, the larger K⁺ and Rb⁺ ions lose nearly twice as many water molecules in the additive C36 model compared to the Drude polarizable model.

Table 1.

Average numbers of water molecules in the ion’s first solvation shell for the ions located in the bulk, forming a direct contact with the DNA, and residing in the minor groove. For the last two occurrences the quantitative changes in the hydration state of the ions relative to the bulk are also provided. Results are shown for all systems simulated using Drude polarizable and C36 additive force fields.

		DRUDE FF					C36 FF
		bulk	direct contact	minor groove	Δ (bulk – direct contact)	Δ (bulk – minor groove)	bulk	direct contact	minor groove	Δ (bulk – direct contact)	Δ (bulk – minor groove)
1DCV	Li+	4.0	3.0	3.9	1.0	0.1	4.1	2.9	4.2	1.2	−0.1
	Na+	5.6	4.3	5.3	1.3	0.3	5.8	4.5	5.5	1.3	0.3
	K+	7.0	5.3	6.1	1.7	0.9	7.1	5.3	5.9	1.8	1.2
	Rb+	8.2	6.0	6.9	2.2	1.3	8.2	4.7	5.9	3.5	2.3
EcoR1	Li+	4.0	3.0	3.9	1.0	0.1	3.8	2.8	4.0	1.0	−0.2
	Na+	5.6	4.2	5.3	1.4	0.3	5.8	4.6	5.4	1.2	0.4
	K+	7.0	5.3	6.3	1.7	0.7	7.0	5.0	5.6	2.0	1.4
	Rb+	8.2	5.9	6.8	2.3	1.4	8.1	4.7	5.7	3.4	2.4
2L8Q	Li+	4.0	3.0	4.0	1.0	0.0	3.8	2.9	4.0	0.9	−0.2
	Na+	5.6	4.2	5.3	1.4	0.3	5.8	4.3	5.5	1.5	0.3
	K+	7.0	5.3	6.3	1.7	0.7	7.0	5.1	5.6	1.9	1.4
	Rb+	8.2	5.9	6.8	2.3	1.4	8.1	5.1	5.9	3.0	2.2

Impact of Different Hydrated Monocations on DNA Conformation

Given the results of the previous section, variations in the DNA minor groove width as a function of ion type observed in the Drude polarizable model²³ are only due to differential impact of the predominantly hydrated ions, meaning all three crucial constituents – DNA, ions and the water – need to be considered. Based on this, we hypothesize that water molecules in the first solvation shell of the ions located in the minor groove form transient hydrogen bonds with the electronegative atoms of the DNA strands, creating structural complexes which we refer to as “Strand(1)–Ion–Strand(2) Hydrogen Bond Bridges” (SIS-HBBs). As follows from the name, at least two water-mediated hydrogen bonds need to be formed (one bond per DNA strand) for a solvated counterion to bridge DNA strands with the potential of modulating the minor groove (see Fig. 1). Next, we assume a number of thermodynamic and kinetic aspects of the SIS–HBB formation play a role in the observed differential modulation of the shape of the DNA exposed to different ionic solutions. These include variations in the ionic hydration state, the lifetime of the SIS–HBB complexes and the number of these complexes formed along the DNA oligomer at a given time.

To address these possibilities, we proceed with identification of SIS–HBB complexes, as elaborated in the Methods section, to verify if they exist and how strong their impact is on DNA conformation as a function of sequences and monocation type. To perform this, we decompose the MD simulation trajectories into two parts, one containing frames when one or more SIS–HBBs are formed, and the other one corresponding to frames when no such complexes are formed, with subsequent structural DNA analysis performed on these two subsets. The results are summarized in Table 2 showing the values of the minor groove width obtained by averaging over the corresponding trajectory parts and also over the entire trajectory for each simulated DNA system. As seen from the data, SIS–HBB complexes involving different ions in the Drude model possess different propensity towards narrowing the DNA minor groove, whose intensity increases in accordance to the following trend, Li⁺ > Na⁺ > K⁺ > Rb⁺. In addition, the effect is a sequence-dependent phenomena as evidenced by the different changes in the three systems studied. The largest minor groove variations occur with the 1DCV sequence in the LiCl ionic buffer where ~70% of the time DNA strands are connected by SIS–HBB complexes resulting in a reduced minor groove width of ~5.7 Å, compared to the unperturbed value of ~7.85 Å. As the ionic size becomes larger, both the fraction of the time when DNA strands are mediated by SIS–HBBs and the extent to which SIS–HBB complexes modulate the minor groove width diminish, resulting in the monotonically increasing value of the average minor groove width. The data indicate that this trend is observed for all systems studied with the Drude FF, with the effect manifested the most in the 1DCV system and the least in the EcoRI dodecamer.

Table 2.

Overall impact of the SIS–HBB formation on the DNA minor groove size. For each DNA system, shown are the average values of the minor groove width derived from the unperturbed DNA conformations (No SIS–HBB), structures affected by solvated cations (With SIS–HBB) and from the entire simulation trajectory (Mean). Values in parentheses denote the percent time in the corresponding DNA states.

	1DCV: DRUDE FF				1DCV: C36 FF
	Li+	Na+	K+	Rb+	Li+	Na+	K+	Rb+
No SIS-HBBs (%) With SIS-HBBs (%) Mean (100%)	7.85 (30) 5.70 (70) 6.34	8.30 (39) 7.16 (61) 7.61	8.35 (50) 7.95 (50) 8.15	8.41 (51) 7.92 (49) 8.17	8.00 (52) 7.82 (48) 7.91	8.02 (50) 7.68 (50) 7.85	8.20 (57) 7.72 (43) 7.99	8.12 (57) 7.63 (43) 7.91
	EcoRI: DRUDE FF				EcoRI: C36 FF
	Li+	Na+	K+	Rb+	Li+	Na+	K+	Rb+
No SIS-HBBs (%) With SIS-HBBs (%) Mean (100%)	8.15 (29) 7.64 (71) 7.79	8.17 (41) 7.86 (59) 7.99	8.09 (52) 7.98 (48) 8.04	8.10 (53) 8.07 (47) 8.09	7.50 (38) 7.21 (62) 7.32	7.45 (32) 7.39 (68) 7.41	7.36 (46) 7.33 (54) 7.34	7.34 (49) 7.30 (51) 7.32
	2L8Q: DRUDE FF				2L8Q: C36 FF
	Li+	Na+	K+	Rb+	Li+	Na+	K+	Rb+
No SIS-HBBs (%) With SIS-HBBs (%) Mean (100%)	7.75 (24) 6.98 (76) 7.12	7.88 (27) 7.35 (73) 7.50	8.17 (49) 7.83 (51) 8.00	8.44 (42) 7.94 (58) 8.15	8.32 (38) 7.96 (62) 8.10	8.45 (44) 8.01 (56) 8.20	8.20 (49) 8.00 (51) 8.10	8.31 (51) 8.08 (49) 8.20

A quite different picture is observed from the additive C36 simulations. Analogous analysis revealed virtually no differential effect of the Li⁺, Na⁺, K⁺ and Rb⁺ monocations participating in SIS–HBB formation on DNA minor groove shape. In particular, the differences between the values of the minor groove width affected by SIS–HBB complexes involving different ions do not exceed ~3% in all systems studied (Table 2). This contrasts the results from the Drude simulations which give analogous values of ~30%, ~13% and 6% for the 1DCV, 2L8Q and EcoRI sequences, respectively. Moreover, the fraction of time corresponding to SIS–HBB formation are very similar for all four cations and for all three additive systems investigated. As a result, the C36 model predicts no substantial differential modulation of the DNA minor groove by solvated Li⁺, Na⁺, K⁺ and Rb⁺ ions, with the results for the three sequences being similar.

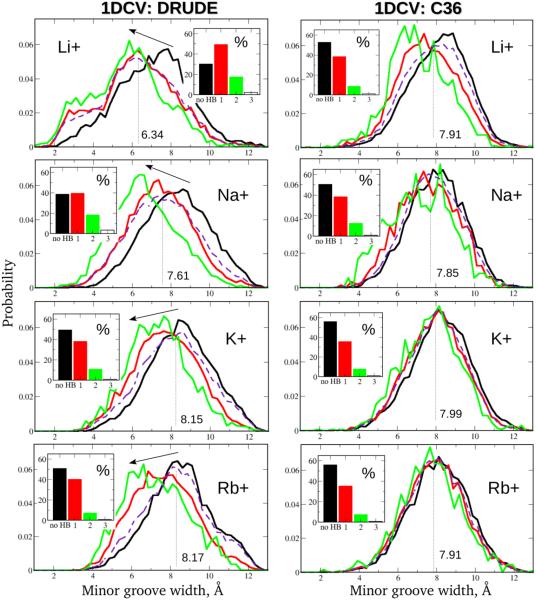
We focus next on a more detailed analysis of how different numbers of SIS–HBBs formed along each DNA oligomer at the same time affect the shape of the minor groove. The data are presented in Fig. 3 for 1DCV simulated with both the Drude and C36 force fields (results for EcoRI and 2L8Q systems are provided in Figs. S4 and S5 of SI). For each ionic solution, minor groove width probability distribution functions are computed from the parts of the MD simulation trajectory composed of the frames corresponding to certain numbers of SIS–HBBs formed. For the 10-base-pair 1DCV sequence, there are three dominant modes which represent the unperturbed by SIS–HBB complexes DNA molecule (black curves), and DNA states when the strands are mediated by one (red curves) and two (green curves) SIS–HB complexes, respectively. The more SIS-HBB complexes formed along the DNA, the larger their impact on the minor groove shape. Besides these modes, there is also a small fraction of instances when three (and more) SIS–HBB bridges occur reducing its size even further. For 1DCV sequence these occurrences are negligible, less than ~3% of the simulation time (white bars in the insets of Fig. 3, no curves shown). However, for longer 12-base-pair EcoRI and 2L8Q oligomers, such instances become more frequent, as seen from Figs. S4 and S5 for the cases of LiCl and NaCl solutions (~5-10% of simulation time, blue bars and curves).

Figure 3.

Relationship between the number of the SIS–HBB complexes formed along the 1DCV oligomer and the size of the minor groove. Results for the LiCl, NaCl, KCl and RbCl salt buffers with the Drude polarizable (left) and C36 additive (right) models are shown. Red and green curves denote minor groove width probability distributions corresponding to occurrences of one and two SIS–HBB complexes, respectively, are formed; black curves indicate the distributions in the absence of SIS–HBBs; dashed purple curves and the values represent the minor groove width distributions and the corresponding averages inferred from the entire MD trajectories. Insets show the time fractions of various binding events. Arrows are placed to emphasize the effect of the increase in the number of the SIS–HBB complexes formed on the minor groove size.

These results confirm our hypothesis that formation of the water-mediated hydrogen bonds between cations located inside the minor groove and DNA electronegative atoms are responsible for differential extent to which Li⁺, Na⁺, K⁺ and Rb⁺ ions modulate minor groove dimensions. The insets of Figs. 3, S4 and S5, showing the time fractions of different binding events, may be thought of as hydrated-ion/DNA “binding patterns” which faithfully characterize various combinations of DNA sequences and ionic solutions involved. For example, irrespective of DNA system, as ion size increases the fraction time corresponding to the unperturbed DNA state (black bar) also increases, with simultaneous decrease in the fractions of bound states (red, green, blue bars). This is rationalized by the lower dehydration penalty for larger cations and, consequently, lesser amount of hydrogen bonds formed between the water molecules solvating the cations and simultaneously two DNA strands. On the other hand, as the length of the DNA oligomer increases, more binding events may occur, such as instantaneous formation of three (and more) SIS–HBB complexes along the macromolecule, as exemplified by the Drude results for the 2L8Q sequence in LiCl and NaCl solutions (Fig. S5). At the same time, DNA sequences of the same length but different sequential content differ in their cation/DNA binding patterns and, consequently, in their overall conformations, as readily seen from comparison of the results for EcoRI and 2L8Q sequences (Figs. S4 and S5).

Figure 5.

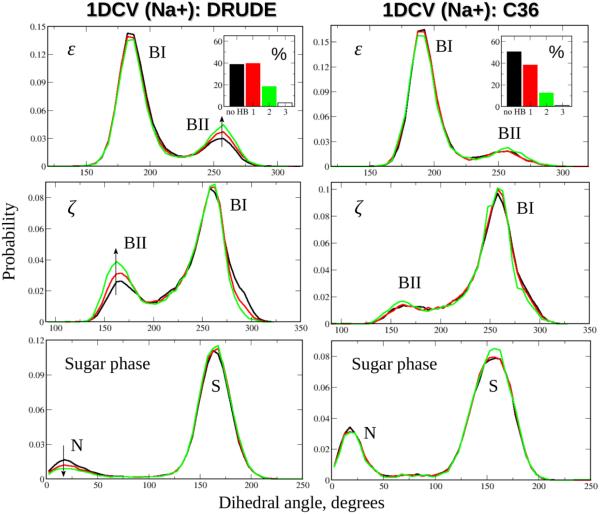
Influence of the number of the SIS–HBB complexes on the conformation of the DNA backbone and sugar moiety. Shown are the probability distribution functions for the ε and ζ dihedral angles of the backbone and pseudorotation angle of the sugar moiety from the Drude (left) and C36 (right) MD simulations of the 1DCV system in NaCl salt buffer. Coloring of the distributions and the time fractions in the insets is the same as in Fig. 3. Arrows indicate the increase in the population of the BII substate of the backbone (ε, ζ) and decrease in the north (N) population of the sugar group as the number of SIS–HBB complexes formed along DNA oligomer increases from zero (black) to one (red) to two (green).

The above analysis provides a clear explanation of the qualitatively different structural responses of the DNA to changes in the chemical content of the ionic buffer observed in the Drude polarizable and C36 additive models.²³ The differences are caused by a number of factors, including: (1) the variations in the hydration state of the cation located in the minor groove, (2) the differences in the hydrated-cation/DNA binding patterns, and (3) a different extent to which SIS–HBB complexes involving a particular cation modulate DNA minor groove.

To summarize the combined effect of all these factors, we reiterate by considering an example of the 1DCV system in KCl solution and comparing the outcomes from the Drude and C36 simulations. As seen from the Figs. 2C and 2D (green curves) and Table 1, hydration patterns of the K⁺ in the minor groove is quite different in the polarizable and additive models. In particular, compared to the C36 model, K⁺ is less dehydrated, possessing, on average, slightly more water molecules in its first solvation shell when the Drude model is employed. This results in a somewhat higher cumulative fraction of the states when DNA strands are mediated by SIS–HBB complexes (Table 2). Next, a closer analysis reveals that different numbers of SIS–HBB complexes formed along the DNA oligomer have a stronger effect on the shape of the minor groove in the Drude model compared to the additive C36 model (Fig. 3) with the differential effect of the number of complexes also being larger. The combination of all these effects results in the different average minor groove widths of 8.15 Å and 7.99 Å for the Drude and C36 models, respectively. When this line of reasoning is applied to other ionic solutions, the overall outcome is that DNA structure is substantially more responsive to the changes in the ionic buffer content in the Drude polarizable model versus the C36 additive model. For the 1DCV sequence, the minor groove width monotonically increases by ~30% when the type of ion in the solvation buffer changes from Li⁺ to Na⁺ to K⁺ to Rb⁺ in the Drude model, with virtually no such effect observed in the additive C36 model (Fig. 3). The two other studied DNA systems, 2L8Q (Fig. S5) and EcoRI (Fig. S4) sequences, give analogous values of ~15% and ~4%, respectively, when the Drude model is utilized, indicating that differential modulation of DNA shape by solvated monocations is a sequence-specific phenomenon based on the critical effect of polarization.

Dynamics of SIS–HBB Formation

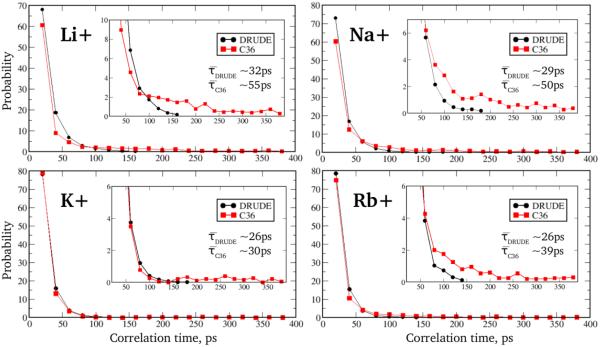
Because formation of SIS–HBBs appears to be a microscopic mechanism for the differential regulation of DNA structure by different monovalent cations, it is important to ensure that the longevity of MD simulations is satisfactory for gaining appropriate statistics of the ion/DNA binding events. A common practice is to require that the MD simulation time be 2-3 orders of magnitude longer than the correlation time of the phenomena being studied – in our case, the residence time of the solvated ions inside the minor groove. To this end, we computed the lifetime distribution functions of SIS–HBB complexes by averaging over residence times of all cations in the minor groove whose solvated water molecules formed hydrogen bonds with DNA strands. Fig. 4 shows the results for 1DCV sequence simulated in different ionic solutions using Drude and C36 force fields (see Fig. S6 of SI summarizing results for EcoRI and 2L8Q systems). It appears that forming/re-forming of SIS–HBB complexes is a highly dynamic process with the 60-80% of events happening on time scales of a few tens of picoseconds, though the rest of the binding/unbinding events cover time scales of up to ~200 ps and ~500 ps in the Drude and C36 models, respectively. Based on these distributions, average lifetimes of ~26-32 ps (Drude model) and ~30-55 ps (C36 model) were estimated, which are about a factor of ~5000 shorter than the MD simulation times of 200 ns. It has to be noted that these lifetimes were computed based on the presence of at least one water-mediated hydrogen bond per DNA strand (see Fig. 1), meaning several hydrogen bonds may form and reform in the process of maintaining a SIS–HB complex, as illustrated in the Fig. S7. For example, individual hydrogen bonds formed between a cation's solvation water molecules and DNA electronegative atoms were found to be very short lived, having an average lifetime of ~3.5 ps, which is almost an order of magnitude smaller than that of the entire SIS–HBB complex. This result is consistent with a recent computational estimate of ~2.8 ps for the average lifetime of the water-mediated hydrogen bond formed between DNA minor groove atoms and a more complex molecular ion, methyl-guanidinium.⁴³ Interestingly, for all three DNA systems studied and for all ionic buffers probed, the lifetimes of the SIS–HBB complexes are systematically shorter in the Drude model compared to the additive C36 model (Figs. 4 and S6). Given the smaller impact of the SIS–HBB complexes on DNA structure in the additive model (Figs. 3, S4 and S5), this is another clear indication that explicit polarization plays a crucial role in a stronger modulation of the DNA by shorter-lived SIS–HBB complexes in the Drude model.

Figure 4.

Lifetime probability distribution functions of the SIS–HBB complexes formed along 1DCV oligomer involving different monovalent ions from the Drude polarizable (circles) and C36 additive (squares) MD simulations. Insets show a expanded view of the Y axis. Average lifetimes derived from these distributions are provided in the insets.

The Role of the BI/BII Structural Equilibrium

The majority of the DNA conformational degrees of freedom reside in the backbone and sugar moieties.^22,32,44 Therefore, we next explored the structural modulation of the DNA by establishing possible correlations between formation of the SIS–HBB complexes and changes in the key dihedral angles of the backbone as well as in the sugar puckering.

Relationships between DNA minor groove dimension and the conformation of the backbone has been addressed previously.^45,46 In the B-form, DNA can adopt two conformations, BI and BII, defined by ε and ζ dihedral angles, with the difference ε – ζ < 0 corresponding to BI and ε – ζ > 0 corresponding to BII.^47,48 In a recent experimental study it was demonstrated that the shape of the minor groove is intrinsically coupled to the sequence-specific BII conformation.⁴⁵ The ability of the Drude polarizable and C36 additive models to satisfactorily reproduce experimentally measured sequential percent of BII for one of the presently studied DNA systems – EcoRI in NaCl salt buffer – was previously reported.^22,32 While studying the effect of sequence on the BII population and the minor groove dimensions would require quantification on the dinucleotide level and, therefore, simulations of considerably more sequences, we focus here on the role of solvated cations in the altering the overall population of the BII substate (i.e. averaged over the full DNA sequence) and the shape of the minor groove.

Shown in the Fig. 5 are the probability distribution functions for selected backbone dihedral angles, ε and ζ, and the pseudorotation angle of the sugar moiety, as functions of the different number of the SIS–HBB complexes formed along the 1DCV sequence simulated in NaCl salt solution using the Drude and additive C36 force fields. It appears that among all phosphodiester torsional degrees of freedom (α, β, γ, δ, ε, ζ), these angles are affected the most by solvated Na⁺ ions, which is also the case with other ionic solutions (not shown). Figs. S8, S9 and S10 show the analogous ε, ζ, and the pseudorotation distributions for 1DCV system simulated in LiCl, KCl and RbCl ionic buffers. Similar correlations are observed for EcoRI and 2L8Q systems in all four salt solutions (not shown). Notably, the correlations only occurs to a significant extent in the Drude model, with no substantial modulations of these (and other) torsional degrees of freedom induced by the increase in the number of SIS–HBB complexes in the additive C36 model.

The bimodal form of the probability distribution functions for ε and ζ angles (Fig. 5) reflects the conformational equilibrium between the dominant BI state (ε~180º and ζ~270º) and occasionally visited BII state (ε~260º and ζ~160º), a process anti-correlated with the puckering of the sugar moiety from the dominant south (S) conformation to the infrequent north (N) conformation.²² As already noted, there is a clear correlation between the number of the SIS–HBB complexes formed along DNA oligomer and the population of the backbone's BII substate. This correlation may be more quantitatively characterized by considering the increase in the percent of the BII population caused by formation of two SIS–HBB complexes relative to the BII population in the unperturbed (by solvated ions) DNA (Table 3). Qualitative differences between the Drude and C36 models are evident. Given that approximately 20% of the base steps (in DNA not bound to protein) populate BII state,⁴⁷ an increase in the BII population of up to ~8% observed in the Drude model indicates an appreciable effect of the solvated cations on DNA conformational properties and emphasizes the importance of properly accounting for the ionic environment when comparing results from Drude simulations with experimental data.

Table 3.

Changes in the population of the BII substate of the backbone induced by formation of the two SIS–HBB complexes (“2") relative to the unperturbed (zero SIS–HBBs, “0”) DNA conformation for all systems and all ionic buffers simulated with the Drude polarizable and C36 additive force fields. Also shown for reference are the actual BII populations corresponding to these states as well as the average values of the BII population computed from the entire MD simulation trajectories (“Average”).

		DRUDE FF				C36 FF
		Average	0	2	Δ (2 – 0)	Average	0	2	Δ (2 – 0)
1DCV	Li+	24.8	24.2	26.7	2.5	28.7	28.5	29.5	1.0
	Na+	21.4	19.5	25.4	5.9	26.5	26.2	27.1	0.9
	K+	19.5	18.3	23.3	5.1	21.6	21.1	22.9	1.8
	Rb+	20.1	17.4	23.9	6.5	18.8	18.5	19.4	0.9
EcoR1	Li+	18.8	15.9	24.1	8.2	18.6	18.1	19.0	0.9
	Na+	12.0	11.8	12.8	1.0	21.2	21.6	21.1	−0.5
	K+	12.8	11.5	16.9	5.4	20.1	20.1	20.2	0.1
	Rb+	14.1	12.3	17.5	5.2	20.4	20.4	20.4	0.0
2L8Q	Li+	21.9	20.5	23.4	2.9	21.4	20.9	22.3	1.4
	Na+	20.3	18.7	22.9	4.2	28.1	27.4	29.0	1.6
	K+	18.3	17.1	20.5	3.4	25.3	25.2	25.5	0.3
	Rb+	16.2	14.8	17.0	2.2	26.0	25.8	26.7	0.9

Impact of Polarization Effects Revealed from Variations in the Dipole Moment of Water

The physical forces driving the dynamics and structural behavior of the DNA in various ionic solutions are different in the C36 and Drude models. The latter model explicitly includes induced polarization providing a more detailed and faithful representation of the microscopic interactions among DNA, ions and water. The different nature of the underlying physics in the additive and Drude models was addressed previously by comparing the evolutions of the dipole moments of individual nucleic acid bases in DNA oligomers²² and peptide backbone in proteins⁴⁹ generated by the additive C36 and Drude polarizable models. In particular, systematically larger values and significant variability of dipole moments in the Drude model – compared to the dipole moments of smaller magnitude and far less variability in the C36 model – indicate that macromolecule’s electronic distribution is sensitive to instantaneous changes in the local electrostatic environment when Drude model is employed.

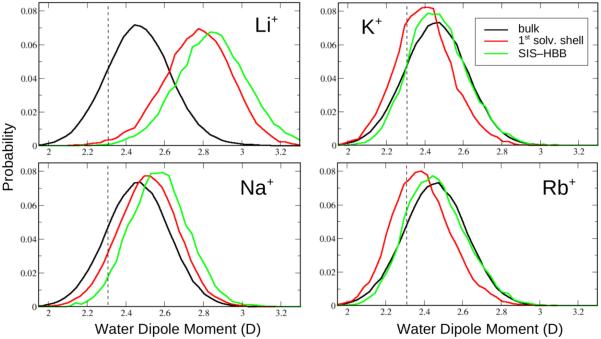
For the presently identified microscopic mechanisms responsible for differential impact of solvated cations on DNA conformational properties observed in the Drude model, it is essential that the direct contribution of polarizability to the phenomena also be identified. Because SIS–HBB complexes involve DNA, ions and water, it is important to monitor the variations in the dipole moments of all three constituents, when DNA is unperturbed and mediated by solvated cations. Such analysis did not reveal any appreciable changes in the dipole moments of the nucleic acid bases and cations upon SIS–HBB formation. However, water molecules demonstrate high sensitivity to changes in the local electrostatic environment, as evidenced in Fig. 6. Shown are the dipole moment distributions of the water molecules located in bulk (~7 Å away from DNA surface, not interacting with cations), contributing to the cation’s first solvation shell and participating in SIS–HBB complexes. It is seen that the extent to which water’s dipole moment varies upon interacting with the ion and with both the ion and DNA depends on the ion’s charge density. For smaller Li⁺ and Na⁺ ions the trends are similar, with the water dipole moment increasing from the average bulk value of 2.45 D to ~2.8 D and ~2.57 D, respectively, when water directly interacts with the ion, with the further increase by ~0.1 D upon interacting with both the ion and DNA. Different changes are observed when larger K⁺ and Rb⁺ ions are involved: upon association with the cation, the water dipole moment first decreases by ~0.1 D relative to the bulk value and then increases by approximately the same amount upon further forming hydrogen bonds with DNA atoms. Such subtle changes in the water electrostatics undoubtedly contribute to the differential structural DNA changes induced by SIS–HBB complexes involving different monocations in the Drude polarizable model. However, it has to be kept in mind that the performed water dipole analysis – while being indicative of the importance of inclusion of polarization effects into the model – cannot be used by itself to interpret the impact of polarization on the obtained results. Indeed, the observed phenomena may be driven by a combination of many factors related to inherent differences between the models tested, and we cannot exclude the possibility that future improvements of the additive C36 parameters for the ions and/or DNA may lead to closer agreement between Drude polarizable and C36 additive results.

Figure 6.

Distributions of the water dipole moments computed from averaging over water molecules located in bulk (black), contributing to the first solvation shell of the cations (red) and participating in the SIS–HBB formation (green). Results are shown for the 1DCV system simulated in different ionic solutions. Vertical dashed lines denote the permanent dipole moment of the water molecules (2.34 D) in the additive C36 model. Values are in Debye.

CONCLUSIONS

The present study is motivated by our recent findings on the differential impact of the monocations Li⁺, Na⁺, K⁺ and Rb⁺ on DNA conformational properties revealed from calculations of the solution-state X-ray scattering profiles and subsequent structural analysis.²³ While the role of the ions in modulation of the scattering spectra and the overall DNA conformation – mainly, via changes in the minor groove dimensions – was appreciated, microscopic mechanisms for such structural behavior were not addressed. Understanding the origin of the DNA minor groove variations is one of the key questions in structural biology.⁴⁵ In a recent experimental study it was demonstrated that disruption of the specific solvation pattern in the minor groove dramatically affects a “direct” readout in remote (5-6 bases away) segments of DNA (e.g. in the major groove),⁴ a result consistent with the more general observation that the minor groove dimensions (but not those of the major groove) are highly variable in protein-DNA complexes.^1,27 Because other experimental and computational studies indicate the presence of various ions inside the minor groove,^{12,14,15,19,21} it is important to provide microscopic insights into the relationship between variations in the minor groove dimensions and changes in the ionic buffer content.²³

Our analysis of the MD simulations was based first on identifying the cations located inside the DNA minor groove and elucidating the extent of their hydration. With those ions found to be predominantly hydrated, maintaining their first solvation shell almost intact, we put forward and confirmed a hypothesis that water-mediated hydrogen bonding between cations and simultaneously two DNA strands was the primary microscopic mechanism for differential minor groove modulation by the first-group monovalent cations. A detailed analysis of the DNA conformational behavior in different ionic buffers indicated that a combination of several factors, such as variations in the lifetime of the hydrogen bond complexes involving the different solvated cations and DNA strands, the number of such complexes simultaneously formed, and the different extent to which such complexes modulate DNA minor groove, provides an explanation for (1) the previously observed dependence of the solution state X-ray spectra on the type of the monovalent ion, and (2) why such dependence is seen only in the Drude polarizable model but not in the additive C36 model.²³ Further analysis revealed that diminishing of the minor groove width induced by solvated cations strongly correlates with the increase in the population of the BII substate, another important result given the increasing evidence of the role of the BI/BII conformational equilibrium in sequence specific and nonspecific protein-DNA recognition,^44,50,51 or even in the ability of the DNA to form nucleosomes.⁴⁴

In summary, our findings indicate an existence of the dual relationship – between water-mediated hydrogen bonding of cations to the DNA minor groove and altering BI/BII backbone conformation, on the one hand, and the backbone behavior and the minor groove dimension, on the other hand. Differential modulation of the DNA minor groove by Li⁺, Na⁺, K⁺ and Rb⁺ monocations predicted by the Drude polarizable model and the proposed microscopic mechanisms explaining the phenomenon may have important implications for a variety of the salt-mediated biological processes involving DNA. The qualitatively different outcomes from the Drude polarizable and C36 additive models, combined with previously demonstrated better agreement between predictions from the Drude model and a set of experimental measurements and theoretical estimations,^{22,23,25,28,52} indicate the importance of the explicit inclusion of electronic polarizability in empirical force fields.