Lesion insertion in the projection domain: Methods and initial results

Abstract

Purpose:

To perform task-based image quality assessment in CT, it is desirable to have a large number of realistic patient images with known diagnostic truth. One effective way of achieving this objective is to create hybrid images that combine patient images with inserted lesions. Because conventional hybrid images generated in the image domain fails to reflect the impact of scan and reconstruction parameters on lesion appearance, this study explored a projection-domain approach.

Methods:

Lesions were segmented from patient images and forward projected to acquire lesion projections. The forward-projection geometry was designed according to a commercial CT scanner and accommodated both axial and helical modes with various focal spot movement patterns. The energy employed by the commercial CT scanner for beam hardening correction was measured and used for the forward projection. The lesion projections were inserted into patient projections decoded from commercial CT projection data. The combined projections were formatted to match those of commercial CT raw data, loaded onto a commercial CT scanner, and reconstructed to create the hybrid images. Two validations were performed. First, to validate the accuracy of the forward-projection geometry, images were reconstructed from the forward projections of a virtual ACR phantom and compared to physically acquired ACR phantom images in terms of CT number accuracy and high-contrast resolution. Second, to validate the realism of the lesion in hybrid images, liver lesions were segmented from patient images and inserted back into the same patients, each at a new location specified by a radiologist. The inserted lesions were compared to the original lesions and visually assessed for realism by two experienced radiologists in a blinded fashion.

Results:

For the validation of the forward-projection geometry, the images reconstructed from the forward projections of the virtual ACR phantom were consistent with the images physically acquired for the ACR phantom in terms of Hounsfield unit and high-contrast resolution. For the validation of the lesion realism, lesions of various types were successfully inserted, including well circumscribed and invasive lesions, homogeneous and heterogeneous lesions, high-contrast and low-contrast lesions, isolated and vessel-attached lesions, and small and large lesions. The two experienced radiologists who reviewed the original and inserted lesions could not identify the lesions that were inserted. The same lesion, when inserted into the projection domain and reconstructed with different parameters, demonstrated a parameter-dependent appearance.

Conclusions:

A framework has been developed for projection-domain insertion of lesions into commercial CT images, which can be potentially expanded to all geometries of CT scanners. Compared to conventional image-domain methods, the authors’ method reflected the impact of scan and reconstruction parameters on lesion appearance. Compared to prior projection-domain methods, the authors’ method has the potential to achieve higher anatomical complexity by employing clinical patient projections and real patient lesions.

1. INTRODUCTION

Assessing CT image quality for lesion detection tasks requires the ground truth for lesion characteristics (size, contrast, texture, boundary, type, and location). Although such information can be collected via chart and image review, the collecting process is time-consuming. Furthermore, the collecting process is retrospective, which means the lesion characteristics cannot be determined prior to the patient scanning. To overcome these barriers, lesions of known characteristics are inserted into patient images to create hybrid images, such that the image quality assessment can be efficiently and prospectively designed.

An easy and common approach to generating hybrid images is the image-domain method, which inserts lesions into reconstructed CT images.^1–5 However, because this method inserts the lesions after image reconstruction, simulating the impact of CT scan and reconstruction parameters (radiation dose, slice thickness, reconstruction algorithm, etc.) on the appearance of lesions becomes extremely challenging. This is especially true with the increasing use of iterative reconstruction algorithms, where the imaging system response at the boundary of the lesion is nonlinear and still under exploration;^6,7 it is almost impossible to simulate the true appearance of lesion boundaries using image-domain lesion insertion methods when iterative reconstruction is applied.

To accurately reflect the impact of scan and reconstruction parameters on the appearance of lesion boundaries, projection-domain methods that insert lesions into projection data prior to reconstruction were explored by Solomon et al.⁸ and Xu et al.,⁹ Xu’s work employed a vendor-developed computer simulation package, drasim,¹⁰ to simulate projections of a virtual anthropomorphic phantom with embedded lesions. The simulated projections were then reformatted to match those of commercial raw data, such that they can be uploaded to commercial CT scanners for image reconstruction. However, the study was fundamentally limited by the fact that, restricted by drasim, only analytical phantoms and lesion models could be used for projection simulation (the virtual anthropomorphic phantom defines organs with nonuniform rational B-spline surfaces,¹¹ not voxels). As a result, subtle anatomical variations such as tissue texture, lesion inhomogeneity and invasive lesion boundaries could not be simulated.

To improve the anatomical complexity and reality of the hybrid images, this study explored a new projection-domain method based on real patient projection data. First, voxelized lesions were extracted from patient CT data sets. Then, lesion projections were obtained using a forward-projection program. The lesion projections were combined with patient projections to generate hybrid images. The forward-projection program precisely simulated the gantry movement of a state-of-the-art commercial CT scanner in both axial and helical modes with various focal spot movement patterns and was evaluated in terms of CT number accuracy and high-contrast resolution. Preliminary evaluations of lesion realism in the hybrid images were performed by radiologists.

2. METHODS

2.A. Lesion insertion in projection domain

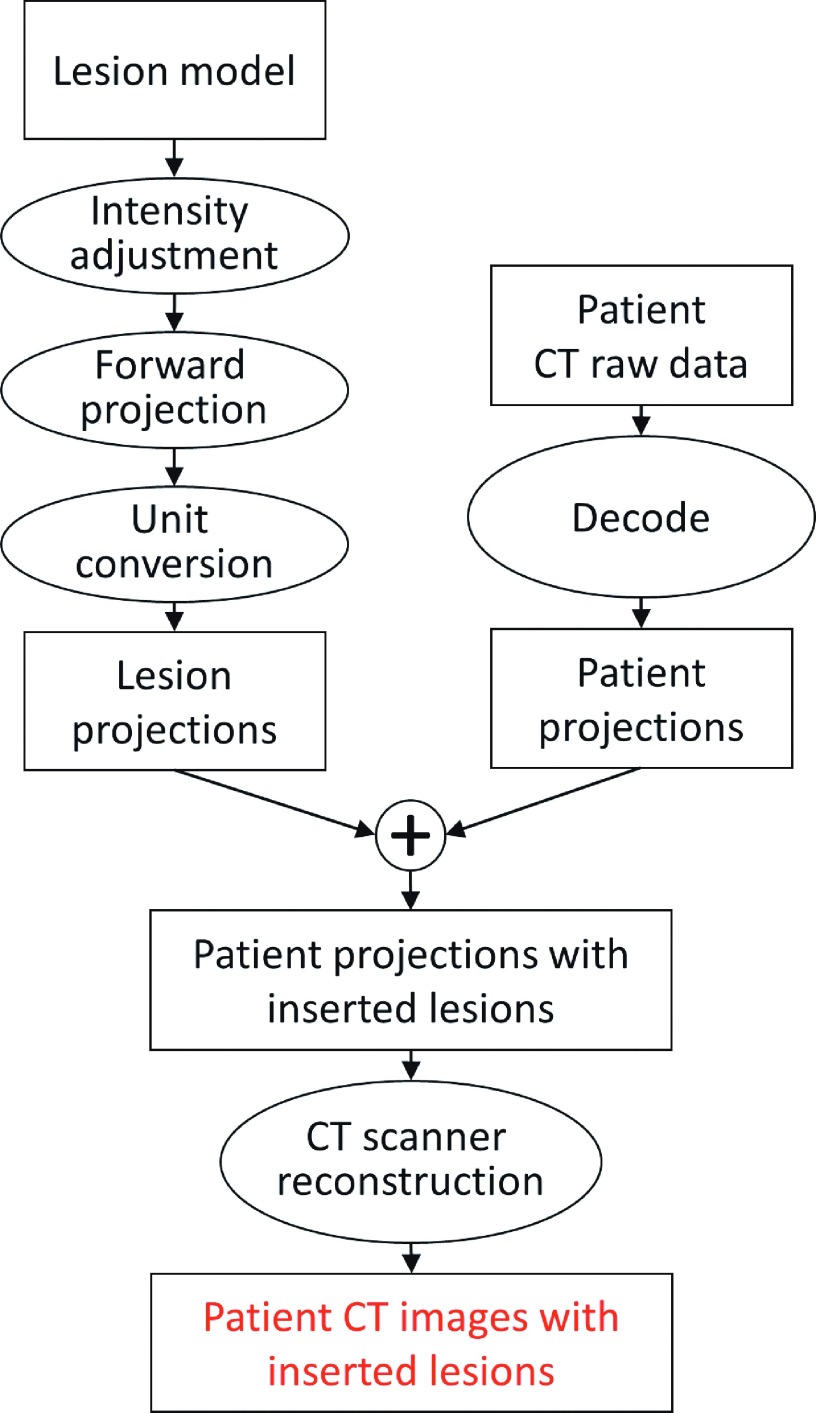
A flowchart of the projection-domain lesion insertion process is shown in Fig. 1. Voxelized lesion models were built upon segmented lesions, forward projected, and combined with patient CT projections. The modified patient projections were then formatted to match that of commercial CT raw data and reconstructed on scanners to yield hybrid images.

FIG. 1.

The process of the projection-domain lesion insertion.

First, voxelized lesion models in the unit of Hounsfield unit (HU) were built upon lesions segmented from patient CT images. The segmentations were performed with free software (Seg3D, University of Utah, Salt Lake City, UT), where the lesion boundaries were manually drawn slice-by-slice under the instruction of a radiologist specialized in abdominal imaging. Basic lesion characteristics such as the volume, contrast, sphericity, and heterogeneity of the lesion were recorded along with the segmented lesion in each lesion model. To minimize the noise while maximizing the resolution of the model, the images for lesion segmentation were reconstructed with an iterative reconstruction algorithm (SAFIRE—Sinogram Affirmed Iterative Reconstruction with strength of 3, Siemens Healthcare, Forchheim, Germany) using a medium sharp I40 kernel, 1 mm image thickness, and 200 mm reconstruction field of view.

The voxel intensity of the segmented lesion model was adjusted in two steps to maintain the lesion’s contrast to the surrounding tissue after it was inserted into the patient images. The first adjustment approximately removed the tissue at the lesion insertion location prior to the insertion, which was done by subtracting the average CT number of the insertion location from the lesion model (assuming that the liver parenchyma at the insertion location is uniform). The second adjustment accounted for the intensity difference between the lesion’s original location and the lesion’s insertion location, which was done by subtracting the background difference from the lesion model. Appendix A mathematically demonstrates how the lesion contrast was maintained through the two adjustments.

Next, a forward-projection program using Siddon’s method¹² was developed to compute lesion projections from the lesion model. Only primary beam was considered during the forward projection, which was reasonable given the fact that each lesion was of limited size. The forward-projection program can potentially be used for geometries of any CT scanner, although this work focused on the geometry of a state-of-art multidetector-row scanner (Somatom Definition Flash, Siemens Healthcare, Forchheim, Germany). Specifically, the program accommodated various acquisition conditions, such as axial and helical scans, 32- and 64-row collimations, and flying focal spot (a periodic motion of focal spot to enhance spatial resolution¹³).

Because the unit of the lesion models was HU, the lesion forward projection needed to undergo an additional unit conversion process to convert CT numbers into linear attenuation coefficients. This conversion requires an x-ray energy spectrum, based on which the water attenuation coefficient can be defined. This spectrum was chosen to be monoenergetic, with its energy equal to the CT vendor’s beam hardening correction energy. This was done because the patient projections, into which the lesion forward projections were inserted, were decoded from commercial CT raw data that had already had beam hardening corrections applied. Therefore, by converting the HU to the linear attenuation coefficient at the CT vendor’s beam hardening correction energy, the lesion forward projections could be readily combined with the patient projections.

The CT vendor’s beam hardening correction energy was proprietary and unknown. To estimate it, a virtual phantom was built from images of an ACR CT accreditation phantom¹⁴ (acquired on a Siemens Definition Flash scanner with highest dose available and reconstructed with 5 mm slice thickness and a sharp H70 kernel), named {I₀}. Forward projections of the virtual phantom were converted from integral of CT number to integral of linear attenuation coefficients under an initial guess of the beam hardening correction energy and formatted to match those of commercial CT raw data. The forward projections were then loaded back to CT scanners and a new set of images named {I₁} were reconstructed. The CT numbers measured from {I₁} were compared to those of {I₀}, according to which the initial guess of the energy can be calibrated. The calibration process is described in detail in Appendix B. The estimation of beam hardening correction energy was performed with multiple materials, including acrylic, polyethylene, and solid water (inserts in Module 1 of the ACR CT accreditation phantom). The estimation was also performed at multiple tube potentials, including 80, 100, 120, and 140 kV. The initial guess of the beam hardening correction energy for each tube potential was the effective energy of the polychromatic beam (53.8, 62.2, 69.7, and 75.8 keV for 80, 100, 120, and 140 kV, respectively¹⁵).

The lesion forward projections after the unit conversion were combined with the patient projections decoded from commercial CT raw data (with the assistance of the vendor). The patient projections with the inserted lesion were then reformatted to match the format of commercial CT projection data and reconstructed on the commercial CT scanner to generate the hybrid images.

2.B. Validation of forward-projection program

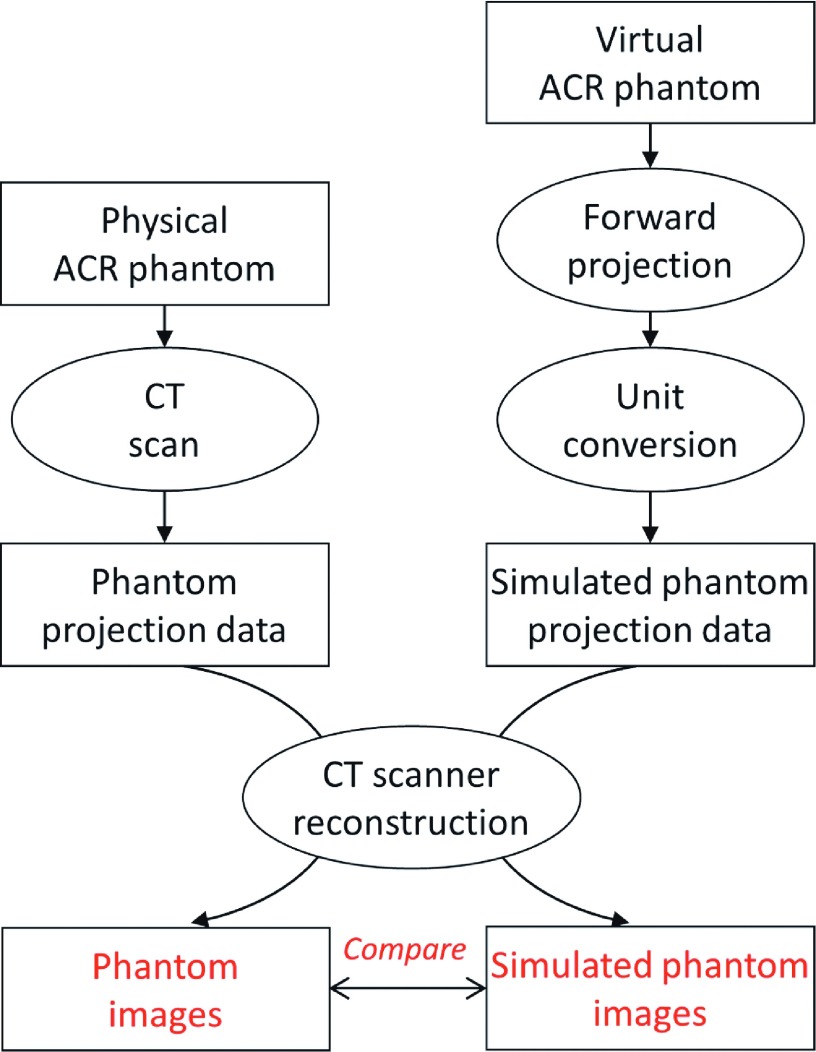
The forward-projection program is the key to projection-domain lesion insertion. To validate its accuracy, forward projections were compared to physically acquired CT projections (decoded from commercial CT raw data) in terms of their reconstructed images, as illustrated in Fig. 2. First, forward projections were computed for the virtual ACR phantom built in Sec. 2.A assuming a helical scan (pitch = 1) and use of the flying focal spot technique (both in-plane and along axial directions). The forward projections were converted into unit of μ ⋅ mm using the beam hardening correction energy estimated in Sec. 2.A and reformatted into the format of commercial CT projection data. Next, CT projection data were physically acquired for an ACR phantom on a Siemens Definition Flash scanner using helical scan of unit pitch and flying focal spot. Both forward projections and commercial projection data were reconstructed on the scanner using a medium sharp B40 kernel, 1 mm slice thickness, and 22 cm field of view. The reconstructed images were compared in terms of HU accuracy (Modules 1 and 2 of the ACR phantom) and high-contrast resolution (Module 4 of the ACR phantom).

FIG. 2.

The process used to validate the forward-projection program.

2.C. Validation of lesion realism

Six liver lesions covering a range of size, boundary type, homogeneity, and contrast were segmented from patient images. As mentioned in Sec. 2.A, the images for segmentation were reconstructed with iterative reconstruction, a medium sharp kernel, thin image thickness, and small field of view, such that the boundary of the lesion was preserved and the noise in the lesion was minimized. The lesions were inserted back into the projection data of the same patients, each at a new location specified by a radiologist. The patient projection data with the inserted lesions were reconstructed on a CT console using clinical protocols (filtered backprojection, medium sharp B40 kernel, 5 mm image thickness, and 320–420 mm field of view) to yield hybrid images. Six lesion pairs (original lesions and the corresponding lesions inserted at a new location) were created from the hybrid images.

To test the realism of the inserted lesions, the six lesion pairs were viewed by two radiologists (both with more than ten years of experience, not the radiologist who specified the lesion insertion location) in the context of the entire liver and across slices. For each lesion pair, the radiologists were blinded to which lesion was inserted and which lesion was original, and chose the lesion in consensus that they thought was inserted. A confidence score on a 1–5 scale was also given to each choice by the radiologists, in consensus, with 1 representing no confidence in their choice and 5 representing full confidence that they had correctly identified the inserted lesion. This assessment of six lesions is limited to a demonstration of feasibility; the small number of lesions does not provide adequate statistical power. In separate work, a full-scale clinical validation study was performed using 51 lesion pairs, and the same methodology and radiologist readers as described here²⁵ (see Sec. 4 for additional information).

To demonstrate the main strength of projection-domain method over image-domain method, which is the ability to reflect the impact of reconstruction parameters on lesion appearance, patient projections with inserted lesion were reconstructed with different reconstruction image thicknesses and kernels to demonstrate the resultant differences of lesion appearance.

3. RESULTS

3.A. Estimation of beam hardening correction energy

Table I lists the estimated energy levels for commercial beam hardening corrections. For 100, 120, and 140 kV, an energy level around 71.1 keV was estimated for materials of acrylic, polyethylene, and solid water. For 80 kV, however, the estimated energy level fluctuated across different materials. This fluctuation was probably caused by beam hardening artifact at 80 kV, which affected the CT number of the virtual ACR phantom and interfered in the energy estimation. The final energy for the beam hardening correction was therefore chosen at 71.1 keV for all kV settings and was used to convert the forward projections from line integral of CT numbers to line integral of linear attenuation coefficients.

TABLE I.

The estimated beam hardening correction energy for various tube potentials. Unit: keV. The air, polyethylene, and solid water materials are provided by inserts in Module 1 of ACR phantom.

	Acrylic	Polyethylene	Solid water	Average
80 kV	73.20	68.40	70.10	70.57
100 kV	71.20	71.10	71.10	71.13
120 kV	70.90	71.20	70.90	71.10
140 kV	71.20	70.90	71.30	71.13

3.B. Validation of forward-projection program

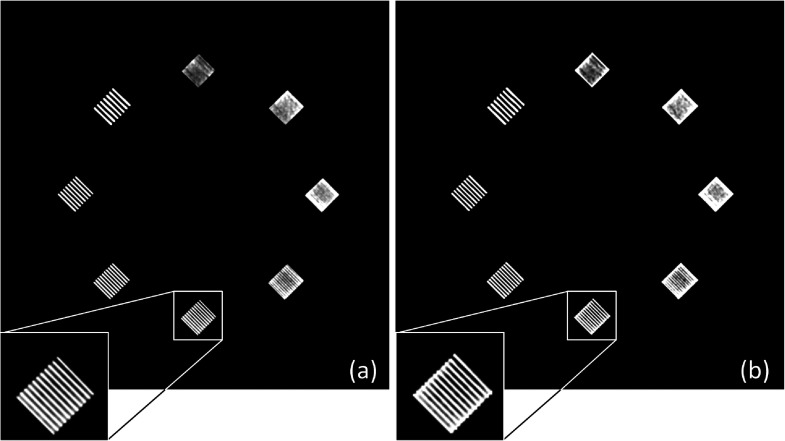
As a validation of CT number accuracy, Table II lists the CT numbers of the inserts in Module 1 of ACR phantom, measured from both physically acquired images and simulated images (reconstructed from the forward projections of the virtual ACR phantom). Across four tube potentials (80, 100, 120, and 140 kV) and five materials (air, acrylic, bone, polyethylene, and solid water), excellent agreement (within 2 HU) was observed. In addition, to validate the CT number accuracy at low-contrast condition, the contrast of the low-contrast insert in Module 2 of ACR phantom (6 HU nominal contrast) were measured from both physically acquired and simulated images. For all four tube potentials (80, 100, 120, and 140 kV), a contrast of six HU was observed. As a validation of high-contrast resolution, Fig. 3 shows that the bar patterns in the physically acquired and simulated ACR phantom images are essentially identical.

TABLE II.

The CT numbers measured from the physically acquired ACR phantom image, “commercial,” and the CT numbers measured from the simulated ACR phantom image, “forward projection.” Unit: HU. The air, acrylic, bone, polyethylene, and solid water materials are provided by inserts in Module 1 of ACR phantom.

		Air	Acrylic	Bone	Polyethylene	Solid water
80 kV	Commercial	−987	102	1178	−111	3
	Forward projection	−988	103	1180	−112	4
100 kV	Commercial	−987	115	980	−93	2
	Forward projection	−988	116	981	−94	2
120 kV	Commercial	−987	121	868	−83	3
	Forward projection	−987	121	868	−82	4
140 kV	Commercial	−985	125	797	−75	3
	Forward projection	−985	126	796	−76	4

FIG. 3.

The high-resolution bar patterns in (a) the physically acquired ACR phantom image at 120 kV and (b) the simulated ACR phantom image at 120 kV. The display window width setting is 200 HU and the level setting is 1000 HU.

3.C. Validation of lesion realism

Figure 4 shows six pairs of original and inserted lesions of various types, including well circumscribed and invasive lesions [Figs. 4(a) and 4(g) and Figs. 4(b) and 4(h), respectively], homogeneous and heterogeneous lesions [Figs. 4(a) and 4(g) and Figs. 4(c) and 4(i), respectively], high-contrast and low-contrast lesions [Figs. 4(a) and 4(g) and Figs. 4(d) and 4(j), respectively], isolated and vessel-attached lesions [Figs. 4(a) and 4(g) and Figs. 4(e) and 4(k), respectively], and small and large lesions [Figs. 4(a) and 4(g) and Figs. 4(f) and 4(l), respectively]. Note that due to partial volume effect (abdominal images are routinely reconstructed with 5 mm slice thickness) and the background differences between original and insertion locations, the inserted lesions do not look exactly the same as the original lesions. However, all inserted locations had realistic appearance and blended naturally into the liver background.

FIG. 4.

Liver lesions were segmented and inserted back into the same patients at a different location. (a)–(f) show the original liver lesions. (g)–(l) show the inserted liver lesions. The display window width setting is 400 HU and the level setting is 40 HU.

When viewed by the radiologists in a blinded, consensus fashion, lesion pairs 1, 2, and 4 in Fig. 4 were correctly classified (i.e., the radiologists correctly chose the inserted lesion from the lesion pair) with confidence scores of 1, meaning that the radiologists made the right choice by randomly guessing. Lesion pair 5 was correctly classified with a confidence score of 5, because the inserted lesion has an unusual orientation (i.e., the flat border of the lesion should instead appear against a vessel). Lesion pairs 3 and 6 were incorrectly classified by the radiologists with confidence scores of 2 and 3, respectively. Overall, the radiologists reported that they could not effectively distinguish between inserted lesions and original pathologies, as demonstrated by this small reader study. Due to the small number of lesions evaluated, this result is not statistically significant. However, a full-scale clinical validation was performed in a subsequent study²⁵ (see Sec. 4).

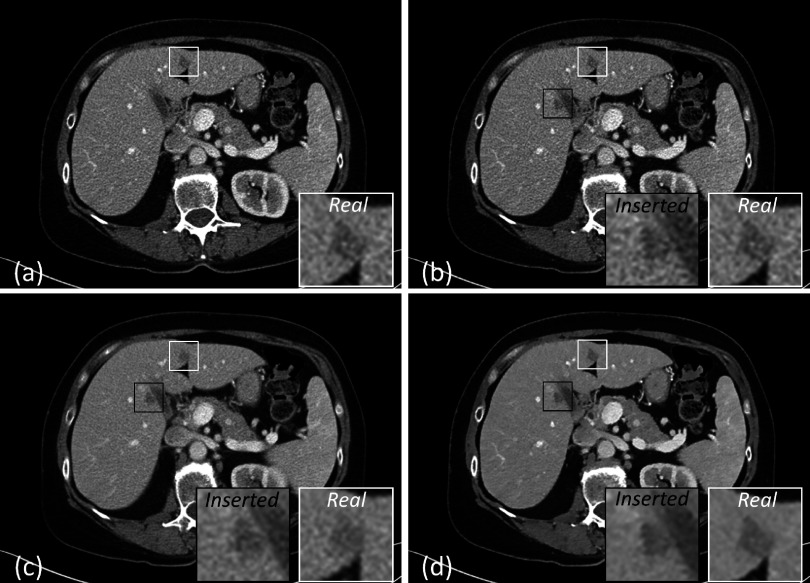
Figure 5 demonstrates the major advantage of our projection-domain lesion insertion method over image-domain methods, which is the ability to reflect the impact of reconstruction parameters on the lesion appearance. Figure 5(a) was reconstructed from the original patient projections (no lesion inserted). Figures 5(b)–5(d) were reconstructed from the same modified patient projections, but using different image thicknesses and kernels. As expected, the inserted lesion appeared smoother with thicker image thicknesses and use of the iterative reconstruction algorithm, reflecting the impact of reconstruction parameters. More importantly, the inserted lesion and the original lesion changed appearance in a similar fashion as reconstruction parameter varied.

FIG. 5.

(a) The patient image reconstructed with a FBP B40f kernel and 2 mm slice thickness. (b) The hybrid image reconstructed with a FBP B40f kernel and 2 mm slice thickness. (c) The hybrid image reconstructed with a FBP B40f kernel and 5 mm slice thickness. (d) The hybrid image reconstructed with a SAFIRE I40f kernel (strength of 5) and 2 mm slice thickness. The display window width setting is 400 HU and the level setting is 40 HU.

4. DISCUSSION

Hybrid images have been widely used in the assessment of image quality. For 2D imaging such as radiography and mammography, because of the anatomical overlap, the hybrid images were mostly created by superimposing the lesions onto the images.^16–19 For 3D imaging such as CT, the creation of hybrid images is much more challenging as the lesions need to be inserted into image volumes.^1,2,9 Moreover, if the lesions are inserted via projection domain instead of image domain, many acquisition parameters need to be precisely simulated, including the energy spectrum of the x-ray and the movement of the focal spot, detector, and patient during the acquisition. This study developed such a projection-domain technique and demonstrated that the technique was capable of precisely simulating acquisition parameters and creating clinically realistic hybrid images.

Because our technique inserted lesions in the projection domain, it reflected the impact of reconstruction parameters on lesion appearance and can be used to study the impact of reconstruction parameters. Because our technique used patient projections and lesions segmented from patient images, the hybrid images demonstrated anatomical complexity typical of clinical images, which is difficult to achieve with projections simulated from anthropomorphic phantoms and mathematical lesions. These strengths enable a number of interesting opportunities. For example, virtual clinical trials could be conducted to evaluate and optimize reconstruction algorithms. Furthermore, the evaluation could be done task-specifically, i.e., with respect to specific lesion characteristics and lesion location, which is required for iterative reconstruction algorithm because multiple studies have shown that the performance of iterative reconstruction is task dependent.^20–22 Another example involves the evaluation of radiation dose reduction. The lesion insertion program could be combined with a previously developed projection-domain noise insertion program²³ to simulate positive cases at lower dose levels, such that the dose reduction potential can be assessed in a task-specific manner.

To improve the anatomical complexity of the hybrid images, patient projections instead of simulated phantom projections were used in this study. However, because the patient projections were decoded from commercial CT raw data with the assistance of the vendor, which is not a common research resource, our lesion-insertion technique might not be easily adopted by other research groups. A potential solution to this drawback is a projection data reference library being developed by our group, which includes patient projections acquired on commercial CT scanners but converted into an extended DICOM format.²⁴ The format is open and vendor-neutral, such that the library can be accessed by the academic community and used for CT projection related research studies.

For observer studies conducted with hybrid images, it is important to precisely control the contrast of the inserted lesion relative to the background tissue. Therefore, a contrast level was assigned to the lesion prior to the insertion, which by default was the same contrast level as the original pathology. For example, if a lesion with a contrast of 50 HU was segmented from 80 kV images and inserted into 120 kV images, despite the tube voltage difference, the contrast of the inserted lesion would be maintained at 50 HU. However, if the user wishes the inserted the lesion to reflect the impact of tube voltage on CT number, the contrast of the lesion can be manually adjusted prior to the insertion.

This study used lesions segmented from patient data, such that the inserted lesion could be compared to the original pathology. One concern about using segmented lesions is that the lesion database might be limited (our current lesion library contains over 100 liver lesions and over 30 pulmonary nodules). However, the orientation, size, and contrast of the segmented lesions can all be adjusted to create new cases. Other lesion models, such as randomly generated mathematical lesions,^1,5,18 could also be used by our lesion-insertion program, as long as the lesion model is voxelized. Another concern about using segmented lesions is that the segmented lesion inherits the noise and boundary blur from the original patient images and introduces them into the hybrid images (i.e., because the segmented lesion has already been imaged once, the forward projected inserted lesion has essentially been imaged twice). The inserted lesion therefore had slightly higher noise than the surrounding tissue and a slightly blurred boundary than the original pathology. We minimized the noise increment by minimizing the noise in the segmented lesion (the lesions for segmentation were reconstructed with iterative reconstruction). We minimized the boundary blur by preserving the edge of the segmented lesion (the lesions for segmentation were reconstructed with a medium sharp kernel). As shown by the six lesion pairs in Fig. 4, the noise increment and boundary blur are barely perceptible. Alternatively, future studies could use mathematical lesions to avoid such noise increment and boundary blur. However, the focus of this paper is the insertion of lesions segmented from patient images, not the creation of lesion models. A third concern about using segmented lesions is that the difference between the inserted lesions and the original pathology, albeit small, may bias the observer performance. However, our intention was not to replicate the original pathology, but to generate hybrid images having realistic looking lesions. In observer studies conducted with the hybrid images, inserted lesions will only be compared to inserted lesions, so that we expect negligible impact of potential bias.

An alternative to validating the forward-projection program with reconstructed images would be to validate the program with projection data, i.e., to compare the projection data simulated from the virtual ACR phantom to the physically acquired projection data. In this study, we chose to compare the reconstructed images because (1) it is hard to translate the differences observed in projection data into differences in reconstructed images, and (2) reconstructed images are what ultimately used for assessment of observer performance.

Although the visual validation of the lesion realism (Figs. 4 and 5) showed that the inserted lesions appeared similar to the original pathologies across varying reconstruction conditions, this quantitative validation of lesion realism in the form of an observer study included only six cases and is thus not statistically significant. To address this, a full-scale observer study was subsequently performed using radiologist readers.²⁵ In that work, 51 lesion pairs (real and inserted) were evaluated by two board-certified radiologists in consensus using methods similar to those described in Sec. 2.C. The results showed that 49% (25/51) of lesion pairs were incorrectly classified (the inserted lesion being identified as the real lesion). Sixty-three percent (32/51) of lesion pairs were classified with a confidence level of 1 or 2, meaning that the radiologists identified the inserted lesion by randomly guessing. Even for the eight lesion pairs that were confidently classified by the radiologists (confidence level of 4 or 5), 38% (3/8) of them were still incorrectly classified.

To conclude, a framework has been developed for projection-domain insertion of lesions into commercial CT images, which could be expanded to all geometries of CT scanners. Compared to conventional image-domain methods, our method reflects the impact of scan and reconstruction parameters on lesion appearance. Compared to prior projection-domain methods, our method has the potential to achieve higher anatomical complexity because it uses clinical patient projections and real patient lesions.

APPENDIX A: ADJUSTMENT OF LESION MODEL VOXEL INTENSITY

The CT number of the lesion model is HU_lesion. With the first adjustment, which aims to remove the tissue at the lesion-insertion location, the CT number of the lesion model becomes

$${\displaystyle {\text{HU}}_{\text{lesion}A1}={\text{HU}}_{\text{lesion}}-{\text{HU}}_{\text{newBG}},}$$

where HU_newBG is the mean CT number of the background tissue at the location of insertion. With the second adjustment, which aims to adjust for the intensity difference between the lesion’s original location and the lesion’s insertion location, the CT number of the lesion model becomes

$${\displaystyle {\text{HU}}_{\text{lesion}A2}={\text{HU}}_{\text{lesion}A1}-\left({\text{HU}}_{\text{oldBG}}-{\text{HU}}_{\text{newBG}}\right)={\text{HU}}_{\text{lesion}}-{\text{HU}}_{\text{oldBG}},}$$

where HU_oldBG is the mean CT number of the lesion’s original background (i.e., the background of the lesion before it is segmented). Assuming that the imaging/forward-projection process F{} and the reconstruction/filtered backprojection process B{} are inverse processes and both linear, the CT number of the inserted lesion can be calculated as

$${\displaystyle {\text{HU}}_{\text{lesion}}^{\prime }=B\{F\left\{{\text{HU}}_{\text{lesion}A2}\right\}+F\left\{{\text{HU}}_{\text{newBG}}\right\}\}=B\left\{F\left\{{\text{HU}}_{\text{lesion}A2}\right\}\right\}+B\left\{F\left\{{\text{HU}}_{\text{newBG}}\right\}\right\}={\text{HU}}_{\text{lesion}A2}+{\text{HU}}_{\text{newBG}}={\text{HU}}_{\text{lesion}}-{\text{HU}}_{\text{oldBG}}+{\text{HU}}_{\text{newBG}}\text{.}}$$

The contrast of the original lesion to the original background is

$${\displaystyle C_{\text{old}}={\text{HU}}_{\text{lesion}}-{\text{HU}}_{\text{oldBG}}.}$$

The contrast of the inserted lesion to the new background is

$${\displaystyle C_{\text{new}}={\text{HU}}_{\text{lesion}}^{\prime }-{\text{HU}}_{\text{newBG}}={\text{HU}}_{\text{lesion}}-{\text{HU}}_{\text{oldBG}}=C_{\text{old}}.}$$

Because C_new equals C_old, the lesion contrast is maintained the same after insertion.

APPENDIX B: ESTIMATION OF BEAM HARDENING CORRECTION ENERGY

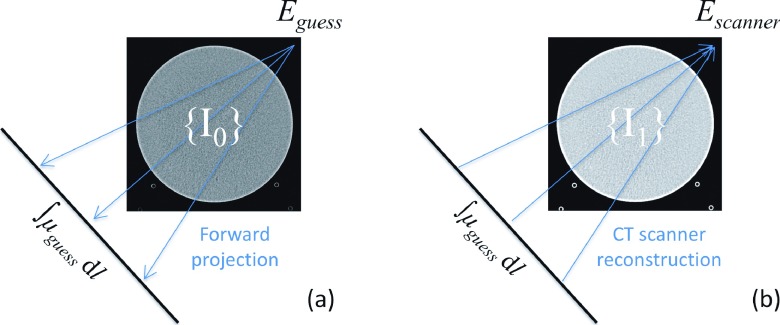
Figure 6 illustrates estimation of the beam hardening correction energy through a calibration process. Forward projections are first calculated for {I₀}, a set of phantom images acquired on a Siemens Definition Flash scanner. During the forward-projection process, the CT numbers of {I₀} (in the units of HU) are converted into attenuation coefficients under an initial guess of the beam hardening correction energy. According to the definition of HU, the relation between the attenuation coefficients and the CT numbers of {I₀} is

$${\displaystyle {\mu }_{\text{guess}}=\left(\frac{{\text{HU}}_{\left\{I_0\right\}}}{1000}+1\right)\cdot {\mu }_{\text{water}}\left(E_{\text{guess}}\right),}$$

where μ_guess is the attenuation coefficient in the forward projections and E_guess is the initial guess of the beam hardening correction energy. The forward projections, formatted to match those of commercial CT raw data, and then reconstructed on a commercial CT scanner to get a new set of images named {I₁}. The CT numbers of {I₁} can be expressed as

$${\displaystyle {\text{HU}}_{\left\{I_1\right\}}=1000\times \left(\frac{{\mu }_{\text{guess}}}{{\mu }_{\text{water}}\left(E_{\text{scanner}}\right)}-1\right),}$$

where E_scanner is the commercial beam hardening correction energy. This equation can be rewritten as

$${\displaystyle {\mu }_{\text{water}}\left(E_{\text{scanner}}\right)=\frac{{\mu }_{\text{guess}}}{\frac{{\text{HU}}_{\left\{I_1\right\}}}{1000}+1}=\frac{\frac{{\text{HU}}_{\left\{I_0\right\}}}{1000}+1}{\frac{{\text{HU}}_{\left\{I_1\right\}}}{1000}+1}\cdot {\mu }_{\text{water}}\left(E_{\text{guess}}\right).}$$

FIG. 6.

(a) Forward projections are calculated for commercial CT images under an initial guess of the beam hardening correction energy. (b) The forward projections are reconstructed by a commercial scanner to yield a new set of CT images, based on which the beam hardening correction energy is derived.

Given the CT numbers of {I₀} and {I₁} (measured from the images) and the attenuation coefficient of water at various energy levels (provided by National Institute of Standards and Technology²⁶), the commercial beam hardening correction energy E_scanner can be numerically solved. Note that in order to accurately estimate E_scanner, the CT numbers in the equation above need to be minimally impacted by the image noise. Therefore, the CT number of a material (acrylic, polyethylene, or water) was averaged from multiple pixels (pixels within a circular region of interest with a diameter of 20 mm).