Abstract
During surgical reconstruction of the aortic valve in the child, the use of foreign graft material can limit durability of the repair due to inability of the graft to grow with the child and to accelerated structural degeneration. In this study we use computer simulation and ex vivo experiments to explore a surgical repair method that has the potential to treat a particular form of congenital aortic regurgitation without the introduction of graft material. Specifically, in an aortic valve that is regurgitant due to a congenitally undersized leaflet, we propose resecting a portion of the aortic root belonging to one of the normal leaflets in order to improve valve closure and eliminate regurgitation. We use a structural finite element model of the aortic valve to simulate the closed, pressurized valve following different strategies for surgical reduction of the aortic root (e.g., triangular versus rectangular resection). Results show that aortic root reduction can improve valve closure and eliminate regurgitation, but the effect is highly dependent on the shape and size of the resected region. Only resection strategies that reduce the size of the aortic root at the level of the annulus produce improved valve closure, and only the strategy of resecting a large rectangular portion-extending the full height of the root and reducing root diameter by approximately 12% – is able to eliminate regurgitation and produce an adequate repair. Ex vivo validation experiments in an isolated porcine aorta corroborate simulation results.
Keywords: Finite element, Aortic valve, Repair, Root, Resect, Congenital, Regurgitation
1. Introduction
The aortic valve is positioned between the left ventricle and the aorta and prevents backflow from the aorta into the heart during diastole – the phase of the cardiac cycle when the ventricles relax and fill. The valve is comprised of three flaps, or leaflets, and the aortic root, which is the vascular wall to which the leaflets attach (Fig. 1A). Three bulges in the aortic root, referred to as sinuses, protrude from the attachments of the leaflets. In the normal valve, the leaflets and sinuses are similar in size and, in diastole, the valve closes symmetrically (Fig. 1B). Aortic regurgitation (AR) is the retrograde flow of blood from the aorta into the left ventricle during diastole. In children, causes of AR include congenital valve abnormalities, endocarditis, and leaflet damage following balloon valvuloplasty for congenital aortic stenosis. Congenital AR is most commonly caused by a bicuspid aortic valve (i.e., a valve with only two leaflets). However, congenital AR has also been reported in three-leaflet valves where one leaflet is abnormally small (Cromme-Dijkhuis and Meuzelaar, 1991; Donofrio et al., 1992; Hashimoto et al., 1984; Hioki et al., 1994; Karimi et al., 2010; Line et al., 1979). Often in these cases, there is annular dilatation (Cromme-Dijkhuis and Meuzelaar, 1991; Donofrio et al., 1992; Hashimoto et al., 1984; Hioki et al., 1994).
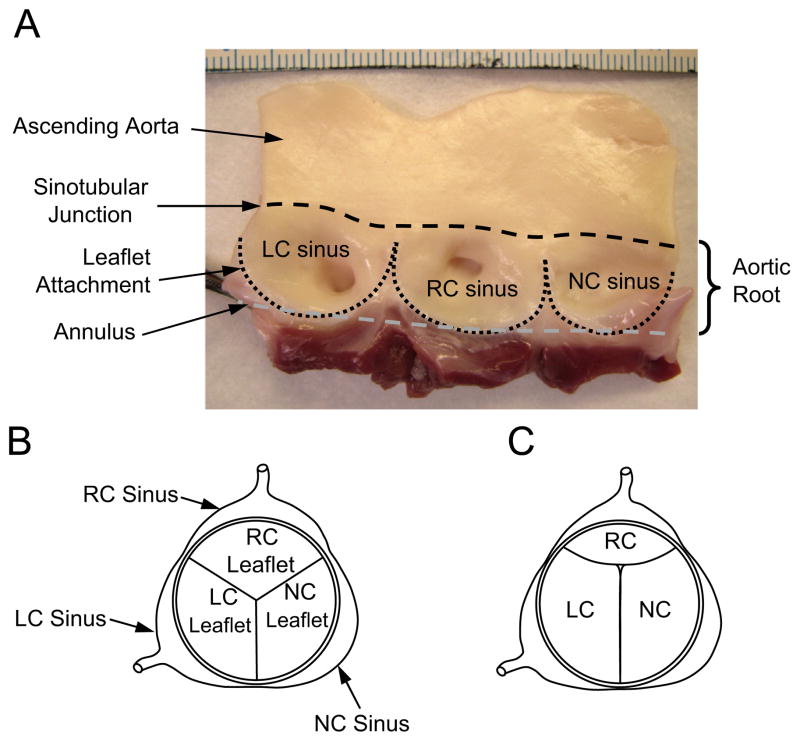
Fig. 1.
(A) Inside wall of the porcine aortic root with leaflets excised. The three sinuses, or bulges, in the aortic root are referred to as the left coronary (LC), right coronary (RC), and noncoronary (NC) sinuses, the former two serving as the origins of their respective coronary arteries. The juncture of the sinuses with the ascending aorta is referred to as the sinotubular junction (black dashed line). The leaflet attachment serves as the hemodynamic boundary between the left ventricle and the aorta (black dotted line). The aortic annulus is used here to describe the plane that passes through the nadirs of the leaflet attachments (gray dashed line). Scale (top of photo) is in millimeters. (B) Top view of aortic valve showing a closed valve in which the three leaflets and sinuses are approximately equal in size. (C) Aortic valve in which the right coronary (RC) leaflet and sinus are significantly smaller than the left coronary (LC) and noncoronary (NC) leaflets and sinuses.
At our center, this latter pathology is not an uncommon finding. These pediatric patients often exhibit moderate to severe AR and a rudimentary leaflet in the right coronary (RC) position (Fig. 1C), and surgery is usually indicated. Case reports describe treatment by replacing the valve with a mechanical valve (Donofrio et al., 1992; Hashimoto et al., 1984) or tissue valve (Cromme-Dijkhuis and Meuzelaar, 1991), however, in children, recent surgical practice favors valve repair (Baird and del Nido, 2009; Jonas, 2010) over replacement. One repair strategy has been to suture the rudimentary leaflet closed to create a bicuspid aortic valve (Hioki et al., 1994), but bicuspid aortic valves are known to have a high early failure rate (Robicsek et al., 2004). A more typical repair strategy would be to augment or replace the undersized RC leaflet with graft material to restore tri-leaflet symmetry and valve competence. A disadvantage of this approach is that currently used leaflet graft tissues (e.g., glutaraldehyde-treated pericardium) do not grow with the child. Furthermore, these grafts are known to degenerate and calcify, eventually requiring reoperation.
Given the limitations of current graft materials, a repair technique that eliminates AR without introducing graft material has appeal. Competent valve closure depends not only on the leaflet sizes but also on the dimensions and proportions of the aortic root. Our intuition based on surgical experience is that the leaflets of a regurgitant, asymmetrical valve can be brought into better approximation by resecting a portion of the aortic root to reduce its size while leaving the leaflets unaltered. Specifically, we hypothesize that it is possible to address AR due to an undersized RC leaflet by reducing the size of the aortic root through resection of tissue from the wall of the noncoronary (NC) sinus. Presumably, this will extend the mobility of the NC leaflet and bring the three leaflets into more complete closure, eliminating regurgitation.
To systematically explore this concept, we use a computational model of the aortic valve. Computational models have been used to study normal aortic valve function (De Hart et al., 2004; Grande et al., 1998; Labrosse et al., 2010; Nicosia et al., 2003) and surgical repair techniques (Grande-Allen et al., 2001; Labrosse et al., 2011; Hammer et al., 2012). For these studies, the primary utility of computational methods is the ability to isolate and quantify the effect of single variables – such as the size, shape, or mechanical properties of a given structure – on measurable outcomes.
We have developed and used a structural finite element model of the aortic valve to study valve function and surgical repair (Hammer et al., 2012, 2014). Our primary goal has been to analyze methods for surgical repair of AR, so our computational methods have focused on predicting valve competence during diastole – the phase of the cardiac cycle when the aortic valve is closed and pressurized. In this study, we apply this modeling method to study how a valve with AR due to one congenitally undersized leaflet can be repaired by resecting tissue from the wall of the aortic root adjacent to one of the other two (normal) leaflets. In this paper, we summarize our aortic valve finite element model and present our method for simulating diastolic function in a valve in which portions of the aortic root have been resected to reduce its overall size. We present simulation results, focusing on quantitative descriptions of the closed configuration of the loaded valve. An ex vivo experimental validation of the model is presented, and experimental and simulation results are compared. Finally we discuss the significance of the findings and study limitations.
2. Methods
2.1. Finite element model of congenital AR and surgical repair
To predict the effect that changing the aortic root geometry has on the competence of the closed valve in diastole, we use a structural finite element model of the aortic valve. The modeling process consists of defining the geometry and mechanical properties of the valve structures, discretizing the structures by meshing, modeling the forces in mesh elements due to deformation, and computing the final loaded state of the mesh resulting from all of the loads acting on mesh elements. These include forces due to transvalvular pressure, tissue deformation forces, inertial forces, damping forces due to leaflet movement through blood, and forces due to leaflet contact.
2.1.1. Model geometry
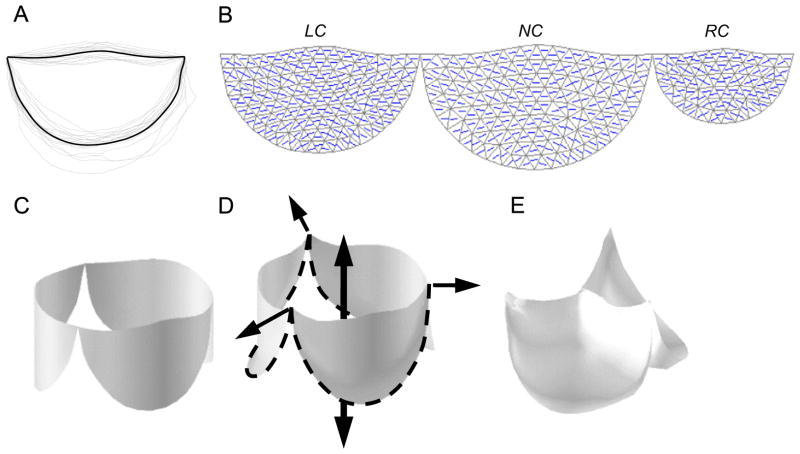
To create a model of a generalized human aortic valve, we scaled the average valve leaflet shape determined from studies of 18 porcine hearts (Fig. 2A) to appropriate relative leaflet sizes for a normal human aortic valve (Sim et al., 2003). Then, to model a valve with a congenitally undersized RC leaflet, we scaled the valve to achieve an aortic valve cross-section in which the portion of the aortic root bounded by the RC leaflet was reduced from approximately one-third to one-quarter of the total circumference, as we typically see on preoperative ultrasound in these patients. To achieve this, we scaled the RC portion of the aortic root and the overall shape of the RC leaflet to two-thirds of their normal size. The scaled leaflet outlines were meshed with triangles (Fig. 2B) and joined at their endpoints. This planar, 3-leaflet mesh was wrapped into a cylinder (Fig. 2C) based on anatomical studies showing that the points of attachment of the leaflets to the aortic root lie on a cylinder (Swanson and Clark, 1974). This cylindrical boundary is further supported by our experimental observations.
Fig. 2.
(A) Aortic valve leaflet shape is determined by averaging the leaflet outlines from 18 porcine hearts. (B) Left coronary (LC), noncoronary (NC), and right coronary (RC) leaflets are scaled to model a human valve with a congenitally undersized RC leaflet, and a mesh of unstructured triangles is generated within each of the three average leaflet outlines. The collagen fiber direction (principal material axis) is also shown. (C) The planar leaflet meshes are wrapped into a cylinder. Closure and loading of the valve is simulated in two steps. (D) First loads are applied to the mesh vertices that lie on the aortic root to simulate the radial and axial dilation of the aortic root in diastole. (E) Then surface normal forces are applied to all leaflet elements to simulate peak diastolic transleaflet pressure.
2.1.2. Finite element methodology
To estimate the forces at mesh vertices due to deformation of the mesh elements representing leaflet tissue, we used a finite element method described by Taylor et al. (2005) for large deformations and unstructured meshes.
For a triangular membrane element in 3D Cartesian space, global position within the triangle for the reference (undeformed) configuration can be expressed as X = ξαXα where Xα are 3D nodal coordinates, ξα are nodal weighting factors, and α is the nodal index. Similarly, for the current (deformed) configuration, x = ξαxα. Relative to the local coordinate system, position within the triangle for the reference configuration can be expressed as Y = ξαYα, where Yα are 2D nodal coordinates and ξα are their respective weighting factors. Similarly, for the current configuration, y = ξαyα.
For finite deformations, we use the Green strain tensor
| (1) |
where I is the 2 × 2 identity matrix, and C is the right Cauchy–Green deformation tensor, typically expressed as C=FTF. Defining J=δY/δξ and j=δy/δξ, the deformation gradient tensor can be written as F=δy/δY=(δy/δξ) (δξ/δY)=jJ−1. Expressing Y and y in terms of X (and x) and weighting factors, ξ, and taking derivatives produces
| (2) |
and
| (3) |
where ΔX21 is the vector from node 1 to 2 of the triangle in the reference configuration, and ΔX31 is the vector from node 1 to 3 (and similarly for Δx21 and Δx31 but in the current configuration).
Green strain from Eq. (1) is rotated to the principal material axes using the standard strain transformation matrix (Hammer et al., 2011), with the principal material direction, corresponding to the local collagen fiber direction, assigned to mesh elements to reflect published data from excised, collagen-stained porcine aortic valve leaflets (Hammer et al., 2014). The Green strain tensor is then used to compute the in-plane element stresses
| (4) |
where S is the second Piola–Kirchhoff stress tensor, E is the Green strain tensor, i and k are indices of the two principal directions, and W is strain energy density. We assume an exponential form
| (5) |
where c is a constant and
| (6) |
Constitutive equation parameters (c=9.7, A1 =49.5, A2 =5.3, A3 = −3.1, A4 =16.0, A5 =A6 =0) were taken from published biaxial test data (Hammer et al., 2011).
Components of the local stress tensor, S, are then transformed back to the local triangle coordinate system and used to compute element nodal forces
| (7) |
where A and H are the area and thickness of the triangle in the reference configuration, and B=Qb, where
| (8) |
and
| (9) |
The nine elements of f are the three components of the force on node 1, followed by those on nodes 2 and 3. The nodal force contributions from all triangles in the mesh are summed to get the net internal forces on nodes throughout the mesh.
2.1.3. Boundary conditions and loading
We simulate the state of diastolic loading in two steps. First, loads are applied to the boundary points where the leaflet mesh meets the aortic root. The edges between these boundary points are common to both the leaflets and the aortic root. The force in each boundary edge due to deformation of the aortic root is decomposed into circumferential and axial components and approximated as
| (10) |
and
| (11) |
where Ec and Ea are elasticities of the root in the circumferential and axial directions (334 and 350 kPa, respectively, Grande-Allen et al., 2001), t is root thickness, λc and λa are the circumferential and axial components of the edge stretch, h is the total height of the root, r is the radius of the root, and N is the number of boundary edges of all 3 leaflets. Diastolic positions of the leaflet attachment points are then determined by the force balance between transaortic pressure (80 mmHg), reaction forces in the aortic root ((10) and (11)), and any reaction forces due to tensile stress in the leaflets as the root distends (7). Then surface normal forces are applied to nodes of the leaflet elements to simulate peak diastolic transleaflet pressure.
2.1.4. Solution method
The equations of motion, discretized using a second-order backward difference method, are solved using semi-implicit numerical integration with adaptive step size control. External forces are included due to transleaflet (diastolic) pressure. Leaflet contact forces are computed using a piecewise function to approximate frictionless contact. As a node approaches the surface of an element, the contact force exponentially approaches a force that just balances the total force due to pressure acting at that node. If a node has passed through an element, a penalty force linearly proportional to interpenetration distance is applied. The stabilized biconjugate gradient method is used to solve the sparse linear system for updated nodal positions. Simulation and analysis software was written in the Matlab programming language (Mathworks, Natick, MA, USA). See our previous work for details (Hammer et al., 2012).
2.1.5. Simulating surgical repair
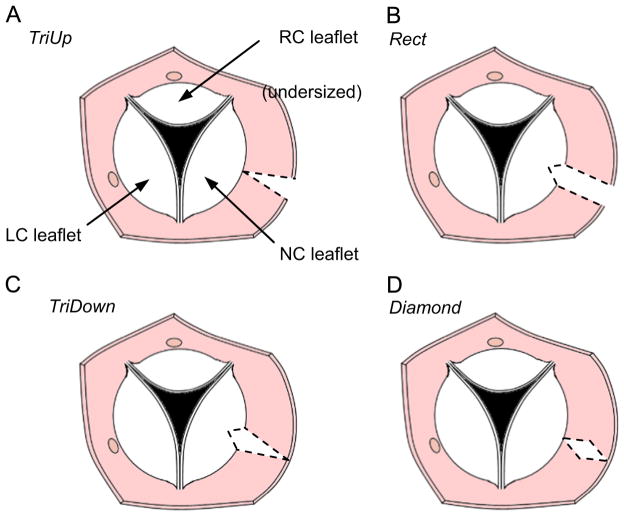
To simulate different surgical strategies for aortic root resection, we move the leaflet boundary points to achieve the modified aortic root shape prior to simulating valve closure. We are interested in the effect of resecting patches of various shapes from the aortic root adjacent to the NC leaflet in order to create the following reductions in aortic root dimensions: (1) a triangular patch oriented such that the aortic root circumference is reduced by 10 mm at the sinotubular junction but unchanged at the level of the annulus, (2) rectangular patches that uniformly reduce the aortic root from the sinotubular junction to the annulus by 5 mm and 10 mm, (3) a triangular patch oriented such that the aortic root circumference is reduced by 10 mm at the annulus but unchanged at the level of the sinotubular junction, and (4) a diamond-shaped patch where the aortic root circumference is reduced by 10 mm at the level halfway between the sinotubular junction and annulus but unchanged at the levels of the annulus and sinotubular junction (Fig. 3). We refer to these resection shapes as TriUp, Rect5, Rect10, TriDown, and Diamond, respectively. We simulate both 5 mm and 10 mm rectangular reductions in the root because the former represents a resected area equal to the other cases while the latter effectively looks at the combined effects of the two triangular resections. Note that for the simulations, resecting a given amount of the aortic root is equal to reducing the circumference of the aortic root by that same amount. In actual surgery, however, this is not the case. Suturing the aortic root back together typically involves a few additional millimeters of tissue, so the reduction in aortic root circumference will be greater than the width of the resection.
Fig. 3.
Drawing of transected aorta showing top view of the aortic valve. Four strategies are shown for resecting a portion (shown with dashed lines) of the NC aortic root to try to compensate for an undersized RC leaflet: (A) triangular resection with base at the level of the commissures, (B) rectangular resection, (C) triangular resection with base at the level of the annulus, and (D) diamond-shaped resection.
For the Rect5, Rect10, and TriDown shapes, the resected portion of the aortic root involves a length of the leaflet attachment, so the NC leaflet meshes are modified to remove a triangular-shaped portion of the mesh that shares the resected attachment. The mesh is stitched back together by applying spring forces to approximate the cut edges during simulated resection and closure.
2.1.6. Quantitative assessment of simulated repair
A normal aortic valve is characterized by several millimeters of overlap (coaptation) between adjacent leaflets when closed, and achieving this redundancy following valve repair is associated with good long-term outcomes (Augoustides et al., 2010). Accordingly, we determine the adequacy of simulated valve closure by computing the minimum extent of coaptation of adjacent leaflets in the closed state as well as the total area of coaptation for a given leaflet.
2.2. Experimental model of congenital AR and surgical repair
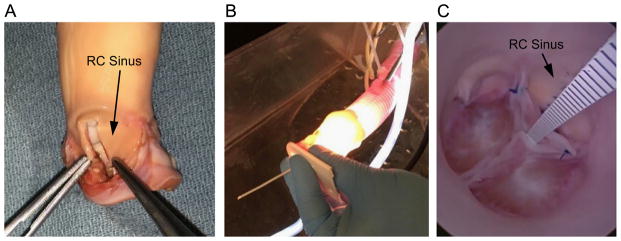
To test the validity of simulation results, we developed an experimental model, in an explanted porcine aorta, of congenital AR due to a deficient leaflet. To reproduce this defect using the porcine root, a 5 mm wide strip of the RC aortic root, extending from the annulus to the sinotubular junction, was resected (Fig. 4A). The excision was closed with a running suture that involved an additional 5 mm of tissue, bringing the total reduction in root circumference to approximately 10 mm. The RC leaflet was excised along its attachment, and approximately 2 mm of leaflet was trimmed from along the annular margin. The leaflet was reattached to the annulus of the diminished RC root with a running suture.
Fig. 4.
(A) Porcine model of congenital AR is created by resecting a 5 mm wide rectangular strip from the wall of the right coronary (RC) sinus, and approximating the cut edges with a running suture. The RC leaflet, which has been excised in the photo, is trimmed along its cut edge and reattached. (Note: aorta has been inverted to facilitate the procedure.) (B) The porcine aorta is attached to a Dacron tube through which the endoscope is inserted for visualizing the pressurized valve. (C) A plastic scale inserted through the closed valve is used to measure central coaptation height.
To assess valve competency, we sutured the distal end of the aorta to a 30 mm diameter Dacron tube connected to a column of water at 80 mmHg of pressure. To inspect the closed valve, an endoscopic camera (camera model 460 H and xenon light source model Dyonics 300XL, Smith and Nephew, London; endoscope model 26046 BA, Storz, Tuttlingen, Germany) was inserted through a purse string suture in the Dacron graft (Fig. 4B). Regurgitant flow at constant diastolic pressure was measured by collecting and measuring retrograde flow. The relative positions of the closed leaflets were measured by inserting a scale through the closed valve that could be read using the endoscope (Fig. 4C).
Repair was reproduced in the experimental porcine model by resecting portions of the aortic root. For the clinical repair, we propose reducing the NC root because (1) there is no coronary artery originating from that sinus so there is no risk of the repair disturbing coronary flow, and (2) it contains the largest of the three leaflets and therefore has the greatest potential to compensate for an undersized opposing leaflet. However, for the experimental model, we chose to reduce the LC root because, in the pig, the LC leaflet is the larger of the two remaining leaflets (Sim et al., 2003), so it better approximates the human repair.
3. Results
3.1. Finite element simulations
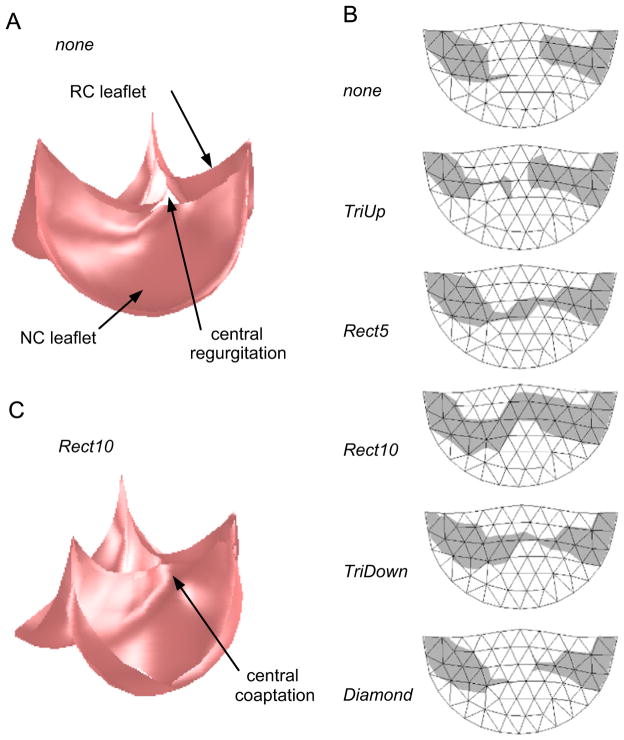
In simulation, a valve in which the RC leaflet has been undersized to mimic the congenital condition exhibited incomplete closure and AR under typical diastolic pressure (Fig. 5A). A map of the portion of the RC leaflet that coapts with the adjacent leaflets shows that a large central portion of the RC leaflet does not contact another leaflet (Fig. 5B). For the root resection strategies that we simulated, only Rect5, Rect10, and TriDown resulted in at least marginal central coaptation (Fig. 5B). Of these, only Rect10 resulted in a repair with acceptable central coaptation. This strategy also resulted in the repair with the largest total area of the RC leaflet involved in coaptation, and the results for total coaptation area generally followed those for central coaptation height (Table 1).
Fig. 5.
Simulation results showing (A) the closed, loaded state of the valve model representing the case of the pathological valve with no resection of the NC aortic root. Note the regurgitant orifice formed due to inability of the three leaflets to meet in the valve center. (B) The region of the RC leaflet that coapts with the other two leaflets (shaded gray) for various root resection shapes. Rect5 and Rect10 refer to the width of the resected rectangle in millimeters. The width of the triangle and diamond regions was approximately 10 mm. (C) The closed, loaded state of the valve model representing the Rect10 resection shape. Note the central coaptation where the three leaflets meet.
Table 1.
Simulation results.
| Resection strategy | Coaptation area (mm2) | Central coaptation height (mm) |
|---|---|---|
| No resection | 31 | 0 |
| TriUp | 31 | 0 |
| Rect5 | 59 | 0.8 |
| Rect10 | 63 | 2.2 |
| TriDown | 58 | 0.3 |
| Diamond | 31 | 0 |
3.2. Experimental validation
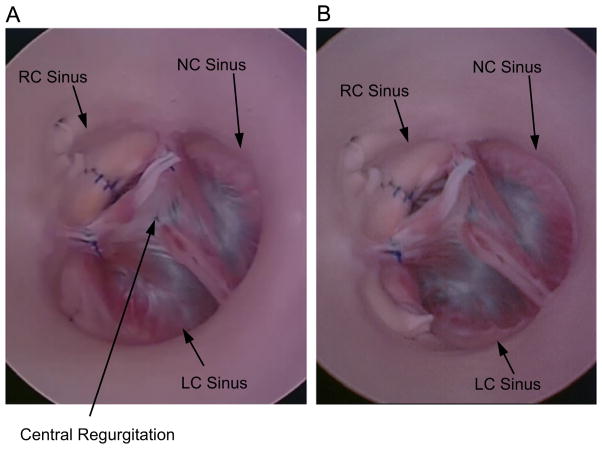
In our ex vivo porcine model of congenital AR, the leaflets exhibited a central gap (no coaptation) where the three leaflets meet under 80 mmHg of transvalvular pressure (Fig. 6A). Regurgitation through the closed valve was central, and a regurgitant flow of 270 ml/min was measured (Table 2). Following a rectangular resection of the LC root that resulted in a 5 mm reduction in root circumference, the valve appeared to close completely (Fig. 6B), with a central coaptation height of 1 mm. Regurgitant flow was reduced to 25 ml/min. Increasing the width of the resection to produce a 10 mm reduction in root circumference resulted in an increase in central coaptation height to 4 mm and a further reduction in regurgitation to 11 ml/min.
Fig. 6.
(A) Top view of experimental model of congenital AR, with valve loaded by a water column at 80 mmHg. Site of central regurgitation is indicated by arrow. (B) Experimental model following reduction of the LC root by approximately 10 mm.
Table 2.
Experimental validation
| Resection strategy | Central coaptation height (mm)
|
Regurgitant volume (ml/min) | |
|---|---|---|---|
| Simulation | Experiment | ||
| No resection | 0 | 0 | 270 |
| Rect5 | 0.8 | 1 | 25 |
| Rect10 | 2.2 | 4 | 11 |
4. Discussion
For this study, simulation serves two purposes. First, creating an ex vivo porcine model of congenital AR is technically difficult; simulation allows a wider range of surgical strategies to be explored than is feasible experimentally. Second, simulation allows the effect of a single variable to be isolated and quantified. This is not possible experimentally due to the variability in valve anatomy and mechanical properties and to the limits of surgical reproducibility. Our simulation results show that AR due to a single undersized leaflet can be eliminated by resecting tissue to reduce the aortic root, and experimental validation corroborates the simulation results. Together the simulation and experimental findings provide evidence that this technique might be effective and appropriate for pediatric patients, in whom introduction of inert graft materials is particularly problematic. A related finding from the simulations is that only the root resection strategies that include the valve annulus effectively eliminate regurgitation. Furthermore, only the case of a 10 mm wide rectangular reduction of the root (corresponding to a 12% reduction in aortic root circumference in our computational and experimental models) produces a repair with adequate central coaptation.
Simulation results help explain the effect of reducing the aortic root at different levels. When resection primarily reduces the diameter of the valve at the level of the commissures (e.g., TriUp), the commissures of the leaflets are moved radially inward causing the free edges of all three leaflets to drop farther under diastolic pressure. For the undersized RC leaflet, whose free edge is too high relative to the other two, this change is beneficial. However, when the free edges of the LC and NC leaflets drop, the leaflets begin to prolapse, or billow, toward the ventricle. This moves the resultant force on each leaflet due to transvalvular pressure so that it points less radially inward and more axially downward. In other words, pulling the commissures together does not result in the leaflets being pushed into tighter closure but rather in their being pushed more downward toward the ventricle. When resection primarily reduces the diameter of the valve at the level of the annulus (e.g., TriDown), the heights of the leaflets along their midlines become more in proportion to the smaller annulus. By resecting or folding the portion of the NC leaflet that had been attached to the now resected section of annulus, billowing is avoided, and the direction of the resultant force vector on that leaflet due to pressure does not shift downward. However, without the reduction of the root at the level of the commissures, the dropping of the undersized RC leaflet is not present, and the valve still does not close with significant coaptation in the center. Rectangular resection reduces the root diameter at both the commissural and annular levels, and both effects described above combine to achieve substantial central coaptation. The efficacy of this strategy depends on the amount of root wall that is resected. Our simulations showed that resecting the aortic root to produce a 5 mm wide reduction does result in full valve closure, but the central coaptation height is marginal. Increasing the width of the rectangular resection to produce a 10 mm root reduction produces acceptable leaflet coaptation.
Although results of our study demonstrate proof-of-concept, further work is necessary to establish robust clinical guidelines. For example it is not clear if a 12% reduction in root circumference is optimal. Furthermore, our simulation and experimental results were based on a valve in which a single leaflet is diminished to two-thirds it normal size; it is not known if this technique can compensate for cases where the diminished leaflet is less than two-thirds its normal size. Another important issue is the impact of aortic root reduction on outflow resistance during systole. Many patients with the type of congenital AR considered here have enlarged aortic roots, so resecting part of the root is, in fact, desirable and unlikely to limit cardiac output. This technique is probably not appropriate for patients whose aortic root is small preoperatively. Further modeling and experimental studies will be necessary to quantify post-repair pressure gradients across the valve in systole. Finally, the simulations are based on a number of simplifying assumptions, including implicit modeling of the aortic root and assignment of normal mechanical properties to a morphologically abnormal leaflet and root. However, the close agreement between simulation and experiment supports the validity our findings. In conclusion, reduction of the aortic root holds promise as a technique for surgical repair of congenital AR that produces a valve with the possibility to grow with the child.
Acknowledgments
This work was supported by NIH grant R01 HL110997.
Footnotes
Conflict of interest statement
None.
References
- Augoustides JG, Szeto WY, Bavaria JE. Advances in aortic valve repair. J Cardiothorac Vasc Anesth. 2010;24:1016–1020. doi: 10.1053/j.jvca.2010.08.007. [DOI] [PubMed] [Google Scholar]
- Baird CW, del Nido PJ. Complex aortic valve disease in children. Oper Tech Thorac Cardiovasc Surg. 2009;14(3):253–263. [Google Scholar]
- Cromme-Dijkhuis AH, Meuzelaar JJ. Congenital aortic regurgitation caused by absence of the right coronary cusp. Eur J Cardiothorac Surg. 1991;5(11):608–609. doi: 10.1016/1010-7940(91)90229-d. [DOI] [PubMed] [Google Scholar]
- De Hart J, Peters GWM, Schreurs PJG, Baaijens FPT. Collagen fibers reduce stresses and stabilize motion of aortic valve leaflets during systole. J Biomech. 2004;37:303–30311. doi: 10.1016/s0021-9290(03)00293-8. [DOI] [PubMed] [Google Scholar]
- Donofrio MT, Engle MA, O’Loughlin JE, Snyder MS, Levin AR, Ehlers KH, Gold J. Congenital aortic Regurgitation: Natural history and management. J Am Coll Cardiol. 1992;20(2):366–372. doi: 10.1016/0735-1097(92)90104-u. [DOI] [PubMed] [Google Scholar]
- Grande KJ, Cochran RP, Reinhall PG, Kunzelman KS. Stress variations in the human aortic root and valve. Ann Biomed Eng. 1998;26(4):534–53545. doi: 10.1114/1.122. [DOI] [PubMed] [Google Scholar]
- Grande-Allen KJ, Cochran RP, Reinhall PG, Kunzelman KS. Finite element analysis of aortic valve-sparing. IEEE Trans Biomed Eng. 2001;48:647–659. doi: 10.1109/10.923783. [DOI] [PubMed] [Google Scholar]
- Hammer PE, Sacks MS, del Nido PJ, Howe RD. Mass–spring model for simulation of heart valve tissue mechanical response. Ann Biomed Eng. 2011;39(6):1668–1679. doi: 10.1007/s10439-011-0278-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammer PE, Chen PC, del Nido PJ, Howe RD. Computational model of aortic valve surgical repair using grafted pericardium. J Biomech. 2012;45(7):1199–1204. doi: 10.1016/j.jbiomech.2012.01.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammer PE, Pacak CA, Howe RD, del Nido PJ. Straightening of curved pattern of collagen fibers under load controls aortic valve shape. J Biomech. 2014;47(2):341–34346. doi: 10.1016/j.jbiomech.2013.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashimoto R, Miyamura H, Eguchi S. Congenital aortic regurgitation in a child with a tricuspid non-stenotic aortic valve. Br Heart J. 1984;51(3):358–360. doi: 10.1136/hrt.51.3.358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hioki M, Iedokoro Y, Matsushima S, Masuda S, Ikeshita M, Shibuya T, Tanaka S, Shoji T. Congenital aortic regurgitation caused by a rudimentary noncoronary cusp: report of a case. Surg Today. 1994;24(5):456–458. doi: 10.1007/BF01427040. [DOI] [PubMed] [Google Scholar]
- Jonas RA. Aortic valve repair for congenital and balloon-induced aortic regurgitation. Pediatr Card Surg Annu. 2010;13:60–65. doi: 10.1053/j.pcsu.2010.01.001. [DOI] [PubMed] [Google Scholar]
- Karimi A, Peiravian F, Amirghofran AA, Kariminejad A. Absent pulmonary valve, intact interventricular septum, rudimentary aortic non-coronary cusp and ascending aortic aneurysm in a single patient. Interact Cardiovasc Thorac Surg. 2010;10(4):636–63638. doi: 10.1510/icvts.2009.225508. [DOI] [PubMed] [Google Scholar]
- Labrosse MR, Lobo K, Beller CJ. Structural analysis of the natural aortic valve in dynamics. J Biomech. 2010;43:1916–191922. doi: 10.1016/j.jbiomech.2010.03.020. [DOI] [PubMed] [Google Scholar]
- Labrosse MR, Boodhwani M, Sohmer B, Beller CJ. Modeling leaflet correction techniques in aortic valve repair: a finite element study. J Biomech. 2011;44:2292–2298. doi: 10.1016/j.jbiomech.2011.05.032. [DOI] [PubMed] [Google Scholar]
- Line DE, Babb JD, Pierce WS. Congenital aortic valve anomaly. Aortic regurgitation with left coronary artery isolation. J Thorac Cardiovasc Surg. 1979;77(4):533–53535. [PubMed] [Google Scholar]
- Nicosia MA, Cochran RP, Einstein DR, Rutland CJ, Kunzelman KS. A coupled fluid-structure finite element model of the aortic valve and root. J Heart Valve Dis. 2003;12(6):781–78789. [PubMed] [Google Scholar]
- Robicsek F, Thubrikar MJ, Cook JW, Fowler B. The congenitally bicuspid aortic valve: how does it function: why does it fail? Ann Thorac Surg. 2004;77:177–185. doi: 10.1016/s0003-4975(03)01249-9. [DOI] [PubMed] [Google Scholar]
- Sim EKW, Muskawad S, Lim CS, Yeo JH, Lim KH, Grignani RT, Durrani A, Lau G, Duran C. Comparison of human and porcine aortic valves. Clin Anat. 2003;16:193–196. doi: 10.1002/ca.10149. [DOI] [PubMed] [Google Scholar]
- Swanson WM, Clark RE. Dimensions and geometric relationships of the human aortic valve as a function of pressure. Circ Res. 1974;35:871–87882. doi: 10.1161/01.res.35.6.871. [DOI] [PubMed] [Google Scholar]
- Taylor RL, Oñate E, Ubach P. Finite element analysis of membrane structures. In: Oñate E, Kröplin G, editors. Textile Composites and Inflatable Structures. Springer; The Netherlands: 2005. [Google Scholar]