Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Nov 5.
Published in final edited form as: J Biomech. 2015 Oct 9;48(14):3937–3944. doi: 10.1016/j.jbiomech.2015.09.018

Shoulder pain and jerk during recovery phase of manual wheelchair propulsion

Chandrasekaran Jayaraman a, Carolyn L Beck a, Jacob J Sosnoff b,*
PMCID: PMC4655152  NIHMSID: NIHMS729047  PMID: 26472307

Abstract

Repetitive loading of the upper limb due to wheelchair propulsion plays a leading role in the development of shoulder pain in manual wheelchair users (mWCUs). There has been minimal inquiry on understanding wheelchair propulsion kinematics from a human movement ergonomics perspective. This investigation employs an ergonomic metric, jerk, to characterize the recovery phase kinematics of two recommended manual wheelchair propulsion patterns: semi-circular and the double loop. Further it examines if jerk is related to shoulder pain in mWCUs. Data from 22 experienced adult mWCUs was analyzed for this study (semi-circular: n=12 (pain/without-pain:6/6); double-loop: n=10 (pain/without-pain:4/6)). Participants propelled their own wheelchair fitted with SMARTWheels on a roller dynamometer at 1.1 m/s for 3 minutes. Kinematic and kinetic data of the upper limbs were recorded. Three dimensional absolute jerk experienced at the shoulder, elbow and wrist joint during the recovery phase of wheelchair propulsion were computed. Two-way ANOVAs were conducted with the recovery pattern type and shoulder pain as between group factors.

Findings

(1) Individuals using a semi-circular pattern experienced lower jerk at their arm joints than those using a double loop pattern (P<0.05, η2=0.32)wrist; (P=0.05, η2=0.19)elbow; (P<0.05, η2=0.34)shoulder and (2) individuals with shoulder pain had lower peak jerk magnitude during the recovery phase (P≤0.05, η2=0.36)wrist; (P≤0.05, η2=0.30)elbow; (P≤0.05, η2=0.31)shoulder.

Conclusions

Jerk during wheelchair propulsion was able to distinguish between pattern types (semi-circular and double loop) and the presence of shoulder pain. Jerk provides novel insights into wheelchair propulsion kinematics and in the future it may be beneficial to incorporate jerk based metric into rehabilitation practice.

Keywords: Repetitive strain injury, shoulder rehabilitation, jerk cost, ergonomics of movement, wheelchair propulsion, motor control

1. Introduction

Approximately 2 million Americans use a manual wheelchair for mobility (LaPlante et al., 2010). Although the use of a manual wheelchair provides numerous benefits (Hosseini et al., 2012), the repetitive strain encountered by the upper limb during propulsion places significant demand on the tissues (Nichols et al., 1979, Gellman et al., 1988, Curtiset al., 1999, Finley et al., 2004) and has been implicated in upper limb injury (Cooper et al., 1998). Indeed up to 70% of manual wheelchair users (mWCUs) report upper extremity pain (Finley et al., 2004). Upper extremity injury in mWCUs has been linked to difficulty performing activities of daily living, decreased physical activity and decreased quality of life (Chow et al., 2011).

Consequently, wheelchair propulsion research has led to guidelines to minimize over-use injuries (Boninger et al., 2002, Koontz et al., 2002, Richter et al., 2007). In general the guidelines suggests that individuals use propulsion patterns such as semi-circular and double loop that maximizes the contact angle. However these guidelines do not discuss other kinematic markers of movement such as jerk, that has been implicated in overuse injuries (Cote JN et al., 2005, Berret et al., 2008, Srinivasan et al., 2012, William et al., 2008, Mark (2012)).

Jerk, the third derivative of position has been widely employed in clinical rehabilitation and human motor control research to quantify movement smoothness and evaluate the performance of upper limb tasks (Hogan et al., 1987, Flash., 1990, Chang et al., 2005, Caimmi et al., 2008). Occupational ergonomics research has revealed distinct differences in arm jerk between movements in individuals with and without shoulder pain (Cote JN et al., 2005). Consequently, the purpose of this investigation is to examine jerk in wheelchair propulsion as a function of recovery pattern and shoulder pain.

To appreciate this research it is important that the reader understands that a typical push-rim wheelchair propulsion has two phases, a push phase (hands in contact with push-rim) and a recovery phase (hands move freely to initiate next push). Four general categories of recovery patterns widely reported in the literature are, semi-circular (SC), single loop (SLOP), double loop (DLOP) and ARC (Shimada et al. 1998, Boninger et al., 2002, Richter et al., 2007). The magnitude of forces and moments experienced by the shoulder joint during recovery phase of wheelchair propulsion can be high as that during the push phase (Mercer JL et al., 2006, Sosnoff et al., 2015). Given this association, it is logical to expect that shoulder pain will influence arm kinematics during the recovery phase of wheelchair propulsion. Indeed recent research shows that mWCUs with shoulder pain employed spatial adaptive strategies to wrist kinematics during the recovery phase of wheelchair propulsion (Jayaraman C et al., 2014).

This analysis examines jerk-based metrics extracted from the three dimensional kinematics of the upper arm joints during wheelchair propulsion. The main goals are (1) to introduce and benchmark a jerk-based framework for wheelchair propulsion and (2) to examine jerk in wheelchair propulsion as a function of recovery pattern and shoulder pain. To accomplish these goals, two recovery pattern types, SC and DLOP patterns were analyzed. A DLOP pattern is characterized by the hands lifting over the propulsion path and crossing the propulsion path to drop below the hand-rim forming a double loop, while a SC pattern is characterized by the hands dropping below the hand-rim during the recovery phase (Sanderson et al., 1985, Shimada et al., 1988, Boninger et al., 2002, Richter et al., 2007).

We postulate two hypotheses; (H1) that individuals using a SC recovery pattern will experience lower jerk magnitudes at their joints than individuals using a DLOP recovery pattern. (H2) that individuals with shoulder pain will minimize peak jerk magnitude at their upper arm joints during the recovery phase kinematics in an effort to avoid pain. H1 rests on the logical rationale that the arm’s movement trajectory during a SC pattern is simpler than a DLOP pattern. H2 is based on the observation that the neuromuscular system avoids large acceleration changes to avoid pain (Berret et al., 2008).

2. Methods

2.1 Participants demographics

Wheelchair propulsion data from 22 experienced adult mWCUs were analyzed. This data constitutes a subset of data from a larger study (n=27) examining wheelchair propulsion and shoulder pain (Sosnoff et al 2015). The total number of participants that employed a SLOP (n=4) or ARC (n=1) were few, hence only SC and DLOP patterns were analyzed. Inclusion criteria for the larger investigation were: (1) between 18–65 years old and (2) use of a manual wheelchair as their primary means of mobility for 1+ year. Table 1 lists the participant demographic information.

Table 1.

Demographic information

Characteristics Recovery pattern type Shoulder pain status
SC (n=12)
Mean(SD)		 DLOP (n=10)
Mean(SD)		 With pain (n=10)
Mean(SD)		 No pain(n=12)
Mean(SD)
Age(years) 25.5(10.68) 21.5(4.1) 25.8(11.11) 22.00(5.31)
Body weight (N) 608.73(235.22) 627.24(180.68) 677.68(216.58) 590.92(194.47)
Arm length (mm) 644.5 (54.51) 630.5 (33.76) 647(47.6) 630.9(45.8)
Current shoulder pain (VAS in cm) 2.11(3.22) 1.83(2.64) 4.16(3.00) * 0.02(0.09) *
WUSPI scores 14.58(22.77) 6.00(6.29) 20.70(22.28)* 2.33(3.75)*
Experience using manual wheelchair (Yrs) 16.83(5.72) 13.05(4.71) 16.45(6.18) 14.09(4.86)
Injury details T6 and below (n=7); Sacral agenesis(n=1), Spinal cyst T6(n=1), Spina bifidia(n=2), C7(n=1). T6 and below (n=5); Amputee(n=2), Spina bifidia (n=3). T6 and below (n=5); Sacral agenesis(n=1), Spinal cyst T6(n=1), Spina bifidia(n=2), Amputee (n=1). T6 and below (n=7); C7(n=1), Spina bifidia(n=3), Amputee (n=1).
Open in a new tab
*

P<0.05

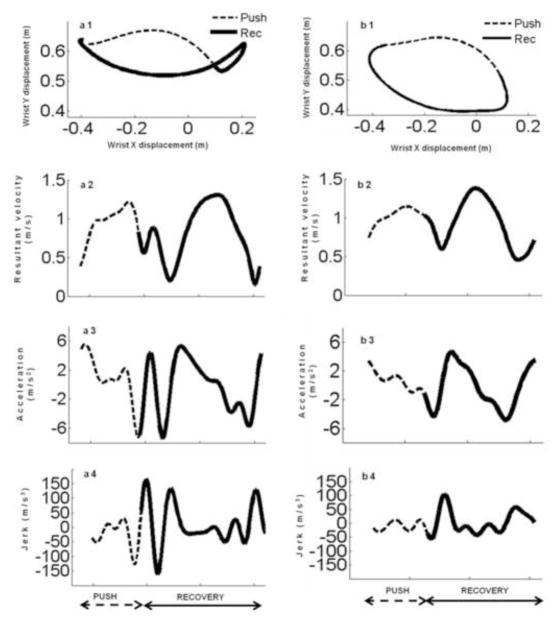
The recovery pattern types were classified using the third metacarpophalangeal joint’s sagittal plane motion (Shimada et al., 1988). A sample DLOP and SC pattern are shown in Fig. 1 (a1–b1) respectively. Twelve individuals used a SC pattern while ten participants used a DLOP pattern. These propulsion patterns were self-selected and no specific instructions regarding pattern were provided.

Figure 1.

Figure 1

Open in a new tab

The instantaneous resultant velocity, acceleration and jerk at wrist from a sample DLOP (a1–a4) and SC (b1–b4) recovery pattern type. The solid lines in all the plots belong to the recovery phase and the dotted line to the push phase. The resultant velocity plot for wrist during the recovery for a DLOP (solid lines - a2) has two asymmetric velocity profile one for each loop as opposed to a SC pattern (solid line - b2). The rate of change of acceleration and deceleration for a DLOP (solid line – a3) is greater than a SC (solid line – b3) pattern. The jerk magnitude for the DLOP (solid line – a4) is greater than a SC (solid line – b4) pattern.

2.2 Protocol

All experimental protocols in this study were approved by the local institutional review board. Upon arrival to the laboratory, the experimental procedures were described to the participants and any questions/concerns they had regarding the experimental protocol were addressed. Once participants became familiar with the procedures, they provide written consent. The participants also provided demographic information (age, height, weight, wheelchair experience, and injury) and self-reported current status of shoulder pain (“Yes”/”No”). Participants also rated their current level of shoulder pain for each shoulder on a 10 cm visual analog scale (VAS) (Campbell et al., 1990). A higher score indicates greater shoulder pain at the time of testing. Using a VAS scale for self reporting current level of pain is a common practice in wheelchair biomechanics literature (Boninger ML et al., 2003, Mulroy SJ et al., 2011). Participants also rated their shoulder pain using the wheelchair user’s shoulder pain index (WUSPI), a 15-item questionnaire (Curtis et al., 1995). Each item is rated between 0 to 10, with 0 representing no interference with functional activities and 10 representing complete interference during the past week due to shoulder pain. The total score is the sum of scores of each of the 15 items. Total score ranges from 0 (no pain)-150 (maximum limitations to daily activities due to pain) (Curtis et al., 1995).

Following the collection of demographic data, the participants’ personal wheelchair was fitted bilaterally with 25 inch diameter SMARTWheels (Three Rivers Holdings; USA). The participant’s wheelchair was then secured to a single roller dynamometer with a fly wheel and tie-down system (Moon et al., 2013).

2.3 Kinematic data collection

Based on the International Society of Biomechanics (ISB) recommendations (Wu et al., 2005), 18 reflective markers were attached at specific bony landmarks to define the trunk, upper arm, forearm, hand, sternum and the jaw (Moon et al., 2013). Reflective markers were also placed on the wheel center and spoke. Kinematic data were collected using a 10 camera system (Cortex 2.5, Motion Analysis Co.; USA) at a sampling rate of 100Hz.

Participants propelled their own wheelchair, fitted with SMARTWheels, at a steady state pace (1.1m/s) on a roller dynamometer for 3 minutes. A speedometer was used to provide real-time visual feedback to the subjects while kinetic data were collected bilaterally at 100Hz. Subjects were given time to acclimate to the dynamometer before the beginning of each trial.

2.4 Data post-processing

The motion data were post- processed and any missing intermediate marker data points were fit using a cubic interpolation. This post-processing was accomplished with Cortex 2.5 Motion Analysis software. The hand-rim kinetic data from the SMARTwheel was used to identify the push and recovery phases from each propulsion cycle. The push phase’s start and end points were located where the moment applied to the hand-rim (Mz) was greater and lower than 1 Nm, respectively, for at least 10 ms (Richter et al., 2011).

The post- processed motion data were filtered using a fourth-order low-pass Butterworth filter with 6 Hz cut-off frequency (Bednarczyk et al., 1994). The wrist motion data was approximated as the mid-point of the radial styloid and ulnar styloid hand segment marker coordinates. The elbow motion data was approximated as the mid-point of olecronon and lateral epicondyl, while the acromion process was used to represent the shoulder kinematics. To test our hypotheses (H1 & H2) we analyzed three dimensional motion data from wrist, elbow and shoulder joints.

Based on recommendation from previous literature, jerk metrics in this analysis were computed from the Cartesian coordinate motion data (Flash (1990), Hreljac (2000)). From the three dimensional motion data (i.e. X, Y and Z coordinate) of the joints, the instantaneous resultant velocity along the trajectory was approximated. To accomplish this, first the individual velocity components from X,Y and Z coordinate motion data were calculated. Then the resultant of these individual velocity components was computed to obtain the instantaneous resultant velocity (Winter (2009)). The acceleration and jerk were approximated by obtaining the successive first and second order time derivatives of the resultant velocity respectively (Winter 2009). The absolute magnitude of the jerk was computed and used for further analyses. For all time derivative approximations, a two point central difference scheme was used (Winter 2009). The data was filtered using a fourth-order low-pass Butterworth filter with 6 Hz cut-off frequency before approximating each time derivative (Cooper et al., 2002, Winter (2009)).

To be consistent across individuals, 50 consecutively occurring recovery phases were extracted from each participant’s data set. Each extracted absolute jerk curve was time normalized to 100 points using a shape preserving cubic spline. Two jerk measures were computed from these absolute jerk curves, namely a jerk cost criteria (Jc) and peak jerk criteria (PJc).

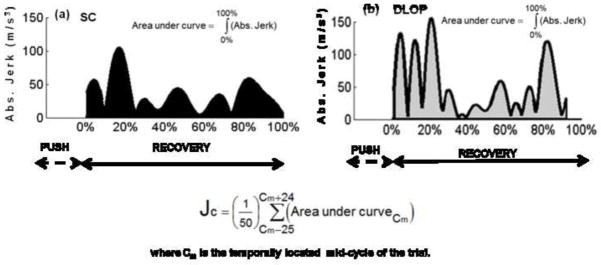
To compute Jc, first the area under the absolute jerk curve for each of the 50 extracted recovery cycles was computed. Jc was computed as the average value of the area under the absolute jerk curve. The scheme used for computing Jc is shown in Fig. 3. The group-wise averaged Jc between the SC and DLOP groups were statistically compared to validate the first hypothesis. For this comparison, data belonging to the dominant hand side was analyzed (right side: n=19(SC=10; DLOP=9); left side: n=3(SC =2, DLOP=1)).

Figure 3.

Figure 3

Open in a new tab

The jerk cost criteria (Jc). (a) & (b) a sample SC and DLOP pattern recovery phase absolute jerk curve depicting the area under curve as shaded regions respectively. The scheme used for computing Jc is shown below the figures. Cm : the propulsion cycle located closest to the mid of the trial (i.e. 90 seconds from the start of trial).

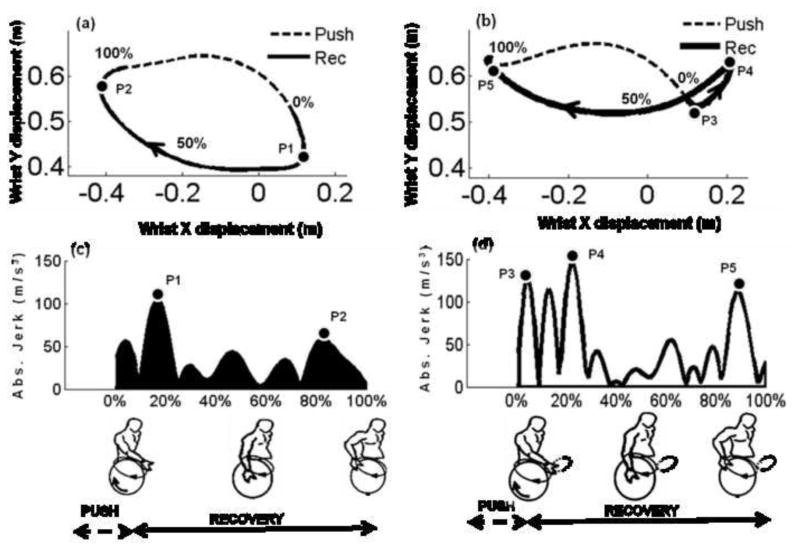
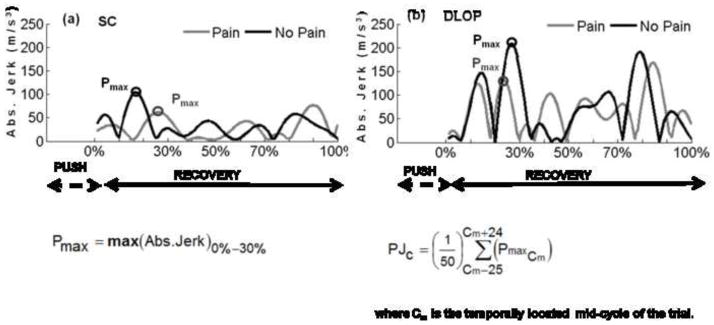
To compute PJc, first the Pmax from each of cycle was extracted. Pmax was defined to be the peak magnitude of absolute jerk that occurred during the recovery trajectory. Two distinct peak jerk magnitude locations were observed, the first between the 0% to 30% (see peak points P1 Fig. 2(c) & P4 Fig. 2(d)) and the other between the 70% to 100% (see peak points P2 Fig. 2(c) & P5 Fig. 2(d)) intervals. PJc (0% to 30%) and PJc (70% to 100%) were computed as the average of the peak magnitude of the absolute jerk (Pmax) (averaged over the 50 consecutive cycles). The scheme used for computing PJc is shown in Fig. 4. The group mean PJc’s from the two intervals were statistically compared between the groups with and without shoulder pain to validate the second hypothesis. The PJc belonging to the side of the hand with the greatest shoulder pain was analyzed for the pain group (right side: n=9 (SC=5; DLOP=4); left side: n=1(SC =1)). The PJc from the dominant hand side was used for the group without shoulder pain, (right side: n=10 (SC=5; DLOP=5); left side: n=2 (SC=1; DLOP=1)).

Figure 2.

Figure 2

Open in a new tab

A sample time normalized (0% – 100% points) recovery trajectory absolute jerk curve at wrist for SC and DLOP patterns. (a) & (b) Push (dotted lines) and recovery (solid lines) phases for a SC and DLOP pattern respectively. The 0% and 100% points represent the start and end of the recovery phase. There are 100 data points between the 0% to 100% points; (c) & (d): Peak jerk magnitudes at wrist during a SC and the DLOP recovery pattern respectively. Peak jerk magnitude at wrist occurred between 0% to 30% (P1,P3,P4) and 70% to 100% (P2,P5) intervals along the recovery trajectory. These peak jerk points typically were seen to occur at those intervals along the recovery phase that required steep acceleration and deceleration rate of change.

Figure 4.

Figure 4

Open in a new tab

The peak jerk criteria (PJc). (a) a sample plot from the SC group comparing Pmax(0%–30%) values between two individuals, with and without shoulder pain. (b) a sample plot from the DLOP group comparing Pmax(0%–30%) values between two individuals, with and without shoulder pain. The scheme used for computing Pmax and PJc is shown below the figures. Cm : the propulsion cycle located closest to the mid of the trial (i.e. 90 seconds from the start of trial).

2.4.1 Kinetic data processing

In addition to the kinematic data, the within individual cycle-wise spatial-temporal propulsion variables were extracted. These included, the mean contact angle, mean push time, mean push speed and mean peak resultant force at hand-rim, each averaged over the 50 cycles considered. A custom developed MATLAB program was used for all computations.

2.5 Statistical analysis

All statistical data analyses were conducted using SPSS (version 21, IBM, Inc.). All values are reported as Mean (SD) unless otherwise noted. The significance level was set to P≤0.05.

2.5.1 Independent variables

Participant demographics information (age, body weight, arm length and manual wheelchair propulsion experience) self reported current level of shoulder pain (VAS scores) and WUSPI scores were treated as independent variables. A series of two tailed independent t-test with propulsion pattern (SC or DLOP) and the shoulder pain (pain vs. no pain) as the between subject factors were conducted to check if statistically significant group differences existed in demographic variables. Two-tailed Mann–Whitney U tests were used to identify if statistical significant difference in VAS and WUSPI scores existed between the pain groups.

2.5.2 Dependant variables

Mean contact angle, mean peak resultant force at hand-rim during push, mean push speed, Jc’s and PJc’s were treated as dependent variables. To test if statistically significant group differences existed in the dependent variables, a series of two-way analysis of variance with propulsion pattern (SC or DLOP) and the shoulder pain status (pain vs. no pain) as the between subject factors were conducted. Bonferroni corrections were applied to account for type I error.

3. Results

3.1 Demographics

No significant between group differences in demographics information as a function of recovery pattern type or shoulder pain status were observed, (P’s>0.05; Table 1). Per design, the group with shoulder pain reported higher pain than the no pain group (VAS: [U=11, P<0.05]; WUSPI. [U=11, P<0.05]). No significant difference in shoulder pain was observed as a function of recovery pattern (P>0.05).

3.2 Spatial-temporal propulsion variables at hand-rim

The group-wise mean (SD) of spatial-temporal propulsion variables are reported in Table 2. No significant between group differences in peak resultant force, push speed or contact angle were observed (P’s>0.05) as a function of pattern type. Push time was significantly different between the SC and DLOP groups [F (1,18)=4.63, P<0.05, η2=0.20] with the SC group having a greater push time. No significant differences were observed in mean spatial-temporal propulsion variables as a function of shoulder pain (P’s>0.05).

Table 2.

Mean (SD) of propulsion variables

Spatial-temporal propulsion variables Recovery pattern type Shoulder pain status
SC (n=12)
Mean(SD)		 DLOP (n=10)
Mean(SD)		 With pain (n=10)
Mean(SD)		 No pain(n=12)
Mean(SD)
Mean peak resultant force at hand-rim (N) 59.07 (18.38) 66.36 (20.81) 64.56(17.99) 60.57(21.11)
Mean push time (sec) 0.54 (0.06)* 0.47 (0.07)* 0.54(0.08) 0.48(0.06)
Mean contact angle (deg) 112.37 (12.21) 101.45 (13.30) 111.69(15.80) 103.84(11.26)
Mean push speed (m/sec) 1.12 (0.04) 1.17 (0.08) 1.12(0.05) 1.16(0.07)
Open in a new tab
*

P<0.05

3.3 Recovery kinematic and jerk metrics

A representative plot of the resultant velocity, acceleration and jerk at the wrist for a DLOP and SC pattern are shown in Fig. 1(a2–a4) and Fig. 1(b2–b4), respectively. A time normalized (0% to 100%) absolute jerk curve computed for the wrist for SC and DLOP pattern are show in Fig. 2(c–d), respectively. Fig. 3(a–b) shows a sample area under the curve for SC and DLOP pattern types. The number of peak jerk points for a DLOP pattern appears higher than that for a SC pattern. The area under the curve for a DLOP pattern is larger than that of a SC pattern.

A sample recovery trajectory comparing peak jerk magnitudes (Pmax) between the groups with and without shoulder pain for the SC and DLOP pattern types are shown in Fig. 4(a–b) respectively. It is clear from the sample data that irrespective of the pattern type, Pmax magnitude for the individual with shoulder pain is lower than that for the individual without shoulder pain.

3.3.1 Jerk criteria (Jc)

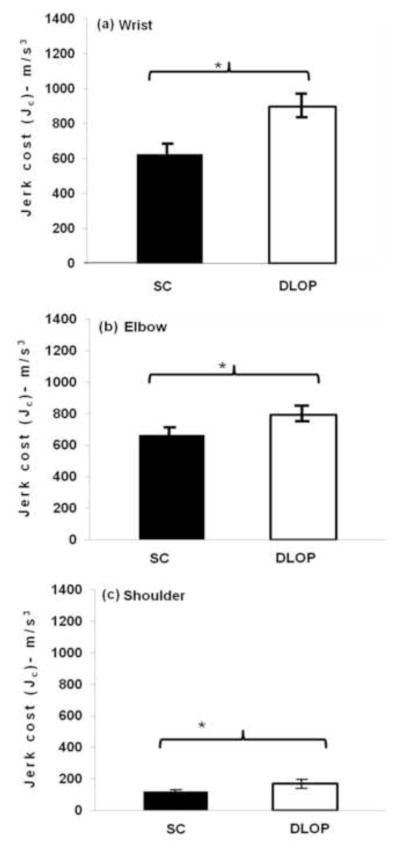
A significant main effect of recovery pattern (SC and DLOP) was observed for Jc at the wrist, elbow and shoulder joint; [F(1,18)=8.49, P<0.05, η2=0.32]wrist; [F(1,18)=4.3, P=0.05, η2=0.19]elbow; [F(1,18)=9.28, P<0.05, η2=0.34]shoulder. The SC group experienced lower mean Jc’s than the DLOP group during the recovery phase (See Fig. 5(a–c)). No significant between group differences in Jc was observed as a function of shoulder pain (P>0.05).

Figure 5.

Figure 5

Open in a new tab

Group mean comparison for Jc at the arm joints between SC and DLOP groups (a) group mean Jc at wrist joint for SC group is lower than that of the DLOP group; (b) group mean Jc at elbow joint for SC group is lower than that of the DLOP group; (c) group mean Jc at shoulder joint for SC group is lower than that of the DLOP group. (*P≤0.05).

3.3.2 Peak jerk criteria (PJc)

A significant main effect of shoulder pain was observed for PJc (0% to 30%); [F(1,18)=10.01, P<0.05, η2=0.36]wrist ; [F(1,18)=7.8, P<0.05, η2=0.30]elbow and [F(1,18)=8.16, P<0.05, η2=0.31]shoulder. The shoulder pain group had lower PJc (0% to 30%) magnitude at all the three joints than the no pain group (See Fig. 6(a–c)). No significant main effect of shoulder pain was observed for PJc(70% to 100%) (P>0.05).

Figure 6.

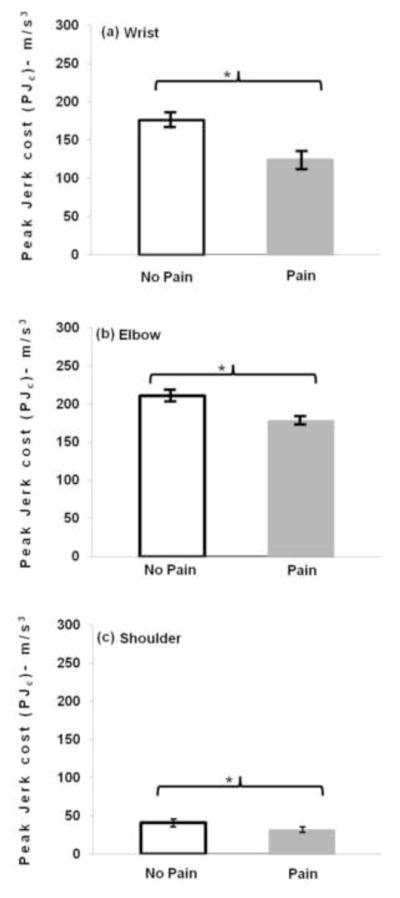
Figure 6

Open in a new tab

Group mean comparison for PJc at arm joints between groups with and without shoulder pain. (a) Group mean PJc at wrist joint for shoulder pain group is lower than that of the group without shoulder pain; (b) Group mean PJc at elbow joint for shoulder pain group is lower than that of the group without shoulder pain; (c) Group mean PJc at shoulder joint for shoulder pain group is lower than that of the group without shoulder pain. (*P≤0.05).

4 DISCUSSION

In this investigation, the jerk characteristics of the upper limb during the recovery phase of manual wheelchair propulsion as a function of propulsion pattern and shoulder pain were examined. In agreement with our postulated hypotheses the SC recovery pattern experienced lower Jc and individuals with shoulder pain had less PJc regardless of propulsion style. Overall, our results suggest that, utilizing a jerk metric while analyzing manual wheelchair propulsion provides novel insights.

The mean spatial-temporal wheelchair propulsion parameters observed in this investigation were consistent with previous literature (Boninger et al., 1997, Shimada et al., 1998, Boninger et al., 2002, Collinger et al., 2008, Richter et al., 2011, Raina, S et al., 2012, Slowik, J.S et al., 2015). This benchmarking was essential to suggest that the observations from our investigation are generalizable and qualitative comparison of our results with previous literature is acceptable.

The logical reason for the DLOP recovery pattern to incur greater Jc is a result of the joints undergoing sharp directional turns, leading to frequent switching between acceleration and deceleration during the recovery trajectory. In contrast, when executing a SC pattern the arm undergoes less directional change resulting in lower jerk. Additionally, the relatively complex DLOP kinematics requires the upper extremity musculature to do additional work to overcome the inertia and gravity. From a jerk minimization perspective, it appears that the SC pattern appears to be superior.

The second novel observation from this investigation is that, individuals with shoulder pain minimized PJc(0% to 30%) at all the three joints, namely, the wrist, elbow and shoulder compared to the group without shoulder pain. This observation is consistent with research observation reported in occupational biomechanics. For instance, individuals with back pain lift a box with less jerk than those without back pain (Slaboda et al., 2005) and it was suggested that those with pain adopt a pain minimizing strategy, characterized by lower jerk. Another investigation revealed that shoulder pain influenced the kinematics of arm joints (Cote JN et al., 2005) with those with shoulder pain having a kinematic movement pattern with lower acceleration magnitudes than those without pain. In the context of our analysis, it is maintained that individuals with shoulder pain adopt a smoother arm motion pattern to reduce momentary discomfort at the shoulder during wheelchair propulsion.

Although the examination of jerk is relatively novel within wheelchair biomechanics research, it is consistent with human motor control research that have implemented jerk based measures to evaluate upper limb movement. Evidence from motor control research suggests that kinematic analysis involving jerk is a viable approach to quantify movement coordination during rehabilitation (Ramos et al., 1997, Teulings et al., 1997, Cozens et al., 2003, Caimmi et al., 2008, Chang et al., 2005). Our results and suggest that integrating jerk metrics with existing analysis procedures can yield an enhanced understanding of wheelchair propulsion mechanics.

For instance, wheelchair propulsion analyses have focused on studying the effect of the different recovery patterns on overall mechanical efficiency (Boninger et al., 2002, de Groot et al., 2004). There are divergent suggestions regarding the overall mechanical efficiency of SC and DLOP patterns (Shimada et al., 1998, Boninger et al., 2002, de Groot et al., 2004, Richter et al., 2007), with both being suggested as the more efficient propulsion technique. However, these studies did not differentiate the influence of different kinematic effects of the recovery phase jerk cost to their overall mechanical efficiency estimates. Perhaps integrating metrics such as jerk with existing wheelchair analysis procedures will yield novel information concerning mechanical efficiency.

5. Limitations

Despite being novel there are limitations that need to be acknowledged. Our sample size was small to investigate the influence of specific injury demographics on the jerk characteristics. However, the diversity of injury could also be viewed as a strength of this study. The results were significant despite having a sample with diverse injury demographics. The sample demographics limited our analysis to SC and DLOP patterns. It is not clear if similar movement characteristics could be identified in other recovery pattern types (ARC and SLOP). However for completeness, the jerk characteristics for a sample SLOP and ARC patterns are provided in the supplementary section. Information on wrist pain was not collected. It is reasonable to expect that wrist pain is unlikely to influence kinematics during the recovery phase since the wrist experiences minimal forces/moments. A last limitation involves the laboratory based roller dynamometer setup utilized which provides a propulsion environment that does not exactly emulate real life propulsion.

6. Conclusions

This research implemented a novel approach integrating metrics and inferences from human movement ergonomics and motor control to understand kinematics of manual wheelchair users with shoulder pain. The analysis indicates that, adopting jerk based quantification of wheelchair propulsion kinematics is worthwhile and yields insightful inferences. Overall the recovery phase kinematics of individuals using a SC recovery pattern placed lower jerk magnitudes than those using a DLOP and (2) mWCUs with shoulder pain had lower peak jerk magnitude during the recovery phase of wheelchair propulsion. In the future it may be beneficial to incorporate jerk based metric into rehabilitation practice.

Supplementary Material

1. Figure S1.

Wrist kinematic characteristics of a sample SLOP pattern: c(1) the hands rise above the hand rim during the recovery phase for a SLOP pattern; the dotted line lines in all the plots belong to the push phase and the solid lines to the recovery phase. The instantaneous resultant velocity (c(2)), acceleration (c(3))and jerk (c(4) at wrist for a sample SLOP pattern.

2
3. Figure S2.

Wrist kinematic characteristics of a sample ARC pattern: c(1) the hands follows the hand rim closely during the recovery phase for a ARC pattern forming a pumping action; the dotted line lines in all the plots belong to the push phase and the solid lines to the recovery phase. The instantaneous resultant velocity (c(2)), acceleration (c(3))and jerk (c(4) at wrist for a sample ARC pattern.

4. Figure S3.

Group mean plots for Jc at the upper arm joints for SLOP and ARC patterns.

Acknowledgments

This project was funded in part by the National Institute of Health (#1R21HD066129-01A1). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. No additional external funding was received for this study. The authors thank Ms. Moon, Ms. Hsu and Dr. Wessels for their assistance. The authors extend their gratitude to the Beckman Institute Illinois Simulator Laboratory.

Footnotes

7. Conflict of interest disclosure

The authors have no conflict of interest to disclose.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Bednarczyk JH, Sanderson DJ. Kinematics of wheelchair propulsion in adults and children with spinal cord injury. Arch Phys Med Rehabil. 1994;75(12):1327–1334. [PubMed] [Google Scholar]
  2. Berret B, Darlot C, Jean F, Pozzo T, Papaxanthis C, Gauthier JP. The Inactivation Principle: Mathematical Solutions Minimizing the Absolute Work and Biological Implications for the Planning of Arm Movements. PLoS Comput Biol. 2008;4(10):e1000194. doi: 10.1371/journal.pcbi.1000194. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Boninger ML, Cooper RA, Robertson RN, Rudy TE. Wrist biomechanics during two speeds of wheelchair propulsion: An analysis using a local coordinate system. Archives of Physical Medicine and Rehabilitation. 1997;78(4):364–372. doi: 10.1016/s0003-9993(97)90227-6. [DOI] [PubMed] [Google Scholar]
  4. Boninger ML, Souza AL, Cooper RA, Fitzgerald SG, Koontz AM, Fay BT. Propulsion patterns and pushrim biomechanics in manual wheelchair propulsion. Archives of Physical Medicine and Rehabilitation. 2002;83(5):718–723. doi: 10.1053/apmr.2002.32455. [DOI] [PubMed] [Google Scholar]
  5. Boninger ML, Cooper RA, Fitzgerald SG, Lin J, Cooper R, Dicianno B, Liu B. Investigating neck pain in wheelchair users. Am J Phys Med Rehabil. 2003;82(3):197–202. doi: 10.1097/01.PHM.0000054217.17816.DD. [DOI] [PubMed] [Google Scholar]
  6. Caimmi M, Carda S, Giovanzana C, Maini ES, Sabatini AM, Smania N, Molteni F. Using Kinematic Analysis to Evaluate Constraint-Induced Movement Therapy in Chronic Stroke Patients. Neurorehabilitation and Neural Repair. 2008;22(1):31–39. doi: 10.1177/1545968307302923. [DOI] [PubMed] [Google Scholar]
  7. Campbell WI, Lewis S. Visual analogue measurement of pain. Ulster Med J. 1990;59(2):149–154. [PMC free article] [PubMed] [Google Scholar]
  8. Chang JJ, Wu TI, Wu WL, Su FC. Kinematical measure for spastic reaching in children with cerebral palsy. Clinical Biomechanics. 2005;20(4):381–388. doi: 10.1016/j.clinbiomech.2004.11.015. [DOI] [PubMed] [Google Scholar]
  9. Chow JW, Levy CE. Wheelchair propulsion biomechanics and wheelers’ quality of life: an exploratory review. Disabil Rehabil Assist Technol. 2011;6(5):365–377. doi: 10.3109/17483107.2010.525290. [DOI] [PubMed] [Google Scholar]
  10. Collinger JL, Boninger ML, Koontz AM, Price R, Sisto SA, Tolerico ML, Cooper RA. Shoulder biomechanics during the push phase of wheelchair propulsion: a multisite study of persons with paraplegia. Arch Phys Med Rehabil. 2008;89(4):667–676. doi: 10.1016/j.apmr.2007.09.052. [DOI] [PubMed] [Google Scholar]
  11. Cooper R, BMaRR Heavy Handed: Repetitive strain injury among manual wheelchair users. Team Rehab Report. 1998;9(2):35–38. [Google Scholar]
  12. Cooper RA, DiGiovine CP, Boninger ML, Shimada SD, Koontz AM, BMA Filter frequency selection for manual wheelchair biomechanics. J Rehabil Res Dev. 2002;39(3):323–336. [PubMed] [Google Scholar]
  13. Cote JN, Raymond D, Mathieu PA, Feldman AG, Levin MF. Differences in multi-joint kinematic patterns of repetitive hammering in healthy, fatigued and shoulder-injured individuals. Clin Biomech. 2005;20(6):581–590. doi: 10.1016/j.clinbiomech.2005.02.012. [DOI] [PubMed] [Google Scholar]
  14. Cozens JA, Bhakta BB. Measuring movement irregularity in the upper motor neurone syndrome using normalised average rectified jerk. Journal of Electromyography and Kinesiology. 2003;13(1):73–81. doi: 10.1016/s1050-6411(02)00070-6. [DOI] [PubMed] [Google Scholar]
  15. Curtis KA, Roach KE, Applegate EB, et al. Development of the Wheelchair User’s Shoulder Pain Index (WUSPI) Paraplegia. 1995;33:290–293. doi: 10.1038/sc.1995.65. [DOI] [PubMed] [Google Scholar]
  16. Curtis KA, Drysdale GA, Lanza RD, Kolber M, Vitolo RS, West R. Shoulder pain in wheelchair users with tetraplegia and paraplegia. Arch Phys Med Rehabil. 1999;80(4):453–457. doi: 10.1016/s0003-9993(99)90285-x. [DOI] [PubMed] [Google Scholar]
  17. de Groot S, Veeger HE, Hollander AP, van der Woude LH. Adaptations in physiology and propulsion techniques during the initial phase of learning manual wheelchair propulsion. Am J Phys Med Rehabil. 2003;82(7):504–510. doi: 10.1097/01.PHM.0000069941.77921.AA. [DOI] [PubMed] [Google Scholar]
  18. de Groot S, Veeger HE, Hollander AP, van der Woude LH. Effect of wheelchair stroke pattern on mechanical efficiency. Am J Phys Med Rehabil. 2004;83(8):640–649. doi: 10.1097/01.phm.0000133437.58810.c6. [DOI] [PubMed] [Google Scholar]
  19. de Groot S, Veeger HE, Hollander AP, van der Woude LH. Influence of task complexity on mechanical efficiency and propulsion technique during learning of hand rim wheelchair propulsion. Med Eng Phys. 2004;27:41–49. doi: 10.1016/j.medengphy.2004.08.007. [DOI] [PubMed] [Google Scholar]
  20. Finley MA, Rasch EK, Keyser RE, Rodgers MM. The biomechanics of wheelchair propulsion in individuals with and without upper-limb impairment. J Rehabil Res Dev. 2004;41(3b):385–395. doi: 10.1682/jrrd.2004.03.0385. [DOI] [PubMed] [Google Scholar]
  21. Flash T. The Organization of Human Arm Trajectory Control. In: Winters J, Woo S-Y, editors. Multiple Muscle Systems. Springer; New York: 1990. pp. 282–301. [Google Scholar]
  22. Gellman H, Sie I, Waters RL. Late complications of the weight-bearing upper extremity in the paraplegic patient. Clin Orthop Relat Res. 1988;(233):132–135. [PubMed] [Google Scholar]
  23. Hogan N, Bizzi E, Mussa-Ivaldi FA, Flash T. Controlling multijoint motor behavior. Exerc Sport Sci Rev. 1987;15:153–190. [PubMed] [Google Scholar]
  24. Hosseini SM, Oyster ML, Kirby RL, Harrington AL, Boninger ML. Manual wheelchair skills capacity predicts quality of life and community integration in persons with spinal cord injury. Arch Phys Med Rehabil. 2012;93(12):2237–2243. doi: 10.1016/j.apmr.2012.05.021. [DOI] [PubMed] [Google Scholar]
  25. Hreljac A. Stride smoothness evaluation of runners and other athletes. Gait & Posture. 2000;11(3):199–206. doi: 10.1016/s0966-6362(00)00045-x. [DOI] [PubMed] [Google Scholar]
  26. Jayaraman C, Moon Y, Rice IM, Hsiao Wecksler ET, Beck CL, et al. Shoulder Pain and Cycle to Cycle Kinematic Spatial Variability during Recovery Phase in Manual Wheelchair Users: A Pilot Investigation. PLoS ONE. 2014;9(3):e89794. doi: 10.1371/journal.pone.0089794. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Koontz AM, Cooper RA, Boninger ML, Souza AL, Fay BT. Shoulder kinematics and kinetics during two speeds of wheelchair propulsion. J Rehabil Res Dev. 2002;39(6):635–649. [PubMed] [Google Scholar]
  28. Koontz AM, Roche BM, Collinger JL, Cooper RA, Boninger ML. Manual Wheelchair Propulsion Patterns on Natural Surfaces During Start-Up Propulsion. Archives of Physical Medicine and Rehabilitation. 2009;90(11):1916–1923. doi: 10.1016/j.apmr.2009.05.022. [DOI] [PubMed] [Google Scholar]
  29. LaPlante MP, Kaye HS. Demographics and Trends in Wheeled Mobility Equipment Use and Accessibility in the Community. Assistive Technology. 2010;22(1):3–17. doi: 10.1080/10400430903501413. [DOI] [PubMed] [Google Scholar]
  30. Mark RLSJ. Introduction to human factors and ergonomics for engineers. CRC press; 2012. [Google Scholar]
  31. Mercer Jennifer L, et al. Shoulder joint kinetics and pathology in manual wheelchair users. Clinical Biomechanics. 2006;21(8):781–789. doi: 10.1016/j.clinbiomech.2006.04.010. [DOI] [PubMed] [Google Scholar]
  32. Moon Y, Jayaraman C, Hsu IM, Rice IM, Hsiao-Wecksler ET, Sosnoff JJ. Variability of peak shoulder force during wheelchair propulsion in manual wheelchair users with and without shoulder pain. Clin Biomech (Bristol, Avon) 2013;28(9–10):967–972. doi: 10.1016/j.clinbiomech.2013.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Mulroy SJ, et al. Strengthening and Optimal Movements for Painful Shoulders (STOMPS) in Chronic Spinal Cord Injury: A Randomized Controlled Trial. Phys Ther. 2011;91:305–324. doi: 10.2522/ptj.20100182. [DOI] [PubMed] [Google Scholar]
  34. Nichols PJ, Norman PA, Ennis JR. Wheelchair user’s shoulder? Shoulder pain in patients with spinal cord lesions. Scand J Rehabil Med. 1979;11(1):29–32. [PubMed] [Google Scholar]
  35. Ramos E, Latash MP, Hurvitz EA, BSH Quantification of upper extremity function using kinematic analysis. Arch Phys Med Rehabil. 1997;78(5):491–196. doi: 10.1016/s0003-9993(97)90162-3. [DOI] [PubMed] [Google Scholar]
  36. Raina S, McNitt-Gray J, Mulroy S, Requejo P. Effect of choice of recovery patterns on handrim kinetics in manual wheelchair users with paraplegia and tetraplegia. The Journal of Spinal Cord Medicine. 2012;35(3):148–155. doi: 10.1179/2045772312Y.0000000013. http://doi.org/10.1179/2045772312Y.0000000013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Rankin JW, Richter WM, Neptune RR. Individual Muscle Contributions to Push and Recovery Subtasks during Wheelchair Propulsion. Journal of biomechanics. 2011;44(7):1246–1252. doi: 10.1016/j.jbiomech.2011.02.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Rice IM, Jayaraman C, Hsiao-Wecksler ET, Sosnoff JJ. Relationship Between Shoulder Pain and Kinetic and Temporal-Spatial Variability in Wheelchair Users. Archives of physical medicine and rehabilitation. 2013 doi: 10.1016/j.apmr.2013.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Richter WM, Kwarciak AM, Guo L, Turner JT. Effects of single-variable biofeedback on wheelchair handrim biomechanics. Archives of Physical Medicine and Rehabilitation. 2011;92(4):572–577. doi: 10.1016/j.apmr.2010.11.001. [DOI] [PubMed] [Google Scholar]
  40. Richter WM, Rodriguez R, Woods KR, Axelson PW. Stroke Pattern and Handrim Biomechanics for Level and Uphill Wheelchair Propulsion at Self-Selected Speeds. Archives of Physical Medicine and Rehabilitation. 2007;88(1):81–87. doi: 10.1016/j.apmr.2006.09.017. [DOI] [PubMed] [Google Scholar]
  41. Sanderson DJ, Sommer HJ., 3rd Kinematic features of wheelchair propulsion. J Biomech. 1985;18(6):423–429. doi: 10.1016/0021-9290(85)90277-5. [DOI] [PubMed] [Google Scholar]
  42. Shimada SD, Robertson RN, Bonninger ML, Cooper RA. Kinematic characterization of wheelchair propulsion. J Rehabil Res Dev. 1998;35(2):210–218. [PubMed] [Google Scholar]
  43. Slaboda JC, Boston JR, Rudy TE, Lieber SJ, Rasetshwane DM. The use of splines to calculate jerk for a lifting task involving chronic lower back pain patients. Neural Systems and Rehabilitation Engineering, IEEE Transactions on. 2005;13(3):406–414. doi: 10.1109/TNSRE.2005.844252. [DOI] [PubMed] [Google Scholar]
  44. Slowik Jonathan S, et al. The influence of speed and grade on wheelchair propulsion hand pattern. Clin Biomech (Bristol, Avon) 2015 Jul 21; doi: 10.1016/j.clinbiomech.2015.07.007. 2015. pii: S0268-0033(15)00192-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Sosnoff JJ, Rice IM, Hsiao-Wecksler ET, Hsu IMK, Jayaraman C, Moon Y. Variability in wheelchair propulsion: a new window into an old problem. Front Bioeng Biotechnol. 2015;3:105. doi: 10.3389/fbioe.2015.00105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Srinivasan D, Mathiassen SE. Motor variability in occupational health and performance. Clin Biomech (Bristol, Avon) 2012;27:979–993. doi: 10.1016/j.clinbiomech.2012.08.007. [DOI] [PubMed] [Google Scholar]
  47. Teulings HL, Contreras-Vidal JL, Stelmach GE, Adler CH. Parkinsonism reduces coordination of fingers, wrist, and arm in fine motor control. Experimental Neurology. 1997;146(1):159–170. doi: 10.1006/exnr.1997.6507. [DOI] [PubMed] [Google Scholar]
  48. Veeger HEJ, van der Woude LHV, Rozendal RH. Load on the upper extremity in manual wheelchair propulsion. Journal of Electromyography and Kinesiology. 1991;1:270–280. doi: 10.1016/1050-6411(91)90014-v. [DOI] [PubMed] [Google Scholar]
  49. William CWRF. Biomechanics of Musculoskeletal Injury. Human Kinetics 2008 [Google Scholar]
  50. Winter DA. Biomechanics and Motor Control of Human Movement. Wiley; 2009. [Google Scholar]
  51. Wu G, van der Helm FC, Veeger HE, Makhsous M, Van Roy P, Anglin C, Nagels J, Karduna AR, McQuade K, Wang X, Werner FW, Buchholz B. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005;38(5):981–992. doi: 10.1016/j.jbiomech.2004.05.042. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1. Figure S1.

Wrist kinematic characteristics of a sample SLOP pattern: c(1) the hands rise above the hand rim during the recovery phase for a SLOP pattern; the dotted line lines in all the plots belong to the push phase and the solid lines to the recovery phase. The instantaneous resultant velocity (c(2)), acceleration (c(3))and jerk (c(4) at wrist for a sample SLOP pattern.

NIHMS729047-supplement-1.tif (83.1KB, tif)
2
NIHMS729047-supplement-2.docx (31.9KB, docx)
3. Figure S2.

Wrist kinematic characteristics of a sample ARC pattern: c(1) the hands follows the hand rim closely during the recovery phase for a ARC pattern forming a pumping action; the dotted line lines in all the plots belong to the push phase and the solid lines to the recovery phase. The instantaneous resultant velocity (c(2)), acceleration (c(3))and jerk (c(4) at wrist for a sample ARC pattern.

NIHMS729047-supplement-3.tif (328.8KB, tif)
4. Figure S3.

Group mean plots for Jc at the upper arm joints for SLOP and ARC patterns.

NIHMS729047-supplement-4.tif (351.7KB, tif)

RESOURCES