The Time Dependent Propensity Function for Acceleration of Spatial Stochastic Simulation of Reaction-Diffusion Systems

Abstract

The inhomogeneous stochastic simulation algorithm (ISSA) is a fundamental method for spatial stochastic simulation. However, when diffusion events occur more frequently than reaction events, simulating the diffusion events by ISSA is quite costly. To reduce this cost, we propose to use the time dependent propensity function in each step. In this way we can avoid simulating individual diffusion events, and use the time interval between two adjacent reaction events as the simulation stepsize. We demonstrate that the new algorithm can achieve orders of magnitude efficiency gains over widely-used exact algorithms, scales well with increasing grid resolution, and maintains a high level of accuracy.

1. Introduction

Stochastic models are widely used in the simulation of biochemical systems at a cellular level, because the populations of some chemical species may be so small that stochastic fluctuations become important [1, 2, 3]. For well-mixed systems, the stochastic simulation algorithm (SSA) [4, 5] is widely used.

The inhomogeneous SSA (ISSA) is a direct extension of the SSA for the simulation of the reaction diffusion master equation (RDME) [6], which governs the dynamics of spatially inhomogeneous stochastic systems. The ISSA discretises a system into subvolumes. In each subvolume, the well-mixed assumption is applied to reactions. Diffusive transfers between adjacent subvolumes are modeled as monomolecular reactions. The efficiency can be improved by the Next Subvolume Method [7], a reformulation of ISSA with lower computational complexity in each step. The NSM has been implemented in software packages such as MesoRD [8] and URDME [9].

Approximation-based methods have also been developed for further speeding up the simulation. The Multinomial Simulation Algorithm (MSA) [10] splits the reaction and diffusion processes. In each step it samples the next reaction time based on the current state, then it samples the position of every particle at the end time of the step using multinomial random variable sampling. Thus it avoids sampling individual diffusion events. After the diffusion process sampling, the MSA updates the system by firing a sampled reaction. The Diffusive Finite State Projection Algorithm (DFSP) [11] employs a similar idea but it allows multiple reaction events to fire in one step. It uses SSA to simulate the reaction process up to the end time of a step. The diffusion process is sampled by solving the diffusion master equation with truncated states. Hybrid methods are another approach for simplifying the simulation. URDME [9] is a software package that has implemented an adaptive hybrid method [12] along with NSM and DFSP, for stochastic reaction-diffusion processes.

In MSA, DFSP and the adaptive hybrid method, the reaction and diffusion processes are decoupled in every step. These methods sample the next reaction time based on the current state, i.e. by assuming that the system state does not change between adjacent chemical reaction events. However, this is an approximation because molecules will be diffusing during that time. In this paper we present a method that uses the time dependent propensity function to sample the reaction events. We will refer to our method as the time dependent propensity for diffusion method (TDPD).

The basic idea in the TDPD method is that it uses the time between adjacent reaction events as the simulation stepsize, which is the same as SSA. The time dependent propensity function takes into account the change of the propensity values during a stepsize due to the diffusion process. Thus the method yields a speedup by avoiding the effort of tracking individual diffusion events, while still enjoying excellent accuracy.

The idea of of using the time dependent propensity in a simulation has previously been introduced in [13], where the Next Reaction Method is extended for time varying Markov processes and some examples are provided. A non-Markov process example is discussed in that paper, where the time dependent propensity, which is a gamma distribution, yields an efficient algorithm for the simulation. In [14], the idea of using the time dependent propensity was incorporated into a hybrid method, where the time dependent propensity of discrete reactions is computed by the values generated from the continuous reactions. A similar idea has also been introduced in [15] for tau-leaping applied to well-mixed chemically reacting systems. It is most advantageous when the stepsize is restricted by a species that is undergoing a rapid relative population change. Making use of the time dependent population of such a species enables the use of larger stepsizes, while still maintaining a high level of accuracy.

The remainder of this paper is organized as follows. In Section 2 we provide a brief introduction to the SSA. In Section 3 we present the new algorithm using the time dependent propensity function. A simple example is used to illustrate the key ideas. Numerical experiments are given in Section 4, including application of the method to a realistic model of blood coagulation, and the algorithm is briefly summarized in Section 5. Detailed mathematical derivations are provided in the Appendix.

2. Stochastic simulation algorithm

Consider a homogeneous system of N species S₁, …, S_N and M reactions R₁, …, R_M. The state vector of the system is denoted by X = {x₁, …, x_N}, where x_i is the population of species i. The SSA is based on the well-mixed assumption. The probability that reaction R_i fires in an infinitesimal interval dt is given by a_i (X)dt, where a_i (X) is the propensity function of R_i. In every step, the algorithm advances the system by sampling the time to the next reaction and the reaction that will fire. Finally it updates the state of the system.

To sample the next reaction time, the SSA uses the total propensity $a_0(\mathit{X})={\sum }_{i=1}^M{a}_i(\mathit{X})$ of the system. As the probability that the system will fire a reaction in the next infinitesimal dt is a₀ (X) dt, the time to the next reaction follows an exponential distribution with parameter a₀ (X). This is the distribution that the SSA uses to sample the next reaction time.

To sample the reaction that the system should fire, the SSA selects the next reaction with probability proportional to its propensity. Thus the probability of choosing reaction i is a_i (X) /a₀ (X). Finally, the SSA updates the system state and repeats these steps until the simulation is completed.

3. Spatial stochastic simulation using the time dependent propensity function (TDPD)

The SSA performs two tasks in each step: select the time to the next reaction and select the reaction to be fired. Analogously, TDPD divides each step of the spatial stochastic simulation into the two tasks described above. In this section we illustrate how these two tasks are performed in TDPD, using the following simple example. In the spatial stochastic simulation, the state X is given by the number of molecules of each species in each voxel.

The example system is composed of two voxels and a reaction $A+B\stackrel{c}{\to }C$, where c is the rate constant of the reaction. An A molecule and a B molecule are able to react only when they are in the same voxel. Molecules A, B and C can jump between the two voxels with diffusion propensities κ^A, κ^B, κ^C respectively. Initially, there are $X_1^A$ A molecules in voxel 1 and $X_2^B$ B molecules in voxel 2.

The first step of our algorithm is to select the next reaction time.

3.1. Select the time to the next reaction using the time dependent propensity

In this section we show how to sample the next reaction time. To achieve this goal, we must find the distribution of next reaction times. This distribution depends on the propensity function, which is a function of time.

3.1.1. The distribution of next reaction times for TDPD

This section basically restates the procedure that SSA uses to obtain the distribution of the next reaction time, but in a spatial setting. The conclusion in this subsection also appeared in [13] and [14] (which can trace back to [16]), where the time dependent propensity is applied for simulation algorithms in different scenarios.

Let X₀ be the initial state of the system and a₀ (t, X₀) the total propensity of the system at time t under the condition that no reaction occurs before t. Then the probability Q (t, X₀) that no reaction occurs before t satisfies

$$Q(t+dt,{\mathbf{X}}_0)=Q(t,{\mathbf{X}}_0)(1-a_0(t,{\mathbf{X}}_0)dt),$$

which yields the ODE

$$\frac{dQ(t,{\mathbf{X}}_0)}{dt}=-Q(t,{\mathbf{X}}_0)a_0(t,{\mathbf{X}}_0),$$

whose solution is given by

$$Q(t,{\mathbf{X}}_0)=e^{-{\int }_0^t{a}_0(s,{\mathbf{X}}_0)ds},$$

$$P(t,{\mathbf{X}}_0)\triangleq 1-Q(t,{\mathbf{X}}_0)=1-e^{-{\int }_0^t{a}_0(s,{\mathbf{X}}_0)ds},$$ (1)

where P (t, X₀) is the probability that the next reaction occurs before time t.

In the SSA, a₀ (t, X₀) is a constant before the next reaction. However, in the spatial case it is a function of time t, because the diffusion process changes the system state over time. Similar to sampling the next reaction time in SSA, the time to the next reaction can be obtained by solving

$$\hat{r}=P(t,{\mathbf{X}}_0),$$ (2)

where r̂ is a uniformly distributed random number in (0, 1). Using (1) and (2) yields

$$-\text{ln}(1-\hat{r})={\int }_0^t{a}_0(s,{\mathbf{X}}_0)ds.$$

Since r ≜ 1 − r̂ is also a uniform random number in (0, 1), it is equivalent to restate the above as

$$-\text{ln}r={\int }_0^t{a}_0(s,{\mathbf{X}}_0)ds.$$ (3)

Next, we must find a₀ (t, X₀).

3.1.2. The time dependent propensity function

As stated above, a₀ (t, X₀) dt is the probability that a reaction will fire in the time interval [t, t + dt], given that no reaction fires before t. This probability is the sum of the probabilities of every possible reaction event during [t, t + dt]. Let us look at a particular A molecule in voxel 1 and a B molecule in voxel 2 in our example. Under the condition that no reaction fires before time t, the probability that they will react during [t, t + dt] is

$$P(\text{the two molecules react in}[t,t+dt])=P(\text{they are in voxel}1\text{at time}t\text{and then react in}[t,t+dt])+P(\text{they are in voxel}2\text{at time}t\text{and then react in}[t,t+dt])=P(\text{they are in voxel}1\text{at time}t)\times cdt+P(\text{they are in voxel}2\text{at time}t)\times cdt,$$ (4)

where c is the reaction rate.

The probability terms in (4) are not trivial. However if we take the assumption that the system is undergoing a pure diffusion process between the reaction events, it simplifies the problem. Under this assumption, molecules diffuse independently and their location distribution is the solution of the master equation of the diffusion process. Thus

$$P(\text{the two molecules are in voxel}1\text{at time}t)=P(\text{A remains in voxel}1\text{at time}t)\times P(\text{B diffuses from voxel}2\text{to voxel}1\text{by time}t)\triangleq p_{11}^A(t)p_{21}^B(t),$$

where $p_{ij}^k(t)$ (i, j = 1, 2; k = A, B) is the probability that the molecule of species k diffuses from voxel i to voxel j by time t.

Now, under the condition that no reaction occurs before t, (4) can be written as

$$P(\text{the two molecules react in}[t,t+dt])=p_{11}^A(t)p_{21}^B(t)cdt+p_{12}^A(t)p_{22}^B(t)cdt.$$ (5)

Another benefit of assuming that the system is governed by a diffusion process between the reaction events is that the master equation of the discrete one dimensional diffusion process with finite voxels and reflecting boundary conditions has a closed form solution (see Appendix A), which also serves as the foundation for constructing the solutions of higher dimensional diffusion processes. In the example case of two voxels, $p_{ij}^k(t)$ (k = A, B) is given by

$$\left(\begin{array}{cc}\hfill p_{11}^k\hfill & \hfill p_{12}^k\hfill \\ \hfill p_{21}^k\hfill & \hfill p_{22}^k\hfill \end{array}\right)=\frac{1}{2}\left(\begin{array}{cc}\hfill 1+e^{-2{\kappa }^{k}t}\hfill & \hfill 1-e^{-2{\kappa }^{k}t}\hfill \\ \hfill 1-e^{-2{\kappa }^{k}t}\hfill & \hfill 1+e^{-2{\kappa }^{k}t}\hfill \end{array}\right),(k=A,B),$$ (6)

where κ^k is the diffusion propensity for species k.

Inserting (6) into (5) yields the probability for a particular pair of molecules to react during [t, t + dt]. Since there are $X_1^A\times X_2^B$ such pairs, the total probability of such events is

$$P(\text{a reaction occurs in}[t,t+dt]\text{given that no reaction occurs before}t)=X_1^A{X}_2^B(p_{11}^A(t)p_{21}^B(t)cdt+p_{12}^A(t)p_{22}^B(t)cdt)=a_0(t,{\mathbf{X}}_0)dt.$$

Thus,

$$a_0(t,{\mathbf{X}}_0)=c{X}_1^A{X}_2^B(p_{11}^A(t)p_{21}^B(t)+p_{12}^A(t)p_{22}^B(t))=\frac{c}{2}{X}_1^A{X}_2^B(1-e^{-2({\kappa }^A+{\kappa }^B)t}).$$ (7)

Inserting (7) into (3) yields the formula for sampling the next reaction time,

$$-\text{ln}r={\int }_0^t{a}_0(s,{\mathbf{X}}_0)ds=\frac{c}{2}{X}_1^A{X}_2^B(t+\frac{e^{-2({\kappa }^A+{\kappa }^B)t}-1}{2({\kappa }^A+{\kappa }^B)}).$$ (8)

Here we note that (6), which results from the assumption that the system is undergoing a diffusion process with reflecting boundary conditions, is only an approximation to the true spatial distribution. To make this point clearer, we denote the true value of $p_{ij}^k$ by ${\tilde{p}}_{ij}^k$ (k = A, B) and take a look at what this value is supposed to be.

3.1.3. Error analysis of $p_{ij}^k$

Consider a particular A molecule that initially remains in voxel 1. Denote by ℛ the set of reaction events in which this molecule is involved as a reactant, and by ℛ̅ the set of all other reaction events. At any time t > 0, under the condition that no event in ℛ̅ occurs before t, there are only three possible states for the observed A molecule: it is in voxel 1, it is in voxel 2, or it is already consumed by a reaction event in ℛ. Denote the probabilities of these three states by p₁ (t), p₂ (t) and p_r (t) respectively. By definition, ${\tilde{p}}_{ij}^A(t)$ is the probability that an A molecule diffuses from voxel i to voxel j at time t, given that no reaction occurs before t. Thus its true value, for example ${\tilde{p}}_{1j}^A(t)$ (j = 1, 2), is given by

$${\tilde{p}}_{1j}^A(t)=\frac{p_j(t)}{p_1(t)+p_2(t)}=\frac{p_j(t)}{p_1(t)+p_2(t)}(p_1(t)+p_2(t)+p_r(t))=p_j(t)+\frac{p_j(t)}{p_1(t)+p_2(t)}{p}_r(t)\triangleq p_j(t)+{\tilde{r}}_j(t),(j=1,2).$$

Here r̃_j (t) is defined as p_r (t)p_j (t)/(p₁(t) + p₂(t)). It is clear that r̃_j (t) ≤ p_r (t), and

$${\tilde{r}}_1(t)+{\tilde{r}}_2(t)=p_r(t).$$ (9)

Since $p_{1j}^A(t)$ is greater than p_j (t) (see Appendix C for the proof), it can also be decomposed into p_j (t) plus some positive value, say r_j (t). Thus the difference between the true value ${\tilde{p}}_{1j}^A(t)$ and its approximation $p_{1j}^A(t)$ can be written as

$$|p_{1j}^A(t)-{\tilde{p}}_{1j}^A(t)|=|(p_j(t)+r_j(t))-(p_j(t)+{\tilde{r}}_j(t))|=|r_j(t)-{\tilde{r}}_j(t)|.$$

We can use this equation to bound the difference between ${\tilde{p}}_{1j}^A(t)$ and $p_{1j}^A(t)$.

A bound for r_j (t) can be obtained from

$$1=\sum _j{p}_{1j}^A(t)=\sum _j(p_j(t)+r_j(t)),$$

which implies

$$\sum _j{r}_j(t)=1-\sum _j{p}_j(t)=p_r(t).$$ (10)

Thus

$$r_j(t)\le p_r(t)(j=1,2),$$

and an upper bound for $|p_{1j}^A(t)-{\tilde{p}}_{1j}^A(t)|$ is given by

$$|p_{1j}^A(t)-{\tilde{p}}_{1j}^A(t)|=|r_j(t)-{\tilde{r}}_j(t)|\le \text{max}(r_j(t),{\tilde{r}}_j(t))\le p_r(t)(j=1,2).$$

The sum of these differences over all voxels is bounded by

$$\sum _j|p_{1j}^A(t)-{\tilde{p}}_{1j}^A(t)|=\sum _j|r_j(t)-{\tilde{r}}_j(t)|\le \sum _j(r_j(t)+{\tilde{r}}_j(t))=\sum _j{r}_j(t)+\sum _j{\tilde{r}}_j(t)=2p_r(t).$$

Here the last equality arises from equations (9) and (10). Thus the error in $p_{1j}^A(t)$ has an upper bound which is determined by p_r (t). But how large can p_r (t) be during a simulation step?

Since p_r (t) by definition is the probability of the observed A molecule being consumed by a reaction before t, given that no reaction events in ℛ̅ occur before t, the longer the time, the larger that probability will be. As our simulation step size τ is the time to the next reaction, p_r (t) in a simulation step will take its maximum value at t = τ. Since τ is a random variable, p_r (τ) itself is also a random variable. It can be shown that the expectation of p_r (τ) has an upper bound given by (see Appendix B)

$$\mathrm{E}(p_r(\tau ))\le \underset{t}{\text{max}}\frac{a(t)}{a_0(t)+a(t)},$$ (11)

where a (t) is the propensity contributed by the observed A molecule, which is defined as a (t) = a₀ (t) − a_ℛ̄ (t) where a₀ (t) is the total propensity of the system at time t given that no reaction occurs before t, i.e. the total propensity of reaction events in ℛ ∪ ℛ̅ at time t given that no reaction events in ℛ ∪ ℛ̅ occur before t. And a_ℛ̄ (t) is the total propensity of the reaction events in ℛ̅ at time t given that no event in ℛ̅ occurs before t. Intuitively, a_ℛ̄ (t) measures the propensity of reaction events where the observed molecule is not involved. Thus a₀(t) − a_ℛ̄ (t) can be regarded as the amount of propensity value that contributed by the observed molecule. When there are many A molecules, E (p_r (τ)) will be small. In this paper we will assume that this condition holds for the systems we consider. i.e. the propensity contributed by a particular molecule is much smaller than the total propensity a₀ of the overall system.

Besides the error analysis, the computational cost of solving (3) is also important. This topic will be discussed in the next subsection.

3.1.4. Complexity of solving (3)

In the two-voxel example, the propensity function has the form (7), and equation (3) leads to the expression in (8). In general if we have L voxels, in voxel i (i = 1, …, L) we initially have $X_i^A$ A molecules and $X_i^B$ B molecules. Then the total propensity is given by

$$a_0(t,{\mathbf{X}}_0)=c\sum _{i=1}^L\sum _{j=1}^L{X}_i^A{X}_j^B(\sum _{k=1}^L{p}_{ik}^A(t)p_{jk}^B(t))=c{({\mathbf{X}}^A)}^T{\mathbf{P}}^A(t){({\mathbf{P}}^B(t))}^T{\mathbf{X}}^B,$$ (12)

where X^A is the population vector of species A and P^A(t) is the transition matrix of species A, whose element at row i and column j is $p_{ij}^A(t)$, and similarly for species B.

From equation (A.5) in Appendix A, the matrix P^A(t) has the form

$${({\mathbf{P}}^A(t))}^T=\mathbf{V}\left(\begin{array}{ccc}\hfill e^{{\kappa }^A{\lambda }_{0}t}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{{\kappa }^A{\lambda }_{L-1}t}\hfill \end{array}\right){\mathbf{V}}^{-1}{({\mathbf{P}}^A(0))}^T.$$ (13)

Here V is the matrix consisting of the eigenvectors of (A.4). In the simulation it is convenient to normalize the eigenvectors, so that V has the properties

$${\mathbf{V}}^{-1}={\mathbf{V}}^T,{\mathbf{V}}^T\mathbf{V}=\mathbf{I}.$$ (14)

P^A(0) is the initial value of the transition matrix P^A(t). In a simulation with given initial positions, P^A(0) = I.

Plugging (13) into (12), noting properties (14) and setting P^A(0) = I, we obtain

$$a_0(t,{\mathbf{X}}_0)=c{({\mathbf{X}}^A)}^T{\mathbf{P}}^A(t){({\mathbf{P}}^B(t))}^T{\mathbf{X}}^B=c{({\mathbf{X}}^A)}^T\mathbf{V}\left(\begin{array}{ccc}\hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_{0}t}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_{L-1}t}\hfill \end{array}\right){\mathbf{V}}^T{\mathbf{X}}^B.$$ (15)

The integral of a₀ (t, X₀) can be expressed analytically using (15), thus (3) becomes, for this example,

$$-\text{ln}r=c{({\mathbf{V}}^T{\mathbf{X}}^A)}^T\left(\begin{array}{ccc}\hfill \frac{e^{({\kappa }^A+{\kappa }^B){\lambda }_{0}t}-1}{({\kappa }^A+{\kappa }^B){\lambda }_0}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \frac{e^{({\kappa }^A+{\kappa }^B){\lambda }_{L-1}t}-1}{({\kappa }^A+{\kappa }^B){\lambda }_{L-1}}\hfill \end{array}\right){\mathbf{V}}^T{\mathbf{X}}^B.$$ (16)

It is clear now that the right hand side of (15) and (16) requires: (a) matrix – vector multiplications (V^TX^A and V^TX^B) and (b) vector – diagonal matrix – vector multiplication. For (a), The computational cost is O (L²). For (b), the computational cost is O (L). If we have multiple such reaction channels, we need to repeat (a) and (b) multiple times. However the cost for (a) can be reduced if a species is a reactant for several reactions, since we need only to perform the matrix – vector multiplication for this species once and reuse the result whenever needed. During the following Newton iterations, (a) brings no additional cost, as it needs only to be computed once when the equation is constructed. However, (b) must be recomputed in every iteration.

The computational cost of solving (16) does not explicitly depend on the population of each species. Increasing the population of species A only changes the elements of vector X^A, which does not affect the computational complexity. However the more molecules in the system, the more reaction events would occur, thus the more simulation steps are required. Therefore, the molecule population still affects the simulation cost, but not by making (16) harder to solve.

It is worth mentioning that the diffusion propensities κ^A and κ^B do not affect the complexity of (16) as well. Unlike the molecule population which may affect the number of reaction events, diffusion propensities affect the number of diffusion events. Since we need only to solve (16) for reaction events, diffusion events do not add computational overhead to the simulation. This is an advantage over the algorithms which track diffusion events. It enables us to simulate systems with large diffusion propensities without extra computational effort. In the case of increasing resolution, e.g. divide each voxel into n smaller voxels, the algorithm incurs the overhead due to the increased value of L. However, algorithms that track diffusion events incur additional costs due to the large propensities for diffusive transfers. A similar analysis applies to second order reactions like A + A → C.

After settling the problem of selecting the next reaction time, our next task is to select a reaction to fire.

3.2. Select the next reaction

In the SSA, the probability that a reaction is selected is proportional to its propensity. For the spatial simulation we will use the same idea. Thus we need first to specify the set of all possible reaction events, and then select one from the set.

3.2.1. The set of reaction events and their propensities

Since we have already sampled the time τ to the next reaction, a typical reaction event is that the system diffuses from the initial state X₀ to a new state Y at time τ and then fires a reaction in the infinitesimal time interval [τ, τ + dt]. The probability p_Y of this event is

$$p_{\mathbf{Y}}=P(\text{diffuse from}{\mathbf{X}}_0\text{to}\mathbf{Y}\text{at time}\tau )\times P(\text{fire a reaction in}[\tau ,\tau +dt]\text{given state}\mathbf{Y}).$$ (17)

Our purpose in this section is to select a possible state Y at time τ, proportional to the probability p_Y, and then select a reaction to fire. It is clear from (17) that if a state Y has no possible reaction to fire, e.g. all A molecules in one voxel and all B molecules in another, then p_Y will be zero and the probability that this state is selected is zero.

3.2.2. The sampling algorithm

Directly using (17) to do the sampling work is not easy. Here we will sample the reaction from another point of view. We sum up the propensities of all potential reaction events at time τ and select one according to its propensity. In our example, the probability of a particular A molecule from voxel i and a particular B molecule from voxel j to diffuse to voxel k at time τ and then react during [τ, τ + dt] is $p_{ik}^A(\tau )p_{jk}^B(\tau )cdt$, so the propensity of this particular reaction event at time τ is $c{p}_{ik}^A(\tau )p_{jk}^B(\tau )$. Summing over all such events yields the total propensity

$$a_0(\tau )=\sum _{i=1}^2\sum _{j=1}^2\sum _{k=1}^2{X}_i^A{X}_j^{B}c{p}_{ik}^A(\tau )p_{jk}^B(\tau ),$$

where $X_i^A$ and $X_j^B$ are the initial populations of A molecules in voxel i and B molecules in voxel j. In the SSA, the probability of a reaction to be selected is proportional to its propensity. Here we use the same idea. The probability that we select an event that an A molecule from voxel i and a B molecule from voxel j react in voxel k at time τ is $X_i^A{X}_j^{B}c{p}_{ik}^A(\tau )p_{jk}^B(\tau )/a_0(\tau )$.

After sampling the reaction event, it is time for us to update the system. Suppose that the sampled reaction event is that an A molecule from voxel i₀ and a B molecule from voxel j₀ react in voxel k₀ at time τ. As the sampling result by definition specifies the voxel location of the two reactant molecules, there is no need to sample a diffusion process for these two molecules. So we first remove an A molecule from voxel i₀ and a B molecule from voxel j₀. Then we sample a diffusion process for the remaining system up to time τ. Finally, we insert a product molecule C into voxel k₀. This completes the procedure of firing the selected reaction.

Now we have completed a step of the simulation for our simple example. The next subsection summarizes the algorithm.

3.3. Summary of the algorithm

In this section we present the algorithm in a more general setting. Suppose that a one dimensional system has M reactions, N species and L voxels. Assume the current state of the system is X, and without loss of generality, the current time is 0. Then the time dependent propensity functions for different types of reactions are

• $\varphi \stackrel{c}{\to }\mathit{\text{something}}$

  $$a(t,\mathbf{X})=n\times c$$

  where n is the number of voxels that contain the reaction.
• $A\stackrel{c}{\to }\mathit{\text{something}}$

  $$a(t,\mathbf{X})=c\sum _{i=1}^L{X}_i^A$$
• $A+B\stackrel{c}{\to }\mathit{\text{something}}$

  $$a(t,\mathbf{X})=c\sum _{i,j,k=1}^L{X}_i^A{X}_j^B{p}_{ik}^A(t)p_{jk}^B(t)$$
• $A+A\stackrel{c}{\to }\mathit{\text{something}}$

  $$a(t,\mathbf{X})=c\sum _{i<j}\sum _{k=1}^L{X}_i^A{X}_j^A{p}_{ik}^A(t)p_{jk}^A(t)+\sum _{i,k=1}^L\frac{c}{2}{X}_i^A(X_i^A-1){(p_{ik}^A(t))}^2=\frac{c}{2}(\sum _{i,j,k=1}^L{X}_i^A{X}_j^A{p}_{ik}^A(t)p_{jk}^A(t)-\sum _{i,k=1}^L{X}_i^A{(p_{ik}^A(t))}^2),$$

  and the total propensity is given by

  $$a_0(t,\mathbf{X})=\sum _{i=1}^M{a}_i(t,\mathbf{X}),$$

  where a_i (t, X) is the propensity function of reaction i at time t given that no reaction occurs before t. Here “→ something” could be “→ ϕ” which denotes a reaction that only consumes molecules.

The simulation steps of the TDPD algorithm are listed below

• 0Compute the eigenvalues and eigenvectors using (A.3) and (A.4) (These values need only to be computed once).

For each realization, do the following:

• 1Initialize the time t = t₀ and the system state X = X₀.
• 2
  With the system in state X at time t, generate a uniform random number r ~ U (0, 1) and solve the following equation to obtain a sample τ of the time to the next reaction,

  $$-\text{ln}r={\int }_0^{\tau }{a}_0(s,\mathbf{X})ds.$$ (18)
• 3Compute the transition matrix p_ij (τ) for each diffusive species using equation (A.5).
• 4
  Sample the reaction R_l to fire. Its index l is an integer random variable between 1 to M with point probabilities

  $$P(l)=\frac{a_l(\tau ,\mathbf{X})}{a_0(\tau ,\mathbf{X})}.$$
• 5
  Sample where the reactant molecules come from and where the product is generated.

  • If in step 4 the sampled reaction R_l is $\varphi \stackrel{c}{\to }\mathit{\text{something}}$, suppose that there are n voxels which contain the reaction, and the reaction occurs in voxel k. Then k is a random variable with point probability

    $$P(k)=\{\begin{array}{cc}1/n\hfill & \text{if voxel}k\text{contains the reaction}\hfill \\ 0\hfill & \text{if voxel}k\text{does not contain the reaction}\hfill \end{array}.$$
  • If in step 4 the sampled reaction R_l is $A\stackrel{c}{\to }\mathit{\text{something}}$, suppose that the reactant originates in voxel i and the product is produced in voxel k. Then (i, k) is a random variable with point probability (Note that voxel i and voxel k are not necessarily adjacent).

    $$P(i,k)=\frac{c{X}_i^A{p}_{ik}^A(\tau )}{a_l(\tau ,\mathbf{X})},i,k=1,\dots ,L.$$
  • If in step 4 the sampled reaction R_l is $A+B\stackrel{c}{\to }\mathit{\text{something}}$, supposing that reactant A originates in voxel i, reactant B originates in voxel j, and the product is produced in voxel k, then (i, j, k) is a random variable with point probability

    $$P(i,j,k)=\frac{c{X}_i^A{X}_j^B{p}_{ik}^A(\tau )p_{jk}^B(\tau )}{a_l(\tau ,\mathbf{X})},i,j,k=1,\dots ,L.$$
  • If in step 4 the sampled reaction R_l is $A+A\stackrel{c}{\to }\mathit{\text{something}}$, supposing that the two molecules originate in voxel i and voxel j, and the product is produced in voxel k, then without loss of generality, we assume i ≤ j. (i, j, k) is a random variable with point probability

    $$P(i,j,k)=\{\begin{array}{cc}\hfill \frac{c{X}_i^A{X}_j^A{p}_{ik}^A(\tau )p_{jk}^A(\tau )}{a_l(\tau ,\mathbf{X})}\hfill & \hfill i<j\hfill \\ \hfill \frac{\frac{c}{2}{X}_i^A(X_i^A-1){(p_{ik}^A(\tau ))}^2}{a_l(\tau ,\mathbf{X})}\hfill & \hfill i=j\hfill \end{array},i,j,k=1,\dots ,L.$$
• 6
  Remove the reactant molecules from the current state X.

  • If in step 4 the sampled reaction R_l is $\varphi \stackrel{c}{\to }\mathit{\text{something}}$, skip this step.
  • If in step 4 the sampled reaction R_l is $A\stackrel{c}{\to }\mathit{\text{something}}$ and in step 5 the sampled voxel where the reactant originates is i, then decrease $X_i^A$ by one.
  • If in step 4 the sampled reaction R_l is $A+B\stackrel{c}{\to }\mathit{\text{something}}$ and in step 5 the sampled voxels where the reactants A, B originate are (i, j) respectively, then decrease $X_i^A$ and $X_j^B$ by one.
  • If in step 4 the sampled reaction R_l is $A+A\stackrel{c}{\to }\mathit{\text{something}}$ and in step 5 the sampled voxels where the two reactants originate are (i, j), decrease $X_i^A$ by one, then decrease $X_j^A$ by one.
• 7
  Sample a diffusion process with reflecting boundary conditions up to time t + τ. For example, for species A, sample a multinomial random variable for each voxel i (i = 1, …, L),

  $${\mathbf{Ŷ}}_i=ℳ(X_i^A,p_{i1}^A(\tau ),\dots ,p_{iL}^A(\tau )).$$

  Here Ŷ_i = (Ŷ_i1, …, Ŷ_iL) is a vector of size L. Ŷ_ij (j = 1, …, L) is the sampled value of the number of A molecules that originated in voxel i at time t and went to voxel j after a time interval τ. Then

  $$\mathbf{Y}=\sum _{i=1}^L{\mathbf{Ŷ}}_i$$ (19)

  is a sample of the distribution of A molecules after the diffusion process. Set the population of species A to be Y. Repeat this procedure for each diffusive species.
• 8Put the product molecules of the sampled reaction (in step 4) into the sampled voxel (in step 5) where they are produced. Set t ← t + τ.
• 9Return to Step 2, or else stop the realization.

3.4. Computational cost of the algorithm

As shown in the algorithm, the majority of the computational cost arises from

1. Compute the stepsize τ (step (2)).

   This has been discussed in Section 3.1.4, where we found that the computational cost is O (ML²).

2. Compute the transition matrix P (τ) (step (3)).

   From equation (A.5), the transition matrix is given by

   $$\mathbf{P}{(t)}^T=\mathbf{V}\left(\begin{array}{ccc}\hfill e^{\kappa {\lambda }_{0}t}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{\kappa {\lambda }_{L-1}t}\hfill \end{array}\right){\mathbf{V}}^T\mathbf{P}{(0)}^T,$$ (20)

   where V and λ₀, …, λ_L−1 are the normalized eigenvector matrix and eigenvalues of the coefficient matrix in Equation (A.1). In the simulation, P (0)^T = I, thus the computation requires a matrix – diagonal matrix multiplication (cost of O (L²)) and a matrix – matrix multiplication (cost of O (L³)). Although we can reduce the cost by using symmetry properties such as p_ij = p_ji = p_{L+1−i,L+1−j} = p_{L+1−j,L+1−i}, the O (L³) complexity still holds.

   One way to decrease the complexity is to set a cut-off tolerance for the computation. For example, when we compute p_1i (i = 1, …, L), we also record the partial sum of the values that we already computed, i.e. psum_k = p₁₁ + p₁₂ + ⋯ + p_1k (k ≤ L). If the value psum_k passes some threshold 1 − ε, then we stop computing and set the remaining variables p_1,k+1, …, p_1,L to zero. The computed values are then normalized by p_1i/psum_k (i = 1, …, k), so that they sum up to one. Here ε is a tolerance chosen small enough so that it does not make a noticeable change to the distribution. This strategy can protect us from computing the huge number of very small probabilities when the space is large and the stepsize is small. In our current code, which is used in Section 4 for the numerical experiments, this tolerance is set to be 0 as the default value. However, we still terminate the computation of p_1i in two cases: (1). p_1i < 0; (2). p_1i > p_1,i−1. When these cases occur, it is clear that the numerical precision is no longer reliable, hence the remaining values of p_1k (i < k ≤ L) may be meaningless.

   The time spent in (b) increases linearly with respect to the number of diffusive species, because we need to compute the matrix for each of them. It does not explicitly depend on the number of reaction channels or the molecule populations. However, if these result in an increment in the number of reaction events, the computational cost will increase since we will need to compute the transition matrix more times.

3. Sample a reaction event (steps (4) and (5)).

   Step (4) samples the reaction to fire from the total of M reactions. It requires the time dependent propensity values of the reactions. For example, the propensity of reaction $A+B\stackrel{c}{\to }C$ can be computed from (15). Since we have already computed V^TX^A and V^TX^B in step (2), computing (15) requires only a vector – diagnal matrix – vector multiplication, which is O(L). Since we may, in the worst case, need to compute all of the reaction propensities, the complexity of step (4) is O(ML).

   Step (5) samples the original positions of the reactant molecules at the beginning of the step and the location where the reaction occurs. This operation can be done with O (L²) cost if the algorithm is carefully designed.

   Let us use reaction $A+B\stackrel{c}{\to }C$ as an example. First we need to sample where the reactant A molecule originates. From the propensity function (15), the propensity contributed by the A molecules in voxel 1 is given by

   $$a^A=c(X_1^A,0,\dots ,0)\mathbf{V}\left(\begin{array}{ccc}\hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_0\tau }\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_{L-1}\tau }\hfill \end{array}\right){\mathbf{V}}^T{\mathbf{X}}^B=c{X}_1^A{\mathbf{v}}_1^T\left(\begin{array}{ccc}\hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_0\tau }\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_{L-1}\tau }\hfill \end{array}\right){\mathbf{V}}^T{\mathbf{X}}^B,$$

   where ${\mathbf{v}}_1^T$ is the first row of the matrix V. Thus the probability that the A molecule originates in voxel 1 is a^A / a_l (τ, X), where a_l (τ, X) is the time dependent propensity of the reaction $A+B\stackrel{c}{\to }C$, which has already been computed in step (4). Since we have already computed V^TX^B in step (2), the computation of a^A basically requires a vector – diagonal matrix – vector multiplication, which is O(L). As the procedure samples over all the voxels in the worst case, it has O (L²) complexity, to locate the voxel from which the A molecule originates.
   The next task is to locate the voxel from which the B molecule originates. Without loss of generality, let us assume that the A molecule originates in voxel 1. Then among a^A, the propensity value contributed by the B molecules from voxel 1 is given by

   $$a^{AB}=c{X}_1^A{\mathbf{v}}_1^T\left(\begin{array}{ccc}\hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_0\tau }\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_{L-1}\tau }\hfill \end{array}\right){\mathbf{V}}^T\left(\begin{array}{c}\hfill X_1^B\hfill \\ \hfill 0\hfill \\ \hfill ⋮\hfill \\ \hfill 0\hfill \end{array}\right)=c{X}_1^A{X}_1^B{\mathbf{v}}_1^T\left(\begin{array}{ccc}\hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_0\tau }\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{({\kappa }^A+{\kappa }^B){\lambda }_{L-1}\tau }\hfill \end{array}\right){\mathbf{v}}_1.$$

   The probability that the B molecule originates in voxel 1 is a^AB / a^A. The computation of a^AB requires a vector – diagonal matrix – vector multiplication, which is O(L). As the algorithm loops over all the voxels in the worst case, the complexity of sampling the B molecule’s position is O (L²).

   The last task in this step is to sample where the reaction event occurs. Without loss of generality, suppose that both the A molecule and the B molecule originate in voxel 1. Then the probability that the reaction event occurs in voxel k is

   $$\frac{c{X}_1^A{X}_1^B{p}_{1k}^A(\tau )p_{1k}^B(\tau )}{a^{AB}}.$$

   Since we must loop over all the voxels in the worst case, the complexity of this task is O(L).

   Putting everything together, step (5) can be implemented with complexity O (L²).

4. Sample the diffusion process (step (7)).

   As shown in step (7), to redistribute A molecules originating in voxel i, we must sample a multinomial random variable, which requires the computation of L − 1 binomial random variables. Thus, to sample the diffusion process for A molecules originating in every voxel, we must generate O (L²) binomial random variables. Once the L multinomial random variables have been generated, we must sum them up as shown in (19), which is an O (L²) operation. As we need to repeat the procedure for every diffusive species, the complexity of step (7) is O (NL²), where N is the number of species. This cost can be reduced if the binomial random variables are sampled in a proper order. For example, to redistribute the A molecules in voxel i, we can first sample the number of molecules that will stay in voxel i, then the number of molecules that will move to voxel i − 1, i + 1, i − 2, i + 2,…, until all of the molecules have been redistributed. Thus if the molecules are all distributed in a few voxels near voxel i, which is usually the case when the time stepsize is small, the computational complexity of the redistribution can be substantially reduced.

3.5. Discussion

The solution of Equation (18)

Newton iteration could be employed to solve Equation (18). However, the iteration may fail to converge occasionally due to a bad initial guess. Changing the initial guess is one way to deal with this problem, but it still does not guarantee that we can find a good initial guess in the following trials. Actually, Equation (18) has some interesting properties that can help us to find its root. $f(t)=\text{ln}r+{\int }_0^t{a}_0(s,\mathbf{X})ds$ is a continuous increasing function of t, and f (0) = ln r < 0 since r is a uniform random number in (0, 1). Our purpose is to find the root in (0, T], where T is the simulation end time. If f (T) < 0, as f (t) is an increasing function, it implies that the root, which is the time to the next reaction event, is not in (0, T]. In this case, we can just sample a diffusion process up to time T and finish the simulation. If f (T) > 0, then the root is between 0 and T. In this case, we first try Newton iteration. If that fails, we use bisection to find the root with a given tolerance ε. We first evaluate f (T/2). If f (T/2) > ε, we search for the root in (0, T/2). If f (T/2) < −ε, we search (T/2, T]. If −ε ≤ f (T/2) ≤ ε, we stop the iteration and set T/2 to be the root. Since f (t) is continuously increasing, bisection search guarantees that we can find the root.

Boundary conditions

In the algorithm as described in this paper, we use reflecting boundary conditions. However, it also works with other boundary conditions as long as one has the closed form transition probabilities for the corresponding diffusion process. For example, it can be applied with periodic boundary conditions (See Appendix A for the solution of discrete diffusion process with periodic boundary conditions).

Extension to higher dimension space

It is straightforward to extend the method to work with a 2D rectangular domain or a 3D cubic domain. For example, on a 2D rectangular domain, the diffusion process in the ‘x’ direction is independent of the diffusion process in the ‘y’ direction. Thus the probability for a molecule to jump from voxel (i₀, j₀) to voxel (i₁, j₁) is the probability that it jumps from column i₀ to i₁ in the ‘x’ direction times the probability that it jumps from row j₀ to j₁ in the ‘y’ direction.

4. Numerical simulation

In this section we present some simulation results generated by our new TDPD algorithm and compare with ISSA and NSM simulation results. Computation times of the three methods were obtained on processor Intel(R) Core(TM) i7-2600 CPU @ 3.40GHz with OS windows 7. Here the ISSA method has been implemented with the dependency graph, thus it updates the propensity functions only when necessary. For NSM the dependency graph for reactions has been implemented, as well as the strategy to reuse the random number for voxels that receive molecules from the neighbours [17]. In addition, the software package MesoRD is used in Example 2 for comparison purposes.

4.1. Example 1

This example is from Section 3. It consists of two voxels and one reaction $A+B\stackrel{c}{\to }C$. The initial values used for the simulation were: 10000 A molecules in the first voxel; 10000 B molecules in the second voxel; no C molecules. The reaction rate constant is 10⁻⁵. The diffusion rates for species A, B and C are 10, 1, 0.1 respectively. The simulation time is 1 second. The first three entries in Table 1 show the CPU time used for the simulation, where it is apparent that the TDPD method achieves an order of magnitude speedup over ISSA and NSM.

Table 1.

CPU times for the one second simulation of Example 1. The first three entries use a resolution of two subvolumes. The last three entries use a resolution of 50 subvolumes.

Method	Realizations	Resolution	Average time per realization
ISSA	100000	2 voxels	0.02756s
TDPD	100000	2 voxels	0.00121s
NSM	100000	2 voxels	0.02979s
ISSA	10000	50 voxels	51.3864s
TDPD	10000	50 voxels	0.13936s
NSM	10000	50 voxels	41.388s

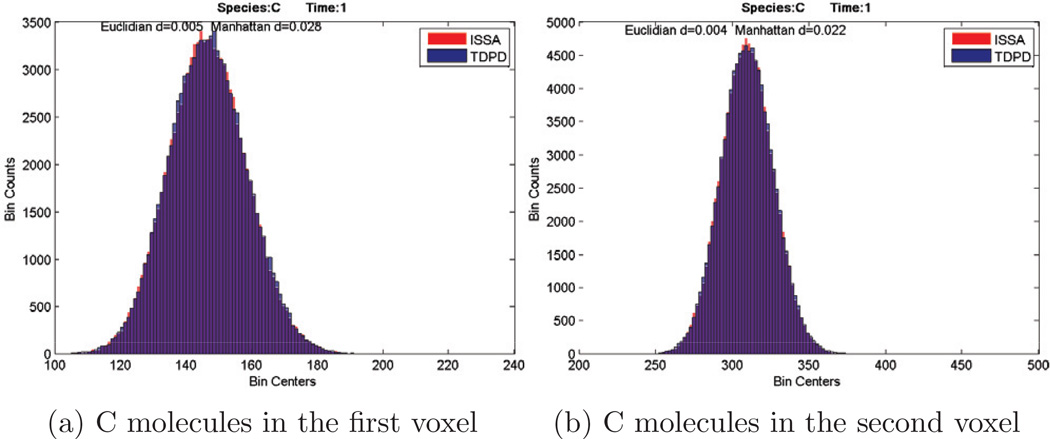
Histograms of species C in the two voxels at time t = 1s are shown in Fig. 1, and reveal that the new TDPD algorithm is quite accurate. At the top of each figure we provide two values to measure the difference of the histograms. The definitions of the two measures are as follows. Let X = (x₁, …, x_n) be a vector that corresponds to a histogram where x_i is the count in bin i, and $\mathbf{x}=\mathbf{X}/{\sum }_{i=1}^n{X}_i$ is the normalized X. Then for two histograms, we have two normalized vectors x and y. The Euclidean distance in the histogram figures is defined as the 2-norm of x − y, i.e. $\sqrt{{\sum }_{i=1}^n{(x_i-y_i)}^2}$. The Manhattan distance is defined as the 1-norm of x − y, i.e. ${\sum }_{i=1}^n|x_i-y_i|$.

Figure 1.

Histograms of species C. Comparison of results given by ISSA and TDPD. Red is ISSA, blue is TDPD, and purple is the overlap of the two histograms.

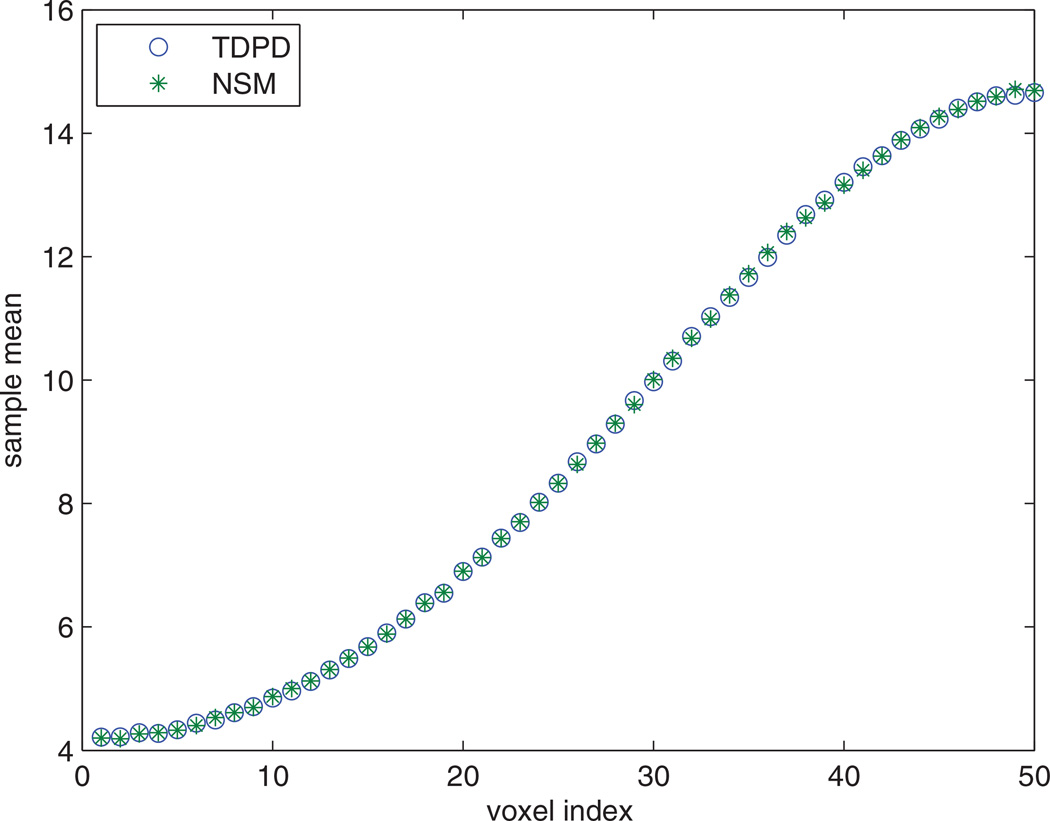
For the next test, we increased the resolution of the one dimensional model from 2 voxels to 50 voxels. The diffusion and reaction rates also changed due to the change of the subvolume size (i.e. the diffusion rates increased 25² times, and the reaction rate increased 25 times). Initially the A and B molecules were located in the two boundary voxels of the one dimensional geometry respectively. The last three entries in Table 1 show the CPU times used for the simulations. Figure 2 shows the average population of species C in each voxel. The TDPD and NSM methods generate nearly identical results.

Figure 2.

Average population of species C in each voxel at t = 1. The resolution is 50 voxels. 10000 realizations are simulated for each method.

In addition to the accuracy, we are interested in the computation time of the algorithm. In the next subsection we will demonstrate how the simulation time scales with the resolution, the species population and the number of reaction channels for this example.

4.1.1. Scaling of simulation time with respect to resolution

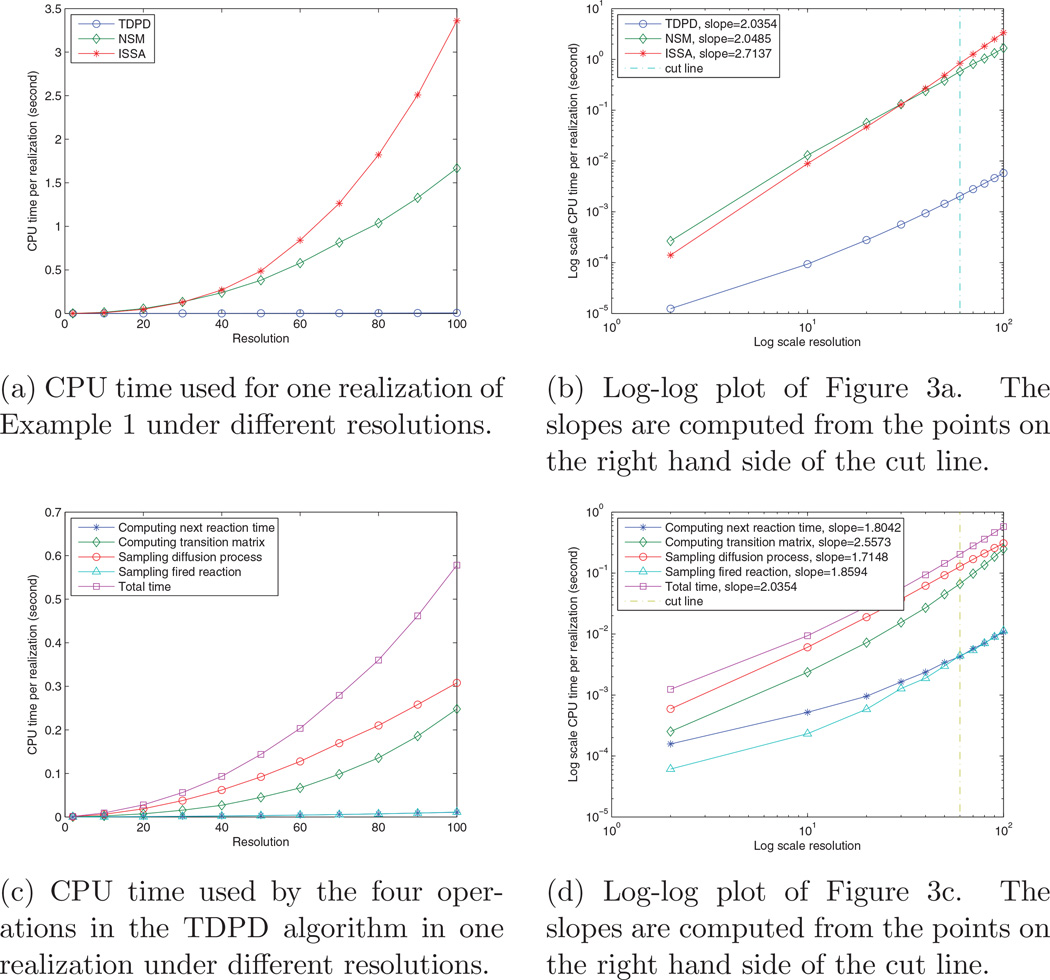
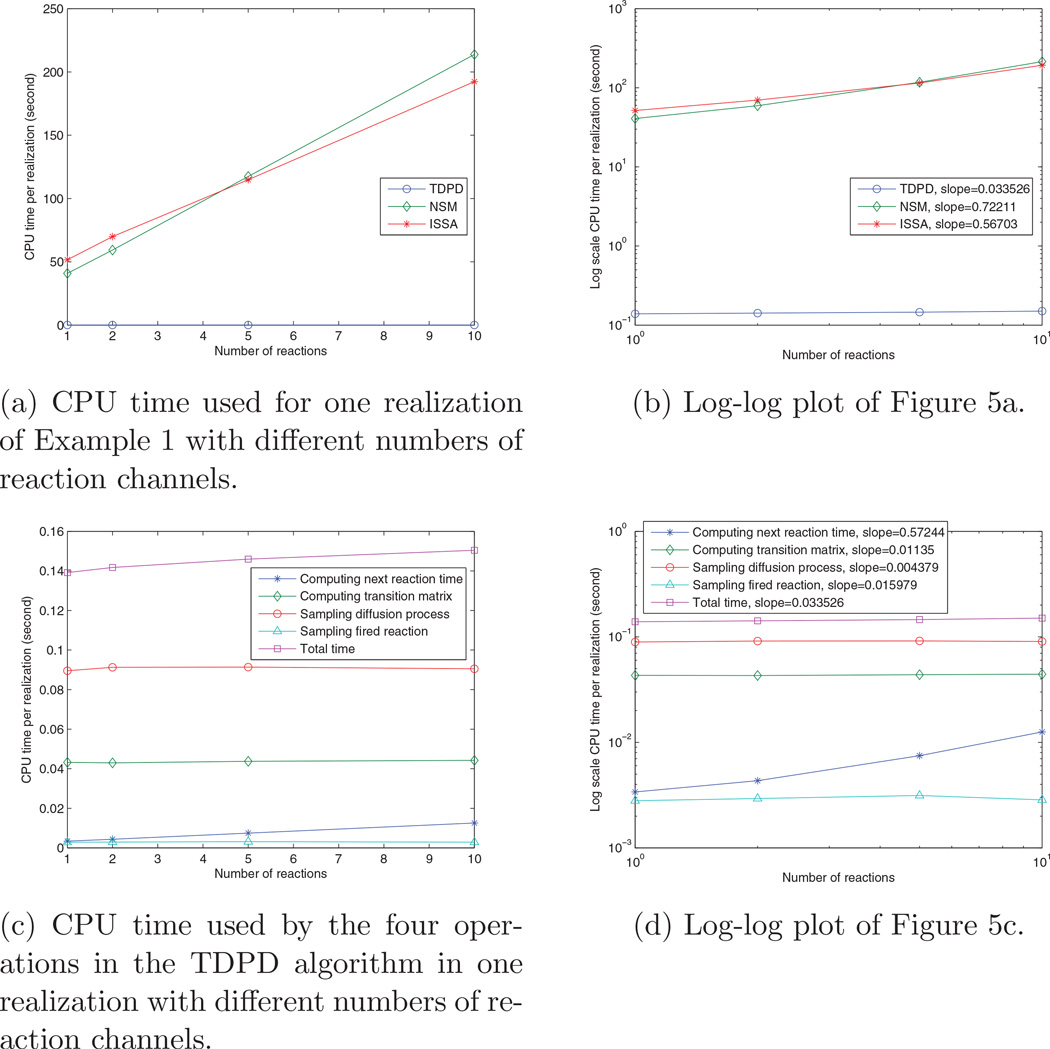
In the previous experiments, we have run the simulation with resolution of 2 and of 50 voxels. In order to show how the simulation time scales with respect to the resolution, we also ran the simulation with resolutions of 10, 20, 30, …, 100 voxels. For each resolution, there are initially 10000 A and B molecules in the two boundary voxels respectively, and 1000 realizations are run with TDPD and with ISSA and NSM for comparison. Figure 3 shows the average CPU time used for one realization. Figure 3a shows that TDPD enjoys an orders of magnitude performance increase over ISSA and NSM. Figure 3b is the log scale plot of Figure 3a. It shows that the TDPD and NSM have similar slopes, which are better than the ISSA’s slope. As we have discussed in Section 3.4, there are four operations in the TDPD algorithm that occupy the majority of computation time. Figure 3c plots the time used by the four operations in each realization under different resolutions. It reveals that sampling the diffusion process (step (7) in the algorithm) is the most expensive operation. The next expensive operation is computing the transition matrix (step (3) in the algorithm). Computing the next reaction time (step (2)) and sampling a reaction event (step (4) (5)) are much cheaper than the previous two operations (they are overlapped in Figure 3c). Figure 3d shows the log scale plot of Figure 3c. Note that even though computing the transition matrix is cheaper than sampling the diffusion process in Figure 3c, it has a larger slope in the log-log plot; thus it may be the most expensive operation when the resolution is very high.

Figure 3.

Scaling of computation time with respect to resolution.

4.1.2. Scaling of simulation time with respect to species’ population

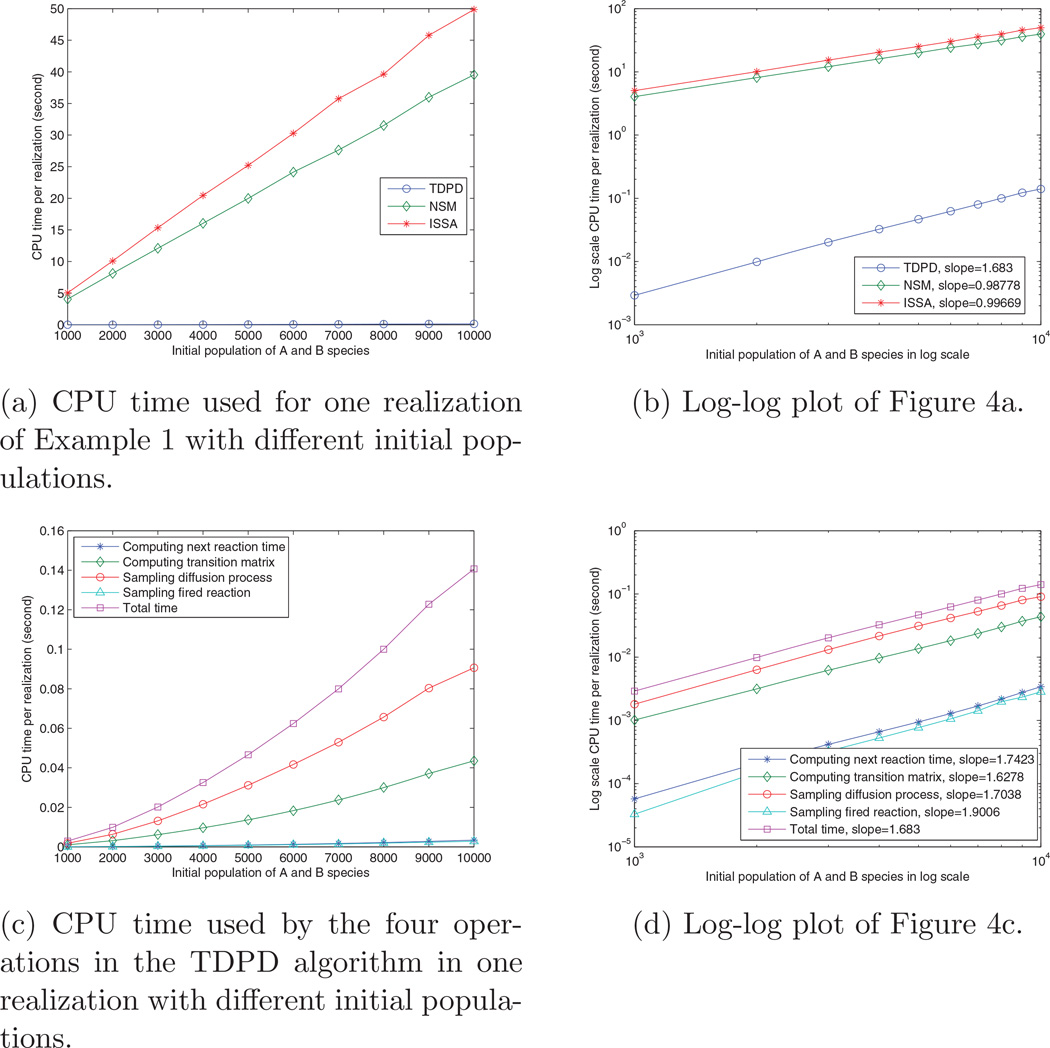
In the previous experiments, we initially have 10000 A molecules and 10000 B molecules in the two boundary voxels respectively. In this subsection, we run a set of simulations with initially 1000, 2000, 3000, …, 10000 A and B molecules in the two boundary voxels respectively. The resolution is set to be 50 voxels. Figure 4 shows the computation times. Figure 4a plots the CPU time used by ISSA, NSM, and TDPD, for one realization with different initial populations. TDPD performs the best of the three. Figure 4b is the log-log plot of Figure 4a. It shows that ISSA and NSM have a slope near one while TDPD has a slope greater than one. This result can be explained as follows: In a system where the number of diffusion events overwhelms the number of reaction events, when the population of A and B molecules increases k times, the number of diffusion events in the system will also increase roughly k times. Thus ISSA and NSM must take roughly k times more steps to run the simulation, which explains why Figure 4a and 4b shows a linear relationship between ISSA, NSM and the initial population. In contrast, the computation time of TDPD is immune from the impact of diffusion. It filters the massive linear increment of diffusion events. However, it must still deal with the increment from reaction events. As the populations of both A and B increase by k times, the time dependent reaction propensity increases k² times at the beginning the simulation, which explains why the computation time of TDPD has a slope larger than one in Figure 4b. Figures 4c and 4d show the time used by the four main operations in TDPD. Figure 4d shows that the four operations have similar slopes.

Figure 4.

Scaling of computation time with respect to the initial population. Values are averaged over 1000 realizations.

4.1.3. Scaling of simulation time with respect to the number of reaction channels

In this subsection we ran a set of simulations with the reaction channel copied k (k = 1, 2, 5, 10) times. For example, when k = 2, the system has two reactions, both of which have the form $A+B\stackrel{c_k}{\to }C$. We set the reaction rate c_k = c/k for all the reaction channels, where c = 10⁻⁵ is the original reaction rate. All of the simulations should have a similar number of reaction events; thus the number of reaction channels will be responsible for the change of computation times. For all the simulations we set the resolution to be 50 voxels, with initially 10000 A molecules at one end, and 10000 B molecules at the other end. The computation times are shown in Figure 5. Figure 5a shows that the computation time for ISSA and NSM increases significantly with respect to the number of reaction channels. The log-log plot of Figure 5b shows that the slope of the computation time of TDPD is much smaller than one, which means that the increase in the number of reaction channels has little influence on the simulation cost of TDPD. Further decomposition of the computation time in TDPD are shown in Figures 5c and 5d. As the number of species is the same for all the simulations, computing the transition matrices and sampling the diffusion processes take a similar amount of time for each simulation. The time spent in sampling the reaction events (steps 4 and 5 in the algorithm) is influenced by the number of reaction channels. In step 4 the index of the reaction channel is sampled, and in step 5 the locations where the reactant molecules originate and where the reaction event occurs are sampled. As analyzed in Section 3.4, the leading term of the complexity comes from step 5, which does not depend on the number of reaction channels. Thus the corresponding curve in Figure 5c looks almost flat. The time spent on computing the next reaction time, however, has a strong relationship with the number of reaction channels. This is because when we solve (18), we need to compute the time dependent propensity for every reaction channel; thus the more channels we have, the more values we need to compute. Figure 5c shows that this part is responsible for almost all of the increase in computation time in the TDPD simulation.

Figure 5.

Scaling of computation time with respect to the number of reaction channels. Values are averaged over 1000 realizations.

4.2. Example 2

Example 2 is a two dimensional problem with 3 × 3 voxels. The chemistry consists of the following first and second order reactions:

$$S_0+S_0\stackrel{c_1}{\to }{S}_1,\hspace{1em}{S}_1\stackrel{c_2}{\to }{S}_0+S_0,\hspace{1em}{S}_0+S_1\stackrel{c_3}{\to }{S}_2,\hspace{1em}{S}_2+S_3\stackrel{c_4}{\to }{S}_3+S_4$$

To make the example spatially inhomogeneous, we begin with one S₃ molecule, which is fixed in the bottom right corner. Thus an S₂ molecule can be converted to S₄ only when it travels to the bottom right voxel and reacts with the S₃ molecule.

Initially we have 10000 S₀ molecules in the top left corner. The rate parameters used in the simulation are given by

$$c_1={10}^{-4},\hspace{1em}{c}_2=0.1,\hspace{1em}{c}_3=0.01,\hspace{1em}{c}_4=0.1,$$

and the diffusion rates for the species are given by

$$S_0:100,\hspace{1em}{S}_1:10,\hspace{1em}{S}_2:5,\hspace{1em}{S}_3:0,\hspace{1em}{S}_4:1.$$

The time used for a ten second simulation is shown in Table 2. The new algorithm has a significant speedup over ISSA and NSM.

Table 2.

Computation time for the ten second simulation of Example 2.

Method	Realizations	Average time per realization
ISSA	100000	8.65476s
NSM	100000	8.13928s
TDPD	100000	0.09501s

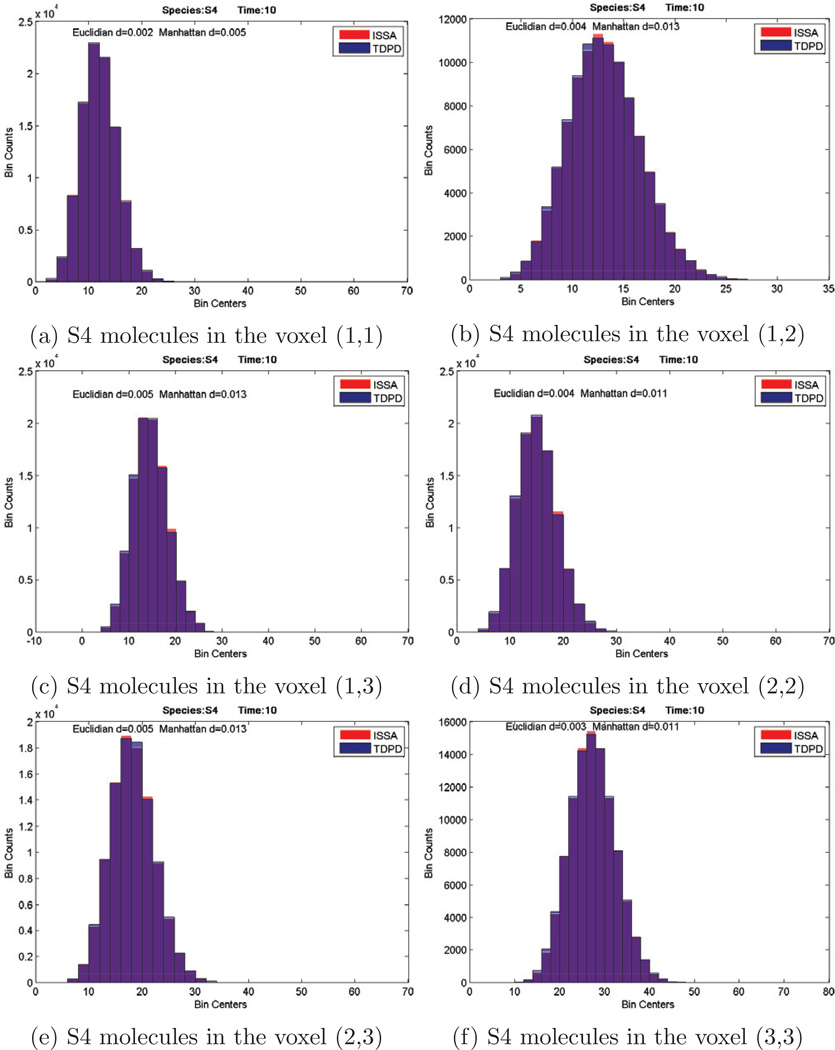
To demonstrate the accuracy of our algorithm, we plotted the histograms of the product S₄ in voxels (1,1), (1,2), (1,3), (2,2), (2,3), (3,3) (Here voxel (i, j) means the voxel at row i and column j), together with the distribution given by ISSA, in Figure 6. It is evident that our algorithm can produce very accurate results.

Figure 6.

Histograms of species S₄. Comparison of result given by ISSA and TDPD. Red is ISSA, blue is TDPD, and purple is the overlap of the two histograms.

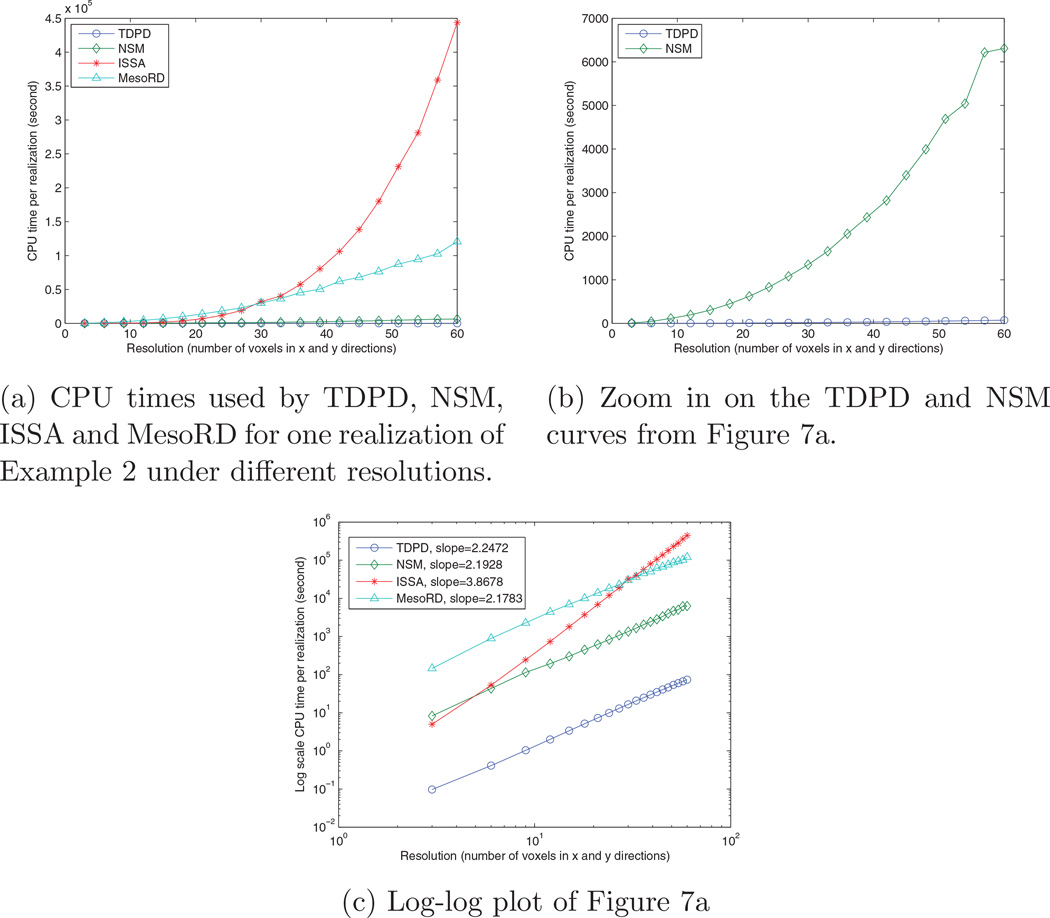
For this model we have also increased the resolution to compare the performance of different methods. Figure 7 shows the CPU times used by different methods for one realization of Example 2. It is evident that TDPD enjoys substantially better performance than the other methods. Figure 7c is the log scale plot of the CPU times. It shows that the computation time of the TDPD method has a similar slope as the NSM and MesoRD, which is smaller than the ISSA’s slope.

Figure 7.

Scaling of computation time with respect to resolution.

4.3. Example 3: Demonstration of the error behavior of the TDPD method

In Section 3.1.3 we noted that the error of the simulation might be large when E (p_r (τ)) is large, where E (p_r (τ)) is bounded by (11). It is evident that when the total propensity of the system a₀(t) is much larger than the propensity contributed by a single molecule a(t), the right hand side of (11) will be small, thus the simulation will have good accuracy. In this section we will use an example to demonstrate this point.

Suppose that we have a one dimensional system with absorbing boundary conditions, with a population of A molecules that are initially in the central voxel. There are 50 voxels on both sides of the central voxel. The diffusion coefficient is set to be 300 for the simulation. The simulation time is one second.

In order to perform the simulation with our algorithm, we modified the system slightly by replacing the escaping diffusion events in the two boundary voxels by absorbing reaction events $A+B\stackrel{c}{\to }B$, where we put one non-diffusive B molecule in each boundary voxel and the reaction rate is also set to be c = 300. It is obvious that the modified system is virtually equivalent to the previous diffusion system with absorbing boundary condition (since species A is governed by the same reaction-diffusion master equation in the two systems), and the “B molecules” are actually the holes in the boundary that allow molecules to escape. Now we have a diffusion system with reflecting boundary conditions, plus an absorbing reaction in the two boundary voxels.

We chose this example in part because its analytical solution is available (See Appendix A). Thus, it is convenient for us to compare the numerical solution with its true solution for error analysis purposes. In this section, we will discuss how the number of molecules, geometry resolution, and number of reaction channels affect the accuracy.

4.3.1. Accuracy with respect to the number of molecules

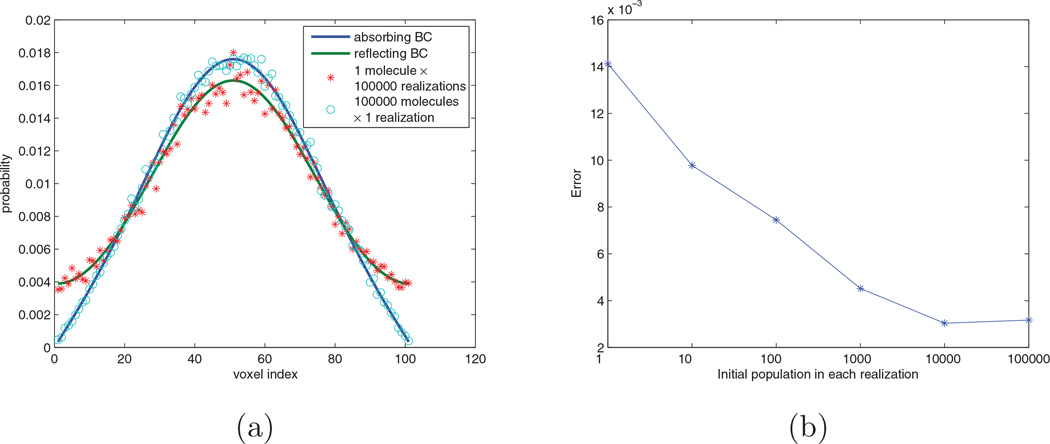
Equation (11) indicates that the simulation may incur a large error when the total propensity a₀(t) is not large compared with the propensity contributed by a single molecule. We can maximize this error by pushing it to an extreme in which the system involves only one molecule initially, thus a₀(t) = a(t). In this case, the algorithm will directly sample the time of the absorbing reaction. If it is larger than the terminating time, the molecule survives and its location will be sampled according to a diffusion process with reflecting boundary conditions, as stated in the algorithm. Thus after 100,000 realizations we obtain a distribution of results (shown in Figure 8a) which suggests that the location of the surviving molecules are that of a diffusion process with reflecting boundary conditions. However, this is obviously not correct, since we know that the solution should be that of a diffusion process with absorbing boundary conditions.

Figure 8.

(a) Simulation results for Example 3. The blue line is the analytical solution of a diffusion process with absorbing boundary conditions. The green line is the analytical solution of a diffusion process with reflecting boundary conditions. The red stars are from 100,000 realizations with one molecule initially. The circles are from one realization with 100,000 molecules initially. (b) Errors for simulations with different initial populations.

Next we created another simulation for comparison. We initially put 100,000 molecules in the central voxel and performed only one realization. This time the total propensity of the system is much larger than the propensity contributed by a single molecule. The analysis in Section 3.1.3 predicts that the simulation should give us a much better result. Figure 8a verifies that this simulation generates a distribution which is quite close to the diffusion process with absorbing boundary condition.

In order to quantitatively show how the error changes with respect to the number of molecules in the simulation, the following simulations were also performed: 10,000 realizations with initial population 10 molecules; 1000 realizations with initial population 100 molecules; 100 realizations with initial population 1000 molecules; and 10 realizations with initial population 10,000 molecules. Each experiment has the same number of molecule samples and generates a probability distribution p_simulate = (p₁, …, p_L), where p_i is the probability that a survived molecule is observed in voxel i. Comparing this result with the analytical solution p_analytical computed from (A.12), we can obtain the error of the simulation as

$$\text{Error}={\Vert {\mathbf{p}}_{\mathit{\text{simulate}}}-{\mathbf{p}}_{\mathit{\text{analytical}}}\Vert }_2.$$ (21)

Figure 8b shows the errors in each simulation. As expected, the error decreases as the initial population increases.

This result can also be explained from another point of view. In each step of the simulation, the algorithm uses the diffusion process with reflecting boundary conditions to approximate the true distribution, which in this example is the diffusion process with absorbing boundary conditions. The true distribution and our approximation start from the same initial condition and diverge as time goes on. Thus the error increases as the stepsize increases. This is quite like using the explicit Euler method for solving ODEs, which uses a straight line to approximate the true solution curve in each step. In the simulation with one molecule in the system, a realization involves at most one reaction event, thus it needs only one step to finish the simulation. As a result, the stepsize is very large and the error will be significant. On the other hand, in the simulation with 100,000 molecules, 7375 reaction events occur. Thus the average stepsize is roughly 1.36 × 10⁻⁴s, which significantly reduces the error of the simulation.

4.3.2. Accuracy with respect to the resolution

In the previous simulations, we have 50 voxels on each side of the central voxel, i.e. 101 voxels in total. In order to explore how the accuracy changes with respect to the resolution, we ran another set of simulations with resolution of 21 voxels, 41 voxels, …, 101 voxels. For each simulation we put 100,000 A molecules in the central voxel initially. The absorbing reactions that occur in the two boundary voxels have a reaction rate that has been set equal to the diffusion rate, which is updated for each simulation due to the change of resolution. Ten realizations are run for each parameter (so there are 1,000,000 molecule samples in total for each simulation). The error of each simulation is computed as in (21). Here the analytical solution is computed with L = 21, 41, …, 101 respectively. Table 3 shows the error under different resolutions. The table suggests that the error does not change much when the resolution changes. As far as (11) is concerned, it means that the ratio between the propensity contributed by a single molecule and the total propensity of the system is similar for each simulation. In this simple system, it implies that in each simulation the total number of molecules that remain in the system is at the same level. The last entry in Table 3 shows the number of survived molecules in each simulation. As we expected, the number of molecules that survived the one second experiment is similar for each simulation with different resolutions. This result agrees with our intuition: the number of molecules that escape the one dimensional channel is a property of the system, which should not depend on the resolution used by a simulation.

Table 3.

Simulation error under different resolutions. Ten realizations are used for each parameter.

Resolution	21	41	61	81	101
Error (×10−4)	9.4304	8.3135	9.1124	9.8801	10.724
Survived molecules	93654.8	92969.4	92696.4	92608.2	92454.2

4.3.3. Accuracy with respect to the number of reaction channels

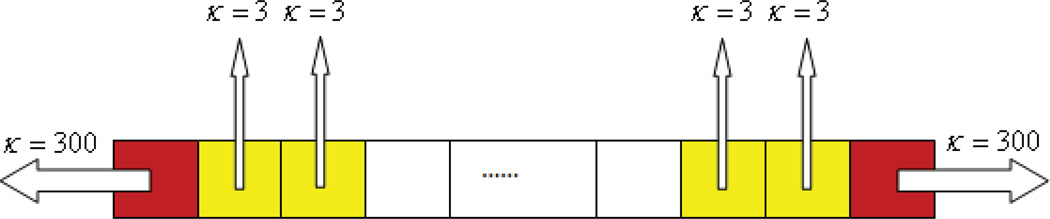
In the previous experiments, molecules can only escape the system from the boundary voxels. In order to show how the error changes with respect to the number of reaction channels, we will run simulations with more and more voxels that have absorbing reaction channels in them. I.e. we drill holes on more and more voxels in the channel. Figure 9 shows how the experiments are designed. For all the simulations we use 101 voxels as the resolution. The initial population in the central voxel is 100,000 molecules. The diffusion rate is 300. The yellow voxels in the figure have absorbing reaction channles in them, whose reaction rates are set to be 3. We will set more and more voxels to be yellow from the two ends of the channel, thus the simulations will have 10, 20, 30, 40, 50 voxels on each end having absoring reactions (including the red voxel at the boundary). Ten realizations are used for each parameter.

Figure 9.

Absorbing reaction channels are added in the yellow voxels, whose reaction rates are set to be 3.

Since for this example the analytical solution is no longer easy to compute, we use the simulation result from exact methods (here we use NSM) instead. Table 4 shows the errors of the simulations. It reveals that the error has an increasing trend as the number of absorbing channels increases. This trend can also be explained by equation (11). The more absorbing channels the system has, the fewer molecules remain in the system. Thus the ratio between the propensity contributed by a single molecule and the total propensity of the system will increase, which implies that the error of the simulation will increase as well. The last entry in Table 4 supports our reasoning: the number of molecules survived the one second simulation decreases significantly as the number of absorbing reaction channel increases.

Table 4.

Simulation error with different number of reaction channels. Ten realizations are used for each parameter.

Number of absorbing reaction channels	20	40	60	80	100
Error (×10−3)	1.0277	1.1830	1.3467	1.9767	4.1608
Survived molecules	90657.6	82230.9	63224.1	30961.2	5152.4

4.4. Coagulation model

The final example is a widely used model of blood coagulation [18] with 43 reactions and 33 species. When a blood vessel is wounded, it exposes Tissue Factor (TF) on the wounded vessel surface. TF initializes the extrinsic pathway of the coagulation cascade, which generates thrombin in the vessel. Thrombin then activates platelets, which form clots to prevent the loss of blood (the latter process is not modeled here).

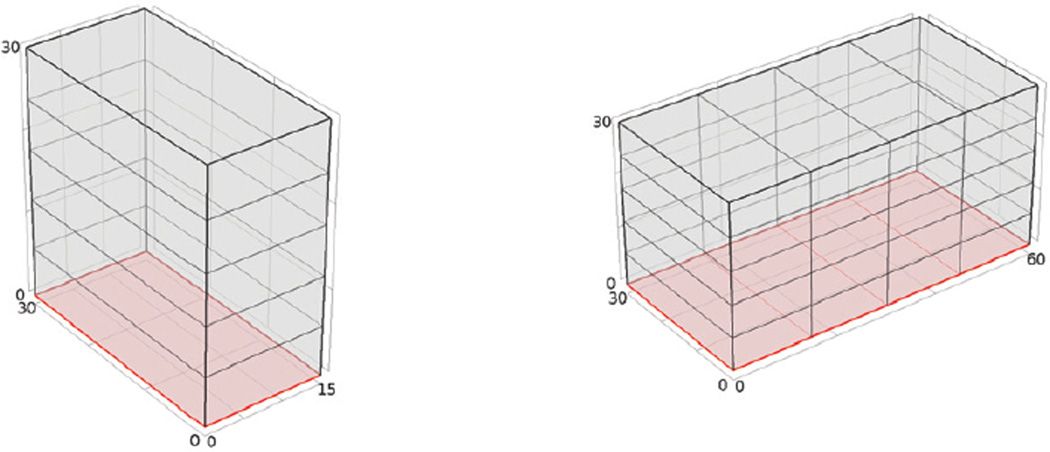
The original ODE model has for its state variables the concentration of each species as opposed to population, which is tracked in discrete stochastic simulation. We converted the concentration to population by selecting a control volume as shown in Figure 10. The bottom surface (the red surface in Figure 10) represents the wounded blood vessel. We begin with a control volume of 30µm × 30µm × 15µm (Figure 10a), where the 30µm × 30µm area is of the same level as the cross section of a capillary. The diffusion rates are set to be 50µm²/s for every species. Since the workload of the simulation is very heavy, it is important for us to reduce the complexity of the model. As the spatial inhomogeneities arise mainly from the species and reactions that belong to the wounded surface, we assume that the system is homogeneous in the ’x’ and ’y’ directions but inhomogeneous in the ’z’ direction. Thus we discretize space in the z direction, yielding a 1D model. In the simulation, we divide the space into five voxels along the z axis. Since TF appears only on the wounded vessel surface, we assume that TF and any compound involving TF exists only in the bottom voxel, and does not diffuse upward. In this example the ISSA simulation is extremely slow (Table 5 shows the ISSA speed). Thus we will compare the results of our method to a PDE simulation (i.e. we compare the dynamics of mean thrombin concentration from the stochastic simulation to the PDE result). Both stochastic and PDE models use the same height of 30µm for the control volume. However, intuition tells us that the larger the control volume, the less the stochastic effect will be. Thus we show the results for another stochastic simulation which increases the length of the control volume (Figure 10b). We expect that the stochastic simulation result should approach the PDE result, as the control volume gets larger.

Figure 10.

The geometry of the control volumes for our simulation. The red surface at the bottom represents the wounded blood vessel surface which contains TF.

Table 5.

The time used for the 700 second simulation of the coagulation model.

Method	Control volume length × width2 (µm3)	Realizations	Average time per realization
TDPD	15 × 302	60	3745s
ISSA	15 × 302	1	56403s
NSM	15 × 302	1	51519s
TDPD	60 × 302	30	84420s

The times required for the 700 second simulation are shown in Table 5. Due to the huge number of molecules, the simulation of diffusion events makes ISSA slow for this model. However, by using the time dependent propensity function in the simulation to avoid sampling of individual diffusion events, we can obtain simulation results at a greatly reduced computational cost.

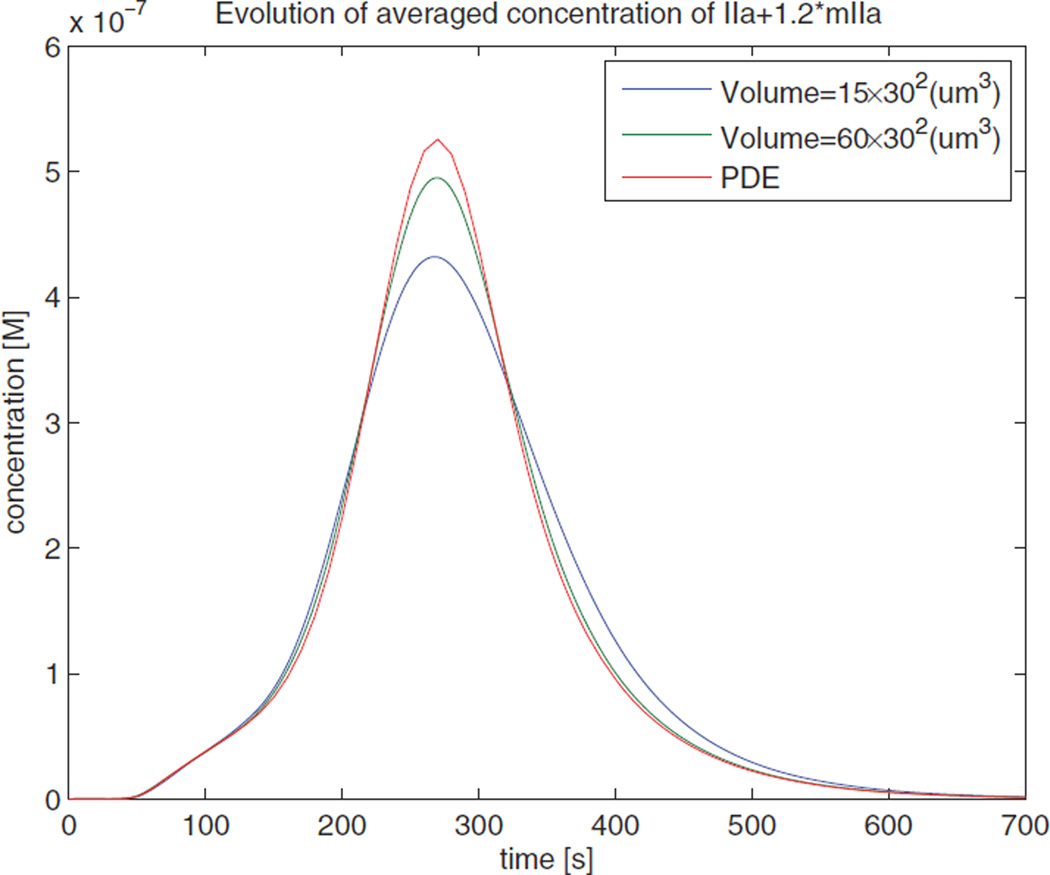
Figure 11 shows the mean values (over space and over all realizations) of the thrombin concentration given by the stochastic simulations and the concentration given by the PDE solution.

Figure 11.

Dynamics of the averaged thrombin concentration for different control volumes. Here IIa is activated thrombin, and mIIa is meizothrombin which is an intermediate that is produced during the conversion of prothrombin to thrombin.

The trend of the curves follows our expectations. It is evident from the figure that when the control volume is small, the peak value of the average thrombin response is low. As the control volume increases, the averaged response is approaching that of the PDE solution. An explanation of the result is the self-propagation of thrombin. Thrombin can accelerate its formation by activating other factors which can form catalysts for thrombin generation. This can also be observed from the PDE curve in Figure 11. (Initially the curve has a small slope; as the concentration of thrombin increases, the slope of the curve increases dramatically). However, in the stochastic model, the situation is more complex.

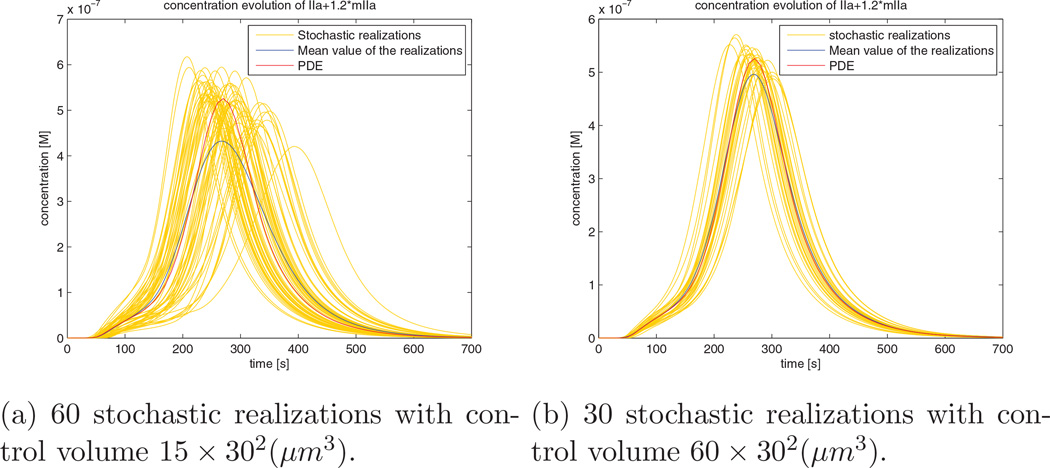
Due to stochastic effects, the initialization time of thrombin response differs among realizations. This can be easily observed if we plot all the trajectory curves. Figure 12a shows that when the control volume is small (15 × 30²µm³), the variation between different realizations can be significant. This variation leads to the fact that the average of the realization curves has a wider bell shape with a lower peak value (the blue curve in Figure 12a) compared with the PDE solution (the red curve in Figure 12a). When we increase the control volume (60 × 30²µm³), as shown in Figure 12b, the variation between realizations becomes smaller. As a result, the bell shape mean response curve becomes narrower and higher (the blue curve in Figure 12b), which more closely matches the PDE curve.

Figure 12.

Stochastic realizations and their averaged responses

5. Conclusion

Spatial stochastic simulation using the time dependent propensity provides a means to accelerate the simulation of systems whose diffusion events overwhelm reaction events. The key point of the method is that it uses the time between adjacent reaction events as the simulation stepsize; individual diffusion events during the step are not tracked. However the effect of the diffusion process is still accounted for by using the time dependent propensity functions for each reaction. Thus the method yields a speedup by avoiding the sampling of the individual diffusion events, while still maintaining excellent accuracy. The idea of the method can also be easily extended for simulations of 2D rectangular regions and 3D cuboid regions.

However, the method still has some limitations.

1. It accelerates the simulation only when the number of diffusion events is much larger than that of the reaction events. When this condition does not hold, the overhead of computing time dependent propensity functions will slow down the simulation compared to an exact method.

2. In the algorithm, a molecule is allowed to diffuse to any subvolume in one step. However in some cases, it is more likely that a molecule walks in a local region as opposed to traversing the whole space during a stepsize. Thus, keeping track of the molecule in a truncated space may greatly decrease the computational cost. As future work, we have designed an algorithm that implements this idea and a general purpose code is now under development.

3. For arbitrary geometry or unstructured meshes, the closed form solution of the probabilities that one molecule jumps from one voxel to another voxel may not be easy to obtain. We may need to use approximation functions (e.g. compute the value at some time points and then do interpolation) in these cases. It might be helpful to store these values so that they can be reused in the simulation.

Appendix A. Solution to the master equation for a one dimensional discrete diffusion process

In this section we derive the probability that a molecule jumps from one voxel to another in a 1D domain. Suppose we discretize a 1D domain into L voxels with reflecting boundary conditions, and that there is a single molecule in the domain. The probability that the molecule jumps to a particular neighbor voxel in the next infinitesimal dt is κdt. Define p_i,j (t) as the probability that the molecule jumps from voxel i to voxel j after a time interval t. Then p_i,j (t) satisfies the following equation

$$p_{i,j}(t+dt)=p_{i,j-1}(t)\kappa dt+p_{i,j+1}(t)\kappa dt+p_{i,j}(t)(1-2\kappa dt)\Rightarrow \frac{d}{dt}{p}_{i,j}(t)=\kappa (p_{i,j-1}(t)+p_{i,j+1}(t)-2p_{i,j}(t)),j=2,\dots ,L-1$$

For j = 1 or j = L we have

$$\frac{d}{dt}{p}_{i,1}(t)=\kappa (p_{i,2}(t)-p_{i,1}),\frac{d}{dt}{p}_{i,L}(t)=\kappa (p_{i,L-1}(t)-p_{i,L}).$$

Rewriting in a more compact form yields

$$\frac{d}{dt}\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill p_{i,2}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L-1}(t)\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right)=\kappa \left(\begin{array}{ccccc}\hfill -1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right)\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill p_{i,2}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L-1}(t)\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right),$$ (A.1)

with initial condition

$$p_{i,j}(0)=\{\begin{array}{cc}1\hfill & i=j\hfill \\ 0\hfill & i\ne j\hfill \end{array}.$$ (A.2)

The eigenvalues of the coefficient matrix in (A.1) are

$${\lambda }_i=2(\text{cos}\frac{i\pi }{L}-1),i=0,\dots ,L-1$$ (A.3)

and the corresponding eigenvectors v_i = (υ_i1, …, υ_iL)^T have elements

$${\upsilon }_{ij}=\text{cos}(\frac{i\pi }{2L}-\frac{ij\pi }{L}),i=0,\dots ,L-1;j=1,\dots ,L.$$ (A.4)

The solution of the ODE (A.1) has the form

$$\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right)=\mathbf{V}\left(\begin{array}{ccc}\hfill e^{\kappa {\lambda }_{0}t}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{\kappa {\lambda }_{L-1}t}\hfill \end{array}\right){\mathbf{V}}^{-1}\left(\begin{array}{c}\hfill p_{i,1}(0)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L}(0)\hfill \end{array}\right),$$ (A.5)

where

$$\mathbf{V}=({\mathbf{v}}_0,\dots ,{\mathbf{v}}_{L-1})$$ (A.6)

is the matrix consisting of the eigenvectors. In the simulation it is convenient to normalize the eigenvectors, in which case V becomes a unit orthogonal matrix and the inverse operation in (A.5) can be replaced by a transpose operation.

Equation (A.5) gives the probability that a molecule jumps from voxel i to voxel j after a time interval t with reflecting boundary conditions. For some other common boundary conditions, the jump probabilities can be expressed similarly. Consider, for example, the case of periodic boundary conditions. Since the first and the last voxels are adjacent, the ODE system for p_ij (t) becomes

$$\frac{d}{dt}\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill p_{i,2}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L-1}(t)\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right)=\kappa \left(\begin{array}{ccccc}\hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill \end{array}\right)\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill p_{i,2}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L-1}(t)\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right).$$ (A.7)

The eigenvalues of the coefficient matrix are

$${\lambda }_i=2\left(\text{cos}\right(\frac{2i\pi }{L})-1),i=0,\dots ,\lfloor \frac{L}{2}\rfloor ,$$ (A.8)

and the corresponding eigenvectors u_i = (u_i1, …, u_iL)^T, v_i = (υ_i1, …, υ_iL)^T for λ_i are

$$u_{ij}=\text{sin}\left(\frac{2ij\pi }{L}\right),i=1,\dots ,\lceil \frac{L}{2}\rceil -1,j=1,\dots ,L,$$

$${\upsilon }_{ij}=\text{cos}\left(\frac{2ij\pi }{L}\right),i=0,\dots ,\lfloor \frac{L}{2}\rfloor ,j=1,\dots ,L,$$ (A.9)

Thus the solution to (A.7) is given by

$$\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right)=\mathbf{V}\left(\begin{array}{cccccc}\hfill e^{\kappa {\lambda }_{0}t}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill e^{\kappa {\lambda }_{1}t}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{\kappa {\lambda }_{1}t}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill e^{\kappa {\lambda }_{2}t}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill e^{\kappa {\lambda }_{2}t}\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill \end{array}\right){\mathbf{V}}^{-1}\left(\begin{array}{c}\hfill p_{i,1}(0)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L}(0)\hfill \end{array}\right),$$ (A.10)

where

$$\mathbf{V}=({\mathbf{v}}_0,{\mathbf{u}}_1,{\mathbf{v}}_1,{\mathbf{u}}_2,{\mathbf{v}}_2,\dots ).$$

In Section 4.3 we need the solution of a diffusion process with absorbing boundary conditions. The ODE system is given by

$$\frac{d}{dt}\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill p_{i,2}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L-1}(t)\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right)=\kappa \left(\begin{array}{ccccc}\hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill \end{array}\right)\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill p_{i,2}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L-1}(t)\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right).$$ (A.11)

The eigenvalues of the coefficient matrix are

$${\lambda }_i=2\left(\text{cos}\right(\frac{i\pi }{L+1})-1),i=1,\dots ,L,$$

and the corresponding eigenvectors v_i = (υ_i1, …, υ_iL)^T for λ_i are

$${\upsilon }_{ij}=\text{sin}\left(\frac{ij\pi }{L+1}\right),i=1,\dots ,L,j=1,\dots ,L.$$

The solution to (A.11) is given by

$$\left(\begin{array}{c}\hfill p_{i,1}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L}(t)\hfill \end{array}\right)=\mathbf{V}\left(\begin{array}{ccc}\hfill e^{\kappa {\lambda }_{1}t}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{\kappa {\lambda }_{L}t}\hfill \end{array}\right){\mathbf{V}}^{-1}\left(\begin{array}{c}\hfill p_{i,1}(0)\hfill \\ \hfill ⋮\hfill \\ \hfill p_{i,L}(0)\hfill \end{array}\right),$$ (A.12)

where

$$\mathbf{V}=({\mathbf{v}}_1,\dots ,{\mathbf{v}}_L).$$

Appendix B. Derivation of the upper bound of E (p(τ))

Let us look at a particular molecule that is a reactant in one or more reactions in the system. We can divide all possible reaction events into two groups ℛ and ℛ̅, where ℛ is the set of possible reaction events in which the observed molecule is involved as a reactant and ℛ̅ the set of possible reaction events that the observed molecule is not involved. Denote by p_r (t) the probability that a reaction event in ℛ occurs before time t, given that no events in ℛ̅ occur before t. We seek an upper bound on the expectation of p_r (τ), where τ is also a random variable which is defined as the time when the first reaction event of the system occurs. In another words, we seek an upper bound for E (p_r (τ)).

Denote by q_r (t) = 1 − p_r (t) the probability that no reaction event in ℛ occurs before t, i.e. the observed molecule does not react before time t, given that no events in ℛ̅ occur before t. To simplify the notation, we denote (𝒰, [t₀, t₁]) as the event that no reaction in 𝒰 occurs during [t₀, t₁] (𝒰 could be ℛ, ℛ̅, etc), thus q_r (t) is equivalent to P ((ℛ, [0, t]) | (ℛ̅, [0, t])), and we have

$$q_r(t+dt)P((\overline{ℛ},[t,t+dt])|(\overline{ℛ},[0,t]))P((\overline{ℛ},[0,t]))=P((ℛ,[0,t+dt])|(\overline{ℛ},[0,t+dt]))P((\overline{ℛ},[0,t+dt]))=P((ℛ\cup \overline{ℛ},[0,t+dt]))=P((ℛ\cup \overline{ℛ},[0,t]))P((ℛ\cup \overline{ℛ},[t,t+dt])|(ℛ\cup \overline{ℛ},[0,t]))=P((ℛ,[0,t])|(\overline{ℛ},[0,t]))P((\overline{ℛ},[0,t]))\times P((ℛ\cup \overline{ℛ},[t,t+dt])|(ℛ\cup \overline{ℛ},[0,t]))=q_r(t)P((\overline{ℛ},[0,t]))P((ℛ\cup \overline{ℛ},[t,t+dt])|(ℛ\cup \overline{ℛ},[0,t])),$$

which implies

$$q_r(t+dt)=q_r(t)\frac{P((ℛ\cup \overline{ℛ},[t,t+dt])|(ℛ\cup \overline{ℛ},[0,t]))}{P((\overline{ℛ},[t,t+dt])|(\overline{ℛ},[0,t]))}.$$ (B.1)

Here the numerator on the right hand side is the probability that no reaction event occurs during [t, t + dt], given that no reaction occurs before t. Thus it equals 1 − a₀(t)dt where a₀(t) is the total propensity of the system at time t given that no reaction occurs before t. Similarly, the denominator equals 1 − a_ℛ̄(t)dt where a_ℛ̄(t) is defined as the propensity of events in ℛ̅ at time t given that no events in ℛ̅ occur before t. Thus (B.1) can be reduced to

$$q_r(t+dt)=q_r(t)\frac{P((ℛ\cup \overline{ℛ},[t,t+dt])|(ℛ\cup \overline{ℛ},[0,t]))}{P((\overline{ℛ},[t,t+dt])|(\overline{ℛ},[0,t]))}=q_r(t)\frac{1-a_0(t)dt}{1-a_{\overline{ℛ}}(t)dt}=q_r(t)(1-a_0(t)dt)(1+a_{\overline{ℛ}}(t)dt+O(d{t}^2))=q_r(t)(1-(a_0(t)-a_{\overline{ℛ}}(t))dt)+O(d{t}^2)\triangleq q_r(t)(1-a(t)dt)+O(d{t}^2).$$ (B.2)

Here a(t) = a₀(t) − a_ℛ̄(t) is the difference between the total propensity and the propensity of the reaction events involving only molecules other than the observed one. Thus it can be considered as the contribution that the observed molecule gives to the total propensity. (B.2) yields an ODE

$$\frac{d}{dt}{q}_r(t)=-q_r(t)a(t)$$

whose solution is

$$q_r(t)=e^{-{\int }_0^{t}a(s)ds}.$$

Thus the probability for the observed molecule to be involved in a reaction event before time t, under the condition that no other reaction event occurs before t, is given by

$$p_r(t)\triangleq 1-q_r(t)=1-e^{-{\int }_0^{t}a(s)ds}.$$ (B.3)

To estimate E (p_r (τ)), it is necessary to find the distribution of τ. Define q (t) to be the probability that the system does not fire a reaction before time t. As a₀ (t) dt is the probability that the system fires a reaction in the infinitesimal [t, t + dt] given that no reaction occurs before t, then we obtain

$$q(t+dt)=q(t)(1-a_0(t)dt)\Rightarrow q(t)=e^{-{\int }_0^t{a}_0(s)ds}$$

$$p(t)\triangleq 1-q(t)=1-e^{-{\int }_0^t{a}_0(s)ds},$$

where p (t) is the probability that the system fires the first reaction before t.

Now we can estimate E (p_r (τ)) as

$$\mathrm{E}(p_r(\tau ))={\int }_0^{\infty }{p}_r(t)dp(t)=p_r(0)+{\int }_0^{\infty }{p}_r^{\prime }(t)(1-p(t))dt={\int }_0^{\infty }a(t)e^{-{\int }_0^t(a(s)+a_0(s))ds}dt={\int }_0^{\infty }\frac{a(t)}{a(t)+a_0(t)}(a(t)+a_0(t))e^{-{\int }_0^t(a(s)+a_0(s))ds}dt\le \underset{t>0}{\text{max}}\frac{a(t)}{a(t)+a_0(t)}{\int }_0^{\infty }{e}^{-{\int }_0^t(a(s)+a_0(s))ds}(a(t)+a_0(t))dt=\underset{t>0}{\text{max}}\frac{a(t)}{a(t)+a_0(t)}{e^{-{\int }_0^t(a(s)+a_0(s))ds}|}_{\infty }^0=\underset{t>0}{\text{max}}\frac{a(t)}{a(t)+a_0(t)}=\frac{1}{1+{\text{min}}_{t>0}\frac{a_0(t)}{a(t)}}.$$ (B.4)

Here the second equality uses integration by parts. Equation (B.4) shows that an upper bound of E (p_r (τ)) is determined by the ratio of the total propensity of the system and the propensity contributed by the observed molecule. E (p_r (τ)) will be a small value when the ratio is large. It is worth mentioning that this value cannot be controlled by decreasing the “stepsize”. This is because the stepsize of this simulation is the time to the next chemical reaction event, which is determined by the behavior of the system rather than a value that can be manipulated at will.

Appendix C. A discussion about the probability that a molecule diffuses to a given subvolume

Suppose we have two one dimensional systems, system 1 and system 2, with reflecting boundary conditions. The two systems are initially identical except that molecules in system 2 are inert, thus that system is simply governed by a diffusion process. Let us look at two molecules of the same species that initially are at the same position but in the different systems. For the observed molecule in system 1, let ℛ be the set of possible reaction events in which the observed molecule is involved as a reactant and ℛ̅ be the set of possible reaction events in which the observed molecule is not involved. Suppose the two molecules are initially in voxel i. Define p̂_i,j (t) as the probability that the molecule in system 1 diffuses to voxel j at time t, under the condition that no event in ℛ̅ occurs before t, and p_i,j (t) the probability of the same event for the molecule in system 2. The purpose of this section is to show that p̂_i,j (t) ≤ p_i,j (t).

Intuitively it is obvious that p̂_i,j (t) ≤ p_i,j (t) because in system 1 the fact that the molecule been observed in voxel j at time t means that it not only has diffused to voxel j but also survived (from reaction) up to time t, thus the probability should be smaller that the value given by system 2 in which the molecules always survive. Here we provide a more rigorous proof of that fact.

Denote the probability that the molecule jumps to a particular neighbor voxel in a infinitesimal dt by κdt. Then in system 2, the diffusion process gives the equation (A.1) with initial condition (A.2). However for system 1 which includes reactions, p̂_i,j (t) satisfies

$${\hat{p}}_{i,j}(t+dt)={\hat{p}}_{i,j-1}(t)\kappa dt+{\hat{p}}_{i,j+1}(t)\kappa dt+{\hat{p}}_{i,j}(t)(1-2\kappa dt-a_j(t)dt)\Rightarrow \frac{d}{dt}{\hat{p}}_{i,j}(t)=\kappa ({\hat{p}}_{i,j-1}(t)+{\hat{p}}_{i,j+1}(t)-2{\hat{p}}_{i,j}(t))-a_j(t){\hat{p}}_{i,j}(t),$$

where a_j (t) is the propensity contributed by the molecule, which is defined as a_j (t) = a₀(j, t) − a_ℛ̄(t) where a₀(j, t) is the total propensity of the system at time t given that no reaction occurs before t and the observed molecule is in voxel j at time t, and a_R̄ (t) is the total propensity of events in ℛ̅ at time t given that no event in ℛ̅ occurs before t. Denoting b_j (t) = a_j (t) p̂_i,j (t), then p̂_i,j (t) satisfies

$$\frac{d}{dt}\left(\begin{array}{c}\hfill {\hat{p}}_{i,1}(t)\hfill \\ \hfill {\hat{p}}_{i,2}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill {\hat{p}}_{i,L-1}(t)\hfill \\ \hfill {\hat{p}}_{i,L}(t)\hfill \end{array}\right)=\kappa \left(\begin{array}{ccccc}\hfill -1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\hat{p}}_{i,1}(t)\hfill \\ \hfill {\hat{p}}_{i,2}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill {\hat{p}}_{i,L-1}(t)\hfill \\ \hfill {\hat{p}}_{i,L}(t)\hfill \end{array}\right)-\left(\begin{array}{c}\hfill b_1(t)\hfill \\ \hfill b_2(t)\hfill \\ \hfill ⋮\hfill \\ \hfill b_{L-1}(t)\hfill \\ \hfill b_L(t)\hfill \end{array}\right)$$ (C.1)

with the same initial condition as in (A.2)

$${\hat{p}}_{i,j}(0)=\{\begin{array}{cc}\hfill 1\hfill & \hfill i=j\hfill \\ \hfill 0\hfill & \hfill i\ne j\hfill \end{array}.$$

Let Δp_i,j (t) = p_i,j (t) − p̂_i,j (t). From (A.1) and (C.1) we obtain

$$\frac{d}{dt}\left(\begin{array}{c}\hfill \mathrm{\Delta }{p}_{i,1}\hfill \\ \hfill \mathrm{\Delta }{p}_{i,2}\hfill \\ \hfill ⋮\hfill \\ \hfill \mathrm{\Delta }{p}_{i,L-1}\hfill \\ \hfill \mathrm{\Delta }{p}_{i,L}\hfill \end{array}\right)=\kappa \left(\begin{array}{ccccc}\hfill -1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathrm{\Delta }{p}_{i,1}\hfill \\ \hfill \mathrm{\Delta }{p}_{i,2}\hfill \\ \hfill ⋮\hfill \\ \hfill \mathrm{\Delta }{p}_{i,L-1}\hfill \\ \hfill \mathrm{\Delta }{p}_{i,L}\hfill \end{array}\right)+\left(\begin{array}{c}\hfill b_1(t)\hfill \\ \hfill b_2(t)\hfill \\ \hfill ⋮\hfill \\ \hfill b_{L-1}(t)\hfill \\ \hfill b_L(t)\hfill \end{array}\right),$$ (C.2)

with initial condition Δp_i,j = 0, j = 1, …, L.

The solution of (C.2) has the form

$$\left(\begin{array}{c}\hfill \mathrm{\Delta }{p}_{i,1}(t)\hfill \\ \hfill ⋮\hfill \\ \hfill \mathrm{\Delta }{p}_{i,L}(t)\hfill \end{array}\right)={\int }_0^t\mathbf{V}\left(\begin{array}{ccc}\hfill e^{\kappa {\lambda }_0(t-s)}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{\kappa {\lambda }_{L-1}(t-s)}\hfill \end{array}\right){\mathbf{V}}^{-1}\left(\begin{array}{c}\hfill b_1(s)\hfill \\ \hfill ⋮\hfill \\ \hfill b_L(s)\hfill \end{array}\right)ds,$$ (C.3)

where λ_i is defined as (A.3) and V is defined as (A.6).

From (A.5) we can see that for any vector p (0) = (p₁(0), …, p_L (0)) whose elements are nonnegative, the following operation:

$$\mathbf{V}\left(\begin{array}{ccc}\hfill e^{\kappa {\lambda }_{0}t}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill e^{\kappa {\lambda }_{L-1}t}\hfill \end{array}\right){\mathbf{V}}^{-1}\left(\begin{array}{c}\hfill p_1(0)\hfill \\ \hfill ⋮\hfill \\ \hfill p_L(0)\hfill \end{array}\right)$$

returns a vector (p₁ (t), …, p_L (t))^T which is also non-negative (every element in the vector is a probability value thus it should be non-negative). Now apply this observation to (C.3). Since b_j (s) = a_j (s) p̂_i,j (s) ≥ 0, it is evident that the overall expression in the integral in (C.3) is also nonnegative. Therefore the result (Δp_i,1, …, Δp_i,L)^T is nonnegative as well, which implies Δp_i,j (t) = p_i,j (t) − p̂_i,j (t) ≥ 0.