Unusual Dynamics of Concentration Fluctuations in Solutions of Weakly Attractive Globular Proteins

Abstract

The globular protein γ_B-crystallin exhibits a complex phase behavior, where liquid–liquid phase separation characterized by a critical volume fraction ϕ_c = 0.154 and a critical temperature T_c = 291.8 K coexists with dynamical arrest on all length scales at volume fractions around ϕ ≈ 0.3–0.35, and an arrest line that extends well into the unstable region below the spinodal. However, although the static properties such as the osmotic compressibility and the static correlation length are in quantitative agreement with predictions for binary liquid mixtures, this is not the case for the dynamics of concentration fluctuations described by the dynamic structure factor S(q,t). Using a combination of dynamic light scattering and neutron spin echo measurements, we demonstrate that the competition between critical slowing down and dynamical arrest results in a much more complex wave vector dependence of S(q,t) than previously anticipated.

Over the past years, an increasing effort has been made to describe transitions between liquid- and solid-like states in colloidal dispersions, and experimental, theoretical, and simulation studies of systems with different interparticle interactions have been reported.¹⁻⁵ The majority of studies have focused on two extreme cases, the occurrence of a hard sphere glass transition at very high densities and the formation of colloidal gels as a result of irreversible aggregation due to strong interparticle attractions.⁶ For colloids with short-range attractions, these two regimes are connected by an arrest line whose location has been investigated primarily by mode coupling theories and computer simulations.⁷⁻¹³ A generic state diagram has been developed that also highlights a possible competition between liquid–liquid phase separation and dynamical arrest,^6,14 which can lead to the phenomenon of an arrested spinodal decomposition. This scenario has been supported by a number of observations in systems as diverse as synthetic and food colloids, emulsions, or small globular proteins.¹⁴⁻¹⁹ A particularly interesting feature of such systems is that, depending on the actual shape of the interaction potential, the arrest line can intersect the (metastable) binodal close to the critical point, that is, in a region where critical fluctuations are still detectable. This leads to an intriguing competition of two mechanisms that both cause a slowing down of dynamical processes: critical slowing down and dynamical arrest. We expect both to act on different length scales, but there is currently no information available on the resulting relaxation time spectra seen for example in the dynamic structure factor S(q,t) probed by dynamic light scattering (DLS) and other quasielastic scattering techniques, such as neutron spin echo (NSE).

Globular proteins have already been used as model systems to study critical phenomena in particle systems.²⁰⁻²² However, the majority of studies have focused on phase diagrams and the behavior of the osmotic compressibility κ_T and the static correlation length ξ_s, and the information on dynamic properties is limited. A notable exception is the work of Fine et al.,²² where DLS has been employed to study the influence of critical phenomena on the collective dynamics of protein solutions. They demonstrated that the decay rate of concentration fluctuations was consistent with the theory for critical dynamics in binary liquids but also noted that an unusually large background contribution had to be assumed to achieve quantitative agreement with theory. However, at that time, the possible existence of an arrest line and its influence on the dynamics had not yet been recognized.

Here, we now address the possible competition between critical slowing down and dynamical arrest in the vicinity of a critical point for particles with short-range attractive potentials. We combine DLS with NSE, a technique accessing dynamics on a range of length scales down to the order of the protein size, thus allowing to disentangle the effects of critical slowing down and dynamical arrest in concentrated protein solutions. We focus on the globular eye lens protein γ_B-crystallin, which has a molecular mass of around 21 kDa and a diameter of about 3.6 nm. The static properties of γ_B-crystallin solutions have been studied intensively in the past, primarily in the context of cataract formation, and are well described by a model of colloidal particles interacting via a short-range attractive potential.^21,23−25

Following the approach of Cardinaux et al.,¹⁷ we first established the state diagram of γ_B-crystallin as a function of the volume fraction ϕ shown in Figure 1. The coexistence curve (binodal) for liquid–liquid phase separation was determined using cloud point measurements²⁶ (fuchsia □) and shallow quenches to temperatures T just below the critical temperature T_c followed by macroscopic phase separation (fuchsia △).²⁷ The spinodal was obtained from static light scattering (SLS) measurements (blue ○).²⁰ We find a critical volume fraction ϕ_c = 0.154 and T_c = 291.8 K. For quenches below 285 K, the solutions undergo a liquid–amorphous solid transition as a result of a spinodal decomposition that eventually becomes arrested when the dense phase forms a space-spanning network, in agreement with the results reported for lysozyme, another globular protein with short-range attractive interactions.¹⁷ The arrest line below the binodal/spinodal (◊) was located by performing temperature quenches deep into the unstable region of the state diagram, followed by centrifugation to separate the solid-like dense from the dilute liquid phase.¹⁷ Additionally, DLS measurements reveal a sharp temperature-independent transition from ergodic (green *) to nonergodic (×) behavior of the protein solutions at a volume fraction ϕ_arr = 0.34 as shown in Figure S3, allowing us to extend the glass line well beyond the binodal. The glass fluidizes on dilution, showing that this arrest transition is a reversible process and not caused by irreversible aggregation and gelation.

Figure 1.

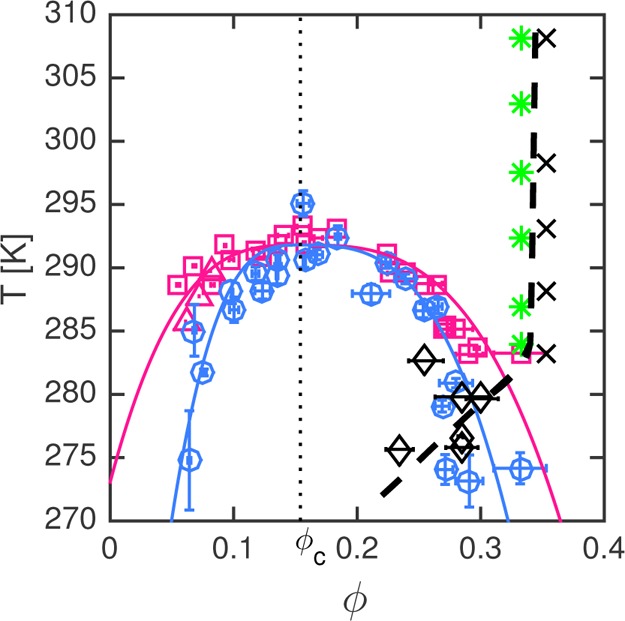
State diagram of γ_B-crystallin in D₂O. Shown are the binodal (fuchsia □, cloud point measurements; fuchsia △, shallow quenches) and the spinodal (blue ○) and the corresponding fits (T = T_c·[1 – A·(|ϕ – ϕ_c|/ϕ_c)^(1/β)], with β = 0.33; binodal, A = 0.065 and 0.029; spinodal, A = 0.248 and 0.057), as well as the arrest line (dashed line) as a function of ϕ. The location of the latter was determined by a combination of deep quenches (◊) and DLS data (green *, ergodic; ×, nonergodic). ϕ_c is marked by the dotted line.

We subsequently used a combination of small-angle X-ray scattering (SAXS) and SLS to investigate the static structure factor S(q) as a measure of structural correlations on different length scales. Here we concentrate on length scales significantly larger than the protein size, that is, on q ≪ 2π/d, where d ≈ 4 nm is the protein diameter. Under these conditions, the total scattering of the proteins S(q,T,ϕ) can be separated into a noncritical background S_noncrit(ϕ) (accounting for the athermal excluded volume interactions) and a strongly temperature-dependent critical component S_crit(q,T,ϕ) that dominates in the vicinity of T_c or the spinodal temperature (T_sp).

The q dependence of S_crit(q) = S_crit(0)/(1 + q²ξ_s²) is given by the Ornstein–Zernike (OZ) equation, where S_crit(0) is related to the osmotic compressibility and ξ_s is the static correlation length as a measure of the characteristic size of density fluctuations caused by critical phenomena, and all relevant structural properties are in quantitative agreement with predictions for critical phenomena in simple binary mixtures (see Supporting Information for details). As both S_crit(0) and ξ_s diverge at T_c and T_sp and given the shape of the spinodal (Figure 1), we therefore also expect them to exhibit a maximum around ϕ_c for a given temperature, which is indeed observed experimentally (Figure 2a,b). We can quantitatively reproduce the experimentally determined T and ϕ dependence of S(0) of γ_B-crystallin solutions using a model of hard ellipsoidal particles interacting via a square-well potential with range Δ = 0.6 nm (Figure 2a, see Supporting Information for more details), providing further evidence that S(0) is indeed closely related to the existence of a critical point.

Figure 2.

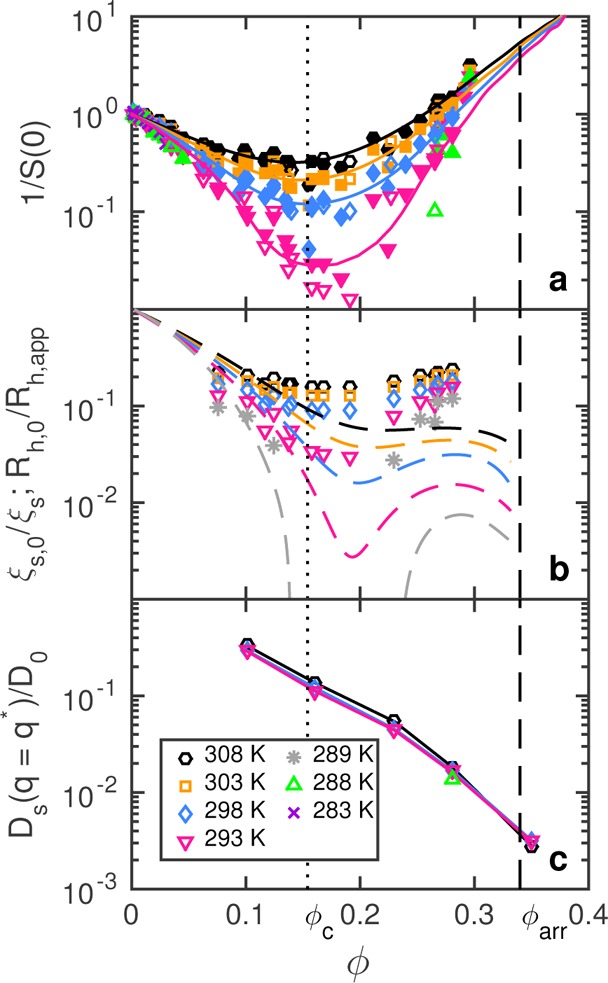
(a) Inverse S(0) from SLS (filled symbols) and SAXS (open symbols) versus ϕ at different T and the corresponding model fits (full lines). (b) Inverse normalized correlation length versus ϕ as a function of T. Symbols, inverse static correlation length (from SAXS); dashed lines, inverse dynamic correlation length (actual data points shown in Supporting Information Figure S2). (c) Normalized short-time diffusion coefficient from NSE versus ϕ as a function of T. The dotted line marks ϕ_c, whereas the dashed line indicates the location of the macroscopic arrest line ϕ_arr (cf. Figure 1).

Having verified that the static properties of the protein solutions are quantitatively captured by a simple coarse-grained model of short-range attractive particles, we next proceed to a characterization of their dynamic properties. Here, we use DLS, which provides a measure of the dynamics of concentration fluctuations on length scales of order 2π/q. We concentrate on the analysis of the initial decay of the measured correlation or intermediate scattering function (ISF) f(q,t), assuming an exponential decay f(q,t) = exp[−2Γ(q)t], where Γ(q) describes the temporal decay of the ISF at the given q value. For fluid-like protein solutions, where dq ≪ 1 and particle motion is diffusive, we thus obtain the collective diffusion coefficient D_c = Γ(q)/q². This allows us to define a dynamic correlation length ξ_d or apparent hydrodynamic radius R_h,app (where ξ_d ≡ R_h,app) through the Stokes–Einstein relation D_c= k_BT/[6πη(T)R_h,app], where k_B is the Boltzmann constant and η(T) the T dependent solvent viscosity. In order to directly compare R_h,app with the corresponding static properties S(0) and ξ_s (Figure 2a,b and Supporting Information Figure S2), we use a normalized quantity D_c/D₀, where D₀ = k_BT/[6πη(T)R_h,0] is the free diffusion coefficient of a noninteracting γ_B-crystallin with R_h,0 = 2.27 nm. Note that D_c/D₀ = R_h,0/R_h,app retains only the T dependence of the apparent hydrodynamic radius.

For simple binary liquids in the vicinity of the critical point or the spinodal line, ξ_d mirrors the behavior of ξ_s and is completely dominated by critical concentration fluctuations. This is obviously not the case for our protein solutions. Here the T dependence of the rescaled dynamic correlation length R_h,0/R_h,app (Figure 2b) shows significant differences to the thermodynamic or static correlation length ξ_s,0/ξ_s, especially at small and large ϕ. Note that R_h,0 is defined as the ϕ → 0 value of R_h,app, while ξ_s,0 is the prefactor appearing in the T dependence of ξ_s, according to ξ_s(T,ϕ) = ξ_s,0(1 – T/T_sp(ϕ))^−ν, where T_sp is the spinodal T and ν the Ising critical exponent (see Supporting Information for more details). Although this explains the differences between the static and the dynamic correlation lengths at small ϕ, the increase of the dynamic correlation length in Figure 2b at large ϕ is due to the (noncritical) slowing down of dynamics as a result of short-ranged interactions, just like for inherently noncritical hard-core systems at higher packing fractions.

This interplay between critical slowing down and dynamical arrest is also reflected in the DLS correlation functions (Figure 3). Here, it is noteworthy to point out the difference to the previously published DLS data from Fine et al.,²² where the authors found correlation functions that were not single exponential. We believe that this is likely due to contributions from multiple scattering, which are completely suppressed in our case due to the use of a 3D cross-correlation scheme for DLS experiments. At ϕ ≈ ϕ_c (Figure 3a), the structural relaxations exhibit the typical exponential decay of a conventional ergodic liquid. Lowering T, that is, approaching criticality, leads to a slowing down of the system dynamics due to critical slowing down, whereas the decay remains exponential. Upon approaching the arrest line at large ϕ (Figure 3b,c), these relaxations become increasingly stretched out and result in a logarithmic, rather than exponential, decay of the ISF. Moreover, a shoulder at long times emerges in the vicinity of the dynamic arrest line that most likely is related to the formation and decay of a transient network driven by temporary bonds induced by the short-range attractions. This second decay is most pronounced close to the glass line but far away from the spinodal, that is, for large ϕ and high T (first two data sets in Figure 3c). However, simultaneously approaching both the spinodal and the glass line results in the previously described logarithmic decay over a range of at least 2 orders of magnitude (last data set in Figure 3c).

Figure 3.

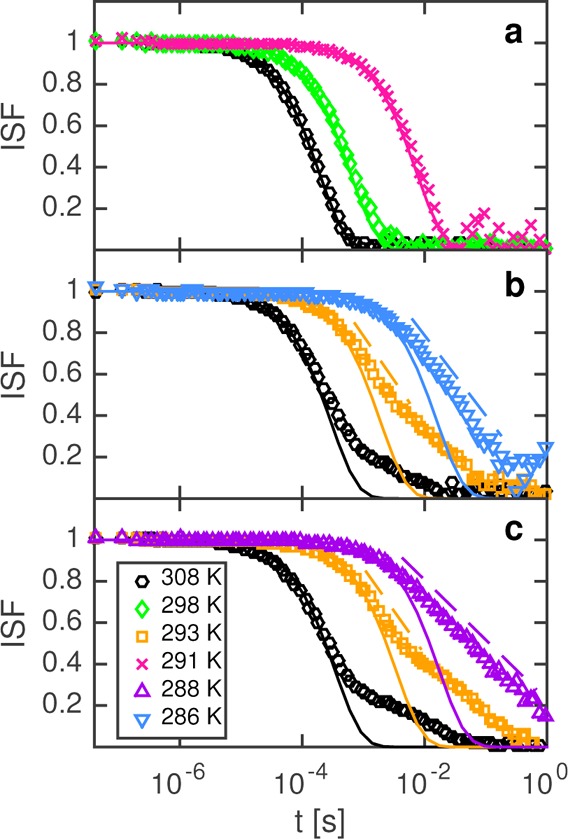
ISFs (symbols) as a function of T for ϕ = (a) 0.157, (b) 0.269, and (c) 0.332 and the corresponding single exponential (full lines) decay fits at θ = 90°, that is, q = 0.0022 Å^–1. Also shown is the logarithmic decay as the dashed lines (offset from actual data for clarity).

These findings are reminiscent of the dynamics near higher-order glass-transition singularities.^2,7,28,29 There, the predicted and observed logarithmic time dependence of the correlation functions is attributed to the interplay between two different arrest scenarios for ϕ ≈ 0.6: caging of particles by their nearest neighbors (repulsion-driven glass) and temporary bonding between the particles (attraction-driven glass). However, despite the evident similarities, there are two major differences between this ”multiple glassy state” system and our concentrated γ_B-crystallin solutions: (1) We find dynamical arrest at much smaller ϕ (around 0.3–0.35, depending on T), where caging due to the hard core repulsion is negligible. (2) The vicinity of the spinodal leads to large-scale concentration fluctuations, strongly affecting the observed collective dynamics. It is thus rather the combination of critical fluctuations at quite large length scales and a true macroscopic arrest that leads to the logarithmic decay of the DLS correlation functions, once critical slowing down has pushed the former process close to the time scale of the attraction-driven bonding processes.

These two effects can be further disentangled with a systematic investigation of the short-time dynamics of γ_B-crystallin solutions on length scales comparable to the nearest-neighbor distance of the proteins. NSE experiments performed at the corresponding q = q* = 0.2 Å^–1 give us access to the local protein short-time diffusion, unaffected by the critical behavior that appears in the DLS data. The effective short-time diffusion coefficients D_s(q) can be extracted from single-exponential decay fits to the initial short-time decay of these ISFs (see Figure S4 in Supporting Information).

Figure 2c shows that the normalized D_s(q = q*)/D₀ (probing the local dynamics over length scales of a protein) is entirely unaffected by large-scale fluctuations around ϕ_c. It also shows that while D_s(q = q*)/D₀ decreases by 2 orders of magnitude upon approaching the arrest line, dynamics on these short length and time scales do not completely arrest, similar to previous observations in hard sphere glasses or dense particle gels,^29,30 quite in contrast to arrest on macroscopic length scales as probed by DLS (Figure 1 and Supporting Information Figure S3). Moreover, D_s(q = q*)/D₀ barely changes with temperature, in agreement with the nearly vertical continuation of the glass line outside of the 2-phase region of the state diagram (Figure 1).

In summary, the static properties of γ_B-crystallin solutions are well described by a coarse-grained model of ellipsoids with a weak square-well attraction. The T and ϕ dependence of the low-q limit of the static structure factor is quantitatively reproduced by a combination of a critical component given by a simple OZ equation, where the parameters follow universal scaling laws for critical phenomena in binary mixtures, and an additional T-independent background contribution that corresponds to the athermal limit due to hard sphere interactions. However, the corresponding dynamic structure factor is much more complex. We observe a rich T and ϕ dependence caused by competing contributions from critical slowing down and dynamical arrest. This results in strongly differing decay scenarios for the ISF at different wave vectors, which can be clearly seen when using a combination of DLS and NSE.

There remain, however, a number of intriguing findings that warrant future investigations. The comparison between the static and dynamic properties (Figure 2) clearly indicates that although the decay of large-scale concentration fluctuations is strongly influenced by critical slowing down and qualitatively follows the static correlation length, this decay is superimposed on a large noncritical background contribution. It is important to understand the origin of this contribution, possibly linked to the presence of an arrest line at quite low values of ϕ. However, we currently lack models that are capable of quantitatively reproducing our data. The relatively low values of ϕ_c and ϕ_arr and the evidence for the formation of transient network structures seen in DLS furthermore indicate that we may need to consider the influence of patchiness, both on the state diagram as well as on the dynamic properties.¹² We believe that these findings are not only relevant for our fundamental understanding of dynamic processes in attractive colloids but may also have implications for the properties of the eye lens. A recent study has demonstrated the existence of a hard sphere-like glass transition in α-crystallin solutions, another major eye lens protein, and has pointed out the importance of various arrest scenarios in dense eye lens protein solutions for cataract and presbyopia.³¹ Our study has now demonstrated that for γ_B-crystallin solutions such liquid–solid transitions can occur already at much lower volume fractions and lead to dramatic changes in the decay of concentration fluctuations responsible for light scattering.

Experimental Methods

Bovine γ_B-crystallin was purified from calf lenses, obtained fresh as a byproduct from a local slaughterhouse, following the method described by Thurston²⁷ (using Superdex 200 prep grade instead of Sephacryl S-200 high resolution for the size-exclusion chromatography). Concentration, determined by UV absorption spectroscopy,²⁷ was converted to volume fraction ϕ using ϕ = c·v, where v = 0.7 mL/g is the protein voluminosity.²¹

LS experiments and transmission measurements were performed on either a home-built multiangle instrument³² or a commercial goniometer system (3D LS Spectrometer, LS Instruments AG), both implementing the so-called 3D cross-correlation technique to suppress contributions from multiple scattering, essential for measurements in the vicinity of a critical point or spinodal line.³³ The q range covered by LS is 0.001–0.003 Å^–1, where the scattering vector q = [4πn(sin (θ/2))]/λ depends on the scattering angle θ, the refractive index n of the solution, and the wavelength λ.

SAXS measurements were performed on a pinhole camera (Ganesha 300 XL, SAXSLAB) covering a q range from 0.003 to 2.5 Å^–1. Dividing the concentration-normalized scattering intensity I(q)/c of a concentrated sample by that of a dilute sample yields the structure factor S(q).

NSE experiments were carried out on IN15 at ILL probing a q range from 0.01 to 0.23 Å^–1 and a Fourier time range between 0.03 and 600 ns. In this Letter, for the analysis of the NSE data, we focus on measurements performed at q = q* = 0.2 Å^–1, where q* closely corresponds to the nearest-neighbor peak in the structure factor of γ_B-crystallin solutions.

Computational Methods

The theoretical isothermal compressibility plots in Figure 2a have been obtained for a monodisperse system of hard ellipsoids (HE, semiaxes a = 2.75 nm, b = 1.625 nm, and c = 1.375 nm), complemented with a square-well (SW) potential, using successive umbrella sampling (SUS) Monte Carlo (MC) simulations.³⁴

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.5b02092.

• Details of sample preparation and the experimental and computational methods. (PDF)

The authors declare no competing financial interest.