An analysis of ozone damage to historical maize and soybean yields in the United States

Significance

Although it has long been known that ground-level ozone (O₃) damages crops and reduces yield, there has never been an estimate of the total loss attributed to ambient O₃ for field-grown maize and soybean in the United States. Knowing the loss caused by this pollutant would be useful for projecting food supply and setting regulatory standards for pollutant emissions. Here we show that ambient O₃ has reduced maize and soybean yields in rain-fed fields by ∼10% and 5%, respectively, based on historical observations from the past 31 y. Results suggest that air-quality regulations in the United States have been effective in reducing crop production losses to O₃, and indicate that further reductions in ground-level [O₃] would be beneficial in the United States and globally.

Abstract

Numerous controlled experiments find that elevated ground-level ozone concentrations ([O₃]) damage crops and reduce yield. There have been no estimates of the actual yield losses in the field in the United States from [O₃], even though such estimates would be valuable for projections of future food production and for cost–benefit analyses of reducing ground-level [O₃]. Regression analysis of historical yield, climate, and [O₃] data for the United States were used to determine the loss of production due to O₃ for maize (Zea mays) and soybean (Glycine max) from 1980 to 2011, showing that over that period production of rain-fed fields of soybean and maize were reduced by roughly 5% and 10%, respectively, costing approximately $9 billion annually. Maize, thought to be inherently resistant to O₃, was at least as sensitive as soybean to O₃ damage. Overcoming this yield loss with improved emission controls or more tolerant germplasm could substantially increase world food and feed supply at a time when a global yield jump is urgently needed.

The United States accounts for over one-third of global maize production and almost one-third of soybean production. It is also the largest exporter of both commodities (1). Numerous controlled environment and field studies have shown that current ozone concentrations ([O₃]) are damaging to the yields of both crops (synthesized by refs. 2 and 3), although soybean is reportedly more sensitive than maize, based on manipulative dose–response experiments (2). This has important implications for current crop production considering that ground-level [O₃] during the Northern Hemisphere growing seasons frequently exceed 40 ppb (4), the threshold concentration for a cumulative exposure index used in Europe, as well as the concentration above which prolonged exposure leads to significant crop yield loss (5, 6). Globally, [O₃] is projected to increase over this century if current high emissions continue (7). Although crop loss from O₃ has been estimated by extrapolating from experimental data to field conditions (8), until recently it has not been possible to quantitatively define crop loss due to O₃ pollution from actual yield data across the major US growing region.

Ozone causes damage by entering leaf intercellular air spaces via stomata, where it reacts with compounds in the exposed wet cell-wall surfaces, causing the production of damaging radicals and signaling that accelerates senescence (9, 10). It also causes chain reactions, creating other reactive oxygen species, which can cause further damage, and large doses of O₃ can induce programmed cell death (11). Because the route of entry is through the stomata, O₃ damage is dependent on stomatal conductance, which is itself dependent on environmental conditions such as water availability. As such, O₃ damage is strongly dependent on environmental conditions and physiological plant properties that affect stomatal conductance. This has led to the expectation that O₃ damage will be less for C₄ species such as maize, given their intrinsically lower stomatal conductance, as well as for plants under drought stress, and in response to rising [CO₂] (9, 12).

Estimating the loss of crop production from ground-level O₃ is valuable for understanding the potential benefits of reducing [O₃] and for projecting future food supply (13). Even though manipulative experiments clearly indicate that elevated [O₃] reduces soybean yields, and to a lesser extent maize yields (2), deriving field-level estimates using data from experimental studies is problematic. The environmental conditions of controlled environment studies represent only a small range of the conditions experienced by crops in fields, and because of the interactions between the effects of [O₃] and microclimate, extrapolating from controlled environment experiments to open-air field conditions is uncertain (14). The few field studies that have been conducted were done at a limited number of locations and with a limited number of genotypes. Dose–response functions created from such studies do not account for the interactions between environment and O₃ damage described above, potentially making extrapolation of losses to entire growing regions unreliable. Multivariable models that include environmental variables as well as [O₃] can account for these interactions, providing better estimates of O₃ damage.

As an alternative to manipulative experiments, studies have used long-term datasets to examine the effects of temperature, precipitation, and [CO₂] on crop yield (15, 16). Ground-level [O₃] has been monitored widely in the United States for the past 30 y, and coupled with long-term county yield records, there is a new opportunity to determine the effect of [O₃] on yields by quantifying the covariance between [O₃] and yield. Using historical [O₃] and yield records requires an accounting of variation in the numerous other factors that affect yield (13, 16, 17). However, this approach has the substantial advantage of allowing for estimation of effects over most of the US growing region, given simultaneous records of surface [O₃]. Furthermore, because these estimates are independent of experimental studies, they provide a separate test and quantification of the damaging effects of O₃ on crop yields.

In this study, we use [O₃] data from the Environmental Protection Agency (EPA) coupled with crop yield data from the National Agriculture Statistics Service and climate data from the Climate Research Unit to estimate production loss of maize and soybean in the United States over the past 30 y by creating a statistical model that accounts for climate, [O₃] and improvements in agronomy, with the objective of estimating production losses of these two crops due to ground-level [O₃]. Results show that from 1980 to 2011 O₃ has reduced maize yields by 10% and soybean by 5%. On a relative basis, both crops are more sensitive to [O₃] in extreme temperatures and dry conditions, and maize is more sensitive to [O₃] than soybean.

Results

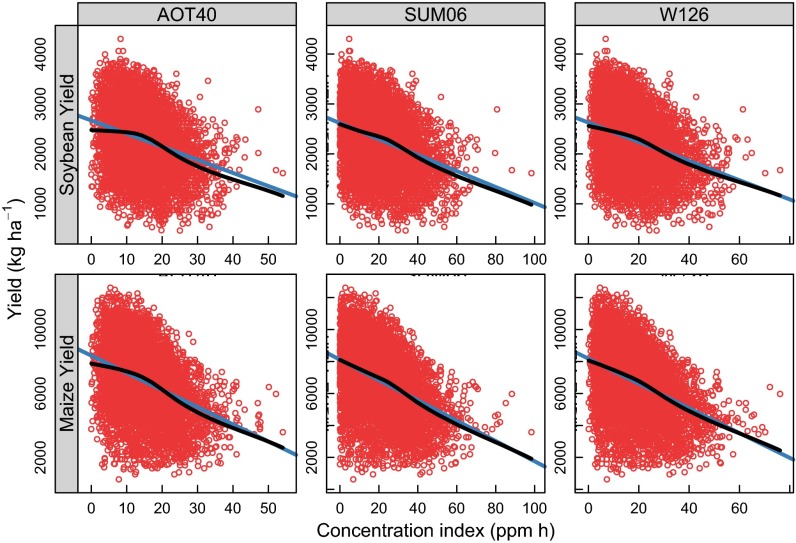
Hourly [O₃] data from 2,700 sites across the United States obtained from the EPA were used to calculate values of three well-established cumulative indices of [O₃]: AOT40, SUM06, and W126 (18). Each of these is a cumulative metric that increases with both duration and dose of O₃ exposure. AOT40 is the sum of hourly [O₃] that are greater than 40 ppb. SUM06 is the sum of hourly concentrations that are greater than 60 ppb, and W126 is the sum of hourly concentrations weighted by a sigmoidal function, such that higher concentrations are given more weight (details are given in Materials and Methods). In each metric, lower [O₃] values are given less weight, which accounts for the observation that doses of low [O₃] over long periods are less damaging to plants than short, high [O₃] doses. All three indices were correlated to yield and showed similar results from which the same conclusions could be drawn (Fig. S1). However, only results for W126 are reported in the main text because the response of yield to W126 was the most linear for both maize and soybean across the entire range of values (Fig. S1), potentially making it the most sensitive index (18), especially at low [O₃].

Fig. S1.

Yield vs. three different O₃ indices for maize and soybean across all locations and times. Points are observations at each site and time. A LOESS fit is shown in black, and a linear fit is shown in blue. The yield response is similar regardless of the index but is closer to linear for W126. The responses in these panels include only the three indices but do not include any of the other effects in Eq. 1. Thus, they do not give a comprehensive view of yield response to [O₃].

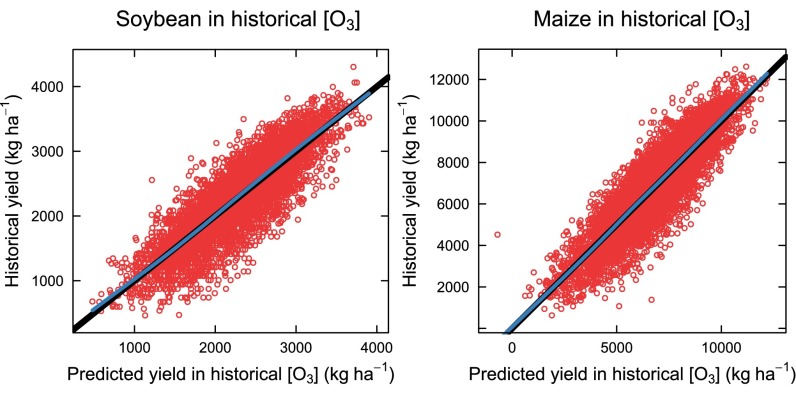
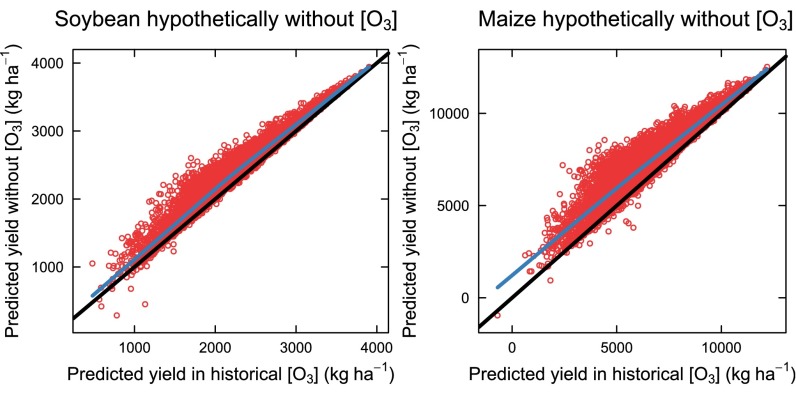
Precipitation over potential evapotranspiration (P/PET), which is a measure of water availability, maximum temperature (T_max), and, in turn, each of AOT40, SUM06, and W126 were used in a linear regression model to determine their effects on yield of soybean and maize. The model was used to predict yield in two conditions: (i) using historical, observed [O₃] indices and (ii) a hypothetical situation assuming no ground-level O₃. The models for soybean and maize accurately predicted historical yields (Fig. S2) and, as expected, predicted higher yields at zero W126 than yields predicted with historical W126 (Fig. S3). The type III sums of squares indicated that the effects of W126, W126*T_max, and W126*T_max² were significant for both soybean and maize, and the W126*(P/PET) and W126*(P/PET)² terms were significant for soybean (Tables 1 and 2), suggesting that even after accounting for other environmental effects, the effect of O₃ still explained a significant proportion of variation in the historical data, and that the response to [O₃] depended on growing season temperature and water status of the crop. Results were similar when using AOT40 or SUM06 (Tables S1 and S2).

Fig. S2.

Measured yields of soybean and maize plotted against yield predicted from the model (Eq. 4) using historical W126 and climate data. Points are individual predictions for each county–year combination. The black line is the expectation for a 1:1 response, and the blue line is a LOESS fit to the points.

Fig. S3.

Yields of soybean and maize predicted from the model (Eq. 4) using zero W126 and historical climate data against yield predicted from the model using historical W126 and climate. Points are individual predictions for each county–year combination. The black line is the expectation for a 1:1 response, and the blue line is a LOESS fit to the points, showing that with zero W126 predicted yield tends to be higher than those predicted with historical W126.

Table 1.

Type III sums of squares for rain-fed soybean yield

Model parameter	Degrees of freedom	Sums of squares	F value	P value†
Intercept	1	42,427,808	377.0	0.002
Year	1	97,894,399	869.8	0.002
County	253	51,990,756	1.8	0.002
Tmax	1	6,534,829	58.1	0.002
P/PET	1	160,418	1.4	0.226
Tmax2	1	6,465,343	57.4	0.002
P/PET2	1	1,086,772	9.7	0.01
W126	1	2,028,804	18.0	0.002
Year*county	253	52,677,918	1.9	0.002
Tmax*P/PET	1	3,579	0.0	0.832
Tmax*P/PET2	1	512,755	4.6	0.032
P/PET*Tmax2	1	20,533	0.2	0.652
W126*P/PET	1	2,834,395	25.2	0.002
W126*Tmax	1	2,534,975	22.5	0.002
W126*P/PET2	1	2,019,730	17.9	0.002
W126*Tmax2	1	2,688,000	23.9	0.002
Residuals	6,210	698,922,185

^†P values were determined by comparing the F value in the table to a null F distribution that was generated by a double bootstrap procedure that accounted for spatial correlation. Thus, the P value in the table is different from that of a standard F test.

Table 2.

Type III sums of squares for rain-fed maize yield

Model parameter	Degrees of freedom	Sums of squares	F value	P value†
Intercept	1	567,895,174	600.4	0.002
Year	1	1,720,503,651	1,818.9	0.002
County	283	888,816,636	3.3	0.002
Tmax	1	54,345,824	57.5	0.002
P/PET	1	380,084	0.4	0.546
Tmax2	1	63,688,564	67.3	0.002
P/PET2	1	5,869,113	6.2	0.016
W126	1	44,226,186	46.8	0.002
Year*county	283	900,103,436	3.4	0.002
Tmax*P/PET	1	1,638,230	1.7	0.21
Tmax*P/PET2	1	1,192,597	1.3	0.258
P/PET*Tmax2	1	2,259,738	2.4	0.12
W126*P/PET	1	1,943,883	2.1	0.134
W126*Tmax	1	51,755,969	54.7	0.002
W126*P/PET2	1	1,068,479	1.1	0.234
W126*Tmax2	1	54,124,209	57.2	0.002
Residuals	6,932	6,556,987,586

^†P values were determined by comparing the F value in the table to a null F distribution that was generated by a double bootstrap procedure that accounted for spatial correlation. Thus, the P value in the table is different from that of a standard F test.

Table S1.

Type III sums of squares for rain-fed soybean or maize yield using AOT40

Model parameter	Degrees of freedom	Sums of squares	F value	Bootstrapped P value†
Soybean
Intercept	1	42,986,422	381.1	0.002
Year	1	109,500,327	970.7	0.002
County	253	51,497,998	1.8	0.002
Tmax	1	6,499,272	57.6	0.002
P/PET	1	231,458	2.1	0.162
Tmax2	1	6,299,699	55.8	0.002
P/PET2	1	1,177,780	10.4	0.01
AOT40	1	2,143,325	19.0	0.002
Year*county	253	52,214,982	1.8	0.002
Tmax*P/PET	1	23,408	0.2	0.65
Tmax*P/PET2	1	638,221	5.7	0.022
P/PET*Tmax2	1	4,135	0.0	0.83
P/PET*AOT40	1	3,220,478	28.6	0.002
Tmax*AOT40	1	2,635,755	23.4	0.002
P/PET2*AOT40	1	2,009,716	17.8	0.002
Tmax2*AOT40	1	2,725,040	24.2	0.002
Residuals	6,210	700,493,337
Maize
Intercept	1	607,930,191	640.3	0.002
Year	1	1,945,329,640	2,048.9	0.002
County	283	872,112,839	3.2	0.002
Tmax	1	63,759,208	67.2	0.002
P/PET	1	14,092	0.01	0.904
Tmax2	1	71,493,397	75.3	0.002
P/PET2	1	10,747,972	11.3	0.002
AOT40	1	52,350,097	55.1	0.002
Year*county	283	883,549,646	3.3	0.002
Tmax*P/PET	1	781,632	0.8	0.384
Tmax*P/PET2	1	3,969,534	4.2	0.046
P/PET*Tmax2	1	1,589,393	1.7	0.218
P/PET*AOT40	1	3,172,799	3.3	0.064
Tmax*AOT40	1	59,760,344	62.9	0.002
P/PET2*AOT40	1	1,285,533	1.4	0.19
Tmax2*AOT40	1	61,096,841	64.3	0.002
Residuals	6,932	6,581,707,260

^†Bootstrapped P values were determined by comparing the F value in the table to a null F distribution that was generated by a double bootstrap procedure that accounted for spatial correlation. Thus, the P value in the table is different from that of a standard F test.

Table S2.

Type III sums of squares for rain-fed soybean yield using SUM06

Model parameter	Degrees of freedom	Sums of squares	F value	Bootstrapped P value†
Soybean
Intercept	1	38,236	0.3	0.688
Year	1	267	0.0	0.984
County	253	51,497,998	1.8	0.002
Tmax	1	6,499,272	57.6	0.002
P/PET	1	231,458	2.1	0.168
Tmax2	1	6,299,699	55.8	0.002
P/PET2	1	1,177,780	10.4	0.008
SUM06	1	2,143,325	19.0	0.002
Year*county	253	52,214,982	1.8	0.002
Tmax*P/PET	1	23,408	0.2	0.69
Tmax*P/PET2	1	638,221	5.7	0.024
P/PET*Tmax2	1	4,135	0.04	0.814
P/PET*SUM06	1	3,220,478	28.6	0.002
Tmax*SUM06	1	2,635,755	23.4	0.002
P/PET2*SUM06	1	2,009,716	17.8	0.002
Tmax2*SUM06	1	2,725,040	24.2	0.002
Residuals	6,210	70,049,3337
Maize
Intercept	1	30,230,016	31.8	0.002
Year	1	23,492,528	24.7	0.002
County	283	872,112,839	3.2	0.002
Tmax	1	63,759,208	67.2	0.002
P/PET	1	14,092	0.01	0.582
Tmax2	1	7,149,3397	75.3	0.002
P/PET2	1	10,747,972	11.3	0.012
SUM06	1	52,350,097	55.1	0.002
Year*county	283	883,549,646	3.3	0.002
Tmax*P/PET	1	781,632	0.8	0.252
Tmax*P/PET2	1	3,969,534	4.2	0.204
P/PET*Tmax2	1	1,589,393	1.7	0.138
P/PET*SUM06	1	3,172,799	3.3	0.022
Tmax*SUM06	1	59,760,344	62.9	0.002
P/PET2*SUM06	1	1,285,533	1.4	0.75
Tmax2*SUM06	1	6,1096,841	64.3	0.002
Residuals	6,932	6,581,707,260

^†Bootstrapped P values were determined by comparing the F value in the table to a null F distribution that was generated by a double bootstrap procedure that accounted for spatial correlation. Thus, the P value in the table is different from that of a standard F test.

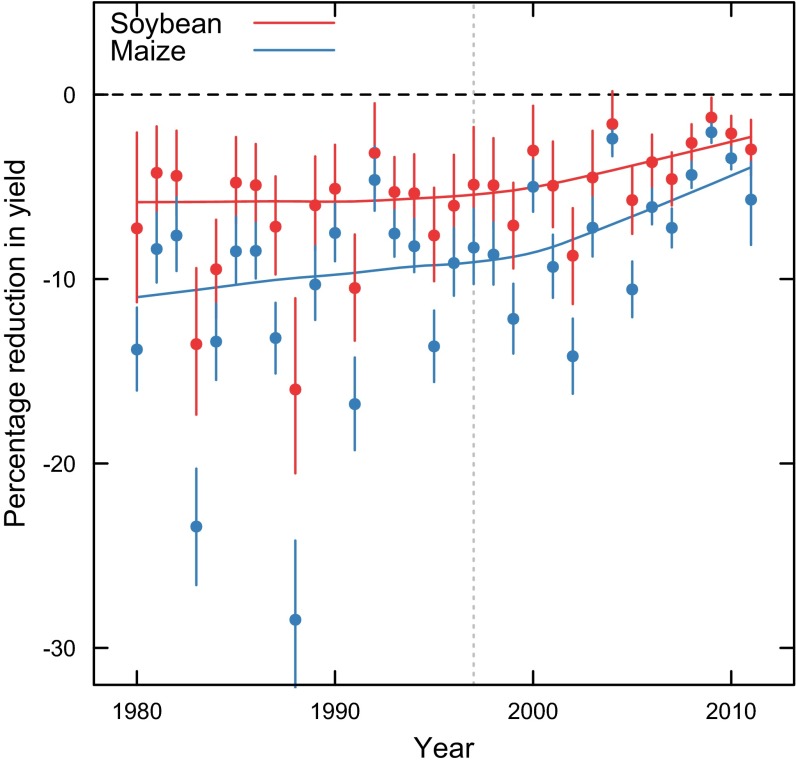
For each set of predictions (i.e., historical [O₃] and a hypothetical situation without O₃), production was summed for all counties and years, and the percentage difference between the two conditions was used to estimate yield loss due to O₃ exposure. Confidence limits for this estimate were obtained using bootstrapping (see Materials and Methods for description). Estimates of production loss ranged from 4–6% for soybean and 8–11% for maize (Table 3), and estimates were similar when using AOT40 or SUM06 (Table S3). Historical yield loss due to O₃ remained relatively constant for soybean until the year 2000, when there was a trend toward less O₃ damage (Fig. 1). For maize, historical yield loss due to O₃ decreased between 1980 and 2000, and like soybean, the trend toward less O₃ damage became greater around year 2000 (Fig. 1).

Table 3.

Percentage increase in crop production estimated from 1980 to 2011 if the ozone index W126 had been 0 instead of the measured historical values

Crop	Mean, %	95% confidence limits from bootstrapping, %
Soybean	5.5	3.3–7.7
Maize	9.8	8.0–11.6

Table S3.

Percentage increase in crop production estimated from 1980 to 201 if AOT40 had been 0 compared with historical values

	AOT40		SUM06
Crop	Mean, %	95% confidence limits from bootstrapping, %	Mean, %	95% confidence limits from bootstrapping, %
Soybean	6.3	3.7–9.0	5.2	3.3–7.0
Maize	11.7	9.4–14.1	9.1	7.4–10.7

Fig. 1.

Estimated percentage reduction of soybean and maize yield from O₃ for 1980–2011. Each point is a weighted mean of percentage reduction for all counties, where the value of a county was weighted by the harvested acreage of soybean or maize in that county. Percentage reduction was estimated by using Eq. 4 to predict yield using historical values of W126 or a value of 0 W126. The lines are a LOESS fit to the points. The black, dashed, horizontal line marks 0 change for reference. The gray, vertical, dotted line indicates when the EPA implemented more stringent standards for O₃ emissions. Bars are 95% confidence intervals of yield reduction for that year.

To examine relative sensitivity of maize and soybean to [O₃], a local regression analysis (LOESS) was used. LOESS models fit low-order polynomial regressions at each data point, using that point’s nearest neighbors, and combine the results into a larger model. Each individual regression uses only a subset of the total dataset, and thus the analysis makes no global assumptions about relationships between model parameters. This sacrifices the ability to make general statements about parameters but allows for better predictions under specific conditions and a more flexible response to parameters, making it well-suited to compare the sensitivity of these crops across the range of conditions seen in the historical data. The parameters used in the LOESS yield model were P/PET, T_max, and W126.

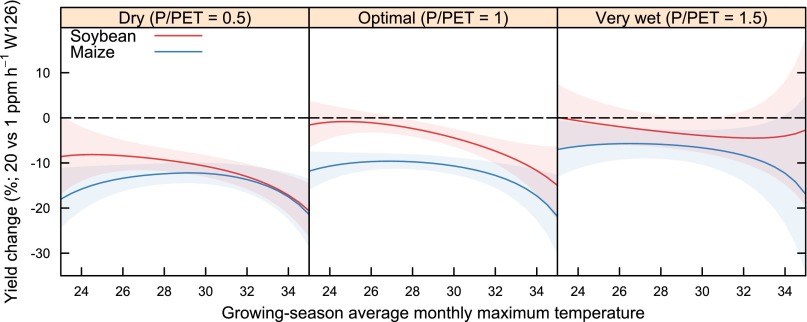
Without the ability to make general conclusions about parameters, a LOESS model can only predict yield using values of P/PET, T_max, and W126 within the ranges used to parameterize the model. Because O₃ is always present at ground level, this means it is not possible with this dataset to use LOESS to predict yield in the absence of O₃. However, there are times and places with very low [O₃]. The lowest W126 value in the dataset was 0.04 ppm h, compared with the mean W126, which was 18 ppm h. Thus, to examine the effect of O₃ the LOESS model was used to predict yields of maize and soybean using a W126 index value of 20 ppm h (which is near the historical mean of 18 ppm h; Table 4) and a value of 1 ppm h (which is small but somewhat larger than the historical minimum of 0.04 ppm h). A W126 value of 0.04 ppm h was not used because the LOESS model uses only nearest neighbors for a given data point, and because 0.04 ppm h is the lowest W126 value, the only nearest neighbors are larger values of W126, giving low power and large confidence limits. By using a W126 value of 1 ppm h, there are nearest neighbors of W126 both smaller and larger than 1 ppm h, giving more power and smaller confidence limits. Moreover, even with complete removal of anthropogenic sources, ground-level [O₃] will never be completely removed, due to natural sources of O₃. Therefore, although the estimate is not for an O₃-free environment, it allows for a useful comparison between the mean [O₃] condition and a low O₃ condition. Results also showed that maize was more sensitive to [O₃] across the entire range of T_max in optimal and very wet conditions, but the crops had similar sensitivities to [O₃] in dry conditions, where both crops were most sensitive to [O₃] (Fig. 2).

Table 4.

Mean environmental conditions for all counties and years included in the analysis of ozone effects on soybean and maize production

Crop	W126, ppm h	Tmax, °C	P/PET
Soybean	17.5	29.4	0.78
Maize	17.4	28.9	0.79

Fig. 2.

Sensitivity of soybean and maize yield to [O₃] across a range of values for P/PET and T_max. Each panel gives estimates of sensitivity at a different P/PET, and values for P/PET are given in the top of each panel. The mean and 95% confidence limits are shown for estimates of percentage reduction of yield in 1 ppm h W126 compared with 20 ppm h W126 from a LOESS model. The black, dashed line indicates no change for reference. Negative values indicate that O₃ decreased yield.

Discussion

Using an approach independent from experimental studies, based on historical records of yield, climate, and ground-level [O₃], we present three major findings. First, ground-level O₃ significantly decreased annual yields of rain-fed soybean and maize in the United States for the period 1980–2011 and regulation of O₃ emissions may have contributed to these losses. Second, the historical relationships suggest that maize yields were more sensitive to [O₃] than soybean yields. Third, O₃ caused substantial damage even in drought conditions, contrary to the expectation that lower stomatal conductance during times of limited water availability would provide protection by limiting O₃ uptake into the plant (19). Data from irrigated fields were not included in the analysis, so these conclusions only apply to rain-fed fields, which describe ∼85% of maize and 90% of soybean growing regions in the United States.

Yield loss from O₃ from 1980 to 2011 was estimated to be 5% for soybean and 10% for maize. The mean value of production from 2009 to 2013 was $65 billion for maize and $39 billion for soybean [National Agricultural Statistics Service (NASS) (www.nass.usda.gov)], implying losses of roughly $7.2 billion per year for maize and $2 billion per year for soybean, ignoring effects of supply and demand. This significant loss of income and food should be a strong impetus to further decrease ground-level [O₃], especially considering that the interaction between [O₃] and high temperatures portends that the effect of O₃ is likely to be greater in the coming decades with intensifying climate change (20).

Although losses from current [O₃] are large, the damage caused by ground-level O₃ has decreased for both crops since 1980 (Fig. 1). Concentrations of O₃ and O₃-producing precursors have decreased in the United States (21), accounting for the reductions in O₃ damage seen here. There is controversy over whether regulatory policies influence air quality, with evidence that some policies have clear effects but other policies have little or no effect (22). However, it is noteworthy that there was an accelerated rate of improvement seen around year 2000 (Fig. 1) following more stringent regulations for O₃ concentrations implemented by the EPA in 1997 (23), indicating that those regulations have had a nationwide positive effect on maize and soybean yield. The EPA currently sets goals for emissions of O₃ and its precursors based on protecting human health, but this has had the fortunate side effect of improving crop yield. However, because nearly 90% of areas have met current [O₃] goals (21), there is little impetus to further reduce ground-level [O₃]. New regulations intended to protect economic production in addition to human health have been considered, but there are currently no regulations in effect. Taken together, the substantial reduction in yield loss since 1980 and the 4–7% loss of production still occurring today indicate that regulating pollutants has had widespread positive benefits on agricultural production, and that further reductions in pollution would produce further benefits. For regions of the world where crop yield loss from pollutants is larger (13), the success in the United States indicates that regulation of air pollutants in those countries would be an effective means of increasing crop yield.

Our analysis used type III sums of squares to account for the effect of interest after including all other terms in the model, so a significant effect indicated that the term was able to further explain variation in the model, even if the newly added term was correlated with terms already included in the model. This is particularly important, because W126 is highly correlated with water availability and temperature, and both environmental parameters strongly and independently affect yield (24). If one were to only check for a significant O₃ effect without already accounting for temperature and precipitation, those effects would be confounded with effects of O₃, biasing the estimate of the O₃ effect and causing erroneous significance. After including major influences on yield such as improved cultivars and agronomy (as a year effect), differences between counties, water availability, and temperature, W126 remained highly significant (Tables 1 and 2), suggesting that O₃ has had a large and quantifiable impact on maize and soybean yields in the United States.

In this analysis, when a term has significant interactions, lower-order effects for that term are often not independently interpretable. This can result in seemingly paradoxical conclusions. For example, for both maize and soybean (P/PET)² was significant, but P/PET was not significant. This does not mean that P/PET had no effect, because the significance of the (P/PET)² term makes the P/PET term uninterpretable on its own. This indicates that yield responded roughly quadratically to P/PET, in that there is a P/PET that is optimal for yield, and too little or too much precipitation reduced yield. The results indicated that O₃ interacted with both temperature and water availability, supported by the significant interactions between W126, T_max, and P/PET for both maize and soybean (Tables 1 and 2). Because of the dependence of the W126 effect on temperature and water availability, it is difficult to make conclusions about O₃ alone, and instead the effects of O₃ are better considered with respect to the environment in which the crop was grown. To help understand these relationships, LOESS analysis was used to determine the effect of O₃ across a range of values of P/PET and growing season temperature. O₃ significantly reduced yield in all conditions, but the effect was most severe in dry conditions with high temperatures (Fig. 2). In very wet conditions, the effect of O₃ was smaller and less dependent on growing season temperature (Fig. 2). Although many studies and reviews have shown that low stomatal conductance under times of drought can limit entry of O₃ into leaves, the response of stomatal conductance to elevated [O₃] is not always consistent (25). There is also evidence that elevated [O₃] impairs abscisic acid (ABA) signaling. ABA is a hormone produced during drought, which signals leaves to reduce stomatal conductance. By impairing ABA signaling, plants under drought stress have greater stomatal conductance when exposed to elevated [O₃], resulting in increased water loss (26). Thus, the greater yield loss under dry conditions seen here could be caused by elevated [O₃] exacerbating drought stress.

Greater variability in precipitation across regions and throughout the year is a predicted consequence of climate change. The interaction between [O₃] and water status seen here implies that [O₃] will modulate the response of precipitation on yield in future climates. However, it is difficult to assess the relative importance of changes in precipitation against changes in O₃ concentration without further experiments or modeling (which is beyond the scope of this study). However, the strong interaction between P/PET and [O₃] seen here has important consequences for increased variability in precipitation, because if [O₃] is high the impact of drought on yield may be magnified. Similarly, global temperatures are predicted to increase, and again without further study it is difficult to assess the relative importance of O₃ vs. increasing temperatures, especially considering that in some regions for some crops temperatures may currently be below what is expected to produce optimal yield. However, for regions and crops where temperatures are currently at or above optimum, damage from increased temperature would potentially be exacerbated if [O₃] is high.

Surprisingly, the yield losses to O₃ were greater for maize than soybean (Fig. 1 and Table 3), even though maize has been considered less sensitive to O₃ than soybean (2, 27). This could be because maize is more sensitive to O₃ or because maize is grown in times and places with greater [O₃] or grown in climates in which crops are more sensitive to O₃. Across all counties and years, the mean W126 index and climate variables were similar for soybean and maize (Table 4), indicating that differences in environment were likely not responsible for the differences in yield loss. In contrast, when normalized to the same conditions, maize yield seemed to be more sensitive to [O₃] in optimal and supraoptimal water-status conditions across a wide range of temperatures (Fig. 2), indicating that greater O₃ sensitivity of maize compared with soybean was responsible for the greater yield loss.

To compare our results with previous studies that have estimated O₃ dose–response functions and crop yield losses for maize and soybean, O₃ sensitivity of both crops was calculated at the mean maximum temperature and P/PET across all sites and years (29 °C, 0.78 P/PET), using 1 ppm h vs. 20 ppm h W126 or 1 ppm h vs. 15 ppm h AOT40, values which are near the minimum and mean concentrations across all sites and years. W126 values were estimated from reported mean [O₃] and duration of fumigation for studies that did not report W126 or AOT40 (27–29). For soybean we found a sensitivity to W126 of 0.45% ppm⁻¹ h⁻¹ compared with 0.4% ppm⁻¹ h⁻¹ (27) and 1.7% ppm⁻¹ h⁻¹ (28), and a sensitivity to AOT40 of 0.49% ppm⁻¹ h⁻¹ compared with 0.5–1% ppm⁻¹ h⁻¹ (2, 30, 31). For maize we found a sensitivity to W126 of 0.52% ppm⁻¹ h⁻¹ compared with 0.12% ppm⁻¹ h⁻¹ (27) and 0.7% ppm⁻¹ h⁻¹ (29), and a sensitivity to AOT40 of 0.62% ppm⁻¹ h⁻¹ compared with 0.4% ppm⁻¹ h⁻¹ (2) and 0.5% ppm⁻¹ h⁻¹ (32). Thus, the sensitivity estimates produced by the current study for the two species are in line with previously reported values. These results suggest that maize is at least as sensitive as soybean to [O₃], and that the reduced stomatal conductance characteristic of species with C₄ photosynthesis does not necessarily protect against O₃ damage. This has important implications for both the benefits that would be obtained by lowering the emissions that give rise to elevated [O₃] in rural regions as well as projections of future food and feed supply.

Elevation of ground-level [O₃] caused by pollution has resulted in very significant losses of maize and soybean yields in the United States and, by extension, other crops. Air-quality regulation has successfully reduced O₃-induced crop damage since 2000 but losses remain at ∼4 and 7% for soybean and maize. Thus, further reducing [O₃] presents an opportunity to increase crop yield at a time when increased food production is needed to feed a growing population (13). Additionally, the exacerbation of O₃ damage by high temperatures indicates O₃ damage could become greater under the temperature increases projected for 2050 if [O₃] is not decreased further. Projections of crop production out to 2050 indicate that maize and soybean will have reduced yield in many growing regions including the United States (33), concluding that the loss is primarily due to changes in climate. These projections, however, do not include interaction between [O₃] and climate, a complication that findings here indicate would make projections more pessimistic in warming regions of the world. However, there are no controlled experimental studies to date in the peer-reviewed literature that have examined how crop yield responds to increased temperature and [O₃] simultaneously under realistic crop production conditions, indicating a large and key knowledge gap in understanding the future of crop production.

Materials and Methods

Annual yields of maize and soybean for each county of the United States were obtained from the US Department of Agriculture NASS (NASS QuickStats; quickstats.nass.usda.gov) for the years 1980–2011. The interaction between water status and [O₃] was of interest, but in irrigated fields P/PET is not an accurate estimate of water status, so data from fields recorded as irrigated were not used. In states where irrigation is the norm, fields are not always recorded as irrigated, so as an additional constraint, data from states that on average irrigate with more than 500 mm were excluded; this step removed about 5% of the remaining observations. Approximately 85% of US maize production and greater than 90% of soybean production is rain-fed (34), so our analysis captured the vast majority of maize and soybean production in the United States. Hourly [O₃] at 2,700 sites across the same years were obtained from the EPA’s Air Quality System (https://aqs.epa.gov/aqs/). To be comparable with yield data, which are reported at the county level, [O₃] indices were calculated at each site, and then indices at sites within a county were averaged. Counties with fewer than 16 y of data were excluded. Hourly data from each EPA monitoring site were used to calculate the values of three widely used cumulative indices of vegetation response to [O₃]: AOT40, SUM06, and W126 (18). AOT40 is a metric of cumulative hours exceeding 40 ppb and was calculated as

$$AOT40={\displaystyle \sum _{h=1}^n{C}_h}\hspace{0.17em}\text{where}\hspace{0.17em}{C}_h=\{\begin{array}{ll}\left[O_h-40\right],\hfill & O_h>40\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array},$$ [1]

where $O_h$ is the [O₃] in parts per million for hour $h$, and $n$ is the total number of observed hours at the site.

SUM06 is a metric of cumulative hours exceeding 60 ppb and was calculated as

$$SUM06={\displaystyle \sum _{h=1}^n{C}_h}\hspace{0.17em}\text{where}\hspace{0.17em}{C}_h=\{\begin{array}{ll}{O}_h,\hfill & O_h>60\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$ [2]

W126 weights [O₃] on a sigmoidal scale and was calculated as

$$W126={\displaystyle \sum _{h=1}^n\left(O_h\mathrm{\cdot }\frac{1}{1+4403\mathrm{\cdot }{e}^{-126\mathrm{\cdot }{O}_h}}\right)},$$ [3]

where $e$ is ∼2.7183.

Indices were summed over the growing season (considered to be June, July, and August) for each year. These months were chosen because they are months in which maize and soybean are typically growing in fields and this definition of the growing season has been used successfully in previous studies (15). All sites were missing some hourly observations when instruments were being repaired or recalibrated; ∼7.6% of expected [O₃] observations were missing. Because these indices are cumulative, they were divided by the number of observed hours ($n$) at each site and then multiplied by the total number of hours in the growing season, so that sites with more missing data would not erroneously have lower values.

Precipitation (P), potential evapotranspiration (PET), and maximum temperature ($T_{max}$) were obtained as monthly, 0.5° × 0.5° gridded datasets (CRU TS 3.2, badc.nerc.ac.uk/data/cru/; cf. ref. 28), and P/PET was calculated as a measure of water availability as has been done previously (16, 35). Crops respond to soil moisture, so P/PET is a better predictor of yield than P alone, because P alone only accounts for inputs to soil moisture, and therefore overestimates water availability. To estimate climate values at a county level, a 0.125° grid was created in which each grid cell was paired with both the county and 0.5° cell that contained the 0.125° cell’s center. The mean of the climate data for all 0.125° cells within a county was used as an estimate of the mean climate for that county (as in ref. 13). The mean climatic values for June, July, and August were calculated for each year. Both photosynthesis and O₃ production only occur during daylight hours, so $T_{max}$ was used as opposed to $T_{min}$, which occurs at night, or $T_{mean}$, which is influenced by day and night temperature. However, the choice of the temperature variable did not affect the results (Table S4).

Table S4.

Relative increase in production estimated from 1980 to 2011 if W126 had been 0 and using T_ave or T_min in the models from Tables 1 and 2

	Tave		Tmin
Crop	Mean, %	95% confidence limits from bootstrapping, %	Mean, %	95% confidence limits from bootstrapping, %
Soybean	5.8	3.7–7.8	5.8	3.8–7.7
Maize	10.2	8.6–11.9	10.8	8.7–11.9

[O₃] is correlated with both P/PET and T_max because both factors affect the reaction rates of processes that form O₃. This results in collinearity of predictor variables in the model, which, although it does not affect the ability to predict yield, can incorrectly attribute effects of one predictor to a different predictor. This could result in attributing effects to O₃ when they are actually due to T_max or P/PET. To examine the severity of collinearity, the standardized W126 index was predicted using T_max and P/PET, including squared terms and interactions. The adjusted r² for this model was 0.21, indicating substantial variation in W126 that is not explained by environmental variables. This is likely due to the fact that precursors for O₃ production will not always be present, even if environmental conditions are favorable for O₃ production. This [O₃] variation that is independent from T_max and P/PET variation allows for estimation of the O₃ effect independent of effects of those two variables.

Data were used in the following linear model to determine the effect on yield of the above climatic variables in combination in turn with each of AOT40, SUM06 and W126:

$$\begin{array}{l}yiel{d}_{ij}={\beta }_0+{\beta }_y\mathrm{\cdot }yea{r}_i+{\displaystyle \sum _{x=1}^{n_c}{\beta }_{c,x}\mathrm{\cdot }count{y}_x}+{\displaystyle \sum _{x=1}^{n_c}{\beta }_{cy,x}\mathrm{\cdot }\left(count{y}_x\mathrm{\cdot }yea{r}_i\right)+{\beta }_T\mathrm{\cdot }{T}_{\mathit{max},ij}+{\beta }_P\mathrm{\cdot }P/PE{T}_{ij}}\\ +{\beta }_{TP}\mathrm{\cdot }\left(T_{\mathit{max},ij}\mathrm{\cdot }P/PE{T}_{ij}\right)+{\beta }_{T2}\mathrm{\cdot }{T}_{\mathit{max},ij}^2+{\beta }_{P2}\mathrm{\cdot }{\left(P/PE{T}_{ij}\right)}^2+{\beta }_{TP2}\mathrm{\cdot }\left(T_{\mathit{max},ij}\mathrm{\cdot }{\left[P/PE{T}_{ij}\right]}^2\right)+{\beta }_{PT2}\mathrm{\cdot }\left(P/PE{T}_{ij}\mathrm{\cdot }{T}_{\mathit{max},ij}^2\right)\\ +{\beta }_o\mathrm{\cdot }{O}_{3,ij}+{\beta }_{PO}\mathrm{\cdot }\left(P/PE{T}_{ij}\mathrm{\cdot }{O}_{3,ij}\right)+{\beta }_{TO}\mathrm{\cdot }\left(T_{\mathit{max},ij}\mathrm{\cdot }{O}_{3,ij}\right)+{\beta }_{P2O}\mathrm{\cdot }\left({\left[P/PE{T}_{ij}\right]}^2\mathrm{\cdot }{O}_{3,ij}\right)+\\ {\beta }_{T2O}\mathrm{\cdot }\left({\left[T_{\mathit{max},ij}\right]}^2\mathrm{\cdot }{O}_{3,ij}\right)+e_{ij},\end{array}$$ [4]

where O₃ is one of the three cumulative [O₃] indexes. The subscripts i and j are indices for year and county, respectively, such that T_max,ij is T_max in year i in county j. n_c is the number of counties, and county_x is a vector of dummy variables (i.e., county_x is 1 when x = j, and is 0 otherwise). Over the period of study (1980–2011), the yields of maize and soybean have increased in the United States due to the release of higher-yielding cultivars and improved agronomic practices. In addition, other factors such as soil type vary regionally. These factors are independent of effects of climate and [O₃], but because they affect yield, they should be included in the model. Therefore, terms for year, county and a year-by-county interaction were included in the model. The term for county accounts for variation in soil type and agronomic practices in different regions, and the year and year-by-county terms account for the increase in yield due to continual development of cultivars and advanced management and agronomic practices over time. Inclusion of these terms in the model accounts for the effects of the numerous variables that alter yield, other than the ones specifically included in the model. The two crops were treated independently and all analyses were performed separately for each crop. Similar models have been used in previous studies (13, 36).

Because many of these observations are recorded near each other, they will be spatially correlated because observations close in space will share factors unexplained by the model, such as soil type and governmental policy. This has the effect of artificially reducing variance estimates and can overestimate significance. To account for spatial correlation, a clustered bootstrap was used (37, 38) as has been done in previous similar studies (39). To determine confidence limits for production loss (Table 1 and Tables S3 and S4 and Dataset S1), all counties within a state for 1 y were treated as a group. Groups were randomly resampled with replacement and parameters from Eq. 4 were estimated. This was repeated 499 times, with the original sample giving 500 bootstrap replicates. The parameter estimates from the original sample and the covariance of all 500 samples were used as the mean and covariance, respectively, of an estimate of multivariate normal distribution of the parameters. By sampling all counties within a state, counties are not treated as independent observations, and this sampling scheme accounts for spatial correlation due to similar environmental conditions in nearby places as well a common policy at the state level. Compared with the multivariate normal distribution estimated using ordinary least-squares regression, this distribution has larger covariance for most parameter pairs and results in larger confidence limits for estimates of production loss. Bootstrapping methods were used for multiple purposes, so for clarity, we refer to this one as the parameter bootstrap.

To determine whether parameters accounted for significant variation, the same clustered approach as the parameter bootstrap described above was used, but observed values of yield were randomly reassigned to counties within each state. By reassigning yield, the null distribution is enforced because yield then has no relation to other observed values. Eq. 4 was used to estimate parameters for the new sample, and the F value for each parameter was recorded. This was repeated 499 times, with the original sample giving 500 estimates, and significance was determined by comparing the F value from the original sample to the bootstrapped null f distribution. We refer to this as the null bootstrap.

An estimate of production loss was determined by summing production across all years and counties for each of the two situations, (i) with historical [O₃] or (ii) a hypothetical situation with no O₃, and production loss was estimated as the percentage reduction in yield. To obtain confidence limits for this estimate, the parameter distributions from the previously described parameter bootstrap were used as input into a second round of bootstrapping. The new parameter estimates were used to predict production loss as described above. This was repeated 2,999 times, with the original sample giving 3,000 estimates, to produce a distribution of production loss, from which the 2.5th and 97.5th percentiles were used as 95% confidence limits (37). We refer to this as the production bootstrap.

For the LOESS analysis, the model included T_max, P/PET, and, in turn, each of the O₃ indexes, AOT40, SUM06, and W126. To understand how the effect of O₃ varies with environmental conditions, yield was estimated in dry, optimal, and overly wet conditions (corresponding to P/PET values of 0.5, 1, and 1.5, respectively) across a range of growing-season average monthly T_max values (23–35 °C). Those estimates were used to calculate the response ratio (Y₂₀/Y₁; where Y₂₀ is yield predicted with a W126 value of 20, and Y₁ is yield predicted with a W126 value of 1), and the natural logarithm of the response ratio to calculate confidence limits (40), which were then converted to percent change for ease of interpretation.