Allowing variance may enlarge the safe operating space for exploited ecosystems

Significance

Humans depend on ecosystems for food, water, pharmaceuticals, and other benefits. Ecosystem managers, industries, and the public want these benefits to be predictable and therefore have low variance over time. However, control of variance for short-term benefits leads to long-term fragility. Here we show that management to reduce short-term variability can drive ecosystems into degraded states, leading to long-term declines of ecosystem services. These risks can be avoided by strategies that tolerate variability within boundaries of safe operating spaces for ecosystem management.

Abstract

Variable flows of food, water, or other ecosystem services complicate planning. Management strategies that decrease variability and increase predictability may therefore be preferred. However, actions to decrease variance over short timescales (2–4 y), when applied continuously, may lead to long-term ecosystem changes with adverse consequences. We investigated the effects of managing short-term variance in three well-understood models of ecosystem services: lake eutrophication, harvest of a wild population, and yield of domestic herbivores on a rangeland. In all cases, actions to decrease variance can increase the risk of crossing critical ecosystem thresholds, resulting in less desirable ecosystem states. Managing to decrease short-term variance creates ecosystem fragility by changing the boundaries of safe operating spaces, suppressing information needed for adaptive management, cancelling signals of declining resilience, and removing pressures that may build tolerance of stress. Thus, the management of variance interacts strongly and inseparably with the management of resilience. By allowing for variation, learning, and flexibility while observing change, managers can detect opportunities and problems as they develop while sustaining the capacity to deal with them.

Massive shifts in ecosystem state have important effects on flows of ecosystem services, the benefits that people obtain from nature (1, 2). Small changes in environmental conditions can trigger large shifts in forests, grasslands, lakes, or marine ecosystems (3–6). Recovery from these transitions can be difficult or impossible, with long-term losses of ecosystem services such as food and clean water. Thus, avoiding thresholds for massive transitions is of utmost importance (7, 8).

Thresholds that bound the favorable states of social–ecological systems delimit a safe operating space (SOS) (9, 10). Inside the SOS, it is unlikely that known critical thresholds will be crossed. A resilient system tends to remain in the SOS, despite disturbance (11). Thus, management for resilience includes close attention to the boundaries of SOS and their changes over time (7, 12, 13). The SOS approach does not impose any particular conditions on the trajectories of ecosystem states, as long as the range of ecosystem behavior remains in the SOS. In this respect, the SOS approach differs from traditional approaches to ecosystem management, such as optimal control or robust control, which address the mean, variance, and other moments of ecosystem behavior (14). So far, there has been little attention paid to the variability of ecosystems within a SOS.

Variability over time may have beneficial or harmful effects on flows of ecosystem services. Low variance is sometimes equated with stability (15). Stability may be sought by constraining harvest or pollutant impacts or by establishing protected reserves that isolate ecosystems from particular types of disturbance. The precautionary principle moderates variability by limiting human actions to those that have succeeded in the past (16). A contrasting view notes that ecosystems in constant environments may be vulnerable to novel disturbances. Stress selects for hardiness. Occasional moderate shocks may build resilience of ecosystems and social–ecological systems (17, 18). Similar arguments are made for human health (19) and psychological development (20). From this point of view, the exclusion of shocks may lead to fragility of complex systems. Holling (ref. 21, p. 21) draws a sharp contrast between ecosystem management that allows for variability and a “stability view that emphasizes the equilibrium, the maintenance of a predictable world, and the harvest of nature’s excess production with as little fluctuation as possible.”

Nonetheless, within a SOS there are reasons to decrease the variability of ecosystem services. When variability is reduced, ecosystem services are more predictable and this predictability facilitates planning by managers, industries, and the public sector. It is especially attractive to decrease short-term variance over timescales of a few years. Central bank policies decrease short-term variance of economic indicators while increasing long-term variance (22). Policies for managing Europe’s forests call for stabilization of yield and suppression of disturbance (23). Populations of large predators, such as wolves in the United States, are managed close to targets that are politically contended and carefully monitored (24). Fish stocks subject to overharvest are held to levels that balance industry profits and sustainability of stocks. Harvest rules that result in lowest variance are preferred (25). Pollutants are managed close to caps that balance industry profits with risk to the public and ecosystems. In these cases, deviations from the mandated target are corrected, and the variance over time is constrained.

Does the variance within the safe operating space affect the boundaries of the safe operating space? If not, then there may be no harm in managing variance. But if control of variance changes the boundaries of the safe operating space, then variance management may lead to large changes in resources that may be costly to society or the people involved.

We investigated this question, using models for three managed systems subject to alternative stable states: a lake subject to eutrophication from phosphorus pollution (26, 27), an exploited fish population (28), and a rangeland subject to collapse from overgrazing by cattle (29). In each case, managers may choose to reduce variance of state variables or outputs to improve the consistency of ecosystem service flows over a time horizon of a few years (21, 30). Variance over this time frame, referred to as short-term variance in this paper, is relevant for planning. Short-term variance is managed by modifying environmental noise or ecosystem variables (input rate of phosphorus, harvest rate of fishes, or mortality of woody vegetation) according to an appropriate weighted average of past years. We then compare outcomes for scenarios with and without management to reduce short-term variance.

Phosphorus Load and Lake Eutrophication

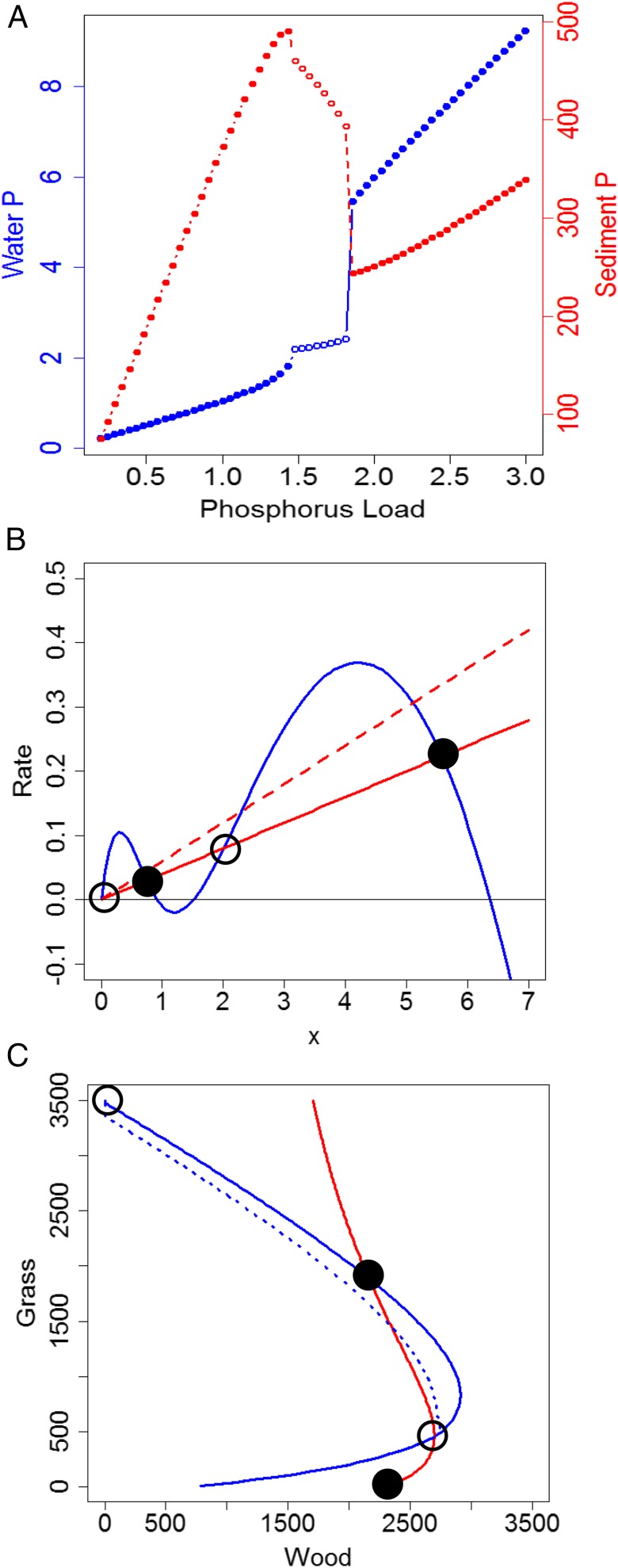
Eutrophication of lakes and reservoirs by excessive phosphorus input is a well-studied case of alternate states, called oligotrophy and eutrophy (26, 31). When phosphorus inputs are low, the lake is in a stable oligotrophic state with clear water. As phosphorus load (input rate) increases, phosphorus builds up in sediments. Eventually critical thresholds are crossed, as shown for a model of Lake Mendota in Wisconsin (Fig. 1A). At phosphorus loads between 1.47 g⋅m⁻²⋅y⁻¹ and 1.84 g⋅m⁻²⋅y⁻¹, cycles of phosphorus exchange occur between sediments and water. When phosphorus load rises above 1.84 g⋅m⁻²⋅y⁻¹, the lake reaches a stable eutrophic state with algae blooms and turbid water. Therefore, the SOS for clean water corresponds to phosphorus load below 1.47 g⋅m⁻²⋅y⁻¹ for Lake Mendota.

Fig. 1.

Deterministic dynamics of the three ecosystem models. (A) Eutrophication model showing response of P mass in the water (blue) and sediment (red) to input rate (load) of phosphorus. Solid circles denote stable points, and open circles denote unstable points. For phosphorus loads between about 1.47 and 1.84 solutions are cyclic. Above a phosphorus load of about 1.84 there is a sharp shift of phosphorus mass from sediment to water, which switches the lake from the oligotrophic (low water phosphorus) to the eutrophic (high water phosphorus) state. (B) Harvest model showing net growth rate of the population (blue line) and nominal harvest rate (solid red line). Solid circles denote stable points, and open circles denote unstable points. With an increase in harvest rate (dashed red line) the upper stable point moves closer to the unstable point. If harvest increases so the red line is tangent to the blue line, the upper stable point disappears and the population collapses to the lower stable point. (C) Isoclines for woody vegetation (red) and grass (blue) in the rangeland model. The equilibrium point with high grass and zero wood is unstable. The equilibrium point with high wood and zero grass is stable. The upper intersection of the isoclines is a stable point. The lower intersection is unstable. If herbivore stocking density is raised from 10 (solid line) to 50 (dashed line), the stable intersection moves closer to the unstable intersection. Thus, there is greater chance that a random event will cross the unstable equilibrium and the ecosystem will collapse to the lower stable point with high woody vegetation and zero grass.

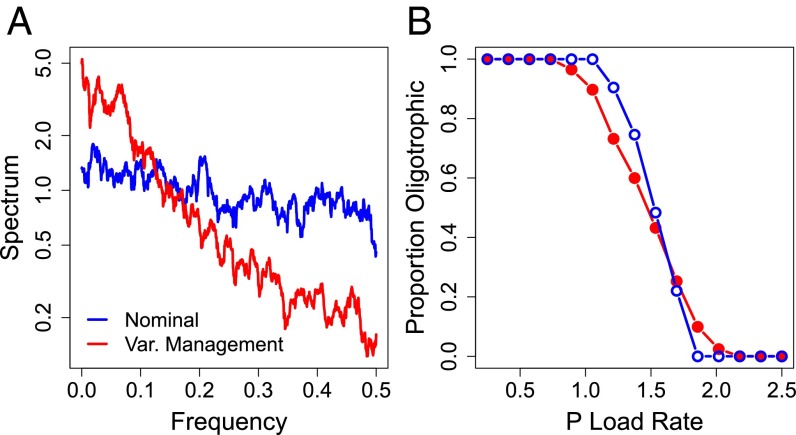
When phosphorus load comes from a point source, such as a sewage plant discharge, the plant operator could manage the autocorrelation of loads, using small brief decrements or increments of load to counter the effects of recent past shocks (SI Text). Such a management scheme can reduce the short-term variance of water quality (Fig. 2A). The spectrum is a plot of variance at a particular frequency vs. frequency. Frequency is scaled so that the period in years is 1/frequency. Thus, the highest frequency corresponds to variability at periods of 2 y or year-to-year variance. The negative slope of the spectra is characteristic of red noise, which characterizes many ecological time series (32).

Fig. 2.

(A) Spectra of time series of water phosphorus concentration in the model of eutrophication by point-source phosphorus pollution (nominal u = 0; variance management u = −0.6). Each point on the spectrum shows variance at a corresponding frequency. Note log scaling. Frequency of 0.5 corresponds to a period of 2 y. (B) Proportion of time spent in the oligotrophic (clear water) ecosystem state vs. phosphorus load rate for the two cases shown in A. Each data point is the proportion of 5,000 time steps.

In this case, management decreases variance for frequencies above about 0.15 (corresponding to periods less than about 1/0.15 ∼ 6 y). The decrease in high-frequency variance of water quality is accompanied by an increase in low-frequency variance. As a consequence the ecosystem transitions out of the oligotrophic state at lower phosphorus load (Fig. 2B). Decreased short-term variance is associated with increased long-term variance and greater fragility of the clear water state of the lake.

This response is analogous to Bode’s law for linear systems (33). However, in lake eutrophication the phosphorus concentration in the lake is the outcome of a nonlinear process. Management of the autocorrelation of point-source phosphorus inputs increases the long-term variability of phosphorus concentration. The short-term variance becomes smaller, but over the long run the lake spends less time in the clear water state.

A Harvested Population

A model of a harvested fish population (28) is often used to illustrate alternate states of living resources (Fig. 1B). Growth of the unharvested population follows the blue line in Fig. 1B. With moderate harvest (solid red line in Fig. 1B) there are four equilibria; the first and third are unstable and the second and fourth are stable. The SOS is the range of harvest values where the upper stable equilibrium exists. If harvest increases (red dashed line in Fig. 1B), the upper two equilibria are closer together. With further increase in slope of the straight line, the two upper equilibria disappear and the population falls to the lower stable equilibrium.

We analyzed two versions of the harvest model: one where an imaginary manager measures the shocks directly and acts to smooth their effects and one where the manager measures harvest directly and seeks to smooth the total catch over time (Materials and Methods).

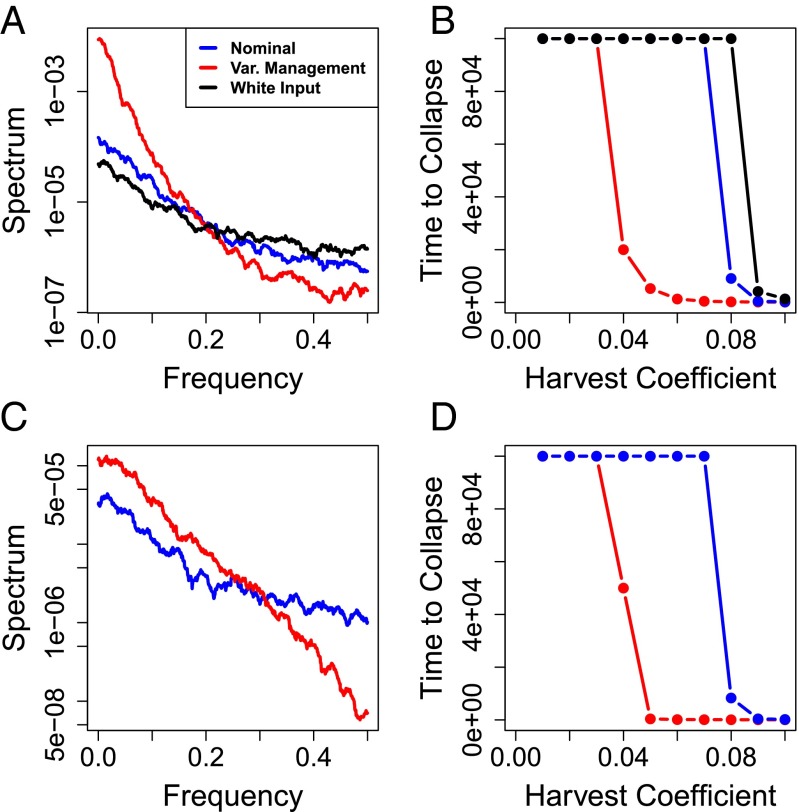
First, we consider the case where environmental noise is managed directly. In this case, management acts directly on the environmental noise and not on the deterministic ecological parameters (SI Text). In the nominal simulation, the variance spectrum of the harvest decreases with frequency (Fig. 3A, blue line). The manager may choose to flatten the spectrum or make it whiter (Fig. 3A, black line). Even with white environmental noise, the spectrum of the harvest time series has a slight negative slope due to critical slowing down near the transition (34). Nonetheless, whitening the environmental noise increases the short-term variance of harvest. Alternatively the manager may choose to decrease the short-term variance of environmental noise and thereby make the spectrum of harvest more red (Fig. 3A, red line). With lower short-term variance (i.e., redder spectrum) the population collapses at lower levels of the harvest coefficient, as has been shown previously for a similar model of a harvested population (28). Thus, the fragility of the resource depends on the variance spectrum imposed by the manager.

Fig. 3.

Harvest model. (A) Spectra of harvest time series for the noise management case (nominal is no variance management, u = 0; variance management is u = 0.8; white input is u = 0 and uncorrelated shocks). Each point on the spectrum shows variance at the corresponding frequency. Note log scaling. Frequency of 0.5 corresponds to a period of 2 y. (B) Average time steps to collapse of the population vs. harvest coefficient for the three cases shown in A. (C) Spectra for the harvest management case (nominal u = 0; variance management u = −0.6). Each point on the spectrum shows variance at the corresponding frequency. Note log scaling. Frequency of 0.5 corresponds to a period of 2 y. (D) Average time steps to collapse of the population vs. harvest coefficient for the two cases shown in C. In B and D, each data point is based on simulation of 100,000 time steps.

This example and the case of lake eutrophication show that management of the noise process alone, without changing the exploitation parameters (i.e., harvest or load), can decrease short-term variance and increase fragility. Management of the noise process may be plausible in some cases of environmental engineering, such as point-source pollutant discharges. However, for many ecosystems the direct modification of the environmental noise may be impossible.

By contrast, it is plausible that the manager can monitor the harvest at each time step and adjust total catch to decrease the short-term variance of the harvest over time. As before, management to decrease short-term variance leads to an increase in long-term variance and redder spectra of the harvest time series (Fig. 3C). With the decrease in short-term variance, the population collapses at a lower value of the harvest coefficient (Fig. 3D). In this version of the harvest model, management to decrease short-term variance has two effects that destabilize the ecosystem: red noise and a small increase in the average harvest.

Grazing in a Semiarid Savanna

Semiarid grasslands can switch irreversibly to woodlands if overgrazing by cattle coincides with drought (29). Therefore, prudent range managers maintain cattle densities within a SOS based on their assessment of soil water and grass conditions. Isoclines for grass and woody plant biomass show two unstable points and two stable points (Fig. 1C). The SOS exists between the upper stable point and the lower unstable point. An increase in cattle density (dashed blue line in Fig. 1C) decreases the size of the SOS.

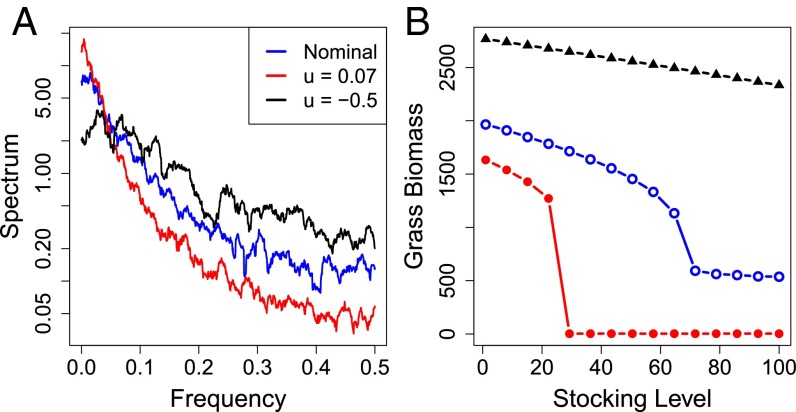
Rangeland managers must cope with varying market prices for meat as well as fluctuating rainfall and grassland conditions (35). Therefore, the manager may wish to reduce the short-term variance of grass biomass. This goal can be achieved by managing woody vegetation, for example using fire, cutting, or herbicides. When the short-term variance of grass biomass is decreased, the spectrum becomes redder (Fig. 4A, red line vs. blue line). Alternatively, the manager could manage woody vegetation to decrease low-frequency variance, thereby increasing high-frequency variance but making the spectrum whiter (black line in Fig. 4A).

Fig. 4.

(A) Spectra of grass biomass time series in the rangeland model (nominal has no variance management, u = 0). Each point on the spectrum shows variance at the corresponding frequency. Note log scaling. Frequency of 0.5 corresponds to a period of 2 y. (B) Average grass biomass for the three cases shown in panel A. Each data point is the mean of 1,000 time steps.

In the nominal case, grass biomass declines smoothly with cattle stocking level (Fig. 4B, blue line) and settles near a value of about 500 (29). Management to decrease short-term variance causes grass biomass to collapse at a lower stocking density (Fig. 4B, red line). In this case, grass biomass falls to the lower stable equilibrium dominated by wood with no grass at all (Fig. 3D, red line). In contrast, management that makes the noise whiter leads to high grass biomass across the range of cattle stocking levels (Fig. 4B, black line). In the white noise case, relatively high short-term variance is associated with high resilience of the grass biomass. Decreasing the short-term variance, as in the red noise case, makes the grass biomass susceptible to collapse.

Discussion

Within a SOS, it may seem reasonable to manage the variance of ecosystem services that support human well-being. Lower variance implies that ecosystem services are more reliable and predictable. It is especially attractive to decrease short-term variance over timescales of a few years that correspond with immediate human needs, election cycles, terms in office, or durations of agency programs. However, managing variance alters ecosystem dynamics and may cause critical transitions. Thus, the management of variance interacts strongly and inseparably with the management of resilience.

Our results show important consequences of managing short-term variance. A decrease in short-term variance is accompanied by an increase in long-term variance. Lower variability in the short term raises the variability in the longer term. This shift in the variance spectrum increases the risk of critical transitions out of the SOS. The risk occurs even if the variance management does not involve any parameters of the deterministic part of the ecosystem model (as shown by the eutrophication model and the noise management case of the harvest model). However, in many real-world cases the reduction of short-term variance may be accomplished by adjusting ecosystem exploitation variables such as harvest or livestock density. In these situations there is a dual effect on stability, through the red shift of variance spectra and the change in ecosystem exploitation variables. In either case, managing variance alters the boundaries of the safe operating space itself.

Management to whiten variance spectra may increase the resilience of ecosystems, as shown by our examples. However, whiter spectra may have higher short-term variance. Higher short-term variability implies that ecosystem services are less reliable and predictable. Therefore, managers and the public may be unwilling to manage ecosystems for whiter variance spectra, despite the long-term benefits of greater resilience.

The tradeoff between mean and variance of an ecosystem service depends on the relative weight placed on these two quantities (SI Text). Reduction of short-term variance increases short-term outputs and makes them more predictable, while increasing the risk of regime shifts with long-term losses of ecosystem services. Thus, the tradeoff between mean output and variance is related to the tradeoff between short-term and long-term benefits (36, 37).

In linear systems, managing short-term variance exposes a waterbed effect (Table 1): By reducing short-term variance, we increase variance at longer timescales (33). The variance does not disappear; it just changes timescale. This phenomenon is known as Bode’s law for linear control systems (33). Stein (33) used the vivid analogy of a box filled with dirt, where the dirt represents that logarithm of variance over all possible frequencies represented by the floor of the box. Shoveling dirt away from certain frequencies piles up dirt at other frequencies. Thus, for linear systems the integral of the logarithm of variance over all frequencies is conserved. The mechanism has been suggested as a cause of fragility in regulatory networks for ecosystem services (38). It has also been used in economics to understand how policy choices to decrease short-term variance create long-term variance (22, 39).

Table 1.

Consequences of managing variance within a safe operating space

Effect of controlling variance	Explanation	Consequence
Frequency shift	Reduced variance at high frequencies guarantees an increase at low frequencies	Long-term cycles may cross thresholds
Change the safe operating space	Reduced short-term variance changes boundaries of the safe operating space	Critical thresholds may be crossed
Missed information	Variability reveals ecosystem behavior under different conditions	Lost opportunity to learn
Lost resilience indicators	Higher variance near critical thresholds indicates loss of resilience	Inability to detect change in resilience
Lock-in of adaptive systems	Without disturbance, adaptive systems become unresponsive to long-term change	Ability to adapt to gradual long-term change is impaired
Impaired hardiness to shocks	Moderate stress promotes capacity to respond to stress	Increased vulnerability to novel disturbance

For the nonlinear systems of ecosystem management, there is no theory as complete and clear as Bode’s law. Nonetheless, suppression of short-term variance can increase long-term variance and shift the location of critical thresholds, as shown by our examples. When shock distributions shift toward lower frequencies, dynamical behavior changes and the risk of critical transitions increases (28, 40).

Management of variance may also change the location of the thresholds that bound the safe operating space (Table 1). A critical transition may be induced simply by decreasing the short-term variance. This effect is evident in all three of our examples covering different ecosystem problems: managing phosphorous pollution of a lake, harvesting a fishery, and managing cattle densities on a rangeland.

A third effect of managing variance is loss of information for learning the behavior of ecosystems (Table 1). Adaptive management, a process of structured learning about managed ecosystems, requires observations of contrasting states of ecosystems (41). Often, the information that drives learning comes from observations of natural variability in ecosystem behavior. If management actively suppresses this variation, then opportunities for learning are lost. Thus, management by the precautionary principle constrains variation in a narrow range and thereby suppresses learning (5, 16).

Measurements of temporal variability also provide information about resilience (Table 1). As an ecosystem approaches a threshold for critical transition, variance increases steeply (42) and the spectrum becomes redder (43). Thus, rising variance and redder spectra are indicators of declining resilience that apply to a wide range of ecosystems and critical transitions (44). However, if managers deliberately manage variance, then its value as an indicator of resilience is compromised.

Management of variance may cause rigidities that decrease adaptive capacity in social–ecological systems (11) (Table 1). Many systems for adaptive control lock in to stable configurations if they are not exposed to a wide range of conditions over time (45). Well-documented examples come from irrigated agriculture. In the Goulbourn–Broken catchment of Australia, emphasis of high-value cash crops created a system that was well tuned to market and climate fluctuations particular to these crops (46). However, standardization of the system of crop production salinized groundwater and brought the entire region near a critical threshold. The Pumpa system of ice-paddy irrigation in Nepal became well tuned to cope with specific fluctuations of climate and hydrology, but in the process became vulnerable to long-term changes in climate and institutional arrangements for water management (47). Thus, there are tradeoffs between resilience of the irrigation system to a small set of known kinds of disturbance and resilience to the vast universe of unknown novel shocks. Resilience to unknown and unforeseeable shocks, or general resilience, remains a major challenge for research and practice (11, 12, 46, 48).

Finally, the diversity of responses to environmental shocks present in an ecosystem is closely related to resilience (12, 49) (Table 1). The development of response diversity may depend on the disturbance history of the ecosystem (50). Thus, management of variance may slow or prevent the development of response diversity that confers resilience.

Insights reported here are based on a limited family of ecosystem models in combination with other literature on ecosystem management. Similar conclusions derive from analyses of complex regulatory systems with dozens of interlocking feedbacks (51). In physiology, such systems are potentially unstable and difficult to control, but the instability often confers functional advantages. Related tradeoffs may exist for managed ecosystems. Exploration of tradeoffs involving mean performance, variability, and stability of more complex managed ecosystems is an important topic for further research.

Early papers on resilience and ecosystem management promoted the maintenance of natural regimes of variability and disturbance (21, 30). Our analyses support this view and expose a richer range of interpretations (Table 1). Actions to decrease temporal variance in ecosystem service flows change the boundaries of safe operating spaces with potentially harmful consequences. By tolerating variability within thresholds that define a safe operating space, we may build the endurance of desirable ecosystem states. The capacity to tolerate disturbance is itself a form of stabilization. If the resulting ecosystem state has high resilience to familiar disturbances but low resilience to novel disturbances, then new risks are created. We are left with the conundrum that it is easier to build resilience to known perturbations than to the full range of potential novel disturbances, some of which are unknown or unimagined (11, 48, 52). Thus, building general resilience to deal with the unknown combined with continuous observation and learning seem to be essential. By observing change while allowing for variation, learning, and flexibility, management systems can discern emerging opportunities and problems while maintaining the capacity to deal with them.

Materials and Methods

Computations were performed in R 3.1.1 and spectra were computed with the multitaper package (53). Programs for the simulations are posted at https://github.com/CFL-UWMadison/SOSvariance. Equations and parameter values are presented in SI Text.

Model Equations and Parameters for Simulations

We simulated discrete-time models such as

$$\begin{array}{c}\mathrm{\Delta }{x}_{t+1}=G\left(x_t\right)-H\left(x_t\right)+\frac{1}{(1-\varphi B)}\sigma {\epsilon }_{t+1}\\ \mathrm{\Delta }{x}_{t+1}\equiv x_{t+1}-x_t.\end{array}$$ [S1]

Ecosystem processes that are not managed follow the deterministic function G(x_t). The deterministic function H(x_t) represents management of nutrient inputs, harvest, or stocking, depending on the ecosystem. The last term of [S1] is the stochastic noise process. B is the backshift operator such that B(x_t) = x_t−1, B²(x_t) = x_t−2, etc. The backshift operator is commonly used to simplify algebra in the statistical time series and control literature (54) (Short Tutorial on Backshift Algebra). The last term of [S1] generates reddened environmental noise, i.e., noise that is shifted toward low frequencies (28). The autoregressive coefficient is $\varphi$ (−1 < ϕ < 1), the $\epsilon$ are independent draws from a unit normal distribution, and $\sigma$ is the SD of the noise.

We define the short-term variance using the variance (or power) spectrum of a time series for a relevant ecosystem variable (54). The spectrum is defined for frequencies from 0 to π and is symmetric around 0. Short-term variance corresponds to the high frequencies, which we define as π/2 to π. In our simulations this range of frequencies corresponds to periods of about 2–4 y. We compute this variance as

$$V\left(x\right)={\displaystyle \underset{\pi /2}{\overset{\pi }{\int }}S\left(\omega \right)d\omega },$$ [S2]

where $S\left(\omega \right)$ is the variance spectrum of the ecosystem output under management (harvest, nutrient levels, or yield).

Lake Eutrophication.

Dynamics involve two state variables, phosphorus in lake water (x_t) and sediment (y_t):

$$\begin{array}{c}\mathrm{\Delta }{x}_{t+1}=\left(\lambda +\frac{1}{1-\varphi B}\sigma {\epsilon }_{t+1}\right)-(s+h)x_t+r{y}_{t}f\left(x_t\right)\\ \mathrm{\Delta }{y}_{t+1}=s{x}_t-b{y}_t-r{y}_{t}f\left(x_t\right)\\ f\left(x_t\right)\equiv \frac{x_t^q}{m^q+x_t^q}.\end{array}$$ [S3]

Parameters include mean rate of phosphorus inputs λ, sedimentation s, hydraulic washout h, phosphorus recycling maximum rate r, half saturation for recycling m, and shape parameter for recycling q. Parameter values were based on 33 y of annual phosphorus budgets for Lake Mendota, WI (55). Parameter values for simulations shown here were b = 0.002, h = 0.252, m = 4, r = 0.019, q = 4, s = 0.748, ϕ = 0.1, and σ = 0.35.

We assumed that the manager could modify the autocorrelation of shocks at each time step, based on observations of previous shocks. This assumption may be plausible for a case of point-source (end-of-pipe) pollution where the mean release of pollutant is regulated but variation around the mean is tolerated. The manager’s intervention was modeled as an additional polynomial in the backshift operator, U(B). This leads to

$$\begin{array}{c}\mathrm{\Delta }{x}_{t+1}=\left(\lambda +\frac{1}{U\left(B\right)(1-\varphi B)}\sigma {\epsilon }_{t+1}\right)-(s+h)x_t+r{y}_{t}f\left(x_t\right)\\ \mathrm{\Delta }{y}_{t+1}=s{x}_t-b{y}_t-r{y}_{t}f\left(x_t\right)\\ f\left(x_t\right)\equiv \frac{x_t^q}{m^q+x_t^q}.\end{array}$$ [S3a]

Clearly if U(B) = 1/(1 – ϕB), then the shocks are converted to the white noise process σε_t. For the sake of simplicity, we used U(B) = 1 − uB. For negative u (−1 < u < 0), simulations show that the spectrum of x_t becomes redder and short-term variance decreases. The opposite occurs for positive values of u (0 < u < 1).

Harvested Population.

Dynamics follow

$$\mathrm{\Delta }{x}_{t+1}=r{x}_t\left(1-\frac{x_t}{K}\right)-\frac{c{x}_t^2}{b^2+x_t^2}-h{x}_t+\frac{1}{1-\varphi B}\sigma {\epsilon }_{t+1}.$$ [S4]

Symbols are logistic growth parameters r and K, sigmoid predation consumption coefficient c, half-saturation constant b, and harvest coefficient h. Parameter values for simulations shown here were r = 0.75, c = 1.35, b = 1, K = 8.8, ϕ = 0.4, and σ = 0.1.

Variance management was studied using two versions of [S4]. In the noise management case the noise is modified to include a process U(B):

$$\mathrm{\Delta }{x}_{t+1}=r{x}_t\left(1-\frac{x_t}{K}\right)-\frac{c{x}_t^2}{b^2+x_t^2}-h{x}_t+\frac{1}{U\left(B\right)(1-\varphi B)}\sigma {\epsilon }_{t+1}.$$ [S4a]

As noted above for the eutrophication model, if U(B) = 1/(1 – ϕB), then the shocks are converted to the white noise process σε_t. If U(B) = 1 − uB with 0 < u < 1, simulations show that the short-term variance of harvest decreases and the spectrum of harvest becomes redder.

The noise management case shows how management can change spectra of ecosystem time series without changing the exploitation parameter term −hx_t. In practice it may be impossible for the manager of a harvested population to directly modify the noise process. However, the manager could modify the harvest process.

In the “harvest management” case, the manager smooths the total allowable catch, using a weighted sum of past harvests. The management term (1 – uB) is applied to the harvest:

$$\mathrm{\Delta }{x}_{t+1}=r{x}_t\left(1-\frac{x_t}{K}\right)-\frac{c{x}_t^2}{b^2+x_t^2}-(1-uB)h{x}_t+\frac{1}{(1-\varphi B)}\sigma {\epsilon }_{t+1}.$$ [S4b]

Thus, at each time step the realized harvest is $(1-\varphi B)(1-uB)h{x}_t=h\left[x_t-(u+\varphi )x_{t-1}+u\varphi x_{t-2}\right]$ instead of hx_t. For −1 < u < 0, simulations show that the spectrum of harvest is reddened and the short-term variance decreases. The opposite occurs for positive values of u (0 < u < 1).

Rangeland Management.

Two state variables are involved, grass biomass x_t and woody plant biomass y_t. Dynamics follow (29)

$$\begin{array}{c}\mathrm{\Delta }{x}_{t+1}=r_{x}I\left(x_t\right)F_x(x_t,y_t)x_t-L_x{x}_t-hQ\left(x_t\right)x_t+\frac{1}{1-\varphi B}\sigma {\epsilon }_{t+1}\\ \mathrm{\Delta }{y}_{t+1}=r_{y}I\left(x_t\right)F_y(x_t,y_t)y_t+\frac{S\left(x_t\right)y_t}{y_t+p}-L_y{y}_t.\end{array}$$ [S5]

Functions used in [S5] are

$$\begin{array}{c}I\left(x_t\right)=\frac{x_t+c_1{i}_0}{x_t+c_1}\\ F_x(x_t,y_t)=\frac{1}{x_t+\alpha y_t+\beta }\\ Q\left(x_t\right)=\max \left(\frac{c_2\left(1-G_0/x_t\right)}{x_t+c_3},0\right)\\ S\left(x_t\right)=r_S\left[1-\frac{x_t}{K(x_t+d_4)}\right]\\ F_y(x_t,y_t)=\frac{1}{y_t+\gamma x_t+\delta }.\end{array}$$ [S6]

The cattle stocking density h is set by the rangeland manager and directly affects the grass dynamics through the term hQ(x_t)x_t of [S5]. The productivity of cattle depends on the stocking density and the grass biomass. We assume that the manager aims to decrease the short-term variability of grass biomass by controlling woody vegetation, for example with cutting, fire, or herbicides. We include variance management in the second equation of [S5],

$$\mathrm{\Delta }{y}_{t+1}=r_{y}I\left(x_t\right)F_y(x_t,y_t)y_t+\frac{S\left(x_t\right)y_t}{y_t+p}-(1-uB)L_y{y}_t.$$ [S5a]

For positive u (0 < u < 1) simulations show that the short-term variance of x_t decreases and the spectrum is redder. For negative u (−1 < u < 0) the spectrum of x_t becomes whiter and the short-term variance increases.

Symbol definitions and parameter values used in our simulations are presented in ref. 29.

The environmental noise parameters were ϕ = 0.2 and σ = 5.

Short Tutorial on Backshift Algebra

In this example we show in detail how to expand the harvesting model subject to noise management [S4a] with U(B) = (1 – uB):

$$\mathrm{\Delta }{x}_{t+1}=G\left(x_t\right)-H\left(x_t\right)+\frac{1}{(1-uB)(1-\varphi B)}\sigma {\epsilon }_{t+1}.$$

We use F(x_t) as shorthand for G(x_t) – H(x_t):

$$\begin{array}{c}\mathrm{\Delta }{x}_{t+1}=F\left(x_t\right)+\frac{1}{(1-uB)(1-\varphi B)}\sigma {\epsilon }_{t+1}\\ \mathrm{\Delta }{x}_{t+1}\left(1-(u+\varphi )B+u\varphi B^2\right)=F\left(x_t\right)\left(1-(u+\varphi )B+u\varphi B^2\right)+\sigma {\epsilon }_{t+1}.\end{array}$$

Now we apply the backshift operators B to $\mathrm{\Delta }{x}_{t+1}$ and F(x_t). Note that B² shifts the position back twice:

$$\mathrm{\Delta }{x}_{t+1}-(u+\varphi )\mathrm{\Delta }{x}_t+u\varphi \mathrm{\Delta }{x}_{t-1}=F\left(x_t\right)-(u+\varphi )F\left(x_{t-1}\right)+u\varphi F\left(x_{t-2}\right)+\sigma {\epsilon }_{t+1}\mathrm{\Delta }{x}_{t+1}=(u+\varphi )\mathrm{\Delta }{x}_t-u\varphi \mathrm{\Delta }{x}_{t-1}+F\left(x_t\right)-(u+\varphi )F\left(x_{t-1}\right)+u\varphi F\left(x_{t-2}\right)+\sigma {\epsilon }_{t+1}.$$

Next expand $\mathrm{\Delta }x$:

$$x_{t+1}=x_t+(u+\varphi )(x_t-x_{t-1})-u\varphi (x_{t-1}-x_{t-2})+F\left(x_t\right)-(u+\varphi )F\left(x_{t-1}\right)+u\varphi F\left(x_{t-2}\right)+\sigma {\epsilon }_{t+1}.$$

The fully expanded equation reads

$$x_{t+1}=x_t+(u+\varphi )(x_t-x_{t-1})-u\varphi (x_{t-1}-x_{t-2})+G\left(x_t\right)-(u+\varphi )G\left(x_{t-1}\right)+u\varphi G\left(x_{t-2}\right)-\left[H\left(x_t\right)-(u+\varphi )H\left(x_{t-1}\right)+u\varphi H\left(x_{t-2}\right)\right]+\sigma {\epsilon }_{t+1}G\left(x_t\right)\equiv r{x}_t\left(1-\frac{x_t}{K}\right)-\frac{c{x}_t^2}{b^2+x_t^2}H\left(x_t\right)\equiv h{x}_t.$$

Expanded Equations Used for Simulations

This section presents the fully expanded equations used for simulations.

Lake Eutrophication.

Expanding the equation for x in [S3a] with U(B) = 1 − uB,

$$x_{t+1}=x_t+(u+\varphi )(x_t-x_{t-1})-u\varphi (x_{t-1}-x_{t-2})+\left[1-(u+\varphi )+u\varphi \right]\lambda +G(x_t,y_t)-(u+\varphi )G(x_{t-1},y_{t-1})+u\varphi G(x_{t-2},y_{t-2})+\sigma {\epsilon }_{t+1}G(x_t,y_t)\equiv -(s+h)x_t+r{y}_{t}f\left(x_t\right)f\left(x_t\right)\equiv \frac{x_t^q}{m^q+x_t^q}.$$

Harvested Population.

For the shock management case, Eq. S4a with U(B) = 1 – uB, the expanded equation is given above in Short Tutorial on Backshift Algebra.

For the harvest management case, expanding Eq. S4b gives

$$x_{t+1}=x_t+\varphi (x_t-x_{t-1})+G\left(x_t\right)-\varphi G\left(x_t\right)-\left[H\left(x_t\right)-(u+\varphi )H\left(x_{t-1}\right)+u\varphi H\left(x_{t-2}\right)\right]+\sigma {\epsilon }_{t+1}G\left(x_t\right)\equiv r{x}_t\left(1-\frac{x_t}{K}\right)-\frac{c{x}_t^2}{b^2+x_t^2}H\left(x_t\right)\equiv h{x}_t.$$

Rangeland Management.

Expanding the equation for y in [S5a],

$$y_{t+1}=y_t+r_{y}I{F}_y{y}_t+\frac{S{y}_t}{y_t+p}-L_y{y}_t+u{L}_y{y}_{t-1}.$$

The Tradeoff Between Mean Output and Its Variance

Analyses presented in this paper assume that the manager’s objective is to maintain a safe operating space while providing an ecosystem service that is sufficiently large with low variance. This problem has a solution if the manager specifies a quantitative weighting of mean output and variance of output. We define a management objective J that reflects the tradeoffs between ecosystem service flow and variability:

$$J=E\left[H\left(x\right)\right]-a\sqrt{V\left(x\right)}.$$ [S7]

The first term E[H(x)] represents the expected flow of ecosystem services. V(x) is the short-term variance of ecosystem service flows calculated from [S2] and a is a weight that measures the manager’s risk preference. Eq. S7 is appropriate for the harvest model and the rangeland model. Management of phosphorus load usually aims to decrease phosphorus concentrations, x. To reflect the desirability of low x the manager’s objective can be defined as

$$J=\frac{1}{1+E\left[x\right]}-a\sqrt{V\left(x\right)}.$$ [S8]

Shifting Ecosystem Variance Toward a Desired Spectrum

This section shows that it is possible to shift ecosystem dynamics some distance toward a desired spectrum by setting the management goal according to a computable function of current and past states.

We seek an averaging process $U\left(B\right)$ to modify the dynamics in expression [S1]. Here $B$ denotes the backshift operator, $B{x}_t=x_{t-1}$. Rewrite [S1] as

$$x_{t+1}=x_t+g\left(x_t\right)-U\left(B\right)h{x}_t+\frac{\theta \left(B\right)}{\varphi \left(B\right)}\delta {\epsilon }_{t+1},$$ [S9]

where $h$ is a management parameter. Define $\delta$ as a small perturbation around a deterministic steady state given h.

Now linearize around $\delta =0$. The equations for the deterministic steady state and the first two derivatives with respect to $\delta$ evaluated at the deterministic steady state are

$$\begin{array}{c}x=x+g\left(x\right)-U\left(B\right)hx\\ x_{t+1}^{\prime }=x_t^{\prime }+g\prime \left(x\right)x_t^{\prime }-U\left(B\right)h{x}_t^{\prime }+\frac{\theta \left(B\right)}{\varphi \left(B\right)}{\epsilon }_{t+1}\\ x_{t+1}^{″}=x_t^{″}+g″\left(x\right)x_t^{\prime }+g\prime \left(x\right)x_t^{″}-U\left(B\right)h{x}_t^{″}.\end{array}$$ [S10]

Thus, a linearized approximation of the steady-state distribution of $x$ given $h$ expanded around $\delta =0$ is

$$x_t(h,\delta )=x(h,0)+x_t^{\prime }(h,0)\delta +(1/2)x_t^{″}(h,0){\delta }^2+\mathrm{....}$$ [S11]

Note that the first term of [S11] does not depend on the noise.

Suppose we approximate the steady-state distribution of the process [S9]. The first derivative with respect to $\delta$ from [S10] is

$$x_{t+1}^{\prime }=x_t^{\prime }+g\prime \left(x\right)x_t^{\prime }-U\left(B\right)h{x}_t^{\prime }+\frac{\theta \left(B\right)}{\varphi \left(B\right)}{\epsilon }_{t+1}.$$ [S12]

We wish to choose $U\left(B\right)$ so that the process described by [S12] is the same as the target process $x_{t+1}^{\prime }=T\left(B\right){\epsilon }_{t+1}$.

Recalling that $B{x}_{t+1}^{\prime }=x_t^{\prime }$, some backshift operator algebra yields

$$x_{t+1}^{\prime }={\left\{1-\left[1+g\prime \left(x\right)-U\left(B\right)h\right]B\right\}}^{-1}\frac{\theta \left(B\right)}{\varphi \left(B\right)}{\epsilon }_{t+1}.$$ [S13]

How do we choose $U\left(B\right)$ so that the spectrum of [S13] is the same as the spectrum of the target process $x_{t+1}^{\prime }=T\left(B\right){\epsilon }_{t+1}$?

For a linear process with mean zero,

$$y_{t+1}=T\left(B\right){\epsilon }_{t+1},\hspace{0.17em}\left\{{\epsilon }_{t+1}\hspace{0.17em}\text{IID}\left(\text{0,}{\sigma }_{\epsilon }^2\right)\right\},$$ [S14]

the spectrum is

$$\begin{array}{c}{g}_y\left(z\right)={\sigma }_e^{2}T\left(z\right)T\left(z^{-1}\right)\\ z\equiv e^{-i\omega }.\end{array}$$ [S15]

So that the spectrum of [S13] will be the same as the spectrum of the target process $x_{t+1}^{\prime }=T\left(B\right){\epsilon }_{t+1}$ with the spectrum given by [S15], we find $U\left(B\right)$ to solve the equation

$${\left\{1-\left[1+g\prime \left(x\right)-U\left(B\right)h\right]B\right\}}^{-1}\frac{\theta \left(B\right)}{\varphi \left(B\right)}=T\left(B\right).$$ [S16]

The solution of [S16] for $U\left(B\right)$ is

$$U\left(B\right)=\frac{1}{hB}\left[\frac{\theta \left(B\right)}{\varphi \left(B\right)T\left(B\right)}-1+B+Bg\prime \left(x\right)\right].$$ [S17]

So that the operator $U\left(B\right)$ gives us a spectrum that will approximate the spectrum of the original Eq. S9 to the first-order approximation in $\delta$, we must locate sufficient conditions for the operator to be of the form

$$U\left(B\right)=u_0+u_{1}B+u_2{B}^2+\mathrm{...},$$ [S18]

i.e., to not contain terms with $B$ raised to a negative power. If the operator $U\left(B\right)$ contained terms of negative power in $B$, it would imply that the manager would have to manage on future values of $\epsilon$ that the manager has no way of observing at dates where actions need to be taken.

If $\left(\theta \left(B\right)/\varphi \left(B\right)\right)/T\left(B\right)$ is of the “fundamental” form

$$\frac{\left(\theta \left(B\right)/\varphi \left(B\right)\right)}{T\left(B\right)}=1+a_{1}B+a_2{B}^2+\mathrm{...},$$ [S19]

then it is clear from [S9] that there are no terms with $B$ raised to a negative power in the operator $U\left(B\right)$. It is sufficient to assume $\theta \left(B\right)/\varphi \left(B\right)$ and $T\left(B\right)$ are of the form

$$\begin{array}{c}\frac{\theta \left(B\right)}{\varphi \left(B\right)}=1+r_{1}B+r_2{B}^2+\mathrm{...}\\ T\left(B\right)=1+t_{1}B+t_2{B}^2+\mathrm{....}\end{array}$$ [S20]

It is easy to check that

$$S\left(B\right)=1+s_{1}B+s_2{B}^2+\mathrm{...}$$ [S21]

is of fundamental form, where $S\left(B\right)=1/T\left(B\right)$, and the product of two operators is of fundamental form when each operator is of fundamental form. Hence [S19] is of fundamental form and the operator $U\left(B\right)$ is of the form [S18]. Note that $U\left(B\right)$ in [S18] may not be of fundamental form because $u_0$ does not have to be one.

Our main point here is simple: A computable function of current and past ecosystem states can be used to shift the spectrum of [S9] toward a desired target spectrum. In computations presented here, we use a simple expression for $U\left(B\right)$. With appropriate parameter choice, the simpler expression succeeds in decreasing the high-frequency variance of [S9], as shown by our simulations.