Growing the terrestrial planets from the gradual accumulation of submeter-sized objects

Significance

The fact that Mars is so much smaller than both Earth and Venus has been a long-standing puzzle of terrestrial planet formation. Here we show that a new mode of planet formation known as “Viscous Stirred Pebble Accretion,” which has recently been shown to produce the giant planets, also naturally explains the small size of Mars and the low mass of the asteroid belt. Thus there is a unified model that can be used to explain all of the basic properties of our solar system.

Abstract

Building the terrestrial planets has been a challenge for planet formation models. In particular, classical theories have been unable to reproduce the small mass of Mars and instead predict that a planet near 1.5 astronomical units (AU) should roughly be the same mass as Earth. Recently, a new model called Viscously Stirred Pebble Accretion (VSPA) has been developed that can explain the formation of the gas giants. This model envisions that the cores of the giant planets formed from 100- to 1,000-km bodies that directly accreted a population of pebbles—submeter-sized objects that slowly grew in the protoplanetary disk. Here we apply this model to the terrestrial planet region and find that it can reproduce the basic structure of the inner solar system, including a small Mars and a low-mass asteroid belt. Our models show that for an initial population of planetesimals with sizes similar to those of the main belt asteroids, VSPA becomes inefficient beyond ∼ 1.5 AU. As a result, Mars’s growth is stunted, and nothing large in the asteroid belt can accumulate.

Classical models of terrestrial planet formation have a problem: The same models that produce reasonable Earth and Venus analogs tend to produce Mars analogs that are far too large (1). The only existing proposed explanations for the small mass of Mars based on classical modes of growth require a severe depletion of solids beyond 1 astronomical unit (AU) (2), involving either not-well-understood nebular processes (3) or a complicated and dramatic migration of the giant planets (4) to solve this problem. Recently, however, it has been shown that a new mode of planet formation known as Viscously Stirred Pebble Accretion (VSPA) can successfully explain the formation of the giant planets (5, 6). Here it is our hypothesis that Mars’s mass may simply be another manifestation of VSPA. To understand how, we need to describe the process.

Review of Pebble Accretion

After the formation of the protoplanetary disk, dust particles, which are suspended in the gas, slowly collide and grow because of electrostatic forces. Once particles become large enough so that their Stokes numbers ($\tau \equiv t_s{\mathrm{\Omega }}_K$, where $t_s$ is the stopping time due to aerodynamic drag and ${\mathrm{\Omega }}_K$ is the orbital frequency) are between $\sim {10}^{-3}$ and 1, depending on the model, these so-called “pebbles” can be concentrated by aerodynamic processes (7–10). Under the appropriate physical conditions (which might not have been satisfied everywhere in the disk), these concentrations become dense enough that they become gravitationally unstable and thus collapse to form planetesimals (11) with radii between $\sim 50$ and $\sim \mathrm{1,000}$ km (10, 12). This process can occur very quickly—on the order of the local orbital period.

Recent research shows that planetesimals embedded in a population of pebbles can grow rapidly via a newly discovered accretion mechanism that is aided by aerodynamic drag on the pebbles themselves (5, 13, 14). In particular, if a pebble’s aerodynamic stopping time is less than or comparable to the time for it to encounter a growing body (hereafter known as an “embryo”), then it is decelerated with respect to the embryo and becomes gravitationally bound. After capture, the pebble spirals toward the embryo due to aerodynamic drag and is accreted. The accretional cross section for this situation is

$${\sigma }_{\text{peb}}\equiv \pi \frac{4G{M}_e{t}_s}{v_{rel}}{\text{exp}}^{-\xi },$$ [1]

where $\xi =2{\left[t_s{v}_{rel}^3/\left(4G{M}_e\right)\right]}^{0.65}$, $M_e$ is the mass of the embryo, and $v_{rel}$ is the relative velocity between the pebble and embryo (13). For the growing planets, ${\sigma }_{\text{peb}}$ can be orders of magnitude larger than the physical cross section alone. Full N-body simulations (6) show that as long as pebbles form continuously over a long enough time period such that embryos have time to gravitationally stir each other, this process can form the observed gas giant planets before the gas disk dissipates.

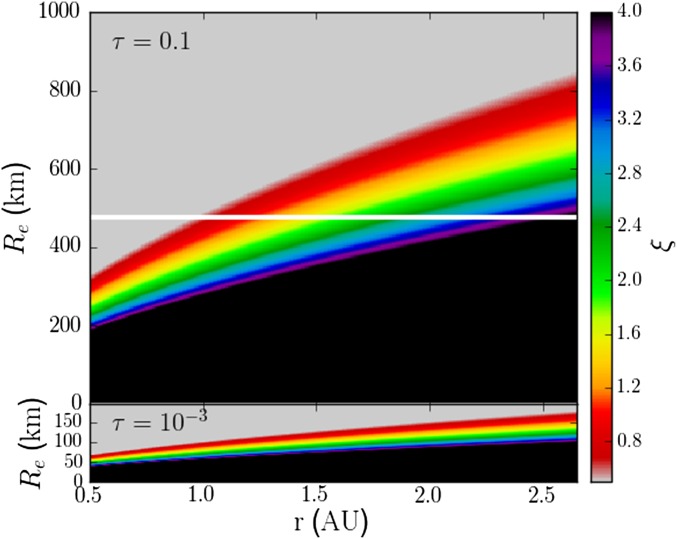
Our hypothesis that this process can also explain Mars’s small size and the low mass of the asteroid belt is based on the $e^{-\xi }$ term in Eq. 1, which says that pebble accretion becomes exponentially less efficient for small embryos because the encounter times for these objects ($4G{M}_e/v_{rel}^3$) becomes short compared with $t_s$. As a result, aerodynamic drag does not have time to change the trajectory of the pebbles, so they are unlikely to be accreted. Eq. 1 therefore predicts a sharp cutoff between small embryos, which cannot grow, and larger objects, which can. In addition, because $t_s$ is a function of location in the disk, this cutoff also varies with location. Fig. 1 shows the value of ξ in our fiducial disk (which is described in Methods) for two values of τ that are consistent with the requirements of the two competing models of planetesimal formation. In particular, Fig. 1, Top employs $\tau =0.1$ pebbles that are required for the so-called “streaming instability” (8, 10, 15), whereas Fig. 1, Bottom uses the $\tau ={10}^{-3}$ pebbles needed by the turbulent concentration models of refs. 7 and 9. As ξ in general increases with heliocentric distance for an embryo of a given size, embryos that can grow in the inner regions cannot grow farther from the Sun. For example, if pebbles have $\tau =0.1$, an object initially the size of Ceres will grow at 1 AU (where $\xi \approx 1$) but not at 2 AU (where ξ becomes large). This argument implies that, initially, all planetesimals could have been the size of currently observed main belt asteroids; those bodies in the asteroid belt did not grow appreciably, whereas those at 1 AU did. Therefore, we postulate that Mars’s small mass and the lack of planets in the asteroid belt might be the result of this cutoff. It is important to note that this figure just shows ξ and does not represent how the entire pebble accretion process will behave. To ascertain that, we must turn to numerical calculations. The remainder of this work presents such simulations.

Fig. 1.

The value of ξ as a function of heliocentric distance (r) and embryo radius ($R_e$) in our fiducial protoplanetary disk, assuming that the embryos have circular (Keplerian) orbits and the pebbles are on orbits as determined by aerodynamic drag. The top and bottom panels are for $\tau =0.1$ and ${10}^{-3}$, respectively. As ξ in general increases with heliocentric distance for an object of a given size, objects that can grow in the inner regions cannot grow farther from the Sun. For reference, the white horizontal line (Top) corresponds to the radius of (1) Ceres.

Methods

To test this hypothesis, we performed a series of N-body calculations of terrestrial planet formation starting with a population of planetesimals embedded in our fiducial gas disk, adopted from ref. 6. We assume a flaring gas disk with a surface density of $\mathrm{\Sigma }={\mathrm{\Sigma }}_0{r}_{\text{AU}}^{-1}$ (16) and a scale height $h=0.047\hspace{0.17em}{r}_{\text{AU}}^{9/7}\hspace{0.17em}\text{AU}$ (17), where $r_{\text{AU}}$ is heliocentric distance in astronomical units. Here we set ${\mathrm{\Sigma }}_0$ initially to 9,000 g/cm², which is roughly 5 times that of the so-called minimum mass solar nebula (18). In this work, we set the density of the planetesimals and pebbles, ${\rho }_s$, to 3 g⋅cm⁻³. Additionally, our disk is assumed to be turbulent with $\alpha =3\times {10}^{-4}$ (19) (although see below).

We allowed the gas surface density to decrease exponentially with a timescale of $t_g=2$ Mya, which is motivated by observations (20). The disk has solar composition so that the solid-to-gas ratio is 0.005 in the terrestrial planet region (21). We convert a fraction $f_{pl}$ of the solids into planetesimals at the beginning of the simulations. We draw our planetesimals from a distribution of radii, s, of the form $dN/ds\propto s^{-3.5}$ such that s is between $s_l$ and $s_u$. The values of $s_l$ and $s_u$ are assumed to be independent of semimajor axis. We set our fiducial value of $s_u$ to the radius of Ceres, 450 km, because we expect little growth in the asteroid belt and we need to produce this object. However, we do vary $s_u$ from 100 to 600 km to test the sensitivity of our results to this value. Because we are interested in building the terrestrial planets and using the asteroid belt as a constraint, we study the growth of planetesimals spread from 0.7 AU to 2.7 AU [the presumed location of the snow line (18)]. As is typical for this type of simulation (1), we do not treat planet formation in the Mercury forming region, to save computer time.

The remaining solids (assumed to be dust) are slowly converted into pebbles with a fixed initial τ, which is a free parameter in our simulations. Following ref. 6, we use a simple prescription to convert dust into pebbles over time that assumes that pebbles form at a rate proportional to the instantaneous dust mass, correcting for dust lost as the gas disk evolves and as pebbles form. The functional form of pebble production can be found in equation 9 in Methods of ref. 6. We scale this function such that the median production timescale is roughly 700,000 y. We assume that all of the pebbles are produced in 2 Mya. For simplicity, we assume that pebbles are randomly created throughout the disk according to the surface density.

We are justified in pursuing the long timescales for pebble formation for the following reasons. Although models of dust coagulation (ref. 22, for example) predict that pebbles should grow on timescales on the order of 100–1,000 orbital periods, this result is observationally problematic. Millimeter- and even centimeter-sized particles, which should have been lost rapidly, are observed in disks of a range of ages (e.g., ref. 23). Although it is possible that the drift of these pebbles could be slowed by variations in the disk structure (24), these trapping models need large, as of yet unobserved, variations in the disk structure. A simpler alternative is that pebbles are continuously formed. Indeed, models in which pebbles slowly form from dust and then are lost due to drift matches some features of observed disks (25). Therefore, we will assume an initial planetesimal population along with pebbles that are steadily produced by the disk over its lifetime.

We also assume that the pebbles involved in terrestrial planet formation formed within 2.7 AU. By having a cutoff at this location, we are assuming that material drifting in from the outer solar system is unable to penetrate the snow line, presumably due to sublimation. However, no matter the mechanism, this assumption is required because solids from the outer solar system are too carbon-rich to have contributed more than a few percent of the mass of the terrestrial planets (see ref. 26). Also, carbon cannot be removed without heating the material to above ∼500 K (27), a temperature not reached in the midplane until well within 1 AU in reasonable disk models.

The values of τ present during VSPA are dependent on which planetesimal formation model we assume and range from $\sim {10}^{-3}$ to $\sim {10}^{-1}$ (7–10). Ideally, here we would prefer to study pebble sizes that cover the complete range required by both models. However, the CPU time required to perform our calculations increases drastically as τ decreases because of two effects. First, the timestep required by our code scales with the pebble’s aerodynamic stopping time. Thus, a smaller τ requires a smaller timestep. In addition, pebbles with small τ have slower radial drift velocities than their larger siblings, and thus spend more time in the calculation. As a result, at any time, there are more objects present in the simulation that the code needs to deal with. This significantly increases the required CPU time per timestep. Therefore, to keep the calculations tractable, we require τ to be larger than $\sim 0.01$. This issue will be addressed again in Discussion.

Each system is evolved for 110 Mya using a the Lagrangian Integrator for Planetary Accretion and Dynamics (LIPAD) (28). LIPAD is the first particle-based (i.e., Lagrangian) code, to our knowledge, that can follow the collisional/accretional/dynamical evolution of a large number of subkilometer objects through the entire growth process to become planets. It is built on top of the symplectic N-body algorithm known as SyMBA (29). To handle the very large number of subkilometer objects required by these simulations, we introduce the concept of a tracer particle. Each tracer represents a large number of small bodies with roughly the same orbit and size and is characterized by three numbers: the physical radius, the bulk density, and the total mass of the disk particles represented by the tracer. LIPAD employs statistical algorithms for viscous stirring, dynamical friction, and collisional damping among the tracers. The tracers mainly dynamically interact with the larger planetary mass objects via the normal N-body routines, which naturally follow changes in the trajectory of tracers due to the gravitational effects of the planets and vice versa. When a body is determined to have suffered an impact, it is assigned a new radius according to the probabilistic outcome of the collision based on a fragmentation law for basalt by ref. 30. In this way, the conglomeration of tracers and full N-body objects represent the size distribution of the evolving population. LIPAD is therefore unique in its ability to accurately handle the mixing and redistribution of material due to gravitational encounters, including planetesimal-driven migration and resonant trapping, while also following the fragmentation and growth of bodies. An extensive suite of tests of LIPAD can be found in ref. 28. For the calculations described here, we will use a version of LIPAD that has been modified to handle the particular needs of pebble accretion (31).

The calculations are performed in three stages. For the first 3 Mya, the terrestrial planet region is evolved in isolation as pebbles continually form and drift inward. At the end of this first stage, all pebbles have either been accreted or lost, and thus no more mass will be added to the system. Because we are interested in constructing systems similar to the solar system, we only continue simulations with the appropriate amount of material (between $2.1\hspace{0.17em}{M}_{\oplus }$ and $2.7\hspace{0.17em}{M}_{\oplus }$) inside 2 AU. If this criterion is met, the simulation is cloned 6 times by adding a random number between $-{10}^{-4}$ AU and ${10}^{-4}$ AU to each component of the position vector of each body. For this second stage, we also add Jupiter and Saturn in orbits consistent with their premigrated configuration (32). In particular, they are placed in their mutual 3:2 mean motion resonance with Jupiter at 5.2 AU and Saturn at 8.6 AU. The evolution is then followed until 100 Mya. For the final stage, Jupiter and Saturn are moved to their current orbits and the system was integrated for an additional 10 Mya.

Simulation Results

In total, we performed 28 simulations to at least 3 Mya, varying $f_{pl}$ between 0.004 and 0.01, and $s_u$ between 100 km and 600 km. For comparison, note that asteroid (1) Ceres has a radius of 476 km. Our small values for $f_{pl}$ were driven by the fact that we wanted to create asteroid belts as close to the observed system as possible assuming that VSPA is not effective there. Unfortunately, however, the smaller we force $f_{pl}$, the more tracers we needed to resolve the system and thus the more CPU time required by the simulation. Our compromise was to choose $f_{pl}$ so that the initial mass between 2.2 AU and 4 AU is roughly between 20 and 50 times the mass currently observed there. These small values of $f_{pl}$ imply that there was, at most, $0.2\hspace{0.17em}{M}_{\oplus }$ of planetesimals between 0.7 AU and 2.7 AU; most of the mass in the final planets comes from accreting pebbles.

We followed 9 of the 28 simulations to completion, making a total of 54 systems including the clones. See Supporting Information for a description of the statistics of our runs.

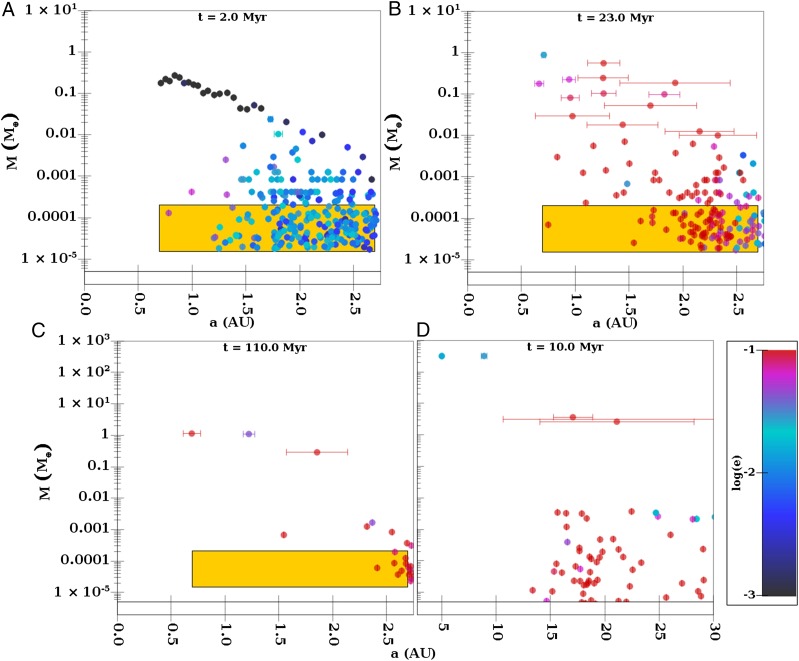
The evolution of a system that produced a reasonable solar system analog is shown in Fig. 2. For this simulation, $\tau =0.1$, s is initially between between 200 km and $450$ km, and $f_{pl}=0.01$. Growth occurs first and fastest closest to the Sun. This happens for two reasons. As described above, ${\sigma }_{\text{peb}}$ is function of semimajor axis. In addition, although we create pebbles randomly throughout our computational domain following the surface density of the gas disk, these objects quickly spiral toward the Sun due to the effects of aerodynamic drag. As a result, a planetesimal encounters pebbles that were created outward of its semimajor axis, and thus the planetesimals closest to the Sun encounter more pebbles.

Fig. 2.

(A–C) The formation of a system of terrestrial planets. Each panel shows the mass of the planetesimals and planetary embryos as a function of semimajor axis, and color indicates their eccentricity. In addition, the error bars, which are only shown for objects larger than $0.01\hspace{0.17em}{M}_{\oplus }$ to decrease clutter, indicate the range of heliocentric distance that an object travels. The yellow box shows the region populated by planetesimals at $t=0$. (A) t = 2.0 Mya, (B) t = 23.0 Mya, and (C) t = 110.0 Mya. B shows the distribution of planetary embryos after pebble accretion but before the dynamical instability. C shows the final system. (D) The fiducial giant planet system constructed in ref. 6.

The era of pebble accretion ends when all of the pebbles have been generated and have either impacted the Sun or been accreted by an embryo. At this time (Fig. 2A), there is a series of 23 embryos with masses greater than $0.01\hspace{0.17em}{M}_{\oplus }$ on quasi-stable, nearly circular orbits. There is a direct correlation between mass and semimajor axis at this time, with no object larger than Mars beyond 1.3 AU and none larger than the Moon beyond 1.9 AU. The largest object in the system is $0.27\hspace{0.17em}{M}_{\oplus }$. This correlation leads to very little mass beyond 1 AU. As expected from Fig. 1, there was little growth beyond 2 AU.

This system remains stable until 20 Mya, at which time the orbits of its embryos cross and they accrete each other. This dynamical instability leads to the formation of two roughly Earth-mass objects at 0.7 AU and 1.2 AU. It is during this instability that a 2.7 Mars-mass object is gravitationally scattered to 1.9 AU by its larger siblings and is stabilized by gravitational interactions with smaller objects found there. This leads to the system shown in Fig. 2C that contains analogs of Earth, Venus, and Mars with roughly the correct masses and orbits. The basic evolution seen here, where the system first develops a series of small planets on nearly circular orbits that suffer an instability at a few tens of millions of years, is a common outcome in our simulations. Thus, this model predicts that the solar system had an initial generation of terrestrial planets—consisting of a large number of small planets—that is now lost. Mars is likely a remnant of this early system. The late timing of the impact that formed the moon (33) resulted, in part, from this instability.

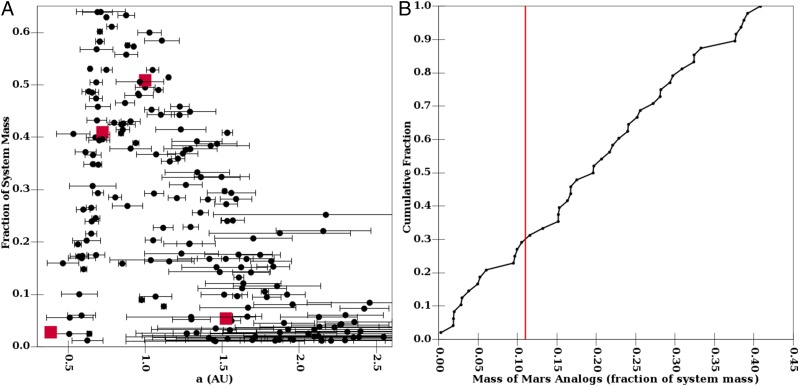
However, due to the chaotic nature of planet formation, not all of our simulations produce good solar system analogs, as shown in Fig. 3A. Also, interpreting this plot, it must be noted that we did not make any attempt to uniformly cover parameter space. Each calculation took many weeks to perform, and thus the survey of parameter space was limited and ad hoc. Thus, the observed distribution shown needs to be viewed with caution. However, we believe that some of the trends are robust. For example, it is common to produce reasonable Earth and Venus analogs. In addition, planets near 1.5 AU are systematically smaller than their siblings interior to 1 AU. No planets grow beyond 2 AU. The objects seen in this region were scattered out during a dynamical instability. The majority of these objects are still on orbits that cross their larger neighbors and thus will eventually be removed. However, a few are on stable orbits. The anomalous and highly processed main belt asteroid (4) Vesta might be an object that was captured in this manner.

Fig. 3.

The finial distribution of our planets. (A) The black dots show a compilation of the planets constructed during our simulations. In particular, we plot the fraction of total system mass in each planet as a function of its semimajor axis. Here we plot the fraction of total system mass because the total mass of our systems varies from run to run due to the stochastic variations in the efficiency of pebble accretion. The error bars indicate the range of heliocentric distance that a planet travels and thus are a function of eccentricity. The red squares indicate the real terrestrial planets in the solar system. (B) The cumulative mass distribution of Mars analogs. Planets to the left of the red line are considered good Mars analogs according to ref. 34.

The natural question is whether VSPA produces good Mars analogs more frequently than the standard planet formation picture. Ref. 34. finds that the standard model produces a good Mars analog in 4% of the simulations with Jupiter and Saturn on circular orbits (their likely state at the time of terrestrial planet formation). They define a “Mars analog” as the largest planet with a semimajor axis both in the range 1.25–2 AU and outside of Earth analog’s orbit. They define an “Earth analog” to be the largest planet between 0.75 AU and 1.25 AU, and, if there is no planet within this range, the Earth analog is the closest planet to 1 AU. A good Mars analog is defined to be an object that is smaller than $0.22\hspace{0.17em}{M}_{\oplus }$ or 11% of the total system mass. Keeping the above caveats about our parameter space coverage in mind, we plot the cumulative mass distribution of Mars analogs from our simulations in Fig. 3B. We find that 30% of our systems produce good analogs. This represents a significant improvement over the standard model. Moreover, ref. 34 finds that the probability that the standard model produces systems with both a good Mars analog and a low-mass asteroid belt is roughly 0.6%. By design, our systems always have a low-mass asteroid belt.

Discussion

The above experiments show that Mars’s small mass is a natural outcome of the process of VSPA. Having said this, there are other issues that need to be considered.

Sizes of Pebbles.

There are currently two independent models in the literature for planetesimal formation directly from pebbles that make very different predictions concerning the size of pebbles: the streaming instability and turbulent concentration. The streaming instability takes advantage of the fact that a clump of pebbles is less affected by aerodynamic drag, and thus moves at a different speed, than free-floating pebbles (8). As a result, individual pebbles catch up with the clump, and the clump grows to the point where it becomes gravitationally bound and collapses to form a planetesimal (10). This mechanism requires $\tau \approx 0.1$–1 (15). On the other hand, turbulent concentration scenarios suggest that objects with $\tau \approx {10}^{-3}$ migrate to the outer edges of turbulent eddies due to centrifugal forces caused by the eddy’s rotation (7, 9). There the pebbles form gravitationally bound clumps that collapse to create planetesimals. Although we are agnostic on which of these are correct and would prefer to cover the whole range of values, as we described above, we cannot perform simulations with τ smaller than $\sim {10}^{-2}$ because the required amount of CPU time makes these calculations impractical.

Unfortunately, there have been recent developments in our understanding of the coagulation of pebbles that call into question whether objects with $\tau \approx 0.01$ can grow in disks. In traditional models, the growth of objects is limited by particle fragmentation (25). With this limitation, particles should grow to $\tau \approx 0.1$ given the known strengths of compacted silicate grains (35). However, some coagulation simulations have identified another barrier to growth, known as the “bouncing barrier,” that halts growth of rocky pebbles at much small sizes (36, 37). If this barrier is proven robust, then pebble growth may halt at $\tau \approx {10}^{-4}-{10}^{-3}$.

The fact that we cannot perform direct LIPAD calculations with $\tau \approx {10}^{-3}$ does not imply that our basic model will not work in this regime. For example, the simple calculation shown in Fig. 1 shows that, regardless of pebble size, there is a radial dependence on the efficiency of pebble accretion. The only difference is that the transition between efficient and inefficient growth occurs at much smaller planetesimal size. This suggests that we would be able to create the same general features seen in Fig. 2C (a low-mass Mars and asteroid belt) for a range of assumed pebble sizes as long as a decrease in pebble size is commensurate with a decrease in the maximum initial planetesimal size.

This trend is already apparent with the range of pebble size we can investigate with LIPAD (see Table S1). For example, when τ was 0.08, reasonable terrestrial analogs were found only when the largest planetesimals initially in the system were bigger than ∼300 km. However, when $\tau =0.025$, simulations that initially contained planetesimals this big grew planets in the asteroid belt. For τ of this value, systems that look like our solar system occurred only when that the maximum initial planetesimal size was ∼100 km. Indeed, recent work indicates that the size distribution of the larger asteroids in the main belt could be explained by planetesimals of roughly this size accreting $\tau \approx {10}^{-3}$ pebbles (38). Therefore, we expect that an initial combination of $\tau \approx {10}^{-3}$ pebbles and planetesimals of a few tens of kilometers would result in systems like our own.

Table S1.

Our completed simulations

			$M\left(<2\hspace{0.17em}\text{AU}\right)$		$M\left(>2.1\hspace{0.17em}\text{AU}\right)$
$f_{pl}$	s, km	τ	($M_{\oplus }$)	Clone	($M_{\text{AB}}$)	$N_{\text{Mars}}$	$N_{\text{Earth}}$
0.004	50–100 km	0.02	3.3
0.004	50–100 km	0.025	2.4
				clone 1	13	1	2
				clone 2	13	0	2
				clone 3	12	0	2
				clone 4	37	1	1
				clone 5	7	0	2
				clone 6	11	0	2
0.004	50–100 km	0.03	1.6
0.004	50–100 km	0.04	1.3
0.004	50–100 km	0.06	1.1
0.004	100–300 km	0.03	3.6
0.004	100–300 km	0.06	3.1
0.004	100–300 km	0.08	2.4
				clone 1	1.2	2	1
				clone 2	11	1	3
				clone 3	82	2	2
				clone 4	112	1	4
				clone 5	31	1	3
				clone 6	37	0	2
0.004	100–300 km	0.1	1.7
0.004	200–450 km	0.03	3.9
0.004	200–450 km	0.06	3.5
0.004	200–450 km	0.08	2.8
				clone 1	2	0	2
				clone 2	7	2	2
				clone 3	5	1	2
				clone 4	10	0	3
				clone 5	17	0	3
				clone 6	50	2	2
0.004	200–450 km	0.1	2.1
				clone 1	81	0	2
				clone 2	12	1	3
				clone 3	72	2	2
				clone 4	9	3	1
				clone 5	18	0	2
				clone 6	6	2	2
0.008	100–300 km	0.03	5.7
0.008	100–300 km	0.06	3.1
0.008	100–300 km	0.08	2.4
				clone 1	82	3	1
				clone 2	32	2	2
				clone 3	110	4	1
				clone 4	31	2	2
				clone 5	17	3	1
				clone 6	19	3	1
0.008	100–300 km	0.1	2
0.008	200–450 km	0.03	5.9
0.008	200–450 km	0.06	3.8
0.008	200–450 km	0.1	2.7
				clone 1	182	3	2
				clone 2	12	2	2
				clone 3	15
				clone 4	15	1	2
				clone 5	224	2	2
				clone 6	113	3	2
0.008	200–450 km	0.3	1.1
0.008	200–600 km	0.1	2.6
				clone 1	57	1	2
				clone 2	208	3	2
				clone 3	16	2	1
				clone 4	42	2	1
				clone 5	22	3	0
				clone 6	17	3	2
0.01	100–300 km	0.06	3.6
0.01	100–300 km	0.08	3.1
0.01	100–300 km	0.1	2.6
				clone 1	0.5	0	2
				clone 2	12	1	2
				clone 3	102	1	2
				clone 4	155	2	3
				clone 5	19	0	2
				clone 6	28	1	3
0.01	200–450 km	0.03	6.3
0.01	200–450 km	0.1	2.7
				clone 1	7	2	2
				clone 2	52	2	3
				clone 3	54	0	2
				clone 4	19	1	2
				clone 5	38	1	2
				clone 6	16	1	2
0.01	200–450 km	0.3	1.2

Having said this, even if the bouncing barrier model is correct, it has some uncertainties and free parameters that might allow larger pebbles to grow, one of the most important being the assumed level of turbulence in the disk. In environments with very little turbulence ($\alpha \approx {10}^{-6}-{10}^{-5}$), it has been demonstrated that small pebbles and dust can combine to form larger aggregates with $\tau \approx {10}^{-1}$ (39).

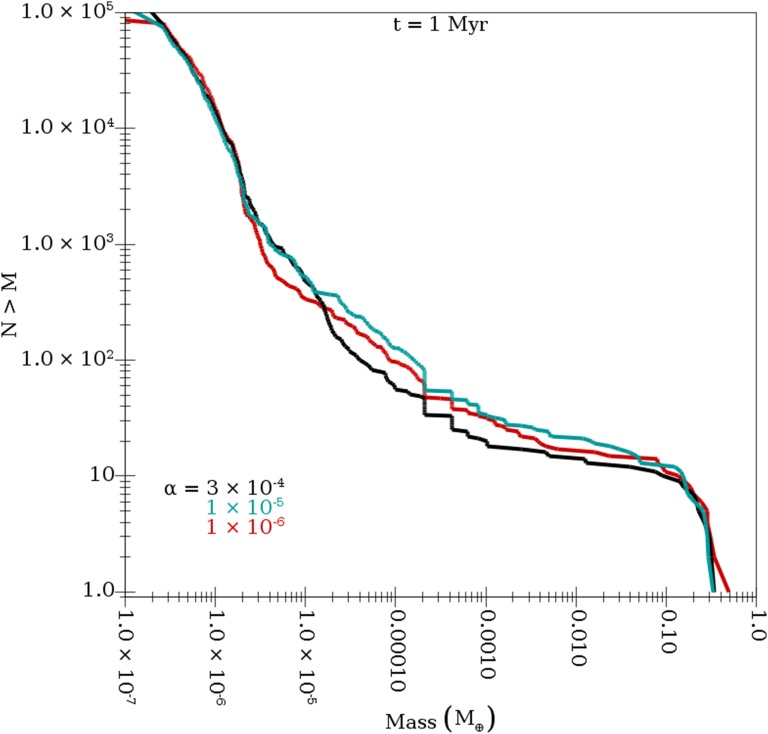
In our simulations, we chose $\alpha =3\times {10}^{-4}$, a value motivated by disk evolution timescales (20) with the assumption that uniform turbulence is driving angular momentum transport in protoplanetary disks. However, while angular momentum must be being transferred in these accretion disks, this does not necessarily imply that there is turbulence at the midplane where the pebbles and planetesimals are located. Indeed, recent models of angular momentum transport in disks suggest that turbulence may be limited to the upper and lower regions of the disk (40) or that disks may not be turbulent at all, and angular momentum may instead by transferred by magnetocentrifulgal disk winds (41). Therefore, we investigated how pebble accretion would behave in more quiescent disks that may be more consistent with our assumed pebble size. We find that the masses of the growing planetary embryos are independent of the assumed level of turbulence for α ranging from ${10}^{-6}$ to our fiducial value of $3\times {10}^{-4}$ (see Fig. S1). As a result, although we did not directly perform simulations in a low-α environment where $\tau \approx {10}^{-1}$ pebbles can form even if the bouncing barrier is important, our results are directly applicable there.

Fig. S1.

The cumulative mass distribution of objects at the end of pebble accretion (i.e., at 1 Mya) in three simulations that are identical except for α. These runs have $f_{pl}=0.004$, $s=50$ – $100$ km, and $\tau =0.025$ (our smallest value). Three values of α were studied; $\alpha =3\times {10}^{-4}$ (our fiducial value; black curve), ${10}^{-5}$ (cyan curve), and ${10}^{-5}$ (red curve). Note that all three curves are basically identical.

Implications for the Asteroid Belt.

This model also has profound implications for both the location and history of the asteroid belt. One of the primary reasons why ξ increases with heliocentric distance in Fig. 1 is because we assume the disk flares (i.e., the ratio between the gas disk scale height and the heliocentric distance increases with heliocentric distance). Although it is observed that most disks are flaring in the outer regions (42), there are not direct observations constraining the disk shape in the terrestrial planet region. Indeed, if a disk is viscously heated and one were to assume that the opacity of the disk is constant with heliocentric distance, then the disk would be flat, with a constant aspect ratio (e.g., ref. 43). However, full radiative transfer models of the structure of viscously heated accretion disks (e.g., ref. 44) show flaring interior to the snow line (which is why we made the assumption we did). This occurs because the dust opacity is expected to increase with decreasing temperatures as water freezes out. In a viscously heated disk, this occurs interior to the midplane snow line because the temperature decreases with height. The change in opacity causes the disk to flare. Thus, a region of increasing ξ is likely associated with snow lines, and VSPA might lead us to expect that asteroid belts are features that are naturally associated with regions interior to snow lines.

Our VSPA calculations also produce asteroid belts that are profoundly different from the standard model. In the standard model, the region between 2 AU and 2.7 AU originally contained several Earth masses of planetesimals—$99.9\text{\%}$ of which were lost either through the dynamical effects of Jupiter and Saturn or by collisional grinding (45) (the asteroid belt currently contains $\sim 5\times {10}^{-4}\hspace{0.17em}{M}_{\oplus }$). Because $f_{pl}$ is always less than 0.1 in our simulations and little growth occurred beyond ∼2 AU, there was never very much mass in the asteroid belt. Indeed, our final planetary systems have asteroid belts with masses between 0.5 and 155 times that currently observed in this region. The model in Fig. 2 has an asteroid belt 3.5 times more massive than the current belt. This is a reasonable value because we expect the asteroid belt to lose between roughly $50\text{\%}$ and $90\text{\%}$ of its mass due to chaotic diffusion, giant planet migration, and collisions during the subsequent evolution of the solar system (4, 46).

As previously noted by ref. 4, an early low-mass asteroid belt might explain several of its most puzzling characteristics. For example, a low-mass main belt is consistent with a limited degree of collisional evolution, as predicted by modeling work (47). Similarly, the 530-km-diameter differentiated asteroid (4) Vesta only has two 400- to 500-km-diameter basins on its surface, and one of them is only ∼1 Gy old (48). These data are a good match to a primordial main belt population that was never very massive. Finally, if Vesta formed as part of a primordial asteroid belt that contained hundreds of times the mass of the current population, then it would be statistically likely to have hundreds of Vesta-like bodies as well. Even a short interval of collisional evolution would produce more basaltic fragments than can be accommodated by the existing collisionally and dynamically evolved main belt (49). All of these observables could be explained by asteroid belts that never contained much mass, like those constructed in our models.

Additionally, we note that by varying the parameters in this model, particularly the initial planetesimal size and the pebble Stokes number, we produce a wide range of different planetary architectures. Although we present parameters that produce systems similar to our own, the natural variability of this process leads us to speculate that VSPA might be able to explain the variety in the observed exoplanetary systems (50).

Unified Picture of the Solar System Formation.

Finally for completeness, Fig. 2D shows a giant planet system constructed within the same disk and using VSPA (6). It shows two gas giant planets plus three ice giants. There is no growth beyond 20 AU because ξ is again large.

We note that we get growth in the giant planet region (6) and not in the asteroid belt for at least three reasons: (i) The initial planetesimals were probably larger in the outer solar system (to be consistent with the larger sizes of object in the Kuiper Belt compared with the asteroid belt). In particular, in this work, we use a maximum planetesimal size in the terrestrial region based on Ceres, whereas, in ref. 6. we used a maximum planetesimal size based on Pluto in the giant planet region. (ii) The pebble sizes were likely also bigger because the pebbles are icy and thus stickier (51). (iii) The giant planets have access to a much larger reservoir of pebbles than the inner solar system due to sublimation of ices at the snow line. In particular, as we explained above, here we assume that pebbles from the outer solar system do not contribute to the growth of the terrestrial planets. As a result, the terrestrial planets only have access to solids out to 2.7 AU. In ref. 6, we assumed that pebbles formed out to $30$ AU and thus the giant planets had access to the substantially larger amount of solids that were between 2.7 AU and 30 AU.

Fig. 2 C and D, therefore shows a consistent planetary system generated by VSPA. This model reproduces the basic structure of our entire planetary system—two roughly Earth-mass objects between 0.5 U and 1 AU, a small Mars, a low-mass asteroid belt, two gas giants, ice giants, and a primordial Kuiper belt that contains objects the mass of (134340) Pluto and (136199) Eris but did not form planets.

Statistics of Our Simulations

Table S1 lists the simulations that we have completed in our investigation of terrestrial planet formation. All of these used the following setup. We used a total surface density distribution of $\mathrm{\Sigma }={\mathrm{\Sigma }}_0{r}_{\text{AU}}^{-1}$, where $r_{\text{AU}}$ is the heliocentric distance in astronomical units, and ${\mathrm{\Sigma }}_0=\mathrm{9,000}\hspace{0.17em}{e}^{-t/2\text{Mya}}\text{g}/{\text{cm}}^2$. The disk flares with a scale height of $h=0.047\hspace{0.17em}{r}_{\text{AU}}^{9/7}\hspace{0.17em}\text{AU}$ (17). We assume a solid-to-gas ratio of 0.005 and a bulk density of 3 g/cm³. Pebbles are slowly generated and follow the same spatial distribution as $\mathrm{\Sigma }$ above. In particular, because pebble generation follows the evolution of the gas disk, the median time for which a pebble is generated is ∼0.7 Mya.

There are three important free parameters that we varied. These are listed in the first three columns of the tables:

• i)The first parameter is the fraction of solids in the disk that are initially converted into planetesimals, $f_{pl}$. For the fiducial simulation, $f_{pl}=0.01$.
• ii)The second parameter is the range of initial radii of the planetesimals. We draw the initial planetesimals from a distribution of radii, s, of the form $dN/ds\propto s^{-3.5}$ (52). For our fiducial simulation, $200\le s\le 450$ km.
• iii)The third parameter is the initial Stokes number of a pebble, τ. Note that as pebbles spiral toward the Sun, their Stokes number changes (generally decreases) because both the gas density and the orbital period vary. For our fiducial simulation, $\tau =0.1$.

The last four columns in Table S1 present the basic characteristics of our systems. In particular, $M\left(<2\hspace{0.17em}\text{AU}\right)$ is the total mass found within 2 AU at 3 Mya. Recall that we only continued to integrate systems for which $2.1\hspace{0.17em}{M}_{\oplus }\le M\left(<2\hspace{0.17em}\text{AU}\right)\le 2.8\hspace{0.17em}{M}_{\oplus }$. We chose this range because it is slightly larger the total of the terrestrial planets ($2.0\hspace{0.17em}{M}_{\oplus }$) and thus allows for some subsequent loss. We created six clones of any run that satisfies the above criterion. The clone identification is listed in the 5th column. The next column, M(>2.1 AU), lists the total mass in the asteroid belt (here defined to be between 2.1 AU and 5 AU) in terms of the currently observed asteroid belt mass ($M_{\text{AB}}$). Finally, the last two columns list the total number of planets with mass between 0.5 Mars mass and $0.5\hspace{0.17em}{M}_{\oplus }$ ($N_{\text{Mars}}$) and the number with mass greater than $0.5\hspace{0.17em}{M}_{\oplus }$ ($N_{\text{Earth}}$), respectively.