Fate of MgSiO₃ melts at core–mantle boundary conditions

Significance

A new technique has been developed to measure in situ the density of amorphous material composed of light elements under extreme conditions of pressure using the X-ray absorption method. At core–mantle boundary (CMB) pressure, the densities of MgSiO₃ glass and melts are similar to the one of the crystalline bridgmanite, within uncertainty. Due to the affinity of iron oxide for silicate liquids, melting in the MgSiO₃–FeSiO₃ system will produce dense melts that could accumulate above the CMB, leading to the formation of a dense basal magma ocean in the early Earth's mantle.

Abstract

One key for understanding the stratification in the deep mantle lies in the determination of the density and structure of matter at high pressures, as well as the density contrast between solid and liquid silicate phases. Indeed, the density contrast is the main control on the entrainment or settlement of matter and is of fundamental importance for understanding the past and present dynamic behavior of the deepest part of the Earth’s mantle. Here, we adapted the X-ray absorption method to the small dimensions of the diamond anvil cell, enabling density measurements of amorphous materials to unprecedented conditions of pressure. Our density data for MgSiO₃ glass up to 127 GPa are considerably higher than those previously derived from Brillouin spectroscopy but validate recent ab initio molecular dynamics simulations. A fourth-order Birch–Murnaghan equation of state reproduces our experimental data over the entire pressure regime of the mantle. At the core–mantle boundary (CMB) pressure, the density of MgSiO₃ glass is 5.48 ± 0.18 g/cm³, which is only 1.6% lower than that of MgSiO₃ bridgmanite at 5.57 g/cm³, i.e., they are the same within the uncertainty. Taking into account the partitioning of iron into the melt, we conclude that melts are denser than the surrounding solid phases in the lowermost mantle and that melts will be trapped above the CMB.

Variations in seismic velocities observed in the deep mantle could be attributed to melting phenomena (1), accumulation of dense matter (2), core–mantle interactions (3), or even a deep hidden geochemical reservoir that dates from the early differentiation of the Earth (4). Indeed, melting phenomena play a critical role in the formation and evolution of terrestrial planets. In the early Earth’s history, large-scale melting events and magma oceans facilitated the segregation of the iron-rich core and the partitioning of elements between the different layers of the Earth (5). Catastrophic events like the moon-forming giant impact may have melted the entire Earth and modified the thermal and chemical state of the planet’s interior (6). It has long been thought that the mantle crystallized from the bottom to the top, with crystals being denser than melts (7). However, the formation of a dense basal magma ocean (BMO) at the bottom of the mantle concomitant to the final accretion of the Earth was proposed as a consequence of partial melting (2). The formation of a BMO requires the accumulation of dense iron-rich silicate melts at the core–mantle boundary (CMB). In this scenario, the mantle starts to crystallize at an intermediate depth, and a raft of crystals continues to grow toward both the bottom and top of the mantle. In the modern mantle, seismic observations highlight ultralow velocity zones (ULVZs) near the CMB (8) that may be caused by melting of deep mantle material (9), potentially feeding sources of hot spots. Alternatively, the ULVZs may be dense remnants from an initial BMO (10, 11). Both scenarios for the formation of the Earth’s mantle and its geodynamical evolution critically depend on the density and fate of silicate melts at high pressure. Indeed, the main parameter that controls the entrainment and/or settling of materials in the deep Earth is the density contrast between crystals and melts at relevant pressures (P) and temperatures (T). Thus, knowledge of the densities of melts and their equation of state (EoS) is of prime importance to understand the past and present structures of the lowermost part of the mantle. However, high-pressure density data are lacking due to experimental challenges. Although many experiments on both melts and glasses densities have been carried out in large volume apparatus to pressures of 20 GPa (12, 13), the few studies conducted in the diamond anvil cell (DAC) were limited to 50–60 GPa (14, 15). Studying glasses is a potential alternative for understanding melts because many of their physical properties are similar to those of melt: from the atomistic scale, with the evolution of the silicon coordination number from fourfold to sixfold from 0 to 40 GPa (15), to the macroscopic scale with similarities in compressibility (16, 17). Using the X-ray absorption technique adapted to the DAC, we more than double the pressure range for density measurements on amorphous materials. We extend the dataset for MgSiO₃ glass to CMB pressures and propose an EoS for MgSiO₃ melts that spans the entire mantle.

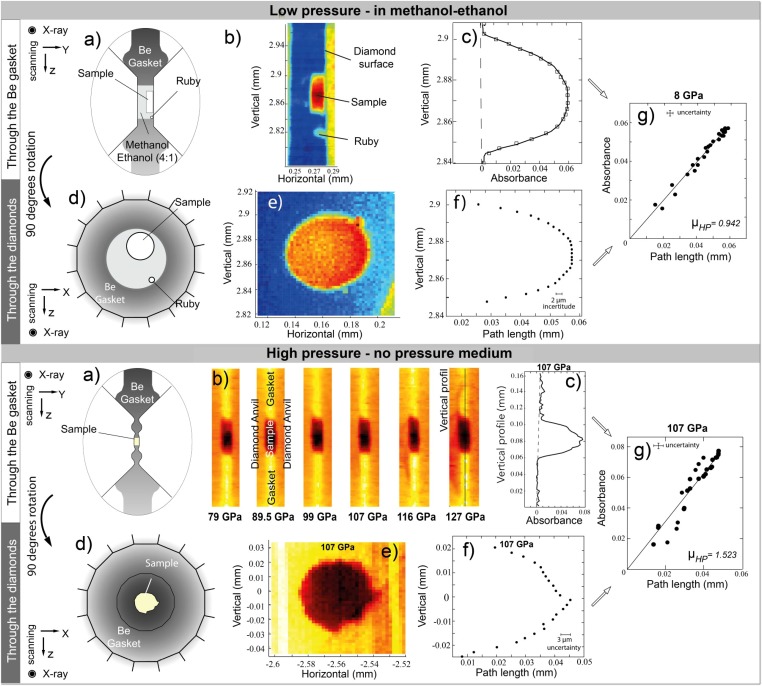
The MgSiO₃ glass starting materials were prepared using an aerodynamic levitation setup (SI Appendix, Fig. S1) and measured in situ at high pressure at the ID13 beamline of the European Synchrotron Radiation Facility (ESRF; Grenoble, France) (SI Appendix, Fig. S3 A and B). Samples were pressurized in DACs and sealed in beryllium (Be) gaskets giving radial access for the X-ray beam. For pressures below 20 GPa, discs of MgSiO₃ glass were cut using a focus ion beam (FIB) (SI Appendix, Fig. S2), loaded in a Be gasket, and immersed in a methanol–ethanol mixture. For pressures above 20 GPa, the sample chamber was filled with MgSiO₃ glass powder only. Pressure was recorded via the ruby luminescence for pressures up to 60 GPa and with the Raman signal of the diamond culet for higher pressures and was kept for about 30 min before the measurements. The X-ray absorbance of the silicate MgSiO₃ glass was monitored through the Be gasket (Fig. 1A) by collecting an absorbance map in the radial geometry (Fig. 1 B and C). The DAC was then rotated at 90°, and an absorbance map was collected along the compression axis (Fig. 1 D and E) to obtain the path lengths of material exposed to the X-rays in the radial geometry (Fig. 1F). The attenuation coefficient at high pressure (µ_HP) was calculated by combining the path lengths of the sample with the absorption map collected in the radial geometry (Fig. 1G and SI Appendix, Fig. S6). The density at high pressure (ρ_HP) was calculated by

$${\rho }_{\mathrm{HP}}/{\mu }_{\mathrm{HP}}={\rho }_{\mathrm{0}}/{\mu }_{\mathrm{0}}.$$ [1]

The attenuation coefficient at ambient pressure (µ₀) was determined from a double-polished plate of MgSiO₃ (SI Appendix, Fig. S4), and the ambient pressure density was measured by the sink/float method (ρ₀ = 2.770 ± 0.028 g/cm³).

Fig. 1.

X-ray absorption measurements in the DAC during low-pressure (Upper) and high-pressure runs (Lower). (A–C) Measurement of the absorption of the sample through the Be gasket. (A) Sample and measurements geometry with respect to the X-rays. (B) Absorbance map through the gasket with (Upper) and without (Lower) transmitting medium. (C) One vertical absorption profile of the sample (one row of pixels). (D–F) Sample dimensions and path length of material exposed to the X-rays. (D) Measurement geometry. (E) Absorbance map through the diamonds. (F) Path length of sample extracted from the map. (G) The combination of C and F is used to measure the absorption coefficient (μ_HP).

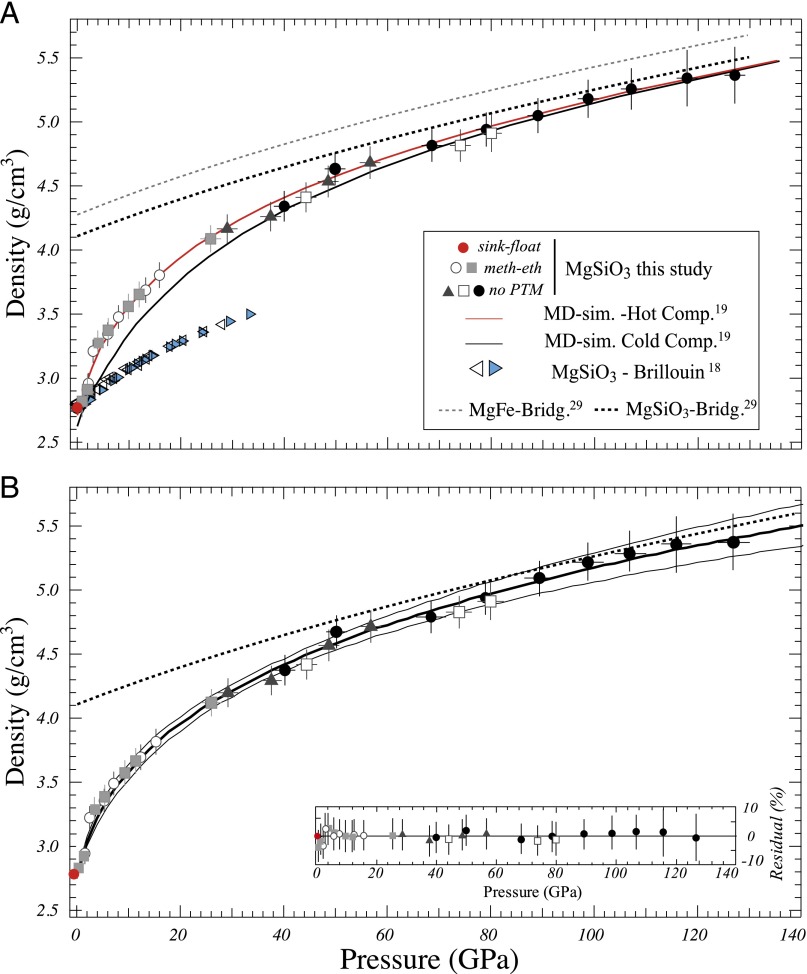
Our densities for MgSiO₃ glass range from 0 to 127 GPa and show a steep increase up to 30 GPa and a moderate increase at higher pressures (Fig. 2 A and B and SI Appendix, Table S2). The density data are consistent independently of the presence or absence of a pressure transmitting medium: both the low-pressure data and high-pressure data overlap at 25 GPa (Fig. 2 A and B). The data can be fitted with a fourth-order Birch–Murnaghan (BM) EoS with V₀ = 36.24 ± 0.36 cm³/mol (fixed by ρ₀), K_T0 = 16.9 ± 3.2 GPa, K′_T0 = 5.9 ± 1.3, and K″_T0 = −0.004 ± 0.77 GPa⁻¹. The EoS reproduces the data within 1.2% (1 SD) (Fig. 2B). Note that a Vinet EoS fits the data nearly as well (1 SD = 1.5%), but with less plausible fit parameters (K_T0 = 14.3± 3.3 GPa, K′_T0 = 8.4± 1.0; SI Appendix, Fig. S9). The densities predicted by the Vinet EoS agree within 1% with those predicted by the BM EoS. At low pressure, MgSiO₃ glass is an order of magnitude more compressible than its bridgmanite counterpart; although K_T increases with increasing pressure and silicon coordination, the glass remains more compressible than the crystalline phase. There is a clear contrast between our data and those derived from Brillouin measurements on the MgSiO₃ glass (18). We found a density of 4.27 ± 0.2 g/cm³ at 33 GPa compared with 3.5 ± 0.01 g/cm³ from the Brillouin data. The bulk moduli also exhibit a large discrepancy: K_T0 = 16.9 ± 3.2 GPa in our study compared with K_T0 = 78.4 ± 0.6 GPa determined from the Brillouin data (18). The densities recalculated from Brillouin data make use of the unrelaxed sound velocities (19). As a result, only elastic, but not the configurational, contributions to the compressibility are probed by Brillouin scattering, and the compressibility is underestimated. In contrast, our data agree well with recent ab initio molecular dynamic (MD) simulations (Fig. 2A) (19). MgSiO₃ glass is as compressible as MgSiO₃ melt with a K_T0 = 16.9 ± 3.2 GPa vs. K_T0 = 20 GPa (20), respectively. Thus, it appears that over a sufficiently large pressure range, our experimental method probes both the elastic and configurational contributions to the compressibility, even for high-viscosity material like glasses. Although both bulk moduli are in good agreement, it is possible that the glass has not reached its full configurational equilibrium and that our density data represent a lower bound, i.e., fully equilibrated melts could be even somewhat denser than our data suggest.

Fig. 2.

Density of MgSiO₃ glass. (A) Density data for five different high-pressure experiments either in methanol-ethanol mixture (meth-eth, gray squares and white circles) or without pressure transmitting medium (PTM) (no PTM, black triangles and circles and white squares). The results from MD simulations (6) for hot (red curve) and cold (black curve) compression, Brillouin spectroscopy measurements (5) (open and blue triangles), and densities for MgSiO₃ (dashed gray) and Mg_0.9 Fe_0.1 SiO₃ (dashed black) bridgmanites are also plotted. (B) Fourth-order BM EoS fit of our data. (Inset) Fit residual. The thick black curve is the best fit; the thin lines bracket the 95% CI.

Starting from our room temperature EoS, we computed melt densities along different isotherms using the formalism in Stixrude et al. (21), which uses the Mie–Gruneisen form with

$$P\left(V,T\right)=P_{\mathrm{c}}\left(V,T_{\mathrm{0}}\right)+P_{\mathrm{th}}\left(V,T\right)=P\mathrm{c}\left(V,T_{\mathrm{0}}\right)+\gamma /vCv\left(T-T_{\mathrm{0}}\right),$$ [2]

and

$$\gamma /vCv\left(T-T_{\mathrm{0}}\right)=\alpha K_T\left(T-T_{\mathrm{0}}\right).$$ [3]

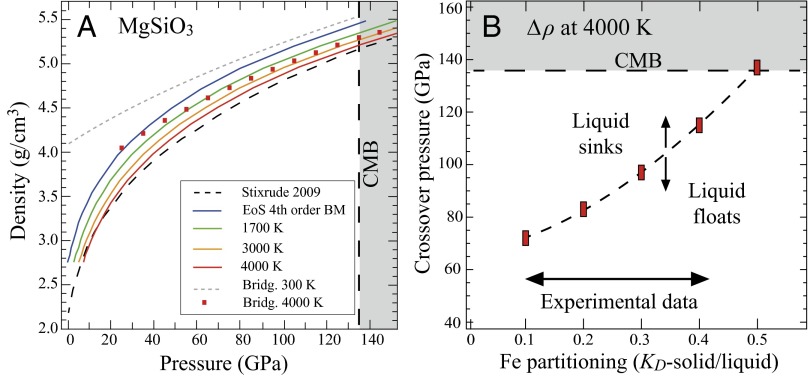
P_c(V,T₀) is the reference equation of state at the reference temperature (300 K), and P_th is the thermal pressure. We used data computed by de Koker et al. (22) for αK_T, which is independent of temperature but varies with volume and can be fitted using a power law curve (SI Appendix, Fig. S10). Our experimental isotherms agree with the isotherms from MD simulations along different isotherms (19, 21, 23) (Fig. 3A). At 4,000 K and 135 GPa, the density contrast between molten and crystalline MgSiO₃ (bridgmanite) is only 1.6% (Fig. 3A). The small density contrast highlights that density cross-overs are probable, and melts can be as dense or even denser than the surrounding solids in the deep mantle, regardless of the presence of a poly-amorphous phase transition near 133 GPa (11), which may lead to a density inversion at even higher pressure as highlighted by shock compression experiments (24) (SI Appendix, Fig. S11). The buoyancy of melts in the deep Earth is strongly influenced by the addition of iron as the main heavy element. Although the partitioning of iron (K_D) between solid and melts remains controversial at lower mantle pressures (9, 25), it is agreed that iron is an incompatible element. Therefore, iron is enriched in the melt phase with a K_D value as low as ∼0.4–0.3 at 25 GPa (26, 27) and most likely even lower at higher pressures. Given that even in the absence of iron, MgSiO₃ melt is already nearly as dense as its crystalline counterpart at CMB conditions (Fig. 3A), melts enriched in iron will be more dense than their equilibrium minerals, regardless of the exact nature of the iron partitioning. With our MgSiO₃ density data at 4,000 K and FeSiO₃ density data at 4,000 K from Ramo and Stixrude (28), we calculated the density cross-over pressure in the MgSiO_3–FeSiO₃ system as a function of iron partitioning. For the available iron partitioning data, a density cross-over will occur in the lower mantle between solid bridgmanite (29) and liquid with a similar composition at 4,000 K (Fig. 3B). However, the thickness of the layer where melts are denser than the solids varies from 1,600 km to only a few tens/hundreds of kilometers depending on the iron partitioning behavior between melts and bridgmanite. For super-Earths, which may have stable postperovskite at pressures above 135 GPa and 4,000 K, the evaluation of density cross-over would require density data of postperovskite end members and iron partitioning behavior for this phase.

Fig. 3.

(A) MgSiO₃ melt density along different isotherms. From the fourth-order BM EoS at 300 K (blue curve), we extrapolate our results to high temperature using the thermal expansion of MgSiO₃ melts. Also reported are the results for MgSiO₃ melts at 4,000 K calculated by Stixrude and Karki (21) (dashed black curve), as well as the EoS for MgSiO₃ bridgmanite (29) at 300 and 4,000 K (29). (B) The density cross-over pressure in the MgSiO₃–FeSiO₃ system. The double arrow represents the range of experimental data for the lower mantle KD.

In conclusion, our experimental density data at CMB pressures confirm the viability of a BMO and the possibility of melts being trapped in the lowermost mantle. Thus, partial melting in the deepest part of the Earth will favor the enrichment and storage of incompatible radiogenic elements at the CMB (27). These trapped melts, or their Fe-rich crystallization products, may explain the large low shear velocity provinces (LLSVPs) area and ULVZs above the CMB and constitute an ideal candidate for a hidden geochemical reservoir.