Collapse of the West Antarctic Ice Sheet after local destabilization of the Amundsen Basin

Significance

The Antarctic Ice Sheet is losing mass at an accelerating rate, and playing a more important role in terms of global sea-level rise. The Amundsen Sea sector of West Antarctica has most likely been destabilized. Although previous numerical modeling studies examined the short-term future evolution of this region, here we take the next step and simulate the long-term evolution of the whole West Antarctic Ice Sheet. Our results show that if the Amundsen Sea sector is destabilized, then the entire marine ice sheet will discharge into the ocean, causing a global sea-level rise of about 3 m. We thus might be witnessing the beginning of a period of self-sustained ice discharge from West Antarctica that requires long-term global adaptation of coastal protection.

Abstract

The future evolution of the Antarctic Ice Sheet represents the largest uncertainty in sea-level projections of this and upcoming centuries. Recently, satellite observations and high-resolution simulations have suggested the initiation of an ice-sheet instability in the Amundsen Sea sector of West Antarctica, caused by the last decades’ enhanced basal ice-shelf melting. Whether this localized destabilization will yield a full discharge of marine ice from West Antarctica, associated with a global sea-level rise of more than 3 m, or whether the ice loss is limited by ice dynamics and topographic features, is unclear. Here we show that in the Parallel Ice Sheet Model, a local destabilization causes a complete disintegration of the marine ice in West Antarctica. In our simulations, at 5-km horizontal resolution, the region disequilibrates after 60 y of currently observed melt rates. Thereafter, the marine ice-sheet instability fully unfolds and is not halted by topographic features. In fact, the ice loss in Amundsen Sea sector shifts the catchment's ice divide toward the Filchner–Ronne and Ross ice shelves, which initiates grounding-line retreat there. Our simulations suggest that if a destabilization of Amundsen Sea sector has indeed been initiated, Antarctica will irrevocably contribute at least 3 m to global sea-level rise during the coming centuries to millennia.

The Antarctic Ice Sheet is losing mass at an accelerating rate, and thus increasingly contributes to global sea-level rise (1, 2). To what extent this is caused by anthropogenic warming of the atmosphere is unclear. The Amundsen Sea sector of West Antarctica accounts for the largest part of the ice loss, manifesting in a speed-up, thinning, and retreat of tributaries such as Pine Island Glacier and Thwaites Glacier during the last 4 decades (3–5). Large portions of the West Antarctic Ice Sheet (WAIS) are grounded on bedrock below sea level (6, 7). These so-called marine parts of the ice sheet hold an ice volume that would elevate global mean sea level by about 3.3 m (8). The bed below this marine ice is generally down-sloping in the inland direction. A grounding line (the line that separates the grounded ice sheet from the floating ice shelf) that is located on such bed has been shown to be potentially unstable (9, 10). The associated marine ice-sheet instability (i.e., self-sustained ice-sheet retreat) can be hindered by the buttressing of ice shelves, which has been investigated in different modeling frameworks (11–14).

The recently inferred destabilization of the Amundsen Sea sector coincides with an increase in the volume and temperature of relatively warm circumpolar deep water that reaches into the ice-shelf cavities in the Amundsen Sea (15, 16). The resulting substantially enhanced sub-ice-shelf melting facilitated the retreat of the grounding line of several tributaries onto the potentially unstable down-sloping bed section. Complex, high-resolution regional modeling studies (17, 18) confined to the Pine Island and Thwaites catchments, respectively, concluded that the retreat of the ice is likely to continue in the near future. The findings are supported by observations that indicate ongoing destabilization (3), including the possibility of a developing marine ice-sheet instability (4). These state-of-the-art regional simulations need to be complemented by simulations of the long-term evolution of the region to deduce implications for the interior region of the WAIS.

Here we provide such simulations and investigate the response of the WAIS to a destabilization of the Amundsen Sea sector in ice-dynamical simulations with the Parallel Ice Sheet Model (PISM). Previous numerical simulations with PISM showed an ocean-triggered destabilization of a basin of marine ice in the Wilkes basin of East Antarctica (19), but no instability in the catchment of the Filchner–Ronne Ice Shelf (20), even for strong projected ocean warming (21). Simulations provided here cover the whole WAIS and allow for an examination of the long-term evolution of the WAIS and its associated sea-level contribution, respectively.

Results and Discussion

Our thermomechanically coupled, 3D, ice-sheet model (22, 23) (Methods) applies a superposition of the shallow-ice and the shallow-shelf approximation (24) of the stress balance that ensures a smooth transition between the different flow regimes of an ice sheet, ranging from bed-frozen inland ice to well-lubricated, fast-flowing ice streams and freely floating ice shelves. Stress transmission across the grounding line allows for the effect of ice-shelf buttressing. The grounding line is free to evolve, and a reversible grounding-line motion that is comparable to results from full-Stokes simulations was demonstrated in the Marine Ice Sheet Model Intercomparison Project for plan-view models for horizontal resolutions of 5 km and finer (25).

Initialization of the Simulations and Model Performance.

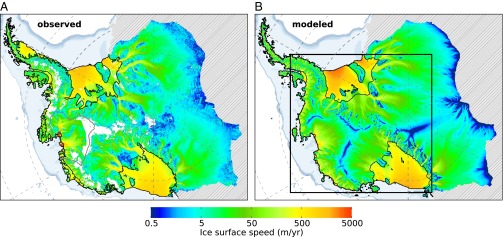
The result of this study is an if–then statement, saying that if the Amundsen Sea Sector is destabilized, then the entire marine part of West Antarctica will be discharged into the ocean. To this end, we spin up our model, using present-day initial ice and bed topography under present-day constant atmosphere conditions and 20th-century sub-ice-shelf melting. The model domain comprises the entire WAIS, the Antarctic Peninsula, and part of East Antarctica (Fig. 1). We obtain an ice sheet in equilibrium with stable ice margins comparable to present-day observations (Fig. 2), with a total ice volume that differs by −1.8% from observations. The largest deviations from the present-day grounding line position occur in the Siple Coast region, (i.e., the Ross Ice Shelf), where our modeled position is landward-biased by several 10 km (Figs. 1B and 2). Difficulties in reproducing the observed grounding-line position with our model arise particularly from the region's flat bed topography beneath the ice streams and from limitations in our parameterization of basal friction (Methods). In contrast, the modeled grounding line is in good agreement with observations for the Filchner–Ronne Ice Shelf (with the exception of some narrow troughs) and in the Amundsen Sea sector (Fig. 1 B and C), which is the relevant region for our perturbation experiments. Although we do not resolve the West Antarctic ice velocity field in full detail, the overall observed flow pattern of the WAIS, including the location of finely branched ice streams, is captured in our equilibrium simulation (compare Fig. 2 A and B). In the Amundsen Sea sector, both the Pine Island and Thwaites tributaries are captured by the model, although they are less separated from each other than observed. The same holds for the Siple Coast ice streams that feed the Ross Ice Shelf from the WAIS direction. The ice streams that originate in East Antarctica and terminate in the Ross Ice Shelf, being strongly confined by the Transantarctic Mountains, are captured individually by the model. Observed and modeled flow patterns match best for the Filchner–Ronne catchment, where most of the East and West Antarctic tributaries are clearly resolved in our simulation.

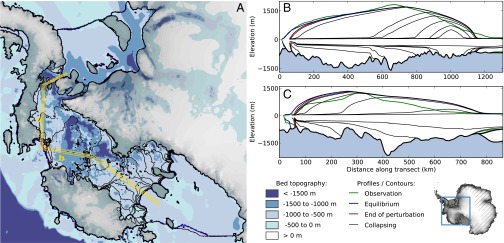
Fig. 1.

Collapse of the WAIS in response to 60 y of currently observed sub-ice-shelf melting in the Amundsen Sea. (A) Simulated initial steady-state grounding line and calving front before perturbation (dark blue contours) and at the end of perturbation (red contours) underlaid by bed topography (blue shading). Grounding-line positions during the collapse in 1,000-y time steps (black contours). Final steady-state grounded ice body in transparent gray with gray contours of surface elevation. Cross sections for ice and bed topography of B and C (yellow lines). (B and C) Transects are displayed from the Amundsen Sea Sector (Left) into the Ross Ice Shelf (B) and Filchner–Ronne Ice Shelf (C) (Right). Colors as in A, with additional profiles from present-day observations (49) in green. (Inset) Region outside the model domain (hatched) and area of A (blue rectangle).

Fig. 2.

(A) Observed present-day (50) and (B) modeled surface speed in equilibrium for the whole model domain (region outside model domain hatched). Observed (49) and modeled grounding line and calving front, respectively (black contours), and bathymetry (light blue shading). Gray contour in A delineates present-day catchment basin of the Amundsen Sea sector (51).

Destabilization of Amundsen Sea Sector.

The field of sub-ice-shelf melting we apply during model spin-up is obtained from a 20th-century simulation of the Finite Element Sea Ice-Ocean Model (Methods) and underestimates present-day sub-ice-shelf melt rates in the Amundsen Sea by an order of magnitude (21). To account for the currently observed enhanced ice-shelf melt that is considered to have destabilized the ice in the Amundsen Sea sector, we perturb our equilibrium state by scaling the regionally underestimated melt-rate field, making the applied melt rates compatible with present-day observations. The perturbation is confined to the Amundsen Sea and is applied as a pulse for periods of different duration (20–200 y), after which the original ocean conditions with melting strongly below the presently observed values are applied.

With the onset of our perturbation of the steady-state ice sheet, the simulated net mass loss from the Amundsen Sea sector increases from approximately zero to an average rate of ∼0.2 mm sea-level equivalent per year (sle/y; black curve in Fig. 3A, see lowermost blue curve for comparison with unperturbed control run). Measurements during the last 2 decades range from a minimum of 0.05 mm sle/y in the mid-1990s to a maximum of 0.32 mm sle/y in 2009 (26). Using the measured rates to extrapolate cumulative net ice loss (dashed lines that span gray area in Fig. 3A), we show that our modeled sea-level contribution from the perturbed region lies well within the range of observations. Simulated average effective melt rates below the Amundsen ice shelves during the perturbation period range from 30 to 33 m/y. Maximum melt rates of 75–145 m/y, in agreement with recent observations for Pine Island and Thwaites glaciers, occur close to the grounding line. For comparison, average observed rates are 16–33 m/y (27, 28), and maximum rates are observed to be above 100 m/y at the grounding line (29). The modeled ice sheet responds to the applied enhanced melting by inland-spreading ice thinning and grounding-line retreat (compare blue with red profiles in Fig. 1 B and C), consistent with the observed present-day situation in the Amundsen catchment basins (3).

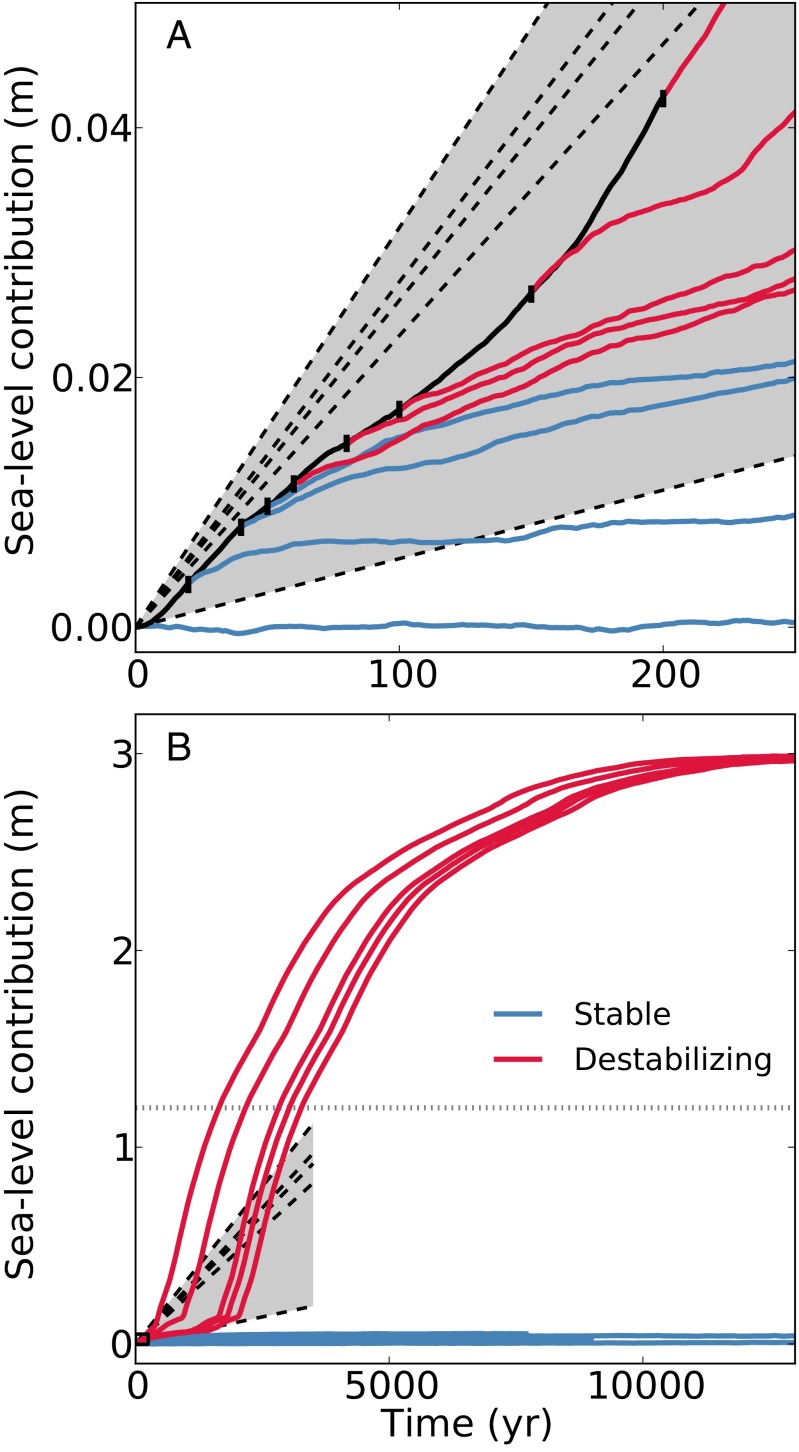
Fig. 3.

Time evolution of the sea-level contribution after the beginning of the perturbation of the equilibrium ice sheet for (A) the first 250 y, covering the perturbation phase (black), and (B) the full simulation. Each colored line represents an individual simulation characterized by a different perturbation duration (end of perturbation after 0, 20, 40, 50, 60, 80, 100, 150, and 200 y, respectively, marked by vertical bars). Stable and unstable simulations in blue and red, respectively. Gray shading shows the range of cumulative sea-level contribution spanned when extrapolating rates of net ice loss from Amundsen Sea sector that were measured for five periods during the last two decades [dashed lines (26)]. Horizontal dotted gray line in B gives the calculated sea level equivalent for a complete drainage of the Amundsen catchment basins (3).

Ice Sheet Response after Destabilization.

After cessation of the perturbation, the original 20th-century melt rates are applied and ice-discharge rates slightly level off (Fig. 3A) during a phase of local ice adjustment. For simulations with a perturbation duration of at least 60 y, an abrupt increase in ice loss then marks the onset of the self-sustained ice loss (Fig. 3B). In these destabilized simulations, the major part of West Antarctica's marine ice disintegrates: The major part of the catchment of the Pine Island and Thwaites glaciers (gray contour in Fig. 2A) is drained in less than 3,000 y (Fig. 4B). The grounding line retreats rapidly inland, following the negative bed gradient into the deep Byrd Subglacial Basin (Figs. 1 and 4 and Movie S1). Further retreat into the interior of the WAIS comes to a halt at the steep bed of the Ellsworth Subglacial Highlands but continues laterally into the marine parts of Ellsworth Land and Marie Byrd Land (Fig. 4C).

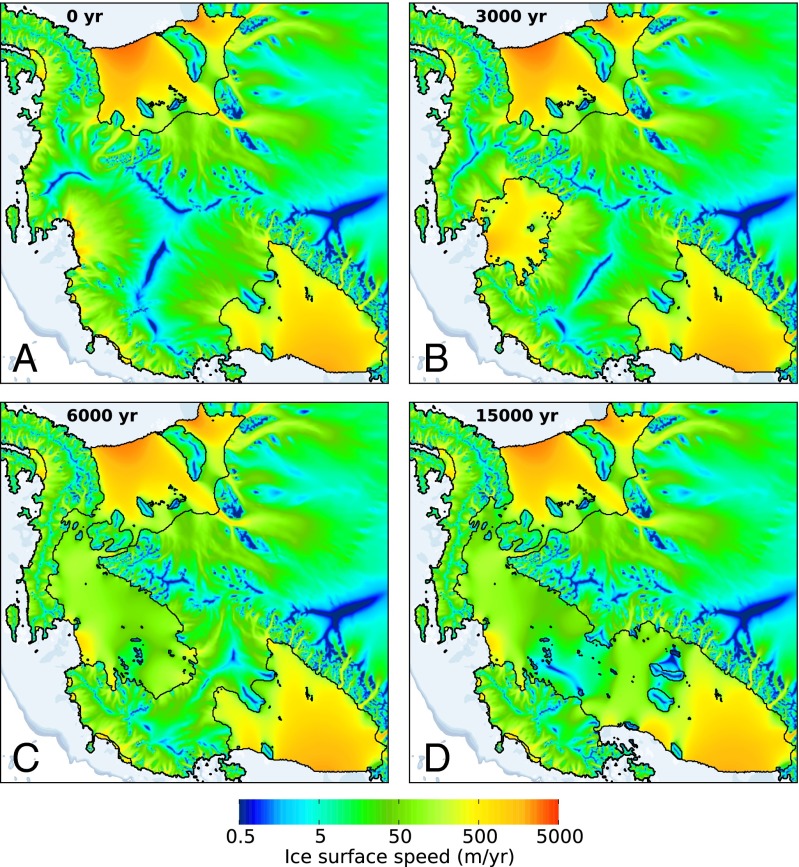
Fig. 4.

Snapshots of modeled surface speed at (A) 0, (B) 3,000, (C) 6,000, and (D) 15,000 y after onset of the 60-y perturbation (zoom into region depicted by rectangle in Fig. 2B, same region as in Fig. 1). Areas of very small ice velocities mark the ice-divide location that shifts from Amundsen into the Ross and Filchner–Ronne basins during ice-sheet retreat (compare A, B, and C). Comparison of B and C reveals grounding-line destabilization from the landward direction in the catchment basin of the Ross Ice Shelf.

Today, these areas act as reservoirs that feed the Filchner–Ronne and Ross ice shelves, respectively. In the course of the destabilization, the widespread thinning causes the ice divides that mark the catchment areas of Pine Island and Thwaites glaciers at present to migrate into the drainage basins of Filchner–Ronne and Ross ice shelves, respectively (indicated by blue regions of small surface speed in Fig. 4 A–C). The thinning signal reaches well beyond the ice divides and eventually arrives at the grounding lines of these basins. This grounding-line perturbation from the landward direction induces ice-sheet destabilization, also from the Filchner–Ronne and Ross directions (black contours in Fig. 1A, also compare Fig. 4 B and C). At some point, the rate of grounding-line retreat is similar for both landward and ocean directions (Fig. 1B). The underlying mechanism has been introduced previously, using a 2D conceptual framework (30), but here it also manifests in a complex, real-world domain that includes the important effect of buttressing.

The remnants of the ice sheet equilibrate after ∼13 ky, and total sea-level contribution by that time has reached about 3 m (Fig. 3B). In the new equilibrium state, an area of around 0.96· 10⁶ km² of originally grounded ice several kilometers in thickness is covered by an extensive ice shelf that is less than 500 m thick on average. The trans-Antarctic seaways between the previously unconnected Amundsen, Weddell, and Ross seas are opened (Fig. 4D), which is a situation that probably prevailed the last time during the Pleistocene (31).

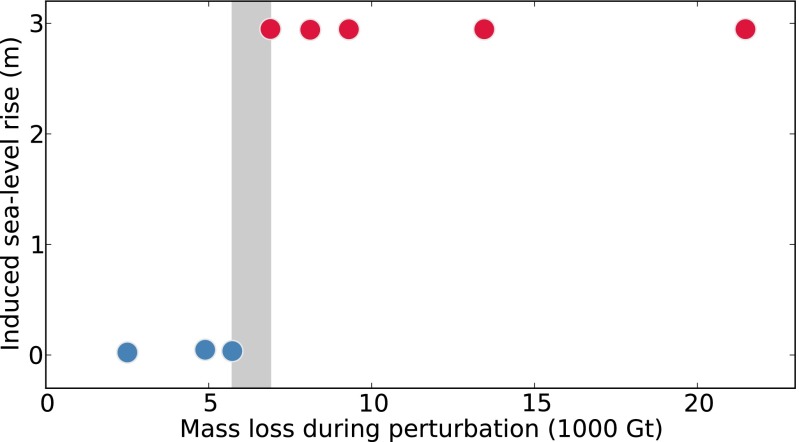
Consistent with previous simulations with models of higher resolution (17, 18), our results show an earlier onset of strong ice loss with increasing forcing duration (Fig. 3B). Independent of the associated mass loss during perturbation, the eventual total sea-level rise contribution of about 3 m is the same for all destabilized simulation runs (Fig. 5, red circles). A difference of ∼1,500 Gt (4.2 mm sle) of ice loss during perturbation between the experiments with 50-y and 60-y long forcing, respectively, separates the stable from the unstable regime in our simulations (Fig. 5, gray shading). Our model's response to basal perturbations has been shown to be faster by a factor of around two compared with full-Stokes simulations (32). Hence, the speed of the WAIS collapse in our experiments might be overestimated.

Fig. 5.

Long-term sea-level contribution as a function of net ice loss from the Amundsen Sea sector during perturbation. Gray shading marks the critical threshold of ice loss between stabilization (blue) and destabilization (red) of the Amundsen Sea sector, followed by disintegration of the WAIS, corresponding to a sea-level rise contribution of almost 3 m.

The constant present-day atmosphere conditions applied during ice-sheet relaxation neglect the effect of rising temperatures and an associated increase in snowfall that are expected in a warming future climate (33). Although increased ice-sheet mass gain through snowfall may counteract imbalance, it can also lead to an increase in ice discharge resulting from the difference in surface elevation change between grounded and floating regions (34). The ice softening through higher surface temperatures tends to intensify ice flow and associated discharge. The question of to which extent these effects might force or inhibit a marine ice-sheet instability remains unanswered by our study. Our approach to apply subshelf melt rates from ocean model simulations unidirectionally to the ice model does not allow for ice–ocean interaction. Although fully coupled ice-sheet climate models are important (35, 36), they represent a compromise between model resolution and coupling degree. Here we account for the main effect of changing ice-shelf thickness on melt rates by applying a pressure-dependent melt adaptation in our model (Methods). Our ice-sheet model applies physically motivated approximations to the stress balance that determines ice-sheet dynamics. While accounting for the relevant stress components, the model allows computationally efficient simulations of the large region covered by the WAIS on a relatively high horizontal resolution over millennial timescales. Other ice-sheet models approximate the stress balance to lesser degree (37), or even solve the full-Stokes stress balance (38), and incorporate elaborated numerical methods such as grid refinement (39), enabling a more accurate simulation of ice-sheet evolution. The application of these models demands much more computational capacity, and to our knowledge, a study such as the one presented here would not be feasible to date.

Conclusions

Using a state-of-the-art continental ice-sheet model, we complement earlier simulations of higher resolution by investigating the long-term response of the WAIS to a destabilization of Amundsen Sea sector. Starting from a simulated equilibrium ice sheet close to observations, we apply a local perturbation to the Amundsen region that is constrained by present-day measurements of net ice loss and observations of sub-ice-shelf melt rates. After destabilization of the Amundsen Sea sector, we find that the marine ice-sheet instability unfolds and is not halted by topographic features. We find that ice thinning spreads far inland and shifts the ice divide of the Amundsen catchment toward the Filchner–Ronne and Ross ice shelves. Consistent with an earlier conceptual study (30), this initiates grounding-line retreat there. Thus, our simulations serve as an example for a scenario in which a destabilization of Amundsen Sea sector will not remain limited to its catchment basins but will lead to a complete disintegration of West Antarctica's marine ice on a millennial timescale. The currently observed retreat in West Antarctica hence might mark the beginning of a millennial period of self-sustained ice discharge from West Antarctica and require long-term global adaptation of coastal protection, such as the building or rebuilding or raising of dykes, the construction of seawalls, or the realization of land fills in the hinterland. For more details on the effects and adaptation strategies to sea-level rise, see the Intergovernmental Panel on Climate Change Working Group II’s latest assessment report (40, 41).

We emphasize that our findings are based on a single realization of an ice-sheet model that applies approximations to the ice dynamics. Thus, further modeling studies using different approaches (including perturbed-physics ensembles; the investigation of different scenarios of surface accumulation and temperature forcing; coupling between atmosphere, ice, and ocean models; or the application of models of higher numerical order) are much needed for comparison, setting our findings into context.

Methods

Ice-Sheet Model.

We use PISM (22, 23) to carry out regional simulations of the WAIS at 5-km horizontal resolution. The model applies a superposition of the shallow-ice approximation and the shallow-shelf approximation. This hybrid scheme ensures a smooth transition between different ice-sheet flow regimes and allows for stress transmission across the grounding line. We adjust for unmodeled anisotropy, as well as for other uncertainties relating to unobserved variations in viscosity and basal resistance in our sheet-shelf system, by using an enhancement factor of 4.5 for the shallow-ice approximation and 0.8 for the shallow-shelf approximation, respectively. A linear interpolation of the freely evolving grounding line, and accordingly interpolated basal friction, enable realistic grounding-line motion also at medium to low horizontal resolution (32). Basal friction is calculated using a nonlinear Weertman-type sliding law (24) with a sliding exponent of 1/3 in combination with a Mohr–Coulomb model for plastic till (42, 43) that accounts for the effect of evolving ice thickness and the associated change in overburden pressure on the basal till (44). The till friction angle is parameterized with bed elevation, as in ref. 42, and the basal pore water pressure is limited to a maximum fraction of 0.93 of the overburden pressure. This friction scheme ensures a continuous transition from quasi-nonslip regimes in elevated regions to the marine areas where basal resistance is low. We use a kinematic first-order calving law (45, 46), with a prescribed proportionality factor of 2·10⁶ m⋅y and a minimum ice thickness at the calving front of 200 m. The physically motivated calving law takes into account the eigenvalues of the horizontal strain-rate tensor, allowing for geographically confined ice shelves and dynamic calving-front positions. A physical stress boundary condition is applied at the calving front to close the equations of the shallow-shelf approximation (23).

Boundary Conditions.

The landward boundary of our model domain is chosen along present-day East Antarctic ice divides, and hence far away from the marine parts of the WAIS. Along this fixed boundary, ice velocities are set to zero, whereas the coastal ice margin is free to evolve.

We spin up the model for 50,000 y under present-day time-constant atmosphere and 20th-century ocean boundary conditions, respectively, to obtain an ice sheet in equilibrium that serves as initial state for our perturbation experiments. Relative drift in total ice volume is less than 10⁻³ % y⁻¹ after 50,000 y.

Subshelf melt rates are applied as an ocean boundary condition in our simulations, taken from the Finite Element Sea Ice-Ocean Model (FESOM) (21). FESOM is a hydrostatic, primitive-equation ocean model that is coupled to a dynamic-thermodynamic sea ice model. The ocean model includes an ice-shelf component that uses a three-equation system for the computation of temperature and salinity in the boundary layer between ice and ocean and the melt rate at the ice-shelf base. The global unstructured grid has a horizontal resolution of 10 km along the Antarctic coast, 7 km under the larger ice shelves in the Ross and Weddell seas, and 4 km under the small ice shelves in the Amundsen and Bellingshausen seas. Ice-shelf draft, cavity geometry, and ocean bathymetry used in FESOM consider data from many of the most recent surveys of the Antarctic continental shelf (47). The ocean model is initialized using temperature and salinity fields from National Oceanic and Atmospheric Administration’s World Ocean Atlas 2001 and is driven by atmospheric conditions from the HadCM3 global climate model (referred to as the HadCM3-20C experiment in ref. 21). Our equilibrium simulation is forced by time-averaged FESOM data for the period 1970–1999, representing 20th-century conditions. Compared with observations, sub-ice-shelf melting from FESOM is reasonably captured for Filchner–Ronne and Ross ice shelves, but significantly underestimated beneath the ice shelves in the Amundsen Sea (figure 10 in ref. 21). For this region, average FESOM melt rates are around 3 m/y, whereas present-day average melt rates are observed to be one order of magnitude larger (15, 29). We thus scale the field of melt rates below the Amundsen ice shelves toward values that are consistent with current observations to represent the observed enhanced melting below these ice shelves, perturbing the equilibrium ice sheet locally. The perturbation is applied for lengths of 20, 40, 50, 60, 80, 100, 150, and 200 y (Fig. 3). After the end of the perturbation pulse, the original (but weaker than observed) 20th-century melt rates are applied, and simulations are integrated for several thousand years until a stable grounding-line position is reached.

In FESOM simulations, the melt rates are computed for fixed present-day ice-shelf geometry and grounding-line position. We hence filled in missing ocean data in regions covered at present by land ice by a simple diffusive algorithm into regions below sea level, leading to melt rates further inland that are similar to the respective ice-shelf cavity melt rates. To account for local ice-shelf thickness change, we apply a pressure adaption of the ocean melt rates in PISM (see supplementary material in ref. 20). Ocean melting is also applied at the grid boxes below sea level, with grounded ice adjacent to the ocean through a buoyancy-dependent basal melt interpolation scheme. Prescribed fields of present-day surface mass balance and temperature obtained from the ALBMAPv1 dataset (48) act as atmospheric boundary conditions in all simulations. Initial bed and ice topography are obtained from the recent Bedmap2 data set (49).