Significance
Many chemical and biomedical techniques rely on slow diffusive transport because existing pressure-based methods or electrokinetic methods can incidentally damage the sample. This study introduces a novel transport concept termed stochastic electrotransport that can selectively and nondestructively expedite transport of electromobile molecules into a porous sample, such as fixed biological tissues. We use the method to rapidly transport several classes of molecules into whole mouse brains and other organs and achieve rapid clearing and staining of the entire tissue in record time without damaging the sample. Our new method may facilitate the application of various molecular techniques to large and dense tissues.
Keywords: stochastic electrotransport, molecular transport, tissue clearing, tissue labeling, CLARITY
Abstract
Nondestructive chemical processing of porous samples such as fixed biological tissues typically relies on molecular diffusion. Diffusion into a porous structure is a slow process that significantly delays completion of chemical processing. Here, we present a novel electrokinetic method termed stochastic electrotransport for rapid nondestructive processing of porous samples. This method uses a rotational electric field to selectively disperse highly electromobile molecules throughout a porous sample without displacing the low-electromobility molecules that constitute the sample. Using computational models, we show that stochastic electrotransport can rapidly disperse electromobile molecules in a porous medium. We apply this method to completely clear mouse organs within 1–3 days and to stain them with nuclear dyes, proteins, and antibodies within 1 day. Our results demonstrate the potential of stochastic electrotransport to process large and dense tissue samples that were previously infeasible in time when relying on diffusion.
Diffusion is a slow process that governs the overall speed of many biochemical and engineering processes. Diffusion is produced by random molecular motion (a “random walk”), and it leads to complete dispersion of particles but is inherently slow (1). Diffusion is, therefore, effective for small-length-scale applications but becomes impractical for applications requiring larger length scales. This is especially true when the sample contains dense architectures with small and tortuous pores that hinder molecular movement. Diffusion of molecules into and out of such a sample (e.g., fixed biological tissues) can take an impractically long time. For instance, it can take weeks for antibodies to diffuse a few millimeters into fixed tissues (2). The slow nature of diffusive transport has long limited the application of many existing and emerging techniques in biology and medicine to small or thin tissue samples (3–7).
External forces can enhance transport of otherwise slowly diffusive molecules into and out of porous samples, but they have many limitations. For instance, hydrodynamic pressure can generate a convective flow across a porous sample (8), but the high pressure required to generate the flow can deform fragile samples such as soft tissues or polymeric materials (9). An electric field can drive electrophoresis of charged particles through a porous sample (10), but if the sample contains charged molecules, the electric field can also damage the sample. For this reason, electrophoresis may not be suitable for tissues or biomolecule–polymer hybrids containing charged endogenous biomolecules (11, 12). To avoid damaging samples, then, conventional chemical and biomedical methods for biological processing rely on the slow but safe diffusion method.
However, with the development of in situ molecular interrogation methods (6, 13, 14) and tissue clearing techniques (2, 15–25) and an emphasis on studying organ-scale tissue as a whole, a pressing need has arisen for a means of expediting the transportation of various molecules into intact tissues. For example, many emerging tissue clearing techniques use surfactant micelles to directly remove lipids from a tissue and thus eliminate light-scattering boundaries to improve optical penetration for holistic visualization (2, 15–25), but transporting these micelles into the intact tissue via diffusion can take weeks (2, 15). Although electrophoresis can speed up this process, as demonstrated in CLARITY, its application has been limited to low electric fields because using high fields can damage tissue structures (2). The problem is compounded by the fact that different regions of a tissue can have widely different electrical properties (26), leading to regions with concentrated electric fields. Electrophoresis, therefore, is ineffective for hastening transport of surfactant micelles into large, dense samples because only low electric fields can be used without risking damage to the sample.
Faster transportation of molecular probes into intact tissue is also needed to reduce the time required to label large tissues. Diverse methods of tissue labeling are used in many areas of biological research and medical diagnosis for visualizing various biomolecules of interest. However, these techniques have been mostly confined to small samples owing to the difficulty of labeling and examining deep structures in large-scale intact tissues (6, 27–31). CLARITY and other emerging tissue-clearing techniques (2, 15–25) render intact tissues optically transparent and macromolecule-permeable, allowing examination deep inside a tissue with light microscopy, but staining such large samples remains challenging because diffusion of molecular probes is very slow; it can take several weeks to deliver molecular probes throughout a mouse-brain-sized tissue for staining (2). Therefore, it is imperative to develop a faster method for labeling thicker and denser tissues.
Here we introduce a novel transport method termed stochastic electrotransport that rapidly and selectively disperses highly electromobile molecules in a porous sample without damaging the charged sample itself. We developed a computational model to theoretically demonstrate that a rotational electric field in a porous sample can enhance the apparent diffusivity of electromobile molecules with a quadratic dependence on their electromobilities. This electrophoretically driven diffusive transport selectively boosts the migration of freely moving molecules with high electromobility while suppressing the displacement of cross-linked endogenous biological molecules with low electromobility within the sample. We then developed an integrated platform to clear and stain intact tissues in record time using stochastic electrotransport. Our work demonstrates the potential of stochastic electrotransport to rapidly and nondestructively process large-scale intact biological systems with various biochemical techniques.
Theory and Computational Modeling of Stochastic Electrotransport
One way to expedite the transport of molecules in a porous sample is by using an electric field. An electric field can drive the electrophoresis of charged molecules down the electrical potential gradient with velocity v based on field strength E and the molecules’ effective electromobility µ. Assuming a Stokes–Einstein model, µ can be described by its effective charge per mole q, its hydrodynamic radius R, and the effective viscosity of the medium η (see SI Appendix for details):
| [1] |
where the lumped term electromobility, , is a constant of proportionality between and (see SI Appendix for details). Thus, particles under an electric field with strength will migrate with velocity based on their electromobility . This means that particles with high electromobility travel faster under an electric field than those with lower electromobility, whereas uncharged materials (e.g., polyacrylamide and agarose gels) remain stationary (10). This becomes a problem, however, when one tries to use electrophoresis to transport molecules into a material that is composed of charged molecules itself, such as endogenous biomolecules (e.g., DNA, RNA, proteins, and small molecules) in fixed tissues. Although the high degree of cross-linking necessary to preserve the physiological architecture significantly lowers the electromobility of the cross-linked molecules (1), the application of sufficiently large electrical forces on these electromobile molecules can strain and damage the sample.
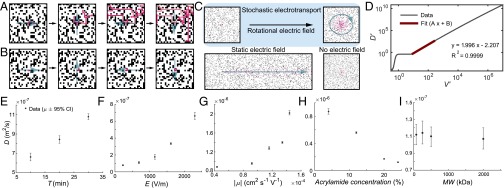
We hypothesized that a rotational electric field could make the migration of charged particles more dispersive and less forceful to the surrounding matrix. The rotational electric field may effectively amplify the differences in electromobilities, allowing more electromobile particles to travel much farther than less electromobile particles. The longer travel length would allow such particles to interact with each other as well as with the surrounding matrix to create a dispersive effect (Fig. 1A), whereas the net movement of particles with low migration velocities would be negligible over time (Fig. 1B). Because free molecules have much higher electromobility compared with the cross-linked molecules that constitute a porous sample, a rotational electric field might be used to selectively disperse the free molecules without straining and damaging the charged sample. This is depicted in the simplified and discretized schematics shown in Fig. 1 A and B.
Fig. 1.
Principles, computational modeling, and experimental characterization of stochastic electrotransport. (A and B) Simplified and discretized illustration of stochastic electrotransport in a porous medium. When migration velocity is high enough compared with rotation period, particles move mainly in the direction of the electric field and disperse as the electric field changes (discretized in four directions here, as opposed to a continuous rotation) and as they encounter blocked sites. (A) When migration velocity is too low compared with rotation speed, there is no dispersive effect. (B) A 25 × 25 lattice with periodic boundary conditions, 0.7 void fraction. (C) Simulation of particle distributions from a point source. Particles (red) start from the middle of the 2D square lattice with randomly distributed pore structures (black). The rotational electric field creates diffusion-like dispersion faster than diffusion alone, whereas a static electric field mainly moves particles in one direction. See Movies S1–S3. (D) Log plot of effective diffusivity versus migration velocity calculated from the KMC modeling. scales quadratically with respect to above a critical point of . (E) Effective diffusivity () increases near-linearly with respect to the period of rotation. (F and G) increases approximately quadratically with respect to increasing the electric field (F) and increasing electromobility (G). (H) decreases almost linearly with respect to increasing acrylamide concentration (or, decreasing porosity). (I) of FITC-dextran molecules with different sizes (but similar electromobilities) was similar.
To simulate the convective–diffusive transport of charged particles in a porous medium under a rotational electric field, we used a pass forward algorithm-based lattice kinetic Monte Carlo model (PFA-LKMC) that allows simulations of field-driven phenomena (32, 33). In this model, convective–diffusive transport is described by the following conservation equation:
| [2] |
| [3] |
where is the solute concentration, is the migration velocity, and is the solute diffusivity. The migration velocity, , as defined above, is linearly proportional to the lumped electromobility and the rotational electric field . The domain is discretized using a uniform square grid with grid points in the and directions with lattice spacing . A solute particle occupies a discrete lattice and can exhibit a diffusive or convective event. The rate, of each event is determined by the timescale of each event as follows:
| [4] |
| [5] |
The PFA-LKMC algorithm identifies the nearest-neighbor connected chains in the direction of the local flow and passes the convective rates of all blocked particles to the leading particle (32). Then, the total convective rate of a particle at the front of a linearly connected chain of particles is given by
| [6] |
After calculating the rate of each event, the algorithm picks a specific event having rate with probability , where is the total rate for all possible events at a given time (not counting the blocked particles). The simulation clock is updated after each event by the time-step increment :
| [7] |
where is the total rate computed using the simplest biasing scheme () and is the total convective rate of all blocked particles in the system.
We first present simulated particle distribution from a point source after equal amounts of time under a rotational electric field, a static electric field, and no electric field (Fig. 1C). The simulations were done on a square lattice of size 1,000 × 1,000 with periodic boundary conditions. The particles were continuously seeded at a set point to simulate the point source. Here, we used for the rotational electric field, for the static electric field, and for the no electric field, where , This simple point-source simulation shows that, indeed, a rotational electric field creates diffusion-like dispersion that is faster than diffusion alone, whereas a static electric field mainly moves the particles in one direction (Fig. 1C and Movies S1–S3). We termed this phenomenon stochastic electrotransport.
We then used this KMC model to analyze when, how, and by how much a rotational electric field can disperse charged particles in a porous medium (see SI Appendix, Supplementary Materials and Methods for more details). The effective diffusivity (in two dimensions) was calculated using the Einstein relation from the ensemble average of the squared distance from the particles’ original positions :
| [8] |
For this simulation, the particles were randomly seeded to a fraction of 0.1. For analysis, we used nondimensionalized diffusivities and velocities:
| [9] |
| [10] |
Here, the velocities and the resulting effective diffusivities were scaled by length scale , which is equal to the grid spacing and the time scale , which is equal to the rotational period. The diffusivity was also normalized by subtracting the molecular diffusivity. The KMC simulation shows that charged particles in a randomly distributed pore structure under a rotational electric field have effective diffusivities, , that scale approximately quadratically with respect to the migration velocity, for (Fig. 1D and Eq. 1):
| [11] |
This scaling was determined through linear regression on the log-log plot of the two variables (Fig. 1D). Dimensionalizing and scaling by the autocorrelation time scale, , yields
| [12] |
Substituting the relationship for migration velocity (Eq. 1) into Eq. 12 yields
| [13] |
This result shows that the action of a rotational electric field is to disperse charged particles with a quadratic dependence on their electromobilities and the electric field strength. This quadratic dependence holds above . For , is approximately invariant with respect to . Below , decreases rapidly to zero with decreasing . As such, if the electric field is sufficiently high (), this approach could theoretically enable selective diffusion-like transport of electromobile molecules.
We hypothesized that the stochastic behavior arises from the rotational trajectory of the particles interacting with blocked sites (or pore walls). We repeated the simulation with no pore structures and observed similar behavior below and between but no quadratic increase above (SI Appendix, Fig. S1). Here, increases rapidly from zero to until around . Above that point, remains approximately invariant with respect to . We also repeated the simulation with different rotation speeds (with the same square lattice shown in Fig. 1D) (SI Appendix, Fig. S2). The effect of changing the rotation speed was to scale the migration velocity by a similar factor.
Experimental Validation and Characterization
To systematically test the model for stochastic electrotransport (Eq. 13), we developed the instrument (see Fig. 4) and studied how varying system parameters (, period of rotation; E, electric field; , electromobility; pore size; and particle size) changes effective diffusivity (D) (Fig. 1 E–I). The instrument applies a rotational electric field to a sample with a controlled field strength and rotation speed. We used this instrument to deliver fluorescein isothiocyanate-conjugated BSA (BSA-FITC), a tracer molecule, into a cylindrical acrylamide gel (4%T, 0.13%C) with a diameter of 14 mm. To quantify the penetration of BSA-FITC from the middle cross-section of the gel cylinders, we measured fluorescence intensity. We smoothed the raw data (containing ∼100–150 pixels) with a moving average of five pixels, normalized the peak intensities (which we knew from our boundary condition), and took an average of four different trials per experimental condition. We then fit the resulting average of the cross-sectional intensity profile to the analytical solution for transient diffusion into a cylinder to estimate the effective diffusivity. Assuming no edge effects and a constant solution concentration, the governing equations are
| [14] |
| [15] |
| [16] |
where Eq. 14 is the conservation equation, Eq. 15 is the boundary condition, and Eq. 16 is the initial condition. An analytical solution that satisfies the governing equations can be obtained by eigenfunction expansion:
| [17] |
where is the Bessel function of order of the first kind and is the root of . For analysis, we clipped the series at . We used a nonlinear least squares method to find the best fit for .
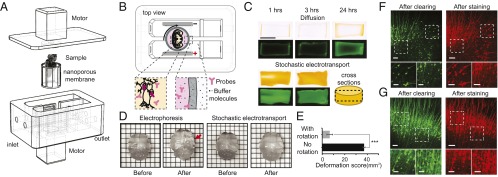
Fig. 4.
Stochastic electrotransport of molecular probes for tissue staining. (A) Device for staining samples using stochastic electrotransport. The tissue is placed in a chamber walled with a nanoporous membrane. A stir bar mixes the solution inside of the sample chamber. (B) Molecular probes penetrate through the tissue and bind to target molecules for imaging. The probes are retained in the sample chamber by the nanoporous membrane. (C) BSA-FITC penetration into cylindrical hydrogel disk following diffusion or stochastic electrotransport. Middle sections were cut and imaged with bright-field (Top) and fluorescence (Bottom) microscopy. (Scale bar, 10 mm.) (D) High electric fields required to drive molecular probes into the tissue cause noticeable damage to the tissue during electrophoresis, but not during stochastic electrotransport. Red arrow points to the deformed region. Grid size, 3 × 3 mm. (E) The deformation score for stochastic electrotransport was significantly smaller than the score for electrophoresis. (F and G) Neurons of Thy1-eGFP mouse brain (cingulate and motor cortical areas), before and after staining with diffusion (F) or stochastic electrotransport (G). In both cases no microscopic deformation was observed. (Scale bars, 100 µm; inset, 10 µm.)
In the first experiment, we systematically varied the electric field strength and the period of the rotation and characterized the resulting effective diffusivities (raw results shown in SI Appendix, Fig. S3). Each experiment was run for 1 h. Fig. 1E compares the effective diffusivity at three different periods of rotation and at . Increasing the period of rotation resulted in an increase in the effective diffusivity. This increase was approximately linear, which agrees with the result of the computational model (SI Appendix, Fig. S2); however, at lower voltages the response was not as apparent (SI Appendix, Fig. S4 A–C). Fig. 1F and SI Appendix, Fig. S4 E–G show how the effective diffusivity changes with increasing electric field strengths. The effective diffusivity scales approximately quadratically with respect to the electric field above . Below this critical point, there is no quadratic behavior.
Next, we varied the pH of the buffer solution to test the effect of electromobility on the effective diffusivities (raw results shown in SI Appendix, Fig. S5 A–E). The environmental pH determines the ionization states of certain amino acid groups in BSA (34), leading to a change in its electromobility. The buffers were made with inorganic buffer molecules possessing similar ionic strengths, osmolarities, and conductivities, to minimize any additional effects (SI Appendix, Supplementary Table 1). All experiments were performed at and for 1 h. Fig. 1G shows how the effective diffusivity changes with increasing electromobilities calculated from the buffer’s pH and ionic strength. The effective diffusivity scaled almost quadratically above pH 7 (or above ), as shown in SI Appendix, Fig. S5 G and H. Although this agrees with the theory, the fit had a low value of 0.7394, perhaps because the electromobilities were calculated based on literature results on BSA, not BSA-FITC—the FITC modification may have introduced a systematic error. Additionally, despite our best efforts to ensure that the buffers were made to minimize additional effects, they varied in their conductivities and osmolalities (SI Appendix, Supplementary Table 1).
We then varied the porosity of the hydrogel to test the applicability of the methodology to media with various solid volume fractions. One way to change the porosity is to change the total polymer concentration while keeping the cross-linker ratios and the reaction conditions constant (35, 36). To isolate the test to the effect of porosity, we used acrylamide gels with varying monomer concentrations but identical cross-linker ratios (4%T, 0.13%C; 12%T, 0.4%C; 20%T, 0.67%C; 24%T, 0.8%C) (SI Appendix, Figs. S6 and S6-2). All experiments were performed at and for 1 h. Fig. 1H shows that stochastic electrotransport can improve the penetration depth across the range of porosities and the effective diffusivity decreased approximately linearly with increasing acrylamide concentration.
Finally, we varied the molecular weight of the compounds to be transported to test whether there would be a limitation on size. We selected FITC-conjugated dextrans (FITC-dextran) of different lengths as tracer molecules (SI Appendix, Fig. S7). All experiments were performed on 4%T, 0.13%C polyacrylamide gels at and . Fig. 1I compares the effective diffusivity for four different sizes of FITC-dextrans: 70, 250, 500, and 2,000 kDa. All of these molecules had similar effective diffusivities, owing to their similar charge-to-mass ratios (and consequently, similar electromobilities), despite their differences in molecular size. This result suggests that stochastic electrotransport does not impose an inherent limit on the molecular size as long as the charged particles are smaller than the pores.
Together, these results validate the key feature of stochastic electrotransport that the effective diffusivity scales quadratically with respect to the electric field and demonstrate the dependence of penetration depth of the molecules on rotation speed, voltage, porosity, and molecular weight.
Application of Stochastic Electrotransport
The unique quadratic dependence of effective diffusivity on electromobility effectively amplifies the differences between the electromobilities of the charged free chemicals to be transported and the electromobilities of the cross-linked endogenous molecules. Therefore, compared with simple electrophoresis, stochastic electrotransport may allow us to rapidly transport charged molecules into and out of intact tissues without significantly straining the tissue structure. We applied this method to enable rapid tissue clearing (by transporting surfactant micelles) and tissue labeling (by transporting molecular probes).
Rapid Clearing of Intact Tissues.
We designed a device that uses stochastic electrotransport to improve the transport of surfactant micelles into tissues without causing tissue damage (Fig. 2 A–C, and detailed in SI Appendix, Figs. S8 and S9). We implemented stochastic electrotransport by continuously rotating a sample chamber with respect to two parallel electrodes positioned next to the sample chamber (Fig. 2C) to create an external rotational electric field with respect to the sample. The sample chamber is immersed in circulating buffer solution (Fig. 2 A and B), and a temperature-controlled circulation system maintains the solution temperature at ∼15 °C to prevent Joule heating from causing thermal damage to the tissue (SI Appendix, Fig. S9). A set of nanoporous membranes (6- to 8-kDa regenerated cellulose; Spectra/Por 1) divides the circulating solution into an inner portion that is in contact with the sample and an outer portion that is in contact with the electrodes (Fig. 2C). The nanoporous membranes also mechanically prevent the sample from directly contacting the electrodes or electrolysis byproducts.
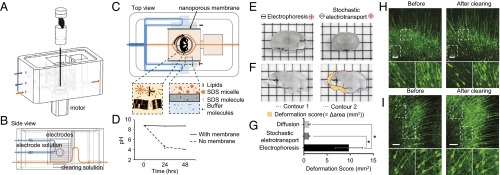
Fig. 2.
Stochastic electrotransport of surfactants for tissue clearing. (A) Device for clearing tissues using stochastic electrotransport. The tissue is rotated with respect to an electric field. (B) Flow fields. Electrode solution provides ions for electrophoresis and flushes the electrode surface, while the clearing solution is driven into the tissue for tissue clearing. (C) Tissue lipids are removed by surfactant micelles, which are concentrated in the clearing solution by the nanoporous membrane. See also SI Appendix, Figs. S8 and S9. (D) pH of the clearing solution versus electrophoresis time at 200 V with or without nanoporous membranes. (E) Whole mouse brains were cut into 1-mm-thick slices after electrophoresis or stochastic electrotransport for 5 h. Grid size, 3 × 3 mm. (F) Deformation score was defined as the absolute sum of mismatched areas between one hemisphere and the mirrored other hemisphere (yellow area). (G) Deformation scores for diffusion and stochastic electrotransport were similar, but the deformation score for static electrophoresis was seven to nine times higher than the score for diffusion and stochastic electrotransport. (H and I) Neurons of Thy1-eGFP mouse brain (cingulate and motor cortical areas), before and after clearing with diffusion (H) or stochastic electrotransport (I). In both cases no microscopic deformation was observed. (Scale bars, 100 µm; inset, 10 µm.)
We chose to use different inner and outer solutions to slow down electro-oxidation of the surfactant molecule, SDS (Fig. 2 A–C). The inner solution consists of 200 mM SDS in lithium borate buffer (25 mM borate buffer titrated to pH 9 using lithium hydroxide at room temperature) and the outer solution consists of 10 mM SDS in lithium borate buffer. We chose an SDS concentration of 200 mM for the inner solution because at that level SDS micelles exhibit the highest stability and detergency (37), and an SDS concentration of 10 mM for the electrophoresis buffer so that 10 mM of SDS monomers can equilibrate across the two channels, given that the critical micelle concentration (above which micelles form) of SDS is ∼10 mM. The concentration of SDS in the inner solution stays high because SDS micelles (∼2 nm in diameter) cannot pass through the nanoporous membranes (Fig. 2C). The outer buffer, which is in contact with the electrodes, has a lower concentration of SDS to slow down the concentration-dependent electro-oxidation of SDS (38). The products of SDS oxidation are sulfuric acid and carbon dioxide (which form carbonic acid) as well as various other alcohols and acids; thus, the net result of oxidative degradation is a decreased pH, but the inner and outer solution setup greatly slows the rate of decrease in pH compared with a setup that does not use divided solutions (Fig. 2D).
To test whether stochastic electrotransport causes significant tissue damage, we used this optimized device to perform stochastic electrotransport on whole adult mouse brains and compared the results with those obtained using static electrophoresis of mouse brains. Five hours of static electrophoresis resulted in substantial tissue deformation (coronal sections of the deformed whole brains shown in Fig. 2E), whereas stochastic electrotransport for the same amount of time produced no macroscopic damage (Fig. 2E). We quantified this macroscopic deformation using a “deformation score,” which we defined as the absolute sum of mismatched areas between one hemisphere and the mirrored other hemisphere (Fig. 2F). If there is no deformation, the deformation score must be close to zero, because the two hemispheres are symmetrical. We compared the deformation scores for stochastic electrotransport, static electrophoresis, and diffusion (by passive incubation of the sample in SDS solution at 37 °C but with shaking for comparison with common practice) after 5 h of treatment (Fig. 2G). One-way ANOVA revealed a significant effect of treatment (F2,7 = 10.22, P < 0.01; n = 3 or 4 for each treatment). Post hoc Bonferroni’s multiple comparison test detected significant differences between diffusion and static electrophoresis (P < 0.05) and between static electrophoresis and stochastic electrotransport (P < 0.05), but not between diffusion and stochastic electrotransport. These results demonstrate that stochastic electrotransport does not significantly alter the tissue shape compared with diffusion, whereas electrophoresis significantly deforms the tissue.
Next, we characterized whether stochastic electrotransport causes microscopic deformations. We compared microscopic images of the same regions (the cingulate and motor cortical areas) of the Thy1-eGFP mouse brain sections from the specimen cleared using stochastic electrotransport and the specimen cleared using diffusion (Fig. 2 H and I). The shape and structure of the neurons at the surface showed no obvious change after clearing in both cases (but more features could be seen in stochastic-electrotransport-cleared sections than in the diffusion-cleared section due to better light penetration). These results show that stochastic electrotransport does not cause either macroscopic or microscopic deformation of the tissue.
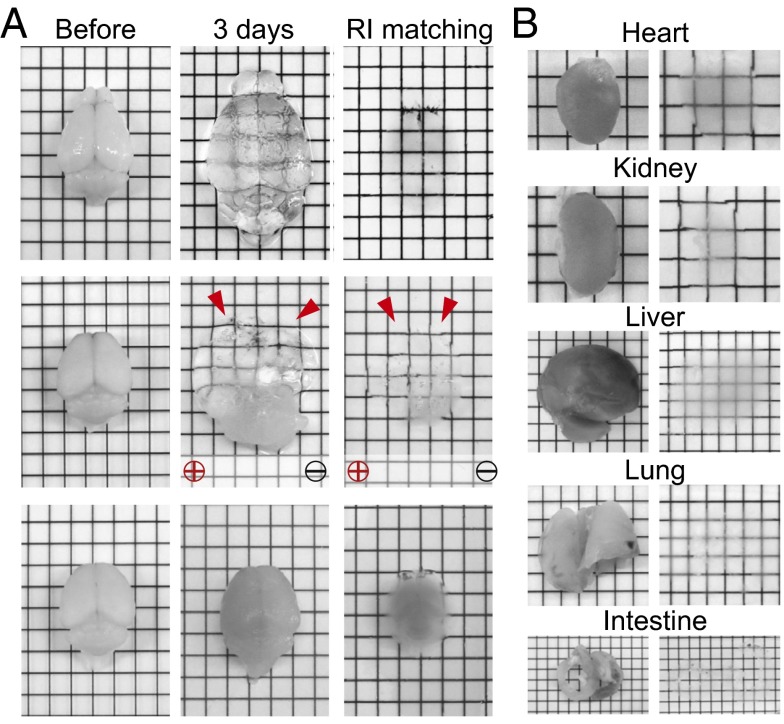
We then tested the degree to which stochastic electrotransport can improve the transport of surfactant micelles into and out of tissues during the clearing process. Fig. 3A compares clearing of hydrogel-embedded mouse brains (2) using stochastic electrotransport, static electrophoresis, and diffusion. Remarkably, stochastic electrotransport cleared the brains within 3 d. However, static electrophoresis asymmetrically cleared and severely damaged the brains, and diffusion only partially cleared the surface of the tissue (also see SI Appendix, Fig. S10 for diffusion at various temperatures). The tissues expanded with clearing due to loss of lipids, but the expansion could be reversed after incubation in a refractive index matching solution (SI Appendix) with high osmolarity. We also applied stochastic electrotransport to other organs: heart, kidney, liver, lung, and intestine. Heart, kidney, and liver cleared within 3 d, lung cleared in 2 d, and intestine cleared in 1 d (Fig. 3B). Taken together, these results demonstrate that stochastic electrotransport effectively and selectively enhances transport of highly electromobile SDS micelles without damaging tissues, thereby enabling rapid intact-tissue clearing without loss of structural information.
Fig. 3.
Rapid clearing of intact tissues. (A) Stochastic electrotransport completely and uniformly cleared the tissue in 3 d. Static electrophoresis caused noticeable tissue damage. Diffusion showed limited tissue clearing. Red arrows indicate the deformed regions of the brains. See SI Appendix, Fig. S10 for passive diffusion results at different temperatures (56 °C and 80 °C). (B) Heart, kidney, and liver were also completely cleared with stochastic electrotransport in 3 d. Lung and intestine took 2 d and 1 d, respectively.
Rapid Staining of Intact Tissues.
To implement stochastic electrotransport for tissue staining, we designed another device to efficiently use molecular probes (Fig. 4 A and B and SI Appendix, Fig. S8). Similar to the device for clearing, this device has a sample chamber that rotates with respect to two parallel electrodes, and it uses a temperature-controlled circulation system, set to 4 °C (SI Appendix, Fig. S9). However, instead of circulating both inner and outer solutions, the inner solution is confined inside of the sample chamber with nanoporous membranes. In this way, molecular probes can be confined to a small volume of several milliliters, which is enough to fully immerse a tissue sample.
We first tested whether stochastic electrotransport can effectively drive large macromolecules such as proteins. We measured the penetration of BSA-FITC into a clear disk-shaped polyacrylamide gel (4%T, 0.13%C) that was larger than a mouse brain (radius, 7 mm; height, 8 mm) with both stochastic electrotransport and diffusion. With stochastic electrotransport, we observed significantly enhanced transport of BSA-FITC into the gel and uniform dispersion of BSA-FITC within 3 h, whereas with diffusion alone BSA-FITC could not reach the core even after 24 h (Fig. 4C).
Next, we tested whether the high voltage necessary to drive large molecules can damage tissues. We compared the deformation of CLARITY-processed intact mouse brains after stochastic electrotransport and after one-dimensional electrophoresis. Within 1 h, the brain under static electrophoresis was noticeably damaged, whereas the brain under stochastic electrotransport remained unchanged (Fig. 4D). Deformation score analysis revealed significant macroscopic deformation with static electrophoresis compared with stochastic electrotransport (Student’s t test, two-tailed, P < 0.001; Fig. 4E). For microscopic analysis, we also stained Thy1-eGFP mouse brain sections against eGFP both passively and via stochastic electrotransport and compared the microscopic images of the same region of the brain before and after staining. The shape and structure of the neurons and the networks remained identical after staining using stochastic electrotransport (Fig. 4 F and G).
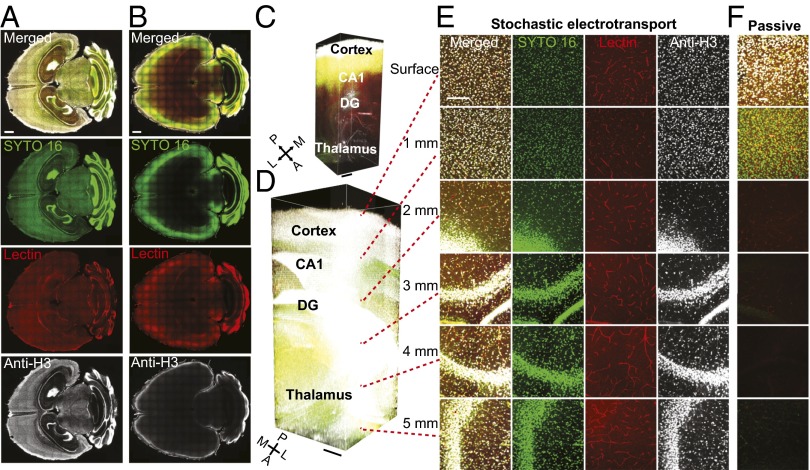
Using this approach, we tested rapid staining using several different classes of molecular probes on CLARITY-processed whole adult mouse brains. To thoroughly evaluate the extent to which stochastic electrotransport can achieve uniform and complete staining, we chose probes whose targets are present throughout the entire brain: SYTO 16, a widely used organic nuclear dye; fluorophore-conjugated Lycopersicon esculentum (tomato) lectin, a carbohydrate-binding protein widely used as an effective blood vessel marker (39–41); and anti-histone H3 protein, an antibody against histone H3 protein that is present in all cell nuclei. Stochastic electrotransport of these probes simultaneously into a mouse brain resulted in uniform and complete staining of their targets throughout the whole brain within a day (Fig. 5 A, D, and E and Movie S4). Diffusion of another CLARITY-processed brain in the probe solution for the same duration (incubated in a tube on a shaker at 4 °C) stained only the surface, and there was virtually no labeling at the core (Fig. 5 B, C, and F). These also demonstrate that molecular probes with a wide range of molecular weights are amenable to stochastic electrotransport into CLARITY-processed tissues; SYTO 16, tomato lectin, and anti-H3 antibody are ∼450 Da, ∼70 kDa, and ∼150 kDa, respectively. Most commonly used molecular probes and functional molecules such as antibodies fall in this size range. Anti-H3 antibodies, the largest among the three molecular probes used, exhibited poor penetration (∼300 µm) in the diffusive staining experiment (Fig. 5F) but complete penetration of the entire depth of imaging in the stochastic electrotransport experiment (Fig. 5E). We also performed stochastic electrotransport of SYTO 16 and tomato lectin into CLARITY-processed heart and intestine and achieved complete staining of all nuclei and blood vessels (Fig. 6). These organs were imaged with a custom-built light-sheet microscope for rapid high-resolution volume imaging. These data demonstrate that stochastic electrotransport enables a rapid, uniform, and system-wide delivery of various molecular probes into various types of tissues, thereby essentially making traditional histochemical techniques scalable to intact tissues.
Fig. 5.
Rapid, uniform, and complete staining of intact brain. (A) Staining using stochastic electrotransport on CLARITY-processed mouse brains with SYTO 16, tomato lectin, and anti-histone H3 antibodies (anti-H3). Horizontal sections show uniform and complete staining of the whole brain with all three probes. (Scale bar, 1 mm.) (B) Passive staining controls shows poor penetration of the probes into the tissue. (Scale bar, 1 mm.) (C and D) Three-dimensional rendering of the hippocampus region of the passively stained brain (C; 2.2 × 1.9 × 5.1 mm3) and stochastic electrotransport-stained brain (D; 2.2 × 1.9 × 5.0 mm3). Imaged with a confocal microscope equipped with a 10× CLARITY-optimized lens (Olympus; N.A. 0.6, WD 8.0 mm). DG, dentate gyrus. (Scale bars, 500 µm.) See Movie S4. (E and F) Optical sections of stochastic electrotransport-stained brain (E) and passive staining control (F) at various depths. (Scale bar, 200 µm.)
Fig. 6.
Staining of various organs. Using stochastic electrotransport, a portion of mouse intestine (A–D) and the whole heart (E–G) were cleared and stained with SYTO 16 and Dylight 594-conjugated tomato lectin to visualize cellular and vascular structures. The stained intestine was imaged using a custom-built light-sheet microscope. Top view (A) and bird’s eye view (B) of 3D rendering of the intestine. (Scale bar, 1 mm.) (C) Horizontal sections at different depths. (Scale bar, 1 mm.) (D) Boxed regions in C. (Scale bar, 100 µm.) (E) Three-dimensional rendering of the heart. (Scale bar, 1 mm.) (F) Horizontal sections at different depth. (Scale bar, 1 mm.) (G) Boxed regions in F. (Scale bar, 100 µm.)
Compatibility with Other Chemical Clearing Methods.
We further tested whether stochastic electrotransport-mediated staining is compatible with other chemical methods in the field. We sought to implement stochastic electrotransport within the protocols of iDISCO (22) and CUBIC (16), the latest representative solvent- and hyperhydration-based clearing methods. For iDISCO, we chemically processed the tissue following the protocol described in the original paper (22) and used stochastic electrotransport for TO-PRO-3 staining. We used TO-PRO-3 as recommended by the original paper because the spectrum of SYTO 16 was altered and Dylight 594 (conjugated to tomato lectin) did not survive in the organic solvent used in iDISCO. Stochastic electrotransport of TO-PRO-3 into a whole adult mouse brain for 1 d labeled only the surface, despite the use of a 25 times higher concentration (5.0 μM) than the suggested concentration (0.2 μM) (SI Appendix, Fig. S11 A and B). For CUBIC (16), we used stochastic electrotransport between the incubation with ScaleCUBIC-1 and ScaleCUBIC-2 to stain with SYTO 16 and tomato lectin. This achieved nearly complete staining of nuclei and blood vessels throughout the adult mouse brain (SI Appendix, Fig. S11 C and D). The resulting image was not as uniform as in the CLARITY-processed brain case (Fig. 5A), perhaps due to limited optical clearing (SI Appendix, Fig. S11C).
Quantitative Analysis of Intact Tissues.
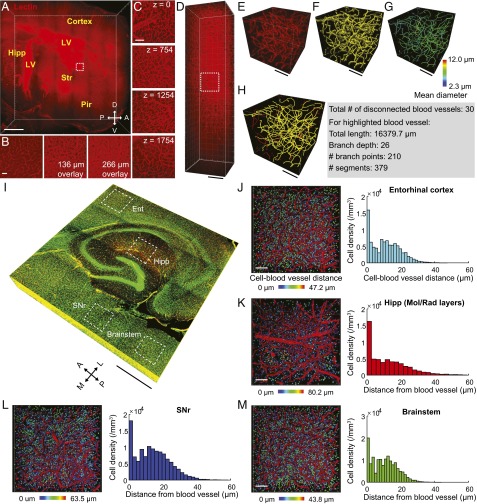
Rapid and uniform labeling of intact tissues using stochastic electrotransport may enable quantitative analysis of tissue architecture, which may not be feasible in conventional 2D histology. To explore this possibility, we labeled the entire vasculature of a mouse hemisphere using stochastic transport within 10 h and then used light-sheet microscopy to rapidly acquire high-resolution volume images. The acquired images displayed uniform staining of both capillaries and larger blood vessels at different depths (Fig. 7 A–D and Movie S5). The uniform labeling with high signal-to-noise ratio that stochastic electrotransport offers allowed us to analyze parameters such as diameter, total length, and number of branch points, using commercially available software (filament and surface tools in IMARIS) (Fig. 7 E–H). In another experiment, we stained the nuclei and the vasculature of a mouse brain with SYTO 16 and lectin and acquired a volume image with 3.41-µm z-steps (half of the theoretical z-resolution of the objective lens) for Nyquist sampling (Fig. 7 I–M). Several distinct brain regions (the entorhinal cortex, hippocampus, substantia nigra pars reticulata, and brainstem) were then vectorized and analyzed for cell density and nuclei–vascular distance with the spot and surface tools of the IMARIS software (Fig. 7 J–M). These parameters are challenging to directly measure in 2D images but are straightforward in 3D datasets. Our preliminary data show that distinct brain regions exhibited different cell body density and nuclei–vascular distance profiles. Such quantitative analysis may reveal important structural or pathological features of the vascular network or cell–vascular interactions in normal or diseased brain tissues (41–44). Together, these results demonstrate that stochastic electrotransport may be useful for rapid and quantitative 3D phenotyping of organ-scale biological systems.
Fig. 7.
Stochastic electrotransport-mediated staining allows quantitative anatomical analyses. (A) A CLARITY-processed mouse hemisphere was uniformly labeled via stochastic electrotransport of lectin. Approximately 10 × 7 × 2 mm3 was imaged using a Zeiss Z-1 light-sheet microscope within 1.5 h (20× CLARITY-optimized objective; N.A. 1.0, WD 5.1 mm; x–y pixel size 0.64 × 0.64 µm2, z-step size 4 µm). See Movie S5. Hipp, hippocampus; LV, lateral ventricle; Str, striatum; Pir, piriform cortex. (Scale bar, 1 mm.) (B) Boxed region in A. Overlays of single and multiple sections are shown. (Scale bar, 100 µm.) (C) Boxed region in A, 100-µm overlay at multiple depths indicated as z (micrometers). (Scale bar, 100 µm.) (D) A single field of view in the striatal region of the same tissue as G imaged with a z-step size of 2 µm within 30 s. (Scale bar, 100 µm.) (E) Three-dimensional rendering of a 300- × 300- × 300-µm3 portion of the boxed region in D. (Scale bar, 100 µm.) (F) Three-dimensional surface reconstruction of blood vessels, dataset from E. (Scale bar, 100 µm.) (G) Vectorized dataset from E, color-coded for the mean blood vessel diameter. (Scale bar, 100 µm.) (H) Analysis of the dataset from E. The largest contiguous blood vessel is highlighted with yellow. (Scale bar, 100 µm.) (I) Another CLARITY-processed mouse brain was stained with both SYTO 16 and lectin using stochastic electrotransport. The hippocampal region was imaged with high resolution [3.9 × 3.9 × 0.5 mm3; x–y pixel size 2.07 × 2.07 µm2, z-step size 3.41 µm (half of the theoretical z-resolution)] using confocal microscopy. Ent, entorhinal cortex. SNr, substantia nigra pars reticulata. Hipp, molecular and radiatum layers of the hippocampus. Brainstem, brainstem regions including the lateral lemniscus and pontine reticular nucleus. (Scale bar, 1 mm.) (J–M) Cell nuclei and blood vessels in the boxed regions in O were vectorized and analyzed to determine the distance between the nuclei and blood vessels in 3D space. (Left) Three-dimensional surface reconstructions of blood vessels and nuclei (represented as spheres). Color-coding indicates the shortest distance to the adjacent blood vessel. (All scale bars, 100 µm.) (Right) Histograms of cell–blood vessel distance and average values.
Discussion
We demonstrated that a rotational electric field can enable diffusion-like transport of electromobile molecules that is orders of magnitude faster than passive diffusion. Our computational model and experimental data show that if migration velocity is sufficiently high (compared with diffusion), the resulting dispersion has a quadratic dependence on the electromobility of the particles and the electric field strength (Eq. 13). This means that stochastic electrotransport can effectively amplify the differences in electromobilities to selectively transport highly electromobile molecules without affecting those with low electromobility.
Based on our simulation without pore structures (SI Appendix, Fig. S1), the dispersive phenomenon seems to come from the particles’ encountering blocked sites (or pore walls, as illustrated in Fig. 1 A and B). These blocked sites introduce variability to the deterministic rotational particle trajectories. This variability in the trajectory leads to dispersion of particles in a manner similar to diffusion. Thus, although the field is deterministic, the net transport of charged particles moving in that field is stochastic. Without the blocked sites to introduce variability, then, there should be no increase in the diffusivity, and indeed, our simulation without pore structures showed a slight increase but no quadratic dependence regime (SI Appendix, Fig. S1). The slight increase in the dispersion may come from the particles as they interact with themselves, acting as blocked sites. This consequently places limitations on the porous samples that can be processed. We hypothesize that charged particles interacting with a large-scale ordered structure would still exhibit dispersive effects. The effect of such an ordered structure would be to lower the variability in the characteristic length scale before a particle encounters a blocked site in its trajectory. It would not, however, eliminate the variability because it would also depend on the random starting point of the particle trajectory. However, if the ordered structure scale was small enough to indeed eliminate the variability (as in the case of rows of infinitely long, one-particle-thin channels), we expect that there would be no dispersive effects. In the opposite limit of a free medium, there could only be a slight increase from particles’ colliding with themselves. Thus, for stochastic electrotransport to work, the porous sample must have some locally random structures to induce dispersion.
Another finding from our simulation is the minimum velocity requirement for the quadratic relationship and a positive correlation between the minimum velocity and rotation speed. We interpret this minimum velocity as the “critical migration velocity” required to ensure a collision with a blocked site in the direction of the migration to induce dispersion. Our simulation with varying rotation speeds showed that as rotation speed increases, the critical migration velocity increases (SI Appendix, Fig. S2). This is because the radius of the rotational trajectory of the particles decreases as rotation speed increases and the particles are less likely to encounter a blocked site in the time required to complete one rotation (Fig. 1B). Under the same condition, however, particles with velocity higher than the critical migration velocity have larger rotational trajectory, and therefore have a higher chance to encounter a blocked site (Fig. 1A). This also means that as rotation speed goes to infinity, the empirical result collapses to standard diffusion. This places another limitation on stochastic electrotransport in terms of rotation speed, migration velocity, and porosity. A more porous sample would require a slower rotation speed and a faster migration velocity for stochastic electrotransport.
Our experimental results on characterizing the system support these insights from the model. Fig. 1E shows that increasing the period of the rotation resulted in an increase in the diffusivities. This means that the velocity autocorrelation time () is indeed coupled with the period of the rotation and they have positive correlation. The autocorrelation time scale can be interpreted as the time required for the particle to forget its deterministic rotational trajectory. It can be interpreted as the characteristic time scale for the particles encountering a blocked site (pore walls or other particles), stopping their deterministic trajectory and creating variability in the particles’ positions. This autocorrelation time scale depends on the rotation speed of the electric field as well as the characteristic length scale of the particle traveling before encountering a blocked site and resetting its trajectory. Fig. 1 F and G demonstrates that the enhancement in the diffusivities is approximately quadratic with respect to the electric field and electromobilities beyond a certain critical migration velocity. Below that critical point, we did not observe the quadratic behavior. This mirrors the critical point phenomenon in our extended KMC simulation. Fig. 1H shows that this quadratic behavior depends on the porosity of the matrices. The effective diffusivities decreased with respect to increasing acrylamide concentration. This agrees with the macroscopic relationship for diffusivities in a porous medium (), where is the diffusivity in a porous medium, is the porosity of the medium, and is the diffusivity in a free medium. Thus, microscopic changes in the stochastic electrotransport phenomenon are also reflected in the macroscopic treatment of the diffusivity.
The strength of stochastic electrotransport is that it can facilitate chemical transport without causing significant damage to the tissue structures. As one can imagine, free molecules have electromobilities that are much greater than those of the cross-linked endogenous molecules that constitute the sample. For this reason, stochastic electrotransport’s quadratic dependence on electromobility would allow for selective dispersion of free molecules while minimizing the displacement of cross-linked molecules. In our experiments on both applications of stochastic electrotransport to clear and to stain tissues, we characterized the degree of deformation both macroscopically (Figs. 2 E–G and 4 D and E) and microscopically (Figs. 2 H and I and 4 F and G). The resulting deformation was minimal and not statistically different from diffusion. Static electrotransport, however, caused significant damage under the high electric fields that we applied. This damage is characteristic of an electric field acting on a less conductive sample (SI Appendix, Fig. S12). Although typical applications using electrophoresis may not use nearly as high of an electric field, we show that the speed of electrophoretic techniques will ultimately be limited by the tissue damage, whereas stochastic electrotransport has more potential for faster clearing, which is currently limited by Joule heating.
In principle, beyond tissue clearing or tissue labeling, stochastic electrotransport may be applicable to any electromobile molecules and any porous samples. For example, RNA probes may be electrically dispersed throughout a tissue for fluorescent in situ hybridization. Reverse transcriptase may be rapidly distributed across a tissue for system-wide cDNA synthesis and subsequent in situ RNA sequencing, to extract transcriptomic data from the same intact tissue from which anatomical and physiological data were obtained (6). Rapid, diffusion-like dispersion of chemicals may also be useful for extending the application of emerging technologies [e.g., expansion microscopy (45)] to large intact tissues by enabling rapid transport of multifunctional probes into noncleared tissues. Finally, the concept of applying a rotational field to rapidly and evenly disperse particles throughout a tissue is not limited to electric force and may be generalizable to other types of forces, such as hydrodynamic pressure and magnetic force for molecular delivery. The broad future implications of stochastic electrotransport are yet to be explored.
Materials and Methods
All experimental protocols were approved by the MIT Institutional Animal Care and Use Committee and Division of Comparative Medicine and were in accordance with guidelines from the National Institutes of Health. Male C57BL/6 mice were perfused with hydrogel monomer solutions and organs were gel-embedded using a modified protocol from the original CLARITY method or using Easy-Gel system (EG-1001; Live Cell Instrument). The stochastic electrotransport system was assembled by connecting custom-built polyacrylate clearing or staining devices, a refrigerated batch circulator, and other accessories. The sample chamber was rotated by motor to implement rotating electric fields. For clearing, pH 9 lithium borate buffer with 200 mM or 10 mM SDS was used; for staining, pH 9 lithium borate buffer with 1% Triton-X was used. Nanoporous membranes were attached to the walls that separated the inner and outer channels in the case of clearing, whereas nanoporous membranes directly walled the sample chambers in the case of staining. For clearing, the inner solution was maintained at 15 °C and 200 V was applied across the sample chamber, while the sample chamber was rotated every 10–30 s. For staining, ∼50–80 V was applied and the sample chamber was rotated every ∼10 min. Staining was performed following conventional protocols (e.g., initial washing and staining followed by final washing) but with our electrophoretic device. Electrophoresis control samples were treated without sample rotation, and diffusion control samples were obtained by shaking in conical tubes. Samples were then optically cleared using a custom-made refractive index matching solution and imaged under a commercially available confocal or light-sheet microscope or a custom-made light-sheet microscope.
Supplementary Material
Acknowledgments
We thank the entire K.C. laboratory for support and helpful discussions. We also acknowledge M. Z. Bazant for advice and Y. J. Lee and J. C. Lee from Live Cell Instrument for fabrication of the devices. S.-Y.K. was supported by the Simons Postdoctoral Fellowship and the Life Sciences Research Foundation. K.C. was supported by Burroughs Wellcome Fund Career Awards at the Scientific Interface, the Searle Scholars Program, the Michael J. Fox Foundation, Defense Advanced Research Projects Agency, the JPB Foundation (PIIF and PNDRF), and NIH Grant 1-U01-NS090473-01. Resources that may help general users to establish the methodology are freely available online (http://chunglab.org/resources/).
Footnotes
Conflict of interest statement: The authors hold intellectual property related to the concept of stochastic transport and its implementation.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1510133112/-/DCSupplemental.
References
- 1.Cussler EL. 2009. Diffusion: Mass Transfer in Fluid Systems (Cambridge Univ Press, Cambridge, UK), 3rd Ed.
- 2.Chung K, et al. Structural and molecular interrogation of intact biological systems. Nature. 2013;497(7449):332–337. doi: 10.1038/nature12107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Piekut DT, Casey SM. Penetration of immunoreagents in Vibratome-sectioned brain: A light and electron microscopic study. J Histochem Cytochem. 1983;31(5):669–674. doi: 10.1177/31.5.6341457. [DOI] [PubMed] [Google Scholar]
- 4.Codling EA, Plank MJ, Benhamou S. Random walk models in biology. J R Soc Interface. 2008;5(25):813–834. doi: 10.1098/rsif.2008.0014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Meurant G. Cell Biological Applications of Confocal Microscopy: Cell Biological Applications of Confocal Microscopy. Academic; New York: 1993. [Google Scholar]
- 6.Lee JH, et al. Highly multiplexed subcellular RNA sequencing in situ. Science. 2014;343(6177):1360–1363. doi: 10.1126/science.1250212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.McAllister LB, Scheller RH, Kandel ER, Axel R. In situ hybridization to study the origin and fate of identified neurons. Science. 1983;222(4625):800–808. doi: 10.1126/science.6356362. [DOI] [PubMed] [Google Scholar]
- 8.Nield DA, Bejan A. Convection in Porous Media. Springer; Berlin: 2012. [Google Scholar]
- 9.Lin DC, Yurke B, Langrana NA. Mechanical properties of a reversible, DNA-crosslinked polyacrylamide hydrogel. J Biomech Eng. 2004;126(1):104–110. doi: 10.1115/1.1645529. [DOI] [PubMed] [Google Scholar]
- 10.Deen WM. 2nd Ed Oxford Univ Press; New York: 2011. Analysis of Transport Phenomena. [Google Scholar]
- 11.Peppas NA, Hilt JZ, Khademhosseini A, Langer R. Hydrogels in biology and medicine: From molecular principles to bionanotechnology. Adv Mater. 2006;18(11):1345–1360. [Google Scholar]
- 12.Slaughter BV, Khurshid SS, Fisher OZ, Khademhosseini A, Peppas NA. Hydrogels in regenerative medicine. Adv Mater. 2009;21(32-33):3307–3329. doi: 10.1002/adma.200802106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Crosetto N, Bienko M, van Oudenaarden A. Spatially resolved transcriptomics and beyond. Nat Rev Genet. 2015;16(1):57–66. doi: 10.1038/nrg3832. [DOI] [PubMed] [Google Scholar]
- 14.Chen KH, Boettiger AN, Moffitt JR, Wang S, Zhuang X. RNA imaging. Spatially resolved, highly multiplexed RNA profiling in single cells. Science. 2015;348(6233):aaa6090. doi: 10.1126/science.aaa6090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tomer R, Ye L, Hsueh B, Deisseroth K. Advanced CLARITY for rapid and high-resolution imaging of intact tissues. Nat Protoc. 2014;9(7):1682–1697. doi: 10.1038/nprot.2014.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Susaki EA, et al. Whole-brain imaging with single-cell resolution using chemical cocktails and computational analysis. Cell. 2014;157(3):726–739. doi: 10.1016/j.cell.2014.03.042. [DOI] [PubMed] [Google Scholar]
- 17.Ke M-T, Fujimoto S, Imai T. SeeDB: A simple and morphology-preserving optical clearing agent for neuronal circuit reconstruction. Nat Neurosci. 2013;16(8):1154–1161. doi: 10.1038/nn.3447. [DOI] [PubMed] [Google Scholar]
- 18.Hama H, et al. Scale: A chemical approach for fluorescence imaging and reconstruction of transparent mouse brain. Nat Neurosci. 2011;14(11):1481–1488. doi: 10.1038/nn.2928. [DOI] [PubMed] [Google Scholar]
- 19.Dodt H-U, et al. Ultramicroscopy: Three-dimensional visualization of neuronal networks in the whole mouse brain. Nat Methods. 2007;4(4):331–336. doi: 10.1038/nmeth1036. [DOI] [PubMed] [Google Scholar]
- 20.Ertürk A, et al. Three-dimensional imaging of solvent-cleared organs using 3DISCO. Nat Protoc. 2012;7(11):1983–1995. doi: 10.1038/nprot.2012.119. [DOI] [PubMed] [Google Scholar]
- 21.Kuwajima T, et al. ClearT: A detergent- and solvent-free clearing method for neuronal and non-neuronal tissue. Development. 2013;140(6):1364–1368. doi: 10.1242/dev.091844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Renier N, et al. iDISCO: A simple, rapid method to immunolabel large tissue samples for volume imaging. Cell. 2014;159(4):896–910. doi: 10.1016/j.cell.2014.10.010. [DOI] [PubMed] [Google Scholar]
- 23.Chung K, Deisseroth K. CLARITY for mapping the nervous system. Nat Methods. 2013;10(6):508–513. doi: 10.1038/nmeth.2481. [DOI] [PubMed] [Google Scholar]
- 24.Kim S-Y, Chung K, Deisseroth K. Light microscopy mapping of connections in the intact brain. Trends Cogn Sci. 2013;17(12):596–599. doi: 10.1016/j.tics.2013.10.005. [DOI] [PubMed] [Google Scholar]
- 25.Richardson DS, Lichtman JW. Clarifying tissue clearing. Cell. 2015;162(2):246–257. doi: 10.1016/j.cell.2015.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lozano AM, Hallett M, editors. Elsevier; Amsterdam: 2013. Brain Stimulation: Handbook of Clinical Neurology. [Google Scholar]
- 27.Hofman FM, Taylor CR. Current Protocols in Immunology. Wiley; New York: 2001. Immunohistochemistry; pp. 21.4.1–21.4.26. [DOI] [PubMed] [Google Scholar]
- 28.Langdale JA. In situ Hybridization. In: Freeling M, Walbot V, editors. The Maize Handbook. Springer; New York: 1994. pp. 165–180. [Google Scholar]
- 29.Oh SW, et al. A mesoscale connectome of the mouse brain. Nature. 2014;508(7495):207–214. doi: 10.1038/nature13186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sharpe J, et al. Optical projection tomography as a tool for 3D microscopy and gene expression studies. Science. 2002;296(5567):541–545. doi: 10.1126/science.1068206. [DOI] [PubMed] [Google Scholar]
- 31.Lovatt D, et al. Transcriptome in vivo analysis (TIVA) of spatially defined single cells in live tissue. Nat Methods. 2014;11(2):190–196. doi: 10.1038/nmeth.2804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Flamm MH, Diamond SL, Sinno T. Lattice kinetic Monte Carlo simulations of convective-diffusive systems. J Chem Phys. 2009;130(9):094904. doi: 10.1063/1.3078518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bulnes FM, Pereyra VD, Riccardo JL. Collective surface diffusion: n-fold way kinetic Monte Carlo simulation. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1998;58(1):86–92. [Google Scholar]
- 34.Jachimska B, Wasilewska M, Adamczyk Z. Characterization of globular protein solutions by dynamic light scattering, electrophoretic mobility, and viscosity measurements. Langmuir. 2008;24(13):6866–6872. doi: 10.1021/la800548p. [DOI] [PubMed] [Google Scholar]
- 35.Orakdogen N, Okay O. Correlation between crosslinking efficiency and spatial inhomogeneity in poly(acrylamide) hydrogels. Polym Bull. 2006;57(5):631–641. [Google Scholar]
- 36.Baker JP, Hong LH, Blanch HW, Prausnitz JM. Effect of initial total monomer concentration on the swelling behavior of cationic acrylamide-based hydrogels. Macromolecules. 1994;27(6):1446–1454. [Google Scholar]
- 37.Patist A, Oh SG, Leung R, Shah DO. Kinetics of micellization: its significance to technological processes. Colloids Surf Physicochem Eng Asp. 2001;176(1):3–16. [Google Scholar]
- 38.Vigo F, Uliana C, Novi M. Electro-oxidation of sodium lauryl sulfate aqueous solutions. J Appl Electrochem. 1988;18(6):904–908. [Google Scholar]
- 39.Alroy J, Goyal V, Skutelsky E. Lectin histochemistry of mammalian endothelium. Histochemistry. 1987;86(6):603–607. doi: 10.1007/BF00489554. [DOI] [PubMed] [Google Scholar]
- 40.Mazzetti S, Frigerio S, Gelati M, Salmaggi A, Vitellaro-Zuccarello L. Lycopersicon esculentum lectin: An effective and versatile endothelial marker of normal and tumoral blood vessels in the central nervous system. Eur J Histochem. 2004;48(4):423–428. doi: 10.4081/916. [DOI] [PubMed] [Google Scholar]
- 41.Jährling N, Becker K, Dodt H-U. 3D-reconstruction of blood vessels by ultramicroscopy. Organogenesis. 2009;5(4):227–230. doi: 10.4161/org.5.4.10403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Whiteus C, Freitas C, Grutzendler J. Perturbed neural activity disrupts cerebral angiogenesis during a postnatal critical period. Nature. 2014;505(7483):407–411. doi: 10.1038/nature12821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Vakoc BJ, et al. Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging. Nat Med. 2009;15(10):1219–1223. doi: 10.1038/nm.1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lacoste B, et al. Sensory-related neural activity regulates the structure of vascular networks in the cerebral cortex. Neuron. 2014;83(5):1117–1130. doi: 10.1016/j.neuron.2014.07.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chen F, Tillberg PW, Boyden ES. Optical imaging. Expansion microscopy. Science. 2015;347(6221):543–548. doi: 10.1126/science.1260088. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.