Significance
Medical predictions rely on probabilistic models that link the risk of future events to diagnostic and therapeutic variables. These models result from epidemiologic studies based on direct observation of events and variables in population samples. They work well for acute diseases in otherwise healthy individuals. For chronic, multiple conditions and diseases, more complex predictive models are needed. Such models have been developed for chemical kinetics problems that are analogous to epidemiologic problems if we view molecules as individuals and macroscopic systems as populations: Deterministic kinetics with one reaction are like most direct epidemiologic studies; the Arrhenius model is analogous to survival analysis. Stochastic systems with time-dependent reaction coefficients are worth exploring for deriving new epidemiologic methods.
Keywords: chemical kinetics, paradigm, noncommunicable disease, epidemiology, stochastic model
Abstract
Calculating the probability of each possible outcome for a patient at any time in the future is currently possible only in the simplest cases: short-term prediction in acute diseases of otherwise healthy persons. This problem is to some extent analogous to predicting the concentrations of species in a reactor when knowing initial concentrations and after examining reaction rates at the individual molecule level. The existing theoretical framework behind predicting contagion and the immediate outcome of acute diseases in previously healthy individuals is largely analogous to deterministic kinetics of chemical systems consisting of one or a few reactions. We show that current statistical models commonly used in chronic disease epidemiology correspond to simple stochastic treatment of single reaction systems. The general problem corresponds to stochastic kinetics of complex reaction systems. We attempt to formulate epidemiologic problems related to chronic diseases in chemical kinetics terms. We review methods that may be adapted for use in epidemiology. We show that some reactions cannot fit into the mass-action law paradigm and solutions to these systems would frequently exhibit an antiportfolio effect. We provide a complete example application of stochastic kinetics modeling for a deductive meta-analysis of two papers on atrial fibrillation incidence, prevalence, and mortality.
Much of the medical progress over the last century can be attributed to the objective assessment of the effect of treatments on the evolution of specific diseases. Treatment effect is measured as the rate of an event such as recovery in a sample of the patient population. Relatively immediate results were obtained from studies involving acute diseases, occurring in previously healthy individuals, in which recovery could be clearly identified. This resulted in the development of effective treatments for most acute diseases affecting children and younger adults and a substantial prolongation of life expectancy (1). Consequently, many acute diseases were treated effectively. This led to the current, more complex situation, in which an elderly population suffers from a combination of chronic conditions. Few older people are strictly healthy, and besides the evolution of the chronic conditions themselves, acute diseases occurring in this setting do not always evolve as in a young, healthy population. This combination of chronic conditions and risk factors amounts to the presence of more heterogenous populations. Thus, samples need to be larger to allow reproducible predictions, compared with those for acute diseases occurring in a young and previously healthy population. Predictions that are also more complex (there is no strict “recovery”) apply to a limited range of cases.
The concepts used by clinicians and epidemiologists to describe the health status of individuals and their prevalence in the population, as well as the rates of change in this status and the general predictive laws, are quite analogous to the concepts used by chemists for predicting the future concentrations of species in a reactor. Early works on the spread of epidemics of communicable diseases (2, 3) made reference to this analogy, unlike later developments in mathematical epidemiology (4, 5). The purpose of current mathematical modeling of epidemiology is mostly the kinetics (or “dynamics” as it is frequently called) of the spread of a communicable disease in an acute epidemic (6), an important and pressing problem when such epidemics occur. The primary phenomenon represented in these models is contagion. The models used are typically deterministic, self-catalytic kinetic models of the whole population, with mass-action law assumption.
The focus of clinical studies in chronic diseases is the risk for various possible outcomes for the patient that are usually distinct from a complete recovery and sometimes of a quantitative nature—for example, how much of the function of an organ is preserved. Kinetics-type mathematical support for this purpose is rarely available, other than a simple statement of risk or relative risk that is directly inferred from a study in a sample.
Deterministic event rates are the basis of virtually all clinical judgement. A typical example is, What is the yearly risk of stroke in patients with atrial fibrillation on either of two treatments, such as warfarin or aspirin? (More individual parameters are usually taken into account when classifying each patient). A lower yearly risk rate in one of the treatment categories is an argument to choose that treatment for a particular patient. This risk rate is usually the rate of stroke that has been directly measured in a study where a sample of patients belonging to certain classes (for example, middle-aged males with atrial fibrillation and no history of stroke) has been followed for some time. The observed event rates are taken as the best estimations for the population sharing the same characteristics as the patients in the sample, a population that is presumed infinite. The event rates are inferred, however, starting from observations made in finite, small, ensembles of individuals (case series). Thus, inference is always probabilistic, as event rates in the population can be estimated only with some uncertainty, even in homogenous populations.
In populations in which individuals have various combinations of underlying pathologies that may each influence the future event rates, this approach may frequently lead to unreproducible results (7, 8). Aiming to predict events that would occur in the more distant future, as needed with chronic disease, further complicates the problem: The longer the prediction time is, the higher the number of other events that may intervene and invalidate the prediction.
Both epidemiology and chemical kinetics have evolved independently over the previous decades, each developing its own stochastic methods with a specific terminology that frequently refers to somewhat similar concepts. Prediction of event rates from relatively small samples, using probabilistic models, is of primary importance for epidemiology. Half a century ago, the factors influencing the recovery from acute diseases in otherwise healthy (that is, homogenous) populations were the main concern. Thus, the problem was to estimate event rates in otherwise simple systems. Models of the epidemiologic equivalent of a single reaction, with a few other parameters, were adequate for this. Probabilistic issues were mostly related to the errors associated with the limited sizes of the samples used, but the inferred rates were typically deterministic. In chemistry, at that time, model development focused on identifying the relatively complex reaction mechanisms that occur, even when only a few initial species are involved, and on describing their kinetics, typically with systems of deterministic differential equations adjusted using macroscopic measurements of species concentrations. Uncertainty due to small molecule numbers was not usually involved. Over the last 70 y, however, chemical kinetics developed new methods, such as models of more complex systems that do not rely on mass-action law (9) or models of single-molecule kinetics that might be closer to the problem of predicting clinical evolution in individual patients. Also, issues that occur in the biochemical kinetics of more complex systems, such as crowding (10), are to some extent analogous to event prediction in heterogenous populations.
The development of numerical methods allows the practical approach to problems that involve systems that are both complex and stochastic and the exploration of uncertain phenomena at both individual and population levels (11). An important clinical problem that cannot, in general, be solved without such a systematic approach is to compute, for an individual, the risks for each possible disease over the next time interval (such as 1 y), given what we know about his or her health status and history and based on currently available epidemiologic data. Solving this problem would allow much more accurate planning of clinical interventions than is possible today.
In this paper, we attempt to compare concepts, methods, and models that have been developed in the two fields, by reformulating the epidemiologic approaches in chemical kinetics terms, to identify chemical kinetics methods that might be adaptable for epidemiologic use. In Supporting Information, we show an example of a deductive meta-analysis of two epidemiology papers, using a stochastic kinetic system.
Unified Terminology
We use the following unique terms to describe either chemical systems or populations of patients: individual, either an individual molecule or a patient; ensemble, a set of individuals; population, a real or imaginary ensemble large enough for deterministic mass laws to occur; sample, a small ensemble in which measurements are performed; species, a binary, yes/no criterion, for classifying individuals and also the subsystem comprising individuals with “yes” for the criterion [it could be a covalent structure for molecules such as warfarin or a diagnostic class (such as “diabetic”) for a patient]; subspecies, a species that is a subset of another species, for example “insulin-dependent diabetic” as a subspecies of diabetic for a patient or a warfarin enantiomer (R or S) as a subspecies of “warfarin” in chemistry; elementary species, a species that contains no subspecies; coverage, a selection of species such that each individual in a population belongs to exactly one species; prevalence is the equivalent of relative concentration, the proportion of individuals of a species in an ensemble; parameter, another measurable term characterizing either the system or each individual, such as temperature or pressure for chemical systems or age, weight, and fasting glycemia for patients; transition, the probabilistic transformation of an individual from one species to another; reaction, the macroscopic process of transition of individuals between two species, possibly going through a number of intermediate species; elementary reaction, a reaction that consists of a single transition, without intermediates; rate is the derivative of the prevalence in time, due to one reaction; rate coefficient is a number, or a function, that characterizes the rate after removing its dependency on the prevalence (concentration); evolution, the succession of species through which an individual progresses in time (for example: susceptible infected recovered); system, a theoretical construction, comprising individuals, species, and reactions; and process, the successive states undergone by a system between two time instants.
The Clinician’s Problem
Restated in these terms, the purpose of clinical research is the prediction of the evolution (state or species transition) of individuals, given variable values at the initial time. The purpose of epidemiological research is the prediction of the prevalence of each species in time, given an initial variable value distribution. An example problem is, Given what we know about an individual, what is the probability of each possible health outcome (status belonging to a species from a coverage) for him or her after a definite period? For example, given a 45-y-old man with uncomplicated diabetes, free of any other disease, on adequate treatment, what is the probability of each disease classification from a coverage 1 y in the future? A simple example of coverage could be (i) alive, healthy, and diabetes free; (ii) the same status as now; (iii) having a new disease; or (iv) dead. The clinical problem, for an individual, is an aspect of the epidemiological problem, for a population, just as chemistry at the macroscopic level is another view of molecular collisions and transformations at the molecular level. The answer to the general clinical problem stated above is typically a probabilistic translation (a “risk” law) derived from an epidemiologic law that was, in its turn, directly inferred from patient sample measurements.
What one cannot usually do, using the current epidemiologic methods, is the equivalent of the prediction of future species concentrations in a chemical reactor: Compute all of the disease and complication risks of the individual, at any time over the next years, such that the sum of the risks is 1 and the result is consistent with experimental data. Such a prediction is usually possible only for the simplest cases: acute diseases in otherwise healthy people and only for the short term.
Types of Data Available from Epidemiology Studies
In chemistry, both measured data and models deal mostly with macroscopic variables (concentrations in time from which rates over finite durations are computed). In epidemiology, models are also at the population level (prevalences, incidences, risk rates) but the data are available only for small samples, starting from measurements in individuals. Measurements consist of diagnostic classifications (such as “atrial fibrillation”) and continuous parameters (such as “serum glucose level”). Sometimes, diagnostic classifications refer to ranges of the continuous parameters, for example “bradycardia,” “normocardia,” and “tachycardia” may refer to a heart rate under 50/min, between 50/min and 100/min, and over 100/min. We denote by x the vector of these n measurements for an individual and by S the set of possible values of x, which is a contiguous subset of , . In a typical experiment, individuals are selected to belong to some subset of S, for example having a certain disease with certain parameters. They are further divided into subgroups, for example by randomly subjecting them to various treatments, say . Each of these subsets corresponds to a species in the unified terminology. Species dealt with in one study may be subspecies of species from other studies or may overlap in various ways. In time t, each individual undergoes changes in his or her status, . Each individual is followed from an initial instant, T, over a finite time interval , to see whether he or she changed into some other subset, named endpoint —for example, if the individual became free of one of the diseases he or she originally had or if he or she died or developed a specific new disease.
The observed frequencies of transition to new states are inferred as rates of transition for the broader population of individuals belonging to or into over the same finite time interval; that is,
| [1] |
In other words, the vast majority of clinical studies that assess the for every and aim in fact to document the master equation that governs the stochastic function. Due to small numbers in samples, the inferred are uncertain, with a confidence interval computed using the binomial distribution that corresponds to the process of random sampling. Alternatively, the probability of the null hypothesis, is reported; a P below a threshold, such as 0.05, results in the conclusion that, for example, . The accuracy of estimation of depends on the product of and the number of cases considered in each study.
Assumptions of Clinical-Epidemiologic Models
Some common assumptions are necessary to extrapolate the observed frequencies to the entire population: (i) that the components of x represent all of the relevant determinants of future values of , this naturally implying that they are all of the known relevant determinants; as a special case, that the previous history of the individual, that is, , does not influence ; (ii) that are properly sampled by the cases reported in the study, and thus refers to any future individual from ; (iii) that do not change over the next years; that is, the current sample is also relevant to future populations (to which the conclusions of the study will be applied); (iv) that for at least some relevant transitions, the transition rate is constant in time or at least that the rate differences observed over are relevant over different time ranges; for example, if a drug is observed to be effective and safe for a disease at exactly 1 mo of treatment, then recommending it for that disease implies the assumption that it will also be safe and effective after 2 wk or 2 mo; although and may not be strictly constant, an assumption is made that, for example, at least for a meaningful range of ; and (v) that the population from which the samples are drawn is infinite, or large enough to be treated as infinite, and thus state transition or reaction rates make sense as macroscopic properties.
The assumption that, for individuals in a region of the parameter space, the probability of transition to another region, , is constant over successive intervals is equivalent to the assumption of mass-action law at the population level. This assumption is explicit in most mathematical epidemiology models, and it is also present in many common judgments that involve, for example, comparing risk rates over specific intervals of time. Many patient evolutions are, however, inconsistent with this assumption. One example is progression through age groups: 40-y-old individuals do not have a constant daily, or monthly, risk of progressing to being 41 y old. Instead, the progression rate is 0 except for the 41st birthday when it is 1. (The same is true irrespective of what time interval we choose for an age group, when we choose age groups with fixed limits as species).
Another example is the cure of an acute infectious disease. The duration of the illness can be given, for example, as a median of 7 d, with an interquartile range of 3–10 d (12). This distribution is inconsistent with a constant rate coefficient, because the rate of cure would then have to be the highest in the first days of the disease. Indeed, the rate of cure is not constant, but given by the time needed for the specific immune response to occur, that is, around 1 wk in most healthy individuals.
Other examples not consistent with constant rates include the time-dependent risks following an acute event. For example, following an acute myocardial infarction, the risk of death is much higher in the first days than in the following days or months.
Thus, the type of kinetics that are suitable for modeling many situations needs to consider reaction coefficients that are functions of time or, at the individual level, stochastic chains that have memory, rather than the mass-action law framework. In some cases, a process that does not conform to mass-action law can still be modeled using mass-action law by assuming that there is more than one species, each with its own constant reaction coefficient. For example, following an acute event, the species C suffering the event E may be split, with a specific probability, in “high-risk” () and “low-risk” () strata (subspecies) having constant reaction coefficients. The kinetics of E will not obey mass-action law, but the components, E and E will.
Methods such as hidden Markov or, more generally, inhomogenous stochastic chains have been used occasionally to approach some epidemiologic problems (13–16).
The General Problem
In general, we need to develop theoretical kinetic systems that are solved in the form of computed results of various hypothetical studies. Parameters of the kinetic systems need to be tuned so that computed results match existing studies. A proposed kinetic system is valid as long as it predicts the results of future studies that were not used for tuning it. In the most general case, these systems would be stochastic reaction–diffusion systems in which reaction (and diffusion) coefficients are stochastic functions of time. Because the history of each individual from the system may influence its current transition probabilities, the solution needs to involve simulation at the individual level. Matching with experimental data must, however, be done at the population (macroscopic) level, as experimental results are available as population models. An example application, in which we check, quantitatively, the consistency of some experimental results (17–19) and some epidemiologic hypotheses (17), using a kinetic system, is shown in Supporting Information.
Description of Time-Dependent Reaction Coefficients
A reaction
| [2] |
where is not constant, can be written at the individual level as a set of transitions
| [3] |
| [4] |
| [5] |
where are subspecies of A, are different transition coefficients that are, each, constant in time, and thus are memoryless transitions, corresponding to constant reaction coefficients. represents a special type of reaction, representing only the memory phenomenon, in which the transition rate is 0 until a specific instant, , when it becomes 1. The time interval , for each individual in species , flows from the instant when it transitioned into species .
This description is equivalent to averaging on intervals.
Typical Epidemiological Studies and Their Chemical Equivalents
Transversal Studies.
Studies called “transversal,” meaning “performed across a population or population sample at a given instant in time,” correspond to the determination, at a specific instant, of the concentrations of a species in a reactor or of the instantaneous rate of production or consumption of that species. Sometimes transversal studies consider the whole population (this type of study is sometimes called “screening”) that is usually large, such as the population of a country, but of course finite. Frequently, the study is performed in a representative sample and the observed prevalences are extrapolated with confidence limits; that is, prevalences in the population are determined as probability distributions. Transversal studies aim to estimate the concentrations at instant . Sometimes an assumption of stationarity is made, so measurements of prevalences (concentrations) performed at one time are supposed to directly predict the prevalences a few years, or decades, later or for any t.
Longitudinal Studies.
Longitudinal studies are repeated transversal studies. Simpler studies are just verifications of the fact that the prevalences are, or are not, stationary. A null hypothesis that they are stationary in the population may be rejected with a statistical test on sample data.
Some long-term surveys monitor the prevalences and incidences of important disease classifications (species) yearly over long periods of time in the whole population of a country. In our notation, this type of study attempts to determine the probability for certain values t.
Cohort Studies.
Cohort studies are longitudinal studies in which the same ensemble, consisting typically of individuals belonging to a single species, is followed for a longer time, and the rates of transition to other species, in time, are recorded. They correspond to observing reactions in reactors where the initial concentrations are well known, for example a single, pure substance, the decomposition of which is monitored in time. In other words, a reaction E is monitored, and the result of the study is an estimation of or or, if successive measurements are made at regular intervals , they are determinations of
| [6] |
or, rather, the probability distribution , where the is the integral rate over some time interval.
Controlled Studies.
Control studies consist of comparing rates in two or more cohort studies in parallel. The differences in rates may be attributed to differences in the initial parameters of the populations that may be introduced (for example, as treatments) by the researchers. Prevalences are usually measured at specific time instants, for example every month, or just at the start and the end of the study. The purpose of a control study, put in kinetic terms, is to compare two integral rates (differences in prevalences) over a specific interval of time. For example, we assume the reactions . We try to estimate the probability that from measurements of at various time instants.
Survival Studies.
Survival studies are control studies in which the timing of the transition from a species to another is recorded for each individual. In a typical approach, using the Cox proportional hazards model (20), an assumption is made that, with the notation above, , where u is a constant. The purpose is to calculate the probability , thus inferring that (t), and also to estimate , sometimes called “relative risk,” that is typically given as an estimate with confidence intervals.
In more sophisticated survival studies, u is given as an exponential of a linear combination of constant population parameters, to estimate the relationship between rate coefficients of numerous population subgroups, for a specific reaction. This is apparently analogous to the Arrhenius model (law). The Arrhenius model relates the rate coefficient to the (inverse of) the temperature with a formula like
| [7] |
where k is the rate coefficient, is the activation energy (specific to the reactant species), R is the gas constant, T is the temperature, and A is a fitting constant.
Proportional hazard models are formulated as
| [8] |
where from survival models corresponds to the prefactor A in the Arrhenius equation. The influencing variable X corresponds to the (inverse of the) temperature and the reaction-specific constant β corresponds to the activation energy . As mentioned above, in some studies, X may be a linear combination of some measurable parameters that are supposed constant for a population subgroup (such as gender, exposure to some environmental factor, genetic variant, etc.).
Theoretical Integration of Experimental Results.
The types of studies described in the previous section are experimental studies for which simple, empirical models are fitted to datasets, equivalent to straightforward chemical or chemometric studies.
The main contribution that might be achieved through analogy with chemical kinetics refers to theoretical integration of such results. Theoretical integration of experimental data in epidemiology can be divided into two categories: meta-analysis and mathematical epidemiology studies. Meta-analysis refers in essence to reducing the uncertainty regarding the estimation of a rate coefficient of a single reaction by pooling the results from multiple studies. Mathematical epidemiology studies usually deal with the phenomenon of contagion and use rate estimates (without confidence intervals) resulting from a number of single-reaction studies to build systems of a few reactions and predict their behavior at the population level.
Predicting the risk profile of a specific individual at a given instant, the prototypical problem we specified in the Introduction, requires a system of many different reactions, corresponding to many combinations of the numerous types of pathologies and evolutions. As the available data are always in relatively small samples, any rates are probabilistic estimations rather than deterministic values observed in a macroscopic setting. This uncertainty needs to be taken into account.
Issues Resulting from System Complexity.
The example below illustrates some of the predictive limitations that arise from not taking into account sufficient aspects of system complexity in the design of a predictive model.
Consider a cohort of initially healthy individuals with two subgroups: low-risk rate , for example younger, , and high-risk rate , for example older, . A pathologic condition, denoted as species F, may occur in subjects from either group, but with a higher rate in :
| [9] |
| [10] |
| [11] |
Suppose an investigator measures the initial () prevalences of and . We denote them as . At time the prevalence of condition F is .
He or she draws the conclusion that the incidence of condition F over y is
| [12] |
If the sampling has been adequate, and the study properly conducted, this conclusion would be directly extrapolated to the evolution of similar populations [with the same initial ratio] over time interval .
However, the incidence of F in this cohort increases in time, as subjects move into the high-risk category. Consequently, the estimation over interval cannot be extrapolated to shorter or longer intervals or to populations in which the initial ratio is different. For example, if the estimated incidence is over 10 y, then it will be lower than 0.1 over 5 y and higher than 0.3 over 15 y.
In a common setup, we would also know and . However, this is sometimes not the case, as the investigations needed to make the initial vs. classification may be expensive or otherwise impractical at time .
Assuming first-order kinetics, we can write the kinetic equations for the system,
| [13] |
| [14] |
| [15] |
| [16] |
where are given constants. A simplistic linear extrapolation of f would be
| [17] |
The error in using a simplistic linear extrapolation is
| [18] |
Usually, one type of transversal study (S1) would consist of examining a large number of patients that just suffered the event F and classify them by the a criterion (were they high or low risk, for example). In another type (S2) the prevalence of the risk class ( vs. ) in the general population could be assessed. These frequencies would allow the direct estimation of and . In yet a different kind of study (S3), the integral incidence is measured for a given value of ; initial and are also known. The problem of the kinetic modeling of such a case could be to estimate given the above frequency estimations. is a monotonous function, and thus the equation can be solved numerically for using, for example, Newton’s method.
In an imaginary example of the above with , , (y), , (/y), (/y) we found , , and , which means an error of about 10% would have been made for with the linear approximation.
In summary, measurement of an event rate after a specific interval (such as 10 y) cannot, in general, be extrapolated to other time intervals or to populations having different distributions of initial parameters than the one in which the measurement was performed, if any of these parameters are correlated with the event rate. For example, an event rate estimated based on direct measurements in a sample of patients that are both younger and older, say between 50 y old and 70 y old, will erroneously estimate the risk for younger patients, say between 50 y old and 55 y old, and indeed it will imply a prediction error for a single individual. To avoid this error, a kinetic model of sufficient complexity needs to be developed.
Determinability of Reaction Coefficients.
Prevalences in epidemiologic studies are usually inferred from (small) samples and are thus known with approximation. For simple mass-action systems, in which we take this uncertainty into account, the rate coefficients have probability distributions that may be calculated analytically. Consider the elementary reaction
| [19] |
Let be the prevalence (concentration) of species A and be the prevalence of species F. We assume that and the prevalence is estimated at time . If we use a large number of cases, the binomial distribution of the real prevalence can be approximated as normally distributed, with the mean and the dispersion . As ,
| [20] |
If we take and is normally distributed, then has a lognormal (ln) distribution with mean
| [21] |
Thus, k also has a lognormal distribution with mean
| [22] |
Successive determinations of the rate of at later time instants allow an iterative improvement of the distribution of k, using a procedure such as that described in ref. 21.
However, if we do not take as being known exactly, but rather as having a probability distribution, then the fraction will exhibit an antiportfolio effect (22) that may reduce the possibility to estimate the value of k very much (the information content of the resulting distribution of k will become very low). A portfolio effect occurs when random variables are combined so that their result has higher information content, such as when we take the average of two measurements of the same noisy event. An antiportfolio effect occurs when combinations, such as multiplication of random variables, result in reduced information, as in solving the above stochastic equation. The presence of an antiportfolio effect provides a previously unidentified explanation for the lack of reproducibility of studies estimating event rates, beyond the reasons stated in ref. 7.
Summary
The computation of the risks of pathological events facing an individual at any future instant in time is not possible with the currently widespread epidemiology theory except for the simplest problems. In general, it requires complex models of his or her possible evolution that are analogous with complex stochastic kinetics systems used in chemistry.
We explored the analogy between common types of clinical/epidemiologic studies and corresponding kinetic models.
Deterministic models that involve only a few reactions/species can be expected to be effective predictors only for the simplest cases, such as acute diseases occurring in otherwise healthy populations. Stochastic descriptions that correspond to a single reaction, directly inferred from sample measurements, that are common in current studies of epidemiologic processes are, by themselves, limited to prediction over a fixed time interval and for populations with a specific composition.
We showed that many common kinetic phenomena that correspond to epidemiologic processes cannot be expected to fit into the mass-action law paradigm. As reaction coefficients are necessarily inferred from small sample measurements, they are uncertainly known. Consequently, some of the more complex systems may exhibit an antiportfolio effect, with a spread of the probability of some solutions on a broad range. Thus, such systems may actually prove to be poor predictors for some problems, due only to this effect. Still, besides stochastic kinetics, no other well-developed theoretical framework is available to approach the essential problem of risk estimation for patients already suffering from multiple diseases and conditions.
A typical, important problem that is rarely approached in the literature is a deductive meta-analysis that is a quantitative synthesis of the results of multiple experimental studies of different types, such as a mortality, an incidence, and a prevalence study. In chemical kinetic terms, this amounts to describing a system consisting of multiple reactions. Data for tuning the system would be obtained from separate experiments involving one reaction each. Concentration measurements would be affected by substantial measurement errors.
We present below, as an illustration of the discussions in the main text, an example application of stochastic chemical kinetics for an epidemiology problem: checking the consistency of observational reports on incidence, mortality, and prevalence of atrial fibrillation (AF) and quantitative check of one hypothesis regarding the increase in AF prevalence over the last 20 y.
The Issue of AF
Permanent heart rhythm, in most humans, is either “sinus rhythm” (SR), which is the normal, regular rhythm, or AF, which is a completely irregular rhythm and a pathologic condition. There are other, much rarer rhythms that we do not consider here (we abstract them out of the model).
AF occurs increasingly with age, starting from around age 50 y. It may be due to other preexisting diseases and conditions, but it mostly occurs idiopathically—without any detectable cause. It is initially reversible, that is, patients may revert to SR, either spontaneously or with specific treatments. Then, AF may occur again. In time, it becomes irreversible.
Patients having AF have a reduction of their heart ability to pump blood, because the atria do not beat anymore, and an increased risk of stroke, because blood clots in the nonbeating atria and the resulting clots may migrate and obstruct various arteries, in particular cerebral arteries.
Because of these, and other reasons, AF is associated with increased mortality. This association was increasingly recognized over the last 20 y, resulting in growing interest in identifying and preventing AF’s causes and complications.
Statement of the Problem
We use data from three sources, all on recent US populations:
-
•
Ref. 17 reports on the incidence and prevalence of AF by gender and age group in a large population sample.
-
•
Ref. 18 reports on AF vs. non-AF mortality by gender and age group.
-
•
Center for Disease Control (19) general mortality data.
The prevalence of AF is a result of its cumulated incidence over time, as well as the different mortality of the patients with AF vs. patients with SR. The first question we try to solve is to check whether the prevalences reported in ref. 17 are quantitatively possible given the incidences from ref. 17 and the mortalities from ref. 18. This type of evaluation is possible only by using a kinetic model. Ref. 17 also finds that AF prevalence has increased from 1993 to 2003 and attributes this increase to a decreased reversibility of AF (possibly due to better diagnosis).
Kinetic Model of Mortality in AF
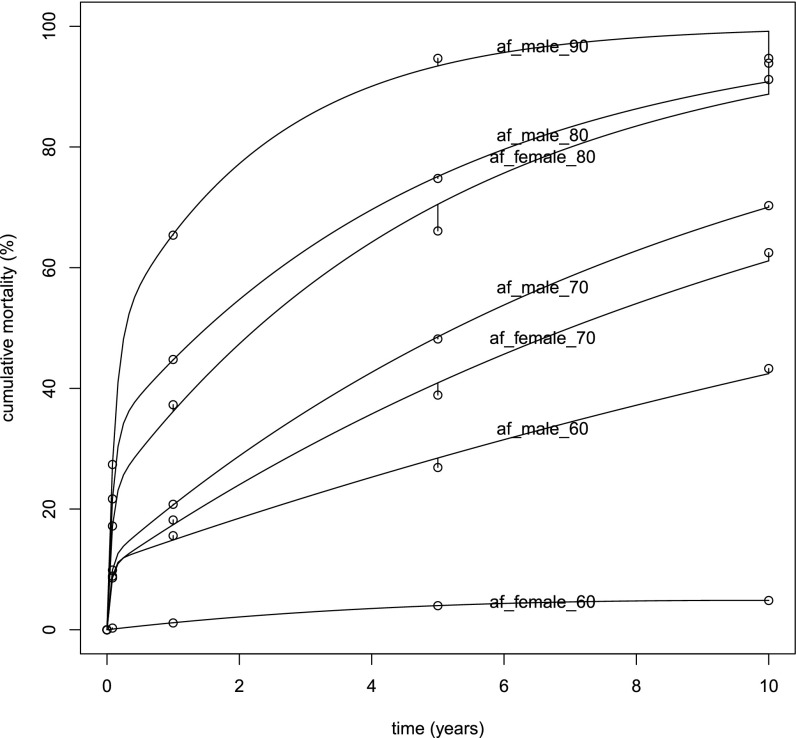
As can be seen in Fig. S1 and in table 2 of ref. 18, the mortality rate in AF is not constant in time after the occurrence of AF. Thus, if is a species that models patients with AF having gender g and age a, the mortality rate cannot be described as a mass-action law reaction , where D represents dead subjects. However, we note that there is a subgroup that dies in the first months after AF occurrence and another group that survives for years, dying at a lower rate, although still higher than subjects without AF.
Fig. S1.
Fit of the kinetic model (Eqs. 1 and 2)—the lines, one for each gender and age group—to data from table 2 of ref. 18 (circles). It shows the extent to which a set of biexponential models, with a high-risk and a low-risk component for age and gender subgroup, fits the observed data and thus justifies why we modeled each age and gender group with the two species.
We call these two groups the high-risk group, and the low-risk group, of AF patients having gender g and age a.
The kinetic equations for the model are thus
| [S1] |
| [S2] |
This two-reaction model, for each age and gender group, is a good fit for the ref. 18 AF mortality data, as shown in Fig. S1, where the variables are the initial ratio of
| [S3] |
and the two mortality rates, and . We denote by the concentration of species X at time t. We estimated the values of these variables by fitting a sum of two exponentials on the data in each row of table 2 of ref. 18, using nonlinear least squares. The percentage values in the table, representing the data against which we performed the fit, correspond to the cumulative mortality
| [S4] |
where time t instants are at 30 d and 1 y, 5 y, and 10 y.
Stochastic Mortality Coefficients
The data in ref. 18, table 2 represent observed frequencies in finite and relatively small samples of 31–268 individuals. Consistent with these observations are population frequencies with the probability distribution , where is the binomial distribution.
We generated 1,000 binomially distributed random samples representing the possible population mortalities corresponding to each data point and, by repeating the fit for each set, obtained a sample of the population distribution of , , and given the observations reported in ref. 18, table 2.
Integration of Mortality, Incidence, and Prevalence Data
To model the incidence and prevalence data from ref. 17 we considered a stationary population to which 100,000 newborns in species (sinus rhythm of gender g and age 0) are added each year.
The non-mass-action law reaction
| [S5] |
represents the age progression from age group a to age group , where the “” coefficient means that individuals in species that were in species for 1 y all move into age group at the end of the year.
Besides [S5], for each age and gender group, we introduced the mass-action law reactions
| [S6] |
| [S7] |
| [S8] |
| [S9] |
| [S10] |
where represents the rate of the reversal of AF to SR. Death rates were taken from ref. 19 as they describe the general population.
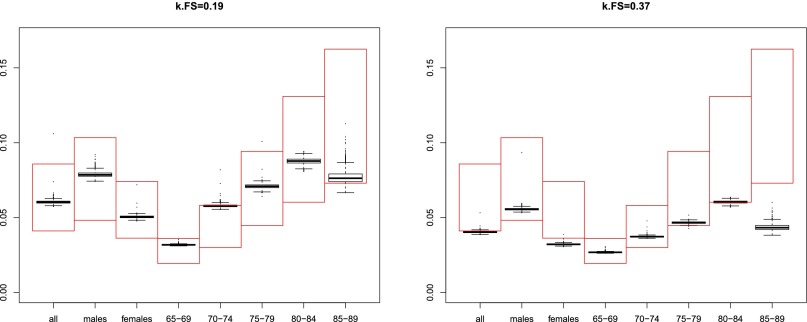
The age progression of subjects with AF fibrillation is, in practice, that they are theoretical species resulting from the biexponential approximation. At stationarity, these prevalences over suitable age and gender groups were compared with prevalences from ref. 17. Fig. S2 presents the results of 2,000 scenarios, 1,000 for and 1,000 for . Each 1,000 scenarios result from the Monte Carlo simulation of the binomial distribution of mortalities in the populations that are possible given the rates observed in ref. 18. The simulated prevalences largely fall within the range of the measured values, using the incidences and the reversal rates reported in the supplementary information of ref. 17. However, these reversal rates do not explain the total differences in prevalence between 1993 and 2007. Also, progression of tprevalence with age was slower in the simulated results compared with observation. This could be due to the fact that we considered a constant reversal rate (constant irrespective of the age and of the duration of fibrillation), as in ref. 17, but in clinical practice this rate is reduced after a few months of continuous AF. The dispersion of values represented by the vertical extent of the whisker plots in Fig. S2 reflects the uncertainty due to small samples sizes of mortality estimations. It can be seen that this factor alone is not the cause of the observed differences between simulations and experimental data.
Fig. S2.
(Left and Right) Simulated and literature results on the prevalence of AF. The y axis shows AF prevalence. The x axis shows various gender and age subgroups. The large, red rectangles represent measured AF prevalences, taken from ref. 17, supplementary table 5. The top level of the range corresponds to year 2007 and the bottom level to year 1993. The whisker plots represent the distributions of the prevalences obtained for each scenario resulting from the Monte Carlo simulation of mortality rates for high- and low-risk AF. Left shows the results obtained with a uniform AF reversal rate of , whereas Right shows a value of (as reported in ref. 17). Ideally, the simulated prevalences (black whisker plots) at Left would be expected to occur toward the top, 2007 level of the measured prevalence range (top of the red box) whereas those at Right would occur toward the bottom, 1993 level. Systematic differences from the expected behavior need to be explained by further refinement of the model, but it can be seen that the uncertainty of the mortality coefficients that is attributable to small sample sizes cannot account for these differences.
Summary
We developed a kinetic model of AF epidemiology as an illustration of the use of kinetic methods for deductive meta-analysis of data sources of different types. Our model demonstrates that the incidence, prevalence, and mortality data from refs. 17–19 are consistent with each other. It also confirms that AF diagnostic reversal, whether due to encoding practices, actual AF reversal, or other reasons, plays a part in the increase of AF prevalence over the last two decades, but also indicates that it may not be the only factor.
Acknowledgments
This work was supported, in part, by the National Science Foundation (CHE 0847073).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1510927112/-/DCSupplemental.
References
- 1.De Flora S, Quaglia A, Bennicelli C, Vercelli M. The epidemiological revolution of the 20th century. FASEB J. 2005;19(8):892–897. doi: 10.1096/fj.04-3541rev. [DOI] [PubMed] [Google Scholar]
- 2.Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond A Contain Pap Math Phys Character. 1927;115(772):700–721. [Google Scholar]
- 3.Muench H. Catalytic Models in Epidemiology. Harvard Univ Press; Cambridge, MA: 1959. [Google Scholar]
- 4.Hairston NG. An analysis of age-prevalence data by catalytic models. A contribution to the study of bilharziasis. Bull World Health Organ. 1965;33(2):163–175. [PMC free article] [PubMed] [Google Scholar]
- 5.Cohen JE. Selective host mortality in a catalytic model applied to schistosomiasis. Am Nat. 1973;107:199–212. [Google Scholar]
- 6.Anderson RM, May R. Infectious Diseases of Humans. Oxford Univ Press; Oxford, UK: 1992. [Google Scholar]
- 7.Ioannidis JPA. Why most published research findings are false. PLoS Med. 2005;2(8):e124. doi: 10.1371/journal.pmed.0020124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Moonesinghe R, Khoury MJ, Janssens ACJW. Most published research findings are false-but a little replication goes a long way. PLoS Med. 2007;4(2):e28. doi: 10.1371/journal.pmed.0040028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ross J, Mazur P. Some deduction from a formal statistical mechanical theory of chemical kinetics. J Chem Phys. 1961;35(1):19–28. [Google Scholar]
- 10.Ryan TA, Myers J, Holowka D, Baird B, Webb WW. Molecular crowding on the cell surface. Science. 1988;239(4835):61–64. doi: 10.1126/science.2962287. [DOI] [PubMed] [Google Scholar]
- 11.Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys. 1976;22:403–434. [Google Scholar]
- 12.Crum-Cianflone NF, et al. Clinical and epidemiologic characteristics of an outbreak of novel H1N1 (swine origin) influenza A virus among United States military beneficiaries. Clin Infect Dis. 2009;49(12):1801–1810. doi: 10.1086/648508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ross JV. On parameter estimation in population models III: Time-inhomogeneous processes and observation error. Theor Popul Biol. 2012;82(1):1–17. doi: 10.1016/j.tpb.2012.03.001. [DOI] [PubMed] [Google Scholar]
- 14.Gil J, et al. Disease progression and survival in ALS: First multi-state model approach. Amyotroph Lateral Scler. 2007;8(4):224–229. doi: 10.1080/17482960701278562. [DOI] [PubMed] [Google Scholar]
- 15.Sweeting MJ, Farewell VT, De Angelis D. Multi-state Markov models for disease progression in the presence of informative examination times: An application to hepatitis C. Stat Med. 2010;29(11):1161–1174. doi: 10.1002/sim.3812. [DOI] [PubMed] [Google Scholar]
- 16.Bureau A, Shiboski S, Hughes JP. Applications of continuous time hidden Markov models to the study of misclassified disease outcomes. Stat Med. 2003;22(3):441–462. doi: 10.1002/sim.1270. [DOI] [PubMed] [Google Scholar]
- 17.Piccini JP, et al. ROCKET AF Steering Committee and Investigators Renal dysfunction as a predictor of stroke and systemic embolism in patients with nonvalvular atrial fibrillation: Validation of the R(2)CHADS(2) index in the ROCKET AF (Rivaroxaban Once-daily, oral, direct factor Xa inhibition Compared with vitamin K antagonism for prevention of stroke and Embolism Trial in Atrial Fibrillation) and ATRIA (AnTicoagulation and Risk factors In Atrial fibrillation) study cohorts. Circulation. 2013;127(2):224–232. doi: 10.1161/CIRCULATIONAHA.112.107128. [DOI] [PubMed] [Google Scholar]
- 18.Benjamin EJ, et al. Impact of atrial fibrillation on the risk of death: The Framingham Heart Study. Circulation. 1998;98(10):946–952. doi: 10.1161/01.cir.98.10.946. [DOI] [PubMed] [Google Scholar]
- 19.Center for Disease Control and Prevention 1998. Mortality Data (Center for Disease Control and Prevention, Atlanta)
- 20.Cox DR. Regression models and life tables. J R Stat Soc B. 1972;34(2):187–220. [Google Scholar]
- 21.Vlad MO, Corlan AD, Morán F, Oefner P, Ross J. Incremental parameter evaluation from incomplete data with application to the population pharmacology of anticoagulants. Proc Natl Acad Sci USA. 2008;105(12):4627–4632. doi: 10.1073/pnas.0711508105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vlad MO, Corlan AD, Popa VT, Ross J. On anti-portfolio effects in science and technology with application to reaction kinetics, chemical synthesis, and molecular biology. Proc Natl Acad Sci USA. 2007;104(47):18398–18403. doi: 10.1073/pnas.0708624104. [DOI] [PMC free article] [PubMed] [Google Scholar]