Brønsted slopes based on single-molecule imaging data help to unveil the chemically coupled rotation in F₁-ATPase

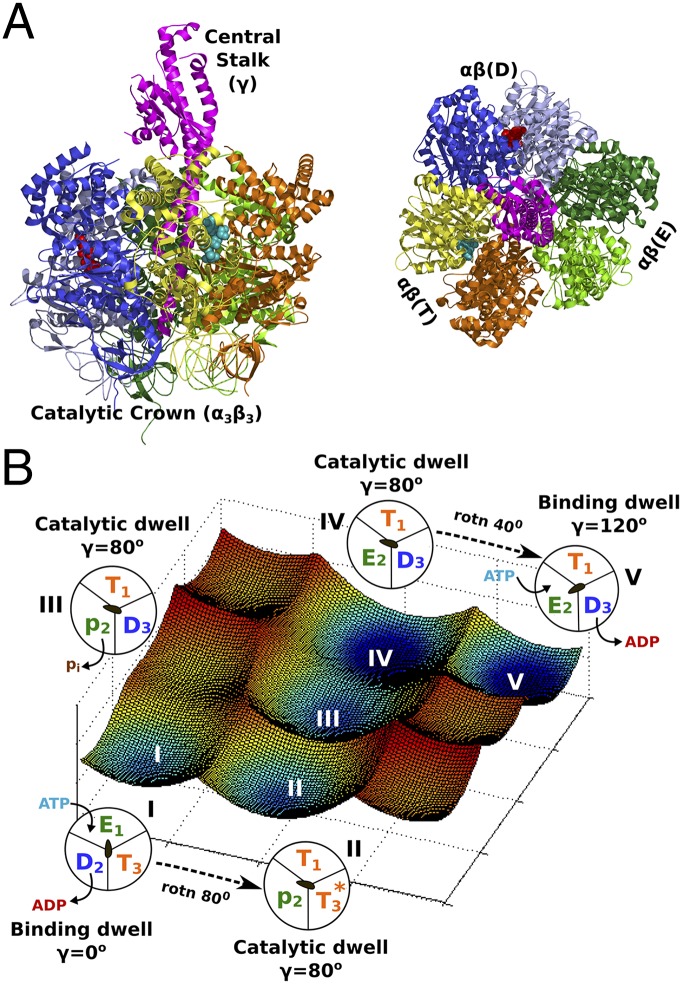
F₁-ATPase, the rotary motor that powers most of the processes in living cells, has challenged scientists, experimentalists, and theoreticians alike to gain deeper understanding of its action. The work on F₁ for more than two decades encompasses elucidation of the complex 3D structure (1) and the analysis of the thermodynamics and kinetics of the chemical steps (2) that led to the revelation of its rotary–chemical action (3). These advances were enhanced by direct observation of the F₁ central stalk (γ) rotation (4) that is tightly coupled to the chemical steps of the ATP binding, hydrolysis, and product release, occurring in the three catalytic subunits of the crown (α/β). The γ rotation was observed to occur in substeps of 80°/40° that were embedded within the waiting dwells, namely, the “ATP binding dwell” before the 80° substep and the “catalytic dwell” before the 40° substep (5) (Fig. 1). Since the initial progress made almost two decades ago, the study of various aspects of F₁ continues to occupy a central position, as ongoing efforts offer more detailed insights into the structure, function, and dynamics of the system (6, 7).

Fig. 1.

(A) The crystal structure of F₁ is shown from sidewise and top-down views of the central stalk γ (in magenta). The catalytic crown consists of three pairs of α/β-subunits in D (blue), T (orange/yellow), and E (green) conformations, where nucleotides ADP and ATP bound to subunits D and T are shown in red and cyan, respectively. For each 120° rotation of the γ, the catalytic subunits changes from D₁E₂T₃ to T₁E₂D₃, where 1, 2, and 3 denote the catalytic subunit number. (B) An analytical free-energy surface depicting the coupled rotary–chemical process for a single ATP molecule hydrolysis and 120° rotation of γ is shown. Schematic representations show that the system moves from state 1 (initial binding dwell with γ = 0°) to state V (next binding dwell with γ = 120°), whereas intermediate states II, III, and IV reflect the 80° rotated conformation in the catalytic dwell undergoing ATP hydrolysis and P_i release. The coupling between the ATP binding/ADP release and the 80° rotation (state I → state II) is investigated in the paper of Volkán-Kacsó and Marcus (15), whereas other studies have investigated the structural basis of the coupling between ATP hydrolysis and P_i release to the 80° dwell and the 80°/40° substep rotational feature (12).

Although much is known from pioneering experimental studies, a large vacuum still persists when one attempts to understand the physical basis of F₁ functionality. There have been insightful structure-based computational studies that revealed various facets of the enzyme’s functionality (8–11). Attempts to study the enzyme as a whole turned out to be problematic, due in part to the huge size of F₁ and its complex multidimensional functionality that commands the need to understand them on wide ranges of timescales. Because a considerable body of 3D structural, ensemble, and real-time single-molecule data exists for F₁, this system is poised to challenge theoreticians to decipher the physical principles that determine its rotary–chemical action. One of the central unresolved questions is associated with the detailed knowledge of the way the chemical free energies (ATP binding, hydrolysis, ADP, and P_i release) are coupled to the conformational changes in the catalytic subunits of the crown (α/β) and the central stalk (γ). This coupling eventually leads to unidirectional rotation and torque generation at the γ unit at the expense of the ATP hydrolysis by the crown. The nature of the coupling between the crown and the stalk also dictates the substep rotational behavior and establishes a precise correlation between the intermittent dwells and the catalytic states (5). Here, at least in principle, one can explore the rotary–chemical coupling and its relationships to the dwells from functionally relevant free-energy surfaces calculated from the 3D structure (Fig. 1B) (12–14). Such an approach can reveal the underlying physical basis of the coupling and also lends theoretical predictions directly comparable to real-time experimental observations.

Although it is promising to obtain the structure–function correlation by computational approaches, an exciting and insightful direction has been opened by the study by Volkán-Kacsó and Marcus published in PNAS (15). The authors have analyzed the coupled rotary–chemical process and related the free energies of the chemical (or binding) steps to the rotation of γ by extending the knowledge of the unified relationship between the kinetics and energetics in chemical processes (known as the Brønsted relationship). If such a generalized theoretical framework is able to highlight the nature of the coupling in F₁ (as done in ref. 15), one can also extract crucial information about the functional free-energy landscape by knowing the relationship between the chemical and mechanical steps. Such an approach should provide a new set of constraints applicable to the free-energy surface that are based on experimental observations. The model of ref. 15 has mainly been applied to the ATP binding and ADP release steps, where the authors used properties like free energies and structural elasticities from ensemble and single-molecule stalling experiments (16) to predict the dependence of rate constants and the equilibrium constants on the stalled rotor angle data, without the use of any adjustable parameters for its predictions. That is, ref. 15 described the two-state binding/release processes in terms of the stalling angle (θ) of the central stalk γ (as used in ref. 16) to explore the corresponding nature of the Brønsted slope, which is given by the following:

$$\alpha =\mathrm{\Delta }{G}^{\ne }\left(\theta \right)/\mathrm{\Delta }{G}_0\left(\theta \right).$$ [1]

Here, $\mathrm{\Delta }{G}^{\ne }\left(\theta \right)$ is the activation barrier at the stall angle and $\mathrm{\Delta }{G}_0\left(\theta \right)$ is the reaction free energy, i.e., the difference between reactants and product free energies. In the case of small coupling between the reactant and product systems, one can write the following (15):

$$\mathrm{\Delta }{G}^{\ne }\left(\theta \right)=W^r+{\left[\lambda +\mathrm{\Delta }{G}^0\right]}^2/4\lambda ,$$ [2]

where $W^r$ is the “work function” associated with bringing the reactants to the point just before passing the reaction barrier. The second term in Eq. 2 represents the energetics of two intersecting parabolas (for the reactant and product systems) where λ is the reorganization energy. The coupling between the reactant and product-state parabolas, could be further modified in case of strong bonding interaction using a bond energy–bond order correction (17). Alternatively, it is very effective to correct the “intersecting parabolas” picture by introducing a resonance correction for the activation free energy, $\mathrm{\Delta }{G}^{\ne }$, as modeled in the empirical valence bond (EVB) approach. Such an example for reactions with large coupling between the reactant and product states is given in ref. 18, and the importance of such resonance corrections has been established for proton translocation in enzymes (19). The $\alpha$ values have also been found to be very useful in analyzing the effects of mutations in actual enzymes (20, 21). The Brønsted slopes, $\alpha$ [or the related linear free-energy relationship (LFER)], have long provided powerful correlations for chemical and electron transfer reactions (22), where Marcus’s theory with two intersecting parabolas clearly pointed to the origin of the Brønsted slopes; the predictability is also reasonable in cases with large coupling. In view of the above discussion, it is likely that the Brønsted slopes considered in ref. 15 would give us instructive insights on the conformational and chemical coupling in F₁. Interestingly, the concepts could also be extended to other complex biological macromolecules where chemical steps are known to couple to long-range mechanical motions. It is worthwhile to note that an early work used the concept of LFER to explore the energetics of ligand binding in the β-subunits of F₁ and correlated the electrostatics-driven free-energy changes with γ rotation (11).

Perhaps the most promising direction of ref. 15 is the division of $\mathrm{\Delta }{G}^{\ne }\left(\theta \right)$ into two contributions (Eq. 2): one from the intersecting parabolas (with additional correction), and another from the “work term” that involves the contribution of the reactant/product motions until the beginning of the process of overcoming the main activation barrier. Implicitly, here, the work terms for binding/release steps have been

The paper by Volkán-Kacsó and Marcus combines theoretical conceptualization with single-molecule imaging data to provide novel ideas about the nature of the rotary–chemical coupling in F₁.

expressed by quadratic approximations in the rotational coordinate of the stall angle θ, which ultimately reflects the free-energy changes upon moving from one dwell state to another. Combining the work term and the Marcus-like barrier (from intersecting parabolas), one can use Eqs. 1 and 2 to directly analyze the experimental results from single-molecule experiments (16) and can also conceptually formulate the contributions coming from different parts of F₁ that produced the observed free-energy barriers. It should be noted that an exact molecular-level interpretation of the different contributions to Eq. 2 is not unique. Such an endeavor requires a knowledge of the complete structure-based landscape in the coupled chemical/conformational space, which should also provide the structural basis for the Brønsted slopes (15).

Obtaining the free-energy landscape for the complete system through atomistic simulations is extremely challenging for complex systems like F₁. At present, the most promising results were obtained by combining a coarse-grained conformational free-energy surface with experimental/theoretical landscapes of chemical steps, to generate a coupled rotary–chemical surface (12). Interestingly, this work has elucidated the 80°/40° substep feature of the rotary–chemical coupling to be an electrostatics-driven process (12). However, it would be exciting to reproduce the phenomenological LFER or the Brønsted slope (15) from 3D structure-based surfaces. We also note that, for a complex system like F₁, there could be nonconcerted reaction coordinates that affect the chemical steps but not so much the mechanical coordinates, or vice versa. This would require more complex descriptions of Brønsted slopes, which is very challenging without simulating the effects of the local environments upon conformational changes. At any rate, the paper by Volkán-Kacsó and Marcus combines theoretical conceptualization with single-molecule imaging data to provide exciting ideas about the nature of the rotary–chemical coupling in F₁, which leads to fresh insights that can be further pursued through structure-based simulations to uncover the molecular language of biological motors.