Extracting Electron Densities in N-Type GaAs From Raman Spectra: Theory

Abstract

In this paper, we present the theory for calculating Raman line shapes as functions of the Fermi energy and finite temperatures in zinc blende, n-type GaAs for donor densities between 10¹⁶ cm⁻³ and 10¹⁹ cm⁻³. Compared to other theories, this theory is unique in two respects: 1) the many-body effects are treated self-consistently and 2) the theory is valid at room temperature for arbitrary values of the ratio R = (Q²/α), where Q is the magnitude of the normalized wave vector and α is the normalized frequency used in the Raman measurements. These calculations solve the charge neutrality equation self-consistently for a two-band model of GaAs at 300 K that includes the effects of high carrier concentrations and dopant densities on the perturbed densities of states used to calculate the Fermi energy as a function of temperature. The results are then applied to obtain the carrier concentrations from Fermi energies in the context of line shapes in Raman spectra due to the coupling between longitudinal optical phonons and plasmons. Raman measurements have been proposed as a non-destructive method for wafer acceptance tests of carrier density in semiconductor epilayers. The interpretation of Raman spectra to determine the majority electron density in n-type semiconductors requires an interdisciplinary effort involving experiments, theory, and computer-based simulations and visualizations of the theoretical calculations.

1. Introduction

The carrier concentration is a key figure of merit associated with a go/no-go decision for determining whether a wafer or an epitaxial layer meets specifications and should undergo further processing. Technology roadmaps from the microelectronics and nanomaterials industries [1–3] call for non-destructive and fast-turn around methods to measure transport properties such as carrier concentrations in semiconductor wafers and epitaxial layers. Non-destructive measurements are economically more significant for III–V compound semiconductor wafers with epitaxial layers than for Si-based wafers with epitaxial layers because the regions of wafers used for making contacts cannot be used for product. Contacting measurement methods may be acceptable for Si wafers, but such destructive methods are much less acceptable for III–V compound semiconductor wafers with epitaxial layers because Si wafers are much less expensive per unit area than compound semiconductor wafers.

Raman spectroscopy has been proposed as one possible way to measure carrier concentrations non-destructively. The shape of the Raman spectral lines due to the longitudinal-optical phonons interacting with the plasmon collective modes of the electron gas (so called coupled longitudinal optical (LO) phonon-plasmon modes) provides information on transport properties of the electron gas in polar semiconductors [4–8]. The frequencies ω of the coupled modes are proportional to carrier concentrations, and the peak widths Δω of the coupled modes are proportional to the scattering rates due to electron-phonon interactions. The qualitative determination of carrier concentration and mobility, which is inversely proportional to the scattering rate, from Raman spectra is reasonably straightforward based on these proportionalities. The quantitative determination of carrier concentrations and mobilities requires more sophisticated modeling of the spectra. Many of these higher level models involve fitting the spectra with the Fermi energy as a parameter and then determining the carrier concentration from knowing the fitted Fermi energy [6].

Most interpretations of Raman measurements on compound semiconductors such as GaAs require physical models and associated input parameters that describe how carrier densities vary with dopant concentrations and Fermi energies. In this paper, we develop the theory for extracting electron densities from Raman measurements of n-type GaAs at room temperature. We introduce two main classes of models that relate carrier concentrations to the Fermi energy for a given temperature and donor dopant density:

1. Bandgap narrowing (BGN) models based on two equivalent bands at the Γ point in the first Brilluoin zone, and

2. Parabolic densities of states (PDOS) models with and without a quartic term in the electron energy dispersion E_cΓ(k) for the Γ conduction sub-band, where k is the wave vector.

The BGN models include many-body quantum effects and bandgap narrowing. The many-body quantum effects describe the electron-electron, electron-hole, and dopant ion-carrier interactions. The results are unique in two respects: 1) the many-body effects are treated self-consistently and 2) the theory is valid at room temperature for arbitrary values of the ratio R = (Q²/α), where Q is the magnitude of the normalized wave vector and α is the normalized frequency used in the Raman measurements. Other reported work either is valid at low temperatures near 0 K for arbitrary ratios (Q²/α) [4] or is valid at arbitrary temperatures for ratios R typically R ≪ 1 [5–7].

2. Theory

Because the Fermi energy is one of the variables for calculating line shapes in the Raman spectra from semiconductors, we first present in Sec. 2.1 the theory for the BGN and PDOS models by which numerical methods give closed-form analytic expressions that relate carrier concentrations to Fermi energy E_F, temperature T, and donor dopant densities N_D. Then, within the context of these BGN and PDOS models, we develop in Sec. 2.2 the theory for calculating the line shapes observed in Raman spectra.

2.1 Fermi Energy and Electron Density

The temperature and donor dopant density are the independent input parameters for evaluating the Raman line shape factor given in Eq. (19). The Fermi energy depends in turn on the dopant density, in this case the donor density N_D and T. For given N_D and T, we present here models to compute the Fermi energy with full Fermi-Dirac statistics for the carriers at finite temperature. By using these models, we calculate the majority electron density as a function of the Fermi energy in zinc blende, n-type GaAs for donor densities between 10¹⁶ cm⁻³ and 10¹⁹ cm⁻³. These calculations solve the charge neutrality equation self-consistently in terms of two main classes of models: the bandgap narrowing (BGN) model and three different parabolic densities of states (PDOS) models.

Some researchers propose that Raman spectra may be a way to determine temperatures with spatial resolutions across wafers on the order of micrometers when the Fermi energy and dopant density are known from other independent measurements. Comparing the results given by the BGN and PDOS models, which are described below, also provides predictions on the sensitivity of the Fermi energy and Raman spectrum to variations in temperature.

2.1.1 BGN Model

The bandgap narrowing (BGN) model is a two-band model with one equivalent conduction band and one equivalent valence band at the Γ point in Brilluoin space. The BGN model is related to earlier work on n-type GaAs [9] and includes modifications to the densities of states due to high concentrations of dopants, bandgap narrowing, and many-body effects associated with carrier-carrier interactions (carrier-carrier exchange and correlation). This BGN model is fully self-consistent and uses the Klauder self-energy (fifth level of approximation) to calculate the distorted-perturbed densities of states for the carriers. This BGN model has the following main features:

1. Many-body quantum effects of carrier-carrier interactions and carrier-dopant ion interactions, bandgap narrowing, and distorted-perturbed densities of states for the carriers [9],

2. Iterative and self-consistent solutions of the coupled charge neutrality equation and Klauder’s fifth level of approximation for the renormalized self-energy propagator from which the distorted-perturbed densities of states are calculated,

3. Full Fermi-Dirac statistics for the carriers at finite temperature, and

4. Statistical analyses to give closed-form analytic expressions from very large, calculated data sets for carrier densities as functions of the Fermi energy. Tables 1 and 2 contain the input parameters for the BGN calculations in Ref. [9] and for the BGN model given here.

Table 1.

Fundamental Constants

Parameter	Symbol	Value	Units
Planck’s constant	ħ	6.5836 × 10−16	eV·s
Boltzmann’s constant	kB	8.6174 × 10−5	eV/K
electron rest mass	m0	9.1072 × 10−28	g
electronic charge	e	−4.802 × 10−10	esu
Bohr radius	aB	0.5291 × 10−8	cm
energy associated with 1 Rydberg	e2/2aB	13.6	eV
speed of light	c	2.9979 × 1010	cm/s
wave length associated with 1 eV	[λ0]	1.2396 × 10−4	cm
wave number associated with 1 eV	[k0]	8.0668 × 103	cm−1
dielectric constant in vacuum	ε	8.854 × 10−12	F/m

Table 2.

BGN model input parameters for intrinsic zinc blende GaAs at 300 K. The energies of the extrema of the conduction and valence sub-bands are referenced to the bottom of the conduction sub-band at the Γ symmetry point in the Brillouin zone of the reciprocal lattice space. The mass of the free electron is m₀. These GaAs data are from Ref. [12].

Parameter	Symbol	Value	Units
bandgap	EG = |−EvΓ|	1.424	eV
effective mass for conduction band (2-band model) density of states	mC	0.067	m0
effective mass for valence band (2-band model) density of states	mV	0.572	m0
number of equivalent conduction bands	NC	1
number of equivalent valence bands	NV	1

The electron n and hole h concentrations in units of cm⁻³ at thermal equilibrium are given, respectively, by

$$n={\displaystyle {\int }_{-\infty }^{+\infty }{f}_0(E){\rho }_{\mathrm{C}}(E)\mathrm{d}E}\mathrm{and}h={\displaystyle {\int }_{-\infty }^{+\infty }\left[1-f_0(E)\right]}{\rho }_{\mathrm{V}}(E)\mathrm{d}E,$$ (1)

where ρ_C(E) and ρ_V(E) are, respectively, the electron density of states for the equivalent conduction band and the hole density of states for the equivalent valence band [9], where f₀(E) = {1 + exp[(E − E_F)/k_BT]}⁻¹ is the Fermi-Dirac distribution function. The calculations incorporate the Thomas-Fermi expression for the screening radius,

$$r_{\mathrm{s}}^2=-\frac{4\pi e^2}{\epsilon {\epsilon }_0}{\displaystyle {\int }_{-\infty }^{+\infty }\frac{\mathrm{d}{f}_0(E)}{\mathrm{d}E}\left[{\rho }_{\mathrm{C}}(E)-{\rho }_{\mathrm{V}}(E)\right]\mathrm{d}E,}$$ (2)

and the charge neutrality condition

$$N_{\mathrm{I}}=n-h,$$ (3)

to compute self-consistently the Fermi energy E_F and the screening radius r_s for given values of the ionized dopant concentration N_I and temperature T. The static dielectric constant is ε and the permittivity of free space is ε₀. The ionized dopant concentration is positive for n-type material (donor ions) and negative for p-type material (acceptor ions). The results reported here are for n-type material. For the case discussed here, N_I = N_D. The results for the screening radius r_s are not reported here because they are not needed to extract carrier concentrations from Raman scattering measurements.

2.1.2 PDOS Models

The PDOS models use parabolic densities of states for all equivalent bands and sub-bands. Unlike the BGN model in Ref. [9], PDOS models such as the four-band PDOS model for GaSb in Ref. [10] do not include modifications to the densities of states due to many-body effects and high concentrations of dopants and carriers because of computational limitations associated with treating a four-band model in the context of the Klauder self-energy method (fifth level of approximation).

The zero of energy is at the minimum energy value (bottom) of the conduction Γ sub-band, E_cΓ0 = 0.0. The bottoms of the conduction L and X sub-bands are, respectively, at E_cL and E_cX. The maximum energy value (top) of the degenerate valence Γ sub-band is −E_G, where E_G is the intrinsic bandgap of GaAs. The split-off valence sub-band at Γ due to spin-orbit coupling is neglected. The probabilities for typical holes in equilibrium to occupy appreciably these states in the split-off valence sub-band at Γ are very low. This means that the Fermi energies should be sufficiently above the valence sub-band maximum at Γ. Placing exact limits on the Fermi energies for which the PDOS models are valid would be tenuous, because knowledge of how the various sub-bands move relative to one another due to the dopant concentrations considered here and due to many body effects is not adequate. Table 3 lists the input parameters for the PDOS models.

Table 3.

PDOS model input parameters for intrinsic zinc blende GaAs at 300 K. The energies of the extrema of the conduction and valence sub-bands are referenced to the bottom of the conduction sub-band at the Γ symmetry point in the Brillouin zone of the reciprocal lattice space. The mass of the free electron is m₀. These GaAs data are from Refs. [11,12].

Parameter	Symbol	Value	Units
bandgap	EG = |−EvΓ|	1.424	eV
bottom of the conduction L sub-band	EcL	0.29	eV
bottom of the conduction X sub-band	EvX	0.48	eV
top of the degenerate valence Γ sub-band	−EvΓ	1.424	eV
spin-orbit splitting	−Eso	0.34	eV
top of the split-off (spin-orbit splitting) valence Γ sub-band	−EsoΓ = −EvΓ − Eso	1.764	eV
effective mass of conduction Γ sub-band	mcΓ	0.063	m0
non-parabolicity factor (quartic term prefactor) for conduction Γ sub-band	ξ	0.824
transverse L sub-band mass	mtL	0.075	m0
longitudinal L sub-band mass	mlL	1.9	m0
effective mass of conduction L sub-band	mcL = (mlL mtL2)1/3	0.222	m0
transverse X sub-band mass	mtX	0.19	m0
longitudinal X sub-band mass	mlX	1.9	m0
effective mass of conduction X sub-band	mcX = (mlX mtX2)1/3	0.409	m0
light hole mass of valence Γ sub-band	mlh	0.082	m0
heavy hole mass of valence Γ sub-band	mhh	0.51	m0
effective mass of valence Γ sub-band	mvΓ	0.53	m0
splitoff band mass of the valence sub-band at Γ	mso	0.15	m0
number of equivalent conduction L sub-bands	NcL	4
number of equivalent conduction X sub-bands	NcX	3

The heavy hole mass m_hh and light hole mass m_lh for the two degenerate sub-bands at the top of the valence band are combined to give an effective mass

$$m_{\mathrm{V}\widetilde{{\rm A}}}={\left(m_{\mathrm{hh}}{}^{3/2}+m_{\mathrm{lh}}{}^{3/2}\right)}^{2/3},$$ (4)

for the valence topmost sub-band, which becomes the equivalent valence band with a hole energy dispersion given by E_νΓ(k) ≈ − E_G − (ħ²k²/2m_νΓm₀).

The general expression for the parabolic densities of states for electrons and holes per band extrema and per spin direction is given by

$$\rho (E)=\frac{N_{\mathrm{e}}4\pi V\sqrt{E}}{\left(8{\pi }^3\right){\left({\hslash }^2/2m^{*}{m}_0\right)}^{3/2}},$$ (5)

where N_e is the number of equivalent ellipsoids in the first Brillouin zone, the volume of the unit cell is V =a_L³, a_L is the lattice constant, m* is one of the effective masses listed in Tables 2 and 3 for the appropriate band extrema, and m₀ is the free electron mass.

We sub-divide the PDOS models into the PDOS2, PDOS2NPG, and PDOS4 models. All three PDOS models include the equivalent valence band described by Eq. (4).

PDOS2 Model

The PDOS2 model uses one equivalent conduction band and one equivalent valence band at the Γ symmetry point in the Brilluoin space for the integrals that appear in Eqs. (1) to (3). The electron energy dispersion for the equivalent conduction band is E_cΓ(k) ≈ E_cΓ0 + (ħ²k²/2m_Cm₀).

PDOS2NPG Model

The PDOS2NPG model is a two-band model with one equivalent conduction band and one equivalent valence band at the Γ point in Brilluoin space. It has no bandgap narrowing, but it includes the non-parabolicity for the electron energy dispersion in the equivalent conduction band at Γ. According to Ref. [11], we may include non-quadratic |k|^l terms in the electron energy dispersion E_cΓ(k) for the conduction Γ sub-band in GaAs when k is small, namely,

$$E_{\mathrm{c}\mathrm{\Gamma }}(\mathit{k})\approx E_{\mathrm{c}\mathrm{\Gamma }0}+\left({\hslash }^2{k}^2/2m_{\mathrm{C}}{m}_0\right)+\left(\xi /E_{\mathrm{G}}\right){\left({\hslash }^2{k}^2/2m_{\mathrm{C}}{m}_0\right)}^2,$$ (6)

where ξ is the non-parabolicity factor. We use the Kane three level k·p model [11], which does not include the conduction sub-bands at L and X, to include quartic terms in E(k) with l = 4.

PDOS4 Model

The PDOS4 model has three conduction sub-bands at the respective Γ, L, and X symmetry points in the Brilluoin space and one equivalent valence band at the Γ symmetry point. For the PDOS4, we modify here the PDOS model for GaSb in Ref. [10] so that it is valid for GaAs. It uses the parabolic electron energy dispersion E_cΓ(k) for the conduction Γ sub-band in GaAs when k is small, namely, E_cΓ(k) ≈ E_cΓ0 + (ħ²k²/2m_Cm₀). The general expression for the temperature dependence of conduction sub-band minima relative to the top of the valence band at Γ is given by [12],

$$E_i=E_{i0}-\left[A_i{T}^2/\left(T+B_i\right)\right]$$ (7)

in units of eV, where i = Γ, L, or X. The values for the coefficients E_i0, A_i, and B_i are listed in Table 4. Because 8 permutations of the wave vector in the (111) direction exist, there are 8 L sub-band ellipsoids with centers located near the boundary of the first Brillouin zone. Also, because 6 permutations of the wave vector in the (100) direction exist, there are 6 X sub-band ellipsoids with centers located near the boundary of the first Brillouin zone. Since about half of each ellipsoid is in the neighboring zone, the number of equivalent sub-bands N_cL for the E_cL is four, and the number of equivalent sub-bands N_cX for the X sub-band is three.

Table 4.

Coefficients for the temperature dependence of the conduction band extrema that are used in Eq. (15). These data are from Ref. [12].

Parameter	Symbol	Value	Units
Γ sub-band coefficients	EΓ0	1.519	eV
	AΓ	5.405 × 10−4	eV/K
	BΓ	204	K
L sub-band coefficients	EL0	1.815	eV
	AL		eV/K
	BL	204	K
X sub-band coefficients	EX0	1.981	eV
	AX	4.60 × 10−4	eV/K
	BX	204	K

In terms of the four-band PDOS4 model for room temperature n-type GaAs, the total density of states ρ_c(E) for the majority carrier electrons in n-type GaAs then becomes

$${\rho }_{\mathrm{c}}(E)={\rho }_{\mathrm{c}\mathrm{\Gamma }}(E)+{\rho }_{\mathrm{cL}}(E)+{\rho }_{\mathrm{cX}}(E),$$ (8)

where ρ_cΓ(E), ρ_cL(E), and ρ_cX(E) are the sub-band densities of states for the conduction Γ, L, and X sub-bands with effective masses of m_cΓ, m_cL, and m_cX, respectively. The density of states for the minority carrier holes is

$${\rho }_{\mathrm{v}}(E)={\rho }_{\mathrm{v}\mathrm{\Gamma }}(E)$$ (9)

with an effective mass of m_vΓ

2.2 Dielectric Response Function

The longitudinal optical (LO) phonons and plasmons interact in polar semiconductors such as GaAs to form LO phonon-plasmon modes. The theoretical line shape function L_A(q,ω) of the Raman spectrum due to longitudinal optical (LO) phonon-plasmon coupled modes is then given for the configuration to which this theory will be applied by [8]

$$L_{\mathrm{A}}(\mathit{q},\omega )={\left(1-e^{-\hslash \omega /k_{\mathrm{B}}T}\right)}^{-1}\left(\frac{{\omega }_0^2-{\omega }^2}{{\omega }_{\text{To}}^2-{\omega }^2}\right)\mathrm{Im}\left\{-\frac{1}{(\mathit{q},\omega )}\right\},$$ (10)

where q is the scattering wave vector, ω is the Raman angular frequency shift, ħ is the Planck constant, k_B is the Boltzmann constant, T is the temperature in Kelvin, ω₀ = ω_TO(1 + C_FH)^1/2 is a parameter with the dimensions of angular frequency, C_FH is the dimensionless Faust-Henry coefficient which includes the LO/transverse optical (TO) phonon scattering ratio, and ω_TO is the TO phonon angular frequency. Table 5 contains values for the parameters in Eq. (10). The total longitudinal dielectric response function ε (q,ω) in the random phase approximation (RPA) is described by

$$\epsilon (\mathit{q},\omega )=1+4\pi {\chi }_{\mathrm{VE}}+4\pi {\chi }_{\mathrm{L}}(\omega )+4\pi {\chi }_{\mathrm{e}}(\mathit{q},\omega ),$$ (11)

where the dielectric susceptibility χ_VE is the contribution from valence electrons, χ_L(ω) is the contribution from the polar lattice phonons, and χ_e(q,ω) is the contribution from the conduction electrons. The high frequency dielectric constant ε_∞ is defined to be ε_∞ = 1 + 4πχ_VE. Equation (11) then becomes for a binary semiconductor,

$$\epsilon (\mathit{q},\omega )={\epsilon }_{\infty }+4\pi {\chi }_{\mathrm{L}}(\omega )+4\pi {\chi }_{\mathrm{e}}(\mathit{q},\omega ).$$ (12)

Table 5.

Dielectric response function input parameters for intrinsic zinc blende GaAs at 300 K. The energies of the extrema of the conduction and valence sub-bands are referenced to the bottom of the conduction sub-band at the Γ symmetry point in the Brillouin zone of the reciprocal lattice space. The mass of the free electron is m₀. These GaAs data are from Ref. [14].

Parameter	Symbol	Value	Units
lattice constant	aL	5.65 ×10−8	cm
static dielectric constant	ε0	13.1
high frequency dielectric constant	ε∞	10.9
longitudinal optical (LO) phonon energy	ħωLO	0.0353	eV
		285	cm−1
transverse optical (TO) phonon energy	ħωTO	0.0332	eV
		268	cm−1
Energy associated with the angular collision frequency Γ	ħΓ	~0.0124	eV
due to electron-phonon and electron-dopant ion interactions		~100	cm−1
Faust-Henry coefficient	CFH	−0.4
effective mass for the single equivalent conduction	mC	0.067	m0
band density of states in Eq. (6)

The contribution of the polar lattice is given by [8]

$$4\pi {\chi }_{\mathrm{L}}(\omega )={\epsilon }_{\infty }\left(\frac{{\omega }_{\mathrm{LO}}^2-{\omega }_{\mathrm{TO}}^2}{{\omega }_{\mathrm{TO}}^2-{\omega }^2}\right),$$ (13)

when phonon damping may be neglected and where ω_LO is the LO phonon angular frequency.

Within the context of the RPA, the Lindhard expression [13] gives the electronic contribution to the dielectric response function 4πχ_e⁰(q,ω) that describes light scattering by the conduction electrons in doped semiconductors. We introduce the collision relaxation time τ that describes the losses associated with electron-phonon and electron-dopant interactions and the corresponding angular collision frequency Γ = τ⁻¹. Mermin [14] showed that replacing ω with ω + iΓ in the Lindhard expression for 4πχ_e⁰(q,ω) fails to conserve the number of local electrons and therefore is not the correct way to include collision broadening in 4πχ_e⁰(q,ω). Instead, Mermin assumed that within the framework of a relaxation time approximation the electron-phonon and electron-dopant interactions relax the electron density matrix to a local equilibrium density matrix [4,14]. He then obtained the following Lindhard-Mermin relation [14] for χ_e(q,ω),

$${\chi }_{\mathrm{e}}(\mathit{q},\omega )=\frac{(\omega +i\Gamma ){\chi }_{\mathrm{e}}{}^0(\mathit{q},0){\chi }_{\mathrm{e}}{}^0(\mathit{q},\omega +i\Gamma )}{\omega {\chi }_{\mathrm{e}}{}^0(\mathit{q},0)+i\Gamma {\chi }_{\mathrm{e}}{}^0(\mathit{q},\omega +i\Gamma )},$$ (14)

where the Lindhard expression χ_e⁰(q,ω + iΓ) for electrons occupying states in a single equivalent conduction band is given by,

$$\begin{array}{l}4\pi {\chi }_{\mathrm{e}}{}^0(\mathit{q},\omega +i\Gamma )=\frac{e^2}{{\pi }^2{q}^2}\int f_0(E)\\ \times \left[{\left(\frac{{\hslash }^2{q}^2}{2m_{\mathrm{C}}{m}_0}+\frac{{\hslash }^2\mathit{q}\cdot \mathit{k}}{m_{\mathrm{C}}{m}_0}-\hslash (\omega +i\Gamma )\right)}^{-1}+{\left(\frac{{\hslash }^2{q}^2}{2m_{\mathrm{C}}{m}_0}-\frac{{\hslash }^2\mathit{q}\cdot \mathit{k}}{m_{\mathrm{C}}{m}_0}+\hslash (\omega +i\Gamma \right)}^{-1}\right]{\mathrm{d}}^3\mathit{k},\end{array}$$ (15)

where f₀(E) = {1 + exp[(E − E_F)/k_BT]}⁻¹ is the Fermi-Dirac distribution function, E_F is the Fermi energy in eV, and T is the temperature in Kelvin.

The integrand in Eq. (15) is independent of the azimuthal angle φ so that,

$${\displaystyle {\int }_0^{\infty }{k}^2\mathrm{d}k{\displaystyle {\int }_0^{\pi }\sin \theta \mathrm{d}\theta {\displaystyle {\int }_0^{2\pi }\mathrm{d}\phi (\dots )}}}=2\pi {\displaystyle {\int }_0^{\infty }{k}^2\mathrm{d}k{\displaystyle {\int }_{-1}^{1}d\mu (\dots )}}$$

where µ = cosθ, dµ = −sinθ, and q·k = qkµ. To simplify Eq. (15) further, we introduce the following dimensionless normalized quantities: Q = qa_B, K = ka_B, $K(E)=\sqrt{\left(2m_0{m}_{\mathrm{C}}{a}_{\mathrm{B}}{}^2/{\hslash }^2\right)E}$, and Ω² = {ħ(ω + iΓ)m_C/13.6 eV} where (e²/2a_B) = (ħ²/2m₀a_B²) = 13.6 eV. Equation (15) then becomes with these definitions the following expression,

$$\begin{array}{l}4\pi {\chi }_{\mathrm{e}}{}^0(\mathit{q},\omega +i\Gamma )\\ =\frac{4m_{\mathrm{C}}}{\pi Q^2}{\displaystyle {\int }_0^{\infty }{K}^2\mathrm{d}K}\\ {\displaystyle {\int }_{-1}^1\mathrm{d}\mu {\left(1+\exp \left[\left\{\left(13.6\mathrm{eV}{K}^2/m_{\mathrm{C}}\right)-E_{\mathrm{F}}\right\}/k_{\mathrm{B}}T\right]\right)}^{-1}}\\ \times \left[{\left(Q^2+2QK\mu -{\mathrm{\Omega }}^2\right)}^{-1}+{\left(Q^2-2QK\mu +{\mathrm{\Omega }}^2\right)}^{-1}\right].\end{array}$$ (16)

Performing analytically the angular integration over µ gives the complex results

$$\begin{array}{l}4\pi {\chi }_{\mathrm{e}}{}^0(\mathit{q},\omega +i\Gamma )\\ =\frac{2m_{\mathrm{C}}}{\pi Q^3}{\displaystyle {\int }_0^{\infty }K\mathrm{d}K{\left(1+\exp [\{(13.6\mathrm{eV}{K}^2/m_{\mathrm{C}})-E_{\mathrm{F}}\}/k_{\mathrm{B}}T]\right)}^{-1}}\\ \times \left[\ln \left(\frac{{\rho }_{+}{}^2+{\gamma }^2}{{\rho }_{-}{}^2+{\gamma }^2}\right)+\ln \left(\frac{{\tau }_{+}{}^2+{\gamma }^2}{{\tau }_{-}{}^2+{\gamma }^2}\right)+i({\eta }_{+}-{\eta }_{-})+i({\sigma }_{+}-{\sigma }_{-})\right],\end{array}$$ (17)

where ρ_± = Q² ± 2QK − α, τ_± = Q² ± 2QK + α, η_± = −sign(ρ_±)arctan(γ/ρ_±) − (π/2)[1 − sign(ρ_±)], σ_± = +sign(τ_±)arctan(γ/τ_±) + (π/2)[1 − sign(τ_±)], Ω² = α + iγ, α = (ħωm_C/13.6 eV), γ = (ħΓm_C/13.6 eV), and −π ≤ arctan(ψ) ≤ π.

When the temperature T = 0, the Fermi function f₀(E) = (1 + exp[{(13.6 eV K²/m_C) − E_F}/k_BT])⁻¹ is the unit step function. Then, the integral in Eq. (17) ${\displaystyle {\int }_0^{\infty }{K}^2\mathrm{d}K(\dots )}$ is ${\displaystyle {\int }_0^{K_{\mathrm{F}}}{K}^2\mathrm{d}K}(\dots )$, and an analytic evaluation is possible [4], where $K_F=\sqrt{m_{\mathrm{C}}{E}_{\mathrm{F}}/13.6\mathrm{eV}}$. But, when T is room temperature, analytic evaluations are not possible. Researchers approximated the integral ${\displaystyle {\int }_0^{\infty }{K}^2\mathrm{d}K(\dots )}$ at finite temperatures by expanding its integrand in terms of the ratio R = (Q²/α) for either very small or large R. However, such expansions do not capture all of the spectral information in Eq. (17).

The theoretical line shape function L_A(q,ω) of the Raman spectrum then becomes

$$\begin{array}{l}{L}_{\mathrm{A}}(\mathit{q},\omega )\\ ={\left(1-e^{-\hslash \omega /k_{\mathrm{B}}T}\right)}^{-1}\left(\frac{{\omega }_0^2-{\omega }^2}{{\omega }_{\mathrm{TO}}^2-{\omega }^2}\right)\left\{\frac{{\epsilon }_{\mathrm{i}}(\mathit{q},\omega )}{{\epsilon }_r{}^2(\mathit{q},\omega )+{\epsilon }_{\mathrm{i}}{}^2(\mathit{q},\omega )}\right\},\end{array}$$ (18)

where $\mathrm{Im}\left\{-\frac{1}{\epsilon (\mathit{q},\omega )}\right\}=\left\{\frac{{\epsilon }_{\mathrm{i}}(\mathit{q},\omega )}{{\epsilon }_r{}^2(\mathit{q},\omega )+{\epsilon }_i{}^2(\mathit{q},\omega )}\right\}$, ${\epsilon }_{\mathrm{r}}(\mathit{q},\omega )=\mathrm{Re}\left\{\epsilon (\mathit{q},\omega )\right\}={\epsilon }_{\infty }\left\{\frac{{\omega }_{\mathrm{LO}}{}^2-{\omega }_{\mathrm{TO}}{}^2}{{\omega }_{\mathrm{TO}}{}^2-{\omega }^2}\right\}+4\pi {\chi }_{\mathrm{re}}(\mathit{q},\omega +i\Gamma )$, and ${\epsilon }_{\mathrm{i}}(\mathit{q},\omega )=\mathrm{Im}\left\{\epsilon (\mathit{q},\omega )\right\}=4\pi {\chi }_{\mathrm{ie}}(\mathit{q},\omega +i\Gamma )$.

The Lindhard-Mermin relation Eq. (14) then gives expressions for χ_re(q,ω + iΓ) = Re{χ_e(q,ω + iΓ)} and χ_ie(q,ω + iΓ) = Im{χ_e(q,ω + iΓ)} as functions of χ_re⁰ (q,ω + iΓ) = Re{χ_e⁰(q,ω + iΓ)} and χ_ie⁰ (q,ω + iΓ) = Im{χ_e⁰(q,ω + iΓ)}. Even though the factors in Eqs. (10) and (18) give the contributions to the Raman line shape for each scattering mechanism, an examination of only the factor

$$\begin{array}{l}\mathrm{Im}\left\{-\frac{1}{\epsilon (\mathit{q},\omega )}\right\}=\left\{\frac{{\epsilon }_i(\mathit{q},\omega )}{{\epsilon }_{\mathrm{r}}{}^2(\mathit{q},\omega )+{\epsilon }_{\mathrm{i}}{}^2(\mathit{q},\omega )}\right\}\\ =\left\{\frac{{\left({\omega }_{\mathrm{TO}}{}^2-{\omega }^2\right)}^{2}4\pi {\chi }_{\mathrm{ie}}(\mathit{q},\omega +i\Gamma )}{D_r{}^2(\mathit{q},\omega +i\Gamma )}\right\}\end{array}$$ (19)

gives the spectral information for extracting the Fermi energy. The denominator in Eq. (19) is given by the expression,

$$\begin{array}{l}{D}_{\mathrm{r}}{}^2(\mathit{q},\omega +i\Gamma )={\epsilon }_{\infty }{}^2{\left({\omega }_{\mathrm{LO}}{}^2-{\omega }_{\mathrm{TO}}{}^2\right)}^2\\ +2{\epsilon }_{\infty }\left({\omega }_{\mathrm{LO}}{}^2-{\omega }^2\right)\left({\omega }_{\mathrm{TO}}{}^2-{\omega }^2\right)4\pi {\chi }_{\mathrm{ie}}(\mathit{q},\omega +i\Gamma )\\ +{\left({\omega }_{\mathrm{TO}}{}^2-{\omega }^2\right)}^2\left[{\left\{4\pi {\chi }_{\mathrm{re}}(\mathit{q},\omega +i\Gamma )\right\}}^2+{\left\{4\pi {\chi }_{\mathrm{ie}}(\mathit{q},\omega +i\Gamma )\right\}}^2\right].\end{array}$$ (20)

Section 3 below contains the procedures for extracting electron densities from the Fermi energies.

3. Numerical Results – Electron Density and Fermi Energy

Because the Fermi energy is one of the variables for calculating the Raman line shape, we give the numerical results for calculating the Fermi energy in terms of the BGN and PDOS models and the analytic expressions that relate the carrier concentrations to the Fermi energy.

3.1 BGN Model

We solve self-consistently, by means of an iterative procedure, Eq. (3) with the distorted-perturbed carrier densities of states ρ_C(E) and ρ_V(E) from Ref. [9] used in the numerical integrations for n and h given by Eq. (1). The ρ_C(E) and ρ_V(E) are in tabular form and have both localized and continuum states. Their associated band edges contain the many body effects related to exchange and correlation. The independent variables are the temperature T and donor density N_D. The Fermi energy is varied for a given temperature until Eq. (3) is satisfied to within an error of plus or minus 10⁻³ × N_D.

Numerical fitting procedures then give a closed-form analytic expression for the dependence of carrier concentration n_BGN on the Fermi energy E_F; namely,

$$\begin{array}{l}{\log }_{10}\left(n_{\mathrm{BGN}}{\mathrm{cm}}^3\right)\\ =a_{\mathrm{BGN}0}+a_{\mathrm{BGN}1}{E}_F+a_{\mathrm{BGN}2}{E}_F^2+\dots +a_{\mathrm{BGN}l}{E}_{\mathrm{F}}^l\dots .\end{array}$$ (21)

During the fitting analyses, we rely substantially on graphics and keep the number of fitting parameters to a minimum, subject to the constraint that the residual standard deviation S_res is acceptably small; i.e., S_res ≤ 0.01. The standard deviation is a measure of the “average” error by which a fitted model represents a set of data points and thereby is a metric for assessing the quality of the fit. A smaller S_res indicates a better fit. The residual standard deviation for a model Y^f = f (Z) is

$$S_{\mathrm{res}}=\sqrt{\left[{\displaystyle \sum _{j=1}^N{\left(Y_j-{\overline{Y}}_j^{\mathrm{f}}\right)}^2/\left(N-P\right)}\right]},$$ (22)

where Y_j are the calculated data values, the ${\overline{Y}}_j^{\mathrm{f}}$ are the predicted values from the fitted model, N is the total number of data points (here N = 28), and P is the total number of parameters to be fitted in the model. We use the NIST-developed DATAPLOT [15] software for both the exploratory graphics and for the statistical analyses.

In addition, we compare the above BGN model results with an equivalent two-band PDOS2 model for which there is no bandgap narrowing and for which the tabular carrier densities of states ρ_C(E) and ρ_V(E) from Ref. [9] are replaced with

$$\begin{array}{l}{\rho }_{\mathrm{C}}\left(E\right)=\frac{N_{C}4\pi V\sqrt{E}}{\left(8{\pi }^3\right){\left({\hslash }^2/2m_{\mathrm{C}}{m}_0\right)}^{3/2}}\mathrm{and}\\ {\rho }_{\mathrm{V}}\left(E\right)=\frac{N_{\mathrm{V}}4\pi V\sqrt{E}}{\left(8{\pi }^3\right){\left({\hslash }^2/2m_{\mathrm{V}}{m}_0\right)}^{3/2}},\mathrm{respectively}.\end{array}$$ (23)

The corresponding polynomial fit for the carrier concentration n₀ versus Fermi energy E_F relation is then denoted by

$${\log }_{10}\left(n_0{\mathrm{cm}}^3\right)=a_{00}+a_{01}{E}_{\mathrm{F}}+a_{02}{E}_{\mathrm{F}}^2+\dots +a_{0l}{E}_{\mathrm{F}}^l\dots .$$ (24)

Figure 1 compares the calculated carrier concentration n_BGN and n₀ data for 28 values of donor densities between 10¹⁶ cm⁻³ and 10¹⁹ cm⁻³. For a given Fermi energy, the electron densities predicted by the BGN model (solid-black curve) are typically factors of two smaller than the electron densities predicted by an equivalent parabolic two-band model (dashed-blue curve).

Figure 1.

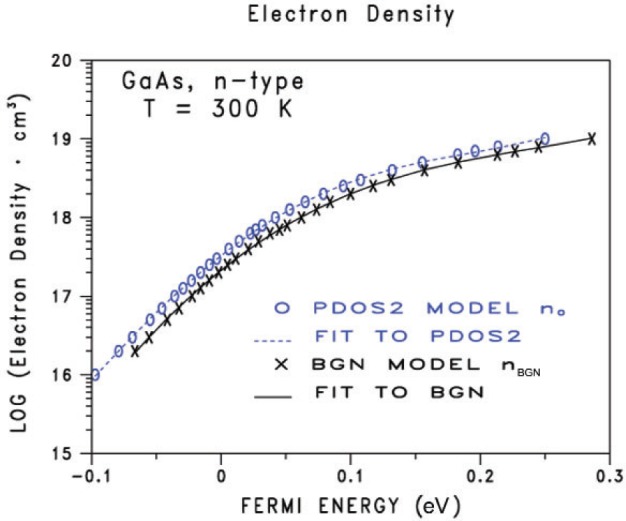
The calculated electron density n_BGN from the BGN model as a function of Fermi energy for n-type GaAs at 300 K is given by the solid-black curve. The calculated electron density n₀ from the two-band PDOS2 model, no bandgap narrowing model, as a function of Fermi energy for n-type GaAs at 300 K is given by the dashed-blue curve. The Fermi energy is relative to the majority conduction band edge at the Γ symmetry point in the first Brillouin zone.

3.2 PDOS Models

We solve self-consistently, by means of an iterative procedure, Eq. (3) with Eq. (5). The independent variables are the temperature T and donor density N_D.

We give here the results for fitting the logarithm to the base 10 of the total electron density and the electron densities in each of the three conduction sub-bands at Γ, L, and X, n_Γ, n_L, and n_X, respectively, to polynomials in E_F, namely,

$${\log }_{10}\left(n_t{\mathrm{cm}}^3\right)=a_{\mathrm{t}0}+a_{\mathrm{tl}}{E}_{\mathrm{F}}+a_{\mathrm{t}2}{E}_{\mathrm{F}}^2+\dots +a_{\mathrm{t}l}{E}_{\mathrm{F}}^l\dots ,$$ (25)

$${\log }_{10}\left(n_{\mathrm{\Gamma }}{\mathrm{cm}}^3\right)=a_{\mathrm{\Gamma }0}+a_{\mathrm{\Gamma }\mathrm{l}}{E}_{\mathrm{F}}+a_{\mathrm{\Gamma }2}{E}_{\mathrm{F}}^2+\dots +a_{\mathrm{\Gamma }l}{E}_{\mathrm{F}}^l\dots ,$$ (26)

$${\log }_{10}\left(n_{\mathrm{L}}{\mathrm{cm}}^3\right)=a_{\mathrm{L}0}+a_{\mathrm{Ll}}{E}_{\mathrm{F}}+a_{\mathrm{L}2}{E}_{\mathrm{F}}^2+\dots +a_{\mathrm{L}l}{E}_{\mathrm{F}}^l\dots ,\mathrm{and}$$ (27)

$${\log }_{10}\left(n_{\mathrm{X}}{\mathrm{cm}}^3\right)=a_{\mathrm{X}0}+a_{\mathrm{Xl}}{E}_{\mathrm{F}}+a_{\mathrm{X}2}{E}_{\mathrm{F}}^2+\dots +a_{\mathrm{X}l}{E}_{\mathrm{F}}^l\dots .$$ (28)

Figures 2 and 3 give the calculated electron densities as functions of the Fermi energy. The corresponding fitted curves are not shown in Figs. 2 and 3 because the pairs of curves (calculated and fitted) for each of the electron densities n_t, n_Γ, n_L, and n_X, lie on top of one another to within the line widths of each curve. Also, since the screening radii for the carriers from Eq. (2) are not needed when interpreting the proposed measurements considered here, the corresponding screening radii are not presented in this paper. Figure 2 compares the results from the PDOS2 model (dashed-blue curve with long spaces), PDOS2NPG model (solid-green curve), and PDOS4 model (dashed-red curve with short spaces). The data for the blue curve in Fig. 1 is the same data for the blue curve in Fig. 2. Figure 3 shows the results for the four-band PDOS4 model. Unlike GaSb, most of the electrons are in the conduction sub-band at Γ. The conduction sub-band at L is only weakly populated at the highest Fermi energies, and the conduction sub-band at X is negligible.

Figure 2.

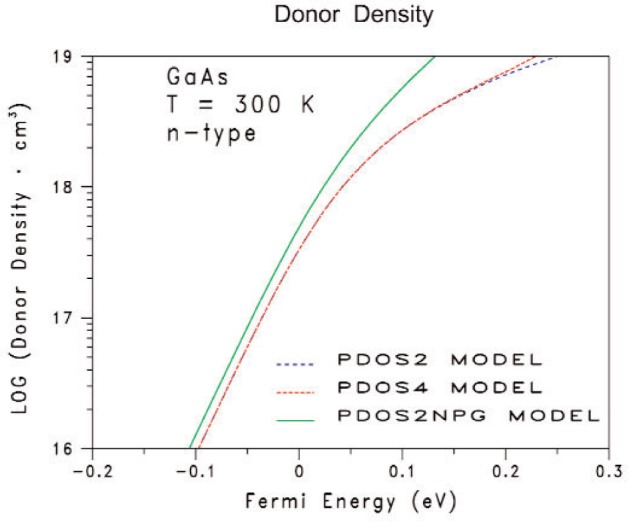
Comparisons among three PDOS models with and without the non-parabolic factor ξ in Eq. (5) for the electron energy dispersion E_cΓ(k). The solid-green curve shows the results for an equivalent two-band model that has one equivalent Γ conduction band with non-parabolicity factor ξ and one equivalent Γ valence band; that is, the PDOS2NPG model. The dashed-blue curve with long spaces shows the results for an equivalent parabolic two-band model PDOS2 (ξ = 0). The dashed-red curve short spaces shows the results for the four-band PDOS4 model. The Fermi energy is relative to the majority conduction band edge at the Γ symmetry point in the first Brillouin zone.

Figure 3.

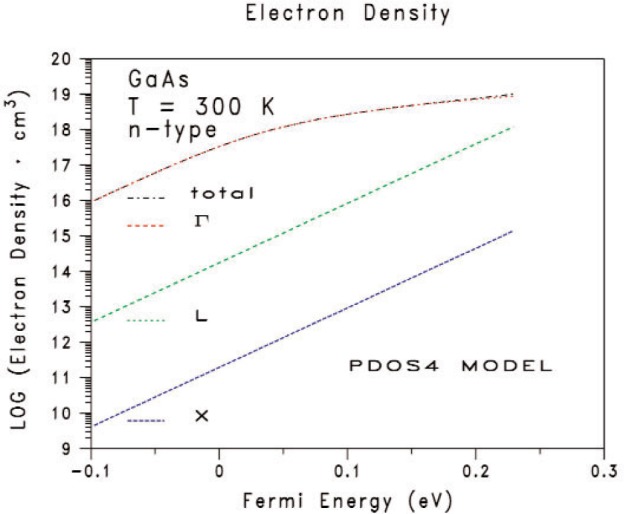
The calculated electron densities n_t, n_Γ, n_L, and n_X from the four-band PDOS4 model as functions of the Fermi energy for n-type GaAs at 300 K. The Fermi energy is relative to the majority conduction band edge at the Γ symmetry point in the first Brillouin zone.

3.3 Polynomial Fits – Closed-Form Analytic Expressions

Tables 6 to 11 give the fitting parameters for polynomial fits to log₁₀(n_BGN cm³), log₁₀(n₀ cm³), log₁₀(n_t cm³), log₁₀(n_Γ cm³), log₁₀(n_L cm³), and log₁₀(n_X cm³) as shown, respectively, in Eqs. (21) and (24) to (28) and the corresponding residual standard deviations S_res. In general, the values of S_res decrease monotonically with increasing number l of terms in these polynomials. But, care must be taken to avoid fitting noise in data sets. The general guideline for many data sets is that when the t-ratio (i.e., the absolute value of the ratio of the estimated parameter value divided by its estimated standard deviation) is less than about 2, then the rate of decrease in S_res with increasing l tends to decrease, and proceeding with higher l values probably is not warranted. Because the changes in values of S_res between l = 4 and l = 5 are not experimentally significant, we use the fitting parameters for the quartic case l = 4 in Eqs. (21) and (24). Similary, because the changes in values of S_res between l = 3 and l = 4 are not experimentally significant, we use the fitting parameters for the cubic l = 3 case in Eqs. (25) to (28).

Table 6.

Bandgap narrowing BGN model for log₁₀(n_BGN cm³). The five fitting parameters for a quartic polynomial fit Eq. (21) of the theoretical calculation for the equivalent conduction band electron density in n-type, zinc blende GaAs at 300 K as a function of the Fermi energy relative to the bottom of the equivalent conduction band at Γ. This quartic polynomial fit, which represents the theoretical results for Eq. (3), is valid only when −0.067 eV ≤ E_F ≤ 0.286 eV. The t-ratio is the absolute value of the estimated fitting parameter |a_BGNi| divided by its estimated standard deviation. The residual standard deviation is S_res = 0.0130.

Fitting parameter	Estimated value	Estimated standard deviation	Units	t-ratio
aBGN0	17.3292	0.4191 × 10−2		4.135 × 103
aBGN1	13.1545	0.7646 × 10−1	eV−1	1.72 × 102
aBGN2	−37.4789	1.473	eV−2	25.45
aBGN3	26.5678	12.86	eV−3	2.067
aBGN4	53.7760	29.43	eV−4	1.827

Table 11.

Four-band PDOS4 model for the electron density X sub-band log₁₀(n_X cm³). The four fitting parameters for a cubic polynomial fit Eq. (28) of the theoretical calculation for the X sub-band electron density in n-type, zinc blende GaAs at 300 K as a function of the Fermi energy relative to the bottom of the conduction Γ sub-band. This cubic polynomial fit, which represents the theoretical results for Eq. (3), is valid only when −0.0974 eV ≤ E_F ≤ 0.229 eV. The t-ratio is the absolute value of the estimated fitting parameter |a_Xi| divided by its estimated standard deviation. The residual standard deviation is S_res = 0.000 019 5.

Fitting parameter	Estimated value	Estimated standard deviation	Units	t-ratio
aX0	11.2919	0.5452 × 10−5		2.071 × 106
aX1	16.7999	0.7862 × 10−4	eV−1	2.137 × 105
aX2	−0.542 16 × 10−3	0.1105 × 10−2	eV−2	0.4905
aX3	−0.4041 × 10−2	0.5426 × 10−2	eV−3	0.7448

4. Conclusions

The foregoing theory for extracting electron densities from Raman spectra is unique in two ways: 1) It treats the many-body effects self-consistently, and 2) it is valid at room temperature for arbitrary values of the ratio R = (Q²/α). When high concentrations of carriers exists, this theory and its associated numerical procedures for determining carrier concentrations from Fermi energies are necessary for interpreting room temperature Raman spectra self-consistently for arbitrary values of the ratio R, even for R ≈ 1. The BGN models presented here include many-body quantum effects and bandgap narrowing. However, obtaining Fermi energies from experimental Raman spectra is beyond the scope of the present paper and involves the following steps to implement contactless measurements of carrier densities:

1. Numerical evaluation of Eq. (17) with adaptive grids to treat the integrable singularities of the integrands,

2. Three-dimensional visualization of computer results for predicted Raman line shapes as functions of Fermi energy and frequency, and

3. Iteration of the predicted Raman line shape with the Fermi energy as a variation parameter to give the best self-consistent fit to the measured Raman line shape.

Table 7.

Two-band, no bandgap narrowing PDOS2 model for log₁₀(n cm³⁰). The five fitting parameters for a quartic polynomial fit Eq. (24) of the theoretical calculation for the L sub-band electron density in n-type, zinc blende GaAs at 300 K as a function of the Fermi energy relative to the bottom of the conduction Γ sub-band. This quartic polynomial fit, which represents the theoretical results for Eq. (3), is valid only when −0.0974 eV ≤ E_F ≤ 0.250 eV. The t-ratio is the absolute value of the estimated fitting parameter |a_0i| divided by the its estimated standard deviation. The residual standard deviation is S_res = 0.0122.

Fitting parameter	Estimated value	Estimated standard deviation	Units	t-ratio
a00	17.5156	0.3411 × 10−2		5.136 × 103
a01	12.8520	0.8063 × 10−1	eV−1	3.1 × 102
a02	−34.5783	0.6672	eV−2	51.83
a03	−27.3728	9.166	eV−3	2.986
a04	223.720	29.54	eV−4	7.573

Table 8.

Four-band PDOS4 model for total electron density log₁₀(n_t cm³). The four fitting parameters for a cubic polynomial fit Eq. (25) of the theoretical calculation for the total electron density in n-type, zinc blende GaAs at 300 K as a function of the Fermi energy relative to the bottom of the conduction Γ sub-band. This cubic polynomial fit, which represents the theoretical results for Eq. (3), is valid only when −0.0974 eV ≤ E_F ≤ 0.229 eV. The t-ratio is the absolute value of the estimated fitting parameter |a_ti| divided by its estimated standard deviation. The residual standard deviation is S_res = 0.0234.

Fitting parameter	Estimated value	Estimated standard deviation	Units	t-ratio
at0	17.5198	0.6519 × 10−2		2.687 × 103
at1	12.3461	0.9401 × 10−1	eV−1	1.31 × 102
at2	−35.5542	1.322	eV−2	26.90
at3	40.1630	6.488	eV−3	6.190

Table 9.

Four-band PDOS4 model for electron density in the Γ sub-band log₁₀(n_Γ cm³). The four fitting parameters for a cubic polynomial fit Eq. (26) of the theoretical calculation for the Γ sub-band electron density in n-type, zinc blende GaAs at 300 K as a function of the Fermi energy relative to the bottom of the conduction Γ sub-band. This cubic polynomial fit, which represents the theoretical results for Eq. (3), is valid only when −0.0974 eV ≤ E_F ≤ 0.229 eV. The t-ratio is the absolute value of the estimated fitting parameter |a _Γi| divided by its estimated standard deviation. The residual standard deviation is S_res = 0.0214.

Fitting parameter	Estimated value	Estimated standard deviation	Units	t-ratio
aΓ0	17.5187	0.5978 × 10−2		2.930 × 103
aΓ1	12.3944	0.8621 × 10−1	eV−1	1.438 × 102
aΓ2	−35.1795	1.212	eV−2	29.03
aΓ3	33.7647	5.950	eV−3	5.675

Table 10.

Four-band PDOS4 model for electron density in the L sub-band log₁₀(n_L cm³). The four fitting parameters for a cubic polynomial fit Eq. (27) of the theoretical calculation for the L sub-band electron density in n-type, zinc blende GaAs at 300 K as a function of the Fermi energy relative to the bottom of the conduction Γ sub-band. This cubic polynomial fit, which represents the theoretical results for Eq. (3), is valid only when −0.0974 eV ≤ E_F ≤ 0.229 eV. The t-ratio is the absolute value of the estimated fitting parameter |a_Li| divided by its estimated standard deviation. The residual standard deviation is S_res = 0.001 17.

Fitting parameter	Estimated value	Estimated standard deviation	Units	t-ratio
aL0	14.2422	0.3269 × 10−3		4.357 × 104
aL1	16.8180	0.4714 × 10−2	eV−1	3.568 × 103
aL2	0.162418	0.6627 × 10−1	eV−2	2.451
aL3	−2.1988	0.3253	eV−3	6.759

Biography

About the authors: Herbert S. Bennett is a NIST Fellow in the Semiconductor Electronics Division of the Electronics and Electrical Engineering Laboratory. He is a Life Fellow of the Institute of Electrical and Electronics Engineers and a Fellow of the American Physical Society. His research interests include improved understanding, metrology, and standards for nanoelectronics, optoelectronics, and magnetic materials and assessing the quality of digital images such as those used in medical imaging. He is active with international industrial consensus building for technology roadmaps on semiconductors and with international standards development for nanoelectrotechnology. The National Institute of Standards and Technology is an agency of the U.S. Department of Commerce.