Abstract
Physical cues exist across all biological scales, from the geometries of molecules to the shapes of complex organisms. While their roles have been identified across a range of scales, i.e. the arrangements of biomolecules and the form and function of tissues, less is known in some intermediate lengths. Particularly, at the cell scale, there is emerging evidence demonstrating the impact of mechanical signals, such as substrate stiffness and confinement, on many critical biological processes and malignancies, especially cancer dissemination. In the context of cell invasion, it is currently unclear how cells select from accessible mechanical paths that result in migratory patterns observed in physiological environments. Here, we devise microchannel decision trees to explore how fundamental and ubiquitous mechanical factors, specifically dimensionality and directionality, affect migratory cell decision making. We then implement strategies based purely on mechanical asymmetries to induce repetitive, non-disseminating motions, in a phenomenon we call iteratio ad nauseam.
Introduction
Cell invasion is a critical component of cancer metastasis, a process associated with many mechanical transport steps through physically complex environments, including cell navigation through the heterogeneous porous medium of the tumor stromal extracellular matrix (ECM), permeation across endothelial barriers, and circulation and trafficking in micro-vessels.1–3 The physical interactions of cancer cells with the mechanical components of these environments are not well understood. To break down this complex process into an addressable form, here we consider quantized cell decision making events during invasion. We assume the scenario of a cell in 3D space with n available tangential paths; this is analogous to a cell in ECM surrounded by n pores of various characteristics. If these paths are all accessible then there is a finite probability Pi, where i = 1, 2,…n, in which the ith path would be chosen. The average displacement of the cell at each decisional step can be represented by the vector <x>, where
| (1a) |
| (1b) |
and xi is the unit step in the direction of the ith path. In general, Pi is a multi-parameter function F of the properties of the ith path, including canonical chemical signals such as chemotactic gradients and physical signals such as substrate stiffness, stress and strain fields, and flow. The ultimate goal is to comprehensively elucidate all of the modulators of Pi in order to be able to predict exact cell trajectories during invasion. While many chemical factors have been identified and associated with cancer, such as the overexpression or deregulation of epidermal growth factor receptors (EGFRs) and G-protein coupled receptors (GPCRs),4 by contrast much less is known about mechanical factors. Therefore, here we focus exclusively on mechanical factors. Previous work has demonstrated the role of substrate stiffness in malignant transformation5 and stiffness gradients in guiding migratory directions via durotaxis.6 More recent work has shown that fibrillar alignment and interstitial flow in 3D ECMs can also direct paths via topography7 and autologous chemotactic gradients,8,9 respectively. However, it is still unclear from these studies how cells select paths at each decisional step. Current state-of-the-art models for cell invasion, which is largely based on cells embedded in 3D ECMs, exhibit an environment that consists of a characteristically heterogeneous fibrillar network of pores with large dispersion in size and local alignment. These features occlude our understanding of the contribution of basic characteristics in the mechanical environment, such as dimensional and directional signals, toward cell invasion. Microchannel-based systems with well-defined features can enable this analysis. Cell-scaled mechanical paths have been shown to promote highly persistent migratory and invasive behavior, and subnucleus gaps and pores rate-limit invasion.10–13 Novel experimental and computational models are emerging that explore the impact of confinement on cell migration.10,14,15 Biochemical gradients generated inside microchannels can be used to investigate chemotaxis and immune cell chemotactic response. For instance, bifurcating microchannels with different chemoattractant profiles, which are generated by controlling the channel lengths between the chemical source (outlet) and sink (inlet), have been used to investigate neutrophil chemotactic response to fMLP (Formyl-methionyl-leucyl-phenylalaine).16 Microgeometries in 2D studies also have been shown to impact cell behavior, from directed migration to stem cell differentiation.17,18 Despite these recent advances, cell migratory decision making, and thus the basic mechanism in the formation of complex invasion patterns, in 3D as a function of mechanical modulators is still unsolved. The goal in our current work is to focus specifically on fundamental mechanical modulators in the microenvironment, so we aim to eliminate externally applied chemical gradients. To do this, in our microchannel devices, we connect the inlet and outlet to a single unifying reservoir. This eliminates chemical and pressure gradients across the channels, as further described in the methods section, and enables our work to emphasize on engineered local mechanical features in the cell invasion path. The physiological local environment (e.g. the ECM) around individual cancer cells contains numerous possible paths that are mechanically disperse (varying pore sizes and fiber orientation),3,19 and currently we cannot predict the path selection behavior based on local mechanical signals. This is critical because mechanical signals are omnipresent, so if they do indeed have an impact on migratory decisional output, identifying their roles could provide fundamental insights toward the very phenomenon of cell invasion, enabling us to better predict and model this process.
Results and discussions
Mechanical decision trees
Our work here aims to develop a system that can elicit migratory decisional processes with well-defined mechanical features that span the cell and subnucleus-scales, which are two scales that induce unique responses in cells,10,11,13 and incorporate directional cues that consider migratory persistence.20 Thus, our approach, through precise microchannel definitions, uniquely integrates a priori ubiquitous differential mechanical modulators of cell behavior and specifically targets their contributions toward cell decision making during invasion. We focused on two mechanical factors – dimensionality and directionality. Their existence is fundamental and ubiquitous in all physical and physiological environments, but their role in cell invasion is not well understood. For instance, during cancer invasion, matrix remodeling could lead to the generation of directionally-guided persistent tracks via proteolytic degradation and aligned ECM fibers via cell tension.19,21,22 These physical cues have been shown to promote cancer cell dissemination and lead to highly persistent migratory states both in native-like matrix models and micropatterned environments.10,23 However, the statistics and dynamics of how cells make migratory decisions in response to these physical properties in their microenvironment have not been systematically studied in a quantitative manner. To address this, we aimed to establish a platform that specifically modulates the local dimensional and directional mechanical signals around individual cells.
We created a microchannel system with binary decision trees implemented for single invading cells. Just as chemotaxis and durotaxis studies probe cell affinities toward a chemotactic or substrate stiffness gradient, the decision tree microchannels here is an enabling and quantitative means to study subtle cell behavior and preferences in response to common mechanical signals in the local environment. In this environment, eqn (1a) simplifies to:
| (2a) |
| (2b) |
As shown in Fig. 1, cells are loaded into the microchannel inlet reservoir. They spontaneously migrate unidirectionally in the cell-scaled channels and encounter the decision tree. Decision trees of the same design are serially patterned in each separate channel, and two different designs are incorporated in parallel. The first design is a circular pattern with two path branches that split at the same angle which is perpendicular to the initial cell path; the larger path at the top has a width of 10 μm and the smaller path at the bottom has a subnucleus width of 3.3 μm. The second design is a semi-circular pattern; the features are identical to the first design except the bottom smaller path is collinear with the original path leading to the decision tree. x1 and x2 in eqn (2a) refer to the top and bottom paths, respectively. The decisional probabilities Pi can then be represented as:
Fig. 1.
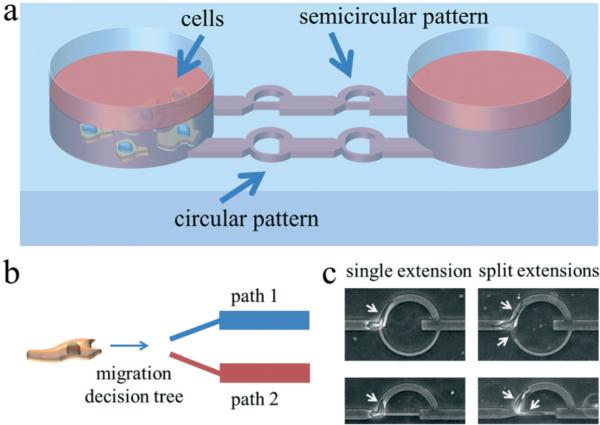
Schematics and images illustrating the decision tree microchannel device concept and operations. a) Cells are loaded into the device via pipetting into the reservoir. They will then spontaneously invade into the microchannels. There are two patterns incorporated into our device design. The first design is a circular pattern with a larger arched top path (cell-scaled, 10 μm) and a smaller arched bottom path that is highly confining (subnucleus-scaled, 3.3 μm), and the second design is a semicircular pattern with the same design features as the circular pattern except that the smaller bottom path is straight and collinear to the original cell path. The height of the channels is 10 μm. b) Conceptual illustration of a cell migrating along a particular direction and encountering an interface with split paths. The goal is to analyze some under-explored but ubiquitous factors that bias the decision making process in route choosing. c) Typical images of cells in the split path device. This matrix of images shows the possible cell–path interactions at the path junction. In both patterns, cells can exhibit a single extension interaction, in which the cell migrates along one leading edge, or a split extension interaction in which two leading edges, with one in each path, compete for the cell's ultimate decision. Leading edges are marked by arrows.
| (2c) |
| (2d) |
for the circular design and
| (2e) |
| (2f) |
for the semicircular design. The goal of this work is to experimentally elucidate P1 and P2 of the different binary trees in order to identify the intrinsic mechanical affinities of invasive cells. For our studies we used the MDA-MB-231 breast adenocarcinoma cell line, which models highly metastatic cancer cells and thus could provide insights toward aggressively invasive behavior.
As shown in Fig. 1c, as an individual cell encounters the decision tree, two scenarios can occur. The cell exhibits either a single extension path choice, in which the cell enters the selected path with no contest, or a split extension path choice, in which the cell splits into two competing edges. In the latter case, as demonstrated in Fig. 2a and b and ESI† videos 1 and 2, the two competing edges both extend and the cell appears to exhibit a highly tensional state. Eventually, one of the edges collapses and the cell is polarized along the remaining edge. This competing edge phenomenon and the subsequent dynamics elicited in the decision tree microchannels are difficult to recreate and analyze in other cell invasion models, such as with cells embedded in 3D ECMs, where the heterogeneous fibrillar meshwork masks the subtle dynamics in mechanical cell decision making.
Fig. 2.
Cell invasion dynamics in decision tree microchannels. a) A cell encounters the decision tree of the circular pattern. Upon entry, the cell exhibits split extensions. Eventually, one side collapses and the cell is polarized along the other edge. b) A cell encounters the decision tree of the semicircular pattern and split extensions are formed. The extensions elongate in competing directions until asymmetric collapse occurs, resulting in the cell being polarized along the remaining leading edge. c, d) Blebbistatin-treated cells typically exhibit an altered cell morphology. They have long and thin extensions that drag the cell body along in a motile mode that resembles a tethered ball. Here, the extension drags the cell along the top path of the circular pattern in (c) and along the bottom path of the semicircular pattern in (d). e) Taxol treated cells tend to be more rounded with less noticeable extensions and have decreased migratory persistence. Arrows point to cell extensions. All time coordinates are in minutes. For scale reference, the width of the top path is 10 μm.
Next we treated the cells with blebbistatin (Bleb) and paclitaxel (Taxol). Both molecules have been demonstrated previously to have an impact on cell invasiveness. Blebbistatin is an inhibitor of non-muscle myosin IIa, which is implicated in cell contractility and tensional force generation.5,7,24–26 Myosin IIa plays an important role in matrix reorganization in 3D, leading to local matrix alignment and enabling cell invasion.7,25 In general, myosin contracts actin filaments in the cytoskeleton, enabling cells to squeeze across constriction points and navigate through dense porous matrices in 3D without necessarily requiring protease activity.27 The amoeboid motile mode is also regulated by actomyosin contractility and can be induced when matrix proteolysis is inhibited.28 Previous studies have demonstrated that blebbistatin can inhibit invasion in 3D gels and can alter traction forces.5,7,25 In particular, cancer cells treated with blebbistatin have decreased capacity in invasion into 3D Matrigel when seeded on the surface and have reduced uropod formation and cell speeds when embedded inside the gel.25 More recent studies have shown that in 3D collagen matrices, actomyosin contractility and proteolytic activity can cooperate or compensate for each other to promote cell invasion and nucleus deformation and translocation across constrictions by modulating force generation and matrix pore size.29 Here we demonstrate that in confined spaces, blebbistatin alters the migratory mode of cells and changes invasion patterns. Blebbistatin-treated cells exhibit morphologies with long and thin extensions and typically have more rounded cell bodies. This phenotype gives semblance of a tethered ball motile mode, as in a thin string pulling on a tethered ball, as shown in Fig. 2c and d and ESI† video 3.
Taxol stabilizes microtubules and is a common chemotherapeutic traditionally used for anti-mitotic effects.30 Microtubule disruption has also been shown to inhibit a cell's ability to permeate through subnucleus-scaled constrictions and impair cell polarity.13,20,31 Taxol-treated cells tend to lose migratory persistence and exhibit a more rounded morphology, as shown in Fig. 2e and ESI† video 4.
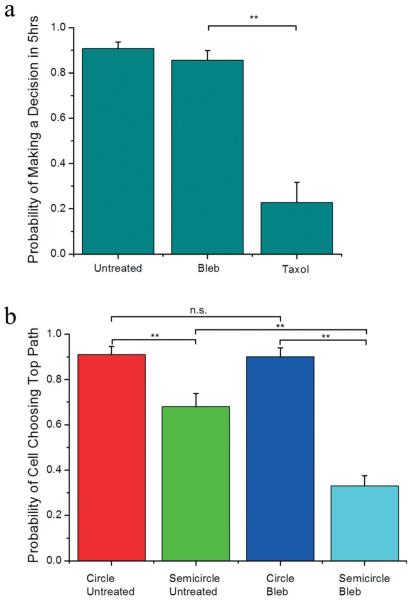
Our results show that as the invading cells encounter the decision tree, >85% of untreated and blebbistatin-treated cells are able to make a path decision within 5 hours, but most taxol-treated cells (>77%) fail to make a decision, as shown in Fig. 3a. This shows that taxol (at 10 μM) is a decision suppressor. Next, we analyzed the decisions of the untreated and blebbistatin-treated cells. In Fig. 3b, our results from the circular pattern show that untreated invading cells have an overwhelmingly high affinity towards larger channels of ≈90%. However, when the directionality of the smaller channel is altered to be collinear with the original cell path as in the semicircular pattern, the affinity for the larger path decreases to 68%, demonstrating that migratory polarization effects can bias cell invasion preferences. When the cells are treated with blebbistatin, the affinity for the collinear route of the smaller path in the semicircular pattern is further increased to 67%, but the affinities are unchanged in the circular pattern. These results suggest inhibition of myosin IIa increases the invading cells' sensitivity to directionality, while maintaining the path size affinity when directional biases are not present. Here, we have shown that dimensional and directional factors, which are present along critical steps during cancer metastasis and other phenomena associated with cell motility, can bias cell decision making in a tunable manner, and molecular inhibitors can further modulate those decisions.
Fig. 3.
Cell decision making statistics. a) Untreated, 50 μM blebbistatin-treated, and 10 μM taxol-treated cells have a probability of making a decision within 5 hours of encountering the decision tree of 0.90 (n = 97), 0.86 (n = 70), and 0.23 (n = 22), respectively, where n is the number of cells. b) The probability of a cell choosing the larger (top) path for untreated cells in the circular pattern, untreated cells in the semicircular pattern, blebbistatin-treated cells in the circular pattern, and blebbistatin-treated cells in the semicircular pattern are 0.91 (n = 66), 0.68 (n = 63), 0.90 (n = 59), 0.33 (n = 104), respectively, where n is the number of decisions observed. ** indicates p < 0.01 and n.s. indicates not statistically different based on the chi-square test. Error bars are standard error of the mean (s.e.m.) calculated from the Bernoulli distribution.
Cell ring traps and iteratio ad nauseam
In understanding some of the mechanical and molecular modulators of cell invasive behavior, we can begin to design strategies to manipulate the patterns of invasion. We have shown that cells have an affinity towards cell-scaled paths over subnucleus-scaled paths that can be altered via directional cues and actomyosin activity inhibition. Here, we designed a new mechanical microenvironment that introduces an invasion path, with directional and dimensional asymmetries, that is aimed to bias and prolong cell residence times in localized regions. We call this a ring trap.
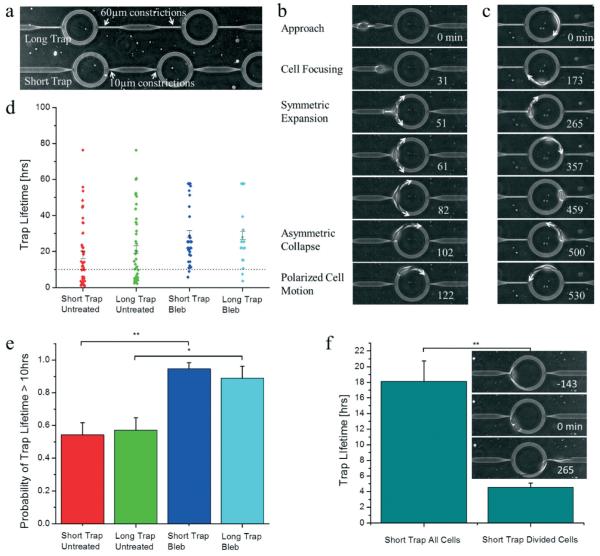
As shown in Fig. 4a, the trap consists of a cell-scaled ring region with subnucleus-scaled entrance/exit paths that are perpendicular to the ring. Two designs are incorporated in parallel – the long trap and the short trap, with long and short exit constrictions, respectively. Since longer traps require permeating cells to undergo larger deformations (and thus require more energy), we hypothesized that this may modulate the trapping stiffness of the rings. The concept is to utilize geometric asymmetry to induce invasive cells to preferentially remain inside the ring and invade in circles.
Fig. 4.
Cell invasion dynamics in ring traps. a) Two different trap designs are incorporated in parallel, the short trap and the long trap with 10 μm long exits and with 60 μm long exits, respectively. The outer ring has a radius of 50 μm. b) As a cell enters the ring trap, it is focused by the subnucleus-scaled constriction. Then it emerges into the trap and expands in a symmetric manner. Next, spontaneous symmetry breaking induces polarized cell migration. Arrows point in the direction of cell extension and migration. c) Cells that enter the trap often exhibit the phenomenon iteratio ad nauseam, during which the cells invade in circular patterns in a confined space rather than disseminate. Arrows point in the direction of cell migration. d) The trap lifetime of untreated cells is over 18 hours, and this is extended by blebbistatin treatment (n = 46, 42, 38, 18 for cells in the short trap untreated, long trap untreated, short trap blebbistatin-treated, and long trap blebbistatin-treated, respectively, where n is the number of trapping events). The horizontal line denotes the 10 hour mark. Note that this data includes censored data points, i.e. the cells are either already in the trap at the beginning of the experiments or are still in the trap at the end of the experiments, so these measurements are under-estimates. e) The probability that a cell spends more than 10 hours in the ring trap is shown for the long and short traps for untreated and blebbistatin treated cells. This enables an assessment of the statistical difference between untreated and blebbistatin-treated cells when including censored data. The probabilities are 0.54, 0.57, 0.95, 0.89 for cells in the short trap untreated, long trap untreated, short trap blebbistatin-treated, and long trap blebbistatin-treated, respectively, for the same data as in (d). Error bars are standard error of the mean (s.e.m.) calculated from the Bernoulli distribution. We note that censored data points under 10 hours (7 out of 151 data points from the raw data) were discarded in order to eliminate arbitrarily short trap lifetimes. f) Cell division promotes escape from the ring traps. Immediately after cell division, the first cell that escapes exhibits a trap lifetime of only around 4.5 hours (n = 21), in comparison to 18+ hours (n = 46) for the overall average in the short trap. We again did not include censored data under 10 hours to eliminate arbitrary short trap lifetimes. We note however that for this data set, only 1 out of 68 data points fell in this category, and including that data point did not alter the statistical significance of our results. Also there were no censored data points for the cell escape after division data. * indicates p < 0.05 and ** indicates p < 0.01. All time stamps on time lapse image stacks are in minutes.
Our experiments show that cell–trap interactions exhibit several phenomena. As cells invade through the subnucleusscaled entrance of the ring trap, typically they enter the ring in a symmetric manner, with split edges extending in opposing directions, as shown in Fig. 4b and ESI† video 5. After several minutes, the cells undergo spontaneous symmetry breaking, inducing the onset of polarized cell migration. Thus, we have shown here a novel way of inducing spontaneous symmetry breaking in single-cells by first focusing the cell with a subnucleus barrier, followed by a mechanical barrier upon exit to induce an initial symmetric response. This is essentially a “cell scattering” experiment, analogous to photon scattering experiments in the Rayleigh (subphoton-scaled) and Mie (photon-scaled) regimes that helped uncover the nature of light–matter interactions. Spontaneous symmetry breaking can then be observed and analyzed at the single-cell level, and since symmetry breaking is a fundamental feature that governs the formation and function of all of life,32–34 enabling experimental apparatuses are important for more in depth studies. In particular, symmetry breaking in single-cell migration, especially in 3D, is not well understood. Thus, we have created a way of systematically inducing single-cell scattering experiments and eliciting the dynamics of cell-mechanical environment interactions.
Next, the well-designed asymmetries in dimensionality and directionality suppress cell dissemination by localizing invasion zones. As shown in Fig. 4c and ESI† video 6, cells typically remain in the ring trap for an extended period of time and invade in circular and repetitive patterns, which we call iteratio ad nauseam. We characterized the trap lifetime and demonstrate in Fig. 4d that cells spend over 18 hours in the ring traps. The trap lifetime can be extended by inhibiting myosin IIa with blebbistatin, which increases the proportion of cells that spend greater than 10 hours in the trap from 55% to 90%, as shown in Fig. 4d and e. The trap lifetime also does not appear to be strongly impacted by the length of the exit constriction. We note here that in our previous studies, we have shown that these aggressive breast cancer cells are highly persistent, maintain speeds on the order of micrometers per minute, and are readily able to permeate through the subnucleus-scaled barriers when no decision trees are presented.13 The strategically designed ring trap architectures here are able to confine cells within a region of 50 μm radius for an extended period of time simply by catering to natural migratory affinities. Finally, we explored the escape mechanisms of cells in the ring traps. We demonstrate in Fig. 4f and ESI† video 7 that cell division within or immediately before entering the ring traps promotes cell escape. The trap lifetime after division is reduced to around 4.5 hours, which is significantly less than the 18+ hours of the general population. This is an interesting result that opens a new perspective for future studies, as existing paradigms typically do not consider any coupling between cell migration and proliferation. Here we have shown that there is causality between the cell cycle and cell invasiveness, suggesting that invasiveness is a dynamic rather than static property that evolves with the natural temporal changes of each cell.
Conclusion
Cell behavior during invasion is a highly complex process that is not well understood. We created microfluidic devices that elicit the decision making process of cells when encountering mechanical asymmetries on the cell and subnucleus scale. By using well-defined geometries and features, we probed the path affinities of invasive cells and explored mechanical and molecular means of modulating these affinities. We demonstrated that dimensional and directional cues can bias cell invasion patterns, actomyosin inhibition can alter migratory decision making, and properly designed mechanical asymmetries can promote the phenomenon iteratio ad nauseam. The devices and experiments shown here can help reveal more complex factors in the dynamics of invasion at the single-cell level. In future studies and next generation modules of our device, the incorporation of angular modulation, additional path choices, alternate geometries of channel entries and exits, and a systematic combinatorial analysis of the effects of mechanical signals can help generate empirical measurements of eqn (1a) for different cell types and elucidate cell behaviors in a well-defined environment that starts to possess the mechanical complexities of physiological 3D matrices. In particular, micro- and nano-topographies at channel entry and exit points could potentially modulate cell force generation and traction, leading to altered cell behavior.17
Additionally, we emphasize from our results that purely mechanical factors in a 3D environment can induce complex cell behavior. This suggests that mechanically modulating tumor microenvironments may be a potential method in altering cancer invasion patterns, and we have shown a particular type of pattern that could trap invasive cells. Future work in developing tissue engineering methods that can strategically alter the architecture of the fibrillar meshwork of the tumor stroma, particularly based on preconceived modules such as the ring trap presented here, may be a new avenue in cancer therapy aimed at suppressing cancer dissemination. Additionally, the trap micropatterns, with its small footprint, may be converted into a micro-pill or particle format that could be injected into local tumor environments and serve as traps for invasive cells. In particular, previously we have shown that non-metastatic breast epithelial cells are less likely to permeate through subnucleus-scaled barriers than highly metastatic cells,12 so these patterns may be able to selectively trap the most aggressive cells. The devices and designs presented here illustrate a means to rapidly prototype mechanical modules that could impact cell migratory behavior and generate complex and tunable patterns of motility.
Methods
Cell culture
MDA-MB-231 cells were obtained from the National Cancer Institute Physical-Sciences in Oncology Centers (NCI PS-OC), originally from the American Tissue Culture Collection (ATCC). They were cultured at 37 °C without CO2 supplement in Leibovitz L-15 media (Life Technologies) with 10% fetal bovine serum (Atlanta Biologicals) and 1% Penicillin-Streptavidin (Life Technologies).
Device fabrication
Devices were fabricated at the Cornell Nanoscale Science and Technology Facility (CNF). Standard photolithography followed by soft lithography was used to fabricate polydimethylsiloxane (PDMS) microfluidic devices. Briefly, SU8 resist was spun onto a wafer and exposed in a UV stepper aligner under a photomask with the designed patterns to create the mold master. PDMS was cast onto the master, cross-linked, and bonded to glass slides to create the final microfluidic devices.
Cell loading into devices
The devices were made hydrophilic via oxygen plasma treatment for 40 seconds. Complete cell growth media (L-15 plus 10% FBS and 1% Penicillin-Streptavidin) was added into the reservoirs and allowed to coat the channels with serum proteins prior to cell loading. Cells in complete media were loaded into the channels by applying a gravity driven pressure gradient between the inlet and outlet reservoirs. After cells were injected into the device, the inlet and outlet reservoirs were filled and connected to the same larger unifying reservoir again filled with complete media. By connecting the inlet and outlet of the channels to the same reservoir, chemical and pressure gradients across the channels were eliminated. A schematic illustrating the integration of the unifying reservoir is shown in ESI† Fig. 1, where the larger reservoir is placed at the top of the device and equilibrates the inlet and outlet to the same pressure. We also traced diffusing cell debris in the channels and show in ESI† Fig. 2 and video 8 that significant flow, with flow rates comparable to those in interstitial flow experiments i.e. around 1 μm s−1,9,35 is not observed across these channels. Complete cell media with serum was used in our experiments in order to maintain the fully functional cell states observed under normal culture conditions. Full deprivation of serum may artificially impair cell invasive capacity.36 We note that through the course of the experiments, autologous gradients may be generated locally inside the channels via serum and nutrient consumption by invading cells. Future experiments with actively perfused media that replenishes the channels continuously and/or the use of serum-free media could help in the investigation of autologous chemical gradients and their impact on cell decision making in response to mechanical cues. By imposing different media constraints, we can gain insights toward the range of possible physiological conditions.
Experiments and analysis
Time lapse video microscopy was used to record cell invasion dynamics in the microfluidic channels, which were kept at 37 °C via a heating plate. Videos were recorded at 3.4 minutes per frame. Image analysis was performed manually on ImageJ. Data processing was performed using custom MATLAB code. For statistical analysis, chi-square and student t-tests were used. Statistical significance is indicated by * and ** for p < 0.05 and p < 0.01, respectively. For pharmacologic treatments, we added the complete growth media with either taxol (Cytoskeleton, Inc.) at 10 μM for 7 hours or blebbistatin (Sigma-Aldrich) at 50 μM for 1 hour in the device reservoir before experimental tracking of cells. Cells were tracked while under continuous drug treatment. Concentrations of the drugs and the time of drug incubation before experiment were chosen based on levels and response times that induce clear and observable phenotypic changes in cell morphology and behavior according to previous studies.10,26 Cell affinity was deduced by observing cells as they invaded towards the mechanical decision trees. Once the body of a cell enters one of the paths, the cell decision is scored for that path. We note that conventional biology studies usually do not consider multiple measurements per cell, and newer single-cell studies typically measure the behavior of each cell once. However, because the cell is dynamic and plastic with the capability of altering morphological states, size, and motile modes, it is important to sample each cell multiple times in order to fully appreciate the capability of each individual cell. Our device design, with decision trees patterned serially along each channel, enables each cell to be probed multiple times. In our experiments, each cell is typically sampled two to four times. Future studies that explore even larger sampling for each individual cell can enable us to address a deeper understanding of the fundamental behaviors and dynamics of single-cells and provide insights toward heterogeneity, plasticity, and ergodicity in cell populations.
It is also noteworthy here that in the confined channels used in our experiments, cells exhibit a 3D environment, as their protrusions are seen to extend both along the center of the channels as well as along the channel side walls (ESI† videos 1–7). Both glass and PDMS are conducive to cell adhesion and migration, especially when the surfaces are hydrophilized (e.g. via oxygen plasma treatment) and coated with serum.37 MDA-MB-231 cells are also capable of invading persistently in confined channels without any substrate coating beyond serum proteins in the media.12,13 In confined microchannel spaces, it has also been previously demonstrated that adhesion sites can form along all three dimensions.38
Supplementary Material
Acknowledgements
The work described was supported by the Cornell Center on the Microenvironment and Metastasis through Award Number U54CA143876 from the National Cancer Institute. This work was performed in part at the Cornell NanoScale Science and Technology Facility, a member of the National Nanotechnology Network, which is supported by the National Science Foundation (grant ECS-0335765). Michael Mak is a National Science Foundation Graduate Research Fellow.
Footnotes
Electronic supplementary information (ESI) available. See DOI: 10.1039/c3lc51173a
References
- 1.Chambers AF, Groom AC, MacDonald IC. Nat. Rev. Cancer. 2002;2:563–572. doi: 10.1038/nrc865. [DOI] [PubMed] [Google Scholar]
- 2.Kumar S, Weaver VM. Cancer Metastasis Rev. 2009;28:113–127. doi: 10.1007/s10555-008-9173-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wolf K, Mazo I, Leung H, Engelke K, Andrian UHV, Deryugina EI, Strongin AY, Bröcker E-B, Friedl P. J. Cell Biol. 2003;160:267–277. doi: 10.1083/jcb.200209006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hanahan D, Weinberg RA. Cell. 2011;144:646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 5.Paszek MJ, Zahir N, Johnson KR, Lakins JN, Rozenberg GI, Gefen A, Reinhart-king CA, Margulies SS, Dembo M, Boettiger D, Hammer DA, Weaver VM. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 6.Lo C-M, Wang H-B, Dembo M, Wang Y-L. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Provenzano PP, Inman DR, Eliceiri KW, Trier SM, Keely PJ. Biophys. J. 2008;95:5374–5384. doi: 10.1529/biophysj.108.133116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shields JD, Fleury ME, Yong C, Tomei AA, Randolph GJ, Swartz MA. Cancer Cell. 2007;11:526–538. doi: 10.1016/j.ccr.2007.04.020. [DOI] [PubMed] [Google Scholar]
- 9.Polacheck WJ, Charest JL, Kamm RD. Proc. Natl. Acad. Sci. U. S. A. 2011;108:11115–11120. doi: 10.1073/pnas.1103581108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Irmia D, Toner M. Integr. Biol. 2009;1:506–512. doi: 10.1039/b908595e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Friedl P, Wolf K, Lammerding J. Curr. Opin. Cell Biol. 2011;23:55–64. doi: 10.1016/j.ceb.2010.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mak M, Reinhart-King CA, Erickson D. PLoS One. 2011;6:e20825. doi: 10.1371/journal.pone.0020825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mak M, Reinhart-King CA, Erickson D. Lab Chip. 2013;13:340–348. doi: 10.1039/c2lc41117b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim M-C, Kim C, Wood L, Neal D, Kamm RD, Asada HH. Integr. Biol. 2012;4:1386–1397. doi: 10.1039/c2ib20159c. [DOI] [PubMed] [Google Scholar]
- 15.Huang Y, Agrawal B, Sun D, Kuo JS, Williams JC. Biomicrofluidics. 2011;5:013412–013417. doi: 10.1063/1.3555195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ambravaneswaran V, Wong IY, Aranyosi AJ, Toner M, Irimia D. Integr. Biol. 2010;2:639–647. doi: 10.1039/c0ib00011f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mahmud G, Campbell CJ, Bishop KJM, Komarova YA, Chaga O, Soh S, Huda S, Kandere-Grzybowska K, Grzybowski BA. Nat. Phys. 2009;5:606–612. [Google Scholar]
- 18.Kilian KA, Bugarija B, Lahn BT, Mrksich M. Proc. Natl. Acad. Sci. U. S. A. 2010;107:4872–4877. doi: 10.1073/pnas.0903269107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wolf K, Friedl P. Biochimie. 2005;87:315–320. doi: 10.1016/j.biochi.2004.10.016. [DOI] [PubMed] [Google Scholar]
- 20.Petrie RJ, Doyle AD, Yamada KM. Nat. Rev. Mol. Cell Biol. 2009;10:538–549. doi: 10.1038/nrm2729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wolf K, Friedl P. Clin. Exp. Metastasis. 2009;26:289–298. doi: 10.1007/s10585-008-9190-2. [DOI] [PubMed] [Google Scholar]
- 22.Wolf K, Wu YI, Liu Y, Geiger J, Tam E, Overall C, Stack MS, Friedl P. Nat. Cell Biol. 2007;9:893–904. doi: 10.1038/ncb1616. [DOI] [PubMed] [Google Scholar]
- 23.Kraning-Rush CM, Carey SP, Lampi MC, Reinhart-King CA. Integr. Biol. 2013;5:606–616. doi: 10.1039/c3ib20196a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Straight AF, Cheung A, Limouze J, Chen I, Westwood NJ, Sellers JR, Mitchison TJ. Science. 2003;299:1743–1747. doi: 10.1126/science.1081412. [DOI] [PubMed] [Google Scholar]
- 25.Poincloux R, Collin O, Lizárraga F, Romao M, Debray M, Piel M, Chavrier P. Proc. Natl. Acad. Sci. U. S. A. 2011;108:1943–1948. doi: 10.1073/pnas.1010396108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kraning-Rush CM, Carey SP, Califano JP, Smith BN, Reinhart-King CA. Phys. Biol. 2011;8:015009. doi: 10.1088/1478-3975/8/1/015009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sahai E. Nat. Rev. Cancer. 2007;7:737–749. doi: 10.1038/nrc2229. [DOI] [PubMed] [Google Scholar]
- 28.Lämmermann T, Sixt M. Curr. Opin. Cell Biol. 2009;21:636–644. doi: 10.1016/j.ceb.2009.05.003. [DOI] [PubMed] [Google Scholar]
- 29.Wolf K, te Lindert M, Krause M, Alexander S, te Riet J, Willis AL, Hoffman RM, Figdor CG, Weiss SJ, Friedl P. J. Cell Biol. 2013;201:1069–1084. doi: 10.1083/jcb.201210152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jordan MA, Wilson L. Nat. Rev. Cancer. 2004;4:253–265. doi: 10.1038/nrc1317. [DOI] [PubMed] [Google Scholar]
- 31.Takesono A, Heasman SJ, Wojciak-Stothard B, Garg R, Ridley AJ. PLoS One. 2010;5:e8774. doi: 10.1371/journal.pone.0008774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cramer LP. Nat. Cell Biol. 2010;12:628–632. doi: 10.1038/ncb0710-628. [DOI] [PubMed] [Google Scholar]
- 33.van Oudenaarden A, Theriot JA. Nat. Cell Biol. 1999;1:493–499. doi: 10.1038/70281. [DOI] [PubMed] [Google Scholar]
- 34.Bornens M. Nat. Rev. Mol. Cell Biol. 2008;9:874–886. doi: 10.1038/nrm2524. [DOI] [PubMed] [Google Scholar]
- 35.Haessler U, Teo JCM, Foretay D, Renaud P, Swartz MA. Integr. Biol. 2012;4:401–409. doi: 10.1039/c1ib00128k. [DOI] [PubMed] [Google Scholar]
- 36.Tong Z, Balzer EM, Dallas MR, Hung W-C, Stebe KJ, Konstantopoulos K. PLoS One. 2012;7:e29211. doi: 10.1371/journal.pone.0029211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Brown XQ, Ookawa K, Wong JY. Biomaterials. 2005;26:3123–3129. doi: 10.1016/j.biomaterials.2004.08.009. [DOI] [PubMed] [Google Scholar]
- 38.Balzer EM, Tong Z, Paul CD, Hung W-C, Stroka KM, Boggs AE, Martin SS, Konstantopoulos K. FASEB J. 2012;26:4045–4056. doi: 10.1096/fj.12-211441. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.