Combined Spectroscopic/Computational Studies of Vitamin B₁₂ Precursors: Geometric and Electronic Structures of Cobinamides

Abstract

Vitamin B₁₂ (cyanocobalamin) and its biologically active derivatives, methylcobalamin and adenosylcobalamin, are members of the family of corrinoids, which also includes cobinamides. As biological precursors to cobalamins, cobinamides possess the same structural core, consisting of a low-spin Co³⁺ ion that is ligated equatorially by the four nitrogens of a highly substituted tetrapyrrole macrocycle (the corrin ring), but differ with respect to the “lower” axial ligation. Specifically, cobinamides possess a water molecule instead of the nucleotide loop that coordinates axially to Co³⁺cobalamins via its dimethylbenzimidazole (DMB) base. Compared to the cobalamin species, cobinamides have proven much more difficult to study experimentally, thus far eluding characterization by X-ray crystallography. In this study, we have utilized combined quantum mechanics/molecular mechanics (QM/MM) computations to generate complete structural models of a representative set of cobinamide species with varying upper axial ligands. To validate the use of this approach, analogous QM/MM geometry optimizations were carried out on entire models of the cobalamin counterparts, for which high-resolution X-ray structural data are available. The accuracy of the cobinamide structures was assessed further by comparing electronic absorption spectra computed using time-dependent density functional theory to those obtained experimentally. Collectively, the results obtained in this study indicate that the DMB→H₂O lower axial ligand switch primarily affects the energies of the Co 3d_z²-based molecular orbital (MO) and, to a lesser extent, the other Co 3d-based MOs as well as the corrin π-based highest energy MO. Thus, while the energies of the lowest-energy electronic transition of cobalamins change considerably as a function of the upper axial ligand, they are nearly invariant for the cobinamides.

Introduction

A wide variety of computational methods have been used in attempts to model the geometric and electronic properties of the naturally occurring macrocyclic cobalt complexes known as corrinoids. Included in this family are the cobalamin (Cbl, Figure 1A) and cobinamide (Cbi, Figure 1B) species. The large size and complex electronic structures of these systems present significant challenges to traditional computational methods, such as molecular mechanics (MM),^{1, 2} ab initio Hartree-Fock,^{3, 4} and density functional theory (DFT).^{5, 6} While significant efforts have been undertaken to obtain much needed insight into the spectral and electronic properties of these corrinoids, success has thus far been quite limited.^{7, 8}

Figure 1.

Chemical structures of cobalamins (A) and cobinamides (B). A variety of ligands can occupy the upper axial coordination site; e.g., R = CH₃⁻, CN⁻, H₂O, and adenosyl.

Corrinoids are characterized by a common structural element known as the corrin macrocycle, a tetradentate ligand that coordinates the cobalt ion in a square planar fashion through four nitrogen atoms. In the cobalamin subfamily (Figure 1A), the lower axial cobalt coordination site is occupied by a dimethylbenzimidazole (DMB) base that is tethered to one of the corrin acetamide side chains via a nucleotide loop. In cobinamides (Figure 1B), this loop terminates just before the phosphate group, leaving an open coordination site on the cobalt ion that is occupied by a water molecule in aqueous solution. A variety of ligands can coordinate to the Co ion in the upper axial position in both cobalamins and cobinamides, such as CN⁻, H₂O, CH₃⁻, and 5′-deoxyadenosyl (Ado⁻). However, only the methyl- and Ado-bound cobalamins, known as methylcobalamin (MeCbl) and adenosylcobalamin (AdoCbl), are biologically active cofactors. Both cobalamins and cobinamides can undergo one-electron reduction to generate Co²⁺Cbl and Co²⁺Cbi⁺, respectively, via release of the upper axial ligand to form a five-coordinate, low-spin (S = ½) Co²⁺ species.

While the corrinoid cofactors are of significant interest to chemists due to their complex geometric and electronic structures, the vital roles they play in biological systems has also caught the attention of biologists and biochemists. AdoCbl and MeCbl are best known for participating in the catalytic mechanisms of carbon skeleton isomerases⁹ and methyltransferases, respectively, serving as essential cofactors for enzymes such as methylmalonyl-CoA mutase,^{10, 11} glutamate mutase,^12–14 dioldehydratase,^{15, 16} and methionine synthase.^{17, 18} Alternatively, cobinamides are key intermediates in the de novo biosynthetic pathway of biologically active cobalamins in lower organisms, acting as substrates for enzymes such as the Co¹⁺corrinoid:ATP adenosyltransferases.^19–22 In addition, cobinamides are extremely useful for investigating the function of the lower axial ligand in “base-off/His-on” cobalamin-dependent enzymes (e.g., methylmalonyl-CoA mutase^{23, 24}) and can serve as interesting analogues to study enzymes that bind the cobalamin cofactors in the “base-off/His-off” fashion (e.g. the corrinoid iron-sulfur protein in methanogens^25–27).

The spectral and electronic properties of corrinoids are known to depend heavily on the identity of the upper and lower axial ligands.^28–30 A combined spectroscopic and computational study published previously by our laboratory described in detail how changing the upper axial ligand perturbs the electronic structures of cobalamins and why the energy of the lowest-energy (i.e., corrin π→π*-based) electronic transition decreases with increasing electron donating power of this ligand.³⁰ Interestingly, the difference in lower axial cobalt coordination that distinguishes the cobalamins from the cobinamides also affects the spectral signatures to a substantial degree. For example, the lowest-energy electronic absorption (Abs) band of AdoCbi⁺ is blue-shifted by ~3000 cm⁻¹ relative to that of AdoCbl (Figure 2). This shift has been attributed to a stabilization of the corrin π-based donor orbital involved in this transition due to the significantly weaker electron donating ability of an axially bound water molecule as compared to the DMB base.³⁰ However, the limited geometric and electronic structure information currently available for cobinamides has greatly limited our understanding of the spectral differences observed between corresponding pairs of cobalamins and cobinamides.

Figure 2.

Electronic absorption spectra (at 4.5 K) of AdoCbl and AdoCbi⁺. A 3000 cm⁻¹ blue-shift of the lowest energy intense feature is observed upon switching the lower axial ligand from the intramolecular DMB base to a solvent-derived H₂O molecule.

In the case of cobalamins, for which X-ray crystallographic structures do exist, two distinct strategies have typically been used to generate computational models. The first strategy involved using high-level DFT methods to optimize the structures of truncated models, where the acetamide side chains (and often the corrin methyl groups, the DMB base, and the adenosyl moiety, Figure 1A) were significantly simplified (to hydrogen atoms, imidazole, and tetrahydrofuran, respectively) or removed altogether.^{7, 31–39} The second strategy relied on classical molecular mechanics (MM) methods to optimize the structures of complete cobalamin models at a lower level of theory.^40–44 DFT geometry optimizations of truncated models of cobalamin species for which X-ray crystallographic structures do exist have been moderately successful in reproducing key structural parameters of the actual cofactors. Typically, the upper axial ligand–cobalt bond lengths were found to deviate from their experimental values by 0.01 to 0.07 Å and the corrin fold angle⁴⁵ was underestimated by as much as 7 – 8°. Particularly poor agreement was achieved for the lower axial Co–N_ax bond length, with average errors being on the order of 0.12 – 0.15 Å (where the largest errors occur for alkylcobalamins, due to the dominance of the Co–C bonding interaction). These significant errors are thought to be due, at least in part, to the lack of the nucleotide loop, which may influence the positioning of the lower axial base and, consequently, the folding of the macrocycle. Thus, DFT models possessing imidazole as the lower axial base often reproduce the experimental structures more closely than those containing the actual DMB base, yielding shorter Co–N_ax bond lengths and larger corrin fold angles.^{31, 35} However, a relatively recent report by Pratt and coworkers suggested that the acetamide side chains may also play an important role in controlling the fold angle of the flexible corrin macrocycle.⁴⁶ Thus, removal of these side chains in silico may further contribute to the discrepancy between computationally predicted and experimentally observed corrin fold angles.

MM computational studies of several cobalamin species employing a standard MM2 force field or an AMBER force field yielded optimized structures in remarkable agreement with those obtained from X-ray crystallographic studies, predicting axial bond lengths within 0.01 to 0.03 Å and fold angles within 2° of the experimental values.^{7, 41, 47–50} However, while a treatment of entire cobalamin and cobinamide models is possible at this lower level of theory, MM methods are unable to provide any insight into the electronic structures of these species. Thus, despite the valuable information they have provided, MM methods are of limited value for obtaining molecular-level insight into the catalytic mechanisms of B₁₂-dependent enzymes.

Combined quantum mechanics/molecular mechanics (QM/MM) calculations offer a means to combine the strengths of both MM and DFT methods.^{51, 52} By treating the relevant portion of the molecule quantum mechanically, the metal-ligand bonding interactions (which largely control the reactivity of these species) can be treated rigorously at a high level of theory, while the steric and electrostatic contributions of the corrin side chains and full nucleotide loop can be accounted for through molecular mechanics. In this study, we validated the use of QM/MM calculation for generating complete models of corrinoids by first optimizing the structures of a series of crystallographically characterized cobalamins whose upper axial ligands span a wide portion of the spectrochemical series (MeCbl, cyanocobalamin (CNCbl), and aquacobalamin (H₂OCbl⁺)). We then employed this QM/MM methodology to generate models of the corresponding cobinamides (i.e., MeCbi⁺, CNCbi⁺, and H₂OCbi²⁺) for which crystal structures are currently unavailable. The optimized structures of these species were evaluated on the basis of a comparison between the absorption spectra computed for our models using time-dependent DFT (TD-DFT) and those obtained experimentally. Together, these studies provide the first fully-optimized, experimentally-validated geometric and electronic structure descriptions for a representative set of cobinamides.

Experimental Section

Chemicals and Cofactors

MeCbl, CNCbl, and [H₂OCbl]Cl were purchased from Sigma and used as obtained. All species were dissolved in doubly distilled water at pH 7. The H₂OCbl⁺ solution was adjusted to pH 5 using 0.1 M HCl (Sigma) to reduce the fraction of hydroxycobalamin in this sample.²⁹ MeCbi⁺ and H₂OCbi²⁺ were prepared according to published procedures.^21,53,54 Base-off CNCbl (our model of CNCbi⁺ for spectroscopic experiments) was generated by the addition of HCl to adjust the pH to < 0, which causes dissociation of the DMB base via protonation of the coordinated N atom (pK_a ≈ 0.11⁵⁵).

Spectroscopy

Abs spectra at 4.5 K were collected using a Jasco J-715 spectropolarimeter in conjunction with an Oxford Instruments SM-4000 8T magnetocryostat. Room temperature Abs spectra were collected on a Varian Cary 5e spectrophotometer to determine sample concentrations spectrophotometrically by using published molar extinction coefficients (ε₅₂₈ = 7,900 M⁻¹ cm⁻¹ for MeCbl,²⁹ ε₅₅₁ = 8,740 M⁻¹ cm⁻¹ for CNCbl,²⁹ ε₅₂₇ = 8,500 for H₂OCbl⁺,²⁹ ε₄₆₀ = 9,470 M⁻¹ cm⁻¹ for AdoCbi⁺,²³ ε₄₆₃ = 8,740 M⁻¹ cm⁻¹ for MeCbi⁺,⁵⁶ ε₅₂₈ = 8,100 M⁻¹ cm⁻¹ for CNCbi⁺,²⁹ and ε₃₄₈ = 28,000 M⁻¹ cm⁻¹ for H₂OCbi²⁺⁵⁷).

Computational Models

Initial geometries for all cobalamin models were based on the corresponding crystal structure coordinates as deposited in the Cambridge structural database; namely, WIKXOD for MeCbl,⁵⁸ WIKXUJ for CNCbl,⁵⁸ and SUNYEF for H₂OCbl⁺.⁵⁹ Hydrogen atoms were added under the assumption that they occupied standard positions with C–H bond lengths of 1.08 Å. Initial geometries for the cobinamide structures were created by modifying the cobalamin crystal structure coordinates in CS Chem3D (CambridgeSoft) to remove the entire nucleotide loop and the DMB base. The water molecule occupying the lower axial coordination site was placed at an initial Co–O distance equivalent to the original Co–N_ax bond length.

Partitioning of QM/MM System

The cobalamin models were partitioned into QM and MM regions as depicted in Figure 3. Our strategy was to treat a significant portion of the molecule at the QM level while simultaneously allowing for the inclusion of all corrin side chains and the full nucleotide loop using MM. In past DFT studies, the macrocycle truncation scheme typically used involved the replacement of all corrin side chains with H atoms.^31–36 Here, we also included the eight CH₃ substituents of the macrocycle in the QM region, but modeled the seven acetamide side chains using MM whereby the first C atom of each side chain was defined as the link atom (for CNCbl and CNCbi⁺, we also added the CH₂ group attached to C¹³ to the QM region due to a unique interaction between this group and the axial CN⁻ ligand). The entire DMB base was included in the QM region with the C atom that connects the DMB to the ribose serving as the link atom, and the full upper axial ligand was treated with QM. Finally, the phosphate group in the MM region was protonated (as shown in Figure 3) to facilitate convergence of the QM/MM geometry optimizations and to account for the fact that the negative charge of this group will be largely neutralized by hydrogen-bond interactions in aqueous solution and protein active sites. The Cbi models were treated in an analogous manner; that is, the side chain originally containing the DMB base and the nucleotide loop were included in the MM region, while the H₂O molecule occupying the lower axial coordination site was assigned to the QM region.

Figure 3.

Schematic depiction of the QM (gray shaded atoms) and MM (unshaded atoms) regions for MeCbl.

QM/MM Calculations

Geometry optimizations were performed using the “new combined quantum mechanics/molecular mechanics” (NEWQMMM) implementation in the Amsterdam Density Functional (ADF) 2008.01 suite of programs^60–62 on an ACE computer cluster consisting of 10 Intel Xeon dual processors. For the DFT portion of the calculations, the ADF TZP basis set (a core double-ζ, valence triple-ζ polarized basis set) was employed with an integration constant of 5.0, along with the Vosko-Wilk-Nusair local density approximation (VWN-LDA)⁶³ and the Perdew-Burke-Ernzerof (PBE) generalized gradient approximation (GGA) for exchange and correlation.^{64, 65} The core orbitals for atoms treated with DFT were frozen through 1s for C, N, and O and through 2p for Co. All models were optimized using the spin-restricted formalism. The MM atoms were parameterized using the standard Amber95 force field⁶⁶ during the MM optimization procedure. The conjugate gradient (CONJGRAD) optimization method was used in all calculations for minimizing the MM energies, which were considered final after 5000 cycles if convergence was not reached at that stage.⁶⁷ Link bonds that cross the boundary between the QM and MM regions (Figure 3) were treated using the capping atoms approach employing the integrated molecular orbital and molecular mechanics (IMOMM) method developed by Maseras and Morokuma.^{68, 69} Simple electrostatic coupling (model 4) was used to model the electrostatic interaction between the QM and MM regions. In this scheme, the point charges of the QM region are updated throughout the geometry optimization using the multipole derived charge (MDC) analysis on the MDC-d charge level. An initial single-point DFT calculation was completed using ADF on each of the X-ray crystal structure-based input geometries to determine atomic charges for the QM/MM input files for all models, though the self-consistent field (SCF) procedure failed to converge for H₂OCbl⁺, H₂OCbi⁺, and CNCbi⁺. The SCF convergence criterion for the QM/MM calculations was set at 1 × 10⁻⁶ hartree and geometries were considered converged when the energy difference between subsequent cycles fell below 1 × 10⁻⁴ hartree and the gradient was less than 0.001 hartree/Å. Atomic coordinates for all optimized models presented in the text are included in the Supporting Information (Tables S1–S6).

Single-Point DFT and TD-DFT Calculations

Single-point DFT and TD-DFT calculations were carried out using the ORCA 2.6.35 software package (Frank Neese, Universität Bonn, Germany)⁷⁰ on suitably truncated models derived from the QM/MM geometry optimized complete cofactor structures. The truncated models included the corrin ring, upper and lower axial ligands (with the DMB replaced by an imidazole for the Cbls), and H atoms instead of the corrin side chains. All single-point calculations were performed spin-restricted using Becke’s three parameter hybrid functional for exchange^{71, 72} and the Lee-Yang-Parr correlation functional (B3LYP/G).⁷³ The VDZ/P (Ahlrichs split valence set with one set of first polarization functions on all atoms) basis set⁷⁴ and the SV/C auxiliary basis were used for all atoms except Co and each atom directly bound to it, which were instead treated with the larger triple-ζ valence plus polarization (TZVP) basis.⁷⁵ An integration grid size of 2 was employed (Lebedev 110 points) and the SCF was considered converged when the change in energy between subsequent cycles fell below 1×10⁻⁶ hartrees. Isosurface plots of molecular orbitals were generated with the gOpenMol program developed by Laaksonen^{76, 77} using an isodensity value of 0.03 au.

Vertical excitation energies and transition dipole moments were calculated by the TD-DFT method^78–80 within the Tamm-Dancoff approximation^{81, 82} by using the same models, basis sets, and functionals as described above for the single-point DFT calculations. To increase computational efficiency, the resolution of the identity approximation^{83, 84} was used in evaluating the Coulomb term. For each model the 60 lowest-energy excited states were calculated by considering all one-electron excitations in an energy window of ±3 hartrees. Transition energies and oscillator strengths from the TD-DFT calculations were used to simulate Abs spectra for a direct comparison with the experimental results. Each electronic transition was assumed to give rise to a Gaussian-shaped band with a full width at half maximum of ν_1/2 = 1700 cm⁻¹, in which case the oscillator strength f is related to the molar extinction coefficient ε_max by f = 4.61×10⁻⁹ ε_maxν_1/2. All simulated spectra were uniformly red-shifted by 5000 cm⁻¹ to compensate for the fact that the TD-DFT method tends to overestimate the transition energies for corrinoids.^{30, 85–87}

Results and Analysis

Cobalamin Geometries

A representative set of complete cobalamin models (MeCbl, CNCbl, and H₂OCbl⁺) were subjected to full geometry optimizations using the combined QM/MM method as described in the Experimental section. While these three Co³⁺Cbl species vary only with respect to the identity of their upper axial ligand, they exhibit distinct differences in their overall geometries, particularly with regards to their axial bond lengths and corrin fold angles.⁸⁸ Thus, these molecules provide an excellent testing ground for assessing the ability of the combined QM/MM approach to accurately model the geometric structures of different corrinoids.

In general, the QM/MM optimized cobalamin structures agree well with those determined crystallographically, accurately reproducing the overall shapes and conformations. To demonstrate this qualitative agreement, the initial (crystal-structure derived) and final (geometry-optimized) models of MeCbl are overlaid in Figure 4 (additional overlay plots for the remaining cobalamins can be found in the Supporting Information, Figures S1–S2). This comparison reveals that the corrin ring and the axial ligands in the optimized structure align particularly well with their crystallographically derived positions. The orientation of the acetamide side chains is also similar in the two structures, displaying only small deviations even far away from the corrin macrocycle. The most noticeable change that occurred during the QM/MM geometry optimization involves a repositioning of a portion of the nucleotide loop that connects the lower axial DMB to the acetamide side chain connected to the corrin ring at C¹⁷. However, this finding is not surprising, given the flexibility of this loop and the fact that crystal-packing effects were not accounted for in our calculations.⁸⁹ Importantly, these geometric differences are not expected to influence the electronic structures, in particular the corrin- and cobalt-based frontier molecular orbitals (MOs), of the Co³⁺Cbl species to any significant degree.³⁰

Figure 4.

Comparison of the X-ray crystallographic (gray) and QM/MM optimized (yellow) structures of MeCbl.

Historically, the corrin fold angle and axial ligand bond lengths have been difficult to reproduce accurately via computational methods and yet they are likely to play an important role with respect to the electronic structures of these species. The comparison between the experimental and computed values for the corrin fold angle and all Co–ligand bond lengths provided in Table 1 demonstrates that the agreement between the experimental and QM/MM optimization cobalamin structures is generally quite good. While the equatorial Co–N_eq bonds are slightly overestimated computationally, by up to 0.03 Å, these error values are consistent with those reported previously in the literature for pure DFT calculations of truncated corrinoid models.^{31, 32, 34–36} The distance between the cobalt ion and the upper axial ligand (R) is accurately reproduced for MeCbl and only slightly underestimated for CNCbl (Δ_QM/MM-Xtal = −0.03 Å). In the case of H₂OCbl⁺, however, the upper axial Co–O bond is significantly overestimated by our calculations, with Δ_QM/MM-Xtal = 0.17 Å. Since the lower axial Co–N_ax bond length has also been difficult to reproduce accurately using DFT methods⁹⁰, it is not surprising that the combined QM/MM method used here overestimates the Co–N_ax bond lengths by 0.01 – 0.11 Å.

Table 1.

Key geometric parameters for the X-ray crystallographic and QM/MM optimized structures of the cobalamins investigated, where R represents the upper axial ligand

Structure	Fold Angle (θ)	Co–R (Å)	Co–Nax (Å)	Co–N21 (Å)	Co–N22 (Å)	Co–-N23 (Å)	Co–N24 (Å)
MeCbl Xtal58	14.8	1.98	2.16	1.88	1.92	1.92	1.87
MeCbl QM/MM	12.0	1.98	2.27	1.88	1.92	1.91	1.90
ΔQM/MM-Xtal	−2.8	0.00	0.11	0.00	0.00	−0.01	0.03
CNCbl Xtal58	18.6	1.89	2.04	1.88	1.91	1.92	1.88
CNCbl QM/MM	16.7	1.86	2.14	1.89	1.93	1.94	1.90
ΔQM/MM-Xtal	−2.1	−0.03	0.10	0.01	0.02	0.02	0.02
H2OCbl Xtal59	18.7	1.95	1.93	1.88	1.90	1.90	1.88
H2OCbl QM/MM	6.8	2.12	1.94	1.89	1.94	1.93	1.90
ΔQM/MM-Xtal	−11.9	0.17	0.01	0.01	0.04	0.03	0.02

Pure DFT-based geometry optimizations of truncated cobalamin models are well-known for their inability to accurately reproduce the experimental corrin fold angle, yielding structures with artificially flat macrocycle conformations. In contrast, our QM/MM calculations are considerably more successful in modeling the corrin fold angles, especially for MeCbl and CNCbl. The larger error values in the upper axial bond length and the fold angle of H₂OCbl⁺, as compared to the other two Co³⁺Cbls studied here, are likely due to, at least in part, to the fact that our calculations did not account for the effects of counterions, intermolecular hydrogen-bonding, and/or crystal packing (also note that in the solid-state structure, 25 solvent water molecules are present for each H₂OCbl⁺ ion). Additionally, in the crystal structure the axially bound water molecule engages in a relatively strong intramolecular hydrogen-bond interaction with the carbonyl oxygen of one of the acetamide side chains. This interaction likely contributes to the distortion of the corrin ring and, more importantly, should lead to a shorter-than-expected axial Co–O(H₂) bond by imposing a small degree of hydroxide character on the water ligand. No such hydrogen-bond interaction is present in our QM/MM optimized model of H₂OCbl⁺. Even with these minor shortcomings, all of the QM/MM optimized Co³⁺Cbl models possess bond lengths in reasonable agreement with those determined crystallographically, and in almost all cases, our values agree more closely with the experimental data than do those obtained in previous DFT calculations on truncated Co³⁺Cbl models.

Cobinamide Geometries

Prompted by the success of the QM/MM calculations in reproducing the geometric structures of a representative set of Co³⁺Cbl species reasonably well, the same computational scheme was applied to the analogous set of Co³⁺Cbi complexes. Initial cobinamide models were generated by in silico modification of the crystallographically-derived structures of their cobalamin counterparts, replacing the axial DMB with a water molecule and the nucleotide loop with an H atom (see the Experimental section for details). As crystal structures are currently unavailable for any cobinamide, our QM/MM optimized models were evaluated on the basis of a structural comparison to the analogous Co³⁺Cbl species and by comparing their computed Abs spectra to those obtained experimentally.

An overlay plot of the QM/MM optimized models of MeCbl and MeCbi⁺ is shown in Figure 5 (overlay plots for the other cobalamin/cobinamide pairs are provided in the Supporting Information, Figures S6 and S7). All of the major structural features of MeCbi⁺, including the corrin ring, the upper axial CH₃⁻ moiety, and a majority of the corrin ring substituents are nearly superimposable on those of MeCbl. Only the acetamide side chains connected to the corrin macrocycle at C² and C¹³ show any significant deviation from their positions in MeCbl, having shifted toward the cavity that used to be occupied by the nucleotide loop. Additionally, the water molecule in the lower axial position moved away from, and slightly shifted to the side of, the central Co ion relative to the position originally occupied by the coordinating N atom of the DMB ligand. Similar structural differences are observed for all of the other pairs of optimized cobinamide and cobalamin models investigated (Figures S6 and S7).

Figure 5.

Comparison of the QM/MM optimized structures of MeCbl (gray) and MeCbi⁺ (yellow).

Key structural parameters of the optimized cobinamide molecules, along with the differences in these parameters between the Co³⁺Cbi and corresponding Co³⁺Cbl structures (Δ_Cbi−Cbl), are provided in Table 2. These data reveal that replacing the DMB base and nucleotide loop with a H₂O molecule has insignificant consequences for the equatorial (Co–N_eq) bond lengths, causing an average shortening by 0.01 Å, but noticeably alters the axial bond lengths. Specifically, in the MeCbi⁺ structure, the Co–C bond is 0.01 Å shorter than in MeCbl, while in CNCbi⁺ and H₂OCbi²⁺, the upper axial ligand approaches the Co center by 0.03 and 0.13 Å, respectively, in response to the DMB→H₂O lower axial ligand switch. However, the greatest geometric differences between corresponding pairs of cobalamin and cobinamide species are in the lower axial bond lengths (see Table 2). This bond is essentially broken in MeCbi⁺ (Δ_Cbi−Cbl = 0.61 Å) and considerably elongated (by ~0.05–0.16 Å) even when the upper axial ligand is a weak to moderately strong σ-donor.

Table 2.

Key geometric parameters for the QM/MM optimized cobinamide structures, where R represents the upper axial ligand. The structural differences for each pair of optimized cobinamide/cobalamin models are expressed in terms of the Δ_Cbi−Cbl values

Structure	Fold Angle (θ)	Co–R (Å)	Co–Oax (Å)	Co–N21 (Å)	Co–N22 (Å)	Co–-N23 (Å)	Co–N24 (Å)
MeCbi+	11.5	1.97	2.88	1.87	1.90	1.90	1.87
ΔCbi−Cbl	−0.5	−0.01	0.61a	−0.01	−0.02	−0.01	−0.03
CNCbi+	17.6	1.83	2.30	1.89	1.92	1.93	1.89
ΔCbi−Cbl	0.09	−0.03	0.16a	0.00	−0.01	−0.01	−0.01
H2OCbi2+	10.3	1.99	1.99	1.90	1.93	1.93	1.90
ΔCbi−Cbl	3.5	−0.13	0.05a	0.01	−0.01	0.00	0.00

^aDifference between Co–O_axand Co–N_ax bond lengths

In optimizing the Co³⁺Cbi structures, the QM/MM calculations did not drastically alter the folding of the corrin macrocycle despite the significant differences in size, basicity, and electron donating properties of the H₂O and DMB lower axial ligands. This finding suggests that the steric and electronic properties of the lower axial ligand may, in fact, have relatively little influence on the fold angle of the corrin macrocycle. Hence, the severe flattening of the corrin macrocycle that typically occurs during pure DFT geometry optimizations may be due, at least in part, to the lack of the acetamide side chains in truncated Co³⁺corrinoid models, as proposed previously.⁴⁶ Consequently, the QM/MM optimized geometries likely provide more accurate representations of the actual Co³⁺Cbi structures than those obtained via pure DFT methods.

TD-DFT Calculations

While comparisons to crystallographically-derived structures provide an easy and indispensable check of the geometries of the QM/MM optimized corrinoid models, a secondary, electronic-structure oriented validation of these models can be achieved by comparing the TD-DFT computed Abs spectra to the experimental spectra. This methodology is particularly useful in the case of the cobinamide species, for which the current lack of crystal structures prevents a direct evaluation of the QM/MM optimized geometries. Because the spectral and electronic properties of Co³⁺corrinoids are dominated by the corrin- and cobalt-based frontier MOs, only the QM cores of the optimized model systems were employed in the TD-DFT calculations, and the DMB ligand of the Co³⁺Cbl species was replaced by an imidazole. The TD-DFT results were then used to simulate Abs spectra, where a uniform red-shift of 5000 cm⁻¹ was applied to compensate for the fact that TD-DFT tends to overestimate transition energies,^64,71 especially when computations are carried out with the B3LYP hybrid functional.^{30, 85–87} With this relatively minor adjustment, excellent agreement between the calculated and experimental Abs spectra was achieved, suggesting that the specific QM/MM approach employed in this study is well suited to reproduce not only the geometric structures (vide supra), but also the electronic properties of Co³⁺corrinoids.

Co³⁺Cobalamins

Figure 6 compares the experimental and TD-DFT computed Abs spectra for the three Co³⁺Cbls included in this study. Overall, the TD-DFT results agree well with our experimental data. In particular, the calculations properly predict a uniform blue-shift of the intense low-energy feature, commonly called the α band (corresponding to band i in the computed spectrum; note that the appearance of several equally spaced bands in this region of the experimental Abs spectrum is due to a vibrational progression associated with a single electronic transition³⁰), as the σ-donor strength of the upper axial ligand decreases from CH₃⁻ to CN⁻ and H₂O. A similar trend is predicted, and experimentally observed, for the dominant feature near 28,000 cm⁻¹ (the γ region). The calculations also successfully reproduce the relative intensities of the α and γ bands in each of the experimental Abs spectra and the striking change in the γ region from a single intense feature with a high-energy shoulder in the H₂OCbl⁺ and CNCbl Abs spectra to a cluster of closely spaced, less-intense bands in the MeCbl spectrum. In addition, the calculated polarizations of the dominant electronic transitions in the α and γ regions (along the C⁵⋯C¹⁵ and C_o⋯C¹⁰ vectors, respectively) are consistent with the results obtained in resonance Raman studies performed previously.³⁰

Figure 6.

Experimental (4.5 K) and TD-DFT calculated Abs spectra for MeCbl (A), CNCbl (B), and H₂OCbl⁺ (C). The simulated spectra were red-shifted by 5000 cm⁻¹ to facilitate a direct comparison with the experimental data. The bands in the calculated spectra that have direct counterparts in the experimental spectra are numbered i–v. The α, β, and γ regions are indicated for the experimental H₂OCbl⁺ Abs spectrum. Detailed TD-DFT computed transition descriptions are provided in the Supporting Information, Tables S7–S9.

Co³⁺Cobinamides

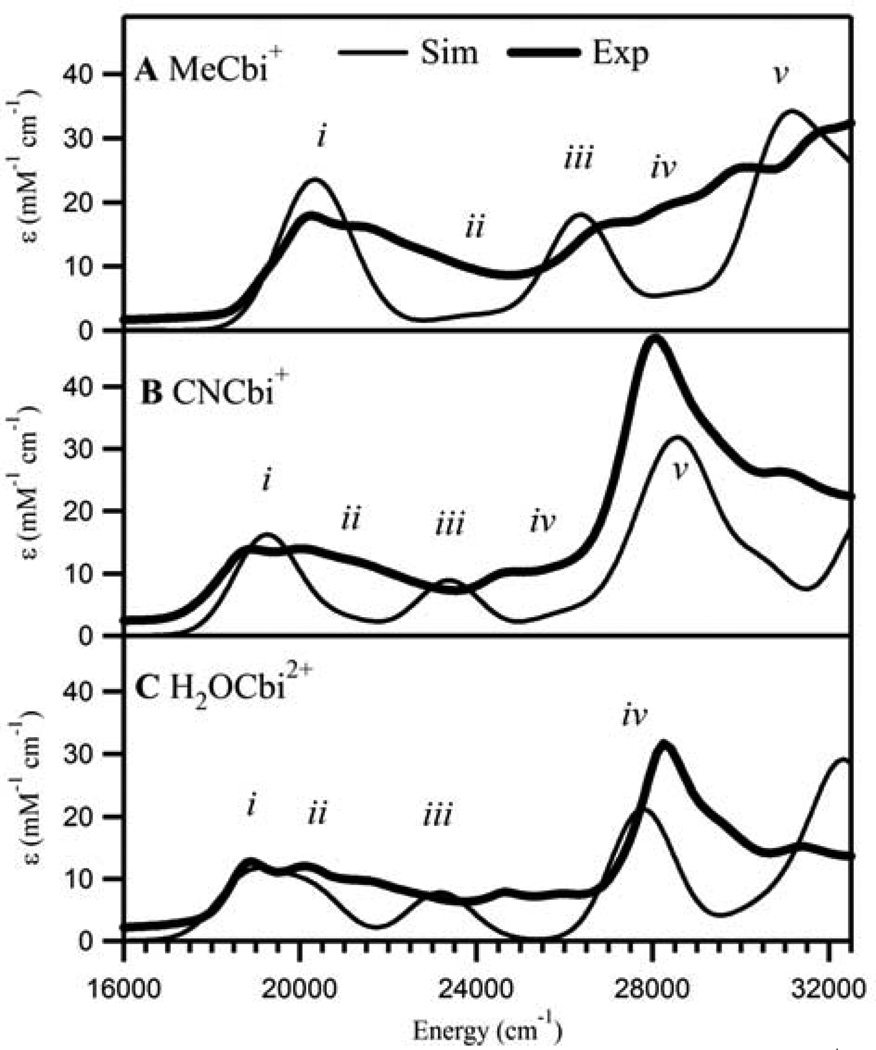
As for the Co³⁺Cbl species, the TD-DFT computed Abs spectra for MeCbi⁺, CNCbi⁺, and H₂OCbi²⁺ also reproduce the key features of the experimental Abs spectra quite well (Figure 7). For MeCbi⁺, the intense low-energy feature centered at 20,300 cm⁻¹ in the simulated spectrum corresponds to the prominent band near 20,250 cm⁻¹ in the experimental spectrum. Thus, our computations correctly predict a significant blue-shift (~3000 cm⁻¹ computationally vs ~2000 cm⁻¹ experimentally) of this low energy transition upon changing the lower axial ligand from the DMB base in MeCbl to a H₂O molecule in MeCbi⁺. Similarly, the TD-DFT predicted shifts of the corresponding transition from CNCbl to CNCbi⁺ (~1500 cm⁻¹) and from H₂OCbl⁺ to H₂OCbi²⁺ (~−200 cm⁻¹) agree reasonably well with those observed experimentally, (~850 and 70 cm⁻¹, respectively). The calculations also correctly reproduce the presence of a very intense feature at ~28,000 cm⁻¹ in the experimental CNCbi⁺ and H₂OCbi²⁺ Abs spectra,⁹¹ as well as the absence of this feature in the Abs spectrum of MeCbi⁺, where this region instead contains multiple less intense bands similar to the γ region of the MeCbl spectrum.

Figure 7.

Experimental (4.5 K) and TD-DFT calculated Abs spectra for MeCbi⁺ (A), CNCbi⁺ (B), and H₂OCbi²⁺ (C). The simulated spectra were red-shifted by 5000 cm⁻¹ to facilitate a direct comparison with the experimental data. The bands in the calculated spectra that have direct counterparts in the experimental spectra are numbered i–v. Detailed TD-DFT calculated transition descriptions are provided in the Supporting Information, Tables S10–S12.

Notably, the TD-DFT computed Abs spectra obtained in this work replicate the experimental spectra significantly better than did those calculated previously for non-optimized, truncated cobinamide models that were derived directly from the corresponding cobalamin structures.³⁰ This finding indicates that our QM/MM optimized models, for which the corrin fold angles are slightly different and the lower axial H₂O ligand is located farther away from the Co ion, provide a better representation of the cobinamide structures.

Electronic Structure Descriptions and Spectral Assignments

The good agreement between the experimental and TD-DFT computed Abs spectra of the Co³⁺corrinoids investigated not only validates the QM/MM optimized structures, but also warrants the use of the DFT calculated molecular orbital (MO) descriptions as the basis for identifying the electronic transitions associated with the key Abs features. These MO descriptions additionally provide an excellent framework for correlating differences in the axial bonding interactions between Co³⁺Cbl and Co³⁺Cbi species with differences in their spectral and electronic properties.

Co³⁺Cobalamins

Relevant portions of the DFT computed MO diagrams for MeCbl, CNCbl, and H₂OCbl⁺ are shown in Figure 8 (a summary of the TD-DFT results and isosurface plots of key MOs for these species are presented in Tables S7–S9 and Figures S8–S10). To facilitate a direct comparison between the different species, the MO diagrams were shifted vertically to match the energies of the lowest-energy corrin π*-based unoccupied MO. Moreover, for each species the one-electron excitations serving as the principal contributors to the electronic transitions responsible for the dominant features in the Abs spectrum are indicated by arrows. Not surprisingly, the general appearance of the MO diagrams and transition assignments for these Co³⁺Cbls are very similar to those obtained previously from DFT and TD-DFT computations for crystal structure-derived truncated cofactor models.³⁰

Figure 8.

Relevant portions of the calculated MO diagrams for MeCbl, CNCbl and H₂OCbl⁺. The individual MO diagrams were shifted vertically to match the energies of the corrin π*-based LUMO (LUMO+1 in the case of H₂OCbl⁺). Note that the HOMO/LUMO gap is not drawn to scale. The MOs are labeled according to their principal contributors, and the relevant electronic transitions contributing to the dominant bands in the TD-DFT calculated Abs spectra (Figure 6) are indicated by arrows (see Tables S7–S9 and Figures S8–S10 for additional information). Circles indicate additional donor orbitals.

(a) MeCbl

In MeCbl, all of the MOs possessing substantial Co 3d-orbital character are considerably higher in energy (relative to the LUMO) than their counterparts in CNCbl and H₂OCbl⁺ (Figure 8). This prediction is consistent with the results obtained in our previous electronic structure studies of Co³⁺Cbls, which suggested that an increase in the σ-donating ability of the upper axial ligand leads to a decrease in the effective nuclear charge of the Co center, thereby causing an overall destabilization of the Co 3d orbitals and, to a lesser extent, the corrin π-based frontier MOs.³⁰ Moreover, because the strongly σ-donating alkyl ligand in MeCbl transfers a moderate amount of electron density into the formally unoccupied Co 3d_z² orbital, the corresponding HOMO exhibits a weak σ-antibonding interaction between the Co 3d_z² orbital and the N_DMB 2p-based “lone pair” of the lower axial base, which destabilizes this corrin π-based MO to a substantial degree.³⁰

The lowest energy transition in the TD-DFT computed Abs spectrum of MeCbl (band i in Figure 6A, which corresponds to the α band in the experimental spectrum) involves a one-electron excitation from the HOMO to the LUMO. This transition formally corresponds to a corrin-based π→π* transition that, nonetheless, should cause a weakening of the Co–C bond as the HOMO is weakly σ-bonding with respect to this bond, whereas the LUMO has no orbital contributions from the upper axial ligand. Indeed, resonance Raman spectra of MeCbl obtained with laser excitation into the α-band region show a substantial enhancement of the Co–C stretching mode.^{92, 93} The dominant contributor to band ii is the HOMO-1 to LUMO+4 transition and contains considerable Co 3d_yz→ Co 3d_xy character. Band iii involves electronic excitation from the HOMO-2 (the Co 3d_xz-based MO) to the LUMO and thus contains substantial metal-to-ligand charge transfer character. Alternatively, band iv is due to a corrin-based π→π* transition, with the principal contributor being the HOMO→ LUMO+1 excitation. Band v, finally, arises from a transition involving multiple one-electron excitations from the HOMO to corrin π*-based MOs and the σ-antibonding Co 3d_z²/C 2p_z-derived MO.

(b) CNCbl

The biggest difference between the electronic structures of CNCbl and MeCbl (Figure 8) is an overall stabilization (relative to the LUMO) of the filled MOs in the former due to the reduction in the σ-donor strength of the upper axial ligand. In particular, the Co 3d_z²-based MO is predicted to be stabilized by ~0.5 eV relative to that of MeCbl, consistent with the 400 mV decrease in the reduction potential from MeCbl to CNCbl.²⁹ Notably, the weaker σ-bonding interaction between the Co ion and the CN⁻ moiety also induces a weaker Co−N_ax σ-antibonding interaction in the HOMO, which partially accounts to the shorter Co−N_ax bond distance in CNCbl than in MeCbl (Table 1).

The major features in both the experimental and the TD-DFT computed CNCbl Abs spectra are shifted to higher energy relative to their counterparts in the MeCbl Abs spectrum (cf Figures 6A and 6B). Band i in the calculated CNCbl spectrum primarily arises from the same transition as band i in the MeCbl spectrum, but due to small contributions from additional one-electron excitations in the case of CNCbl, this transition now occurs at slightly higher energy. Band ii arises from another corrin-based π→π* transition, while the dominant contributors to band iii are the HOMO→LUMO+2 and HOMO→LUMO+3 excitations (formally corrin π→Co 3d_z² and corrin π→Co 3d_xy charge transfer transitions, respectively). The corrin π→Co 3d_z² transition is therefore predicted to occur at significantly lower energy in CNCbl than in MeCbl (where it contributes mostly to band v), which again reflects the large stabilization of the Co 3d_z²-based MO from MeCbl to CNCbl. The most significant contributors to band iv, which accounts for the dominant feature in the γ region of the experimental CNCbl Abs spectrum, are corrin-based π→π* excitations that terminate in the LUMO.

(c) H₂OCbl⁺

The weak interaction between the H₂O ligand and the Co center in H₂OCbl⁺ causes the Co 3d orbitals to drop significantly in energy relative to the frontier orbitals of the corrin macrocycle (Figure 8). This energetic stabilization suppresses the mixing between the filled Co 3d orbitals and the corrin π-based frontier MOs, which is particularly obvious from the MO plots for H₂OCbl⁺ (Figure S10). Additionally, the Co 3d_z²-based MO is predicted to be stabilized by 1.67 eV over that of MeCbl, correlating well with the 1.5 V lowering of the reduction potential from MeCbl to H₂OCbl⁺.²⁹

Unique to the Abs spectrum of H₂OCbl⁺ (Figure 6C) is the presence of a very weak feature at lower energy than the prominent α band (band i). This feature (band 0), which is centered around 14,500 cm⁻¹, arises from an electronic excitation between the corrin π-based HOMO and the Co 3d_z²-based LUMO. The distinctly different compositions of these two MOs account for the negligible intensity of this band in both the experimental³⁰ and the computed Abs spectra. Bands i and iv arise from the same corrin-based π→π* transitions as those responsible for bands i and iv in the Abs spectrum of MeCbl. Alternatively, bands ii and iii in the H₂OCbl⁺ Abs spectrum arise from electronic excitations from the corrin π-based HOMO-1 to the lowest-energy corrin π*-based MO (LUMO+1) and to the Co 3d_z²-based LUMO, respectively. As for CNCbl, only a single intense feature is observed in the γ region of the H₂OCbl⁺ Abs spectrum, since the stabilization of the Co 3d orbitals results in a smaller number of available corrin π- and Co 3d-based donor MOs for electronic transitions in this spectral range.

Co³⁺Cobinamides

Figure 9 provides a comparison of the relevant portions of the DFT-computed MO diagrams for MeCbi⁺, CNCbi⁺, and H₂OCbi²⁺ (tables summarizing the TD-DFT results and isosurface plots of key MOs for these species are presented in Tables S10–S12 and Figures S8–S10). As for the Co³⁺Cbls, all MO energy levels were shifted vertically to align the energies of the corrin π*-based LUMO (LUMO+1 in the case of H₂OCbi²⁺), and the principal contributors to the dominant electronic transitions are indicated by arrows.

Figure 9.

Relevant portions of the calculated MO diagrams for MeCbi⁺, CNCbi⁺, and H₂OCbi²⁺. The individual MO diagrams were shifted vertically to match the energies of the corrin π*-based LUMO (LUMO+1 in the case of H₂OCbi²⁺). Note that the HOMO/LUMO gap is not drawn to scale. The MOs are labeled according to their principal contributors, and the electronic transitions associated with to the dominant bands in the TD-DFT calculated Abs spectra (Figure 7) are indicated by arrows (see Tables S10–S12 and Figures S8–S10 for additional information). Circles indicate additional donor orbitals.

(a) MeCbi⁺

The MO plots in Figure 9 reveal that most of the Co 3d-based MOs are significantly higher in energy (relative to the LUMO) in MeCbi⁺ than in CNCbi⁺ and H₂OCbi²⁺. This destabilization of the Co 3d-based MOs of MeCbi⁺ again reflects the large σ-donor strength of the methyl ligand and the consequent decrease in the effective nuclear charge of the cobalt center. A critical difference between the frontier MOs of MeCbl and MeCbi⁺ is that the lower axial H₂O ligand in the latter is a much weaker σ-donor than the DMB of the former, with the O 2p-based lone pairs being too low in energy to interact appreciably with the Co 3d_z² orbital. The differences in axial bonding interactions between MeCbl and MeCbi⁺ can be quantified by examining the calculated Co–C and Co–N/O bond orders from a Mayer population analysis (Table 3).^94–96 Interestingly, the Co–C bond order remains almost unchanged (reduction by 0.03) upon substitution of the DMB ligand by a H₂O molecule, even though the lower axial bonding interaction changes dramatically (reduction in bond order by > 0.2).

Table 3.

Calculated bond orders based on a Mayer population analysis^85–87

	Cobalamins		Cobinamides
R	Co–R	Co–Nax	Co–R	Co–Oax
Me	1.11	0.31	1.08	< 0.10
CN	0.96	0.41	0.98	0.21
H2O	0.40	0.74	0.56	0.53

The Abs spectrum of MeCbi⁺ (Figure 7) is comprised of 5 main features between 16,000 and 32,000 cm⁻¹. The fairly intense band i arises from an electronic excitation between the corrin π-based HOMO and the corrin π*-based LUMO and is analogous to band i in the MeCbl Abs spectrum (Figure 6). The weaker band ii is associated primarily with transitions involving electronic excitations from the HOMO-3 and HOMO-4 (Co 3d_x²–y²/3d_yz-based MOs) to the LUMO, and additionally with a transition from the HOMO-2 (the Co 3d_xz-based MO) to the LUMO+4 (the Co 3d_xy-based MO), similar to band ii in the computed MeCbl Abs spectrum. Establishing specific assignments for bands iii through v is complicated by the fact that each transition has contributions from multiple one-electron excitations. In general, these excitations are from filled corrin π- and Co 3d-based MOs to empty corrin π*-based MOs and the corrin π*/Co 3d_z²/C 2p_z-derived MO.

(b) CNCbi⁺

With the exception of the HOMO, all of the MOs of CNCbi⁺ are stabilized in energy (relative the LUMO) from their counterparts in MeCbi⁺ (Figure 9). Most notably, the relative energies of the Co 3d-based MOs drop by 0.2 – 0.6 eV from MeCbi⁺ to CNCbi⁺, similar to trend observed from MeCbl to CNCbl (Figure 8). Despite these large changes in electronic structure from MeCbi⁺ to CNCbi⁺, Mayer population analyses indicate only a slight weakening of the Co–C bond in CNCbi⁺ versus MeCbi⁺ (Co−C bond orders of 0.96 and 1.08, respectively; see Table 3). Note, however, that the Co–C bonding interaction is purely σ-type in MeCbi⁺, but may also contain some π-bonding contributions in CNCbi⁺. The decrease in the Co–C bond order correlates with a strengthening, and thus a shortening, of the lower axial Co–OH₂ bond from MeCbi⁺ to CNCbi⁺, typical of a normal trans influence.

The lower energy portion (below 25,000 cm⁻¹) of the TD-DFT computed Abs spectrum of CNCbi⁺ is qualitatively similar to that of MeCbi⁺ (Figure 7). In contrast, the higher energy region is strikingly different, containing one intense band with a high energy shoulder as opposed to several moderately intense features. Band i is assigned as the HOMO to LUMO (corrin-based π→π*) transition, as for MeCbi⁺ and CNCbl. Band ii is due to a transition that primarily involves the HOMO (corrin π-based MO) to LUMO+1 (corrin π*/Co 3d_z²/CN-based MO) excitation, though it also has a significant contribution from the HOMO-1 (corrin π/Co 3d_yz-based MO) to LUMO excitation. This assignment is more similar to that for CNCbl than for MeCbi⁺, because the Co 3d-based MOs donor orbitals for the transitions associated with band ii in the computed MeCbi⁺ Abs spectrum are significantly stabilized in CNCbi⁺, where instead they serve as the donor orbitals for the transitions associated with band iv (Figure 7). Band iii in the computed CNCbi⁺ Abs spectrum is associated with a transition primarily involving HOMO-1→LUMO excitation (formally a corrin-based π→π* transition). Finally, the dominant Abs feature (band v) has significant contributions from corrin-based π→π* transitions (HOMO and HOMO-1→LUMO+2 excitations).

(c) H₂OCbi²⁺

The MO diagram for H₂OCbi²⁺ is quite different from those of the other two cobinamides described above (Figure 9). The presence of two weak σ-donors in the axial positions of the Co ion in H₂OCbi²⁺ leads to a large stabilization of the Co 3d orbitals and, thus, to minimal mixing between these orbitals and the corrin π-based MOs, which is particularly evident from the extremely “pure” Co 3d- and corrin π-based MOs calculated for this species (Figure S10). Consistent with a normal trans influence, replacement of the strongly σ-donating methyl group by a weakly donating H₂O ligand in the upper axial position causes a significant strengthening, and thus shortening, of the lower axial bond from MeCbi⁺ to H₂OCbi⁺ (computed Co-O_ax bond orders of < 0.10 and 0.53, respectively; see Table 3).

The TD-DFT computed Abs spectrum for H₂OCbi²⁺ is similar in general appearance to that obtained for CNCbi⁺, having three prominent features in the energy range shown in Figure 7. However, due to the large stabilization of the Co 3d-based MOs relative to the corrin π/π*-based MOs in H₂OCbi²⁺, an additional very weak feature at 14000 cm⁻¹ (band 0) is predicted for this species. This feature arises from the HOMO to LUMO transition of H₂OCbi²⁺, but in this species the Co 3d_z²-based MO is lower in energy than the lowest-energy corrin π*-based MO and thus serves as the LUMO. Consequently, it is band i in the computed Abs spectrum of H₂OCbi²⁺, at ~19,000 cm⁻¹, that arises from the corrin-based π→π* transition responsible for band i in the Abs spectra of the other Co³⁺Cbi species. Band ii is associated with a transition that has a large contribution from the HOMO to LUMO+2 (Co 3d_xy-based MO) excitation and a smaller contribution from the HOMO to LUMO+1 (corrin π→π*) excitation, similar to band ii in the computed CNCbi⁺ Abs spectrum. Finally, the transitions responsible for bands iii and iv in the H₂OCbi²⁺ Abs spectrum are similar in nature to those associated with bands iii and v in the CNCbi⁺ Abs spectrum, both involving excitations between corrin π- and π*-based MOs containing very little Co 3d orbital contributions as a direct result of the low σ-donor strength of the H₂O ligands that occupy the axial coordination sites of the cobalt ion.

Discussion

Major advances in computational chemistry occurring over the last decade, including improvements to both the theoretical framework and computing power, have allowed researchers to tackle progressively larger and more complicated systems. Members of the corrinoid family are structurally and electronically complex molecules whose properties and reactivities have attracted the attention of chemists and biochemists alike, making them ideal targets for testing the limits of currently available computational methods. While the large size of these species continues to represent a major challenge for full treatment using density functional theory (DFT), the desire to obtain both geometric and electronic structure descriptions by using computational chemistry limits the relevance of pure molecular mechanics (MM) methods. A hybrid of these two methods is the foundation of the combined quantum mechanics/molecular mechanics (QM/MM) approach employed in this study.

The application of QM/MM methods to corrinoids is not novel, with several reports having appeared in the literature over the last decade.^{7, 39, 89, 97–110} Interestingly, however, the ability of QM/MM computations to accurately reproduce the geometric and electronic structures of the free cobalamin cofactors has only been verified on a case-by-case basis. In addition, the QM/MM method has never been used to generate complete models for members of the corrinoid family whose structures have not yet been determined by X-ray crystallography, such as the cobinamides. In this study, we have tested the use of QM/MM calculations for generating reasonable structural models of a series of Co³⁺Cbl and Co³⁺Cbi species whose upper axial ligands span a wide range of the spectrochemical series. The models were evaluated on the basis of X-ray crystallographic data when available and by comparing the TD-DFT computed Abs spectra to those obtained experimentally. The computed electronic structure descriptions for these experimentally-validated models provide significant new insight into the similarities and differences between the spectral and electronic properties of corresponding pairs of cobalamin and cobinamide species.

Validation of QM/MM optimized models

To validate our computational approach, full QM/MM geometry optimizations were performed on a representative set of cobalamin species. In each case, the optimized geometry was found to be in good agreement with the corresponding X-ray crystallographic structure, though in the case of H₂OCbl⁺ the differences in the corrin fold angle and upper axial Co–O bond length were somewhat larger than expected. Nonetheless, the cofactor models obtained in this process represent a significant improvement over those based on truncated counterparts generated via pure DFT geometry optimization.¹¹¹ Although DFT geometry optimizations of complete corrinoid models have recently become viable,¹¹² they are immensely time-consuming and thus not practical on a routine basis. Additionally, to model larger systems where the corrinoid cofactors are bound to an enzyme active site, the use of a combined QM/MM approach is inevitable. Our results indicate that such an approach should be well suited to study the geometric and electronic properties of enzyme-bound corrinoid cofactors, as long as the computational results be carefully evaluated on the basis of experimental data.

As an additional means to validate the QM/MM optimized models, Abs spectra were calculated for the corresponding QM cores using TD-DFT. Excellent agreement was achieved between the experimental and computed spectra, especially with regards to the major trends in band positions and intensities (Figures 6 and 7). Thus, the QM/MM optimized models not only represent realistic structural mimics of the actual corrinoids, but also provide an excellent basis for investigating their spectral and electronic properties.

Geometric structures of Co³⁺cobinamides

Overall, the core geometries of the cobinamides appear to be very similar to those of the analogous cobalamins. The corrin macrocycles of all of the cobinamides are similarly folded as those of their cobalamin counterparts, and not flattened to the large extent (by ~5–10°) predicted by previous DFT calculations on truncated models. Substitution of the intramolecular DMB moiety by a H₂O molecule causes a lengthening of the lower axial ligand bonds by 0.05 – 0.61 Å, with the bond length change varying inversely to the σ-donor strength of the upper axial ligand. The upper axial bond lengths are predicted to change only modestly upon DMB → H₂O substitution, shortening by 0.01 to 0.13 Å, where again the magnitude is inversely proportional to the σ-donor strength of the upper axial ligand. In the case of MeCbl/MeCbi⁺, the strongly σ-donating CH₃⁻ moiety dominates the axial bonding scheme, which renders the Co–C bond length largely insensitive to changes in the lower axial ligation (Δr(Co−C_Me) = 0.01 Å for this pair). CN⁻ and H₂O are considerably weaker σ-donor ligands, thus allowing the lower axial ligand to play a more important role in the axial bonding scheme. Consequently, the upper axial ligand bond lengths of CNCbl and H₂OCbl⁺ are more sensitive to changes in the lower axial ligation, decreasing by 0.03 and 0.13 Å, respectively, upon DMB → H₂O substitution. Our QM/MM calculations also predict a small, but consistent, contraction of the equatorial Co–N_eq bond lengths in the cobinamide models relative to their cobalamin counterparts, presumably due to the increase in the effective nuclear charge of the cobalt ion accompanying the ligand switch from DMB to H₂O.

Comparison of the Cobalamin and Cobinamide Electronic Structures

Because cobalamins and cobinamides differ primarily with respect to the identity of the lower axial ligand, the largest electronic-structure differences between corresponding Co³⁺Cbl/Co³⁺Cbi pairs involve the Co 3d_z²-based MO and, to a lesser extent via modulation of the effective nuclear charge of the cobalt ion, the other Co 3d-based MOs. Specifically, our computations reveal that the replacement of the DMB ligand with a more weakly σ-donating H₂O molecule leads to a stabilization of the Co 3d_z²-based MO relative to the corrin π*-based LUMO (or LUMO+1) by 0.8 eV for MeCbi⁺, 0.5 eV for CNCbi⁺, and 0.8 eV for H₂OCbi²⁺.

A shift of the prominent low-energy Abs feature is observed for each pair of Co³⁺Cbl/Co³⁺Cbi species whose magnitude varies considerably as a function of the upper axial ligand. This feature, commonly referred to as the α band, has been assigned as an electronic transition from the HOMO, a corrin π-based MO containing a variable amount of Co 3d_z² orbital character, to the LUMO (or LUMO+1 for H₂OCbl⁺ and H₂OCbi²⁺), a corrin π*-based MO (Figure 10). In the cobalamins, the HOMO exhibits a σ-antibonding interaction between the formally unoccupied Co 3d_z² orbital and the N_DMB 2p-based “lone pair” that increases in magnitude as a function of the σ-donor strength of the upper axial ligand. The DMB→H₂O axial ligand substitution effectively eliminates this σ-antibonding interaction, causing a species-dependent stabilization of the HOMO relative to the LUMO (or LUMO+1). Consequently, for a given Co³⁺Cbi, the α band is typically blue-shifted from its position in the Abs spectrum of the corresponding Co³⁺Cbl. The magnitude of this blue-shift correlates roughly with the percentage of Co 3d_z² orbital character in the HOMO of the cobalamin (Figure 10). Specifically, the largest blue-shift of ~3500 cm⁻¹ is observed for the MeCbl/MeCbi⁺ pair (~6% Co 3d_z² orbital contribution to the HOMO of MeCbl), followed by ~1500 cm⁻¹ for the CNCbl/CNCbi⁺ pair (~2% Co 3d_z² character in the HOMO of CNCbl) and the H₂OCbl⁺/H₂OCbi²⁺ pair (~1% Co 3d_z² orbital character in the HOMO of H₂OCbl⁺), for which a minor red-shift of ~200 cm⁻¹ is actually observed.

Figure 10.

MO correlation diagram depicting the modulation of the energy of the α-band transition (vertical arrows; not drawn to scale) upon upper and lower axial ligand substitutions. The LUMOs (or LUMO+1 for H₂OCbl⁺ and H₂OCbi²⁺) were set to be of equal energies. The horizontal dashed line connecting the HOMOs of the cobinamides highlights the roughly isoenergetic nature of these orbitals relative to the corresponding LUMOs. Isosurface plots of the donor MOs (i.e. the HOMOs) are shown at the bottom along with the percentage of Co 3d_z² orbital character they contain.

Interestingly, while the energies of the α-band transition of the cobalamins change considerably as a function of the upper axial ligand, they are nearly invariant for the cobinamides. This difference can be understood by comparing the axial bonding interactions that exist in the cobalamins and the cobinamides. The HOMOs of the cobalamins exhibit a σ-antibonding interaction between the Co 3d_z² orbital and the N_DMB 2p-based “lone pair” of the DMB base. As the σ-donor strength of the upper axial ligand increases from H₂O to CN⁻ and CH₃⁻, the Co 3d_z² orbital contribution to the HOMO and, thus, the σ-antibonding interaction with the lower axial ligand increase. As a result, the HOMO is raised in energy and the α band undergoes a red-shift. Alternatively, due to the low energy of the O 2p-based “lone pair” of the lower axial H₂O ligand in the cobinamides, the HOMOs of these species lack any significant axial σ-antibonding interactions involving the Co 3d_z² orbital, and alterations in the σ-donating strength of the upper axial ligand will thus not noticeably alter the energy of the HOMO.

Conclusions

By carrying out QM/MM and TD-DFT computations, we have been able to generate experimentally-validated geometric and electronic structure descriptions for a representative set of cobalamin and cobinamide species. As a result, significant new insight has been obtained into the similarities and differences between these two corrinoid subfamilies. Our results indicate that the DMB→H₂O lower axial ligand switch primarily affects the energies of the Co 3d_z²-based MO and, to a lesser extent, the other Co 3d-based MOs as well as the corrin π-based highest energy MO. This renders the energy of the α-band transition of cobinamides nearly invariant to changes in the upper axial ligation, while for cobalamins this transition has been shown to redshift considerably with increasing σ-donor strength of the upper axial ligand. This research also provides a sound basis for future experimental and computational studies of these biologically-relevant species. In particular, the combined QM/MM approach can be extended to model larger systems, including select active-site residues or entire subunits of cobalamin-dependent enzymes. Additionally, the improved electronic structure descriptions for the cobinamides provide an excellent framework for interpreting spectral changes observed when these cofactor analogues are utilized to probe protein/cofactor interactions.