Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Feb 1.
Published in final edited form as: Ultrasonics. 2015 Sep 28;65:258–267. doi: 10.1016/j.ultras.2015.09.016

Impedance Matching Network for High Frequency Ultrasonic Transducer for Cellular Applications

Min Gon Kim 1, Sangpil Yoon 1,*, Hyung Ham Kim 1, K Kirk Shung 1
PMCID: PMC4656103  NIHMSID: NIHMS726549  PMID: 26442434

Abstract

An approach for the design of an impedance matching network (IMN) for high frequency ultrasonic transducers with large apertures based on impedance analysis for cellular applications is presented in this paper. The main objectives were to maximize energy transmission from the excitation source to the ultrasonic transducers for cell manipulation and to achieve low input parameters for the safe operation of an ultrasonic transducer because the piezoelectric material in high frequency ultrasonic transducers is prone to breakage due to its being extremely thin. Two ultrasonic transducers, which were made of lithium niobate single crystal with the thickness of 15 μm, having apertures of 4.3 mm (fnumber = 1.23) and 2.6 mm (fnumber = 0.75) were tested. L-type IMN was selected for high sensitivity and compact design of the ultrasonic transducers. The target center frequency was chosen as the frequency where the electrical admittance (∣Y∣) and phase angle (θz) from impedance analysis was maximal and zero, respectively. The reference center frequency and reference echo magnitude were selected as the center frequency and echo magnitude, measured by pulse-echo testing, of the ultrasonic transducer without IMN. Initial component values and topology of IMN were determined using the Smith chart, and pulse-echo testing was analyzed to verify the performance of the ultrasonic transducers with and without IMN. After several iterations between changing component values and topology of IMN, and pulse-echo measurement of the ultrasonic transducer with IMN, optimized component values and topology of IMN were chosen when the measured center frequency from pulse-echo testing was comparable to the target frequency, and the measured echo magnitude was at least 30% larger than the reference echo magnitude. Performance of an ultrasonic transducer with and without IMN was tested by observing a tangible dent on the surface of a plastic petridish and single cell response after an acoustic pulse was applied on a target cell.

Keywords: L-type impedance matching network, large aperture high frequency ultrasonic transducer, impedance analysis, optimization of impedance matching network, single-cell application

I. INTRODUCTION

An ultrasonic transducer/array is a crucial component of an ultrasonic scanner such as those widely used in clinical diagnosis [1-7]. There has been a growing interest in transducers in the frequency range higher than 100 MHz for applications in single cell analysis, acoustic trapping, and studying mechanotransduction with improved lateral resolution [8-12]. In these applications, a highly focused acoustic beam is required [13]. When making highly focused ultrasonic transducers, those having a large aperture are much easier to press-focus. A transducer with a large aperture also generates a stronger pressure field under the same input parameters, such as voltage and pulse duration. Therefore, to generate the same acoustic pressure field, a transducer with a large aperture is safer and more effective than a transducer with a small aperture because lower input voltage and shorter pulse duration are needed.

The advantages of a transducer with a large aperture are true only when the electrical impedance between the ultrasonic transducer and auxiliary components are matched. As the operating frequency approaches the resonance frequency of the piezoelectric material, the magnitude of the acoustic pulse becomes larger because the energy transfer condition is optimized [14]. In other words, at the resonance, the magnitude of the electrical impedance of the ultrasonic transducer becomes optimized allowing maximal energy conversion. Energy conversion optimization depends upon the input electrical impedance of the transducer which in turn depends upon the dielectric constant of the piezoelectric material [15]. Electrical impedance mismatch between the ultrasonic transducer and excitation source leads to a large energy reflection between them thereby wasting energy, which results in excessive power consumption when trying to achieve the same acoustic pressure field. [16-19]. Therefore, an impedance matching network (IMN) is essential for the optimization of power transfer and efficiency by minimizing reflections between the ultrasonic transducer and the excitation source. This is particularly acute in applying large aperture high frequency transducers, which have extremely low electrical impedance at the resonance frequency, to a number of cellular applications [8-13] given that popular and highly sensitive piezoelectric materials typically have fairly high dielectric constants, which are unfavorable for the design of large aperture devices.

Various schemes of broadband IMN have been adopted for ultrasound imaging applications so as to obtain wide bandwidth because it helps to improve axial resolution [20-24]. Broadband IMN produces a spectral response that has a wide bandwidth with a gradual peak and echo signal energy distributed over a broad range of frequencies [25]. Therefore, broadband IMN may not be appropriate in applications where maximum intensity at the resonance frequency is required [26].

The commercially available transducer simulation software, PiezoCAD (Sonic Concepts, Bothell, WA), has been widely used in transducer design, however, it is very challenging to fabricate transducers in the frequency range above 100 MHz based on PiezoCAD modeling. Because PiezoCAD modeling does not take into account the effects of variations in thickness of the piezoelectric material at higher frequency and the electromechanical effects resulting from press-focusing, PiezoCAD modeling is not likely to show good agreement in terms of magnitude of admittance (∣Y∣), phase angle (θz), the real (R) and the imaginary (X) values compared with impedance analysis based on the real fabricated transducer [16, 27-29]. For low frequency transducers, PiezoCAD modeling agrees well with impedance analysis based on the real fabricated transducer because the thickness variations and other aspects of the transducer design process have a more negligible impact on the characteristics of the transducers. For high frequency transducers, however, small variations have a direct influence on the characteristics of the transducers. We therefore chose a design method for the impedance matching network (IMN) using impedance analysis based on the real fabricated transducer and the Smith chart to determine the appropriate component values and topology of IMN instead of a design method based on PiezoCAD modeling.

In this paper, we developed an L-type IMN for a large aperture high frequency transducer, which achieved a much sharper peak at the resonance frequency by sacrificing bandwidth [30], allowing a greater acoustic pulse at the resonant frequency to be generated than that generated by an ultrasonic transducer without IMN. The L-type IMN could be easy to tune the matching network with a reliable performance using the combination of inductor and capacitor in the frequency range from kHz to GHz depending on ultrasonic transducers’ electrical impedance compared to transmission line IMN [20]. A detailed description of the design process for the optimization of an impedance matching network (IMN) for a large aperture high frequency transducer is presented. The IMN design process follows five steps; (1) measuring maximum magnitude of admittance (∣Y∣) and zero phase angle (θz) from impedance analysis and estimating the resonance frequency that would be termed as the target center frequency of the ultrasonic transducer; (2) determining the appropriate component values and topology of IMN using the Smith chart based on the real (R) and the imaginary (X) values obtained from the impedance analysis; (3) performance verification of the ultrasonic transducer with and without IMN by pulse-echo measurement; (4) optimizing component values and topology of IMN by trial and error after comparing the target center frequency and measured center frequency from pulse-echo measurement; (5) determined component values and topology implemented on a Printed Circuit Board (PCB), and integrated with the ultrasonic transducer. The optimized center frequency was set to a value similar to the target center frequency, measured from impedance analysis. At the same time, the optimized echo magnitude was set to a value at least 30% larger than the reference echo magnitude obtained by pulse-echo testing of the same ultrasonic transducer without IMN. Under the same input parameters, such as peak-to-peak voltage (Vpp) and treatment time (Tt), cell response and the effects on the surface of a plastic petridish by the acoustic pressure field, generated by ultrasonic transducers with and without IMN, were observed by microscope.

II. MATERIALS AND METHODS

A. Ultrasonic transducers, impedance analyzer, pulse-echo and insertion loss measurement system

Two ultrasonic transducers were fabricated and tested. Single element lithium niobate (LiNbO3) ultrasonic transducers were fabricated with conventional approaches [28]. The aperture sizes of the first (TR1) and the second (TR2) ultrasonic transducers were 4.3 mm and 2.6 mm, respectively. The fnumber of TR1 and TR2 were 1.23 and 0.75, respectively. The designed center frequencies of TR1 and TR2 were 110 MHz and 150 MHz, respectively. The characteristics of the ultrasonic transducer were measured by an impedance analyzer (Agilent E4991, Agilent Technologies, Santa Clara, CA), which has an operating frequency range from 1 MHz to 3 GHz. The magnitude of electrical impedance (∣Z∣) and admittance (∣Y∣), phase angle (θz), real (R) and imaginary (X) values of the electrical characteristics were measured.

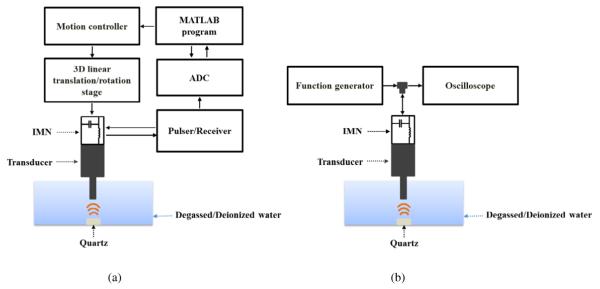
To verify the performance of the impedance matching network (IMN), pulse-echo and insertion loss (IL) measurement of the ultrasonic transducers with and without IMN was conducted [31]. For the pulse-echo measurement, an imaging system was developed as shown in Fig. 1(a). It was comprised of a pulser/receiver (5900PR, Olympus NDT Inc., Waltham, MA), 12-bit analog to digital converter (ADC) with up to 2 GS/s sampling (CS122G1, Dynamics Signals LLC., Lockport, IL), a 3D linear translation/rotation stage (ILS100HA, Newport, Irvine, CA), motion controller (ESP301-3N, Newport, Irvine, CA), and a custom-built MATLAB (MathWorks Inc., Natick, MA) program. An ultrasonic transducer with or without IMN was excited by the pulser/receiver with 200 Hz pulse repetition frequency. The measurements were performed in the degassed/ deionized water and the focal depth was aligned using a 3D linear translation/rotation stage with a motion controller and a custom-built MATLAB program. The reflected echo signals from a quartz target, placed at the focal point, were amplified by the pulser/receiver. Received signals were digitized with ADC at 1 GHz sampling rate. Digitized signals were transferred to the custom-built MATLAB program to visualize pulse-echo responses.

Fig. 1.

Fig. 1

Open in a new tab

Experimental setups for (a) pulse-echo and (b) insertion loss (IL) measurement.

For the insertion loss (IL) measurement as presented in Fig. 1(b), a sine burst 5 V signal of 30 cycles generated from a function generator (AFG 3251, Tektronix, Beaverton, Oregon) was used to excite ultrasonic transducers with and without IMN, and the reflected echo signal from a quartz target placed at the focal distance was recorded in an oscilloscope (TDS 5052, Tektronix, Beaverton, Oregon) set to 1 MΩ coupling. IL was measured by voltage ratio of the echo signal to the sine burst signal, expressed in decibels (dB) over a range of −6 dB bandwidth (BW). The measured value was then compensated for the attenuation in water (0.0002 dB/mm/MHz2) [29] and reflection from the quartz target (1.9 dB).

B. Design of impedance matching network

An impedance matching network (IMN) was used to transform the real value and cancel the imaginary value of the input electrical impedance of an ultrasonic transducer. The real value (R2) measured by impedance analysis was compared to the electrical impedance of the excitation source (R1), usually 50 Ω, in order to determine whether IMN was placed in shunt with R2 (lowers R2) or in series with R2 (boosts R2) as shown in Figs. 2(a) and (b), respectively. Once IMN was determined in shunt or in series with R2, the component values and topology such as capacitor (C)/inductor (L), C/C, L/L and L/C were determined by using the Smith chart, based on measured real and imaginary values of the electrical impedance of the ultrasonic transducer. A series-added inductor (L) moved the impedance in an upward direction, which led to a clockwise rotation along a constant circle of resistance, while a series-added capacitor (C) moved the impedance in the downward direction, which led to a counter clockwise rotation along a constant circle of resistance. A shunt-added inductor (L) moved the impedance upward, which led to a counter clockwise rotation along a constant circle of conductance, while a shunt-added capacitor (C) moved the impedance downward, which led to a clockwise rotation along a constant circle of conductance [20, 32]. For example, as presented in Fig. 2(c), when measured real and imaginary values of electrical impedance were 2.5 Ω and −5.5 Ω at target center frequency (TCF) of 130 MHz, respectively, by selecting series-added inductor (L) of 20 nH, electrical impedance was moved to a clockwise rotation along a constant circle of resistance, and real and imaginary values were 2.5 Ω and 11.5 Ω at TCF, respectively. The electrical impedance was then transformed a clockwise rotation along a constant circle of conductance by shunt-added capacitor (C) of 100 pF, and real and imaginary values were 50 Ω and −0.2 Ω at TCF, respectively. As a result, the input electrical impedance of the ultrasonic transducer moved toward the center of the Smith Chart by selecting appropriate component values and topology at the target center frequency.

Fig. 2.

Fig. 2

Open in a new tab

Schematic diagram of impedance matching network (IMN) for an ultrasonic transducer. Zin represents input impedance seen from the excitation source and should be equal to the complex conjugate of the Z1. Z1 and Z2 indicate the electrical impedance of the excitation source and ultrasonic transducer, respectively. (a) When R1 < R2, IMN is placed in shunt with R2 to lower R2 (b) When R1 > R2, IMN is placed in series with R2 to boost R2. The component values and topology such as capacitor (C)/inductor (L), C/C, L/L and L/C were dependent upon measured real and imaginary values of electrical impedance of the ultrasonic transducer at the target center frequency on a Smith chart. (c) The example of IMN design procedure. The input electrical impedance of the ultrasonic transducer moved toward the center of the Smith Chart by appropriate inductor and capacitor component values and topology at the target center frequency. (d) Picture of IMN with ultrasonic transducer 1. The printed circuit board (PCB) was implemented with shunt-added capacitor of 100 pF and series-added inductor of 8 nH, and an overall size was 21 by 11 mm2.

The target center frequency of the ultrasonic transducer with impedance matching network (IMN) was chosen because it was the frequency where the magnitude of electrical admittance (∣Y∣) and the phase angle (θz) of the transducer was maximal and zero, respectively [33]. The design criterion was that the echo magnitude of the ultrasonic transducer with impedance matching network (IMN) at the target frequency should be at least 30% greater than the reference echo magnitude, acquired from the pulse-echo test using the ultrasound transducer without IMN. When the design criterion was not satisfied, the topology and component values of IMN should be optimized according the optimization approach. For the optimization approach, a topology selection should be taken into consideration of availability of components and frequency response related to applications; high-pass IMN (series-added capacitor/shunt-added inductor) for blocking low frequency oscillating signals, and low-pass IMN (series-added inductor/shunt-added capacitor) for filtering harmonic signals [34,35]. Also, specifying component values was taken account of the target center frequency sweep (20% bandwidth) and component values with a given tolerance [36]. Since electrical impedance is changed as a function of frequency on the Smith chart and initially determined component values does not take account of the given tolerances, the component values and topology were adjusted by sweeping the target center frequency (20% bandwidth) and its tolerance ranges. The optimization process of the topology and component values was repeated until the criterion was met.

The printed circuit board (PCB) was implemented on 0.062” fiberglass epoxy laminate (FR-4) with a loss tangent of 0.0153 and dielectric constant of 4.5, with an overall size of 21 by 11 mm2. IMN was made using the optimized component values and topology, and then was connected to the ultrasonic transducer as shown in Fig. 2(d).

C. Validation of IMN and cell applications

Fig. 3 illustrates the experimental arrangement which has been used to study high frequency ultrasonic microbeam transducers for acoustic-transfection in our laboratory. It was used to demonstrate the usefulness of such an impedance matching network (IMN) in enhancing energy delivery of a large aperture transducer at a designated frequency. The experimental setup was composed of transducer 1 (TR1) with or without IMN, a pulser/receiver, an oscilloscope (LC534, LeCroy, Chestnut Ridge, NY), a 3D linear translation/rotation stage, a customized LabVIEW (National Instruments, Austin, TX) program for focusing TR1, the function generator and a 50 dB power amplifier (525LA, ENI, Rochester, NY) for the generation of an acoustic pulse using TR1. An Epi-microscope (IX71, Olympus Corporation of the Americas, Center Valley, PA) was integrated with the ultrasound system for cell imaging.

Fig. 3.

Fig. 3

Open in a new tab

Experimental setup for the validation of impedance matching network (IMN) and cell applications. Precise focal depth of the ultrasonic transducer 1 (TR1) with IMN was found by moving TR1, attached to a 3D linear translation/rotation stage, while finding the optimized echo magnitude using a pulser/receiver and an oscilloscope. After focusing TR1 with IMN, an acoustic pulse with peak-to-peak voltage (Vpp) and treatment time (Tt) was applied to the surface of a plastic petridish and HeLa cells. Tt was composed of the number of sine waves with the optimized center frequency of TR1. The test and experiment were carried out comparing tangible effects obtained by TR1 with and without IMN.

The ultrasonic transducer 1 (TR1) was accurately moved by a 3D linear translation/rotation stage to locate TR1’s focal point at the desired position by finding the optimized echo magnitude. The focal point was positioned at the center of the microscope’s field of view. Once focusing of TR1 with IMN was completed, TR1 with IMN was excited by an electrical pulse with peak-to-peak voltage (Vpp) and treatment time (Tt) as shown in Fig. 3. Tt was determined by the number of cycles of sine waves with the optimized center frequency, which was found during the optimization process of TR1 with IMN.

We applied an acoustic pulse, generated by TR1 with and without IMN, with peak to peak voltage (Vpp) ranging from 40 V to 70 V and treatment time (Tt) of 420 μs on the surface of a 35 mm plastic petridish. The effects of the applied acoustic pulse on the surface of the 35 mm petridish were recorded by taking still shot images using the epi-fluorescence microscope.

Experiments on a single cell were also conducted using human cervical cancer cells (HeLa). HeLa cells were grown in eagle's minimum essential medium (EMEM) supplemented with 10% fetal bovine serum (FBS). The cells were plated on a 35 mm petridish and incubated for 2 days in 5% CO2 at 37°C. An acoustic pulse was applied on cells with the treatment conditions of Vpp of 55 V and Tt of 420 μs. Immediately after the treatment, cells were incubated with EMEM in 5% CO2 at 37°C for 4 hours. Cell viability was conducted with a LIVE/DEAD Cell Imaging kit (Life Technologies Corp., Carlsbad, CA) according to the manufacturer’s instructions. Bright-field and fluorescence images were taken with the epi- fluorescence microscope. In the case of the live/dead assay, stained live cells have bright green fluorescence, while stained dead cells have intense red fluorescence. In order to compare the performance of the IMN, the experiment was repeated with the same ultrasonic transducer without IMN under the same conditions and input parameters.

III. RESULTS

A. Impedance analysis results

Figs. 4(a) and (b) represent magnitude measurements of electrical admittance (∣Y∣), phase angle (θz), real (R) and imaginary (X) values of the electrical impedance of ultrasonic transducer 1 (TR1) and ultrasonic transducer 2 (TR2) based on impedance analysis, respectively. Left column in Fig. 4 indicates ∣Y∣ and θz measurements and right column shows R and X values of electrical impedance of TR1 and TR2. From ∣Y∣ and θz measurements, the target center frequencies of TR1 and TR2 were determined as 105 MHz and 150 MHz, respectively. These target center frequencies are denoted as solid arrows in Figs. 4(a) and (b). At these target center frequencies, measured R and X values are 1.5 Ω and 0.2 Ω for TR1 and 2.5 Ω and 0.1 Ω for TR2, respectively. Since the real value of the two ultrasonic transducers at the target center frequency was less than 50 Ω, impedance matching network (IMN) was placed in series with the ultrasonic transducers to boost the real value of impedance of the two ultrasonic transducers.

Fig. 4.

Fig. 4

Open in a new tab

Measured magnitude of electrical admittance (∣Y∣), phase angle on the left column (θz), real (R) and imaginary (X) values on the right column of electrical impedance of (a) transducer 1 (TR1) and (b) transducer 2 (TR2). The target center frequency (TCF) of TR1 and TR2 were measured as 105 MHz and 150 MHz, respectively, when ∣Y∣ was maximum value and θz was zero as indicated with solid arrows in left column in (a) and (b). At the target center frequency, measured R and X were 1.5 Ω and 0.2 Ω for TR1 and 2.5 Ω and 0.1 Ω for TR2, respectively.

B. Optimization of impedance matching network

The measured pulse-echo waveform and echo spectrum of ultrasonic transducer 1 (TR1) and ultrasonic transducer 2 (TR2) are presented in Figs. 5(a) and (b), respectively. Left column and right column in Figs. 5(a) and (b) indicate the pulse-echo measurements without impedance matching network (IMN) and with IMN, respectively. Table 1 summarizes the optimization process of IMN.

Fig. 5.

Fig. 5

Open in a new tab

Pulse-echo waveform and echo spectrum of (a) ultrasonic transducer 1 (TR1) and (b) ultrasonic transducer 2 (TR2). Left column represents the pulse-echo measurement without impedance matching network (IMN) and right column shows the pulse-echo measurement with IMN. For TR1, the optimized center frequency (OCF) was almost the same as the target center frequency (TCF, 105 MHz) and the optimized echo magnitude (OEM) in the right column of (a) was increased by 65% compared to the reference echo magnitude (REM) in the left column of (a). For TR2, the optimized center frequency (OCF) was similar to the target center frequency (TCF, 150 MHz), measured by impedance analysis and the optimized echo magnitude (OEM) in the right column of (b) was enhanced by 33% compared to the reference echo magnitude (REM) in the left column of (b).

TABLE1.

Summary of the optimization of impedance matching network (IMN) for ultrasonic transducer 1 (TR1) and ultrasonic transducer 2 (TR2). The optimized component values and topology of IMN were 100 pF/8 nH and topology of capacitor/inductor for TR1 and 47 nH/25 pF and topology of inductor/capacitor for TR2. Optimized center frequency and optimized echo magnitude were 111 MHz and 3.3 V for TR1 and 140 MHz and 1.6 V for TR2, respectively. For TR1, the optimized center frequency was close to the target center frequency and the optimized echo magnitude was improved by 65%. For TR2, the optimized center frequency was 140 MHz while the target center frequency was 150 MHz and the optimized echo magnitude was enhanced by 33%.

Impedance matching network
(IMN)		 Transducer 1 (TR1) Transducer 2 (TR2)
without # of Optimization
 without # of Optimization
IMN 1st 2nd … Final IMN 1st 2nd … Final
Target center frequency (MHz) 105 - - … - 150 - - … -
Reference center frequency (MHz) 113 - - … - 120 - - … -
Optimized center frequency (MHz) - 86 114 … 111 - 163 114 … 140
Reference echo magnitude (V) 2.0 - - … - 1.2 - - … -
Optimized echo magnitude (V) - 2.8 0.6 … 3.3 - 0.4 1.0 … 1.6
Inductor (nH) - 24 14 … 8 - 8 9 … 47
Capacitor (pF) - 146 740 … 100 - 45 90 … 25
Topology - graphic file with name nihms-726549-t0011.jpg graphic file with name nihms-726549-t0012.jpg … graphic file with name nihms-726549-t0013.jpg - graphic file with name nihms-726549-t0014.jpg graphic file with name nihms-726549-t0015.jpg … graphic file with name nihms-726549-t0016.jpg
Open in a new tab

Left column in Fig. 5(a) shows the reference center frequency and the reference echo magnitude that were measured as 113 MHz and 2.0 V, respectively. For TR1 with IMN, the combination of 146 pF/24 nH and topology of capacitor/inductor were initially determined and tested. The center frequency of the pulse-echo response was measured at 86 MHz, whereas echo magnitude was increased from 2.0 V to 2.8 V compared to TR1 without IMN. Since the center frequency was too low, the second optimization process was conducted with updated component values of 14 nH/740 pF and topology of inductor/capacitor. The center frequency was 114 MHz, but the received echo magnitude was decreased to 0.6 V compared to TR1 without IMN. After the optimization process was repeated, the optimized component values and topology of IMN were 100 pF/8 nH and capacitor/inductor, respectively. The optimized echo magnitude of TR1 with IMN was 65% greater than TR1 without IMN while the optimized center frequency of TR1 with IMN was 111 MHz which was similar to the target center frequency (105 MHz) measured by an impedance analysis as shown in the right column of Fig. 5(a).

Left column in Fig. 5(b) indicates the reference center frequency and the reference echo magnitude which were measured as 120 MHz and 1.2 V from pulse-echo testing, respectively. For TR2 with IMN, the combination of 8 nH/45 pF and topology of inductor/capacitor were initially selected by using the Smith chart. The center frequency of the pulse-echo measurement was improved to 163 MHz, whereas echo magnitude was decreased from 1.2 V to 0.4 V. Since the echo magnitude was too low, it was necessary for further optimization. A second optimization process was conducted with updated component values of 90 pF/9 nH and topology of capacitor/inductor. The center frequency and the received echo magnitude were simultaneously decreased. After the optimization process was repeated, the optimized component values and topology of IMN were 47 nH/25 pF and inductor/capacitor, respectively. The optimized center frequency of TR2 with IMN was 140 MHz which was similar to the target center frequency (150 MHz) measured by impedance analysis, and the optimized echo magnitude of TR2 with IMN was improved by 33% compared to the reference echo magnitude as shown in the right column of Fig. 5(b).

C. Electrical characteristics of optimized impedance matching network

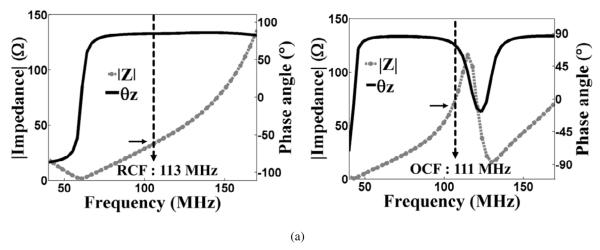
Figs. 6(a), (b) and (c) indicate electrical performance of two ultrasonic transducers without and with optimized impedance matching network (IMN). The electrical properties of the cable are 6 inch (153 mm) length, 50 Ω impedance, insertion loss of 0.05 dB and return loss of 37 dB in the frequency range from 100 MHz to 200 MHz. Left column in Figs. 6(a) and (b) represents ∣Z∣ and θz measurements that are 35 Ω and 85° for TR1 without IMN, and 32 Ω and 77° for TR2 without IMN at the reference center frequency (RCF), respectively. Right column in Figs. 6(a) and (b) shows ∣Z∣ and θz measurements of 65 Ω and 76° for TR1 with IMN, and 52 Ω and −40° for TR2 with IMN at the optimized center frequency (OCF), respectively. After compensation for the attenuation caused by water and reflection from the quartz target, the insertion loss (IL) values over a range of −6 dB bandwidth (BW) are shown in Fig. 6(c). Left column in Fig. 6(c) indicates IL is calculated as −21.5 dB for TR1 without IMN at the RCF and −13 dB for TR1 with IMN at the OCF, respectively. Right column in Fig 6(c) shows IL is measured as −34 dB for TR2 without IMN at the RCF and −29 dB for TR2 with IMN at the OCF, respectively.

Fig. 6.

Fig. 6

Fig. 6

Open in a new tab

Measured electrical performance of ultrasonic transducers without and with impedance matching network (IMN). (a) Magnitude of electrical impedance (∣Z∣), (b) phase angle (θz) and (c) insertion loss (IL) of ultrasonic transducer 1 (TR1) without and with IMN and ultrasonic transducer 2 (TR2) without and with IMN, respectively. For TR1, ∣Z∣, (θz) and IL were measured as 35 Ω, 85° and −21.5 dB at the reference center frequency (RCF) without IMN, and 65 Ω, 76° and −13 dB at the optimized center frequency (OCF) with IMN, respectively. For TR2, ∣Z∣, (θz) and IL were 32 Ω, 77° and −34 dB at the RCF without IMN, and 52 Ω, −40° and −29 dB at the OCF with IMN, respectively.

D. Validation of the approach in a cellular application

Fig. 7(a) demonstrates noticeable circular dents, produced by ultrasonic transducer 1 (TR1) with impedance matching network (IMN). In contrast, the acoustic pulse generated by TR1 without IMN did not produce recognizable circular dents as shown in Fig. 7(b). The locations of the acoustic pulse are indicated as dashed circles in Fig. 7. The scale bars indicate 20 μm.

Fig. 7.

Fig. 7

Open in a new tab

Circular dents on a 35 mm plastic petridish generated by acoustic pulses from ultrasonic transducer 1 (TR1) (a) with impedance matching network (IMN) (b) without IMN. Acoustic pulses were generated from the peak-to-peak voltage (Vpp) ranged from 40 V (left) to 70 V (right) with increments of 10 V and treatment time (Tt) of 420 μs. The scale bar indicates 20 μm.

Bright-field and fluorescence images of a HeLa cell treated by ultrasonic transducer 1 (TR1) with impedance matching network (IMN) and without IMN are shown in Figs. 8(a)-(c) and Figs. 8(d)-(f), respectively. Fig. 8(a) shows a circular dent which was found in the middle of a HeLa cell right after one acoustic pulse was applied. The cell, which was treated by TR1 with IMN, was dead after 4 hours of incubation. Red fluorescence from propidium iodide was clearly seen in Fig. 8(c). However, the cell, which was treated by TR1 without IMN, was alive after 4 hours of incubation. The retention of fluorescent from calcein (green fluorescence) in the cell was observed as shown in Fig. 8(e). TR1 with IMN generated a higher pressure field than TR1 without IMN under the same peak-to-peak voltage and treatment time.

Fig. 8.

Fig. 8

Fig. 8

Open in a new tab

Cell responses to an acoustic pulse generated by ultrasonic transducer 1 (TR1) with impedance matching network (IMN) and TR1 without IMN. Peak-to-peak voltage (Vpp) and treatment time (Tt) were 55 V and 420 μs, respectively. Arrows indicate the area where the acoustic pulse was applied. The scale bars indicate 20 μm. (a)-(c) TR1 with IMN (a) Bright-field image of a HeLa cell was acquired right after treatment. The circular dent in the middle of the cell was generated by the acoustic pulse. (b) Fluorescence image of the same cell stained with calcein was captured. (c) Fluorescence image of the same cell stained with propidium iodide (PI) was acquired. After 4 hours of incubation after treatment, the cell treated by TR1 with IMN was dead. (d)-(f) TR1 without IMN (d) Bright-field image of a HeLa cell was taken right after treatment. (e) Fluorescence image of the same cell stained with calcein was taken. (f) Fluorescence image of the same cell stained with PI was captured. After 4 hours of incubation after treatment, the cell exposed to the treatment was alive.

IV. DISCUSSION

To demonstrate the effectiveness of an impedance matching network (IMN) in improving energy transfer of a large aperture high frequency ultrasonic transducer, two ultrasonic transducers were tested. After optimization, the center frequency approached the target center frequency, measured by an impedance analysis, and, at the same time, the optimized echo magnitude was improved by at least 30% compared to the reference echo magnitude, measured and defined from the pulse-echo and insertion loss test using the ultrasonic transducer without impedance matching network (IMN). For ultrasonic transducer 1 (TR1), the optimized center frequency of TR1 with IMN was 111 MHz, which was similar to the target center frequency, and the optimized echo magnitude of TR1 with IMN was increased from 2 V to 3.3 V (65%). Insertion loss was measured as −21.5 dB for TR1 without IMN at the reference center frequency, −13 dB for TR1 with IMN at the target and optimized center frequency, respectively. For ultrasonic transducer 2 (TR2), the optimized center frequency of TR2 with IMN was almost the same as the target center frequency, and the optimized echo magnitude of TR2 with IMN was improved from 1.2 V to 1.6 V (33%). Insertion loss was −34 dB for TR2 without IMN at the reference center frequency, −18 dB and −29 dB for TR2 with IMN at the target and optimized center frequency, respectively. Although the measured insertion loss results were slightly different between the target and optimized center frequency, these results demonstrate a great improvement on sensitivity, which is essential for high frequency ultrasonic transducers.

There were some remarkable differences between simulation results obtained by using the Smith chart and experimental results acquired by pulse-echo measurement. Most notably, non-ideal properties such as equivalent series resistance (ESR) were not taken into consideration in simulation. ESR, however, is a very important characteristic and should be considered in practice. As the frequency increases, non-ideal inductor and capacitor values were simply modeled as an ideal inductor and capacitor in series with ESR [37, 38]. Additionally, circuit board performance such as trace characteristics, which might be attributed to the experimental results, was not taken into account for the simulation. Moreover, even if the above mentioned characteristics were taken into consideration in simulation, designed component values might be slightly different from the commercially available component values. Therefore, the repeated optimization process was required to acquire the desired values of optimized center frequency and optimized echo magnitude.

The tested ultrasonic transducer 1 (TR1) with IMN was able to generate clear circular dents on the plastic petridish, however, TR1 without IMN did not produce recognizable circular dents with the same peak-to-peak voltage (Vpp) and treatment time (Tt) as shown in Fig. 7. These experimental results indicate that the ultrasonic transducer with IMN can effectively generate a stronger pressure field at its focal area without damaging the ultrasonic transducer. We can expect that an acoustic pulse generated by the ultrasonic transducer with IMN under lower input voltage and/or lower PRF will be capable of inducing similar effects to the ultrasonic transducer without IMN.

Cell response could be controlled by adjusting treatment conditions, i.e., peak-to-peak voltage (Vpp) and treatment time (Tt), according to the purpose of the application. We can induce cell lysis or death as shown in Figs. 8(a)-(c). Cells are treated to increase permeability so as to introduce foreign molecules inside cell cytoplasm by applying gentle and/or repeated acoustic pulses. An ultrasonic transducer with IMN can be used in both cases more effectively without damaging the transducer.

V. CONCLUSIONS

The design of impedance matching network (IMN) for high frequency ultrasonic transducers with large apertures based on impedance analysis for cellular applications was discussed in this paper. Our approach was to maximize energy transfer and efficiency from the excitation source to the ultrasonic transducers to manipulate cells with low input parameters for safe operation of the ultrasonic transducers. The performance of IMN was verified by pulse-echo measurement. The optimized echo magnitude was enhanced by at least 30% compared to the reference echo magnitude and at the same time, the optimized center frequency was comparable to the target center frequency. For validation of the approach in cellular applications, a tangible circular dent on the surface of a plastic petridish and single cell response were investigated after an acoustic pulse was applied on a target cell. The experimental results have shown that an acoustic pulse may be better controlled with IMN and without damaging the ultrasonic transducer.

Highlights.

  1. The IMN design for large aperture high frequency ultrasonic transducers.

  2. At least 30 % improvement of echo magnitude was achieved with IMN at the resonance.

  3. The acoustic pulse with IMN yields more efficient transmission of energy.

  4. IMN enables cell manipulation without damaging transducer according to applications.

Acknowledgments

This work was supported by the National Institutes of Health under grant No. P41-EB002182.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

VI. REFERENCES

  • [1].Silverman RH, Lizzi FL, Ursea BG, Cozzarelli L, Ketterling JA, Deng CX, Folberg R, Colemen DJ. Safety levels for exposure of cornea and lens to very high-frequency ultrasound. Journal of Ultrasound in Medicine. 2001;20(no. 9):979–986. doi: 10.7863/jum.2001.20.9.979. [DOI] [PubMed] [Google Scholar]
  • [2].Merks EJW, Bom N, Bouakaz A, de Jong N, van der Steen AFW. Design of a multi-layer transducer for acoustic bladder volume assessment. IEEE Ultrasonics Symposium.2004. pp. 145–148. [Google Scholar]
  • [3].Lockwood GR, Turnbull DH, Christopher DA, Foster FS. Beyond 30 MHz: Applications of high frequency ultrasonic imaging. IEEE Engineering in Medicine and Biology Magazine. 1996;15(no.6):60–71. [Google Scholar]
  • [4].Paeng DG, Choi MJ, Yoon SW, Shung KK. Echogenicity from disturbed blood flow by an eccentric stenosis under pulsatile flow. Journal of the Acoustical Society of America. 2004;116(no. 4):2560. [Google Scholar]
  • [5].Kim MG, Choi H, Kim HH, Shung KK. Bipolar pulse generator for very high frequency (> 100 MHz) ultrasound applications. IEEE Ultrasonics Symposium. 2013:1567–1570. [Google Scholar]
  • [6].Yoon S, Kim MG, Williams JA, Yoon C, Kang BJ, Cabrera-Munoz N, Shung KK, Kim HH. Dual element needle transducer for intravascular ultrasound imaging. J Med Imaging. 2015;2(no. 2):027001. doi: 10.1117/1.JMI.2.2.027001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [7].Yoon S, Williams JA, Kang BJ, Yoon C, Cabrera-Munoz N, Jeong JS, Lee SG, Shung KK, Kim HH. Angled- focused 45 MHz PMN-PT single element transducer for intravascular ultrasound imaging. Sens Actuators A Phys. 2015;228(no. 1):16–22. doi: 10.1016/j.sna.2015.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [8].Hwang JY, Yoon CW, Lim HG, Park J, Yoon S, Lee J, Shung KK. Acoustic tweezers for studying intracellular calcium signaling in SKBR-3 human breast cancer cells. Ultrasonics. 2015;63:94–101. doi: 10.1016/j.ultras.2015.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [9].Hwang JY, Lim HG, Yoon CW, Lam KH, Yoon S, Lee C, Chiu CT, Kang BJ, Shung KK. Non-contact high-frequency ultrasound microbeam stimulation for studying mechanotransduction in human umbilical vein endothelial cells. Ultrasound in Medicine and Biology. 2014;40(no. 9):2172–2182. doi: 10.1016/j.ultrasmedbio.2014.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [10].Hwang JY, Lee C, Lam KH, Kim HH, Lee J, Shung KK. Cell membrane deformation induced by a fibronectin-coated polystyrene microbead in a 200-MHz acoustic trap. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 2014;61(no. 3):399–406. doi: 10.1109/TUFFC.2014.2925. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [11].Lee J, Teh SY, Lee A, Kim HH, Lee C, Shung KK. Single beam acoustic trapping. Applied Physics Letters. 2009;95(no. 7):1–3. doi: 10.1063/1.3206910. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [12].Lee J, Lee C, Kim HH, Jakob A, Lemor R, Teh S-Y, Lee A, Shung KK. Targeted cell immobilization by ultrasound microbeam. Biotechnology and Bioengineering. 2011;108(no. 7):1643–1650. doi: 10.1002/bit.23073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [13].Lee J, Teh SY, Lee A, Kim HH, Lee C, Shung KK. Transverse acoustic trapping using a gaussian focused ultrasound. Ultrasound in Medicine and Biology. 2010;36(no. 2):350–355. doi: 10.1016/j.ultrasmedbio.2009.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [14].Ben Yaakov S., Krihely N. Modeling and driving piezoelectric resonant blade elements. Applied Power Electronics Conference and Exposition. 2004;3:1733–1739. [Google Scholar]
  • [15].Snook KA, Zhao JZ, Alves CH, Cannata JM, Chen WH, Meyer RJ, Jr., Ritter TA, Shung KK. Design, fabrication, and evaluation of high frequency, single-element transducers incorporating different materials. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 2002;49(no. 2):169–176. doi: 10.1109/58.985701. [DOI] [PubMed] [Google Scholar]
  • [16].Cannata JM, Ritter TA, Chen WH, Silverman RH, Shung KK. Design of efficient, broadband single-element (20-80 MHz) ultrasonic transducers for medical imaging applications. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 2003;50(no. 11):1548–1557. doi: 10.1109/tuffc.2003.1251138. [DOI] [PubMed] [Google Scholar]
  • [17].Stephen NG. On the Maximum Power Transfer Theorem Within Electromechanical Systems. Journal of Mechanical Engineering Science. 2006;220(no. 8):1261–1267. [Google Scholar]
  • [18].Kong CS. A general maximum power transfer theorem. IEEE Transactions on Education. 1995;38(no. 3):296–298. [Google Scholar]
  • [19].Bhuiyan R, Islam M, Huang H. Wireless excitation and electrical impedance matching of piezoelectric wafer active sensors. ASME Conference on Smart Materials, Adaptive Structures and Intelligent Systems. 2012;2:271–276. [Google Scholar]
  • [20].Pozar DM. Microwave Engineering. 2nd ed Wiley; New York: 1998. [Google Scholar]
  • [21].Youla DC. A New Theory of Broad-band Matching. IEEE Transactions on Circuit Theory. 1964;11(no. 1):30–50. [Google Scholar]
  • [22].Augustine LJ, Andersen J. An algorithm for the design of transformerless broadband equalizers of ultrasonic transducers. The Journal of the Acoustical Society of America. 1979;66:629–635. [Google Scholar]
  • [23].Andersen J, Wilkins L. The Design of Optimum Lumped Broadband Equalizers for Ultrasonic Transducers. IEEE Ultrasonics Symposium. 1977:422–427. [Google Scholar]
  • [24].Shung KK. Diagnostic Ultrasound: Imaging and Blood Flow Measurements. Taylor and Francis; London, UK: 2005. [Google Scholar]
  • [25].Duffer CE, Burger CP. Narrow Band Laser Ultrasonic NDE. Review of Progress in Quantitative Nondestructive Evaluation. 1995;15:593–600. [Google Scholar]
  • [26].Hoarau C, Bailly PE, Arnould JD, Ferrari P, Xavier P. A RF tunable impedance matching network with a complete design and measurement methodology. Microwave Conference. 2007:751–754. [Google Scholar]
  • [27].Herickhoff CD, Grant GA, Britz GW, Smith SW. Dual-mode intracranial catheter integrating 3-D ultrasound imaging and hyperthermia for neuro-oncology: Feasibility study. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 2010;57(no. 11):2572–2584. doi: 10.1109/TUFFC.2010.1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [28].Lam KH, Hsu H-S, Li Y, Lee C, Lin A, Zhou Q, Kim ES, Shung KK. Ultrahigh frequency lensless ultrasonic transducers for acoustic tweezers application. Biotechnology and Bioengineering. 2013;110(no. 3):881–886. doi: 10.1002/bit.24735. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [29].Cannata JM, Ritter TA, Chen W, Shung KK. Design of focused single element (50-100 MHz) transducers using lithium niobate. Medical Imaging, Proc. SPIE. 2001;4325:28–35. [Google Scholar]
  • [30].Gonzalez G. Microwave Transistor Amplifier Analysis and DeSign. 2nd ed Prentice Hall; New Jersey: 1996. [Google Scholar]
  • [31].Lam KH, Ji HF, Zheng F, Ren W, Zhou Q, Shung KK. Development of lead-free single-element ultrahigh frequency (170-320 MHz) ultrasonic transducers. Ultrasonics. 2013;53:1033–1038. doi: 10.1016/j.ultras.2013.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [32].Rhea R. The Yin-Yang of Matching: Part 2 – Practical Matching Techniques. High Frequency Electronics. 2006 [Google Scholar]
  • [33].Kuang Y, Jin Y, Cochran S, Huang Z. Resonance tracking and vibration stablilization for high power ultrasonic transducers. Ultrasonics. 2014;54(no.1):187–194. doi: 10.1016/j.ultras.2013.07.001. [DOI] [PubMed] [Google Scholar]
  • [34].Huang Y, Boyle K. Antennas: From Theory to Practice. Wiley; New York: 2008. [Google Scholar]
  • [35].Rogers J, Plett C. Radio Frequency Integrated Circuit Design. Artech House. 2003 [Google Scholar]
  • [36].ILUMOKA A, SPENCE R. Parameter tolerance design for electrical circuits. Quality and Reliability Engineering International. 1988;4:87–94. [Google Scholar]
  • [37].Piwowarska E, Sidlarewicz A. Analysis of spiral inductor model in CMOS circuit. The International Conference of Mixed Design of Integrated Circuits and System. 2006:454–459. [Google Scholar]
  • [38].Li YL, Figueroa DG, Rodriguez JP, Huang L, Liao JC, Taniguchi M, Canner J, Kondo T. A new technique for high frequency characterization of capacitors. Electronic Components & Technology Conference. 1998:1384–1390. [Google Scholar]

RESOURCES