Molecular Dynamics Simulations of 441 Two-Residue Peptides in Aqueous Solution: Conformational Preferences and Neighboring Residue Effects with the Amber ff99SB-ildn-nmr Force Field

Abstract

Understanding the intrinsic conformational preferences of amino acids and the extent to which they are modulated by neighboring residues is a key issue for developing predictive models of protein folding and stability. Here we present the results of 441 independent explicit-solvent MD simulations of all possible two-residue peptides that contain the 20 standard amino acids with histidine modeled in both its neutral and protonated states. ³Jhnh_α coupling constants and δh_α chemical shifts calculated from the MD simulations correlate quite well with recently published experimental measurements for a corresponding set of two-residue peptides. Neighboring residue effects (NREs) on the average ³Jhnh_α and δh_α values of adjacent residues are also reasonably well reproduced, with the large NREs exerted experimentally by aromatic residues, in particular, being accurately captured. NREs on the secondary structure preferences of adjacent amino acids have been computed and compared with corresponding effects observed in a coil library and the average β-turn preferences of all amino acid types have been determined. Finally, the intrinsic conformational preferences of histidine, and its NREs on the conformational preferences of adjacent residues, are both shown to be strongly affected by the protonation state of the imidazole ring.

Introduction

Molecular dynamics (MD) simulations using pairwise-additive force fields have been used for many years to model the conformational dynamics of biological macromolecules.¹ While current protein force fields generally work quite well, one important recent trend has been the use of NMR data to thoroughly test force fields and to identify areas for improvement.² For example, combined computational and experimental studies of ³J coupling constants in alanine peptides,³ and subsequent MD studies,^{2b, 4} have explored reweighting of conformations sampled during MD in order to improve agreement with experiment. Comparisons with experimental ³J couplings for these and other peptides^{3, 5} have led to the development of improved backbone dihedral energy terms⁶ for the Amber ff99SB force field.⁷ Improved backbone terms for the same force field have also been developed through iterative comparisons with chemical shift data for proteins,⁸ and an extended version of the force field also parameterized against residual dipolar coupling (RDC) data has been reported.⁹ Importantly, in a large-scale comparison of simulated and experimental chemical shifts and ³J couplings for peptide systems, these modified Amber ff99SB force fields produced the best performances of the many force field and water model combinations tested.^2c

Combined applications of computational and experimental methods to peptide systems^{3, 10} can be especially valuable for identifying limitations in simulations.¹¹ Eventually, of course, one might hope that MD force fields will develop to the point at which their predictive abilities are beyond question. Until that time, however, there remains a need for good experimental datasets that can be used to test and further refine force fields.¹¹ One such dataset comes from a very recent 2D NMR study¹² that reported ³Jhnh_α coupling constants and δhn and δh_α chemical shifts for each residue in a comprehensive set of 361 blocked two-residue peptides; that work built upon an earlier 1D study performed by the same authors.¹³ While analysis of these data enabled the authors of that work to compile a comprehensive view of neighboring residue effects (NREs) on both ³J couplings and chemical shifts in peptides, the same dataset also clearly provides an excellent new opportunity to test simulation force fields.

In recent work we have described the use of long explicit-solvent MD simulations to model the interaction thermodynamics of all possible pairs of amino acids; the resulting simulation data provided the basis for deriving a simple coarse-grained simulation force field which we named COFFDROP.¹⁴ Here we describe a similar large-scale effort aimed instead at modeling the conformational landscapes of all possible two-residue peptides. In separate work we use these data to derive coarse-grained backbone potential functions for incorporation into COFFDROP, but here we focus on analysis of the conformational properties of the peptides and how the simulation results compare with experimental data. We use a combination of the Amber ff99SB-ildn-nmr force field^{7-8, 15} and the TIP4P-Ew water model¹⁶ to perform all simulations given the success that this combination has achieved in reproducing NMR observables for peptide systems.^2c We employ the same procedures to compute ³Jhnh_α coupling constants¹⁷ and δh_α chemical shifts¹⁸ as used in that previous study^2c and we compare our results to the corresponding experimental data for as many of the peptides as possible.¹² The comparisons indicate a reasonably high level of correspondence between the simulations and experiment and provide the first truly comprehensive description obtained from explicit-solvent MD simulations of the effects of neighboring residues on the conformational preferences of amino acids.

Materials and Methods

Molecular dynamics (MD) simulation protocol

The systems studied here consist of all possible two-residue peptides, each immersed in its own 35 × 35 × 35 Å box containing explicit solvent molecules. Since one of our principal objectives was to sample the conformational behavior that peptides would exhibit when embedded within protein sequences, each two-residue peptide was capped (blocked) with an acetyl group (Ace) at the N-terminus and an N-methyl group (Nme) at the C-terminus in order to mimic the adjacent residues that would be present in proteins. Every two-residue peptide that was simulated was therefore of the form Ace-Xaa-Yaa-Nme, where Xaa and Yaa represent amino acids. We note that throughout this manuscript we use the term “two-residue peptide” to describe these molecules instead of “dipeptide” as the latter is used in multiple ways in the literature (i.e. sometimes it is meant to describe a single amino acid with peptide bonds at both the N- and C-termini – as in the alanine dipeptide¹⁹ – and sometimes it is used to mean two amino acids connected by a single peptide bond¹²). Since we model histidine (His) in both its neutral and protonated states, a total of 21 × 21 = 441 possible two-residue peptides have been simulated.

All simulations were performed using the MD software package GROMACS version 4.5.1²⁰ and all systems were modeled using the Amber ff99SB-ildn-nmr^{7-8, 15} force field together with the TIP4P-Ew¹⁶ water model. Systems were first energy minimized using steepest descent minimization for 1000 steps, gradually heated to 298 K over the course of 350 ps, and then equilibrated for a period of 1 ns. Production simulations were then carried out in the NPT ensemble for 300 ns, with the temperature maintained at 298 K using the Nosé-Hoover thermostat,²¹ and the pressure maintained at 1 atm using the Parrinello-Rahman barostat.²² A cutoff of 10 Å was applied to short-range nonbonded interactions and the PME method²³ was used to calculate all long-range electrostatic interactions. Covalent bonds were constrained to their equilibrium lengths using the LINCS algorithm,²⁴ allowing a 2.5 fs time step to be employed. Coordinates of the solutes were collected every 0.1 ps giving a total of 3 million structures for analysis for each two-residue peptide.

Analysis and convergence of molecular dynamics simulations

To assess the completeness of sampling in the MD simulations, we calculated the standard deviations of the population distribution for the backbone dihedral angles ϕ and ψ. For each two-residue peptide, the 300 ns simulation period was divided into three time intervals (0-100, 100-200, 200-300 ns). The GROMACS utility g_rama was used to calculate the backbone dihedral angles ϕ and ψ of each residue during the course of each of the three time intervals. 2D histograms of the sampled ϕ and ψ values were then constructed using a bin size of 5° and the standard deviation for each bin was calculated over the three 100 ns intervals. The standard deviations of all bins were summed to obtain total standard deviations for both the N-terminal and C-terminal positions of each two-residue peptide and the two results were averaged to give a single number for each peptide. For the peptides that were found to give the largest average standard deviations (Ile-Pro, Ile-Tyr, Trp-Arg), two independent additional MD simulations, also of 300 ns duration, were performed in order to demonstrate that sampling is likely to be sufficient. A full description of our analysis of convergence of the simulations is provided in the Supporting Information (Figures S1 & S2).

To aid comparison of the conformational preferences of different peptides, each 2D histogram of ϕ and ψ values was converted into free energy form using the relation ΔG = −RT ln (f/f_max), where f is the frequency of sampling a particular bin in the 2D ϕ,ψ histogram and f_max is the maximum frequency found in any of the bins. Since each of the 441 two-residue peptides has two residues, a total of 882 2D free energy distributions were constructed in this way. The data in these histograms were also expressed in an alternative, more concise form as fractional populations of the four major backbone conformations (right-handed helix α, near right-handed helix α’, β-strand, and PPII) computed by summing the populations in the relevant bins of the histograms; definitions for these secondary structure conformations were taken from the literature:²⁵ α: −100° ≤ ϕ ≤ 0°, −80° ≤ ψ ≤ 40°; α’: −160° ≤ ϕ < −100°, −80° ≤ ψ ≤ 60°; β: −180° ≤ ϕ < −100°, 70° ≤ ψ ≤ 180°; PPII: −100° ≤ ϕ ≤ 0°, 70° ≤ ψ ≤ 180°.

To obtain average 2D free energy maps and average secondary structure populations that describe the intrinsic conformational preferences of each type of amino acid when at the N- and C-terminal positions, we summed all frequency distributions for peptides that contained the residue of interest, excluding those peptides that had Gly or Pro as neighbors. For example, to calculate the average fractional populations of the different secondary structures for an Ala residue at the N-terminal position, the fractional populations of the N-terminal residue in the peptides Ala-Ala, Ala-Cys, Ala-Gln … Ala-Val (excluding Ala-Gly and Ala-Pro) were all combined.

To describe the average effects exerted by each type of amino acid on the properties of neighboring amino acids (i.e. neighboring residue effects: NREs), we used the same procedure used by the Cho group to compute NREs on ³Jhnh_α and δh_α values,¹² which we illustrate as follows. To compute the average NRE exerted by a C-terminal Trp on the α population at the N-terminal position, for example, we consider in turn each of the peptides Ala-Trp, Cys-Trp, Gln-Trp … Val-Trp (excluding Gly-Trp and Pro-Trp). For Ala-Trp, we calculate the difference between: (a) the α population at the N-terminal Ala in Ala-Trp, and (b) the mean α population at the same position in all peptides Ala-Ala, Ala-Cys, Ala-Gln … Ala-Val (excluding Ala-Gly and Ala-Pro). We carry out similar calculations for the Cys in Cys-Trp, the Gln in Gln-Trp etc and average the results to obtain the mean change in α population at the N-terminal position induced by the presence of a C-terminal Trp. Similar calculations can be performed for all other types of secondary structure populations and for ³Jhnh_α and δh_α values (see below).

To compute populations of β-turn conformations, which are defined in terms of the backbone conformations of four consecutive residues i, i+1, i+2, and i+3, we identify i with the acetyl capping group (Ace), i+1 with the N-terminal amino acid, i+2 with the C-terminal amino acid, and i+3 with the N-methyl capping group (Nme). We consider all possible β-turns that can be formed with peptide bonds in trans configurations using definitions provided in the literature;²⁶ note that these definitions depend only on ϕ and ψ of residues i+1 and i+2 and so can be meaningfully applied to the capped two-residue peptides studied here even though they do not possess complete amino acids at the i and i+3 positions.

Calculation of ³Jhnh_α coupling constants

Since the work of Karplus, ³J coupling constants have been interpreted in terms of the dihedral angle connecting the two coupled nuclei.²⁷ To compute ³Jhnh_α coupling constants from the simulations, the ϕ backbone dihedral angles of each amino acid were computed for every simulation snapshot and converted using an empirical Karplus relation of the following form: ³J(ϕ) = A cos²(ϕ + θ) + B cos(ϕ + θ) + C, where θ denotes a phase shift value, and A, B, C represent parameters. In this study, we used the parameterization of Hu and Bax,¹⁷ for which A = 7.09, B = −1.42, C = 1.55, and θ = −60°. While a large number of alternative parameterizations are available,^{3, 17, 28} including at least one that has been derived from MD simulations of proteins,²⁹ the particular parameterization used here has been selected for consistency with the earlier study of the Pande group^2c and with other studies;^{2b, 3} other studies have shown that correlation coefficients between simulation and experimental ³Jhnh_α values are insensitive to the specific choice of Karplus parameters.^{2c, 30} As is usual,^{2b, 2c} we assume for most calculations that a single parameterization of the Karplus equation applies equally well to all residue types; we also, however, consider the possibility of deriving residue-specific Karplus parameters in Results.

In comparing with the experimental data reported by the Cho group¹² we omit all peptides containing either Asp or Glu. We have elected to do this because the experiments for these peptides were performed at pH values between 4 and 5 where we expect the sidechains to be partially deprotonated, while our simulations were all performed with the Asp and Glu sidechains in fully deprotonated forms (i.e. more appropriate to a pH of 7). For comparison with experiment, we also omit ³Jhnh_α coupling constants of Gly residues since the experimental data do not identify which of the two Hα protons is probed: experimentally, it has been shown that the ³Jhnh_α values for the two Hα atoms can differ enormously (e.g. by 5.1 Hz for Gly79 in staphylococcal nuclease^28a).

Calculation of chemical shifts

Calculations of δh_α chemical shifts for both residues in each two-residue peptide were performed using the SPARTA+ program;¹⁸ owing to the greater computational expense of these calculations they were carried out only on simulation snapshots sampled at 1 ps intervals (a total of 30,000 snapshots for each peptide). SPARTA+, in common with other chemical shift prediction algorithms,³¹ uses information on the ϕ, ψ angles at neighboring residues i-1 and i+1 when calculating the chemical shifts at position i. This makes use of the program to calculate chemical shifts in our peptides challenging, since the first residue is capped with an acetyl group and so does not have a complete neighbor at the i-1 position, and the second residue is capped with a N-methyl group and so does not have a complete neighbor at the i+1 position. This problem can be mitigated by renaming the two capping groups as Ala residues: this is done by renaming the appropriate atoms and residues in the structure (pdb) file of each snapshot. This simple approach allows us to obtain quite good results for the δh_α chemical shifts, although it works less well for δhn chemical shifts, which are in any case predicted more poorly by SPARTA+;¹⁸ we therefore report only the former here. We also note that while a chemical shift prediction program has recently been reported that has been specifically parameterized using MD data on proteins,³² the peptides studied here are apparently too short to be used with that program.

Results

Comparison of experimental and simulated ³Jhnh_α coupling constants

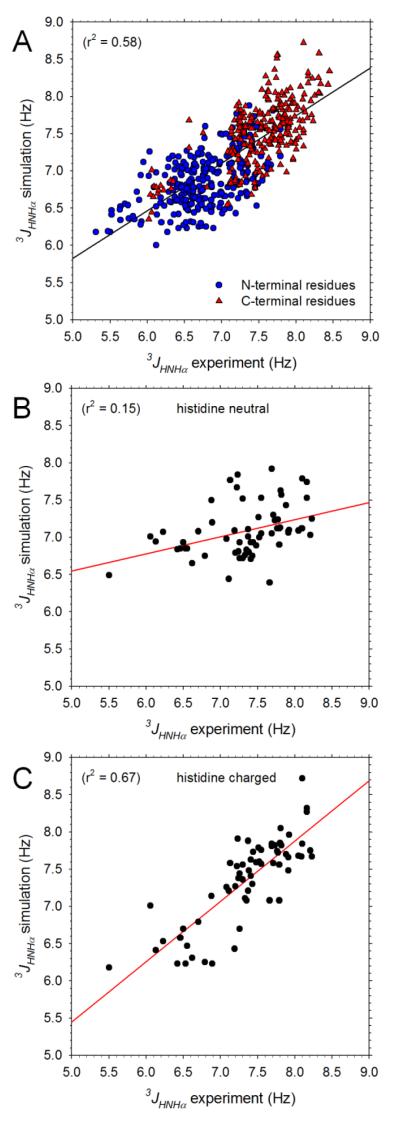
Before analyzing the conformational behavior of the peptides in detail it is first important to determine the extent to which they are consistent with experimental data.¹² Figure 1A compares the simulated and experimental ³Jhnh_α coupling constants for all peptides that do not contain an Asp or Glu residue; owing to uncertainties in experimental assignments we also omit coupling constants for Gly residues (see Methods). The overall level of agreement between the 544 computed and experimental ³Jhnh_α coupling constants is quite reasonable: r² = 0.58. When this figure is replotted including data for Gly residues the r² actually improves significantly to 0.68, but as expected, when data for peptides containing Asp or Glu are added, the r² worsens again to 0.64 (not shown). The degree of agreement with experiment obtained here is similar to that reported recently³⁰ when the same force field and Karplus parameterization was applied to ³Jhnh_α coupling constants of 19 dipeptides (i.e. capped single amino acids):³³ the Pearson correlation coefficient between simulation and experiment is 0.76 here, while that reported previously for the dipeptides is 0.62.³⁰ In addition, however, the simulations reported here also reproduce the experimental observation¹² that, within any given peptide, the ³Jhnh_α coupling constants of residues at the C-terminal position are generally significantly higher than those at the N-terminal position: in Figure 1A, C-terminal ³Jhnh_α coupling constants (red triangles) are consistently shifted upwards relative to N-terminal ³Jhnh_α coupling constants (blue circles).

Figure 1. Comparison of computed and experimental ³Jhnh_α coupling constants.

A. Plot comparing simulation and experimental ³Jhnh_α coupling constants for all non-Gly residues in peptides that do not contain Pro, Asp or Glu; experimental data taken from Jung et al.;¹² black line shows linear regression. B. Comparison of simulation and experimental ³Jhnh_α coupling constants for residues in histidine-containing peptides; simulations modeled histidine using the neutral, His residue type. C. Same as B but plotting data obtained from simulations that modeled histidine using the charged, Hip residue type.

With the exception of the Asp/Glu-containing peptides, all of the experiments were performed at pH 2;¹² at this pH value we expect all histidine sidechains to be in a fully protonated form. We should therefore expect to obtain better agreement with experiment from those simulations that modeled the protonated form of the residue (Hip) than from those that modeled the neutral form (His). Figures 1B and 1C show that this expectation is fulfilled. Figure 1B compares the computed and experimental ³Jhnh_α coupling constants for those peptides that contain histidines using data from simulations that employed the neutral His residue type; the agreement is clearly very poor (r² = 0.15). Figure 1C, on the other hand, shows a corresponding comparison using data obtained from simulations that employed the charged Hip residue type; in this case, the agreement is much better (r² = 0.67), thereby arguing that the simulations are correctly sensing the overall effects of the sidechain’s charge state on the conformational properties of the peptide backbone.

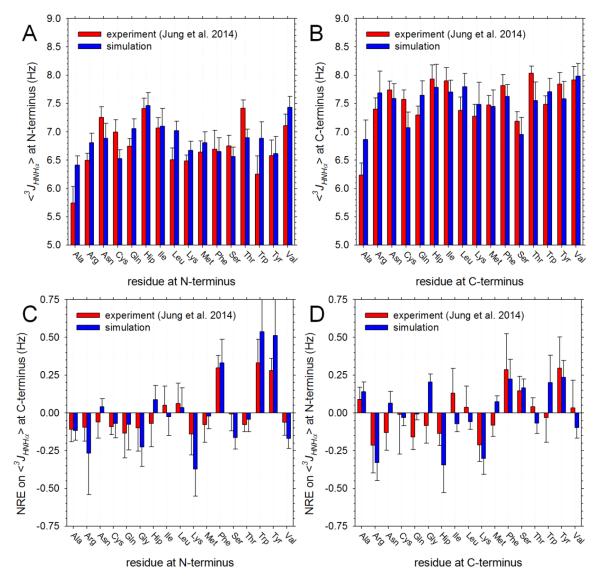
The above results indicate that the simulations perform quite well in reproducing the experimental ³Jhnh_α coupling constants. As might be expected, however, when the data are examined in more detail, significant discrepancies between simulation and experiment emerge. Figure 2A compares the average computed and experimental ³Jhnh_α coupling constants of each type of amino acid when at the N-terminal position of a two-residue peptide. The agreement between the two sets of data is far from perfect (r² = 0.33): in particular, relative to their experimental values, the simulation-average ³Jhnh_α coupling constants for Ala, Leu, Trp and Val are too high while those of Asn, Cys, Ser and Thr are too low. Again, these results are in line with those reported recently for simulations of capped single amino acids using the same force field:³⁰ in that work, Ala and Val were again noted as being too high, while Asn, Cys and Ser were too low. Similar discrepancies between the average computed and experimental ³Jhnh_α coupling constants are also apparent at the C-terminal position of the two-residue peptides (Figure 2B), although here the agreement between simulation and experiment is somewhat higher (r² = 0.45).

Figure 2. Comparison of computed and experimental ³Jhnh_α coupling constants averaged by type of amino acid.

A. Plot showing average ³Jhnh_α coupling constant of each type of amino acid when present at the N-terminal position; all averages obtained from data on 17 peptides (all peptides that do not involve Pro, Asp or Glu); error bars indicate standard deviations. B. Same as A but showing results for each type of amino acid when present at the C-terminal position. C. Plot showing the effect of each type of amino acid, when present at the N-terminal position, on the average ³Jhnh_α coupling constant of amino acids at the C-terminal position (see text); error bars indicate standard deviations. D. Same as C but showing effect of each type of amino acid, when present at the C-terminal position, on the average ³Jhnh_α coupling constant of amino acids at the N-terminal position.

As is considered further below, discrepancies between the computed and experimental ³Jhnh_α coupling constants could be caused by a number of different factors, the most likely of which may be the accuracy of the force field. A comparison between simulation and experiment that we anticipate might be less dependent upon potential errors in the force field is to compare the effect of a given residue type on the average ³Jhnh_α coupling constant at a neighboring position. Figure 2C shows the effects that each type of amino acid, when present at the N-terminal position, has on the average ³Jhnh_α coupling constant at the C-terminal position of the same peptide: red bars show the experimental values calculated as recently described¹² (see Methods), while blue bars show the corresponding simulation values. As noted by the Cho group,¹² the most noticeable effect in the experimental data is that aromatic residues at the N-terminal position increase the average ³Jhnh_α coupling constants of C-terminal residues by ~0.3 Hz. Importantly, this effect is nicely reproduced by the simulations: we find that Phe, Trp and Tyr at the N-terminus cause upward shifts of the average ³Jhnh_α coupling constant at the C-terminus of 0.32, 0.51 and 0.50 Hz, respectively. In fact, the overall level of agreement between the computed and experimental neighboring residue effects (NREs) of N-terminal amino acids is quite high: r² = 0.80, and for 14 out of the 17 residue types studied, the sign of the NRE is correctly reproduced.

For the NREs caused by amino acids at the C-terminal position (Figure 2D), the agreement is considerably less good but still reasonable (r² = 0.39). The largest effects seen in the experimental data are provided by the aromatic amino acids Phe and Tyr, which increase the average ³Jhnh_α coupling constants of N-terminal residues by ~0.3 Hz, and the positively charged amino acids Arg and Lys, which decrease them by ~0.2 Hz. Both of these effects are correctly captured by the simulations. Nevertheless, other significant effects that are predicted by the simulations are not apparent in the experimental data. Gly and Trp, for example, are both predicted to exert positive NREs on the ³Jhnh_α values at the N-terminus, but these are not supported by the experimental data; Hip, on the other hand, is predicted to cause a large negative NRE, and while this is qualitatively supported by the experimental data, the experimental effect is significantly smaller in magnitude.

Origins of discrepancies between experimental and simulated ³Jhch_α coupling constants

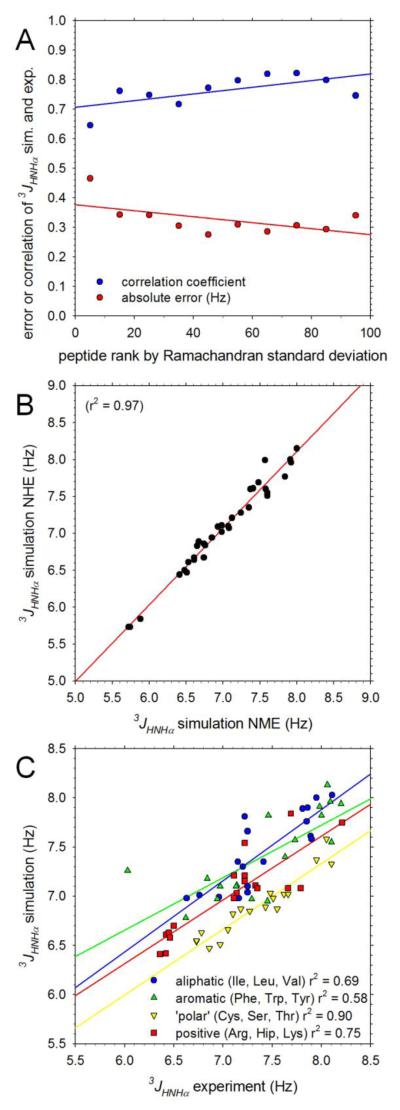
While the overall level of agreement between the computed and experimental ³Jhnh_α coupling constants is quite good, it is clear from the scatter in Figure 1A and from the more detailed comparisons in Figure 2 that there are notable discrepancies. While the obvious and most likely potential source of disagreement is inadequacies of the simulation force field, there are other factors that might play contributing roles. One possible factor is the degree of convergence of the simulations: it might easily be imagined, for example, that simulations that are less completely sampled might produce worse agreement with experimental ³Jhnh_α coupling constants than simulations that are well sampled. To examine this issue we first arranged the peptides studied experimentally in order of increasing standard deviation of their simulated Ramachandran maps (see Supporting Information). We then computed correlation coefficients between the computed and experimental ³Jhnh_α coupling constants for each of the 10 different groups of peptides with ranks in the range 0-10%, 10-20%, … 90-100%; we also computed the mean absolute difference between the computed and experimental ³Jhnh_α coupling constants for each ranked group of peptides. The resulting correlation coefficients and average absolute errors are plotted versus the average rank in each group in Figure 3A. There is no compelling relationship between the extent of conformational sampling and the degree of correlation between the computed and experimental ³Jhnh_α coupling constants. In fact, surprisingly, those peptides for which sampling of the Ramachandran maps is probably the best (left-most datapoints in Figure 3A) produce a somewhat worse correlation with experiment (blue circles), and a higher error (red triangles) than those for which sampling is likely to be worst (right-hand side of Figure 3A).

Figure 3. Factors influencing agreement between computed and experimental ³Jhnh_α coupling constants.

A. Plot showing correlation coefficient (blue) and mean unsigned difference (red) between simulation and experimental ³Jhnh_α coupling constants as a function of the standard deviations of the Ramachandran maps sampled during MD simulations. Peptides are grouped according to their rank in an ordered list of Ramachandran map standard deviations; the datapoints at far-left show the correlation coefficient and error obtained for those peptides with standard deviations in the lowest 10%; the datapoints at far-right show the same for those peptides with standard deviations in the highest 10%. B. Plot comparing computed ³Jhnh_α coupling constants obtained from simulations of identical peptides using NHE (simple amide) and NME (N-methylamide) capping groups. C. Plot comparing simulation and experimental ³Jhnh_α coupling constants for peptides grouped according to their constituent amino acids: datapoints marked aliphatic (blue), for example, are for peptides that contain only Ile, Leu or Val residues.

A second possible factor that might contribute to differences between the computed and experimental ³Jhnh_α coupling constants is the identity of the capping group employed at the C-terminus of the peptides. In the experiments of the Cho group¹² a simple amide group (NH₂) was used at the C-terminus, whereas in the simulations an N-methyl group (NHCH₃) was used since a parallel objective of our work was to generate raw data for deriving coarse-grained potential functions for proteins (see Introduction & Methods); at the N-terminus, both the experiments and the simulations used an acetyl group. To test the potential effects of the difference at the C-terminus we randomly selected 20 peptides and performed replicate 300 ns MD simulations using the same amide C-terminal capping group used in the experiments. As shown in Figure 3B, the ³Jhnh_α coupling constants calculated from simulations using the NH₂ capping group (residue-type NHE) are effectively identical with those calculated from simulations using the NHCH₃ capping group (residue-type NME): the difference between the two corresponding ³Jhnh_α coupling constants averages 0.09 ± 0.09 Hz, with the largest discrepancy (0.42 Hz) being for Met-Trp which is likely to be comparatively poorly sampled (see Supporting Information). This suggests that differences in the termini are not likely to be a significant cause of discrepancies with experiment.

With the above two issues dealt with, we can consider whether inaccuracies in the force field are likely to be responsible for differences between the simulated and experimental ³Jhnh_α values. One very real possibility is that differences in the intrinsic conformational preferences of different amino acids might be incorrectly described by the force field.^{30, 34} An indication that this might be the case is provided by Figure 3C, which shows that quite different regression lines are obtained when the computed and experimental ³Jhnh_α values are compared separately for aliphatic (Ile, Leu, Val), aromatic (Phe, Trp, Tyr), ‘polar’ (Cys, Ser, Thr) and positively charged amino acids (Arg, Hip, Lys): in particular, the regression line for ‘polar’ amino acids (yellow) is shifted down by ~0.5 Hz relative to that for aliphatic amino acids (blue). We note in passing that an alternative explanation that might be considered for this result is that different parameterizations of the Karplus equation might be required for different types of amino acids. Figure S3 shows that the agreement between computed and experimental ³Jhnh_α couplings can be significantly improved if Karplus parameters are optimized separately for individual residue types; a full listing of the resulting residue-specific Karplus parameters is provided in Table S1.

Comparison of experimental and simulated chemical shifts

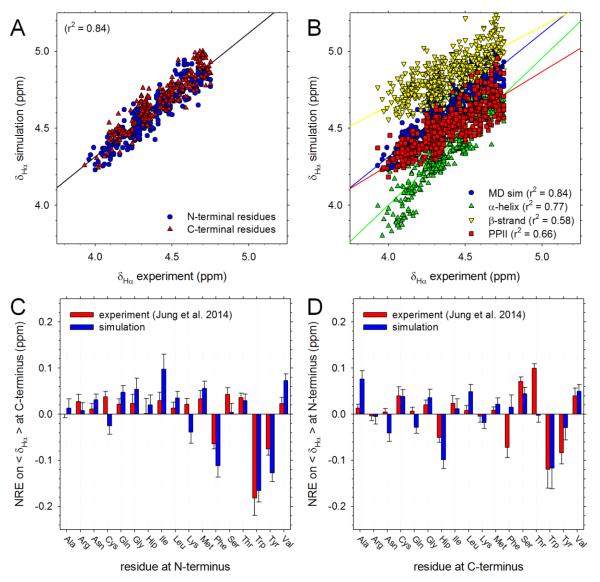
In addition to ³Jhnh_α coupling constants, the Cho group also reported δh_α and δhn chemical shifts for both residues in 361 two-residue peptides. To compare with their data, we used the SPARTA+ program¹⁸ (see Methods). Figure 4A compares the computed and experimental δh_α chemical shifts for all peptides that do not contain an Asp or Glu residue; as before, we also omit values for Gly residues owing to assignment ambiguities (see Methods). The correlation between simulation and experiment is good although the simulated values are clearly shifted upwards by ~0.3 ppm relative to experiment: it is possible that this upward shift is a consequence of our artificially redefining the capping groups as alanine residues (see Methods). While the generally high level of agreement is an encouraging result, it is important to determine the extent to which this results from correct sampling of conformations in the simulations: the chemical shift calculations use a neural network that takes as input the identity of the amino acids involved,¹⁸ so it is possible that this information is instead primarily responsible for the good agreement. To explore this issue, we repeated the chemical shift calculations of all peptides with each built in the following idealized backbone conformations: α-helix, β-strand and PPII. If correct sampling of the backbone distributions is responsible for the good agreement shown in Figure 4A then we should expect to obtain poorer agreement with experiment when a single backbone conformation is used in the calculations. Figure 4B compares the computed δh_α values of all peptides with the corresponding experimental values. All three secondary structures produce good correlations with experiment, with that of the α–helical conformation, surprisingly, being the highest (r² = 0.77). Importantly, however, the correlation coefficient obtained from the MD simulations is considerably higher (r² = 0.84), thereby suggesting that MD’s reasonably realistic sampling of different backbone conformations plays a significant role in determining the agreement with experiment.

Figure 4. Comparison of computed and experimental δh_αchemical shifts.

A. Plot comparing computed and experimental δh_α chemical shifts for all non-Gly residues in peptides that do not contain Pro, Asp or Glu. B. Same as A, but showing results computed when each peptide is restricted to one of three different backbone conformations. C. Plot showing the effect of each type of amino acid, when present at the N-terminal position, on the average δh_α value of amino acids at the C-terminal position (see text); error bars indicate standard deviations. D. Same as C but showing effect of each type of amino acid, when present at the C-terminal position, on the average δh_α value of amino acids at the N-terminal position.

In the same way that NREs on ³Jhnh_α coupling constants can be compared with experiment, it is possible to compare NREs on the average δh_α chemical shifts. Figure 4C shows the effects that each type of amino acid, when present at the N-terminal position, has on the average δh_α coupling constant at the C-terminal position of the same peptide: red bars show the experimental values calculated as recently described,¹² while blue bars show the corresponding simulation values. Experimentally, the largest NREs are again due to the aromatic residues, each of which causes a decrease in the average δh_α chemical shift at a C-terminal position of ~0.1 ppm. Qualitatively, these effects are correctly reproduced by the simulations – the three largest NREs are all due to the aromatic residues – but there are other effects predicted by the simulations that are not mirrored in the experiments: e.g. Ile and Val are both predicted to cause large increases in the average δh_α chemical shifts at the C-terminal position, but much smaller effects are seen experimentally. Despite these discrepancies, the overall level of agreement between the computed and experimental neighboring residue effects (NREs) of N-terminal amino acids is quite high: r² = 0.70, with the sign of the NRE being correct for 14 out of the 17 residue types studied. As was the case with the ³Jhnh_α coupling constants, the agreement for NREs exerted by C-terminal residues on the average δh_α chemical shifts at the N-terminal position is lower (Figure 4D): r² = 0.40, even though the sign of the NREs is correctly predicted for 13 out of 17 residue types.

Average intrinsic backbone conformational preferences of each amino acid

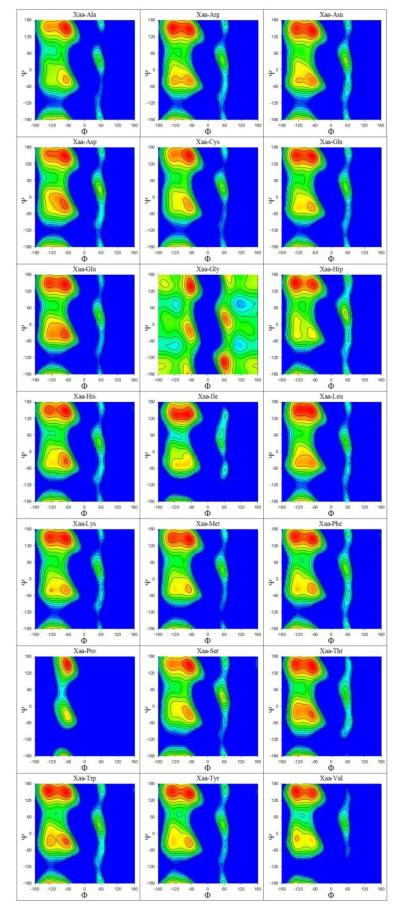
We proceed now with an analysis of the conformational distributions of all 441 two-residue peptides predicted by the simulations. The individual Ramachandran maps (ϕ/ψ distributions) of all peptides are plotted separately for residues at the N-terminal and C-terminal positions in Figures S4 and S5 respectively. Composite maps that describe the intrinsic backbone conformational preferences of each type of amino acid averaged over all possible types of neighboring residues (see Methods) are shown in Figures 5 and 6 for N-terminal and C-terminal positions respectively. Since in all cases we average only over those neighboring residues that are not Gly or Pro, each of the results shown in Figures 5 and 6 represents an average of 19 × 300 ns = 5.7 μs of simulation data; we therefore expect them to be more reliable than Ramachandran maps of any individual system. Figures 7A and 7B show the corresponding average fractional populations of the four major backbone conformations that we consider here (α, α’, β, PPII) for each residue type at the N-terminal and C-terminal positions, respectively. As was the case with the ³Jhnh_α coupling constants described earlier, the average fractional populations of (α + α’), β and PPII obtained from the present simulations are very similar to those reported recently from replica-exchange simulations of 19 dipeptides (capped single residues) performed using the same force field:³⁴ r² = 0.91 (Figure S6).

Figure 5. Average Ramachandran maps at the N-terminus.

Plots showing simulation Ramachandran maps expressed in free energy form for all 21 types of amino acids averaged over all possible C-terminal residues excluding Pro and Gly. Map at top-left, for example, shows the average Ramachandran map of the N-terminal Ala in all peptides of the form Ala-Ala, Ala-Cys, Ala-Gln, Ala-Glu, etc. Free energies are colored in descending order from blue to red.

Figure 6. Average Ramachandran maps at the C-terminus.

Plots showing simulation Ramachandran maps expressed in free energy form for all 21 types of amino acids averaged over all possible N-terminal residues excluding Pro and Gly. Map at top-left, for example, shows the average Ramachandran map of the C-terminal Ala in all peptides of the form Ala-Ala, Cys-Ala, Gln-Ala, Glu-Ala, etc. Free energies are colored in descending order from blue to red.

Figure 7. Fractional populations of four major backbone conformations.

A. Simulated fractional populations of α, α’, β and PPII conformations for all 21 types of amino acids when present at the N-terminal position; results are averaged over all possible C-terminal residues excluding Pro and Gly. B. Same as A but showing results for all 21 types of amino acids when present at the C-terminal position; results are averaged over all possible N-terminal residues excluding Pro and Gly. C. Plot showing effect of each type of amino acid, when present at the N-terminal position, on the average fractional populations of α, α’, β and PPII conformations of amino acids at the C-terminal position. D. Same as C but showing effect of each type of amino acid, when present at the C-terminal position, on the average fractional populations at the N-terminal position. E. Plot comparing the simulated effect of each type of amino acid, when present at the N-terminal position, on the average fractional PPII population at the C-terminal position with that obtained from analysis of a coil library.³⁵ F. Same as E but comparing the simulated effect of each type of amino acid, when present at the C-terminal position, on the average fractional PPII population at the N-terminal position.

Generally speaking, for all non-Pro and non-Gly residue types, the PPII conformation (red squares) is the most preferred conformation, with β-strand (yellow downward triangles) being the next most preferred conformation (Figures 7A and 7B). Amino acids with less clear preferences for PPII include the negatively charged Asp and Glu, protonated His (Hip) and the small polar amino acids Thr and Ser. Asp and Glu show an increased preference for α-helical conformations (blue circles) at both the N- and C-terminal positions, and when found at the N-terminal position (Figure 7A), their α-helical populations are competitive with those of the PPII conformation. For Hip, on the other hand, the preferred conformation in the simulations is the β-strand, regardless of whether it is at the N- or C-terminal position. Other residues showing comparatively high preferences for the β-strand conformation when at the C-terminal position include the three aromatic amino acids (Phe, Trp and Tyr), Arg and Val. One final notable effect is that while the α conformation is clearly preferred over α’ for residues at the N-terminal position (compare blue circles with green upward triangles), this preference larger disappears for residues at the C-terminal position (Figure 7B).

Neighboring residue effects on average backbone conformational distributions

In addition to examining the intrinsic conformational preferences of each type of amino acid, it is also of interest to compute the average effects of each type of amino acid on the conformational preferences of their neighboring residues (see Methods). Figure 7C shows the effects that each type of amino acid, when present at the N-terminal position, has on the average fractional population of each type of secondary structure at the C-terminal position of the same peptide: positive numbers indicate an increase in the average fractional population, while negative numbers indicate a decrease. Perhaps the most obvious effect is that the presence of an aromatic residue (Phe, Trp, Tyr; also His) at the N-terminal position strongly decreases the chances of finding a PPII conformation at the C-terminal position (red squares) and, with the exception of His, also has the surprising added effect of increasing the preference for the α’ conformation (green upward triangles). Importantly, it is this increase in the α’ population at the C-terminal position that is most responsible for the increases in the average computed ³Jhnh_α coupling constants caused by the aromatic residue types in Figure 2C, not an increase in the β population (see Discussion). A second clear effect is that the presence of the positively charged amino acids Arg and Lys at the N-terminal position increases the average PPII population (red squares) at the C-terminal position while suppressing both the α and α’ populations (Figure 7C); the former effect is responsible for the decrease in the average computed ³Jhnh_α coupling constants caused by these residue types in Figure 2C. A third significant observation is that very different NREs are exerted by the different protonation states of the histidine sidechain: the neutral form, His, increases the α and α’ populations (blue circles and green upward triangles, respectively) at the expense of β and PPII, while the protonated form, Hip, does the opposite.

Figure 7D is a corresponding plot showing the effects that each amino acid type, when present at the C-terminal position, has on secondary structure populations at the N-terminal position. The presence of a Pro at the C-terminal position strongly decreases the chances of finding a N-terminal residue in either the α or α’ conformations and accentuates its preference for a PPII conformation; this is in marked contrast to the very minor effects exerted by a N-terminal Pro on the conformational preferences at the C-terminal position (Figure 7C). Again, the presence of a positively charged amino acid (Arg, Hip, Lys) at the C-terminal position increases the population of the PPII conformation at the N-terminal position, and a corresponding but smaller effect results from the presence of a β-branched amino acid at the C-terminal position (Ile, Val). Again, the two protonation states of histidine produce quite different NREs on the conformational properties of N-terminal residues: a C-terminal Hip increases the average PPII population at an N-terminal position by ~8%, while a C-terminal His decreases it by ~5%.

We can compare all of the above changes in populations with corresponding results obtained from a Bayesian statistical analysis of the ‘TCB’ coil library carried out by the Dunbrack group.³⁵ Figure 7E compares the change in average PPII populations at the C-terminus associated with each type of N-terminal amino acid; Figure 7F shows corresponding effects exerted by C-terminal amino acids on populations at the N-terminus. Analogous plots for NREs exerted on α-helical and β-strand populations are shown in Figure S7. For NREs exerted by N-terminal residues (Figure 7E), correspondence between the simulations and the PDB analysis is quite poor: a scatter plot of the two datasets has r² = 0.28 and for only 13 out of 20 residue types are the same qualitative effects predicted. For NREs exerted by C-terminal residues (Figure 7F), on the other hand, agreement is much better: r² = 0.78, and qualitative agreement is obtained for 15 out of 20 residue types. In particular, the very strong effect exerted by a C-terminal Pro seen in the PDB analysis is reproduced (as expected) by the simulations, as is the tendency for aromatic residues at the C-terminal position to decrease the average populations of PPII for N-terminal residues, and for the β-branched residues Ile and Val to increase the populations of PPII. The tendency for Arg and Lys to modestly increase the PPII conformation at neighboring residues is also a consistent feature of the simulations and the PDB analysis.

β-turn populations

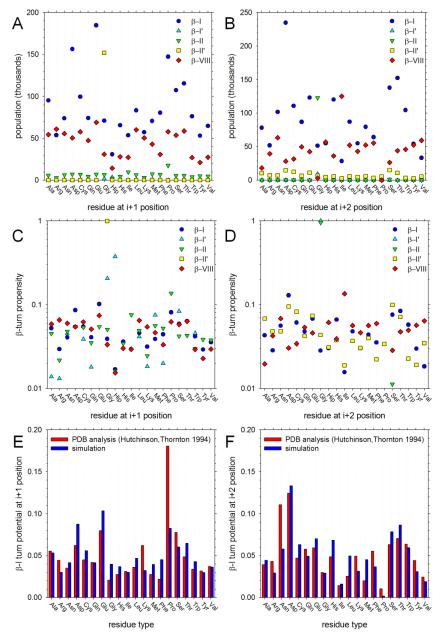
Since our two-residue peptides contain acetyl groups at the N-terminus and N-methyl groups at the C-terminus they can be considered minimal model systems capable of adopting β-turn conformations (see Methods). The average populations of each of the various types of β-turns that can form with all-trans peptide bonds are shown in Figure 8. In the simulations, the populations of β-I (blue circles) and β-VIII (red diamonds) turns are, in general, much higher than those of the remaining turn types β-I’, β-II and β-II’; exceptions include the finding that β-II’ (yellow squares) is common in peptides that contain a Gly at the N-terminal position (i.e. the “i+1” position of a β-turn involving residues i, i+1, i+2 and i+3) and β-II (green downward triangles) is common in peptides containing a Gly at the C-terminal position (i.e. the “i+2” position). For almost all residue types the population of β-I turns is higher than that of β-VIII; exceptions involve peptides containing N-terminal Arg and Lys residues, for which the populations are similar (Figure 8A) and peptides containing C-terminal Ile and Val residues, for which the β-VIII population is clearly higher (Figure 8B).

Figure 8. Sampling of β-turn conformations.

A. MD-sampled populations of five types of β-turn conformation plotted as a function of the identity of the amino acid at the ‘i+1’ (i.e. N-terminal) position (see text). B. Same as A but plotted as a function of the identity of the amino acid at the ‘i+2’ (i.e. C-terminal) position. C. Plot showing the propensity of each type of amino acid to be found at the ‘i+1’ position for each type of β-turn (see text). D. Same as C but showing the propensity of each type of amino acid to be found at the ‘i+2’ position. E. Plot comparing the MD-computed turn potential of each type of amino acid for the ‘i+1’ position of type β-I turns with that obtained from analysis of PDB structures.²⁶ F. Same as E but showing results for the ‘i+2’ position.

The preferences of amino acids for forming different β-turn types are expressed in the form of β-turn potentials²⁶ in Figures 8C and 8D for the N-terminal and C-terminal positions, respectively. Each set of symbols refers to a different type of β-turn; the β-turn ‘potential’ then indicates the fraction of all occurrences of that turn type found in all simulations that involved a residue of a given type. For example, Figure 8C shows that in the combined set of (infrequently sampled) β-I’ conformations (cyan upward triangles), the residue most often found at the N-terminal (i+1) position is Hip, with Gly being a close second; Figure 8D, on the other hand, shows that in the combined set of β-II conformations (green downward triangles) – which are also infrequently sampled – the residue at the C-terminal (i+2) position is almost always a Gly.

For the more frequently sampled turn types (β-I, β-II and β-VIII), the simulation data can be compared with statistics compiled from the PDB.²⁶ Given that 60% of all β-turns formed in the simulations are β-I type turns we show results only for this type of turn; for comparison, 57% of the turns identified by Hutchinson and Thornton in their PDB analysis were of this type.²⁶ Figures 8E and 8F compare the β-turn potentials of β-I type turns reported by Hutchinson and Thornton with those calculated here; Figure 8E shows results for residues at the i+1 (N-terminal) position, Figure 8F shows results for the i+2 (C-terminal) position. For the i+1 position, the correspondence is only modest (r² = 0.40), and the dramatic preference for a Pro residue apparent in the PDB analysis is not mimicked by the simulations. For the i+2 position, on the other hand, the correspondence is more convincing (r² = 0.63): in particular, the simulations reproduce the finding that polar sidechains have high β-I type turn potentials while Pro and the β-branched Ile and Val have low β-I type turn potentials. No closer correspondence is obtained when we compare with an updated β-turn database.³⁶

Discussion

The simulations reported here provide a reasonably comprehensive view of the conformational properties of two-residue peptides simulated with a very widely used force field and water model combination. The comparisons with experimental ³Jhnh_α coupling constants and δh_α chemical shifts show that the simulations achieve an encouraging level of correspondence with experiment. In particular, neighboring residue effects on the ³Jhnh_α and δh_α values are quite well reproduced (Figures 2C, 2D, 4C and 4D). Discrepancies with experiment are likely to be primarily a function of inadequacies in the force field since we have found that neither the convergence of sampling (Figure 3A) nor the type of capping group (Figure 3B) appear to play significant roles in dictating the level of correspondence with experiment; it appears quite possible, however, that residue-specific Karplus parameterizations might ultimately be required for quantitative reproduction of experiment (Figure S3; see below). Agreement between the simulations and previous analyses of conformational distributions in the PDB is less good (e.g. Figure 7E), but there are obvious structural differences between two-residue peptides and proteins that would place limits on the level of correspondence to be expected.

Owing to the large number of systems simulated here – 441 – the computational demands of the present study were significant, and it was principally for reasons of expense that we chose to sample conformational behavior using equilibrium MD simulations: the combined simulation time of the simulations reported here amounts to 130 μs. In the future, it should be possible to exploit increases in computer power to make use of more effective sampling techniques that have thus far typically only been used on much smaller numbers of systems. Examples include: (a) the metadynamics³⁷ method used to study single amino acids with a variety of force fields³⁸ – and which showed that there was little consensus among the tested force fields regarding backbone conformational preferences – (b) the Hamiltonian replica-exchange MD (REMD) methods that have been used to study neighbor effects on the conformational behavior of a number of small Ala, Val, or Phe-containing peptides,³⁹ and (c) the more conventional replica exchange methods⁴⁰ used in the iterative development of the recent RSFF1³⁰ and RSFF2³⁴ force fields. Improved sampling would have the added benefit of enabling comparisons between simulation and experiment to be performed on an individual peptide-by-peptide basis with confidence. This could be important given that the Cho group has noted¹² that the NREs exerted by a given type of amino acid can vary significantly depending on the identity of the other amino acid being examined: for example, the NRE exerted by a C-terminal Trp on the ³Jhnh_α of an N-terminal Arg is −0.32 Hz while that exerted on an N-terminal Asn is +0.27 Hz.

Reproduction of experimental results

Although the force field and water model combination used in this study has already been shown to be one of the best currently available for reproducing a variety of NMR observables in both peptide^2c and protein systems,⁴¹ the simulations reported here provide an opportunity to explore its ability to reproduce a much larger body of NMR data for two-residue peptides. The generally good reproduction of the experimental ³Jhnh_α values for two-residue peptides appears notable since the force field was optimized to reproduce NMR data for proteins, not peptide systems,⁸ and since the original parameterization did not consider scalar coupling constants but focused instead on chemical shifts. This, together with the observation that the NREs on ³Jhnh_α and δh_α values can also be reasonably well captured (see below) reiterates the point made by others that the force field selected here performs quite well;^2c it is to be noted, however, that it has recently been shown to be incapable of producing a stable structure for the GB1 hairpin.³⁴

That said, the agreement between the computed and experimental ³Jhnh_α values is far from perfect. Sampling issues aside, it appears most likely that this is due to errors in the force field’s description of the intrinsic conformational preferences of individual residue types since there are systematic differences between the average ³Jhnh_α values measured in the simulations and those measured experimentally (Figures 2C and 2D) that appear to depend on the type of the amino acid. Discrepancies between the computed and experimental ³Jhnh_α values for capped single amino acids using the same force field have also been reported recently,³⁰ and the authors of that work have shown that a reparameterization of the Amber ff99SB force field to match conformational distributions observed in a coil library gave ³Jhnh_α values for capped single amino acids in much better agreement with experimental values.³⁴ For the future, therefore, it will be of interest to examine whether that new force field, RSFF2, leads to improved agreement with experiment for ³Jhnh_α couplings of two-residue peptides.

While we think that the force field is the most likely cause of the discrepancies between computed and experimental ³Jhnh_α values, it is intriguing to note that better agreement can also be achieved using Karplus parameters that are optimized independently for each type of amino acid (Figure S3 and Table S1). It has long been recognized that ³J (vicinal) coupling constants can be sensitive to factors in addition to the dihedral angle connecting the nuclei, e.g. substituent effects,⁴² and the possibility of using residue-specific Karplus parameterizations in the analysis of MD simulations has been noted by others.^{2b, 6} A comprehensive determination of all of the factors that determine ³Jhnh_α values in peptides and proteins may in the future come from mixed quantum mechanical-molecular mechanical (QM-MM) calculation methods that have recently been applied to proteins.⁴³

Neighboring residue effects

An understanding of the effects that neighboring residues exert on the conformational behavior of other residues is essential for accurate predictions of the conformational ensembles of proteins;¹¹ such effects have been the subject of a very recent comprehensive review by Toal and Schweitzer-Stenner.⁴⁴ NREs can be manifested in a number of ways: the PPII propensities⁴⁵ and chemical shifts⁴⁶ of amino acids in short peptides, for example, can depend significantly upon the sequence in which they are embedded, and ³Jhnh_α values in unfolded proteins are typically higher for residues that are preceded by bulky, branched or aromatic residues;⁴⁷ NREs can also be inferred by conformational analysis of protein structure databases.^{35, 48} Here, the focus has been on NREs between amino acids that are adjacent to each other in sequence, but it should be remembered that statistical analysis of coil conformations indicates that interactions between residues at i-1 and i+1, for example, can alter the conformational preferences of an intervening residue i,⁴⁹ and that steric interactions of residues that are not immediate neighbors can also affect the conformational possibilities open to oligopeptides.⁵⁰

To our knowledge, this is the first simulation effort aimed at explicitly reproducing experimental NREs in a comprehensive set of peptide systems. Implicit solvent simulations performed by the Freed and Sosnick groups on a number of two- and three-residue peptides had previously shown that the conformational properties of Ala are sensitive to the identity and conformation of neighboring residues and showed that these NREs were also sensitive to the simulation force field.⁵¹ Monte Carlo simulations performed by the Pappu group using purely steric potential functions explored the influences of neighboring Gly, Ala, Phe, Val and Pro residues on the secondary structure preferences of amino acids in pentameric host-guest peptides;⁵² we find little correspondence with their data (not shown) but this is not surprising given the differences in the peptides and potential functions used in the two studies.

More recently, the Liu group³⁹ has reported using Hamiltonian-REMD simulations together with the GROMOS 53A6 force field⁵³ to explore the conformational free energies of a variety of peptide systems, in particular exploring the NREs exerted by Ala, Phe and Val residues on the conformational behavior of a neighboring Ala. Their study showed that the backbone conformation adopted by the neighboring residue could in some cases play a more significant role in influencing the conformational preferences of a residue of interest than the neighboring residue’s identity;³⁹ an important implication of their study, therefore, is that errors in the intrinsic backbone preferences of amino acids – which are apparent for the force field used here (see above) – could lead to errors in their computed NREs. Finally, the Cho group has used equilibrium MD simulations of 30 ns duration each to model the conformational behavior of the two-residue peptides that they studied experimentally;¹³ the computed free energy differences between the PPII and β-strand conformations obtained from their MD simulations, however, yielded no correlation with the corresponding experimentally derived values.⁵⁴ It is not clear to what extent the poor correlation that they obtained might have been due to the comparatively short simulation time, the force field used (Amber ff03⁵⁵), or to the decision to average the two ³Jhnh_α values measured for each two-residue peptide in order to obtain average PPII and β-strand populations.

While the correspondence between the simulation and experimental results reported here is by no means quantitative, one clear success of the simulations is in reproducing the experimental results¹² showing that δh_α chemical shifts and ³Jhnh_α values in two-residue peptides are altered significantly by neighboring aromatic residues. A previous analysis of a protein coil library had suggested that bulky, branched or aromatic residues (analyzed as a single group) tended to increase the β-strand population of following residues,⁴⁷ and this effect had been interpreted in terms of electrostatic solvation free energy differences between bulky and non-bulky residues in a β-strand model of an (Ala)₉ peptide.⁵⁶ It is apparently in light of these earlier studies that the Cho group has interpreted the increased ³Jhnh_α values caused by neighboring aromatic residues as indicating an increase in the fractional β-strand population.¹² Interestingly, however, while the simulations reported here nicely reproduce the experimental changes in ³Jhnh_α values due to neighboring aromatic residues (Figure 2C), the origins of these changes are quite different: here, they are instead caused primarily by an increase in the α’ population. Importantly, both interpretations represent plausible explanations of the experimental results: the ϕ angle ranges of α’ and β conformations are similar and their ³Jhnh_α values are also, therefore, expected to be similar. If the increases in α’ population predicted by the simulations were to be confirmed by direct experimentation it would provide nice support for the idea of using simulations as a means of rationalizing and interpreting experimental results.

Protonation state effects

A final important result of the work reported here is that the protonation state of the histidine sidechain can significantly affect both its backbone conformational preferences and those of adjacent residues. Although not explicitly commented upon by the authors, the finding that the protonation state of a residue can affect its intrinsic backbone conformational preferences is apparent also in simulation work by the Vondrášek group for histidine and for a number of other amino acids.³⁸ Importantly, the finding that backbone preferences of amino acids can be affected by their protonation state is also supported by experimental work³³ showing pH-dependent changes of ~0.5 Hz in the ³Jhnh_α values for Asp and Glu; these have been interpreted in terms of protonation-state dependent alterations in the populations of β-strand conformations.¹⁹ Other experimental work has indicated that the PPII propensity of Asp also depends significantly upon the protonation state of its sidechain.^45c

While the effects of sidechain protonation state on the intrinsic conformational preferences of amino acids have been noted elsewhere, the results reported here provide, to our knowledge, the first indication that significant effects can also be exerted on the conformational preferences of neighboring residues. The largest such effect is seen on the average α-helical population of residues C-terminal to histidine: the average equilibrium constant for the α:PPII equilibrium changes from (0.32/0.25 = 1.3) with His at the N-terminus to (0.04/0.45 = 0.10) with Hip at the N-terminus: in free energy terms this amounts to a relative change in the ΔG for the α:PPII interconversion of ~1.4 kcal/mol at 298 K. If validated experimentally, such a change would have obvious potential implications for attempts to understand how changes in protonation state contribute to the pH dependence of protein stability.