Ion specific effects: decoupling ion-ion and ion-water interactions

Abstract

Ion-specific effects in aqueous solution, known as the Hofmeister effect is prevalent in diverse systems ranging from pure ionic to complex protein solutions. The objective of this paper is to explicitly demonstrate how complex ion-ion and ion-water interactions manifest themselves in the Hofmeister effects, based on a series of recent experimental observation. These effects are not considered in the classical description of ion effects, such as the Deryaguin-Landau-Verwey-Overbeek (DLVO) theory that, likely for that reason, fail to describe the origin of the phenomenological Hofmeister effect. However, given that models considering the basic forces of electrostatic and van der Waals interactions can offer rationalization for the core experimental observations, a universal interaction model stands a chance to be developed. In this perspective, we separately derive the contribution from ion-ion electrostatic interaction and ion-water interaction from second harmonic generation (SHG) data at the air-ion solution interface, which yields an estimate of ion-water interactions in solution. Hofmeister ion effects observed on biological solutes in solution should be similarly influenced by contributions from ion-ion and ion-water interactions, where the same ion-water interaction parameters derived from SHG data at the air-ion solution interface could be applicable. A key experimental data set available from solution systems to probe ion-water interaction is the modulation of water diffusion dynamics near ions in bulk ion solution, as well as near biological liposome surfaces. It is obtained from Overhauser dynamic nuclear polarization (ODNP), a nuclear magnetic resonance (NMR) relaxometry technique. The surface water diffusivity is influenced by the contribution from ion-water interactions, both from localized surface charges and adsorbed ions, although the relative contribution of the former is larger on liposome surfaces. In this perspective, ion-water interaction energy values derived from experimental data for various ions are compared with theoretical values in the literature. Ultimately, quantifying ion-induced changes in surface energy for the purpose of developing valid theoretical models for ion-water interaction, will be critical to rationalizing the Hofmeister effect.

1. Specific ion effects: basis for the general effect underlying diverse solution systems

Specific ion effect, also known as the Hofmeister effect has been shown in diverse phenomena since F. Hofmeister first published the paper “about the science of effect of salts” in 1888^{1, 2}. In the original work, he showed that ion’s ability of changing the egg globulin solubility was different from ion to ion. Although a vast of focus was manifested in his protein precipitation study, he also showed that the same phenomena occur in isinglass, colloidal ferric acid, and sodium oleate with a specific order of ion’s ability that change the precipitation behavior of different materials, known as the Hofmeister series, as follows³:

$$\begin{array}{l}{{\text{SO}}_4}^{2-}>{\mathrm{F}}^{-}>{{\text{HPO}}_4}^{2-}>{\text{CH}}_3{\text{COO}}^{-}>{\text{Cl}}^{-}>{\text{Br}}^{-}\approx {{\text{NO}}_3}^{-}>{\mathrm{I}}^{-}>{{\text{CIO}}_4}^{-}>{\text{SCN}}^{-}\\ {{\text{NH}}_4}^{+}>{\mathrm{K}}^{+}\approx {\text{Na}}^{+}>{\text{Li}}^{+}>{\text{Ca}}^{2+}\gg {\text{GuH}}^{+}\end{array}$$

The specific ion effect is so prevalent that it manifests itself across vastly diverse systems. The pH of water and buffer depends on the ion species in solution⁴, and the viscosity of water changes with ion types, which is known as the Jones-Dole effect^{5, 6}. The surface tension^7–9 and the surface potential^10–12 of ion solutions, and therefore the liquid bubble coalescence which is driven by surface tension, is inhibited by ions to different extent from ion to ion^{13, 14}. Not only do different ions affect the solubility of small molecules such as benzene¹⁵ and various amino acids^{16, 17}, ion’s property themselves are differentially affected by the structure of the solvent as shown in the variation in ion conductance¹⁸. Also, the carbon chain of octadecylamine monolayers¹⁹ and of lipid bilayers^{20, 21} rigidify to different extent depending on the ion species in solution.

Even when focusing on the phase behavior of macromolecules and complex structure formation/aggregation of biomolecules, specific ion effects play an important role as summarized in many reviews^{3, 22–27}. This covers a broad range of phenomena, from changes in the critical micelle concentration of alkyltrimethyl ammonium²⁸, phase diagram of microemulsion made of DDAB/decane/water²⁹, hyaluronan film swelling³⁰, critical temperature of PNIPAM³¹, repeat distance of a multilamellar bilayer membrane³², gel-fluid phase transition temperature and lamellar to inverted hexagonal phase transition temperature of POPE³³, colloid stability^{22, 33–35}, and lysozyme cloud-point temperature³⁶. The equilibrium constant for the formation of biomolecular complexes such as β-sheet rich amyloid fibrils³⁷, collagen-fold³⁸, or that of γ-cyclodextrin and carboxylate in α-hemolysin nanopore³⁹ also depend on ion species in solution.

Aqueous ion solutions are very interesting systems, not only because they are the medium of biological importance, but also because they show the specific effect of ion chemistry that leads to the failure of the Deryaguin-Landau-Verwey-Overbeek (DLVO) theory to describe charged interparticle interactions⁴⁰. The DLVO theory relies on a discrete physical origin of the electric field with its fluctuation expressed in terms of van der Waals and electrostatic forces. It is not clear whether the DLVO theory can still hold when the unknowns of specific ions, such as their spatial distribution, are taken into account, or whether the DLVO model fundamentally fails with ions given the complexity of the involved interactions. However, the common empirical trend seen in macromolecular interactions induced by ions persistently following trends of the Hofmeister effect, and thus offers evidence that systematic variations in ion properties are the effectors.

The characteristics of aqueous ion solutions are intrinsically complex because at least three components, the cation, the anion and solvent water molecules, as well as their interactions must be considered. Furthermore, each of the components may experience complex anisotropic interactions with each other, depending on the chemistry of the ions and solvent molecules, whose nature is still a current topic of research. Somehow, the interplay of these many interactions manifests itself in a clear-cut trend known as the Hofmeister effect that offers a common empirical denominator to which we can trace back and test a model that attempts to describe the fundamental interactions between ions and water. Here, the surface concentration of ions⁴¹ has been considered as the most important parameter to bridge the fundamental interactions between ions and water and the phenomenological Hofmeister effect⁴². Based on equilibrium statistical physics, the surface ion concentration is determined by the ion’s energy at the surface versus in the bulk. When the surface ion concentration is known, surface properties that follow the Hofmeister series, such as changes in the surface tension and the interaction between two surfaces can be calculated. However, even though the surface ion concentration may be a key parameter in order to understand the Hofmeister effect, it is not the fundamental modulator because it is determined by the ion’s interaction energy at the surface versus in the bulk. Ion’s interaction energy, which is microscopically decomposed into ion-ion and ion-water interactions, is the most fundamental modulator, which still is an unknown quantity and a topic of ongoing debate and research.

In this perspective, an approach of using the surface ion concentration as a key connecting parameter will be tested with experimentally derived excess charge density values, which is defined as the difference between the anion and cation concentration at the surface. First, the excess charge density at various air-ion solution interfaces will be presented, whose magnitude follows the Hofmeister series. Second, the ion’s energy is inferred from the excess charge density and quantitatively compared with various theoretical or simulated potential energies proposed in the literature. Third, the surface tension increment at various air-ion solution interfaces, as well as the interaction between model surfaces are calculated with the known or modeled surface ion concentration, and compared with experimental results. Finally, ion’s effect on water diffusion near small chemical probes in solution, as well as near various surfaces will be presented as an independent indicator to evaluate the nature of ion-water interaction.

2. Surface ion concentration: theoretical and experimental studies

When ions are dissolved in water, cations and anions are dissociated. In the presence of a solute or a macroscopic surface or interface, the concentration of the cation and anion can be different up to a certain distance from the surface, although their concentrations eventually converge to be equal to that in bulk solution to achieve charge neutrality. The most notable experimental exhibition of the mismatch between cation and anion concentration at a surface can be seen by x-ray photoelectron spectroscopy of the liquid/vapor interface in a saturated ion solution. In their study, S. Ghosal et al. irradiated x-rays at the aerosol made of saturated ion solutions and measured the photoemission from the potassium cation and bromide/iodide anion⁴³. The higher the x-ray intensity, the deeper the x-ray penetrates into the liquid/vapor interface, so that it yields the photoemission intensity ratio of cation and anion as a function of the distance from the surface. Surprisingly, there are more anions closer to the interface, and the iodide/potassium ratio was larger than the bromide/potassium ratio. Not only is the surface concentration of cation and anion different, but there are also ion-specific variations.

The first attempt to calculate the surface concentration of cations and anions of different sizes, and the surface tension was by L. Onsager et al. in 1934⁴⁴, whose objective was to explain the measured surface tension increase by ions in solution⁴⁵. Onsager was aware that the air-ion solution interface is a dielectrically discontinuous interface so that charged ions have an image charge potential from the interface. With the image charge potential that depends on the distance of the ion from the interface, he calculated the surface ion concentration from the Boltzmann distribution and the surface tension from the calculated surface ion concentration. Table 1 shows the unhydrated radius of various ions and their image charge potential at the distance corresponding to the ion radius. As the size of the ion increases, the image charge potential decreases. So, while ions in general are excluded from the air-ion solution interface, larger size ions are less excluded. A similar analysis was extended to include the dispersion forces at various interfaces by B. W. Ninham et al.^{40, 46–48}, whose origin lie in the quantum mechanical polarization response from a given material, also known as the van der Waals force^{49, 50}. Unfortunately, these dispersion forces are non-additive, and not easily predictable for different surfaces. However, by making assumptions to determine a few parameters such as the excess polarizability and the electron affinity of ions, the surface ion concentration was numerically calculated using the Poisson-Boltzmann distribution⁴⁰.

Table 1.

Unhydrated radius, self-energy, image charge potential, and hydrogen-bond perturbation energy of various ions.

ion species	unhydrated radiusa [Å]	self-energy in bulka [kBT]	image charge potential at the interfaceb [kBT]	hydrogen-bond perturbation energyc [kBT]
Na+	0.95	−3.66	1.83	0.43
K+	1.33	−2.61	1.31	1.18
NH4+	1.48	−2.35	1.17	1.62
F−	1.36	−2.56	1.28	1.26
Cl−	1.81	−1.92	0.96	2.96
Br−	1.95	−1.78	0.89	3.71
I−	2.16	−1.61	0.80	5.04
NO3−	2.64	−1.32	0.66	9.20

^aUnhydrated radius is from the book by J. Israelachvili⁶⁵ and ion’s self-energy was calculated with water dielectric constant ε_water ~ 80.

^bFrom the equation by L. Onsager et al.⁴⁴ at the distance of ion’s unhydrated radius and at infinite dilution.

^cFrom hydrogen-bond perturbation energy 0.5 k_BT/Ų by Y. Levin⁵⁴.

P. Jungwirth et al.^{41, 51, 52} simulated the ion concentration at the air-ion solution interface and calculated the surface tension from this, while including the polarization potential of ions⁵³. Their results described the experimental trends for ion surface concentration and surface tension changes induced by specific ions fairly well, but large ion polarizability had to be included empirically for the polarizable potential, whose physical origin is not validated. Y. Levin⁵⁴ adopted the water hydrogen-bond perturbation energy from hydrophobic hydrations⁵⁵, and calculated the ion concentration at the air-water interface with hydrogen-bond perturbation energy as the driving force for ions to reside at the interface, as listed in Table 1. However, because the ion’s potential energy in aqueous solution and the air-ion solution interface is not derived from a known physical origin or too simplified as in the image charge potential, often alternative approaches were taken by optimizing parameters of force fields in molecular dynamics simulation to obtain the ion’s potential energy⁵⁶, and from there infer the origin of molecular interaction between ion and water molecules. Although molecular dynamics simulations pursues to describe interactions modulated by specific ion with molecular details at realistic interfaces, such as lipid bilayers^{57, 58},, the results strongly depend on the force fields used⁵⁷.

The current status of theoretical calculations of surface ion concentration based on the Poisson-Boltzmann distribution of ions exploits two approaches. One is to model the potential energies, calculate the surface ion concentration and surface tension, and to compare them with experimental results to validate the proposed potential energy model. This approach has the advantage of offering a physical origin for the proposed potential in advance, but has not been successful in finding a general working model for the ion’s potential energy. The other is to start from experimental results on the surface ion concentration and surface tension, then trace back the ion’s potential energy, and decompose the energy into the force-field parameters with known forms as in molecular dynamics simulation. However, this approach suffers from insufficient data to find optimal fitting for many basic interaction parameters.

Experimentally measuring ion concentrations at any interface directly is extremely difficult, and subject to assumptions about the depth of the interface. Grazing incidence x-ray fluorescence can infer the cation and anion concentration at the interface as a ratio with bulk ion concentration⁵⁹, while x-ray photoemission spectroscopy can get the concentration ratio between the cation and anions at the interface, but not the absolute concentration values⁴³. From the ion-specific swelling behavior and changes in area per lipid under osmotic pressure in lipid bilayer system, the ion concentration adsorbed at the lipid surface can be indirectly inferred from^{60, 61}. The ion concentration at the air-ion solution interface can also be obtained with second harmonic generation (SHG), which is intrinsically a surface-specific optical technique. Because SHG is based on the induced electric dipole moment, its signal only appears where the centrosymmetry is broken, such as at the interface between isotropic media. R. J. Saykally et al. calculated the iodide concentration at the air-ion solution interface, assuming that the second-order susceptibility tensor creates the second harmonic electric field, and thus the SHG signal, that changes with ion concentration⁶². J. Song et al., on the other hand, determined the excess charge density at the air-ion solution interface by using cationic SHG probes, as will be further discussed in detail^{63, 64}. Because there is no omnipotent experimental tool for determining surface ion concentration free of assumptions, experimental insight from various experimental techniques has to be put together to validate ion concentrations at the surface.

3. Excess charge density at the interface: separating electrostatic and ion-water interactions

In the previous section, surface ion concentration has been proposed to be the bridging parameter between fundamental ion/water interaction and the phenomenological Hofmeister effect. When the cation and anion concentrations were known as a function of distance from the surface, the excess charge density defined as the the difference in cation and anion concentration can be obtained, but these are not easily experimentally determined. There is a way to overcome these difficulties by using charged probes that adsorb at the surface, whose adsorbed amount increases with increasing excess charge density. The excess charge density at the interface is a function of the distance from the interface, and eventually disappears with the distance from the interface to the bulk. Importantly, the excess charge density can yield valuable predictions on key surface properties, such as the surface tension, as will be closely examined in a later section.

Using charged probes that adsorb at the interface with excess charge density σ, the adsorption Gibbs free energy ΔG of N charged probes at a surface that faces a solution with a bulk inverse Debye screening length κ can be calculated. Assuming a two-state model with the probe molecule either in the surface or the bulk state, the adsorption free energy can be calculated from changes in the energy and entropy associated with adsorption. From linearized Poisson-Boltzmann equation, the electric field E at a flat surface with charge density per unit area σ and facing a solution with bulk inverse Debye screening length κ as shown in Fig. 1(a) is expressed as⁶⁶

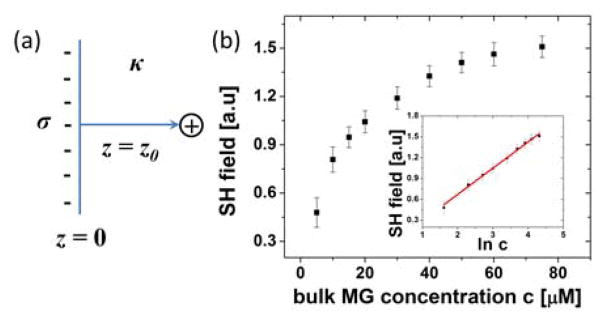
Figure 1.

(a) Illustration of the surface of charge density σ and the bulk inverse Debye screening length κ for oppositely charged probe molecules to adsorb. z is the distance from the interface. (b) Malachite Green (MG), a cationic SHG probe molecule, the adsorption isotherm at the air-ion solution interface with 1M bulk KCl concentration in solution, with data taken from ref. 64. The SHG field is proportional to the adsorbed MG concentration. In the inset, the SHG field is plotted over the natural logarithm of the bulk MG concentration, ln c, with the solid, a linear fit with Eq. (7).

$$E=-4\pi l_B{k}_{B}T\sigma e^{-\kappa z},$$ (1)

at a distance z from the surface. Here, l_B is the Bjerrum length, T is the temperature in Kelvin unit, and k_B is the Boltzmann constant. Therefore, the electrostatic energy gain of a oppositely-charged probe to be at the position z₀ from the surface, U(z₀), is

$$U\left(z_0\right)=\underset{\infty }{\overset{z_0}{\int }}4\pi l_B{k}_B\sigma e^{-\kappa z}dz={-\frac{4\pi l_B{k}_{B}T\sigma e^{-\kappa z}}{\kappa }|}_{\infty }^{z_0}=-\frac{4\pi l_B{k}_{B}T\sigma e^{-\kappa z_0}}{\kappa }.$$ (2)

$$U(0)=-\frac{4\pi l_B{k}_{B}T\sigma }{\kappa }.$$ (3)

To decouple the electrostatic energy of the charged surface from other types of energies, let E_b and E_s stand for the energies of one probe molecule in the bulk and one probe molecule at the surface, excluding electrostatic energy from the surface due to its excess charge density, respectively. As listed in Table 1, the source of the bulk and the surface energy may include image charge potential, dispersion energy, hydrogen-bond breaking energy, and the attraction potential between solvent water and the charged probe molecule. From the surface energy E_s and the electrostatic term as expressed in Eq. (3), the gain of surface energy, U_S(N), for N molecules to be at the surface can be expressed as⁶³

$$U_S(N)=\underset{0}{\overset{N}{\int }}\left[E_S-\frac{4\pi l_B{k}_{B}T}{\kappa }\left(\sigma -\frac{x}{A}\right)\right]dx=\left(E_S-\frac{4\pi l_B{k}_{B}T\sigma }{\kappa }\right)N+\frac{2\pi l_B{k}_{B}T}{\kappa }\frac{N^2}{A}.$$ (4)

with the decrease in the excess charge density σ by the adsorption of the oppositely charged probe molecule taken into account. In contrast, the bulk energy, U_b(N), of N molecules to be in the bulk solution is U_b(N) = E_bN.

Neglecting contribution of the 2D entropy on a surface that is smaller compared to in bulk ⁶⁷ and in the thermodynamic limit, the net entropy loss for moving N probes from the bulk to the surface, ΔS_b, can be expressed as⁶⁶

$$\mathit{\Delta }{S}_b=-k_{B}TN\left[ln\left(c{\upsilon }_0\right)-1\right],$$ (5)

where c is the bulk concentration of charged probe molecules and υ₀ the specific volume of the charged probe molecule. From Eq.s (4) and (5) and defining ψ = E_s - E_b, the Gibbs free energy change for N probe molecules to adsorb at the surface from bulk solution is then⁶³

$$\mathit{\Delta }G=U_S(N)-U_b(N)+T\mathit{\Delta }{S}_b(N)=\left(\psi -\frac{4\pi l_B{k}_{B}T\sigma }{\kappa }\right)N+\frac{2\pi l_B{k}_{B}T}{\kappa }\frac{N^2}{A}+k_{B}TN\left[ln\left(c{\upsilon }_0\right)-1\right].$$ (6)

The number of adsorbed probe molecules at the surface in equilibrium, N₀, that minimizes the Gibbs free energy for adsorption, according to Eq. (6), is as follows⁶³,

$$\frac{N_0}{A}=\frac{\kappa }{4\pi l_B}\left[ln\left(c{\upsilon }_0\right)-\left(\frac{\psi }{k_{B}T}+1-\frac{4\pi l_B\sigma }{\kappa }\right)\right].$$ (7)

When the interface is not charged, therefore in the absence of the electrostatic term in Eq. (6) which is proportional to σ and N², the number of molecules adsorbed at the surface in equilibrium follows the Langmuir adsorption isotherm^{63, 67}. From Eq. (7), we can see that the larger the excess charge density, σ, at the surface, the greater N₀, i.e. the more oppositely charged probe molecules will adsorb at the surface.

Because anion concentration is known to be larger than the cation concentration at the air-ion solution interface as it is closer to the interface^{43, 51, 59}, in effect the interface is negatively charged. Using Malachite Green (MG) with size of ~ 1 nm as a cationic SHG probe of valence 1, in resonance at the 420 nm wavelength, the excess charge density at the air-ion solution interface was obtained for different ions at varying bulk ion concentration^{63, 64} by analyzing the MG adsorption isotherm. In resonance SHG, the number of SHG probes, MG in this case, is proportional to the second harmonic (SH) field, which is the square root of the measured SH intensity. The SH field at 20 μM MG concentration in 1 M NaCl solution was arbitrarily set to 1 and is proportional to N₀. Fig. 1(b) shows a typical MG adsorption isotherm at an air-ion solution interface at 1M bulk KCl concentration, as plotted from data in ref. ⁶⁴. In the inset, the natural logarithm of the bulk MG concentration, ln c, was used as the x-axis, so that the expected linear-dependence of the SH field that is proportional to N₀ as expressed in Eq. (7), can be verified. MG is soluble in water up to 200 mM at room temperature, implying that there are no specific interaction between MG and the electrolyte ions. Because the concentration between the MG probe (~100 μM) and the added ions (50 mM ~ 1M) used in the experiment is different by orders of magnitude, while MG does not display specific interactions with added ions at dilute concentrations of ~100 μM, the excess surface charge density and screening of electrostatic interactions can be assumed to be from the added ions. Thus, MG can be treated as a dilute probe charge that is attracted to the surface with excess negative charges. The justification for these assumptions and the linearization of the Poisson-Boltzmann equations has been empirically verified, as the experimentally obtained MG adsorption isotherm and the excess charge density follow the predictions of the theory presented here with Eqns. (7) as shown in the insets in Figure 1(b).

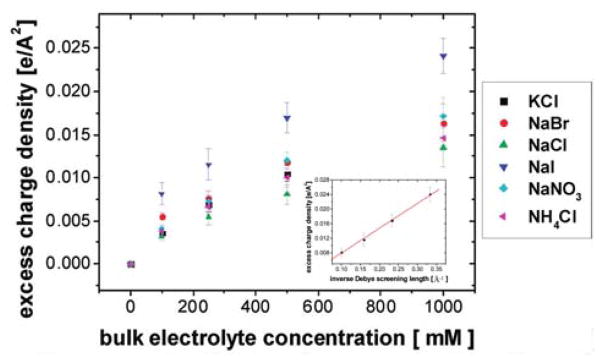
By fitting the measured MG adsorption isotherm at the air-ion solution interface with different ions in solution with Eq. (7), the excess charge density σ can be obtained as a function of bulk ion concentration and ion species. As the SH field is proportional to N₀ up to one molecular layer⁶⁸, the obtained σ is the excess charge density within 1 nm from the air-ion solution boundary. Fig. 2 shows the excess charge density at various ion concentrations for different ions⁶⁴, and demonstrates that the excess charge density increases with bulk ion concentration with trends that follow the Hofmeister series for anions at a given bulk ion concentration. However, the same trend is not clearly discernable for cations.

Figure 2.

Excess charge density at various ion concentrations for various ions⁶⁴. In the inset, x-axis was converted to the inverse Debye screening length κ for the excess charge density at air-NaI solution interface and the solid line is a linear fit with Eq. (10)⁶⁴.

Suppose that there are no probe molecules, but only cations and anions from the electrolytes that adsorb at the surface. By sequentially adsorbing N₊ cations and N₋ anions at the surface, the surface energy gain from cation and anion adsorption can be expressed as follows,

$$\begin{array}{c}{U}_S\left(N_{+},N_{-}\right)=\underset{0}{\overset{N_{+}}{\int }}\left[E_{+S}-\frac{4\pi l_B{k}_{B}T}{\kappa }\frac{x_{+}}{A}\right]{dx}_{+}+\underset{0}{\overset{N_{-}}{\int }}\left[E_{-S}-\frac{4\pi l_B{k}_{B}T}{\kappa A}\left(N_{+}-x_{-}\right)\right]{dx}_{-}\\ =E_{+S}{N}_{+}+E_{-S}{N}_{-}+\frac{4\pi l_B{k}_{B}T}{\kappa A}{\left(N_{+}-N_{-}\right)}^2\end{array}$$ (8)

with E_±s expressing the surface energy of one cation and one anion excluding the electrostatic energy, respectively. Therefore, the total adsorption Gibbs free energy for both cation and anion is⁶³

$$\mathit{\Delta }G={\psi }_{+}{N}_{+}+{\psi }_{-}{N}_{-}+\frac{2\pi l_B{k}_{B}T}{\kappa A}{\left(N_{+}-N_{-}\right)}^2-N_{+}{k}_{B}T\left[ln\left(c_i{\upsilon }_0\right)-1\right]-N_{-}{k}_{B}T\left[ln\left(c_i{\upsilon }_0\right)-1\right].$$ (9)

with c_i expressing the ion concentration in bulk, which is different from the probe concentration c previously used in Eq. (6), with ψ_± that is equal to the difference in energy for a cation and an anion to be at the surface E_±s and in the bulk E_±b, respectively, i.e., ψ_±= E_±s - E_±b. The specific volume for the cation and anion can be different, but it was assumed to be equal for simplicity. If so, the excess charge density σ, is expressed as follows^{63, 64}:

$$\sigma =\frac{\left(N_{0+}-N_{0-}\right)}{A}=-\frac{\kappa }{8\pi l_B{k}_{B}T}\left({\psi }_{+}-{\psi }_{-}\right)$$ (10)

obtained by minimizing the adsorption Gibbs free energy expression in Eq. (9) with respect to N₊ and N₋ separately, and then taking the difference of the resulting equations. Here, because a two-state model was used, the term adsorption is defined as referring to ions at the surface within ~ 1 nm depth of SHG molecule probe size. As can be seen from Eq. (10), the excess charge density depends on the inverse Debye screening length κ, whose squared value equals 4πl_BΣ_ic_iZ_i². Here, c_i is the ion concentration and Z_i is the valence of the cation and anion. The summation goes over all cations and anions in solution. The excess charge density increases with κ, and thus with the square root of the bulk ion concentration⁶⁹, as indicated in Eq. (10). The x-axis in the inset of Fig. 2 was converted to κ from the bulk ion concentration, c_i. As predicted, the excess charge density at the air-ion solution interface, here of NaI, was found to increase linearly with κ, following the relationship derived above for analyzing the MG adsorption isotherm with Eq. (10), which again supports the validity of the linearization of the Poisson-Boltzmann equation, as implicitly assumed from Eq. (1) to (10).

Notably in Eq. (10), the excess charge density, σ, is proportional to ψ₊ - ψ₋, in which ψ_± is the difference in energy for a cation and an anion to be at the surface E_±,s and in the bulk E_±,b, respectively. For an ion either a cation or an anion, the larger ψ_± is, the smaller the surface ion concentration is because it costs more energy to be at the surface than in bulk. As shown in Eq. (10), the larger the difference in ψ₊ and ψ₋, Δψ, the larger is the negative excess charge density. Larger Δψ means that it costs more energy for the cation to be at the surface than the anion, so that the surface is net negatively charged as the negative sign for the expression in Eq. (10) indicates. Because cations and anions are always correlated together and SHG is dependent on σ, not N₊ and N₋ separately, it is difficult to measure ψ₊ and ψ₋ separately, except with a spectroscopic technique such as photoemission spectroscopy that can determine N₊ and N₋ separately⁴³. In any case, Δψ can be used to estimate the origin of the ion’s effect on the energetics at the surface and in bulk. Note that the electrostatic interaction between ions is excluded from the expression for ψ_±, as it was explicitly separated in Eq. (8).

Table 2 summarizes the values for Δψ as obtained from the excess charge density σ using Eq. (10), as displayed in Fig. 2 in various ion solutions. The calculated values for Δψ using various surface and bulk energies as proposed in the literature are listed in Table 2 for comparison. The 3^rd column in Table 2 used the image charge potential at the interface (listed in the 4^th column in Table 1) to calculate the ion’s surface energy E_±s and the bare ion’s perturbation in hydrogen-bond network in bulk water, here termed bulk water hydrogen-bond perturbation energy (cavitation energy), for the ion’s bulk energy E_±b⁵⁴ (listed in the 5^th column in Table 1). The 4^th column in Table 2 used again the image charge potential at the interface to calculate the ion’s surface energy, but this time the hydrophobic hydration energy⁵⁵ was used as the ion’s bulk energy E_±b. The hydrophobic hydration energy is essentially the same as the bulk water hydrogen-bond perturbation energy used in the 3^rd column in Table 2 except that here, the ion’s hydrated size, i.e. the bare ion radius plus the effective packing radius of H₂O 1.4 Å⁶⁵, is considered. The empirical polarizable energy as used in some molecular dynamics simulation^{53, 70} was not considered. The experimentally measured values for Δψ for a two-state model as listed in Table 2, first column, are larger than the values from the simulations for surfaces whose solvent density or solvent dielectric constant is assumed to vary continuously across the surfaces^70–72. For anions consisting of a single atom such as Cl⁻, Br⁻, and I⁻, the calculated Δψ matches the experimental Δψ value better when the image charge potential⁴⁴ at the surface and its hydrophobic hydration energy of the hydrated ion radius are considered. Therefore, it can be speculated that these ions have a strong first hydration shell⁷³, where the ion and water molecules in the first hydration layer are strongly coupled together. However, for NO₃⁻ ion, considering the bulk water hydrogen-bond perturbation energy using the unhydrated bare ion radius matches the experimental Δψ value better. This exemplifies why knowledge of the detailed hydration structure is important for rationalizing the surface excess charge density. The energy needed to place an ion in the gas phase into the solution state is the hydration enthalpy. The more negative the hydration enthalpy, the more energetically favorable it is for the ion to be in solution state. The difference in hydration enthalpy is found to correlate well with Δψ for anions with the cation fixed as Na⁺. However, when the anion is fixed as Cl⁻, for K⁺ and NH₄⁺, not only do the hydration enthalpy values not correlate with the Δψ values for the cations, even the sign is opposite between the difference in ψ and the difference in ΔH⁰_hyd. This indicates that the ion’s energy in solution is not the sole determinant of their differential concentration at the surface, but the ion’s energy at the interface must contribute significantly to determining the excess charge density.

Table 2.

^a The measured values for Δψ obtained from the excess charge density in Fig. 2 using Eq. (10). ^b Calculated values for Δψ when the image charge potential at the interface (listed in the 4^th column in Table 1) and ion’s perturbation in bulk water hydrogen-bond network due to bare ion radius (listed in the 5^th column in Table 1) are considered. ^c Calculated values for Δψ when the image charge potential at the interface and its hydrophobic hydration energy with ion’s hydrated size of unhydrated ion radius + effective packing radius of H₂O 1.4 Å⁶⁵ are considered^d From Ref⁷⁴. Hydration enthalpy is the energy needed in the reaction cation⁺ (g) + anion⁻ (g) → cation⁺ (aq) + anion⁻ (aq). The more ΔH⁰_hyd is negative, the more readily an ion is hydrated in the solution than in the air.

salt	measured Δψa [kBT]	calculated image charge + H-bond perturbationb [kBT]	calculated image charge + hydrated ionc [kBT]	calculated ΔH0hyd,− - ΔH0hyd,+d [kBT]
NaCl	7.2 ± 1.2	3.4	6.9	11.3
NaBr	8.2 ± 1.2	4.2	8.3	25.0
NaNO3	10.4 ± 1.2	9.9	17.1	38.3
NaI	12.2 ± 1.7	5.6	10.7	42.0
KCl	9.4 ± 1.4	2.1	4.2	−23.8
NH4Cl	8.3 ± 1.1	1.6	3.0	−29.9

^aFrom Ref. 64.

^bFrom image charge potential⁴⁴ and hydrogen-bond perturbation energy⁵⁴ calculated in Table 1.

^cFrom image charge potential⁴⁴ and hydrophobic hydration energy⁵⁵ with hydrated ion size of unhydrated ion radius + effective packing radius of H₂O 1.4 Å⁶⁵.

^dFrom Ref. 74.

Thus far it has been presented how to infer ion’s surface and bulk energy from measured excess charge density at the surface to. However, there are limitations in determining the excess charge density, as the interfacial depth that SHG probes corresponds to the probe’s moleculear size, while the proposed potential energies used to calculate the excess charge density (Table 1 and 2) are extracted using greatly simplified and empirical models. In reality, the surface is not a discontinuous dielectric boundary, i.e. there is a spatially discrete gradient in the dielectric response across the surface, and the structure of the surface is not sharp relative to the ion radius, so that the image charge potential that assumes a sharp dielectric boundary may not be valid. Therefore, ions can act differently depending on their exact location from the surface with what the surrounding water density varies. In the calculation of hydrophobic hydration energy, ions were assumed to be spherical and the electrostatic interaction between ion and water assumed to be negligible. For molecular ions such as NO₃⁻, ion interaction with water can be anisotropic. However, even for single atom ions such as Cl⁻ and I⁻, their charge distribution is deformable from a spherical shape at the surface, so that the ion’s response to the local electric field that is anisotropic at the surface can be complicated. Because of the complexity of the nature of the ion and water interaction and the solvation structure, values for Δψ as obtained from SHG experiments must be combined with other independent experimental observations that offer corroborating clues to the nature of ion and water interaction to converge to a unified interaction model between ions and water.

4. Surface properties and macromolecular interaction

4. 1. Surface tension

As noted earlier, the surface ion concentration can be used a bridging parameter between fundamental ion interaction and the phenomenological Hofmeister effect. In the previous section, the surface ion concentration in the form of excess charge density was obtained from SHG data. Now from this, the extraction of key surface properties such as the surface tension and the interaction between two macromolecular surfaces will be rationalized.

The surface tension at the air-ion solution interface is conventionally calculated from the ion concentration at the interface based on the Gibbs adsorption equation⁷⁵ as established in 1934 by L. Onsager et al.⁴⁴ and Y. Levin et al.^{76, 77}, whose study also includes the oil-water interface. While L. Onsager et al.⁴⁴ used the mean activity coefficient from the Debye-Huckel approximation to determine the ion chemical potential for correlated charged systems, the Kirkwood-Buff formula can be used to calculate the surface tension⁷⁸ without knowing the Gibbs dividing surface of the water solvent and the details of the chemical potential for the charged system, as long as the local normal and tangential direction of the interface can be defined. The latter approach is taken in this perspective. The Kirkwood-Buff formula is a microscopic description for surface tension that is equivalent to the statistical definition of the surface tension γ^{75, 78},

$$\gamma ={\left(\frac{\partial E}{\partial A}\right)}_{V,S},$$ (11)

which is the change in surface energy E per unit area A change when the volume and the entropy of the system is fixed. When the adsorbed ions at the surface interact with each other with the distance-dependent potential energy U(r₁₂), then the Kirkwood-Buff formula expresses the surface tension as follows^{75, 78},

$$\begin{array}{c}\gamma =\frac{1}{4A}\int d^3{\overrightarrow{r}}_1\int d^3{\overrightarrow{r}}_{12}{\rho }^{(2)}\left({\overrightarrow{r}}_1,{\overrightarrow{r}}_2\right)\frac{dU\left(r_{12}\right)}{d{r}_{12}}\left(\frac{x_{12}^2+y_{12}^2-2z_{12}^2}{r_{12}}\right),\\ =\frac{1}{A}\int d^3{\overrightarrow{r}}_1\left[P_N\left({\overrightarrow{r}}_1\right)-P_T\left({\overrightarrow{r}}_1\right)\right]\end{array}$$ (12)

where r₁ and r₂ are positions in space and r₁₂ is the vector from r₁ to r₂. ρ⁽²⁾ is the density pair correlation function. So, the surface tension can be essentially expressed as the difference between the local normal pressure P_N and local tangential pressure P_T, as can be seen in Eq. (12). At the air-ion solution interfaces, the normal pressure is due to the osmotic pressure that increases linearly with ion concentration in bulk and the tangential pressure is due to the electrostatic repulsion between ions. When taking the Yukawa type of potential to express the screened Coulomb interaction^{65, 66} as the potential between excess surface charges, the self-exerting force per unit area F_ES due to the excess charge density becomes⁶⁴,

$$F_{ES}=\frac{1}{2}{\sigma }^2\times {\int }_{a_{\mathit{min}}}^{\infty }\left[-\frac{d}{dr}\left\{\frac{e^2}{4\pi {\epsilon }_{w}r}{e}^{-{\kappa }_{i}r}\right\}\right]\mathit{rdr}\approx \frac{e^2{\sigma }^2}{4{\epsilon }_w}{e}^{-{\kappa }_i{a}_{\mathit{min}}},$$ (13)

as approximated to the leading order in an exponential decay. Here, a_min is the minimum distance between ions at the surface, ε_w is the dielectric constant of water and κ_i is the inverse Debye screening length at the interface. Here, κ_i is equal to the square root of 4πl_BΣ_ic_sZ_i², except now the surface ion concentration, c_s, is considered to be different from the bulk ion concentration c_i. The value a_min is inversely proportional to the square root of c_s, so that the exponent κ_ia_min is a constant, independent of the surface ion concentration. Taken together, when using the osmotic pressure as the normal pressure and the electrostatic repulsion as expressed in Eq. (13) as the tangential pressure in Eq. (12), the surface tension increase at the air-ion solution interface can be expressed as,

$$\mathit{\Delta }\gamma =\left[2w_1{k}_{B}T-\frac{w_2}{4k_{B}T}{\left({\psi }_{+}-{\psi }_{-}\right)}^2\right]c_i,$$ (14)

where c_i is the bulk ion concentration, w₁ the interfacial depth and w₂ equal to w₁ multiplied by e^−κiamin. Here, Eq. (10) was used to replace σ in Eq. (13). Essentially, Eq. (14) expresses that the surface tension increases linearly with the bulk ion concentration relative to the neat water surface tension, in agreement with experimental reports on surface tension for various ion species over a wide range of bulk ion concentration^{7, 8}. Taking these together, the surface tension increment (STI), which is the ratio of the surface tension increase, Δγ, with the bulk ion concentration increase, c_i, can be expressed as,

$$\mathit{STI}=\frac{d\gamma }{{dc}_i}=2w_1{k}_{B}T-\frac{w_2}{4k_{B}T}{\left({\psi }_{+}-{\psi }_{-}\right)}^2.$$ (15)

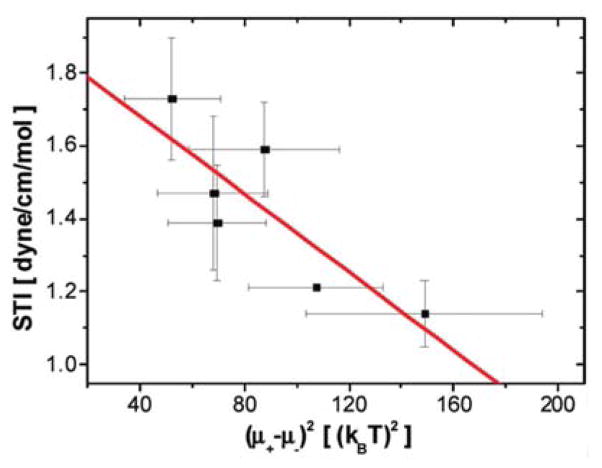
According to Eq. (15), the surface tension at the air-ion solution interface increases to counteract the osmotic pressure exerted by the ions in the bulk (first term) and decreases due to the repulsion between the excess ions charges giving rise ψ₊ - ψ₋, Δψ, (second term) that acts to increase the surface area by the repelling excess charges. Note that the osmotic pressure term (first term) works as predicted by the Gibbs adsorption equation and the second term comes from a modification of the Gibbs adsorption equation due to the interaction between ions at the surface. The validity of this model is tested using STI values taken from Ref^{7, 8} and plotted as a function of (ψ₊ - ψ₋)²,⁶⁴ as obtained from SHG measurements that were introduced in the previous section, shown in Fig. 3. Indeed, the trend shows a negative linear correlation between these quantities across various ions, as predicted by Eq. (15), which also indicates that the assumption of a relatively constant interfacial depth, w₁, over a variety of ions appears to bevalid.

Figure 3.

Excess charge density at various ion concentrations for various ions⁶⁴. In the inset, x-axis was converted to the inverse Debye screening length κ for the excess charge density at air-NaI solution interface and the solid line is a linear fit with Eq. (10)⁶⁴.

It should be noted that the calculation of the surface tension as presented in this section is not entirely rigorous. Specifically, the expression for the surface tension in Eq. (12) is rigorously derived from the definition of the surface tension as presented in Eq. (11). However, the Yukawa potential for screened Coulomb interaction between excess ion charges and the truncation used in the integration as expressed in Eq. (13) are approximations, although reasonable justifications are provided. The spatial distribution of surface ions over the interfacial depth w₁ was also neglected. While details as these have to be more carefully worked out in future numerical calculation with Eq. (12), the approximate model presented in Eq. (15) can already capture the trends of the Hofmeister effect in the STI values at the various air-ion solution interfaces with the excess charge density, which follows the Hofmeister series.

4. 2. Macromolecular aggregation

Many macromolecules show ion-specific aggregation^37–39 and changes in the phase transition temperature with ion types^{31, 33, 36}, which indicates that specific ion can change the intermolecular interactions to a different extent in an ion-specific way. Let’s consider a model macromolecular surface as shown in Fig. 4(a). For simplicity, let’s assume that the macromolecular surface does not undergo directly ion-induced structural changes. Instead, at the macromolecular surface, the surface ion concentration and bulk ion concentration can be different, and there can be an excess charge density accumulated at the macromolecular surface, similar to as found at the air-ion solution interface. When two macromolecular surfaces such as that of proteins approach closer than the interfacial depth, w₁, where the surface ion concentration deviates from the bulk ion concentration, this will induce depletion interaction, while at the same time any excess charge at one macromolecular surface will also interact with the excess charge at the other macromolecular surface electrostatically, as schematically illustrated in Fig. 4(a). Because the depletion interaction, as well as the electrostatic interaction at high ion concentration is short-ranged, we propose that a binary mixture model⁶⁶ is appropriate to describe the phase transition. Basically, this is a mean-field Ising model that describes the transition between a homogeneously distributed and phase-separated state.

Figure 4.

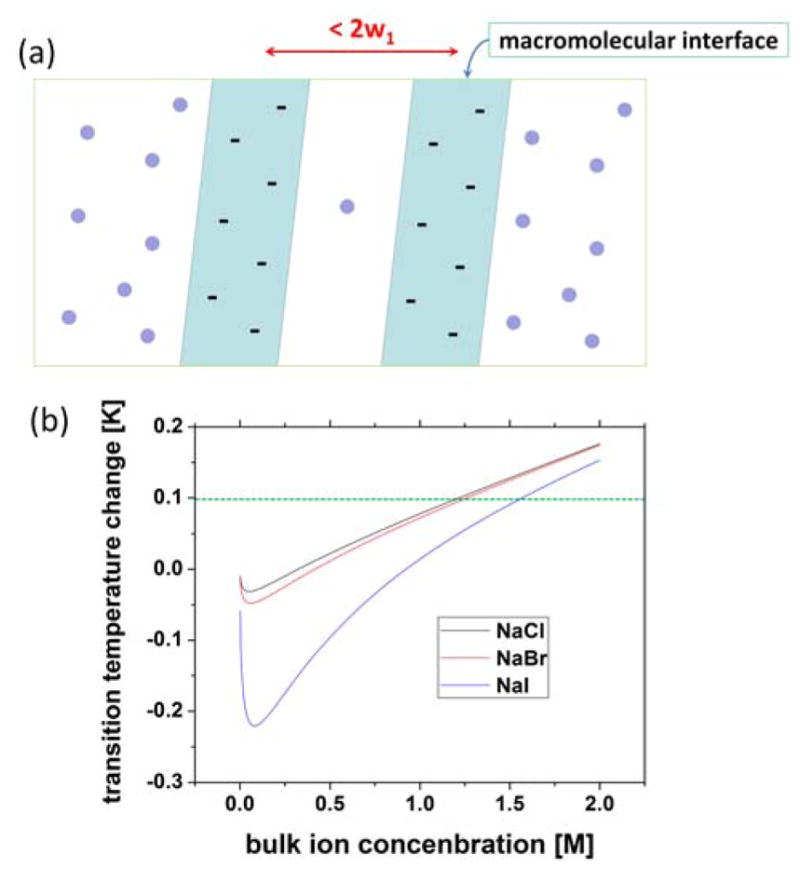
(a) Schematic of two macromolecules ion solutions. Ions were drawn as spheres. (b) Calculated phase transition temperature change, Tc - Tc⁰ by Eq. (21) with Bjerrum length l_B at room temperature 7 Å, and d₁ ~ 10 Å in NaCl, NaBr and NaI solution at various bulk ion concentration. Excess charge density values at the air-ion solution interface using Table 2 and Eq. (10) were used. The dotted line indicates the room temperature, which was set arbitrarily as Tc⁰ + 0.1.

The free energy per unit volume of the binary mixture, f, can be written as follows⁶⁶,

$$f=\frac{F}{V}=k_{B}T\left[\varphi ln\varphi +(1-\varphi )ln(1-\varphi )\right]+\frac{J_0}{2}\varphi (1-\varphi ),$$ (17)

where F is the total free energy of the whole system in volume V, _ is the volume fraction of macromolecules and J₀ is the energy difference between the macromolecule that is aggregated and isolated. The first term, which is proportional to k_BT, represents the entropy of mixing and favors a homogeneously distributed state. The second term, which is proportional to J₀, represents the energy change due to aggregation. A binary mixture with this free energy is known to have a phase transition temperature of k_BT_c⁰ at J₀/4⁶⁶, above which the macromolecules homogeneously distribute in solution and below which the macromolecules phase-separate.

When two macromolecular surfaces approach to a distance smaller than 2w₁, which is the range where the surface ion concentration c_s differs from the bulk ion concentration c_i, as said before, macromolecules feel the attractive force when ions are depleted from the macromolecular surface, which is proportional to the concentration difference, c_i - c_s. However, as noted before, measuring ion concentration near the macromolecular surface is difficult. Furthermore, the distance dependence of the depletion force requires the surface ion concentration to be known as a function of distance from the surface, which is very difficult to measure. Therefore, for simplicity, it will be assumed that the cation and anion concentration at the macromolecular surface, c_s+ and c_s−, respectively is negligible, so that the macromolecular interaction changes due to the depletion force can be estimated. Under this assumption, macromolecular surfaces will experience a depletion attraction of value 2c_ik_BT when two surfaces approach closer than 2w₁. The change in the second term involving J₀ in Eq. (17) with ion can be analytically calculated by the energy difference per unit area, ΔU_contact/A, between two macromolecular surfaces in contact at distance d₁ and the macromolecular surfaces at infinite distance using ion-induced depletion and electrostatic forces. Here, surfaces in contact at distance d₁ roughly represent the aggregated state and surfaces at infinite distance the homogeneously distributed state. The expression for ΔU_contact/A, which is equal to −ΔJ, i.e. the negative value of the change in J₀, can be expressed as,

$$\frac{\mathit{\Delta }{U}_{\mathit{contact}}}{A}=-\mathit{\Theta }\left(2w_1-d_1\right)2c_i{d}_1{k}_{B}T+e^{-\kappa d_1}\frac{4\pi l_B{k}_{B}T}{\kappa }{\sigma }_s^2,$$ (18)

where a factor of 2 for the depletion attraction in the first term comes from the fact that there are both cations and anions. Θ(x), a step function which is 0 for x<0, and 1 for x>0, is used to describe the depletion interaction being effective for d₁ < 2w₁. The second term, the electrostatic repulsion between the excess charge density is calculated with the electric field as expressed in Eq. (1), from the linearized Poisson-Boltzmann equation. When the ion concentration c_s at the interface becomes significant, the bulk ion concentration c_i in the depletion force term can be replaced by c_i - c_s. While the ion’s bulk energy is the same as that at the air-ion solution interface, the ion’s surface energy at a macromolecular surface can be different from that at the air-ion solution interface, depending on the nature of the interaction between the ion and the surface. Therefore, ψ_s± is different from ψ_±, and as a result, the electrostatic repulsion due to the excess charge density at the macromolecular surface σ_s, is different from σ at the air-ion solution interface. Because Eq. (10) still holds, it follows that

$$\frac{\mathit{\Delta }{U}_{\mathit{contact}}}{A}=-\mathit{\Theta }\left(2w_1-d_1\right)2c_i{d}_1{k}_{B}T+e^{-\kappa d_1}\frac{\kappa }{4\pi l_B{k}_{B}T}{\left({\psi }_{s+}-{\psi }_{s-}\right)}^2.$$ (19)

In summary, the depletion attraction pushes towards the aggregation of the macromolecule, while the excess charge repulsion pushes towards the homogeneous distribution of the macromolecules in solution, as expressed in Eq. (19).

The ions ranked higher in the Hofmeister series such as Cl⁻, have smaller ion concentration at the surface, and thus smaller excess charge density at the surface compared with ions ranked lower in the Hofmesiter series such as Br⁻ and I⁻. Therefore, both depletion attraction and excess charge repulsion act in a concerted way to favor macromolecular aggregation in the direction going from I⁻ to Cl⁻. Now, the energy difference between macromolecules aggregated vs. isolated state in the binary mixture model, J₀ for solution without ion will be changed to J for solution in the presence of ions, as expressed as,

$$J=J_0+2c_i{k}_{B}T-\frac{e^{-\kappa d_1}}{d_1}\frac{\kappa }{16\pi l_B{k}_{B}T}{\left({\psi }_{s+}-{\psi }_{s-}\right)}^2.$$ (20)

Therefore, the transition temperature for macromolecules between the phase-separated to homogenously distributed state is,

$$k_B{T}_c=k_B{T}_c^0+\frac{c_i}{2}{k}_B{T}_c-\frac{e^{-{\kappa }_c{d}_1}}{d_1}\frac{{\kappa }_c}{16\pi l_{B,c}{k}_B{T}_c}{\left({\psi }_{s+}-{\psi }_{s-}\right)}^2,$$ (21)

where k_BT_c⁰ equals to J₀/4, the phase transition temperature for macromolecular aggregation in solution without ion.

Fig. 4(b) shows that the calculated change in the phase transition temperature, Tc - Tc⁰, with bulk ion concentration, c_i, follows trends predicted by Eq. (21) when using the Bjerrum length l_B at room temperature of ~7 Å and a surface separation distance d₁ of ~ 10 Å. Note that the inverse Debye screening length κ and the Bjerrum length l_B are also functions of temperature. However, for simplicity to a first approximation, all temperature-dependent parameters of Eq. (21), κ and l_B, are calculated at room temperature. For the excess charge density at the air-ion solution interface, the values for ψ₊ - ψ₋ as listed in the 2^nd column in Table 2 were used, although the values for ψ_s+ - ψ_s− can be different from ψ₊ - ψ₋. As expected, the ion ranked higher in the Hofmeister series, such as Cl⁻, prefers the aggregated, phase-separated, state even at higher temperature than the ions ranked lower in the Hofmeister series, such as Br⁻ and I⁻. When the macromolecular aggregation occurs and phase separation follows by adding ions, the ion concentration, c_i*, at which the phase transition occurs is where the phase transition temperature in Eq. (21) is equal to room temperature so that,

$$k_B{T}_{\mathit{room}}=k_B{T}_0+\frac{c_i^{\ast }}{2}{k}_B{T}_{\mathit{room}}-\frac{e^{-{\kappa }_{\mathit{room}}^{\ast }{d}_1}}{d_1}\frac{{\kappa }_{\mathit{room}}^{\ast }}{16\pi l_{B,\mathit{room}}{k}_B{T}_{\mathit{room}}}{\left({\psi }_{s+}-{\psi }_{s-}\right)}^2.$$ (22)

Note the inverse Debye screening length κ is also a function of ion concentration in solution, although it is assumed here to be a constant for simplicity. As for the Hofmeister’s original experiment, the globulin protein has a phase transition temperature Tc⁰ that is lower than room temperature, so that it dissolves homogeneously in solution at room temperature. In Fig. 4(b), the ion-induced changes in the phase transition temperature, T-Tc⁰, as obtained from Eq. (22) is presented. As predicted, when the ion concentration increases, the phase transition temperature increases at high ion concentration. At the ion concentration where the phase transition temperature equals the room temperature, which was set arbitrarily as Tc⁰ + 0.1 and shown as the dashed line in Fig. 4(b), phase separation occurs. The free energy of the two macroscopic surfaces at a distance d as expressed in Eq. (17) when using the interaction energy from Eq. (20) is essentially the same as defining a grand potential per unit area between colloidal surfaces at a distance L, as presented by A. P. dos Santos et al.⁷⁹ The difference is that the macromolecular surface considered in this perspective is neutral, so that the larger the concentration difference between the anion and cation, the larger the repulsion between surfaces. In contrast, A. P. dos Santos et al. considered positively charged colloidal surfaces⁷⁹, where the larger the concentration difference between the anion and cation at the colloidal surfaces, the more the colloidal surface is neutralized. Therefore, the remaining van der Waals attraction results in the coagulation of the colloids. For neutral surface as considered in this perspective, it is the depletion force that mainly drives the aggregation between surface.

As was the case with the calculation of surface tension, the derivation presented here for ion-induced changes in the phase separation temperature is not rigorous. Specifically, the spatial distribution of surface ions over the interfacial depth w₁ was ignored in estimating the energy as presented in Eq. (18), which is important to calculate the double layer potential, although the square dependence of the energy on the excess charge density contains the contribution from the double layer potential, giving non-zero values even under net charge-neutrality condition. There are no systematic or sufficient experimental data on surface ion concentration over a wide range of ion species and concentration that can be used in numerical calculations to date. However, the approach and model presented here captures the trend of the Hofmeister effect in macromolecular aggregation through the excess charge density, and offers useful hints at the physical origin of this effect. Importantly, the calculation of ion-induced STI presented in the previous section and the phase transition temperature change presented in this section did not require the consideration of interactions beyond the level of DLVO theory, except it utilized the excess charge density, i.e., the ion-specific interaction parameters as obtained from SHG measurement. The theoretical calculation of the excess charge density requires detailed knowledge of the ion-water interaction, such as whether the ion is strongly or weakly hydrated, in order to quantitatively rationalize the empirically obtained values. However, when the excess charge density is experimentally obtained, macromolecular interaction change induced by the ion can be calculated without the detailed knowledge of ion-water interaction. Thus, the access to experimentally determined excess charge density is invaluable.

4. 3. Macromolecular precipitation

Some macromolecules in ion solutions precipitate rather than aggregate. Here, the term precipitation is referred to when the density of the macromolecules becomes larger than the density of the solution. In this case, the size of the macromolecules may or may not change upon precipitation, contrary to the aggregation of macromolecules that implies their assembly.

Self-assembled structures such as multilamellar vesicle (MLV) made of many lipids whose specific volume is smaller than the specific volume of water⁸⁰ precipitate in low salt solutions but refloat in high salt solutions⁸¹. The solvent density, which is the inverse of the specific volume of the solvent, increases with ion concentration, so that at an ion concentration lower than c_i*, where the solvent density ρ_w matches the lipid density ρ_L, the MLVs precipitate out

$$c_i^{\ast }=\frac{{\rho }_L-{\rho }_w}{{\delta }_i}.$$ (16)

At a higher concentration than c_i*, the MLVs refloat in solution. In Eq. (16), δ_i is the slope of the solvent density increase per unit ion concentration. The ions ranked higher in the Hofmeister series such as Cl⁻ display a smaller δ_i than the ions ranked lower in the Hofmeister series such as Br⁻ and I⁻. Therefore, in NaCl solution macromolecules precipitate across a wider range of ion concentration than in NaBr or NaI solution. Although this precipitation model only considers the ion-dependent solvent density and neglects the electrostatic repulsion between macromolecules that homogeneously disperses the macromolecules in solution, neglects any differential surface ion concentration at membrane surfaces compared with in bulk solution, as well as ion-specific membrane structural changes, it captures characteristic features found in precipitation when varying ion types in solution.

For example, large unilamellar vesicles (LUV) made of POPC precipitates at low concentration of NaCl solution. However, it takes a few days for LUVs to precipitate and when the precipitated solution is vortexed and redispersed, their hydrodynamic radius according to dynamic light scattering (DLS) stays unaltered. This implies that POPC LUVs do not aggregate to form a larger-sized complex and that the LUV’s individual structure is unchanged upon precipitation. Table 3 lists the hydrodynamic radius R_h of POPC LUVs extruded with 200 nm-pore polycarbonate filter as measured by DLS, radius of gyration R_g, molecular weight of LUV M_g, and the second virial coefficient υ₂ determined by static light scattering (SLS). The second virial coefficient υ₂ was obtained from a Zimm plot⁸². The values for R_h, R_g, and M_g indicate that the size of the vesicle depends on the ion species, such that ions ranked higher in the Hofmeister series such as Cl⁻ yield larger vesicles than ions ranked lower in the Hofmeister series such as Br⁻ and I⁻. The same is true for cations. However, the second virial coefficient υ₂ indicates that the interaction between the vesicles is very small and shows no consistent trend with variation in ion species. For reference, the second virial coefficient υ₂ = 2.4 × 10⁻⁷ cm³mol/g² for LUVs of 250 nm diameter in 100 mM NaCl solution is comparable to that of spheres of 200 nm diameter, when only taking the excluded volume (hard sphere) interaction into account. This indicates that the ions alter the individual POPC vesicle structure, as manifested in changes in the vesicle size with varying ion type, but not the interaction between vesicles, consistent with the precipitation picture of POPC MLVs as introduced by A. Parsegian et al.⁸¹ and with the precipitation picture described in this perspective, with further simplification by neglecting the effect of adsorption of the ion at the liposome surface.

Table 3.

The hydrodynamic radius, R_h, of large unilamellar POPC vesicles (LUVs) extruded with a 200 nm pore polycarbonate filter as measured by dynamic light scattering (DLS), the radius of gyration R_g, molecular weight, M_g, and the second virial coefficient υ₂ by static light scattering (SLS) with Zimm plot⁸².

salt	hydrodynamic radius Rh [nm]	radius of gyration Rg [nm]	molecular weight Mg [g/mol]	second virial coefficient υ2 [cm3mol/g2]
de-ionized watera	178 ± 6	169 ± 22	1.0 × 109 ± 2.1 × 108	5.2 × 10−7 ± 2.0 × 10−7
NaCl 100 mM	135 ± 7	105 ± 10	3.4 × 108 ± 8.6 × 107	2.4 × 10−7 ± 2.7 × 10−8
NaBr 100 mM	105 ± 2	80 ± 4	1.5 × 108 ± 5.7 × 106	7.9 × 10−7 ± 2.1 × 10−7
NaI 100 mM	78 ± 7	63 ± 11	1.4 × 108 ± 1.0 × 108	5.3 × 10−7 ± 6.2 × 10−7
CaCl2 100 mM	111 ± 22	91 ± 8	1.37 × 108 ± 8.6 × 107	9.5 × 10−7 ± 2.9 × 10−7

^ade-ionized water from Millipore with resistance 18.2 MΩ/cm.

4. 4. Ion-induced changes of macromolecular structures

Inter-molecular interactions become more complicated when ions induce changes in the macromolecular structure, as found with lipid bilayers in which lateral interactions between lipid molecules can be changed by added ions that may contribute to directly altering the phase of the self-assembled structure, as well as the interaction between the self-assembled structures themselves³³. E. Leontidis et al. used small angle x-ray scattering of stable multilamellar bilayer structures made of DPPC, under applied osmotic stress by using high molecular-weight polymers such as PEG in solution, to quantify changes in the bilayer structure induced by various ions under external pressure^{60, 83}. It was found that the swelling of the bilayer as observed with increases in the multilamellar repeat distances increases, together with the area per lipid, with added ions ranked lower in the Hofmesiter series such as I⁻. However, their effort to model the perpendicular and lateral equation-of-state of the lipid bilayer system failed. The authors attribute this to two factors. First, at maximum swelling in the presence of electrolytes the osmotic pressure of the bilayer system cannot be set equal to zero. Second, at high salt concentrations an additional repulsion appears to come into effect in the presence of strongly adsorbing anions such as iodide. It is possibly because the osmotic pressure applied may not be the same for bilayers hydrated in different ion solutions and/or because there is an additional repulsion between bilayers due to ions contributing differentially to the excess charge density at the bilayer surface.

Another example of manifested complex interactions induced by ions are found with macromolecules with lower critical solution temperature (LCST)^{31, 84} that are soluble at low temperature, but insoluble at high temperature. Thus, LCST cannot be explained without thermally induced changes of the macromolecular structure itself or changes in the water-macromolecular interaction. This phenomenon is in contrast to the properties of systems described by the binary mixture model previously, in which the homogeneous distribution of macromolecules are driven by entropy, so that macromolecules are soluble at high temperature but insoluble at low temperature.

5. Ion-water interaction as reflected in water dynamics

Ions are known to change the water viscosity as a function of ion concentration following^{5, 6, 85},

$$\frac{{\eta }_i}{{\eta }_0}=1+A\sqrt{c_i}+B{c}_i,$$ (23)

which relation is known as the Jones-Dole effect, where η_i is the viscosity of the ion solutions and η₀ that of pure water. The A-coefficient originates from ion-ion correlation due to electrostatic interaction between the cations and anions, while the B-coefficient expresses the effect of ion-water interaction on the solution viscosity⁸⁵. While the calculated A-coefficient from the Debye-Huckel approximation is in good agreement with experimental values⁸⁶, the origin of the B-coefficient is not very clear despite long-standing efforts in the literature, as described in the following. J. Hubbard and L. Onsager treated an ion as a charged sphere moving in a continuous dielectric medium with hydrodynamic dissipation that gives rise to the B-coefficient^{87, 88} that may depend on the boundary condition for the ion-solvent contact^{89, 90}. D. Laage et al. simulated the changes of the ion-induced solution viscosity, and so the B-coefficient by using a polarizable force field for the ions and including the geometrical restriction of the hydrogen bonds in bulk water in their molecular dynamics simulation⁹¹.

The electron binding energy is the energy to take one valence electron out from ions into aqueous solution. The difference in electron binding energy in aqueous solution and in the gas phase is the free energy penalty for disrupting the local solvent structure, also known as the solvent reorganization energy. The experimentally measured electron binding energy probed by photoelectron spectroscopy⁹² is surprisingly well explained by a dielectric cavity model, which is the energy to generate a charged cavity with the ion’s radius in a continuous dielectric medium. This indicates that the interaction between the ion and solvent, water in this case, is determined by electrostatic energy. Although the ion-water interaction can be very strong within the first hydration shell of the ion, ion effects on the water structure are suggested to still not exceed the first hydration shell^{93, 94}. Even with di- and tri-valent ions, neither the water density nor the water orientation has been found to be directly affected by ions more than 5Å away⁹⁵. Still within the first hydration shell of some ions, the water orientational correlation time is ~ 10 ps⁷³ which indicates fairly dynamic water near these ions.

As can be seen with the Jones-Dole effect expressed with Eq. (23), the ion-induced changes in water viscosity, i.e. the water diffusion coefficient, reflect on the ion-water interaction via the B-coefficient. Thus, especially the local water diffusion as measured near the ions, which is sensitive to the local water structure around the ions⁹⁶, would be a sensitive reporter of ion-water interaction. However, such measurements have only recently become available with Overhauser dynamic nuclear polarization⁹⁷ (ODNP) relaxometry that can measure the local water diffusion within ~10 Å near spin labels or spin probes harboring an unpaired electron spin^98–102. ODNP relies on the dipolar interaction energy between magnetic spins of an electron spin of the spin label or spin probe and the nuclear spin of the water proton. The dipolar interaction energy depends on the distance between the electron spin and the water proton spin, r, to r^−3.102 The change in dipolar interaction energy between the spins that is typically induced by the change in r gives rise to spin state transitions, as reflected in the spatial correlation with time, i.e. water diffusion^{98, 102}. Because the dipolar interaction falls with r⁻³, the transition rates depends on r⁻⁶ so that 99% of the proton spin state transitions due to the electron spin occur within 10 Å from the spin label^{98, 101, 102}. These transition of the water proton spin states induced by the external spin label lead to amplified proton nuclear magnetic resonance (NMR) signal and shortened proton spin-lattice relaxation time, T₁, both of which are functions of the electron spin-induced nuclear spin transition rates¹⁰⁰. By analyzing these rates with the force-free hard sphere water diffusion model (FFHS)⁹⁹, the local water diffusion constant near a spin label can be obtained. FFHS assumes no water proton density within the hard sphere size of the spin label and no interaction between the spin label and water. In addition, water protons are freely diffusing so that the distance between spin label and water proton increases with time t as t^0.5. By attaching the spin label physically or chemically at a surface of interest¹⁰³, the local water diffusion constant within ~10 Å of this surface can be measured by ODNP relaxometry.

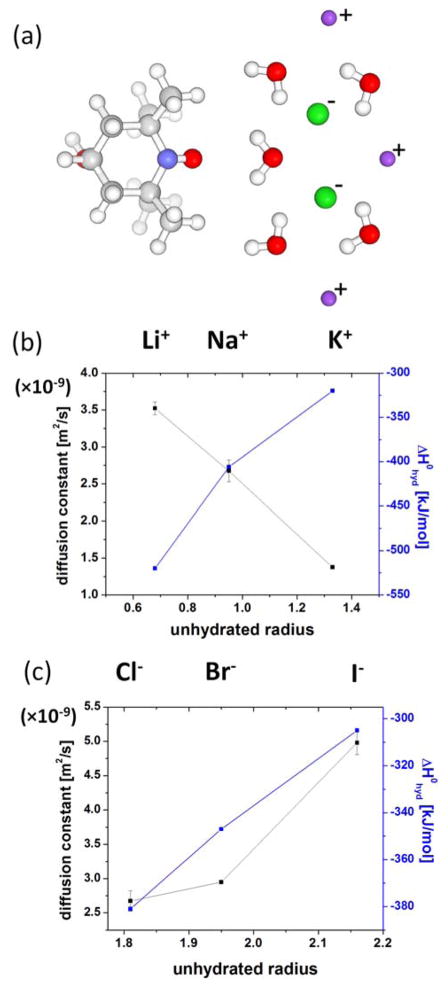
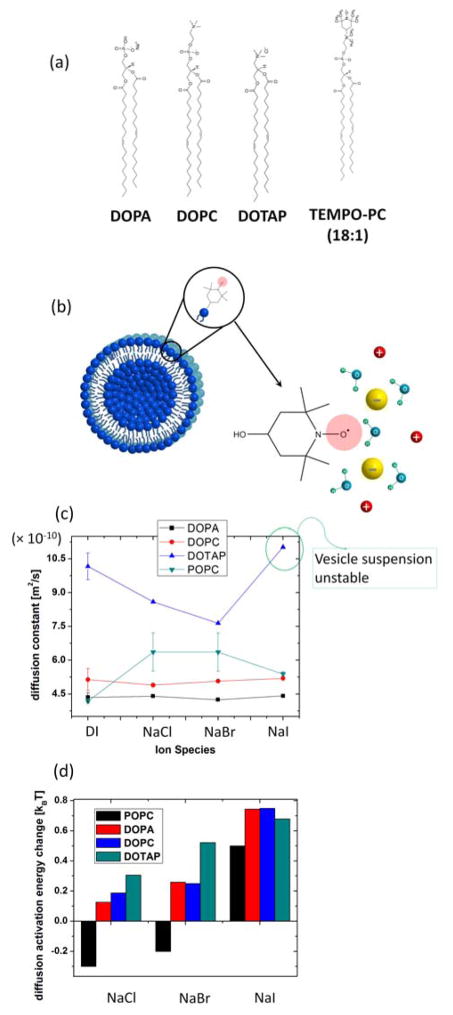
Fig. 5 present ODNP relaxometry-derived changes in local hydration water diffusion near 4-hydroxy-TEMPO, a small molecular spin probe, with varying cation type, while fixing the counter anion as Cl⁻, and with varying anion type, while fixing the counter cation as Na⁺ at 100 mM ion concentration¹⁰⁴. The changes in local water diffusion constant together with the change in enthalpy of hydration⁷⁴ for the cation is plotted as a function of the unhydrated ion radius in Fig. 5, with values listed in Table 1. As the cation radius increases, the water diffusion constant decreases, i.e., water near the 4-hydroxy-TEMPO spin probe in the ion solution diffuses slower. In contrast, when the anion radius increases as shown in Fig. 5(c), local water diffusion constant increases, i.e., water near the 4-hydroxy-TEMPO spin probe in ion solution diffuses faster. Near the nitroxide (N-O) moiety of 4-hydroxy-TEMPO, the hydrogen of water has a longer residence time than the oxygen of water¹⁰⁵, so that the ions outside the first hydration water layer of 4-hydroxy-TEMPO exerts a larger force on the water oxygen than on the water hydrogen, simply because the water oxygen is closer to the ion approaching this water from the bulk. In this picture, cations outside the first hydration layer of 4-hydroxy-TEMPO attract the oxygen of the water molecules, and so tend to pull on the water of the 4-hydroxy-TEMPO hydration layer, while anions tend to push the water oxygen of the 4-hydroxy-TEMPO hydration layer via electrostatic interactions. When the anion is fixed as Cl⁻, as the counter cation size increases and thus its charge density decreases, the strength of the counter cation’s pulling force on the water oxygen decreases. As a result, water is more closely attracted to, and can less freely diffuse away from 4-hydroxy-TEMPO. When the cation is fixed, as the counter anion size increases, now the pushing force becomes smaller so that the water molecules diffuse faster. The observation of clearly opposite effects exerted by the cations versus the anions on the water diffusivity suggests that the local water diffusion around a chemical defect, here the 4-hydroxy-TEMPO spin probe, is modulated by electrostatic interactions with nearby ions in solution. This means that the interaction between ion and water is at least partially electrostatic, so that the diffusion of water hydrating the spin probe is affected by cations and anions with opposite signs.

Figure 5.

(a) Molecular schematics of spin label, water and ions. Red spheres are oxygens, white are protons, blue is nitrogen, grey are carbons. Green spheres are anions and violet spheres are cations. Not drawn in scale. (b) Water diffusion changes by the cations while the anion is fixed as Cl⁻ and the enthalpy of hydration⁷⁴ for the cations as a function of unhydrated ion radius in Table 1. Redrawn from Ref. ¹⁰⁴. (c) Water diffusion changes by the anions while the cation is fixed as Na⁺ and the enthalpy of hydration⁷⁴ for the anions as a function of unhydrated ion radius in Table 1. Redrawn from Ref. ¹⁰⁴.

6. Ion-specific effects on lipid vesicle surfaces

Having established that ion-water interactions can be experimentally probed by surface water diffusion constants, the effects of ions on modulating these interactions will be next examined on extended surfaces. Here, we specifically focus on large unilamellar vesicle (LUV) surfaces constituted of negatively charged, neutral, or positively charged lipids, whose molecular structure is shown in Fig. 6(a). The electron spin label is covalently tethered on the choline group of the lipid head group, constituting TEMPO-PC that surveys the hydration shell of the LUV surface, as illustrated in Fig. 6(b). 2 mol % of this spin labeled lipid is mixed with un-spin labeled lipids to constitute the LUVs. Both, the effects of ions that constitute the lipid headgroups, as well as of those externally added to the solution will be examined. Fig. 6(c) shows the surface water diffusion constant measured at the LUV surface by ODNP employing the PC-tethered spin label. The negative charge of the lipid surfaces comes from the phosphate group and positive charge from the choline group, while the zwitterionic lipid headgroup contains both the phosphate and choline group. The water diffusion constant within the hydration layer of the negatively charged DOPA LUV is found to be much slower than the positively charged DOTAP LUV, with the neutral DOPC LUV displaying intermediate diffusion constant for surface hydration water, but with values rather closer to that of the negatively charged LUVs, as shown in Fig. 6(c). This suggests that both phosphate and choline at the lipid headgroup are interacting with the water molecules¹⁰⁶, but that the phosphate group is more strongly hydrated than the choline group. This is possibly because the negative charge in a phosphate is spatially delocalized over four oxygens, and thus readily exposed to the small hydrogen of water that can more closely approach the phosphate group of the lipid headgroup, while the positive charge in choline may be spatially localized closely within the nitrogen atom, so that the larger oxygen of water may not as readily approach the choline moiety.

Figure 6.

(a) Molecular structure of negatively charged DOPA, neutral DOPC and positively charged DOTAP. Not drawn in scale. (b) LUV made of 2 mol % spin labeled lipid and 98 mol % un-spin labeled lipid. (c) Water diffusion at LUV surfaces made of DOPA, DOPC, POPC and DOTAP in various ion solutions. POPC data were taken from Ref. ¹⁰⁴. Bulk ion concentration is 100 mM. (d) The change in ΔE_a = E_{a, surface} - E_{a, bulk} at LUV surfaces made of various lipids with different ions in solution. POPC data were taken from Ref. 104.

The activation energy of water diffusion is reflective of the local water structure. The “tighter” the local water structure, the more energy is needed for a water molecule to break the local structure to diffuse. By measuring the water diffusion constant near the LUV surface and in bulk, the difference in activation energy of water diffusion at the surface E_{a, surface} and in bulk E_{a, bulk} was obtained, which is ΔE_a = E_{a, surface} - E_{a, bulk}. Fig. 6(d) shows the change in ΔE_a at LUV surfaces made of various lipids with different added ions in solution. Regardless of the lipid used, the ion-induced change in ΔE_a follows the Hofmeister series. Here, the change in ΔE_a with ion is simultaneously affected by the surface ion concentration as well as each ion’s ability to change the local hydration structure¹⁰⁴. Importantly, the permanently installed surface charges of the lipid headgroups of LUV made of DOPA or DOTAP are significant, and should be taken into account for calculating adsorption free energy according to Eqs. (8) and (9), while any excess charge density σ will be due to the externally added ions from solution.

As is the case with ψ_±, where the ion’s bulk energy contribution is larger than the ion’s surface energy contribution, as shown in Table 1 and 2, the activation energy of water diffusion in bulk ion solution contributes most strongly to ΔE_a, rather than the activation energy of water diffusion at the surface. This can be concluded from observing that the ions do not affect the absolute values for the hydration water diffusion near LUV surfaces as much as they do in bulk water, as seen in Fig. 6(c) when comparing with Fig 5 (b–c). In fact, on the surfaces of DOPC and DOPA LUVs, the effect of the intrinsic lipid headgroup charges seem to dominate the observed surface water diffusion constants, and no modulation with added ions are discernable. This implies that the surface ion concentration on DOPC and DOPA LUV surface is not significantly affected by the added ions. However, added ions from solution do induce modulations on the surface water diffusivity with the ion types near DOTAP surfaces. Anions such as Cl⁻ and Br⁻ on positively charged LUV surfaces made of DOTAP were found to induce small, but clear, decreases in hydration water diffusion. It can be suggested that this is due to the slight preference in anion adsorption at the positively charged surface, where more anions are adsorbed at the surface with increasing trends from Cl⁻ to Br⁻, likely due to the enhanced anion adsorption with increasing anion size. In this case, the water diffusion constant at the surface will decrease, when the hydration of the adsorbed ions are stronger than that of the lipid headgroup’s choline group, whose hydration was found to be weaker than that of the phosphate moiety. Importantly, the differential modulation of DOTAP’s surface water diffusion with added Cl⁻ to Br⁻ can only be explained when strong differences in ion-water interaction is taken into account. Interestingly when iodide is added, i.e. the largest anion size used, the positively charged LUVs aggregate, as observed by eye. This observation may be attributed to sufficiently large surface iodide concentration that is large enough to neutralize the intrinsic surface charge of DOTAP headgroups, and/or the iodide bridging two positively charged surfaces, given the ion’s large size with negative charges distributed over its surface that may attract the positive charge of LUVs on both sides. The iodide-induced aggregation between DOTAP cannot be explained by the mean-field binary mixture model as described in the previous section, as that model neglects the effects of strong charge-charge correlation^{107, 108}. At POPC LUV surfaces, added ions have also been observed to modulate the surface water diffusion constant, but with approximately the opposite trend as seen with DOTAP LUV surfaces. In case of POPC, the added ions are known to affect the vesicle structures, such as their sizes (listed in Table 3), so that the effects of the ions may be more complex. Added NaCl and NaBr were observed to increase the surface water diffusion at POPC LUV surfaces. This means the water structure at the membrane surface is weakened by the added ions, which may be due to ions outside the first hydration layer of LUV surfaces competing with ions of the LUV headgroups to attract hydration water. Iodide falls outside of this trend, while no clear modulation is observed on DOPC LUV surfaces. Clearly, much more data is needed to support any of these possibilities, especially because the added ions do change the POPC LUV sizes, as presented in Table 3. However, the trend in water diffusion is not correlated with changes in the vesicle size nor interaction between LUVs as expressed in the second virial coefficient υ₂. It can be concluded that the surface water diffusion is clearly not affected by only one factor, such as the surface ion concentration, but also by the ion’s ability to change the local hydration structure, and also where the ion exactly is located near the surface. As discussed for the case of DOTAP vs. POPC LUV surfaces, ions adsorbed at the surface vs. near the surface, but outside the first hydration shell, can be conceptualized to yield opposite effects on the surface water diffusion dynamics.

Taken together, the study of local water diffusion near a small chemical defect, 4-hydroxy-TEMPO, and a spin label positioned at the surface of large vesicle models that represent more complex chemical and structural topology show that water differentially interacts with local surface charges, such as phosphate and choline of the lipid groups of LUV, or adsorbed or nearby ions from solution, yielding greatly varying values for the surface water diffusion constants. Crucially, the experimental access and approach to measuring surface water diffusion constants offers the opportunity to explore interactions between complex ions and water near complex surfaces.

The nature of ion-water and water-water interactions are both of partially electrostatic origin, in terms of the charge distribution and the van der Waals radius typically used in molecular simulations, the details of which are not generally agreed upon. In many cases, water properties, especially their dynamics, are not easily understood by considering only classical interactions, so there are ab initio simulations describing water-water interactions of quantum mechanical origin^{109, 110}. In either case, the experimentally determined modulation of water diffusion constant at surfaces with different chemical and structural topology and with varying ion types and concentration will provide currently unavailable data to test models that describe ion-water interactions.

7. Towards a unified model for ion-water interaction

In this perspective, models and experimental approaches were presented to decouple ion-ion interactions originating from electrostatic interactions from ion-water interactions to explain ion-modulated surface properties, such as the surface ion concentration, the surface tension increment at the air-ion solution interface and the propensity for macromolecular aggregation. Although the ion-water interaction included in ψ_± is decoupled from the inter-ion electrostatic interactions, this ion-water interaction as reflected in ion-induced changes of local water diffusion constants is at least partially due to electrostatic interaction between the ion and water species. It was also found that including contribution from water hydrogen bond perturbation energy is important to even qualitatively describe the experimentally derived excess charge density at the air-ion solution interface, which strongly depends on the spatial and geometric considerations of the ion, such as its radius and spatial distribution due to its chemistry.

It has been attempted in the past to find a unified parameter to describe ion-water interaction, such as the ion radius, but it is clear that the nature of ion-water interactions is more complicated, so that it not only depends on the ion radius, but also asymmetrically on the sign of the charges. This is because the water counterpart of positive ions, namely the oxygen of water has a different size and charge distribution from the water counterpart of negative ions, the proton of water. Further, the spatial distribution and delocalization of the charges of a given ion at a surface, such as the phosphate and choline groups at lipid surfaces, and how well the hydrated or unhydrated external ions adsorbed at the surface accommodate the water structure near the surface vs. in the bulk are important factors. Clear answers to these questions are not simple and beyond the scope of the current literature. Theory should provide the physical basis for the origin of interactions between ion and water, while simulation should provide the molecular interaction model and numerical output values for experimentally testable parameters. Ultimately, experiments of surface ion or ion-induced properties should provide the key testable information for theory and simulation. All of these efforts need to be combined to stand a chance in developing a unified model for ion-water interactions.