Abstract
Although Ca2+ is the principal regulator of contraction in striated muscle, in vitro evidence suggests that some actin-myosin interaction is still possible even in its absence. Whether this Ca2+-independent activation (CIA) occurs under physiological conditions remains unclear, as does its potential impact on the function of intact cardiac muscle. The purpose of this study was to investigate CIA using computational analysis. We added a structurally motivated representation of this phenomenon to an existing myofilament model, which allowed predictions of CIA-dependent muscle behavior. We found that a certain amount of CIA was essential for the model to reproduce reported effects of nonfunctional troponin C on myofilament force generation. Consequently, those data enabled estimation of ΔGCIA, the energy barrier for activating a thin filament regulatory unit in the absence of Ca2+. Using this estimate of ΔGCIA as a point of reference (∼7 kJ mol−1), we examined its impact on various aspects of muscle function through additional simulations. CIA decreased the Hill coefficient of steady-state force while increasing myofilament Ca2+ sensitivity. At the same time, CIA had minimal effect on the rate of force redevelopment after slack/restretch. Simulations of twitch tension show that the presence of CIA increases peak tension while profoundly delaying relaxation. We tested the model’s ability to represent perturbations to the Ca2+ regulatory mechanism by analyzing twitch records measured in transgenic mice expressing a cardiac troponin I mutation (R145G). The effects of the mutation on twitch dynamics were fully reproduced by a single parameter change, namely lowering ΔGCIA by 2.3 kJ mol−1 relative to its wild-type value. Our analyses suggest that CIA is present in cardiac muscle under normal conditions and that its modulation by gene mutations or other factors can alter both systolic and diastolic function.
Introduction
Ventricular relaxation occurs as intracellular Ca2+ drops to resting levels. Under low Ca2+ conditions, contraction is inhibited by the troponin/tropomyosin complex (see Gordon et al. (1) for review). However, experimental evidence has long suggested that some degree of actin-myosin interaction is possible even in the absence of Ca2+ (2, 3, 4, 5). Under Ca2+-free conditions, as many as 5% of actin binding sites are occupied by myosin, according to some estimates made from solution studies of purified myofilament components (3, 4).
Despite abundant in vitro evidence for Ca2+-independent activation (CIA), its relevance to in vivo cardiac function is not clear. Striated muscle preparations can produce small amounts of actin-myosin-based force under low Ca2+ conditions, especially near physiological temperatures (6, 7). This suggests that residual actin-myosin crossbridges resist diastolic filling, adding to the resistance provided by other structures such as collagen and titin (8). However, distinguishing the contributions of these various factors is technically challenging, and cross bridge-based diastolic stiffness remains controversial (9).
Beyond any impact during diastole, it seems possible that the same molecular mechanisms that underlie CIA could also impact behavior of the muscle when Ca2+ is present. Lehrer and Geeves (10) recently proposed myosin-induced dissociation of troponin I (TnI) from the surface of actin as one such mechanism. This notion was embodied in a new structural state they call M−, a state in which myosin is bound to actin even though the associated troponin complex lacks Ca2+. They observed that adding the M− state into their model predicted not only an increase in myosin S1 binding at low Ca2+, but also an increase in Ca2+ sensitivity and a reduction in the Hill coefficient of the activity-pCa relationship. By their own interpretation, permitting the M− state perturbs thin filament equilibrium in favor of activation, thereby enhancing activity at all submaximal Ca2+ levels.
We have furthered the analysis of Lehrer and Geeves (10) by comparing our own model of CIA against mechanical measurements made in functioning cardiac preparations. In the process, we have been able to use specific data sets to constrain the extent of CIA in a more physiologically relevant context. That enabled a systematic study of its contribution not only to steady-state levels of activation, but also dynamic phenomena such as the rate of force redevelopment (ktr), the rate of tension development following Ca2+ activation (kact), and twitch contraction events. Our analyses provide evidence that CIA has wide-ranging effects on the behavior of cardiac muscle, and that it can be used as the basis for describing the effects of certain cardiomyopathy-associated mutations on twitch kinetics.
Materials and Methods
Background for model development
To explore consequences of CIA on myofilament behavior, we added a new Ca2+-independent activation pathway to our previous model of thin filament regulation and myosin binding (11). In the earlier model, we had assumed that transition of tropomyosin (Tm) out of the blocked position was impossible without having Ca2+ bound to troponin C (TnC). This has been referred to as the tight coupling premise (12). Here, we considered the possibility of loose coupling (13), wherein Tm can occasionally move from a blocked to closed state even in the absence of Ca2+. Justification for assuming some degree of loose coupling comes from considering the function of TnI as presently understood (see Kobayashi and Solaro (14) for review). Under conditions of low Ca2+, the inhibitory region (IR) of TnI is bound to the surface of actin, thereby pinning Tm in the blocked state. Tm is able to leave the blocked state only after the IR dissociates from actin, which is facilitated by the binding of the switch region (SR) of TnI to the N-terminal lobe of TnC. When Ca2+ is bound to site II on TnC, this enhances the affinity of the SR for TnC, thereby causing activation to be Ca2+-sensitive. With this in mind, CIA could reasonably occur as a consequence of either spontaneous IR dissociation from actin or spontaneous binding of the SR to Ca2+-free TnC. We have lumped these two putative phenomena into a single Ca2+-independent activation pathway in the model presented here.
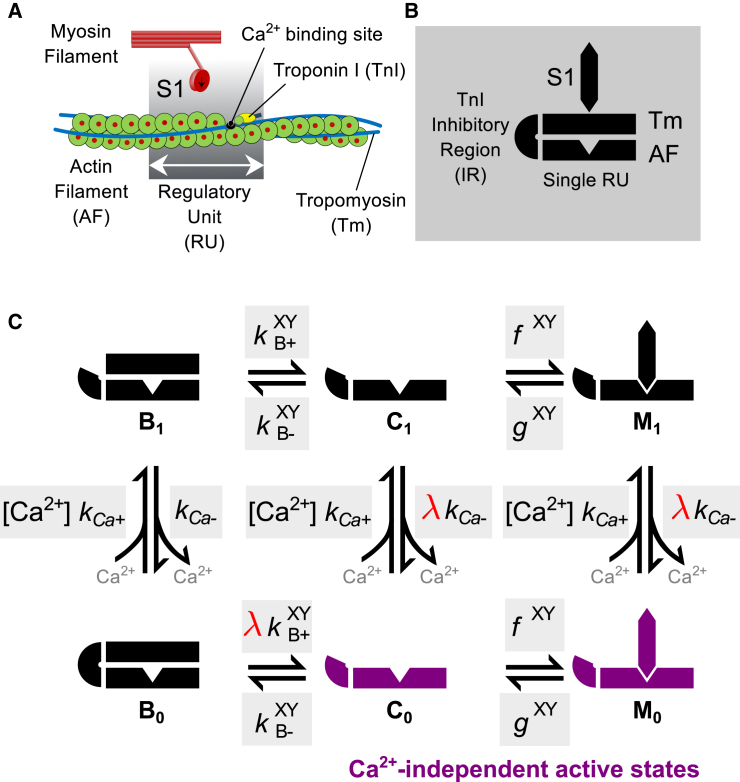
This model follows the formulation of discrete myofilament structural states as described previously by Campbell et al. (11), as shown in Fig. 1. The actin thin filament is discretized into a linear series of N = 26 regulatory units (RUs), each composed of 7-actin monomers, 1 Tm molecule, and 1 troponin (Tn) complex. For simplicity, each RU is assumed to contain a single myosin S1 binding site. The behavior of each RU is described by a three-state model corresponding to the known structural positions of Tm on the actin surface—namely, the blocked position B (myosin binding sites on actin are sterically blocked by Tm), closed position C (only weak binding of S1 to actin is permissible), and the open position M (corresponding to the presence of strongly bound S1) (3, 15). Ca2+-dependent control of the B ↔ C transition is represented by partitioning B into Ca2+-free and Ca2+-bound states (B0 and B1, respectively). The representation of structural overlap of Tm molecules between nearest-neighbor RUs is retained from the original model formulation (11).
Figure 1.
Schematic diagram of model components and states. (A) The model represents the function of individual thin filament regulatory units (RUs), as well as their interactions with myosin S1 and nearest neighbor RUs along the thin filament. (B) Illustration of symbols used to represent key myofilament components, including a single RU, the TnI inhibitory region (IR), tropomyosin (Tm), and myosin S1. (C) State diagram showing the assumed six possible regulatory states for an individual RU. (Shaded boxes) Kinetic rates for each state transition. From the B0 state, activation can proceed through Ca2+ binding, which causes the IR to dissociate from actin, or through spontaneous transfer of TnI from actin to TnC (see main text for details). The degree of Ca2+-independent activation is controlled by the parameter λ (red). When λ > 0, the Ca2+-independent activated states C0 and M0 (purple) can be occupied. Superscripts X and Y on some rates indicate that they are subject to these states occupied by neighboring RUs along the thin filament. To see this figure in color, go online.
An additional two structural RU states are needed to represent CIA caused by spontaneous TnI activity. These states are labeled C0 and M0, with the subscript 0 denoting the absence of Ca2+ bound to TnC. Similarly, we have added a subscript 1 to the former C and M states to explicitly indicate the presence of Ca2+. The final kinetic diagram showing these new states, along with the associated kinetic rates, is shown schematically in Fig. 1 C. Within each RU, transitions between the six states are governed by their differences in free energy as well as the states occupied by their nearest-neighboring RUs. Kinetic rates for the model are derived from these free energy terms as explained in the next section.
Simultaneous representation of loose coupling and nearest-neighbor interactions
Identical to our previous analysis (11), we assume some free energy difference between B and C states that arises from interactions between Tm and the surface of the actin filament. This energy difference assumes reference conditions in which both neighboring RUs occupy the C state. Using the Gibbs relation, we obtain a reference equilibrium constant between B and C states:
| (1) |
We can add to this description of the B ↔ C equilibrium by considering other factors that contribute to the free energy landscape. Interactions of each RU with its nearest neighbors (via Tm-Tm overlap) are assumed to add additional energy terms that influence this equilibrium. For instance, an RU transitioning into the C state while its neighbor remains in the B state will have to induce a significant amount of local bending at their shared Tm-Tm junction. Hence, a neighbor-dependent description of the B ↔ C energy difference can be written as follows:
| (2) |
The terms and represent the energy differences induced by Tm-Tm interactions with left and right neighboring RUs, respectively. The superscripts X and Y correspond to this Tm status (B, C, or M) of left and right RU neighbors. Applying the Gibbs relation separately to and terms in Eq. 2, we can now describe the neighbor-dependent B ↔ C equilibrium constant as the product of a reference equilibrium constant and a cooperative coefficient γ(XY):
| (3) |
Equation 3 suffices for the description of the equilibrium between Ca2+-bound states B1 and C1. However, the free energy difference between the Ca2+-free states B0 and C0 requires another term to account for the additional energy required for IR dissociation from actin or SR binding to TnC in the absence of Ca2+:
| (4) |
ΔGCIA is a generic energy term in the sense that it does not distinguish between IR and SR activity but instead represents in a lumped sense the properties of Ca2+-independent RU activation in the myofilament system. Similar to γ(XY), ΔGCIA can be transformed into a coefficient affecting the B ↔ C equilibrium constant via the Gibbs relation:
| (5) |
Thus, the overall equilibrium constant relating states B0 and C0 is
| (6) |
The free energy between C{0,1} and M{0,1} states and the associated equilibrium constants can be derived using a similar procedure. This yields
| (7) |
where is the reference C ↔ M equilibrium constant and μ(XY) is a cooperative coefficient analogous to γ(XY) representing the impact of neighboring RU states on the C ↔ M equilibrium.
For convenience, we define the contribution of a single B or M neighbor, respectively, on the B ↔ C equilibrium as the coefficients
| (8) |
The free energy term is the energy imposed by a neighboring RU in the B state on a B → C transition. Similarly, is the energy imposed by a neighboring RU in the M state on a B → C transition. Using these coefficients, the overall cooperative coefficient γ(XY) for any combination of neighbor states is given by
| (9) |
In like manner, the cooperative coefficient μ(XY) is defined as
| (10) |
By this formulation, whenever at least one of the cooperative coefficients (γB, γM, μB, or μM) has a value greater than unity, each RU will be affected by the states occupied by its neighbors. These interactions in sufficient strength can cause the Hill coefficient of steady-state force (nH) to be much greater than 1. As in the previous formulation, microscopic reversibility constrains γM and μB to be equal in value (11).
Up to this point, the model equations have been derived from free energy differences between thin filament states, which allow a thermodynamically consistent and unambiguous formulation of cooperative coefficients and equilibrium constants. While the cooperative coefficients are retained as free parameters in the model, equilibrium constants are generally not, due to practical considerations. Because we wish to conduct not only equilibrium but also dynamic simulations, equilibrium constants are insufficient on their own and it is necessary to specify either a pair of kinetic rates (forward and reverse) or one of the rates together with the equilibrium constant. Kinetic rates for Tm transitions relate to the reference equilibrium coefficients as follows:
| (11) |
| (12) |
Here, is the reference rate of transition B → C, and is the reference rate for C → B. We assume C ↔ M transitions to be driven by the cycling of cross bridges, hence the kinetic rates fref and gref assume the familiar identities of the rates of cross-bridge attachment and detachment, respectively.
To determine the final kinetic rates for Tm transitions, the nearest-neighbor cooperative coefficients must be partitioned between forward and reverse directions. This we accomplish with the scaling parameters r and q. It can be shown that final kinetic parameters of the following form satisfy Eqs. 3 and 7:
| (13) |
| (14) |
| (15) |
| (16) |
Equations 15 and 16 apply identically to the C1 ↔ M1 and C0 ↔ M0 transitions, ignoring the Ca2+ binding status of the RU. Likewise, the reverse transitions C1 → B1 and C0 → B0 are assumed to be Ca2+-independent, both following Eq. 14. However, the rate shown in Eq. 13 applies only to the Ca2+-bound case of B1 → C1. Recalling Eq. 6, the final transition rate for B0 → C0 (assuming that the energy barrier ΔGCIA applies to the forward rate only) must be
| (17) |
One nonobvious consequence of invoking loose coupling in this manner is that, to satisfy microscopic reversibility, λ must appear in one of the other kinetic rates around the loop of states (B0 - B1 - C1 - C0 - B0). (The product of rate constants clockwise around a loop must equal the product of rate constants around the counterclockwise direction.) It has been demonstrated that the rate of Ca2+ dissociation from TnC is greatly reduced by thin filament activation (16). Accordingly, we scale the Ca2+ dissociation rate by λ for the case where Ca2+ dissociates from an RU in the C1 state. Because λ takes on values of 0 < λ < 1, this has the effect of increasing the Ca2+ affinity of the troponin complex under conditions of activation (in accordance with experiments), while also ensuring that microscopic reversibility is preserved. A similar construction has been used by Rice et al. (17). Assuming that TnC-Ca2+ affinity is similar in closed and open states, the dissociation rate of Ca2+ from M1 is also scaled by λ. Note that this is also necessary to satisfy microscopic reversibility in the scheme’s other loop (C0 - C1 - M1 - M0 - C0). Hence, the rate of Ca2+ binding to an RU is governed by the second-order rate constant kCa+ irrespective of Tm position, but the dissociation rate is kCa− for B1 → B0, and λkCa− for C1 → C0 and M1 → M0 (Fig. 1 C).
Markov chain-Monte Carlo simulations
We employed a standard Markov chain-Monte Carlo (MCMC) algorithm to simulate activation of a full-length cardiac thin filament composed of N coupled RUs (N = 26). Each RU behaves according to the scheme described above and depicted in Fig. 1 C. The initial state of the system at time t = 0 was always specified by placing all 26 RUs in the B0 state. To advance the system in time, repeated steps of Δt were taken. At each time step, the state of every individual RU in the filament was updated in turn by comparing a randomly drawn number R ∈ (0,1) with a set of transition probabilities that correspond to the RU’s state. Transition probabilities are computed by , where kl represents the lth transition rate among n total transitions leading away from the state in question.
For example, consider an RU occupying the B0 state. In total, there are n = 2 transitions leading away from this state (B0 → B1, B0 → C0; see Fig. 1), with corresponding transition probabilities and . The MCMC algorithm determines the new state of the RU (Zt+Δt) according to the following rules:
| (18) |
This construction partitions the interval of R into three regions that correspond to B0 → B1, B0 → C0, or no change (the RU remains in B0). Updates for RUs in the B1, M1, and M0 states, which also have n = 2 transitions, are analogous. For the states C0 and C1, each of which have n = 3 possible transitions, updates are similar to Eq. 18 except that the (0,1) interval of R is subdivided into four regions rather than three. Before each simulation, the full set of model parameters was analyzed automatically to determine an overall value for Δt, such that
| (19) |
for each of the six possible RU states. In other words, Δt was chosen such that no state had a cumulative transition probability for a single time step that exceeded 70%. Values for Δt ranged from 0.64 to 70 μs in the simulations reported here.
Because many of the kinetic rates depend upon these states of an RU’s nearest neighbors (Eqs. 13–16), the corresponding transition probabilities were updated for each RU at the beginning of every time step. RUs on either extreme of the thin filament were assigned to the B0 state and not permitted to transition during simulation, thereby acting as boundary conditions for the domain of the filament.
The state Zi,t occupied by the ith RU in the simulated thin filament was recorded at every time point t for postprocessing. Force was calculated at each time point by counting up M{0,1} states along the entire filament span:
| (20) |
To obtain meaningful results from these stochastic simulations, each time series was repeated J times. The final average force at any given time step t is given by
| (21) |
where Fj,t is the force produced at t (Eq. 20) for the jth repetition. J = 1024 repetitions were performed for all simulations reported herein.
The computational demand of these MCMC simulations was offset by implementing the model in CUDA C++ to take advantage of parallelism offered by graphics processing units (GPUs). Simulations were run on a Tesla K40 GPU (NVIDIA, Santa Clara, CA), with scripting and data postprocessing performed using MATLAB (The MathWorks, Natick, MA). A single averaged force response like those shown in Fig. 2 required 1.5 s of wall clock time for typical parameter sets, the equivalent of 525,000 thin filament state updates per second. This was an ∼30,000× speedup over a naive MATLAB implementation of the model run on a 6-core Intel i7 processor (Santa Clara, CA).
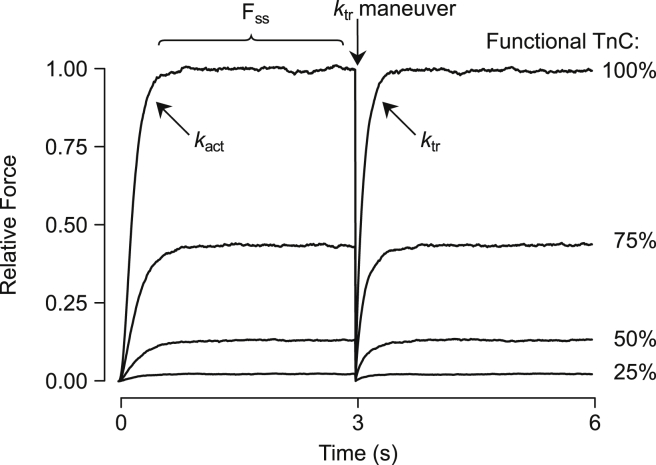
Figure 2.
Model output for typical simulations. The model predicts contractile force produced by the myofilaments during sudden exposure to Ca2+. pCa was set to 4 in these records at time zero. After a period of rapid change (described by the rate constant kact), force reached a steady-state level (FSS). A slack/restretch maneuver was then mimicked by instantaneously removing all attached cross bridges and observing the rate of force redevelopment (ktr). Simulations were also performed in which Ca2+ binding to some fraction of randomly selected RUs was eliminated, imitating experiments in which nonfunctional troponin C (TnC) was incorporated into myofilaments (19, 20). Initial simulations with the tightly coupled model (i.e., λ = 0) are shown here under conditions of 100, 75, 50, and 25% functional TnC. Force is shown relative to FSS of the 100% functional TnC curve.
Simulation protocols
Model parameters and conditions were adjusted to mimic various experimental scenarios. In a typical simulation (Fig. 2), Ca2+ concentration was set at a constant value, and force output of the system was computed for 3000 ms. For all parameter sets used, this was sufficient time for the system to reach steady state. After 3 s are elapsed, all RUs occupying M states were set to the corresponding C state (C0 or C1) to simulate a ktr maneuver in which cross bridges are instantaneously broken. Force redevelopment was observed by continuing simulation for another 3000 ms postmaneuver. Values of ktr were computed assuming an exponential rise in force after breaking of cross bridges (18). kact, the rate of force development after Ca2+ activation, was calculated in the same manner. We constructed steady-state force-pCa curves by repeating this simulation protocol at several Ca2+ concentrations, and computing the force at steady state for each case.
We also simulated experiments where myofilaments are reconstituted with nonfunctional, non-Ca2+ binding TnC (xTnC) (19, 20). This was implemented by randomly designating RUs as normal or xTnC-containing before each repetition. xTnC-containing RUs had their kinetic models altered such that they remained permanently in the Ca2+-free states (B0, C0, or M0). Varying proportions of xTnC were incorporated into simulations to study its effects on properties such as Ca2+-activated force and ktr.
Finally, we simulated Ca2+-activated isometric twitches by causing Ca2+ concentration to vary with time. A representative Ca2+ transient, recorded in rat trabecula by Janssen and de Tombe (21) was digitized and used as Ca2+ input for some twitch simulations. Representative transients were also digitized from Wen et al. (22) for model analysis of the TnI R145G mutation.
Parameter optimization was used to generate baseline parameter sets corresponding to data from skinned rat trabeculae at 25°C (19), intact rat trabeculae at 22°C (21), and intact mouse papillary muscle at room temperature (22). These sets, shown in Table 1, were obtained using a particle swarm optimization algorithm (23). For set 1 (skinned rat trabeculae), optimization was performed to minimize the least-squares error between measured and modeled values of maximally activated force under different levels of xTnC, the baseline force-pCa relationship (0% xTnC), and the baseline ktr-pCa relationship. Simultaneous fitting to all three curves constrained λ to its final estimated value of 0.06. Intact muscle parameter sets (sets 2 and 3) were obtained by fixing λ at 0.06 and adjusting other model parameters until the least-squares error between the measured and simulated twitch time courses was minimized. The parameter differences seen between sets are most likely due to the effects of muscle skinning (24) (between sets 1 and 2) and interspecies differences (rat in sets 1 and 2 versus mouse in set 3). Except where noted, the simulations reported here used parameter set 1.
Table 1.
Model parameter values
| Set | λ | kCa+ (μM–1ms–1) | kCa− (ms–1) | (ms–1) | (ms–1) | fref (ms–1) | gref (ms–1) | γB | γM | μM | q | r |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.06 | 1.14 | 10.0 | 17.0 | 0.084 | 0.0034 | 0.007 | 96 | 1.1 | 1.0 | 1.0 | 1.0 |
| 2 | 0.06 | 5.02 | 3.81 | 195 | 2.19 | 0.7 | 0.243 | 153 | 1.6 | 1.8 | 0.5 | 1.0 |
| 3 | 0.06 | 10.0 | 9.21 | 82.3 | 2.25 | 1.0 | 0.610 | 61 | 2.0 | 1.91 | 0.97 | 0.33 |
The values optimized to fit data from skinned rat trabeculae at 25°C (set 1), intact rat trabeculae at 22°C (set 2), and intact mouse papillary muscle at room temperature (set 3).
Results
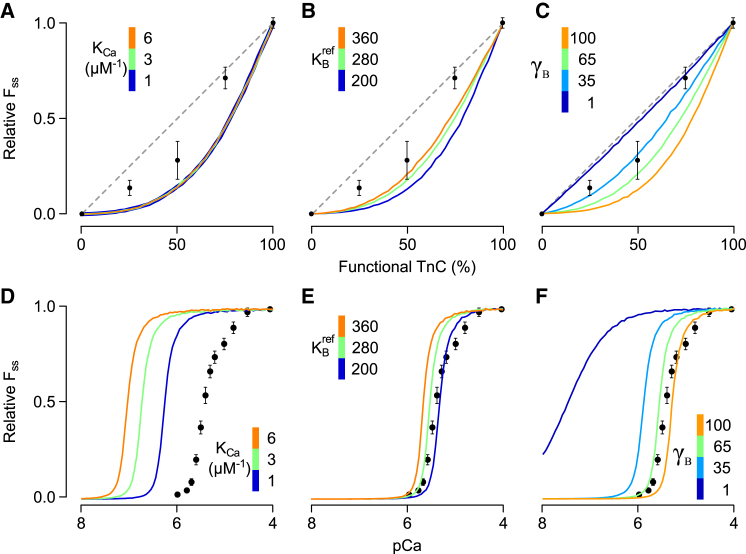
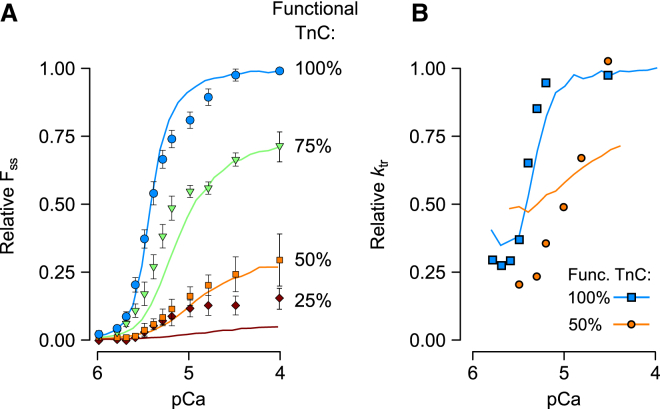
We first sought means of estimating the value of λ, the parameter representing the extent of Ca2+-independent regulatory unit activation (CIA). Our overall approach was to identify a data set that a tightly coupled model (λ = 0) could not reproduce and then determine an approximate λ-value that reconciled the discrepancy. In previous work (11), we showed that the tightly coupled model exhibits some systematic deviations from measurements in which nonfunctional TnC (xTnC) is exchanged into skinned cardiac muscle preparations (19). Simulations overestimated the inhibitory effect of xTnC on maximal Ca2+-activated force (e.g., Fig. 3 A).
Figure 3.
Sensitivity of the tightly coupled model to various parameter changes. The dependence of FSS on % functional TnC (A–C) and on pCa (D–F) was studied in the tightly coupled model (λ = 0) while perturbing other key model parameters. Perturbations included large changes in the Ca2+-TnC equilibrium constant (KCa, A and D), the equilibrium constant governing the B → C transition (, B and E), and the cooperative coefficient γB (C and F). Measured FSS-functional TnC and FSS-pCa relationships were digitized from Gillis et al. (19) and are shown here for comparison. (A–C, dashed line) Generic 1:1 relationship between FSS and % functional TnC for reference. Under conditions of tight coupling, none of the parameter changes were capable of producing curves rising above the 1:1 line or having the characteristic inflection point implied by data from experiments. Changes that tended to improve agreement with the data in (A)–(C) shifted the corresponding curves away from measurements in (D)–(F). To see this figure in color, go online.
To confirm that the tightly coupled model was incapable of reproducing the reported FSS-xTnC relationship, we systematically perturbed other key model parameters while holding λ equal to zero (Fig. 3). Simulations were repeated with wide-ranging values for the TnC Ca2+ affinity (KCa), the reference equilibrium constant between B and C states , and the cooperative coefficient γB. In xTnC simulations, changing KCa had no effect upon the FSS-xTnC relationship whatsoever (Fig. 3 A). Increasing so that functional RUs favored the C rather than B state did increase the force at each intermediate level of % functional TnC, but even at extreme values the model produced no inflection point between 50 and 75% functional TnC as implied by the data (see overlain data points in Fig. 3 B). The model showed greatest sensitivity to variations in γB. In the extreme case (γB = 1), no cooperative interactions exist between neighbors and a 1:1 relationship between % functional TnC and maximum force was produced (Fig. 3 C), a result also observed by Tanner et al. (25). Although adjustment to γB allowed the predicted xTnC-maximum force relationship to pass nearer to data points, it too lacked an inflection point. For each parameter set used in Fig. 3, A–C, we also simulated the corresponding FSS-pCa relationship under conditions of 100% functional TnC (Fig. 3, D–F). Parameter changes that tended to improve the FSS-xTnC relationship invariably increased Ca2+ sensitivity of FSS, shifting curves far to the left of experimental measurements.
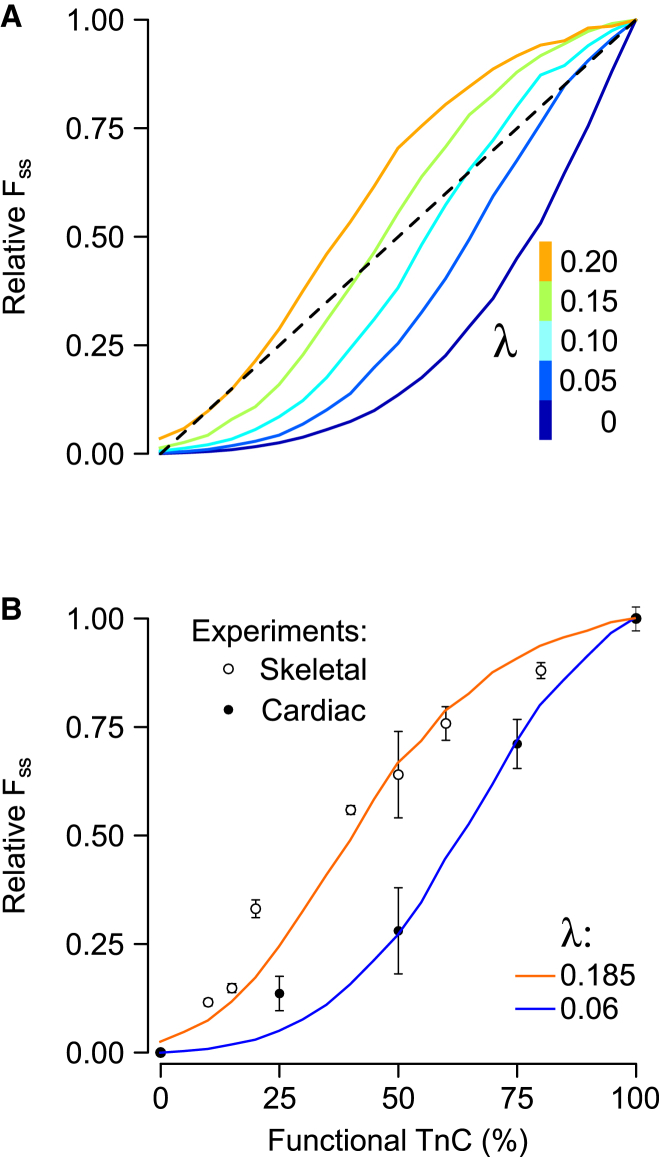
Having established that none of the original model parameters were capable of reconciling differences between simulated and measured effects of xTnC, we repeated xTnC simulations for values of λ > 0. Introducing CIA into the model in this way gives rise to an inflection point in the FSS-xTnC curve (Fig. 4 A), in stark contrast to the other parameter changes studied (Fig. 3). Another unique effect of λ was its ability to allow curves to range above the 1:1 line. Furthermore, we found that it was possible to match FSS-xTnC curves from both cardiac (19) and skeletal muscle (20) simply by adjusting the value of λ (Fig. 4 B).
Figure 4.
The effect of Ca2+-independent activation (λ) on the FSS-xTnC relationship. (A) FSS-xTnC curves were computed for values of λ ranging between 0 and 0.2. (B) λ-values of 0.06 and 0.185 most closely reproduced experimental data reported in cardiac (19) and skeletal muscle preparations (20), respectively. To see this figure in color, go online.
The fact that λ conferred unique characteristics to xTnC simulations indicated that, in combination with other measurements, the xTnC dataset could be used to constrain the value of λ to within reasonable limits. Besides the FSS-xTnC relationship, Gillis et al. (19) also reported the FSS-pCa and ktr-pCa relationships for skinned rat trabeculae. We performed a global model fit to these three datasets using particle swarm optimization, yielding parameter set 1 (Table 1). This consensus set represents parameter values that lead to the best overall simultaneous reproduction of the FSS-xTnC relationship (Fig. 4 B) and FSS-/ktr-pCa relationships under conditions of 100% functional TnC (light blue curves; see Fig. 5). Within parameter set 1, λ is constrained in the sense that either increasing or decreasing its value causes the global fit to deteriorate. The converged value of λ (0.06) is equivalent to a free energy barrier to Ca2+-independent RU activation (ΔGCIA) of 7 kJ mol–1 at 25°C (Eq. 5).
Figure 5.
Predicted effects of xTnC on FSS-pCa relationships (A) and ktr-pCa relationships (B). The 100% functional TnC curves (light blue in A and B) were obtained by fitting the model simultaneously to the experimentally reported values from Gillis et al. (19) for both relationships, along with the FSS-xTnC relationship reported in that same study (Fig. 4B). Fitted values are listed under set 1 in Table 1. Predictions of FSS and ktr (solid lines) in the presence of xTnC were produced using set 1, but with increasing levels of simulated xTnC. (Symbols) Data digitized from the study of Gillis et al. (19). To see this figure in color, go online.
A certain degree of independent validation for parameter set 1, including the final value of λ, was obtained by predicting full FSS-pCa and ktr-pCa curves for intermediate levels of functional TnC (Fig. 5). As seen in experiments, the addition of xTnC shifted the modeled force-pCa curves rightward while diminishing maximal force. The model also reproduced in qualitative fashion the dynamic effects of xTnC, as seen through measurements of the rate of force redevelopment (ktr, Fig. 5 B). In experiments, conditions of 50% functional TnC were seen to greatly slow ktr at submaximal pCa levels, shifting the entire curve rightward. Model predictions of ktr for 50% functional TnC capture this dynamic effect as well (Fig. 5 B, orange curve). In the model, this behavior arises because RUs containing xTnC are only recruited after myosin binding takes place in neighboring RUs—a process that takes time and hence slows force redevelopment (26). This slowing effect is less apparent at high Ca2+ concentrations, where Ca2+, and not recruitment, is the primary source of activation.
These results support the idea that CIA is not merely an in vitro phenomenon, but present to some degree in functioning muscle fibers as well. Simulations with the optimized parameter set predict that at the half-activation mark (pCa 5.4), roughly 5% of all RUs reside in one of the Ca2+-free active states (C0 or M0). They also suggest that ∼12% of force at half-activation comes from RUs that do not contain bound Ca2+ (Fig. S1 in the Supporting Material). Having established a reasonable estimate of the magnitude of CIA (λ = 0.06), we performed additional simulations to explore the different ways in which CIA might manifest itself in cardiac muscle behavior.
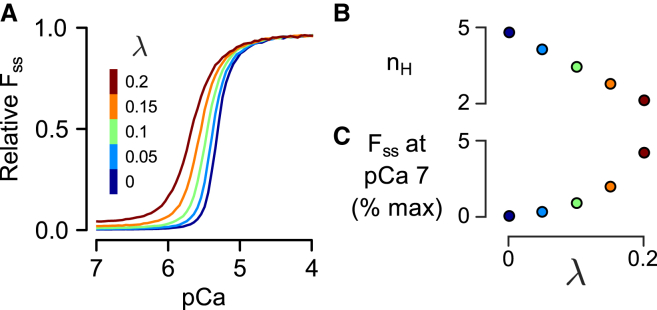
Using parameter set 1 as a baseline, we examined the effects of CIA on the FSS-pCa relationship by varying λ-values between 0 and 0.2 (Fig. 6). Increasing CIA (increasing λ) shifted the FSS-pCa curve leftward, increasing Ca2+ sensitivity (Fig. 6 A). At the same time, the Hill coefficient (nH) decreased linearly with increasing λ (Fig. 6 B), demonstrating that thin filament cooperativity and CIA are inversely coupled. Not surprisingly, another effect of enhanced CIA was increased force at low Ca2+ (Fig. 6 C), indicating an inability of the myofilaments to completely inhibit contraction as λ is increased. Besides FSS, rates of force generation (kact and ktr) as functions of pCa and λ were also extracted from simulation records (see Fig. S2). The ktr was minimally effected by the degree of CIA, only shifting in Ca2+ sensitivity in a manner similar to the FSS-pCa relationship. On the other hand, kact exhibited complex, nonlinear changes in response to perturbations of λ (Fig. S2, C and D).
Figure 6.
Effects of the parameter λ on the steady-state force (FSS). (A) FSS as a function of pCa is shown for several different values of λ. (Dark blue line) Tight coupling case (λ = 0). Increasing degrees of loose coupling or Ca2+-independent activation (λ > 0) are shown by other colors, as labeled. (B) Increased λ reduces the Hill coefficient (nH) of the FSS-pCa curves in a linear fashion. (C) Increasing λ increases the relative force produced by the model under low Ca2+ conditions (pCa 7). To see this figure in color, go online.
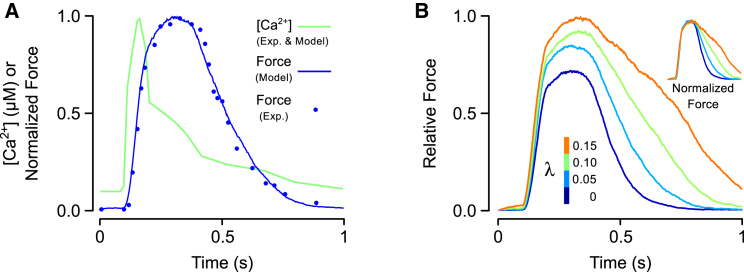
To examine the effects of CIA in a more physiological context, we also simulated isometric twitches while varying the parameter λ. We began by first fitting model parameters to an isometric twitch measured in a sarcomere length-clamped rat trabecular preparation (21), resulting in parameter set 2 (Table 1). The intracellular Ca2+ transient measured in that study was used to drive activation of the model (Fig. 7 A). The twitch tension produced as a result of parameter fitting showed excellent agreement with the measured response (Fig. 7 A). Next, we repeated the twitch simulation at several different levels of CIA, ranging from none (λ = 0) to λ = 0.15 (Fig. 7 B). Over this range, the time required to reach peak contraction changed by only 10%. At the same time, peak tension increased by 40% and the relaxation time (time from peak contraction to 50% relaxation), increased by 172%. These results suggest that CIA could be a potent modulator of relaxation in particular.
Figure 7.
Simulations of cardiac twitch events. (A) A Ca2+ transient was digitized from a study of rat cardiac trabeculae (21) and used as an input to the model (green trace). The predicted twitch force was compared against a measured twitch response from the same study. Model parameters were adjusted to minimize error between the measured and simulated twitches (Table 1, set 2). (B) The effect of Ca2+-independent activation on twitch force was examined by simulating twitches while varying λ between 0 and 0.15. The Ca2+ transient shown in (A) was used to elicit each contraction. Twitch magnitude has been scaled to the peak twitch force for λ = 0.15, at which 70% of RUs contained attached cross bridges. (Inset, B) Overlay of twitches after each has been normalized to its own peak. To see this figure in color, go online.
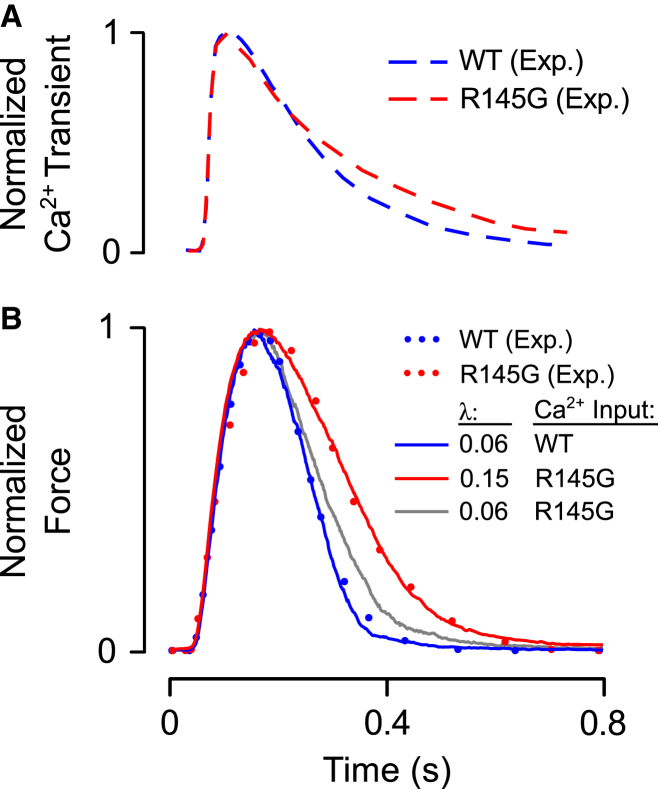
Having observed a meaningful impact of CIA on twitch kinetics, we considered conditions under which this muscle property might be perturbed. Among the possible sources of CIA as represented in our model is the relative affinity of the TnI IR for actin. We therefore used the model to analyze data obtained from intact papillary muscles of mice expressing a mutant R145G TnI transgene (22). This mutation results in the loss of a positively charged central residue within the IR domain on TnI, and could conceivably disrupt normal electrostatic interactions that promote inhibitory region-actin (IR-actin) binding. To determine whether the new model parameter λ could capture the phenotypic consequences of the R145G mutation, we undertook the following procedure: to start, isometric twitches were simulated in response to a measured wild-type (WT) mouse papillary Ca2+ transient, also reported by Wen et al. (22) (Fig. 8 A, blue trace). Next, model parameters were adjusted such that the simulated twitch response matched the measured twitch time course (Fig. 8 B, blue trace). This parameter set is shown in Table 1, set 3. Then, the Ca2+ input into the model was switched from the WT record to one measured in a mutant muscle (Fig. 8 A, red trace) and a new twitch tension was predicted. The mutant Ca2+ transient’s slower decay did cause a slight prolongation of the simulated twitch relative to the WT case (Fig. 8 B, gray trace), but substantial differences remained relative to the measured R145G twitch. Ultimately, we found that besides the change in Ca2+ transient it was necessary to increase λ from its WT value of 0.06 up to a new value of 0.15 in order achieve a close fit to the reported data (Fig. 8 B). This λ-change amounts to a prediction that the R145G mutation weakens IR-actin affinity, lowering binding energy by 2.3 kJ mol−1 at 25°C (see Eq. 5). These results therefore suggest a specific mechanism whereby this TnI mutation can exert substantial effects on the rate of twitch relaxation.
Figure 8.
Analysis of the functional consequences of the TnI mutation R145G. (A) Ca2+ transients were digitized from a study of papillary muscles taken from WT mice and R145G mutants by Wen et al. (22). (B) Simulated twitch responses (solid traces) were obtained by driving the model with Ca2+ transients shown in (A). Model parameters were adjusted until output force (blue trace) matched a measured WT twitch record (blue dots). The fitted parameters are reported in Table 1, set 3. Then, driving the model with the R145G transient, the parameter λ was increased to determine whether this change was capable of explaining the effects of the mutation. Increasing λ from 0.06 to 0.15 allowed the model (red trace) to reproduce the measured R145G twitch record (red dots). To illustrate that the change in λ exerted substantial effects on twitch independent of the differences in WT and R145G Ca2+ transients, λ was set to 0.06 once again and the model was driven with the R145G transient (gray trace). To see this figure in color, go online.
Discussion
Lehrer and Geeves (10) recently contemplated the impact of loose coupling on myofilament activity, primarily drawing on observations from in vitro solution studies of myofilament proteins. They found that the addition of a myosin-induced, Ca2+-independent state increased Ca2+ sensitivity and Ca2+-independent actin/myosin activity while lowering nH. We have attempted to place their findings in a more physiological context by fitting our own model to data obtained from preparations with intact sarcomeres. This yielded evidence supporting the existence of meaningful CIA within functioning muscle, based on analysis of the xTnC data set of Gillis et al. (19). Similar to Lehrer and Geeves (10), we found that CIA modulated Ca2+ sensitivity, Ca2+-independent force, and cooperativity of steady-state force (Fig. 6 A). Beyond steady-state type results, we were able to extend the model to study the effects of CIA on dynamic responses. Of particular interest were the findings that CIA has a strong impact on twitch relaxation and that such a mechanism can explain the measured effects of a TnI mutation on twitch contraction.
Our study suggests some practical bounds for the extent of generic CIA in cardiac muscle. We found that λ-values of 0.06 worked best when fitting parameters to data sets (Figs. 4 and 5). In terms of the model, this means that RU activation proceeds 17× more slowly in the absence of Ca2+. When this is coupled with the inhibition imposed by inactive nearest neighbors (as would be the case on average for a muscle at rest), this value allows for loose coupling while still maintaining the requisite Ca2+ regulation of contraction. The thermodynamic constraint in our model that dissociation of Ca2+ from C or M state RUs also be slowed by the same factor λ actually reinforces the value of 0.06 as being reasonable: a 17× slower dissociation rate is of the same order as the 8× decrease in dissociation rate measured by Davis et al. (16) when regulated actin is treated with myosin S1 fragments. Hence, while we cannot now estimate a value of λ with absolute certainty, the values used here seem plausible.
Far-reaching effects of the parameter λ in our model suggest that tuning CIA could be an important regulatory mechanism in the heart. The value λ had marked effects on twitch relaxation rate, with relatively minor effects on other aspects of contraction (Fig. 7). This raises the possibility that posttranslational modifications of TnI that impact either its inhibitory or switch regions (e.g., PKC phosphorylation of threonine 144) mediate lusitropic regulation with high specificity. Indeed, transgenic mice with pseudophosphorylated PKC sites on TnI exhibited slowed twitch relaxation (27). According to the model, these molecular perturbations would exert their effects through lowering ΔGCIA, possibly by weakening the binding affinity of the IR for the surface of actin. Similarly, we showed that lowering ΔGCIA (increasing λ) prolonged relaxation in a manner that precisely resembled the effects of the TnI R145G mutation expressed in mice (22) (Fig. 8). The model therefore explains in quantitative and mechanistic terms how modifications to TnI’s inhibitory region can act as potent regulators of cardiac relaxation.
Although the parameter λ can capture the effects of specific IR-actin perturbations such as the R145G mutation to TnI, it is necessary to emphasize that λ is a lumped term that likely represents not only IR-actin interactions, but also binding of the adjacent TnI switch region to TnC (Eq. 5). As such, it cannot be used to distinguish between IR-actin and switch region-TnC (SR-TnC) effects unless perturbations are targeted (as in the case of the R145G mutation). In other words, muscle behavior that is described by an increase in λ could indicate either a decrease in IR-actin affinity or an increase in SR-TnC affinity—both have the net effect of promoting dissociation of the IR from actin. Indeed, λ could conceivably represent any mechanism capable of encouraging the displacement of the IR from actin, such as spontaneous fluctuations in Tm position or forcible displacement of Tm by myosin.
One striking result yielded by the model was its ability to represent the divergent responses of cardiac and skeletal fibers to xTnC with a single change to the parameter λ (Fig. 4 B). This analysis suggests that the differing xTnC responses can be explained by well-known differences in troponin isoforms between the two muscle types (28, 29). This is an alternate viewpoint to the interpretation offered in the original studies, namely that the distinct responses were indicative of fundamentally different sources of cooperativity (19, 20). It was suggested that in skeletal muscle each Ca2+ binding site regulates myosin binding sites beyond the seven that are structurally associated with a single RU. In this manner, a Ca2+-containing RU could activate neighboring stretches of the thin filament, even sites that should be inhibited by xTnC (20). It was further argued that the behavior of cardiac preparations could be explained if, in that muscle type, each Ca2+-containing RU activated less than seven myosin binding sites (19). They concluded that Tm is more flexible in cardiac muscle than in skeletal, and, by extension, that Tm-Tm interactions could not be the main source of cardiac muscle cooperativity. Our analysis does not require any assumption of differences in Tm flexibility, and as such supports the view that the mechanisms of cooperative Ca2+ activation are similar in the two muscle types. This perspective may be more consistent with the broader collection of findings regarding Tm flexibility. Although some studies have suggested persistence lengths for Tm that are on the order of a single RU (30), several others have reported values corresponding to roughly 12 regulatory units (31, 32), substantially more stiff than previously believed. Furthermore, rodent fast skeletal and cardiac muscle preparations like those used in the xTnC studies both express primarily α-Tm (33), making differential Tm isoform expression an unlikely source of functional divergence.
Ultimately, further experiments will be required to resolve which mechanism accounts for skeletal and cardiac differences in the xTnC response. However, the model results reported here provide important insight in the form of testable hypotheses. For instance, given that the model explains TnI R145G twitch results on the basis of decreased actin-IR affinity, we predict that repeating the xTnC experiments of Gillis et al. (19) in preparations containing the TnI R145G mutation will cause cardiac muscle to shift toward a more skeletal-type response (Fig. 4 B). Such experiments seem feasible and would directly test the model’s validity.
It should be acknowledged that the model has resolution only at the level of single RUs, and does not consider fine regulation of the seven individual myosin binding sites within each (34, 35). The ability of the model to reproduce key experimental phenomena despite this coarse-grained approach suggests that activation events are rarely limited to single RUs. Rather, they consist of several contiguous RUs that transition in concert, forming islands of activation (Fig. S3). Statistical analysis of raw MCMC model output shows that in the model activation occurs preferentially in islands, even at low pCa (Fig. S4). Elegant experiments by Desai et al. (36) have recently provided direct visualization of this type of clustered activation along the thin filament. To do so, they stretched single actin filaments between latex beads and tracked the binding of fluorescently labeled myosins. Binding events tended to cluster in contiguous regions along the filament, rather than occurring at random. The abundant structural evidence for strong Tm-Tm coupling (15, 37) and the recent data of Desai et al. (36) leave little doubt that activation spreads through nearest neighbors along the thin filament. Several computational models of the thin filament, including our own, elevate the significance of Tm-Tm coupling by demonstrating that it can single-handedly account for a number of experimentally observed phenomena, including realistic Hill coefficients for steady-state activation, the Ca2+-dependence of ktr, and the effects of NEM-S1 on activation. In this article, we add to this list by successfully recapitulating the measured effects of xTnC on steady-state and dynamic aspects of thin filament activation.
At the same time, key questions regarding differences between skeletal and cardiac muscle remain unanswered. While we find the xTnC analysis convincing (Fig. 4 B), by their nature the xTnC experiments probably highlight differences in IR-actin binding between the two muscle types while eliminating the effects of any SR-TnC differences. The xTnC molecules used in those studies were engineered to disrupt Ca2+ binding to TnC, which in turn should block SR-TnC interactions for xTnC-containing RUs. In the absence of SR-TnC interactions, the two distinct λ-values fit to the data likely represent different IR-actin binding affinities. The implication is that the IR of cardiac TnI has a greater affinity for actin than that of skeletal TnI, a result which is intriguing given the fact that their amino-acid sequences in the inhibitory region differ by a single residue (28), with measurable consequences to function (38). A more comprehensive comparison of CIA between cardiac and skeletal muscle would use conditions that allow both IR-actin and SR-TnC binding. SR-TnC affinity seems likely to differ between skeletal and cardiac muscles, considering stark differences in their respective TnI and TnC isoform sequences (28, 29).
Aside from our model and that of Lehrer and Geeves (10), others have included CIA in varying forms. Some allow myosin to remain attached even after dissociation of Ca2+, but do now allow Ca2+-free crossbridge formation (39). Others include an explicit Ca2+-independent activation pathway that resembles the one presented here (17, 25, 40, 41). Dobrunz et al. (40) presented a four-state model that allows a force-generating permissive state without requiring the binding of Ca2+ to the troponin complex. Their four-state RU model is the rough equivalent of the one that would be obtained by taking our six-state representation (Fig. 1 C) and merging closed states with open states (C0 with M0 and C1 with M1). Rice et al. (17) also used a four-state model with a Ca2+-free permissive state, while adding thermodynamic constraints very similar to those we have adopted. Although the main purpose of their study was to examine the impact of nearest-neighbor Tm interactions on cooperativity, they conducted some simulations under increasing amounts of CIA and noted the same impact on the FSS-pCa relationship as we did (Fig. 6 A). The additional results presented here indicate that models with representations of CIA are more likely to exhibit realistic dynamic myofilament behavior and enable the analysis of targeted perturbations such as mutations to TnI.
While the model presented here is generally successful in reproducing experimental observations, it does have some systematic deviations from the data. Careful consideration of these discrepancies is instructive. We note, for instance, that the simulations underestimate tension produced under conditions of 25% functional TnC in cardiac muscle (Fig. 4 B, blue trace). We believe that this is a consequence of the model assuming a fixed RU span—when activation spreads along the thin filament in our model, one complete RU is the smallest increment available. As such, the model does not have adequate resolution to account for recruitment of neighboring myosin binding sites within single RUs along the thin filament. This is particularly critical in transition zones, or points along the filament where inactive RUs are found adjacent to active ones (see Fig. S3). At higher fractions of functional TnC, this assumption is reasonable because long contiguous stretches of the filament can still be activated together, and there are few transition zones. In contrast, there will be many more transition zones at 25% functional TnC, and the model, lacking intra-RU resolution, loses some accuracy. This may also explain why ktr values for 50% functional TnC are overestimated by the model (Fig. 5 B, orange trace). Therefore, refining the spatial resolution of the model to include individual myosin binding sites (25, 34, 35) is an important future direction for this work, insofar as it may reconcile remaining discrepancies with the measured data.
Author Contributions
Y.A., J.A.B., K.J.M., and S.G.C. designed and implemented the computational model; Y.A., J.A.B., and K.J.M. performed simulations; and Y.A., J.A.B., and S.G.C. wrote the article.
Acknowledgments
The authors acknowledge Sander Land for helpful discussions and comments on an early draft of the article.
This work was supported in part by the facilities and staff of the Yale University Faculty of Arts and Sciences High Performance Computing Center. It was also supported in part by National Institutes of Health award No. 1R21HL126025 to S.G.C. and Clinical and Translational Science Award No. UL1 TR000142 from the National Center for Advancing Translational Science, a component of the National Institutes of Health.
Its contents are solely the responsibility of the authors and do not necessarily represent the official view of the National Institutes of Health.
Editor: David Warshaw.
Footnotes
Yasser Aboelkassem’s current address is Institute for Computational Medicine, Johns Hopkins University, Baltimore, Maryland.
Four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00999-6.
Supporting Material
References
- 1.Gordon A.M., Homsher E., Regnier M. Regulation of contraction in striated muscle. Physiol. Rev. 2000;80:853–924. doi: 10.1152/physrev.2000.80.2.853. [DOI] [PubMed] [Google Scholar]
- 2.Fuchs F. Thermal inactivation of the calcium regulatory mechanism of human skeletal muscle actomyosin: a possible contributing factor in the rigidity of malignant hyperthermia. Anesthesiology. 1975;42:584–589. doi: 10.1097/00000542-197505000-00014. [DOI] [PubMed] [Google Scholar]
- 3.McKillop D.F., Geeves M.A. Regulation of the interaction between actin and myosin subfragment 1: evidence for three states of the thin filament. Biophys. J. 1993;65:693–701. doi: 10.1016/S0006-3495(93)81110-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schaertl S., Lehrer S.S., Geeves M.A. Separation and characterization of the two functional regions of troponin involved in muscle thin filament regulation. Biochemistry. 1995;34:15890–15894. doi: 10.1021/bi00049a003. [DOI] [PubMed] [Google Scholar]
- 5.Maytum R., Westerdorf B., Geeves M.A. Differential regulation of the actomyosin interaction by skeletal and cardiac troponin isoforms. J. Biol. Chem. 2003;278:6696–6701. doi: 10.1074/jbc.M210690200. [DOI] [PubMed] [Google Scholar]
- 6.Ranatunga K.W. Thermal stress and Ca-independent contractile activation in mammalian skeletal muscle fibers at high temperatures. Biophys. J. 1994;66:1531–1541. doi: 10.1016/S0006-3495(94)80944-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Campbell K.S., Patel J.R., Moss R.L. Cycling cross-bridges increase myocardial stiffness at submaximal levels of Ca2+ activation. Biophys. J. 2003;84:3807–3815. doi: 10.1016/S0006-3495(03)75108-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wu Y., Cazorla O., Granzier H. Changes in titin and collagen underlie diastolic stiffness diversity of cardiac muscle. J. Mol. Cell. Cardiol. 2000;32:2151–2161. doi: 10.1006/jmcc.2000.1281. [DOI] [PubMed] [Google Scholar]
- 9.Kass D.A., Bronzwaer J.G.F., Paulus W.J. What mechanisms underlie diastolic dysfunction in heart failure? Circ. Res. 2004;94:1533–1542. doi: 10.1161/01.RES.0000129254.25507.d6. [DOI] [PubMed] [Google Scholar]
- 10.Lehrer S.S., Geeves M.A. The myosin-activated thin filament regulatory state, M–-open: a link to hypertrophic cardiomyopathy (HCM) J. Muscle Res. Cell Motil. 2014;35:153–160. doi: 10.1007/s10974-014-9383-z. [DOI] [PubMed] [Google Scholar]
- 11.Campbell S.G., Lionetti F.V., McCulloch A.D. Coupling of adjacent tropomyosins enhances cross-bridge-mediated cooperative activation in a Markov model of the cardiac thin filament. Biophys. J. 2010;98:2254–2264. doi: 10.1016/j.bpj.2010.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Robinson J.M., Wang Y., Cheung H.C. Activation of striated muscle: nearest-neighbor regulatory-unit and cross-bridge influence on myofilament kinetics. J. Mol. Biol. 2002;322:1065–1088. doi: 10.1016/s0022-2836(02)00855-0. [DOI] [PubMed] [Google Scholar]
- 13.Smith D.A., Geeves M.A. Cooperative regulation of myosin-actin interactions by a continuous flexible chain II: actin-tropomyosin-troponin and regulation by calcium. Biophys. J. 2003;84:3168–3180. doi: 10.1016/S0006-3495(03)70041-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kobayashi T., Solaro R.J. Calcium, thin filaments, and the integrative biology of cardiac contractility. Annu. Rev. Physiol. 2005;67:39–67. doi: 10.1146/annurev.physiol.67.040403.114025. [DOI] [PubMed] [Google Scholar]
- 15.Vibert P., Craig R., Lehman W. Steric-model for activation of muscle thin filaments. J. Mol. Biol. 1997;266:8–14. doi: 10.1006/jmbi.1996.0800. [DOI] [PubMed] [Google Scholar]
- 16.Davis J.P., Norman C., Tikunova S.B. Effects of thin and thick filament proteins on calcium binding and exchange with cardiac troponin C. Biophys. J. 2007;92:3195–3206. doi: 10.1529/biophysj.106.095406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rice J.J., Stolovitzky G., de Tombe P.P. Ising model of cardiac thin filament activation with nearest-neighbor cooperative interactions. Biophys. J. 2003;84:897–909. doi: 10.1016/S0006-3495(03)74907-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Campbell K.S., Holbrook A.M. The rate of tension recovery in cardiac muscle correlates with the relative residual tension prevailing after restretch. Am. J. Physiol. Heart Circ. Physiol. 2007;292:H2020–H2022. doi: 10.1152/ajpheart.00714.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gillis T.E., Martyn D.A., Regnier M. Investigation of thin filament near-neighbour regulatory unit interactions during force development in skinned cardiac and skeletal muscle. J. Physiol. 2007;580:561–576. doi: 10.1113/jphysiol.2007.128975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Regnier M., Rivera A.J., Gordon A.M. Thin filament near-neighbour regulatory unit interactions affect rabbit skeletal muscle steady-state force-Ca2+ relations. J. Physiol. 2002;540:485–497. doi: 10.1113/jphysiol.2001.013179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Janssen P.M., de Tombe P.P. Uncontrolled sarcomere shortening increases intracellular Ca2+ transient in rat cardiac trabeculae. Am. J. Physiol. 1997;272:H1892–H1897. doi: 10.1152/ajpheart.1997.272.4.H1892. [DOI] [PubMed] [Google Scholar]
- 22.Wen Y., Pinto J.R., Kerrick W.G.L. Functional consequences of the human cardiac troponin I hypertrophic cardiomyopathy mutation R145G in transgenic mice. J. Biol. Chem. 2008;283:20484–20494. doi: 10.1074/jbc.M801661200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kennedy J., Eberhart R.C., Shi Y. Morgan Kaufmann; San Francisco, CA: 2001. Swarm Intelligence. [Google Scholar]
- 24.Gao W.D., Backx P.H., Marban E. Myofilament Ca2+ sensitivity in intact versus skinned rat ventricular muscle. Circ. Res. 1994;74:408–415. doi: 10.1161/01.res.74.3.408. [DOI] [PubMed] [Google Scholar]
- 25.Tanner B.C.W., Daniel T.L., Regnier M. Filament compliance influences cooperative activation of thin filaments and the dynamics of force production in skeletal muscle. PLOS Comput. Biol. 2012;8:e1002506. doi: 10.1371/journal.pcbi.1002506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Campbell K. Rate constant of muscle force redevelopment reflects cooperative activation as well as cross-bridge kinetics. Biophys. J. 1997;72:254–262. doi: 10.1016/S0006-3495(97)78664-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kirk J.A., MacGowan G.A., Shroff S.G. Left ventricular and myocardial function in mice expressing constitutively pseudophosphorylated cardiac troponin I. Circ. Res. 2009;105:1232–1239. doi: 10.1161/CIRCRESAHA.109.205427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wilkinson J.M., Grand R.J. Comparison of amino acid sequence of troponin I from different striated muscles. Nature. 1978;271:31–35. doi: 10.1038/271031a0. [DOI] [PubMed] [Google Scholar]
- 29.van Eerd J.P., Takahashi K. The amino acid sequence of bovine cardiac tamponin-C. Comparison with rabbit skeletal troponin-C. Biochem. Biophys. Res. Commun. 1975;64:122–127. doi: 10.1016/0006-291x(75)90227-2. [DOI] [PubMed] [Google Scholar]
- 30.Loong C.K.P., Zhou H.-X., Chase P.B. Persistence length of human cardiac α-tropomyosin measured by single molecule direct probe microscopy. PLoS One. 2012;7:e39676. doi: 10.1371/journal.pone.0039676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Li X.E., Lehman W., Fischer S. The relationship between curvature, flexibility and persistence length in the tropomyosin coiled-coil. J. Struct. Biol. 2010;170:313–318. doi: 10.1016/j.jsb.2010.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li X.E., Orzechowski M., Fischer S. Structure and flexibility of the tropomyosin overlap junction. Biochem. Biophys. Res. Commun. 2014;446:304–308. doi: 10.1016/j.bbrc.2014.02.097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cummins P., Perry S.V. Chemical and immunochemical characteristics of tropomyosins from striated and smooth muscle. Biochem. J. 1974;141:43–49. doi: 10.1042/bj1410043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zou G., Phillips G.N., Jr. A cellular automaton model for the regulatory behavior of muscle thin filaments. Biophys. J. 1994;67:11–28. doi: 10.1016/S0006-3495(94)80475-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tanner B.C., Daniel T.L., Regnier M. Sarcomere lattice geometry influences cooperative myosin binding in muscle. PLOS Comput. sBiol. 2007;3:e115. doi: 10.1371/journal.pcbi.0030115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Desai R., Geeves M.A., Kad N.M. Using fluorescent myosin to directly visualize cooperative activation of thin filaments. J. Biol. Chem. 2015;290:1915–1925. doi: 10.1074/jbc.M114.609743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Murakami K., Stewart M., Wakabayashi T. Structural basis for tropomyosin overlap in thin (actin) filaments and the generation of a molecular swivel by troponin-T. Proc. Natl. Acad. Sci. USA. 2008;105:7200–7205. doi: 10.1073/pnas.0801950105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tachampa K., Wang H., de Tombe P.P. Cardiac troponin I threonine 144: role in myofilament length dependent activation. Circ. Res. 2007;101:1081–1083. doi: 10.1161/CIRCRESAHA.107.165258. [DOI] [PubMed] [Google Scholar]
- 39.Landesberg A., Sideman S. Mechanical regulation of cardiac muscle by coupling calcium kinetics with cross-bridge cycling: a dynamic model. Am. J. Physiol. 1994;267:H779–H795. doi: 10.1152/ajpheart.1994.267.2.H779. [DOI] [PubMed] [Google Scholar]
- 40.Dobrunz L.E., Backx P.H., Yue D.T. Steady-state [Ca2+]i-force relationship in intact twitching cardiac muscle: direct evidence for modulation by isoproterenol and EMD 53998. Biophys. J. 1995;69:189–201. doi: 10.1016/S0006-3495(95)79889-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rice J.J., Wang F., de Tombe P.P. Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophys. J. 2008;95:2368–2390. doi: 10.1529/biophysj.107.119487. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.