Bacillus subtilis Bacteria Generate an Internal Mechanical Force within a Biofilm

Abstract

A key issue in understanding why biofilms are the most prevalent mode of bacterial life is the origin of the degree of resistance and protection that bacteria gain from self-organizing into biofilm communities. Our experiments suggest that their mechanical properties are a key factor. Experiments on pellicles, or floating biofilms, of Bacillus subtilis showed that while they are multiplying and secreting extracellular substances, bacteria create an internal force (associated with a −80 ± 25 Pa stress) within the biofilms, similar to the forces that self-equilibrate and strengthen plants, organs, and some engineered buildings. Here, we found that this force, or stress, is associated with growth-induced pressure. Our observations indicate that due to such forces, biofilms spread after any cut or ablation by up to 15–20% of their initial size. The force relaxes over very short timescales (tens of milliseconds). We conclude that this force helps bacteria to shape the biofilm, improve its mechanical resistance, and facilitate its invasion and self-repair.

Introduction

Although biofilms are one of the first primitive forms of living communities, existing for more than 1 billion years (1), little is known about their physical properties. In the classical view, a biofilm is an edifice that colonizes a surface or an interface, and where cells may differentiate from their planktonic counterparts (2, 3, 4). Some microorganisms produce extracellular substances composed mostly of polysaccharides, proteins, and DNA (5, 6, 7, 8).

Previous observations suggested a heterogeneous structure in which the extracellular matrix is interspersed with water pores and channels. It also tends to be denser very close to the solid surfaces and may be composed of amyloid fibers (9, 10, 11, 12, 13). This intricate matrix confers cohesion to the cells and constitutes a highly protective hydrogel in which cells can survive even in hostile environments. This is probably why biofilms are ubiquitous and are the predominant life mode of bacteria that are able to colonize tissues, plant roots, and every natural, industrial, or medical setting and environment.

Some force analyses have already been done to explore the mechanical softness of biofilms in response to an external perturbation. In general, biofilms that are immersed in a liquid and attached to solid surfaces behave like viscoelastic matter, the rigidity of which may vary by a factor of 10⁵ depending on the biofilm and the method used (11). The biofilms studied here, which float on top of a liquid and are often called pellicles, exhibit somewhat similar mechanical properties (13, 14, 15). Most mechanical studies published to date analyzed biofilms as a static biomaterial, at a given stage in the life of the biofilm. They did not take into account the bacteria’s ability to produce a mass that may create a mechanical stress inside the structure. To understand the formation of macroscopic wrinkles, we considered this notion in a previous study (15) and hypothesized the existence of such a stress (the residual stress, or prestress) acting within the biofilm.

The residual stress within solid matter or an edifice corresponds to the internal stress (force per area unit) that remains inside the system after it has been processed. In civil engineering, this process is currently being considered in the construction of edifices whose supporting elements are prestrained and stressed before or during their assembly, such as bridges (16, 17). It allows one to strengthen the edifice at low density without overloading or oversizing it. Note that the forces self-equilibrate within the structures and their presence may not be apparent at first glance. As early as 1850, researchers observed tensions in plants after cutting and separating the different parts of living tissues (18). Subsequently, force and stress were measured on living systems ranging from plants to tissues, organs, and arteries (19, 20, 21, 22, 23), and similar concepts have been introduced to explain the cytoskeletal mechanical properties of eukaryotic cells (24). In fact, the residual stress in all of these living systems originates from molecular motors and/or their growth under constraints (25, 26, 27, 28). Without any physical constraints, i.e., in an open space without borders and heterogeneities, the growth would generate no stress. However, such a situation is never encountered in nature.

Biofilms formed both in vitro and in vivo are usually attached to solid surfaces, confined by their surroundings, and may be heterogeneous. Attachment to underlying surfaces may confine them by preventing lateral expansion of the lower surface. The appearance of wrinkles in such systems supports the hypothesis that biofilms can be mechanically stressed locally without any external load. To our knowledge, the presence of internal forces in biofilms has not been previously reported. Here, by studying floating pellicles of a wild-type strain of Bacillus subtilis, a bacterial species that very often serves as a model in the laboratory, we obtained direct evidence of the presence of internal forces within a biofilm. The liquid state of the surface allowed us to directly separate the contributions made by the solid biofilm and the liquid substrate to the measured force. We also used a rich liquid medium to favor bacterial growth and allow the bacteria to secrete a large amount of extracellular substances that could generate high, detectable force values. We followed the traditional method of cut, excision, and ablation to visualize the presence of such forces. A force sensor was connected to a plate dipped into the bacterial solution. When the pellicle grew, it attached to the plate and closely surrounded it. We monitored the forces after cutting and removing part of the surrounding pellicle. Changes in the geometry allowed us to identify the origin of the forces without hypothesis or modeling. We recorded the shape of the biofilms at different steps using a camera and observed a rapid expansion after the pellicle was released and the forces relaxed. We also compared the responses of a naturally self-stressed biofilm and a released biofilm subjected to a puncture. Finally, we examined the role played by such forces in the morphology, mechanical resistance, and mechanobiology of biofilms.

Materials and Methods

Bacteria culture

We used the wild-type strain NCIB3610 of B. subtilis for this study. A single colony isolated on an agar plate was cultured overnight in LB medium (10 g NaCl, 5 g yeast extract, and 10 g tryptone per liter) at 30°C under shaking (240 rpm). The bacteria were then diluted 1000 times in LB medium and incubated in the same conditions up to an optical density (OD) at 600 nm (OD600) ≈ 0.1. The cells were then inoculated in a biofilm medium (LB supplemented with 0.1 mM MnCl₂ and 3% glycerol) at a final initial concentration of OD600 ≈ 10⁻³. We used different-sized rectangular plastic dishes (inner dimensions: 6.1 × 4.6 cm, 9 × 6.1 cm, and 20 × 7.5 cm) and adjusted the liquid volume from 25 mL to 160 mL to obtain a liquid height equal to 0.5–1 cm. Two large pellicles were formed in a specific dish (49.5 × 14 cm) containing 750 mL of biofilm liquid medium (Fig. S2 in the Supporting Material). The mobile plate of the force sensor was placed in the dish, and the samples were then incubated at 23°C in a safety cabinet. Biofilms were studied ∼48 h after the inoculation, i.e., when the biofilm morphology remained flat and before they started to form vertical structures such as wrinkles and folds. We performed only one force F measurement per sample and replaced the sample for each measurement. We studied ∼70 biofilms to characterize the internal forces in relation to their self-compressed state.

Force sensor

We used three high-sensitivity force sensors to obtain the results presented here. As described in Trejo et al. (15), each force sensor was composed of a double-cantilever spring whose stiffness (19.5, 26.7 and 30.3 N/m) was measured by a precalibration performed on different elastic materials. Behind each spring we placed a capacitive gauge (Fogale Nanotech, Nimes, France), and in front of each spring we placed a mobile vertical plastic plate that was in contact with the biofilm. Then, when the biofilm generated a force onto the plate, it pulled or pushed the plate and moved it to a distance that depended on the spring stiffness and was measured by the capacitive gauge. For example, 1.2 mN of force moved the plate ∼50 μm. Note that we defined the zero level of the sensor as the force value measured in the pellicle-free situation in which no horizontal force acted on the plate. A negative force value indicated a pushing force of the biofilm on the mobile plate. Finally, it may be recalled that a 1 mN force is equivalent to the gravitational force of a 0.1 mg object pushing a 40 mm plate.

Thickness measurements

In a previous study (15), we used two methods—one noninvasive and one invasive—to measure the pellicle thickness. The invasive method consisted of inserting a needle inside the biofilm in a series of vertical steps and detecting the steps at which the needle entered and exited the biofilm. Although this method was successful in determining the thickness of the intact confined pellicle, we found it to be too invasive for the relaxed pellicle: the needle insertion induced a reduction of its thickness and created a hole after a few vertical steps. This effect showed the relative fragility of the relaxed biofilm. For the noninvasive method, we imaged the biofilm using a Macroscope (Leica Z16 APO A objective 5× and ZoomDrive 20×) and a high-performance camera (Orca R2; Hamamatsu). We Z scanned the pellicle at different vertical planes separated by a 10 μm step and recorded the images obtained at each plane. As a background image appeared when scanning at planes out of the biofilm (above and below), we simply detected by visually inspecting each series of images the step position at which the biofilms stood against the background.

Results and Discussion

Detection of a compressive force

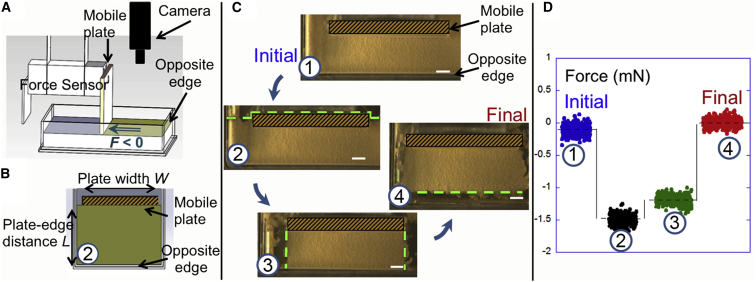
Fig. 1 shows schematic views of the experimental setup. Biofilms were grown in a rectangular dish delimited by four fixed vertical edges and with one vertical mobile plate that was set at a distance L from one edge. The plate of width W was connected to a high-sensitivity force sensor as previously described (15) (see Materials and Methods).

Figure 1.

Direct measurement of the compressive force. (A and B) Schematic oblique (A) and top (B) views of the setup. We studied the force generated by a floating pellicle located between a mobile plate and the opposite edge. As the pellicle covered the whole air-liquid surface, we successively cut different parts of the pellicle to keep only one rectangular piece intact. The views in (A) and (B) illustrate the state of the pellicle at cutting step 2. A negative force corresponded to the case in which the plate moved away from the opposite edge. (C) Top views of the cutting steps. For clarity, a well-marked hatched rectangle is superimposed on the mobile plate and the green dashed lines show the successive cuts. Step 1: in the initial state, the pellicle covered the whole liquid surface and closely surrounded the mobile plate. During its formation, it attached to the vertical walls of the dish’s edges and the mobile plate. Step 2: part of the pellicle located behind the plate was cut and removed. Step 3: the pellicle sides were removed and a pellicle band of dimensions L and W stood between the mobile plate and the opposite edge. Step 4: in the final state, the biofilm was detached and released by moving the plate away from the opposite edge (scale bars = 5 mm). (D) Force measurements. At each cutting step, we measured the forces acting on the mobile plate (blue, step 1; black, step 2; green, step 3; red, step 4). To see this figure in color, go online.

After ∼2 days of incubation at 23°C, the bacterial biofilm formed a flat pellicle that floated on top of the liquid and was naturally attached to the mobile plate and the edges of the dish. At the initial stage, the pellicle surrounded the plate and no force could be detected on the plate (step 1, blue data in Fig. 1 B). We then produced a series of cuts on the pellicle biofilm using a scalpel and recorded the force values at each step. Fig. S1 shows a detailed sequence of the cutting steps. In the second step, we kept the pellicle between the plate and the opposite edge intact and removed the pellicle on the other side of the plate (above the dashed lines in Fig. 1 B, step 2, as illustrated in Fig. 1, A and B). Concomitantly, the force went toward negative values (step 2, black data), meaning that the sensor detected a pushing compressive force and that the remaining part of the pellicle pushed the plate. In the initial state, this force was counterbalancing the opposite force exerted by the removed part of the pellicle. This result demonstrated the ability of bacteria to generate a pushing force within a biofilm.

In the third step, we maintained a rectangular pellicle band of width W and length L, and removed the pellicle sides that previously confined the film laterally. Straight line cuts suppressed the curvatures of the lateral surfaces that bowed outward just after the sides were removed (see Fig. S1). The resulting force was lower in magnitude than before, but was still negative. We subsequently recorded this force value F (equal to −1.2 mN in Fig. 1 B, step 3, green data). Finally, in the last step, we detached the pellicle from the opposite edge and horizontally shifted the container to let the pellicle relax and be released. The force then returned to its initial zero value, indicating that this force was strictly related to confinement of the pellicle (Fig. 1 B, step 4, red data).

A constant force value

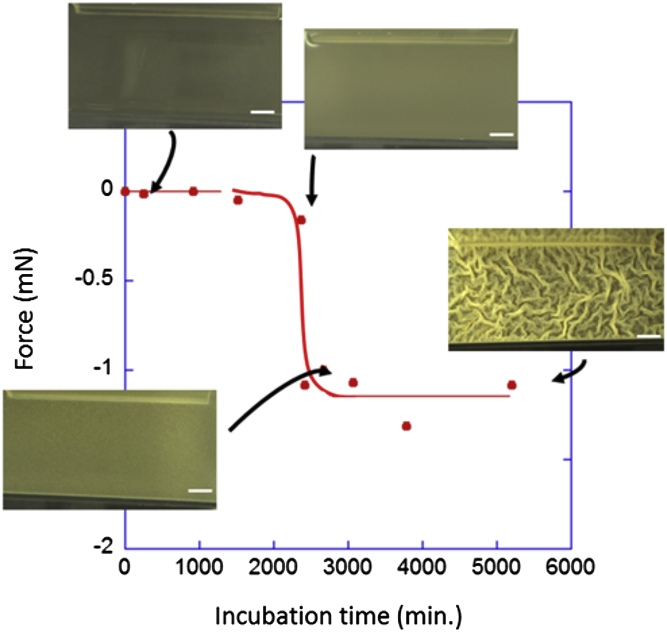
We repeated the measurements at different incubation times on different samples as shown in Fig. 2. Up to 36 h, the culture remained liquid and no force was created. After that, the force dropped to −1.2 mN as soon as a flat pellicle covered the liquid surface. The bacteria then continued to multiply and to secrete extracellular substances while the matrix was already compressed. The force stabilized at this value and did not change even when vertical ripples and large folds emerged. This seems to indicate the existence of a force regulation and that this force value is an important parameter of the pellicle’s properties regardless of its degree of maturation. In subsequent experiments, we mainly worked on flat pellicles at the prewrinkled stage, 45 h after the bacteria inoculation.

Figure 2.

Force generated by the bacterial biofilm during its growth. At the beginning of the incubation period, no force was measured. As the biofilm developed, the force suddenly became compressive and remained constant regardless of the degree of maturation. This suggests the existence of a critical step for biofilm development (scale bar = 5 mm). The continuous red lines are just visual guidelines. To see this figure in color, go online.

An internal stress

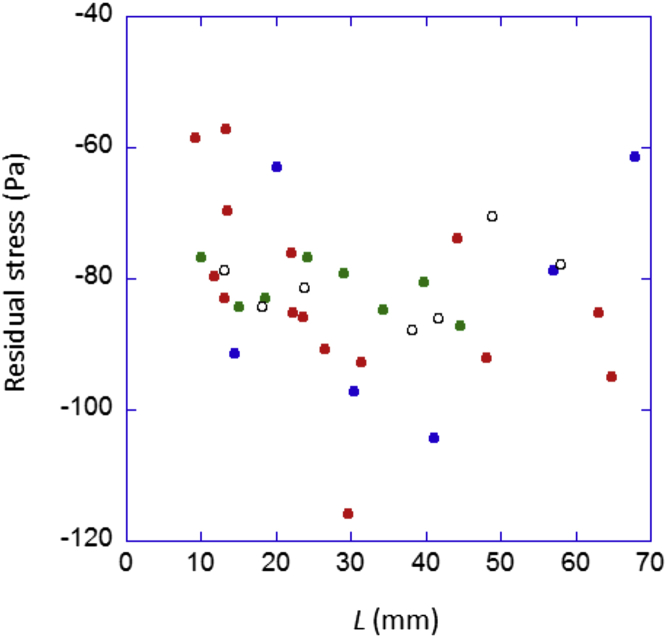
To understand the origin of this force, we varied the plate-to-edge distance, L, and the plate width, W. We measured negative force values ranging from approximately −0.5 to about −2.5 mN (see Fig. S2) depending on W. Because the cross-sectional surface area of the biofilm in contact with the plate was the product of the plate width W and the top-to-bottom biofilm thickness h, we divided F by this area to get the mechanical stress (the force per area unit in the actual configuration). The biofilm thickness h was estimated to be ≈350 ± 50 μm (15) (see Fig. 5 C). The results are plotted in Fig. 3 for different values of W and L. We observed a constant and very low stress of σ = −80 ± 25 Pa independently of the macroscopic dimensions L and W. This means that this stress is not macroscopic, and instead is local and internal to the biofilm. The biofilm experienced a compressive local stress originating from its local growth in a limited space. This stress is a passive growth-induced pressure. Here, the term “local” refers to a scale of the element unit that generated the stress and might include several bacteria and units of extracellular fibers and matrices, in other words, to a size equivalent to the biofilm thickness. The magnitude of the recorded stress was very low (for comparison, internal stresses are typically 1–20 kPa in microtissues and skin) (29, 30).

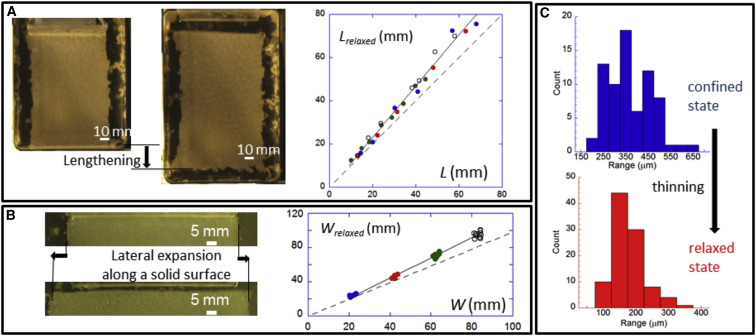
Figure 5.

Expansion and thinning of the pellicle after its detachment and release. (A and B) We focused on three types of expansion and thinning: (A) longitudinal bulk expansion, where lengths of relaxed and confined pellicles, L_relaxed and L, were related by the fit expression (black line) L_relaxed = −0.67 + 1.19L (R = 0.993); and (B) expansion of the biofilm surface in contact with the solid plate, and where the widths of the detached and attached pellicles, W_detached and W, are closely related by the linear fit (black line) W_detached = −2.56 + 1.17W (R = 0.997). Dashed lines show the case in which the two lengths (A) or the two widths (B) remain equal. (C) Histograms of thickness. The horizontal expansion implies thinning of the pellicle that we measured at different places on the same biofilm and on different biofilms. In the confined state, we found that the mean thickness h = 350 μm, in agreement with previous measurements (15) with a large 100 μm standard deviation reflecting the high rugosity of the pellicle. In the relaxed state, the mean thickness reduced to h_relaxed = 170 μm and the standard deviation reduced to 50 μm. To see this figure in color, go online.

Figure 3.

Dividing the different force values by the area of the biofilm surface in contact with the mobile plate reveals the presence of a unique and local stress. Force values were measured using plates of different widths W, represented here by symbols of different colors (blue, 20 mm; red, 40 mm; green, 60 mm; open black, 80 mm) as a function of L. The stress is constant and independent of the macroscopic dimensions. To see this figure in color, go online.

Confined versus released pellicles: stress relaxation

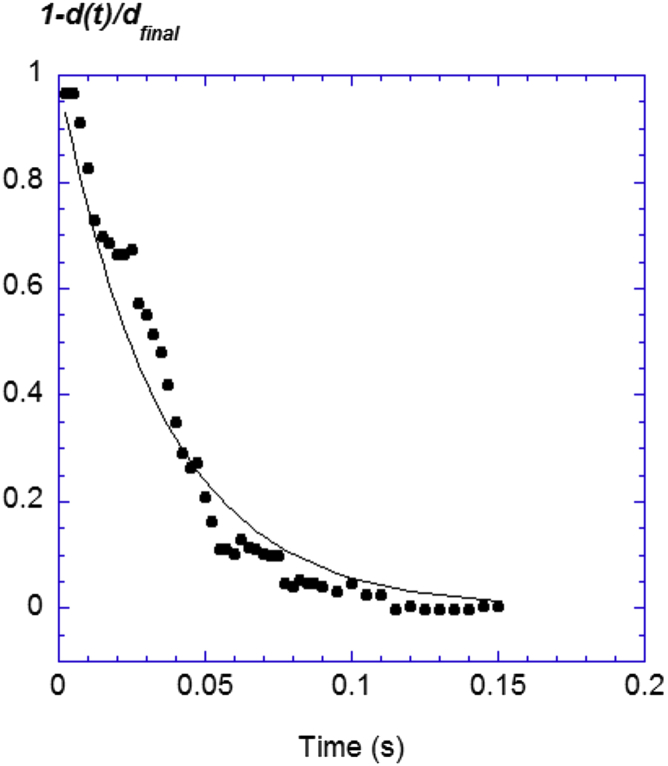
As we detected when we manipulated the pellicle, the force relaxed to zero only after the pellicle became detached and released. At the same time, we also observed that the biofilm immediately spread out on the liquid. To determine the relaxation time, we used a high-speed camera (FASTCAM SA3; Photron) to visualize the biofilm expansion. Movie S1 (scale bar = 5 mm) shows the expansion of a pellicle band after the removal of one plate. For this experiment, the biofilm grew in a small Petri dish and covered the whole air-liquid interface. We then cut a quasi-rectangular band confined between two opposite vertical borders of the dish and placed a plate (a razor blade) between them. Keeping the pellicle band intact on only one side of the razor blade, we monitored the expansion that followed the removal of the blade at a speed of 4000 frames/s. Fig. 4 illustrates the biofilm margin position versus time. Defining d(t) the square root of the square displacement of a point located at the margin level at any time t and d_final its final value, the relative displacement 1− d(t)/d_final is plotted versus time. We found that it may be adjusted by a simple exponential decay e^-t/τR of the relaxation time, τ_R = 30 ± 10 ms.

Figure 4.

Relaxation of the pellicle. Using a high-speed camera, we were able to measure the temporal displacement of the pellicle margin during its release. The relaxation may be adjusted by an exponential decay of characteristic time τ_R = 30 ± 10 ms (straight line). To see this figure in color, go online.

As observed by Bonnet et al. (31) after severing epithelial tissue, a dynamical retraction or expansion (in our case) is the first sign of the existence of a prestress. The relaxing biofilm experiences two types of friction: external friction on the supporting medium (the liquid) and internal friction within the tissue, allowing internal motion with local redistributions that reflect the fluidity and its viscoelasticity. According to Bonnet et al. (31), the starting motion would be sensitive mainly to the external friction. Since the supporting liquid moved once we took off the blade, the method we used here did not allow us to measure the effects of external friction. Defining the biofilm internal viscosity η by the expression η = Y τ_R, which relates the three parameters that characterize the viscoelasticity of any soft material of elastic modulus Y (Y = 300 Pa (15)), we found a viscosity equal to 10 Pa⋅s. Therefore, the biofilm’s internal viscosity was 10⁴ higher than the typical water and culture-media viscosity, and on the order of the viscosity of physical networks such as entangled polymers in solution (32).

Note that the viscoelastic relaxation times reported in the literature are rather long, typically a few minutes or tens of minutes (33), compared with the characteristic time in this study. These relaxation times correspond to the time required for the biofilms to rearrange over different scale lengths to relax the applied macroscopic stress or strain. Relaxation implies microscopic as well as macroscopic rearrangements, and the stress and strain fields also may not be uniform. We interpret the short relaxation time τ_R in this study as being a result of local friction accompanying the release of the pellicle. The friction remains local within the pellicle and does not imply long-range rearrangements as would be required by straining or loading biofilms macroscopically. Here, we might consider the expansion as a process involving multiple simple and local dilations that occur within the same short period. Images of the relaxed structure (e.g., see Fig. 5 A) show the presence of grains that are not visible in the confined state. When the grainy structure is compressed (data not shown), the grains are no longer visible and the structure looks homogeneous like the initial confined structure. A more detailed analysis of the local structure and the rearrangement of the grains during relaxation would help to precisely identify the friction mechanisms involved.

Confined versus released pellicles: extension and thinning

As shown in Movie S1, the pellicle extended its size by 20%. To perform a systematic study of this extension, we cultivated biofilms in rectangular dishes at the prewrinkled stage and measured on rectangular biofilm bands the longitudinal extension (lengthening) perpendicular to the plate and to the edge (Fig. 5 A). Different dimensions were cut. From the slope of the linear fit, we obtained a geometrical strain during the relaxation equal to −19% irrespective of the plate width. In addition to the horizontal extension, we observed a thinning of the pellicles. By scanning the samples in confined and relaxed states on different vertical planes with a Macroscope (cf. Materials and Methods), we were able to measure the local thickness reduction. As shown by the histograms in Fig. 5 C, the thickness distributions were broad and the mean thickness was reduced by +50%. Although these strain values may seem high, the prestrains are close to the values measured in soft tissues (34), which range from +43% in arteries (35) to −14% in wood (36). Because the pellicle growth is likely isotropic, we can hypothesize that the pellicle spread out on the liquid equally in every direction when the isotropic residual stress was relaxed. If the pellicle behaves like a simple elastic plate, biaxial elastic strain ε_e and stress σ_e are related by Hooke’s law through the expression σ_e = Y/(1 − ν) ε_e, where Y denotes the plate Young’s modulus (= 300 Pa (15)) and ν is Poisson’s ratio (37). The vertical elastic strain ε_z is also expected to depend on the horizontal strain as ε_z/ε_e = −2ν /(1 − ν). Subjected to the strain ε_e = −19% and stress σ_e = −80 Pa, the elastic plate equivalent to the biofilm would then have a Poisson’s ratio on the order of 0.30–0.50, which is a common range that is characteristic of the compressibility of many materials (e.g., steel, foam, wood, bone, and cells (38)). Picioreanu et al. (39) reviewed the literature on biofilm mechanics and reported a similar value. To the best of our knowledge, no more recent measurement of the Poisson’s ratio has been reported. This value implies that the biofilm is weakly compressible, which can be explained by small fluid exchanges with the surrounding bath (as in a sponge).

Finally, we focused on the lateral expansion near the plate (Fig. 5 B). Here, the biofilm had attached to the solid plate surface during pellicle development (40). Once it detached, we also observed that the detached biofilm spread laterally to a relative strain equal to 17%, a value on the order of the bulk strain. This indicates that the biofilm near a solid surface experienced a lateral compressive force parallel to the solid surface. Note that the two expansions (in the bulk and along the solid surface) originated from two different geometrical constraints: 1) confinement limited by two opposite borders in the direction of the growth (Fig. 5 A) and 2) attachment to a solid surface in the direction perpendicular to the growth (Fig. 5 B), respectively. In Fig. S3, we illustrate the bottleneck-like shape of the detached part observed when the pellicle was partially released before it detached.

Response when punctured

Taken together, our results clearly show the existence of internal forces that compress a biofilm. These forces and the associated spreading prevent the formation of a hole or crack in the biofilm, and therefore the biofilm can spontaneously (within <100 ms) spread toward free surrounding spaces and may cover any holes that appear within its structure. Movies S2 and S3 show examples of biofilm reorganization after the puncturing of compressed (Movie S2) and released (Movie S3) biofilms. The self-compressed biofilm rapidly but partially closed the large opening, whereas a fairly large hole appeared on the released and deformed pellicle. Therefore, this release facilitates and directs surface colonization and self-repair, and helps maintain the biofilm’s integrity. These forces also help to strengthen the overall structure, in the sense that any mechanical treatment must apply a force that at least exceeds the internal forces that stretch and disrupt the biofilm.

The constant stress predicted by a buckling mechanical model

Interestingly, there is a mechanism of force regulation within a biofilm that ensures that the stress is constant, assuming that the local thickness of the biofilm does not change over time.

If the growth of bacteria, the production of biomass, and the composition of the extracellular matrix are controlled by biological mechanisms, we suspect that a physical mechanism, such as the buckling effect, regulates internal stress. The buckling model predicts that when an elastic sheet is progressively confined on top of a liquid, the flat sheet will start to buckle (i.e., wrinkle) when the horizontal mechanical stress reaches a critical value σ_c = −2 (BK)^1/2/h, which depends on the bending stiffness (B) of the sheet and the stiffness (K) and thickness (h) of the liquid substrate (41). Once this value is reached, the stress will remain constant and will not be sensitive to further confinement. In this context, the stress we measured in biofilms would correspond to that critical value and further biofilm growth would occur by increasing the wrinkle amplitude in the vertical dimension, rather than compressing the biofilm horizontally, thus keeping the horizontal stress value constant. The presence of an internal force would then contribute to shape the biofilm morphology.

A quantitative analysis can be achieved because most of the parameters have been estimated (fluid density ρ ∼ 10³ kg/m³, gravitational acceleration g ∼ 10 m/s², Young’s modulus Y = 300 Pa, Poisson’s ratio ν = 0.4, thickness h = 350 μm). From these values, we expect a bending rigidity of the pellicle B = Yh³/12(1 − ν ²) = 1.3 10⁻⁹ Pa/ m³, a fluid substrate stiffness K = ρ g ∼ 10⁴ Pa/m, and finally a critical stress σ_c = −20 Pa. This theoretical estimate agrees with the magnitude of σ_c, but is still four times lower than the experimental value. We reported a similar discrepancy in our previous study (15). The predicted wavelength of the pellicle wrinkles scales as λ_b = 2π(B/K)^1/4 and was found to be 3.5 times higher than the measured value, λ_b ∼ 1.5 mm. In that study, we suspected the existence of a mechanically active layer within the pellicle that was much thinner than the measured value: a low h value would reduce the bending rigidity B and therefore the wavelength λ_b. With regard to stress, this hypothesis seems to be wrong, since a decrease of h would diminish the critical value σ_c and increase the discrepancy between the predicted and measured values. The only way to account for both discrepancies (regarding the critical stress and the wavelength) is to increase the substrate stiffness K: higher K would lead to higher σ_c and lower λ_b at the same time.

In the model, the substrate stiffness K accounts for the action of the fluid substrate on the pellicle and describes the magnitude of a vertical force that opposes a vertical displacement of the liquid. To match the experimental values for both critical stress and wavelength, K must be 16 times larger than the actual value (10⁴ Pa/m), which is not possible. This suggests the existence of another vertical force with a stiffness 16 times higher than the actual gravitational force of the liquid. The pellicle would then be firmly stuck to the flat surface of the fluid. However, the kind of force that would be responsible for this effect remains to be elucidated.

Finally, our discussion about constant stress is based on the assumption that the thickness h does not vary over time. If the thickness were to increase over time, the internal stress would then decrease as 1/h and there would be no clear physical explanation for the force steady state (Fig. 2). The buckling threshold would increase over time as h^1/2 and the wavelength of the wrinkles would increase as h^3/4. This increase of wavelength does not agree with our previous observations, i.e., an increase in the wrinkles’ amplitude over time and no change in the wavelength. Those observations support our assumption.

Conclusions

Our experiments demonstrate that the pellicles formed by the wild-type strain NCIB3610 of B. subtilis are subjected to internal mechanical forces, and suggest that biofilms are engineered by bacteria like strengthened edifices combining prestrain and internal stresses. These forces are generated by the growth of the biofilms: bacteria secrete extracellular matrix, are embedded in a developing network, and in turn become stressed mechanically (compressed). By monitoring a biofilm’s response to injury, we were able to show one of the benefits of a biofilm being naturally compressed rather than released: the force maintains the biofilm’s integrity and contributes to its self-repair.

A closer look at how these forces distribute within a heterogeneous body may inspire new models and approaches in the field of biofilm mechanobiology. In our approach, the low Pa value (−80) corresponds to a mechanical stress averaged over the whole thickness and does not provide information about the local force heterogeneity. Importantly, higher local forces may serve as mechanical cues to activate a cell’s mechanosensors (42).

We plan to extend this work to other types of growing biofilms. As indicated by the presence of wrinkles in many biofilms cultured on liquids or gels, and in rich or poor media, an internal pushing force could exist in various systems and produce macroscopic wrinkles. Even in spherical, unattached, growing spheres (e.g., flocs), growth may induce wrinkles (43) because the specific geometry limits stress-free growth. The emergence of a compressive or tensile residual stress depends on this growth, which may be radial or circumferential (43).

Here, we found two types of geometrical constraints: confinement and attachment of a growing system. That suggests that biofilms that are attached to a solid surface and immersed in a liquid medium could be subjected to an internal force as well. However, this hypothesis is difficult to verify. In the latter situation, the conventional view holds that some bacteria attach to an underlying solid surface and initiate the biofilm by dividing themselves and producing extracellular matrix. These biofilms are not confined by lateral walls and may cover a macroscopic underlying surface or may remain isolated and dispersed in patches or clusters. Growth conditions such as nutrient diffusion-limited conditions and liquid flows directly impact the biofilms’ morphology and the clusters’ shape. Our experiments suggest that the attachment of growing matter to a solid wall may be a geometrical constraint that is able to generate an internal stress parallel to the underlying surface.

Author Contributions

C.D., J.-M.A., and E.R. discussed the experimental approach and the results, and wrote the manuscript. C.D. and E.R. conceived and designed the experiments, and analyzed the data. E.R. performed the measurements.

Editor: Dennis Bray.