Abstract
The water solubility of lyotropic liquid crystals (LCs) makes them very attractive to study the behavior of biological microorganisms in an environment where local symmetry is broken (as often encountered in nature). Several recent studies have shown a dramatic change in the behavior of flagellated bacteria when swimming in solutions of the lyotropic LC disodium cromoglycate (DSCG). In this study, the movements of Escherichia coli bacteria in DSCG-water solutions of different concentrations are observed to improve our understanding of this phenomenon. In addition, the viscosity of DSCG aqueous solutions is measured as a function of concentration at room temperature. We also experimentally identify a previously undescribed isotropic pretransition zone where bacteria start sticking to each other and to surfaces. Simple estimations show that the unbalanced osmotic pressure induced depletion force might be responsible for this sticking phenomenon. An estimate of the bacteria propulsive force and the DSCG aggregates length (versus concentration) are calculated from the measured viscosity of the medium. All these quantities are found to undergo a strong increase in the pretransition zone, starting at a threshold concentration of 6 ± 1 wt % DSCG that is well below the known isotropic-LC transition (∼10 wt %). This study also shines light on the motility of flagellated bacteria in realistic environments, and it opens new avenues for interesting applications such as the use of motile microorganisms to probe the physical properties of their host or smart bandages that could guide bacteria out of wounds.
Introduction
Many biological processes occur under a very delicate balance of forces. Weak disturbances in this equilibrium may bring drastic changes to these processes. For instance, the swimming of flagellated bacteria is subject to multiple forces and constraints, and it was recently shown that this behavior dramatically changes in anisotropic environments (whose properties vary with direction) (1, 2, 3, 4, 5). Interestingly, many natural environments show some level of anisotropy. For example, several studies have shown that a liquid crystal (LC) phase (anisotropic phase) can be observed in a solution of isolated biological molecules such as chitin or collagen (6). Even if the concentration needed to obtain this anisotropic phase is generally higher than those found in nature, we expect that environments enriched with those molecules can have local LC domains. Natural mucus can also show an LC phase when it is exposed to air for a few hours (7, 8, 9). This state could be necessary to form the compact granule of mucus found in mucosa cells (7). Synovial fluid, used for the lubrication in cartilage, is also known to be an LC (10). Some motile bacteria can be found in this lubricant, for instance Borrelia burgdorferi, which is responsible for the Lyme disease, Pseudomonas aeruginosa, and Yersinia enterocolitica (11, 12). Finally, although biofilms are not strictly speaking LCs, they can exhibit anisotropic properties (13, 14), and a recent study has shown that swimming bacteria can infiltrate the biofilm, enhancing its viability or in some cases, causing its destruction (15).
Although the use of LCs in consumer electronic products (such as displays (16) and lenses (17)) has been widely explored in the scientific literature, their combination with biological systems, for diagnostics (18) and sensing (19), is relatively recent. Because they are biocompatible, aqueous solutions of lyotropic LCs have been used in several recent reports to study the behavior of flagellated bacteria in anisotropic environments. Exciting research was conducted in many groups to extend these studies to the behavior of several types of bacteria in biocompatible LCs. The three-dimensional (3D) random trajectories followed by bacteria swimming in an aqueous (isotropic) environment (20, 21, 22) have been shown to be radically modified by the presence of an orientational order in the motility medium (2, 2, 3, 4, 5). For example, it was shown that individual bacteria move along (forward and backward) the direction of the anisotropy axis in a lyotropic LC environment (water solution of disodium cromoglycate, DSCG) (2). It was also discovered that the presence of bacteria in such medium may result in a delicate coupling of the orientational order and bacterial activities resulting in local phase transitions (3). Finally, an orientational deformation mediated sticking (or trapping) between two bacteria has been observed in the anisotropic phase of the host (15 wt % DSCG) (4), and the interface between coexisting isotropic and LC phases has been used to probe how mechanical anisotropy and defects in LC ordering influence fundamental bacterial behaviors (5).
In this work, we present a detailed study of the bacterial motility at different concentrations of DSCG, bringing the medium from isotropic to anisotropic states. Our results uncover a previously undescribed (to the best of our knowledge) pretransition zone between the isotropic and anisotropic phases. Measurements of the viscosity of the solution as a function of DSCG concentration show an exponential increase in viscosity in this pretransition zone (after a threshold of ∼6 wt % DSCG that is well before the nematic transition occurring at 10 to 11 wt %) that we attempt to understand using a qualitative model of the DSCG molecules’ aggregation.
Materials and Methods
Cell culture
Escherichia coli (E. coli) strain HCB33 (wild-type, the same strain as RP437 (23)) was used in our experiments with motile bacteria and strain JY25 (wild-type modified to obtain a strain without filament, and in HCB33 (24)) in those with nonmotile bacteria. Single bacterial colonies were grown on agar plate (15 g agar, 10 g Bacto-Tryptone, and 5 g NaCl in 1 liter) at 37°C for 24 h. Then, bacteria from one colony were picked and grown to saturated phase in Terrific Broth (10g Bacto-Tryptone and 5g NaCl in 1 liter) at 34°C for 15 h in a shaking incubator at 200 rpm. Next, 100 μl of saturated culture was diluted in 10 ml of Terrific Broth and grown to exponential phase at 34°C for 4 h in a shaking incubator at 200 rpm. The cells were washed once with motility buffer (MB) (10 mM KPO4, 0.1 mM EDTA, 10 mM lactic acid, and 20 mM glucose) and then suspended in ∼5 ml of MB to obtain a bacterial concentration of OD600 ∼ 0.8. Finally, 20 μl from this suspension was diluted into a DSCG solution at the desired concentration to obtain a total volume of 160 μl.
LC mixture
The DSCG (Sigma-Aldrich, St. Louis, MO) was used to prepare the solution of LC. To make different concentrations of DSCG LC, a stock solution was made by mixing 16.0 wt % DSCG with 84 wt % MB. This mixture was heated for at least 10 min at 55°C and then shaken for ∼1 min to ensure complete solubility. The stock solution was stored at 4°C. Before making the final DSCG solution, the stock solution was heated again for 5 min at 55°C and shaken for 1 min to ensure complete homogeneity. A small amount of the stock LC was then diluted into a solution with a total volume of 160 μl containing a concentration of either bacteria of OD600 ∼ 0.15 or polystyrene microspheres (see below) with a diameter of 0.75 μm (Polysciences, Warrington, PA) to obtain a DSCG concentration from 0 to 13.7 wt %. The temperature in all our experiments was 22.5°C ± 0.5°C. At this temperature, DSCG forms a nematic LC phase above ∼11 wt % and an isotropic phase below ∼10 wt %. Between these two concentrations both phases coexist. The detailed concentration/temperature phase diagram of the mixture may be found in Lydon (25).
LC chamber
To make an optical chamber for our experiment, a coating of PI-150 1% (Nissan Chemical, Houston, TX) was first applied onto two glass cover slips by spin coating. This surface was then rubbed unidirectionally with a technique described in Seo et al. (26). Finally, a cavity was created by sticking together two cover slips with UV glue (Optical Adhesive 65, Norland, Cranbury, NJ) containing 60 μm glass microspheres used as spacers (Duke Scientific, Palo Alto, CA) (see Fig. S10 in the Supporting Material for more information and Duchesne et al. (27)). The solution was inserted by capillarity in the sandwich-like chamber. To prevent the movement of fluid and evaporation of water, the chamber was closed with transparent nail polish. Results obtained for each concentration were measured with at least three different samples made from at least two different stock solutions.
Bacteria observations
To visualize bacteria and microspheres, an IX71 Olympus inverted microscope equipped with crossed polarizers and an EMCCD iXon3 888 camera (Andor Technology, South Windsor, CT) was used. To observe the motility of bacteria, a 60× oil objective with 1.25NA (Olympus UPLFLN 60XOIPH, Tokyo, Japan) was employed in brightfield microscopy. Videos between 5 and 10 s long at a frame rate of 30 fps were recorded using a custom LabVIEW program (National Instruments, Austin, TX).
Videos of motile bacteria were analyzed with a custom particle tracking algorithm in MATLAB (The MathWorks, Natick, MA). To determine the average speed of bacteria for each concentration of DSCG, the centroids of every bacterium in each frame were identified and then linked together to create a trajectory. The difference in the bacterium position between two consecutive frames was divided by the acquisition time of the camera to obtain the instantaneous speed. Then, the average speed for every trajectory at the same concentration was computed. The image moment of every cell in each frame was used to obtain the angle between the long axis of the rod-shaped bacterium and the horizontal axis. Finally, the standard deviation of this angle for every trajectory at the same concentration was computed. Trajectories with less than 20 frames were discarded.
Viscosity measurements
To measure the effective viscosity along the axis parallel and perpendicular to the director n (showing the axis of the anisotropy of the LC (28)), the Brownian motion of polystyrene microspheres (with a diameter of 0.75 μm) was recorded by using the technique described in Duchesne et al. (27) (see also Saveyn et al. (29)). To visualize those particles, a guided-light dark-field microscope (27) with a 50× objective with 0.5 NA (Olympus LMPLFLN 50X, Tokyo, Japan) was used. For the calculation of the viscosity values sensed in each direction (1D), the following equation was used:
| (1) |
where is the Boltzmann constant, is the temperature in Kelvin, is the acquisition time, is the diameter of the microspheres, and is the average step length executed in . The weighted average viscosity for every DSCG concentration was computed from these data. The orientation of n was determined by using the technique described in Duchesne et al. (27). The mean squared displacement (MSD) was plotted as a function of time to make sure that the diffusion of microspheres was always normal, i.e., that the relationship was linear (27, 30, 31). Trajectories with less than 10 frames were discarded.
Results
Motility of bacteria in anisotropic environment
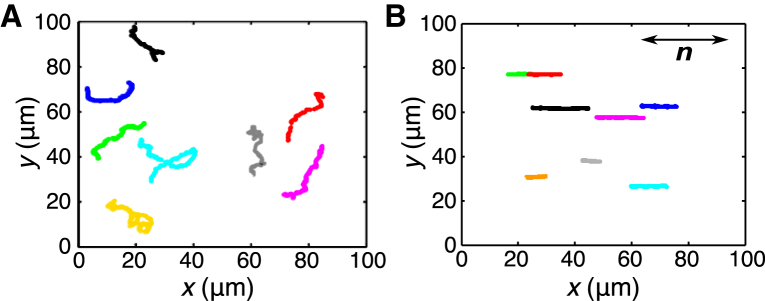
This work began by carefully recording the trajectories of more than 1800 E. coli bacteria swimming in water solutions of DSCG with concentrations varying from 0 to 13.7 wt %. Above these concentrations, the motility of the bacteria is strongly reduced and it becomes difficult to track them. Fig. 1 shows the dramatic contrast between typical trajectories (the position of the center of gravity versus time) of bacteria recorded in isotropic and anisotropic phases (at low and high DSCG concentrations, respectively). In the anisotropic (nematic) phase of the medium (Fig. 1 B), all bacteria swim along a single axis in both directions, that is they make forward and backward movements in one dimension (1D). This behavior is very different from the random 3D movements observed in isotropic media ((20) and Fig. 1 A). Because the distance between the sample and the microscope objective is fixed during the acquisition of each movie, our recorded tracks are two-dimensional projections of the 3D trajectories. That explains why the tracks are relatively short in the isotropic phase (1 s on average) because bacteria disappear from the image when they move by more than a few micrometers out of focus. In the anisotropic regime, the tracks appear even shorter, but it is only because of the lower bacterial speed and their forward and backward movements in 1D. These data confirm that, as previously reported in earlier studies (2, 3, 4), the bacterial trajectories in an anisotropic medium are confined to the direction of n.
Figure 1.
Trajectories of motile bacteria in isotropic and anisotropic solutions. (A) E. coli swimming tracks in isotropic media at 0 wt % DSCG and (B) in anisotropic media at 12 wt % DSCG (at 22.5 ± 0.5°C). In (B), the x axis is parallel to the rubbing direction of the chamber. To see this figure in color, go online.
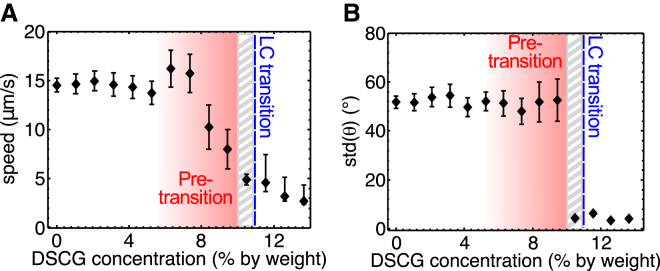
Analysis of the recorded videos also lead to the measurement of the mean speed of bacteria and the variations in the bacterial body orientation as a function of DSCG concentration. Fig. 2 A shows, the speed in the isotropic phase (from 0 to 7 wt % DSCG) does not change significantly and has a value of ∼15 μm/s as previously reported in the literature (20, 21, 22). The speed starts to decrease at 8 wt % and, after the LC transition (above ∼10 wt %), the speed slows down significantly to ∼5 μm/s at 10.5 wt % and continues to decrease to reach a value of ∼2.5 μm/s at 13.7 wt %. Note that the speed in the biphasic region (at 10.2 wt %) has been recorded in zones where the solution exhibited a nematic phase.
Figure 2.
Characterization of the motility of bacteria in DSCG solutions. (A) Bacterial speed and (B) standard deviation of the orientation of the bacterial body as a function of the DSCG concentration. The standard deviation (SD) was used as the error bars. All experiments were made at 22.5 ± 0.5°C. The number of data acquired for each concentration is shown in Table S3 (1808 individual bacteria in total, and more than 83,500 positions). The gray hatched zone represents the DSCG concentration range where both phases coexist (isotropic and anisotropic). The gradient shaded zone represents the DSCG concentration range where the pretransition phenomena are observed (see main text for details). To see this figure in color, go online.
To quantify the degree of unidirectionality of the bacterial trajectories, the standard deviation of the bacterial body orientation angle was computed (shown on Fig. 2 B). We observe that the bacteria orientations are randomly distributed in the isotropic environment (because the standard deviation of a random distribution with values between 0° to 180° is ∼52°), whereas the bacteria are all aligned along one direction in the anisotropic environment (the standard deviation of the angle is ∼4°).
Pretransition zone
Although some of the above-mentioned behaviors had already been reported (2), this much larger and detailed study led to the observation of an unexpected and distinct behavior of bacteria between 6 and 10 wt % DSCG concentration. In this concentration interval (further referred to as the pretransition zone), the bacteria experience significant difficulties for swimming; they are very sticky and stop swimming as soon as they touch any surface or other bacteria (see Section S5 for examples of images). In some rare cases, bacteria are able to detach themselves and swim away, but most of the time they remain stuck. When the bacterial concentration was raised to OD600 ∼ 3, big aggregates of bacteria were formed. At a DSCG concentration below 6 wt %, this sticky behavior is rarely observed, but it becomes more common as the concentration increases, up to 10 wt %. Because of that effect, the number of swimming bacteria that could be tracked in this region is limited. It is difficult to determine if the sticky effect is still present above 10 wt % because, in the anisotropic phase, each bacterium moves along its own straight line, so that collisions with the chamber’s top and bottom surfaces occur much less often and that collision between bacteria are described by the elastic interactions (4) (which is different from the interactions observed in the pretransition zone, see Discussion).
Viscosity of the DSCG solution
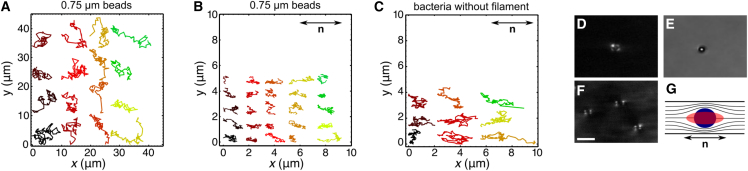
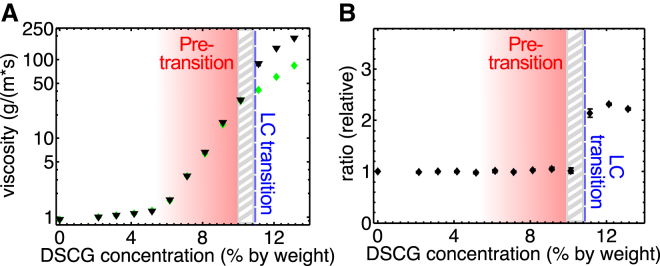
The swimming of E. coli is characterized by a low Reynolds number (Re ∼ 10−4), which means that the viscous forces are much more important than the inertial forces (32). Obviously, the elastic forces, involved in the deformation of the aligned LC environment, also play an important role at high DSCG concentration when the medium is anisotropic (4). However, the pretransition zone described above is not in the anisotropic LC phase. To investigate what could cause the existence of three distinct regimes in bacterial motility (purely isotropic, pretransition, and anisotropic regimes), we measured the effective viscosity of the medium in the directions parallel and perpendicular to n. To do so, the Brownian diffusion of more than 11,800 polystyrene microspheres (with a diameter of 0.75 μm) was tracked in DSCG solutions of various concentrations (in motility buffer MB). Fig. 3, A and B, shows typical trajectories of microspheres diffusing in isotropic and anisotropic environments. As expected, the average distance traveled by microspheres in isotropic media is identical in any direction, which is not the case in anisotropic media. The viscosity was measured from these trajectories (see Duchesne et al. (27) for details), and the results can be seen in Fig. 4. The viscosity of DSCG solutions increases very slightly at low concentration, but it suddenly starts to increase exponentially ∼6 wt %. Up to ∼10 wt % (the LC transition), the viscosity is the same in every directions, but, not surprisingly, the viscosity in the direction parallel to the director becomes lower than the one in the perpendicular direction once the system enters its anisotropic phase (28). The ratio of viscosities in these two directions is measured to be ∼2.2 ± 0.1. This ratio is rather large compared with thermotropic LCs as IS-8200, 5CB, or MBBA (ranging from 1.35 to 1.7) (30, 33, 34). Above 10 wt % (the LC transition), the viscosity in the two directions still increases exponentially, but at lower rate. To our knowledge, this is the first complete study of the viscosity of DSCG solutions as a function of concentration, and the first measurement of the ratio between the viscosities perpendicular and parallel to the director in the anisotropic phase.
Figure 3.
Diffusion of beads and nonmotile bacteria in DSCG solutions and anchoring of the DSCG molecules on their surfaces. (A) Trajectories of the diffusion of 0.75 μm diameter microspheres in an isotropic solution with 0 wt % DSCG and (B) in an anisotropic solution with 13.2 wt % DSCG. (C) Trajectories of the diffusion of paralyzed bacteria (without flagellum) in a solution with 13.2 wt % DSCG. (D) Image of a 3 μm polystyrene microsphere taken in brightfield with crossed polarizers and (E) without polarizers. (F) Image of three bacteria taken between crossed polarizers and (G) schematic representation of the perturbation of n around a polystyrene microsphere (circle) and a bacterium (ellipse). All experiments were made at 22.5 ± 0.5°C. The white bar in (F) measures 10 μm. To see this figure in color, go online.
Figure 4.
Characterization of the viscosity of DSCG solutions. (A) Viscosity parallel (diamonds) and perpendicular (triangles) to n and (B) anisotropy of the viscosity of DSCG solution as a function of concentration. Microspheres with a diameter of 0.75 μm were used. Each point was measured from a data set containing at least 230 microspheres and 8000 positions (11,800 individual microspheres in total, and more than 270,000 positions). The standard error of the mean was used as the error bars, but these are generally too small to be visible in figures. The unit of viscosity is equivalent to (mPa s) or cP. To see this figure in color, go online.
Interestingly, the three distinct regimes observed in the viscosity measurements correspond very closely to the three different types of behaviors we have observed in the motility of bacteria. In the purely isotropic regime, at low concentration of DSCG, bacteria swim as they usually do in water and the viscosity changes very little. In the second regime, the bacteria become very sticky and the viscosity increases exponentially. In the third regime, the bacterial trajectories and the viscosity become anisotropic along with noticeable slowing down of the viscosity growth (Figs. 2 and 4). It is certainly expected that the viscosity would increase with DSCG concentration, but we are not aware of any previous report of the three regimes described above (some pretransitional fluctuations, when the temperature of the solution is changed at constant DSCG concentration, were studied in Nastishin et al. (35)).
Note that the measured viscosity is independent of the microsphere diameter (in the range of bead diameters that we explored, between 0.2 and 2 μm, the difference was at most 20%; see Duchesne et al. (27) for details), so we only used beads of 0.75 μm diameter. Furthermore, we performed the same viscosity measurements in distilled (DI) water and the results were similar (27). Finally, to complete the analysis of the diffusion data, the relation between the MSD and time was computed. For every concentration of DSCG, the relationship between the MSD and time was linear (see Section S1). The diffusion of particles in the nematic phase of DSCG solution is therefore normal on a timescale above the minimal acquisition time we used during our experiments, namely 0.4 s. This result is in agreement with a previous report that showed anomalous diffusion only below 0.5 s in 13 wt % DSCG solution (30) (see also Duchesne et al. (27)).
Finally, it is useful to know that the alignment and anchoring of the director on the surface of the polystyrene particles and of E. coli is tangential. As Fig. 3, D and F, shows, the light pattern around particles, taken with crossed polarizers, is typical of a tangential surface anchoring (36, 37).
Discussion
Propulsive force of bacteria
Many bacteria (for example, E. coli and Salmonella) swim by rotating their flagella, which are long helical filaments anchored in the membrane by a rotary motor (38). Because the physical properties of the medium change with DSCG concentration, it is relevant to ask whether the propulsive force generated by the bacterial flagella also varies. When bacteria swim, the propulsive force applied by the flagella rotation must be equal to the drag force. To estimate this propulsive force, we approximated the shape of the bacterial body by a prolate spheroid (see Fig. 5 A). The propulsive force we calculate is an approximation because the following two effects are ignored: 1) the drag force on the filament (to our knowledge this calculation has never been done), and 2) the viscosity dependence on the speed of the object because this relation is unknown. In the particular case where the spheroid moves along its long axis, the drag force is described by the following equation (39):
| (2) |
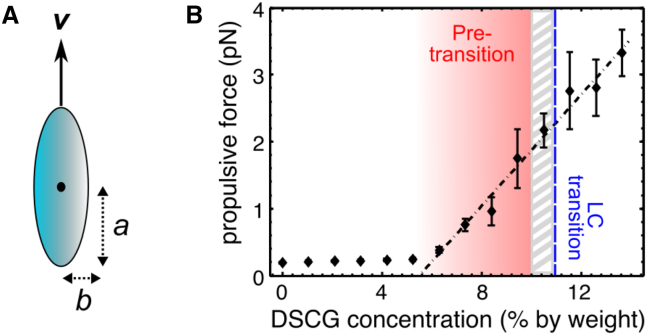
where η is the viscosity, v is the speed, a is the semi-major axis, and b the semi-minor axis of the spheroid. Our speed and viscosity measurements can thus be used to calculate the propulsive force exerted by the bacteria for each DSCG concentration. We estimated a = 1.5 ± 0.4 μm and b = 0.5 ± 0.1 μm from the images in our videos. In the anisotropic phase, the viscosity parallel to n was used for the calculation. The propulsive force that we find in MB (0 wt %) is in agreement with the one obtained for E. coli in previous reports, namely ∼0.19 pN for our bacteria strain with a swimming speed of 15 μm/s compared with 0.32 pN for bacteria strain with a swimming speed of 30 μm/s (40). Interestingly, the propulsive force increases linearly both in the pretransition zone and in the anisotropic phase, whereas it remains stable for lower DSCG concentration (Fig. 5 B). Two principal hypotheses could explain this increase in propulsive force: either the torque provided by the motor increases or the propulsion efficiency is higher. The flagellar motor can work in two distinct regimes: 1) at high angular speed (high swimming speed) the torque exerted by the motor increases linearly when the speed decreases, and 2) at low angular speed (low swimming speed) the torque remains constant. Calculations show that the variable torque regime could explain the increase in the propulsive force only below a DSCG concentration of 7.2 wt % (Section S2). Above that concentration, the torque should remain constant and we therefore conclude that the observed increase in propulsive force is because of a higher propulsion efficiency. A similar situation arises in unbranched polymer solutions (non-Newtonian fluid) where the bacteria are observed to swim faster when the solution viscosity is increased. This phenomenon is believed to be caused by the interaction of the flagella with the structured network created by the unbranched polymers in the solution (41, 42, 43, 44). A recent report has demonstrated that this phenomenon could rather be explained by the fact that the filaments see a different viscosity than the body does (39). We think that the same effect is observed here in the pretransition zone: the length of the DSCG aggregates must become suddenly long enough to form a nonaligned (isotropic) structured network (non-Newtonian solution). Below the 6 wt % threshold, the aggregates are presumably much smaller, and the solution is Newtonian.
Figure 5.
Propulsive force of the bacteria in DSCG solutions computed by modeling the shape of bacteria with a prolate spheroid. (A) Transversal cut of a prolate spheroid moving in the direction of its major axis and (B) estimation (using our viscosity measurements) of the propulsive force applied by the bacteria when it swims as a function of the DSCG concentration. The linear increase of the propulsive force (with a slope of [0.42 ± 0.09]pN/%) is represented in (B) with the dotted line. The gray hatched zone represents the DSCG concentration range where both phases coexist (isotropic and anisotropic). To see this figure in color, go online.
It is also instructive to compare the speed of the bacteria as a function of the viscosity of the DSCG solution (see Fig. S11) with the speed obtained in previous work in viscous solution of long polymers. We then find that the speed in the pretransition zone is similar to the speed in solution with the same viscosity, but that the speed in the anisotropic phase is higher. Indeed, in the pretransition zone, at a viscosity of 15 ± 0.2 g/(m × s), we obtain a relative speed of ∼ (where is the speed in MB) as in solutions of linear polymers (39, 45). Therefore, the solutions of DSCG in the pretransition zone seem to have the same properties as the solutions of long linear polymers. In the anisotropic phase, the relative speed of the bacteria is ∼ at a viscosity of 84 ± 1 g/(m × s). This is similar to the speed measured in Martinez et al. (39), but the viscosity was ∼35 g/(m × s) in that case. In addition, that speed is higher than the one obtained in Atsumi et al. (45), namely at a viscosity of ∼100 g/(m × s). We therefore conclude that the anisotropic phase of DSCG solutions exhibit non-Newtonian properties that are more important than in solutions of linear polymers.
Sticky behavior
In an earlier study (25), Lydon presented a phase diagram for the DSCG-water solution (versus temperature and concentration), according to which, at room temperature, the material undergoes a phase transition starting from ∼8 wt % DSCG. The zone between 8 and 12 wt % is labeled as a two-phase region. In our experiments however, this two-phase region was observed only between 10 and 11 wt %; no nematic domains were observed below 10 wt % (see Section S5) and the medium in the pretransition zone was always isotropic. Thus, the sticky behavior we observed seems to be different from the trapping by elastic forces (to minimize the elastic energy of deformation of the n field), described by Mushenheim et al. (4). Our observation that some bacteria succeed to break apart in the pretransition zone further supports the above statement. Indeed, for the separation to be possible, the sticky force must be of the same order of magnitude as the propulsive force produced by our bacteria, which is ∼2 pN (see Fig. 5 B and Mushenheim et al. (4)). This force is much weaker than the trapping elastic force on similar bacteria in a solution of 15 wt % DSCG estimated in (4). Interestingly, although our force estimates show that the pretransition sticking process is weaker than the trapping elastic forces in the anistropic phase (above 10 wt % DSCG), we do not observe the same type of sticking phenomenon in the latter phase. As mentioned before, this might simply be because of the fact that interactions with surfaces are much less frequent and because the interactions between two bacteria are dominated by the elastic forces in an anisotropic medium. If the elastic deformation forces are absent in the pretransition zone, then the attraction between bacteria and surfaces must originate from other local (e.g., electrostatic or depletion) interactions.
Because the aggregates’ length should increase in the pretransition zone (see section below), one could also imagine that the formation of some microscopic phase transition (that would not be observable by the techniques we are using, see also Lydon (25)) might cause the sticky effect. However, by increasing the temperature up to 37°C in a solution with 9.2 wt % DSCG, we observe no difference in the stickiness of bacteria (compared with our observations at 22.5°C). Because the local anisotropic phase should become isotropic at 37°C, this scenario becomes less plausible.
In colloidal suspension, when big particles are in the presence of much smaller ones, a depletion effect is observable. In this process, when the distance between the surfaces of two big particles become smaller or equal to the characteristic size of the small particles, the latter have the tendencies to be exclude from the space between the big particles. This exclusion create an unbalanced osmotic pressure that causes an effective force pushing together the big particles (46, 47). The depletion effect becomes particularly important when the size of the small species becomes much larger than the molecular size. This phenomenon has been shown to form aggregates of bacteria in solutions with large molecules or polymers (48, 49). Interestingly, this aggregation can be reversed simply by shaking the solution. Because the DSCG aggregates’ length should suddenly become larger in the pretransition zone (see below), the depletion effect should also drastically increase in this zone. To verify whether the depletion force is sufficient to explain the sticky effect in the pretransition zone, we estimated the strength of this effect by considering the bacteria as big spheres and the aggregates as small rods (see Section S3) (46, 47). We estimated this force by using the aggregation model of the DSCG described below for the concentrations between 6.2 and 10.2 wt %. The maximum depletion force (when the membranes of the two bacteria are in contact) increases from 90 pN at 6.2 wt % to 150 pN at 10.2 wt % (see Fig. S3). Thus, the strength of the depletion force is more than enough to create the sticky effect observed between the bacteria because the propulsive force in the pretransition zone is ∼2 pN. However, we observed that some bacteria in the pretransition zone are able to detach themselves from surfaces or bacterial aggregates, suggesting that the propulsive force must be of the same order of magnitude as the sticky effect. We estimated the critical distance between two bacteria needed to have the same depletion force as the propulsion force (see Fig. S3, inset), and we found that it vary from ∼5 nm at 6.2 wt % to ∼12 nm at 9.2 wt %. We expect that the wall of two bacteria cannot be fully in contact because there are many proteins at the surface of the membrane that cause many protuberances. This should increase the minimal interbacterial distance and reduce the maximum effective depletion force sensed by the bacteria. Furthermore, the depletion effect can be perturbed by the propulsive apparatus (e.g., a filament can penetrate between the two bacteria) causing the effective force to be reduced.
We think that the depletion effect is the main mechanism that explains the sticky effect in the pretransition zone because it is in agreement with several of our observations. 1) The bacteria in aggregates can be momentarily resuspended in the solution by shaking the chamber, just like the bacterial aggregates caused by the depletion effect reported in Schwarz-Linek et al. (48). 2) Because the aggregates’ length should drastically increase in the pretransition zone, the depletion force should be much more important in that zone, as the sticky effect. 3) The maximum depletion force being larger than the propulsive force, it can explain why the majority of bacteria stay stuck to each other or to the wall of the chamber. 4) Even if the propulsion force is smaller than the maximum possible depletion force, the imperfection on the surface of the bacteria and the perturbation created by the flagellar motor can explain why some bacteria are able to detach from the aggregates because the minimal distance needed for two bacteria to detach is relatively small. 5) Finally, the depletion effect can also explain why the sticky effect becomes more important as the DSCG concentration is raised because the depletion force increases with the length of the aggregates (growing with the DSCG concentration).
Aggregates length
Our measurements show that the medium’s viscosity is undergoing a drastic (exponential) increase in the pretransition zone, but the link between this increasing viscosity and the stickiness of bacteria was not clear initially. Many models describe how the viscosity of a fluid increases when molecules or particles in solution aggregate (50, 51, 52, 53). Using the Krieger and Dougherty model (53, 54), we calculated how the DSCG aggregates increase in length in the pretransition zone, as the increase in propulsive force seems to suggest. This section will describe the details of this calculation.
The Krieger and Dougherty model (53, 54) is one of the models that describe the behavior of the viscosity when rigid spheres form clusters in a solvent. We used this theory to estimate the length of DSCG aggregates in our system. In this model, the following equation describes the relative viscosity of the solution:
| (3) |
where is the intrinsic viscosity and is the volume fraction of particles in an aggregate. The volume fraction of aggregates in the solution is given by , where ϕ is the volume fraction of particles in the solution, is the aggregates radius, is the particles radius, and is the fractal dimension of aggregates. The relative viscosity is given by , where η is the viscosity of the solution and is the viscosity of the solvent without particles.
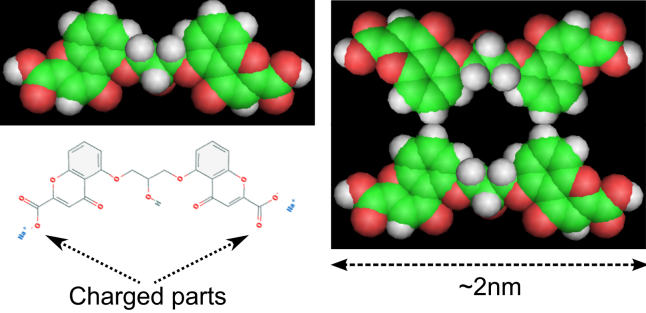
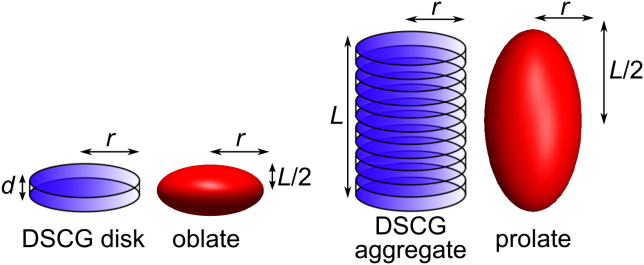
To estimate the length of DSCG aggregates from the viscosity of the solution, we have to make some assumptions. First, we assume that aggregates are assembled from stacked disks formed by two DSCG molecules. These molecules are coupled by the aromatic rings to maximize the distance between the charged groups on the opposite side (see Fig. 6). This model is based on the conclusions of Dickinson et al. (55). The space between two disks is 0.34 nm (56), so the thickness of the disk is chosen to be also 0.34 nm (Fig. 7 d), which means that there is no empty space between two disks. At the DSCG concentrations considered in this work, we suppose that molecules are always coupled two by two, in agreement with an earlier study (25). Therefore single particles are considered to be disk of two DSCG molecules (with a radius r of 1 nm). Furthermore, we assume that the volume occupied by a disk in the solution does not change when they are in aggregates. The measured volume fraction ϕ at each weight fraction is shown in Table S1.
Figure 6.
Scheme of a DSCG molecule and disk-like arrangement. To see this figure in color, go online.
Figure 7.
Scheme of DSCG disk and aggregate and their representation as spheroid. To see this figure in color, go online.
Another assumption is that the shape of the aggregates is estimated to be spheroid to simplify the calculation of (see Fig. 7). In that case, the expression for is given by the following (57):
| (4) |
where is the Avogadro constant, M is the molecular weight of aggregates, and is the hydrodynamic volume of aggregates. For an oblate spheroid (disk-like), ν is given by the following:
| (5) |
where (57). For a prolate spheroid (rod-like), ν is given by the following:
| (6) |
where .
To obtain the length of the aggregates, the equivalent Stokes radius of a spheroid is used to calculate . This radius is given by the following (the Stokes radius of a spheroid corresponds to the radius of a sphere with the same volume):
| (7) |
By using Eqs. 3 and 7 and isolating L, the aggregate length, on the left side of Eq. 3, we find the following:
| (8) |
Because depend also on L, the value of in the exponent was varied numerically to obtain the same value of L in the equation of than in Eq. 8 with a precision of 0.01 nm.
The numerical values of the different constants used in the calculation are summarized in Table S4. The volume fraction of molecules in aggregates consists in the ratio between the volume occupied by a molecule and the volume occupied by holes in an aggregate. In DSCG, this factor does not change with the size of the aggregates because of their rod-shaped symmetry. Furthermore, we suppose the arrangement of disk to be densely packed with , a value similar to the aggregation of hard spheres (50). The hydrodynamic volume of aggregates involves a comparison between the volumes occupied by DSCG molecules and by the solvent in an aggregate, multiplied by . As for a hard sphere, we suppose that no solvent enters inside the holes of the aggregates because the center hole is exposed to the hydrophobic parts of the DSCG molecule (Fig. 6, uncharged parts). Therefore, and . Finally, by observing the geometry of the aggregate (Fig. 7, cylinder), one finds that the length of the aggregate increases by one unit of length (the thickness of the DSCG disk) for each added disk, which corresponds to a fractal dimension of . Even if a more detailed model of the aggregates were to lead to a more precise value of , that would simply affect the size of the aggregates, but not our conclusions.
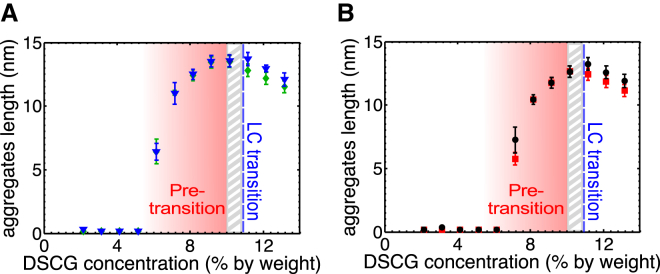
As Fig. 8 shows, the calculated length of aggregates is stable for DSCG concentrations below 6.2 wt % for MB solutions and 7.2 wt % for DI water solutions, and it dramatically increases above this concentration. After the LC transition, the calculation indicates that length of aggregates slightly decreases, which is probably not realistic. It is important to note that this model does not take into account any electrostatic forces between aggregates, so the breakdown of the model at high concentrations is not surprising.
Figure 8.
Estimation of the aggregates length computed with the Krieger and Dougherty model as a function of DSCG concentration. (A) The length of DSCG aggregates calculated from the viscosity of MB solution in the direction parallel (triangles) and perpendicular (diamonds) to n. (B) The length of DSCG aggregates calculated from the viscosity of DI water solution in the direction parallel (squares) and perpendicular (dots) to n (viscosity data taken from Duchesne et al. (27)). The gray hatched zone represents the DSCG concentration range where both phases coexist (isotropic and anisotropic). To see this figure in color, go online.
Additional information about motility conditions
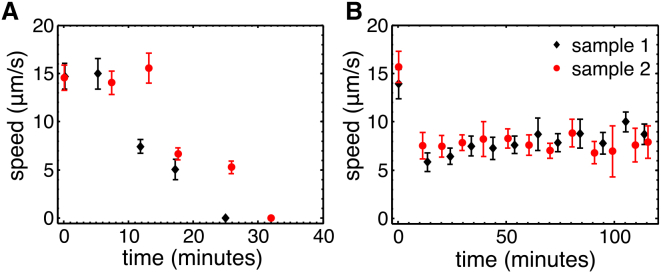
In contrast to the results presented in Fig. 2 A, Kumar et al. (2) did not observe a significant difference in bacterial speed before and after the LC transition. In these experiments, a fluorophore (with an excitation wavelength in the blue) was used to visualize the bacteria, whereas our study was performed in brightfield microscopy. It is well established that atmospheric oxygen can react with fluorophores by photobleaching it. These reactions create reactive oxygen that can break lipid chains, thus compromising the membrane of the bacteria (58, 59). We experimentally demonstrated (see Section S4) that the slow bacterial speed at DSCG concentrations below the LC transition (∼4 μm/s, see Fig. S4 C), reported in Kumar et al. (2), was attributable to the effect of the reactive oxygen. Obviously, this effect can be inhibited by anaerobic conditions. As it takes at least 25 min (after the chamber is sealed) for DSCG aggregates to align, it is likely that the observations performed above the LC transition were done in the absence of oxygen (consumed by bacteria) (see Fig. S4 D). This would explain why the speed above the LC transition (∼3 μm/s) is the same in both experiments.
Previous reports have shown that the motility of bacteria slows down when the oxygen is consumed in a solution containing glucose or stops if no glucose is present (60, 61). However, we are not aware of any measurement of the influence of oxygen on the swimming speed of bacteria in a solution containing glucose. To quantify that relationship, we recorded the speed of bacteria swimming in MB containing glucose (or not) over long periods of time (2 h). The results are shown on Fig. 9. When no glucose is available, the bacteria run out of oxygen and stop swimming in less than 30 min. When glucose is present, bacteria can use it to carry out mixed acid fermentation and continue to swim in anaerobic conditions (for at least 2 h), albeit at a lower speed. From Fig. 9 B we note that the oxygenated speed is about two times higher than the speed when oxygen is exhausted (15 vs. 8 μm/s). These experiments were made with a high concentration of bacteria (OD600 = 1). When this concentration was decreased around the one used in DSCG experiments (OD600 ∼ 0.15), the time before the complete exhaustion of oxygen greatly differed from sample to sample, varying from 15 min to more than 1 h. This phenomenon was probably caused by fluctuations in the starting oxygen concentration in each cell. Because all observations at DSCG concentrations below 11 wt % were made within 10 min, we are confident that we recorded oxygenated speeds for all concentrations below the LC transition. For the three higher concentrations in Fig. 2 A, our observations may have been made in anaerobic conditions and the equivalent oxygenated speed could have been up to twice as high. The asymmetric error bars on the last three points reflect that uncertainty.
Figure 9.
Effect of oxygen and glucose on the speed of bacteria in a closed chamber. (A) Speed of bacteria as a function of time in closed cells with a high bacterial concentration (OD600 = 1) in a MB without glucose and (B) with 0.02 M glucose. The SD was used as the error bars. To see this figure in color, go online.
Before concluding, we would like to discuss a couple of additional observations. First, by looking closely at the bacterial tracks (shown on Fig. 1 B), one observes a Brownian diffusion in the y axis (perpendicular to the director) similar to the one obtained with microspheres (Fig. 3 B). This indicates that the active machinery that allows the bacteria to swim (the flagella) acts almost exclusively in the direction parallel to the director (the x axis). The cell body is constrained (by the LC elastic forces) to maintain its long axis along the director n, as was also previously reported (4).
To ensure that the observed trajectories in the LC nematic phase were not the result of passive diffusion, we also tracked more than 100 nonmotile bacteria whose filaments were genetically removed. Because the trajectories of these nonmotile bacteria (Fig. 3 C) are qualitatively equivalent to those of microspheres (Fig. 3 B), we conclude that the anisotropic swimming behavior of active bacteria does not simply come from the elongated shape of their bodies. Therefore, we hypothesize that the filaments (thin helicoids long of several body lengths) should also be aligned with the director and push the bacteria in the direction of n. More research is needed on this topic, but it is very clear that the active displacement of bacteria is significantly different from the diffusion of microscopic objects in the same anisotropic environment.
Finally, although it is not affecting our key conclusions, we would like to address one discrepancy between the viscosity measurements reported in our study and the data we can find in the literature (4, 30). Indeed, for a DSCG solution with a concentration of 15 wt % and a temperature of 25°C, the viscosity measured by a rheology method was found to be ∼ (4). This is to be compared with our values of and at 13 wt %. The trend of our viscosity versus concentration plot in Fig. 4 A is reassuring because, for lower concentrations of the DSCG, our viscosity value is converging toward , as it is expected for water (see also the calibration of this technique in Duchesne et al. (27) that confirms its accuracy). It is hard to believe, however, that the viscosity could increase by an order of magnitude between 13 and 15 wt % DSCG to reach the value . At this stage, we do not know yet the reason for this discrepancy, but our best hypothesis would be that this difference is caused by the different methods used. Indeed, it has previously been shown that the viscosity measured with rheology method in Sunset Yellow (another chromonic LC) could change by a factor of 2 when the shear rate is modified during the measurement (62). Other measurements turned out to be very sensitive to the particle surfaces and LC anchoring conditions (33, 63, 64).
Conclusions
Our study shows that the motility of bacteria in DSCG-water solutions (LC) is sensitive to the morphology and microstructure of the host. The combined effect of alignment of bacterial body (by elastic forces in the LC phase of the host) and of the anisotropic viscosity of the host (lower in the direction parallel to its anisotropy axis) favors its movement along linear traces. In addition to these pure elastic energy considerations, the strongly anisotropic viscosity of the host media should create an effective dynamic torque favoring the anisotropic swimming. These effects cannot, however, fully explain the behavior of the bacteria (like the reversals in direction), and the observation of the flagella movements should complete this explanation.
Our quantitative studies of the bacterial motility and of the diffusion of microspheres in DSCG solutions of various concentrations have uncovered the existence of a pretransition zone (between 6 and 10 wt %) where the DSCG-water solution has not yet gone through its isotropic-anisotropic phase transition. In that zone, the viscosity of the medium is undergoing an exponential growth with DSCG concentration, the propulsive force of bacteria increases and their motility is strongly limited because they stick to each other and to surfaces. Based on the measured increase in the solution’s viscosity and in the propulsive force, we think that the size of DSCG aggregates drastically increases in that pretransition zone. Because of that increase in aggregates size, it seems likely that the depletion effect becomes important in this zone and generates the observed sticking phenomenon in the isotropic phase of the medium. Our data suggest a threshold, at a concentration of ∼6 ± 1 wt %, where the length of DSCG aggregates starts to increase rapidly.
It is interesting (almost ironic) to note that new physical properties of a material (exponential increase of viscosity, pretransition zone, etc.) were discovered by observing the behavior of bacteria, which are themselves not fully understood yet. At the same time, it shows that bacteria could be used as qualitative or even quantitative probes to detect physical properties in biocompatible media (such as aggregation, anisotropy, non-Newtonian fluid properties, etc.) This study reveals yet another layer of rich complexity in the physical characteristics of lyotropic LCs, which are bound to play an increasingly important role in our technologies thanks to their biocompatibility. Understanding the behavior of living microorganisms in these LCs promises to open extraordinary possibilities for further study of biological systems and the control of their movements. For example, we can imagine various applications in the areas of lab-on-a-chip (to control the bacteria movements) or of smart bandages where an anisotropic gel would force bacteria to move on the outskirts of the wound.
Author Contributions
I.D., S.R., and T.G. designed the experiments and wrote the manuscript. I.D. conducted all the experiments and analyses.
Acknowledgments
We acknowledge the financial support of the Canada Foundation for Innovation (CFI), the Natural Sciences and Engineering Research Council of Canada (NSERC), and CREATE. T.G. thanks Canada Research Chair in Liquid Crystals and Behavioral Biophotonics and Manning Innovation price for financial support. We are grateful to G. Paradis, K. Allahverdyan, and Dr. A. Tork (from LensVector and TLCL Optical Research, Inc.) for their help during our experiments, to the group of H.C. Berg for bacterial strains, and to Remy Colin for sharing with us his tracking algorithm. We also acknowledge the important contribution of Wilson Poon for bringing the depletion mechanism to our attention and his other thoughtful comments on the manuscript.
Editor: Dennis Bray.
Footnotes
Supporting Materials and Methods, eleven figures, and four tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)01007-3.
Supporting Citations
References (65, 66) appear in the Supporting Material.
Supporting Material
References
- 1.Smalyukh I.I., Butler J., Wong G.C.L. Elasticity-mediated nematiclike bacterial organization in model extracellular DNA matrix. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:030701. doi: 10.1103/PhysRevE.78.030701. [DOI] [PubMed] [Google Scholar]
- 2.Kumar A., Galstian T., Rainville S. The motility of bacteria in an anisotropic liquid environment. Mol. Cryst. Liq. Cryst. 2013;574:33–39. [Google Scholar]
- 3.Zhou S., Sokolov A., Aranson I.S. Living liquid crystals. Proc. Natl. Acad. Sci. USA. 2014;111:1265–1270. doi: 10.1073/pnas.1321926111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mushenheim P.C., Trivedi R.R., Abbott N.L. Dynamic self-assembly of motile bacteria in liquid crystals. Soft Matter. 2014;10:88–95. doi: 10.1039/c3sm52423j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mushenheim P.C., Trivedi R.R., Abbott N.L. Using liquid crystals to reveal how mechanical anisotropy changes interfacial behaviors of motile bacteria. Biophys. J. 2014;107:255–265. doi: 10.1016/j.bpj.2014.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rey A.D., Herrera-Valencia E.E., Murugesan Y.K. Structure and dynamics of biological liquid crystals. Liq. Cryst. 2014;41:430–451. [Google Scholar]
- 7.Viney C., Huber A.E., Verdugo P. Liquid crystalline order in mucus. Macromolecules. 1993;26:852–855. doi: 10.1021/ma00056a044. [DOI] [PubMed] [Google Scholar]
- 8.Viney C. Mucus liquid crystallinity: is function related to microstructural domain size? Biorheology. 1999;36:319–323. [PubMed] [Google Scholar]
- 9.Davies J.M., Viney C. Water–mucin phases: conditions for mucus liquid crystallinity. Thermochim. Acta. 1998;315:39–49. [Google Scholar]
- 10.Kupchinov B.I., Ermako S.F., Kestelman V.N. Role of liquid crystals in the lubrication of living joints. Smart Mater. Struct. 1993;2:7. [Google Scholar]
- 11.Nocton J.J., Dressler F., Steere A.C. Detection of Borrelia burgdorferi DNA by polymerase chain reaction in synovial fluid from patients with Lyme arthritis. N. Engl. J. Med. 1994;330:229–234. doi: 10.1056/NEJM199401273300401. [DOI] [PubMed] [Google Scholar]
- 12.Hughes J.G., Vetter E.A., Cockerill F.R., 3rd Culture with BACTEC Peds Plus/F bottle compared with conventional methods for detection of bacteria in synovial fluid. J. Clin. Microbiol. 2001;39:4468–4471. doi: 10.1128/JCM.39.12.4468-4471.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hermanowicz S., Schindler U., Wilderer P. Anisotropic morphology and fractal dimensions of biofilms. Water Res. 1996;30:753–755. [Google Scholar]
- 14.Van Wey A.S., Cookson A.L., Shorten P.R. Anisotropic nutrient transport in three-dimensional single species bacterial biofilms. Biotechnol. Bioeng. 2012;109:1280–1292. doi: 10.1002/bit.24390. [DOI] [PubMed] [Google Scholar]
- 15.Houry A., Gohar M., Briandet R. Bacterial swimmers that infiltrate and take over the biofilm matrix. Proc. Natl. Acad. Sci. USA. 2012;109:13088–13093. doi: 10.1073/pnas.1200791109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yeh P., Gu C. John Wiley & Sons; Hoboken, NJ: 2010. Optics of Liquid Crystal Displays. [Google Scholar]
- 17.Galstian T.V. CRC Press; Boca Raton, FL: 2013. Smart mini-cameras. [Google Scholar]
- 18.Tomilin M.G., Stafeev S.K., Stepanova A. Influenza viruses optical detection based on liquid crystals. Proc. SPIE. 2006;6398:639813. [Google Scholar]
- 19.Shiyanovskii S.V., Lavrentovich O.D., Doane K.J. Lyotropic chromonic liquid crystals for biological sensing applications. Mol. Cryst. Liq. Cryst. 2005;434 259/[587]–270/[598] [Google Scholar]
- 20.Berg H.C., Brown D.A. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature. 1972;239:500–504. doi: 10.1038/239500a0. [DOI] [PubMed] [Google Scholar]
- 21.Frymier P.D., Ford R.M., Cummings P.T. Three-dimensional tracking of motile bacteria near a solid planar surface. Proc. Natl. Acad. Sci. USA. 1995;92:6195–6199. doi: 10.1073/pnas.92.13.6195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Molaei M., Barry M., Sheng J. Failed escape: solid surfaces prevent tumbling of Escherichia coli. Phys. Rev. Lett. 2014;113:068103. doi: 10.1103/PhysRevLett.113.068103. [DOI] [PubMed] [Google Scholar]
- 23.Parkinson J.S. Complementation analysis and deletion mapping of Escherichia coli mutants defective in chemotaxis. J. Bacteriol. 1978;135:45–53. doi: 10.1128/jb.135.1.45-53.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yuan J., Berg H.C. Thermal and solvent-isotope effects on the flagellar rotary motor near zero load. Biophys. J. 2010;98:2121–2126. doi: 10.1016/j.bpj.2010.01.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lydon J. Chromonic liquid crystalline phases. Liq. Cryst. 2011;38:1663–1681. [Google Scholar]
- 26.Seo D.S., Matsuda H., Kobayashi S. Alignment of nematic liquid crystal(5CB) on the treated substrates: characterization of orientation films, generation of pretilt angles, and surface anchoring strength. Mol. Cryst. Liq. Cryst. 1993;224:13–31. [Google Scholar]
- 27.Duchesne I., Rainville S., Galstian T. Application of a microrheology technique to measure the viscosity of disodium cromoglycate liquid crystal. Mol. Cryst. Liq. Cryst. 2015 Submitted. [Google Scholar]
- 28.de Gennes P.G., Prost J. Clarendon Press; New York: 1995. The Physics of Liquid Crystals. [Google Scholar]
- 29.Saveyn H., De Baets B., Van der Meeren P. Accurate particle size distribution determination by nanoparticle tracking analysis based on 2-D Brownian dynamics simulation. J. Colloid Interface Sci. 2010;352:593–600. doi: 10.1016/j.jcis.2010.09.006. [DOI] [PubMed] [Google Scholar]
- 30.Turiv T., Lazo I., Lavrentovich O.D. Effect of collective molecular reorientations on Brownian motion of colloids in nematic liquid crystal. Science. 2013;342:1351–1354. doi: 10.1126/science.1240591. [DOI] [PubMed] [Google Scholar]
- 31.Berezhkovskii A.M., Dagdug L., Bezrukov S.M. Discriminating between anomalous diffusion and transient behavior in microheterogeneous environments. Biophys. J. 2014;106:L09–L11. doi: 10.1016/j.bpj.2013.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Purcell E.M. Life at low Reynolds number. Am. J. Phys. 1977;45:3–11. [Google Scholar]
- 33.Stark H., Ventzki D. Stokes drag of spherical particles in a nematic environment at low Ericksen numbers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2001;64:031711. doi: 10.1103/PhysRevE.64.031711. [DOI] [PubMed] [Google Scholar]
- 34.Ryzhkova A.V., Muševič I. Particle size effects on nanocolloidal interactions in nematic liquid crystals. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013;87:032501. doi: 10.1103/PhysRevE.87.062501. [DOI] [PubMed] [Google Scholar]
- 35.Nastishin Y.A., Liu H., Anisimov M.A. Pretransitional fluctuations in the isotropic phase of a lyotropic chromonic liquid crystal. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;70:051706. doi: 10.1103/PhysRevE.70.051706. [DOI] [PubMed] [Google Scholar]
- 36.Smalyukh I.I., Lavrentovich O.D., Prasad P.N. Elasticity-mediated self-organization and colloidal interactions of solid spheres with tangential anchoring in a nematic liquid crystal. Phys. Rev. Lett. 2005;95:157801. doi: 10.1103/PhysRevLett.95.157801. [DOI] [PubMed] [Google Scholar]
- 37.Poulin P., Weitz D.A. Inverted and multiple nematic emulsions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 1998;57:626–637. [Google Scholar]
- 38.Sowa Y., Berry R.M. Bacterial flagellar motor. Q. Rev. Biophys. 2008;41:103–132. doi: 10.1017/S0033583508004691. [DOI] [PubMed] [Google Scholar]
- 39.Martinez V.A., Schwarz-Linek J., Poon W.C.K. Flagellated bacterial motility in polymer solutions. Proc. Natl. Acad. Sci. USA. 2014;111:17771–17776. doi: 10.1073/pnas.1415460111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Darnton N.C., Turner L., Berg H.C. On torque and tumbling in swimming Escherichia coli. J. Bacteriol. 2007;189:1756–1764. doi: 10.1128/JB.01501-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Berg H.C., Turner L. Movement of microorganisms in viscous environments. Nature. 1979;278:349–351. doi: 10.1038/278349a0. [DOI] [PubMed] [Google Scholar]
- 42.Schneider W.R., Doetsch R.N. Effect of viscosity on bacterial motility. J. Bacteriol. 1974;117:696–701. doi: 10.1128/jb.117.2.696-701.1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Magariyama Y., Kudo S. A mathematical explanation of an increase in bacterial swimming speed with viscosity in linear-polymer solutions. Biophys. J. 2002;83:733–739. doi: 10.1016/S0006-3495(02)75204-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nakamura S., Adachi Y., Magariyama Y. Improvement in motion efficiency of the spirochete Brachyspira pilosicoli in viscous environments. Biophys. J. 2006;90:3019–3026. doi: 10.1529/biophysj.105.074336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Atsumi T., Maekawa Y., Homma M. Effect of viscosity on swimming by the lateral and polar flagella of Vibrio alginolyticus. J. Bacteriol. 1996;178:5024–5026. doi: 10.1128/jb.178.16.5024-5026.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Mao Y., Cates M.E., Lekkerkerker H.N.W. Theory of the depletion force due to rodlike polymers. J. Chem. Phys. 1997;106:3721–3729. [Google Scholar]
- 47.Yaman K., Jeppesen C., Marques C.M. Depletion forces between two spheres in a rod solution. Europhys. Lett. 1998;42:221. [Google Scholar]
- 48.Schwarz-Linek J., Dorken G., Poon W.C.K. Polymer-induced phase separation in suspensions of bacteria. Europhys. Lett. 2010;89:68003. [Google Scholar]
- 49.Dorken G., Ferguson G.P., Poon W.C.K. Aggregation by depletion attraction in cultures of bacteria producing exopolysaccharide. J. R. Soc. Interface. 2012;9:3490–3502. doi: 10.1098/rsif.2012.0498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rubio-Hernández F.J., Ayúcar-Rubio M.F., Galindo-Rosales F.J. Intrinsic viscosity of SiO2, Al2O3 and TiO2 aqueous suspensions. J. Colloid Interface Sci. 2006;298:967–972. doi: 10.1016/j.jcis.2006.01.009. [DOI] [PubMed] [Google Scholar]
- 51.Kovalchuk N., Starov V., Holdich R. Effect of aggregation on viscosity of colloidal suspension. Colloid J. 2010;72:647–652. [Google Scholar]
- 52.Barthelmes G., Pratsinis S.E., Buggisch H. Particle size distributions and viscosity of suspensions undergoing shear-induced coagulation and fragmentation. Chem. Eng. Sci. 2003;58:2893–2902. [Google Scholar]
- 53.Duan F., Kwek D., Crivoi A. Viscosity affected by nanoparticle aggregation in Al2O3-water nanofluids. Nanoscale Res. Lett. 2011;6:248. doi: 10.1186/1556-276X-6-248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Krieger I.M., Dougherty T.J. A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 1959;3:137–152. [Google Scholar]
- 55.Dickinson A.J., LaRacuente N.D., Collings P.J. Aggregate structure and free energy changes in chromonic liquid crystals. Mol. Cryst. Liq. Cryst. 2009;509 9/[751]–20/[762] [Google Scholar]
- 56.Hartshorne N.H., Woodard G.D. Mesomorphism in the system disodium chromoglycate-water. Mol. Cryst. Liq. Cryst. 1973;23:343–368. [Google Scholar]
- 57.Tanford C. Wiley and Sons; New York: 1961. Physical Chemistry of Macromolecules. [Google Scholar]
- 58.Hadjur C., Lange N., Wagnières G. Spectroscopic studies of photobleaching and photoproduct formation of meta(tetrahydroxyphenyl)chlorin (m-THPC) used in photodynamic therapy. The production of singlet oxygen by m-THPC. J. Photochem. Photobiol. B. 1998;45:170–178. [Google Scholar]
- 59.Heiser I., Oswald W., Elstner E.F. The formation of reactive oxygen species by fungal and bacterial phytotoxins. Plant Physiol. Biochem. 1998;36:703–713. [Google Scholar]
- 60.Adler J., Templeton B. The effect of environmental conditions on the motility of Escherichia coli. J. Gen. Microbiol. 1967;46:175–184. doi: 10.1099/00221287-46-2-175. [DOI] [PubMed] [Google Scholar]
- 61.Douarche C., Buguin A., Libchaber A. E. coli and oxygen: a motility transition. Phys. Rev. Lett. 2009;102:198101. doi: 10.1103/PhysRevLett.102.198101. [DOI] [PubMed] [Google Scholar]
- 62.Prasad S.K., Nair G.G., Jayalakshmi V. Evidence of wormlike micellar behavior in chromonic liquid crystals: rheological, x-ray, and dielectric studies. J. Phys. Chem. B. 2007;111:9741–9746. doi: 10.1021/jp073190+. [DOI] [PubMed] [Google Scholar]
- 63.Senyuk B., Glugla D., Smalyukh I.I. Rotational and translational diffusion of anisotropic gold nanoparticles in liquid crystals controlled by varying surface anchoring. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013;88:062507. doi: 10.1103/PhysRevE.88.062507. [DOI] [PubMed] [Google Scholar]
- 64.Koenig G.M., Jr., Ong R., Abbott N.L. Single nanoparticle tracking reveals influence of chemical functionality of nanoparticles on local ordering of liquid crystals and nanoparticle diffusion coefficients. Nano Lett. 2009;9:2794–2801. doi: 10.1021/nl901498d. [DOI] [PubMed] [Google Scholar]
- 65.Purcell E.M. The efficiency of propulsion by a rotating flagellum. Proc. Natl. Acad. Sci. USA. 1997;94:11307–11311. doi: 10.1073/pnas.94.21.11307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Chattopadhyay S., Moldovan R., Wu X.L. Swimming efficiency of bacterium Escherichia coli. Proc. Natl. Acad. Sci. USA. 2006;103:13712–13717. doi: 10.1073/pnas.0602043103. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.