Abstract
The assembly of various proteins into fibrillar aggregates is an important phenomenon with wide implications ranging from human disease to nanoscience. Using general kinetic results of nucleation theory, we analyze the polymerization of protein into linear or helical fibrils in the framework of the Oosawa-Kasai (OK) model. We show that while within the original OK model of linear polymerization the process does not involve nucleation, within a modified OK model it is nucleation-mediated. Expressions are derived for the size of the fibril nucleus, the work for fibril formation, the nucleation barrier, the equilibrium and stationary fibril size distributions, and the stationary fibril nucleation rate. Under otherwise equal conditions, this rate decreases considerably when the short (subnucleus) fibrils lose monomers much more frequently than the long (supernucleus) fibrils, a feature that should be born in mind when designing a strategy for stymying or stimulating fibril nucleation. The obtained dependence of the nucleation rate on the concentration of monomeric protein is convenient for experimental verification and for use in rate equations accounting for nucleation-mediated fibril formation. The analysis and the results obtained for linear fibrils are fully applicable to helical fibrils whose formation is describable by a simplified OK model.
Introduction
Polymerization of protein into fibrillar aggregates is much studied both because protein fibrils are involved in scores of human diseases (1, 2) and because they could be useful for various technological applications (3, 4). Describing the kinetics of the process is particularly challenging due to the plethora of possible pathways that could be taken by the protein monomers in their filamentous self-assembly (1, 2, 5, 6, 7, 8, 9, 10). Because the description is greatly simplified by modeling the process as evolving along a single pathway, most of the theoretical studies on the kinetics of protein polymerization are based on such modeling. A recent comprehensive analysis of nucleation-mediated protein fibrillation with competing off-pathway aggregation is that of Powers and Powers (11).
In a pioneering article, Oosawa and Kasai (12) considered protein fibrils resulting from one-dimensional arrangement of dissolved protein monomers either along a straight line or along a spiraling line, two cases that they called linear and helical polymerization, respectively (see also Oosawa and Kasai (13), Oosawa and Higashi (14), and Oosawa and Asakura (15)). Although the Oosawa-Kasai (OK) model (12) has its limitations (16), it became a valuable tool in the kinetic analysis of protein fibrillation, because it and the ensuing extended models led to the formulation of rate equations allowing description of the process at the molecular level (e.g., see the literature (12, 14, 15, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35); see also a review by Gillam and McPhee (36) and references therein). In their study, Oosawa and Kasai (12) focused on the helical polymerization and dealt only briefly with the linear one. In contrast, this analysis is concerned above all with linear polymerization in the framework of the OK model. Helical polymerization within this model can be treated in a similar fashion, but the problem is mathematically more complicated and requires a separate study unless the model is not simplified. The simplification considered here allows describing the helical polymerization in precisely the same way as the linear one.
Most generally, the filamentous self-assembly of protein is a particular case of formation and growth of condensed phases during first-order phase transitions. Despite that this was recognized long ago (12, 14, 15, 37), hitherto, general results of droplet or crystal nucleation and growth theories have relatively rarely been employed in thermodynamic and kinetic studies of protein fibrillation (e.g., see the literature (5, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51)). In particular, the OK model has not been analyzed from the viewpoint of nucleation theory to verify whether it admits of nucleation, and if so, to determine the fibril nucleation barrier and rate. Such an analysis is much needed, because both the original (12) and some generalized (14, 15, 20, 22, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36) rate equations of the OK model do not provide a self-contained description of the fibrillation kinetics. Namely, they operate with a semiempirical quantity called the fibril nucleation rate and are introduced ad hoc to account for the effect of nucleation on the overall fibrillation process. As it will be seen below, this quantity disappears from the rate equations of the OK model when fibrillation is analyzed by employing general kinetic results of the classical nucleation theory (CNT) (52, 53, 54).
The objective of this study is to apply the CNT kinetic approach to the OK model of linear polymerization to 1) clarify the role of nucleation in the formation of linear fibrils; 2) derive expressions for the fibril formation work, size distribution, nucleation barrier, and nucleation rate (when fibrils appear via nucleation); and 3) reveal the physical meaning of the semiempirical quantity in the rate equations of the model.
Materials and Methods
In this study, we use standard materials for analytical calculations as well as a standard personal computer. Our method is very simple: we apply known general kinetic expressions of CNT to the OK model of linear polymerization. These are given and briefly explained below.
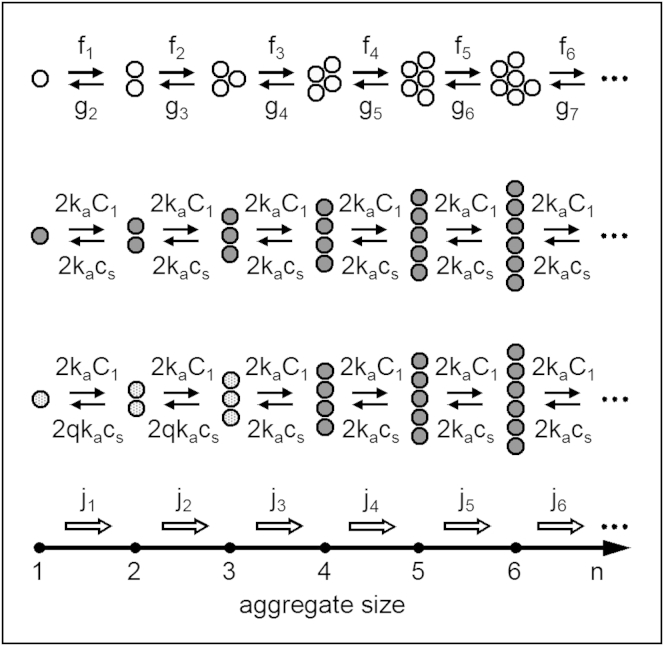
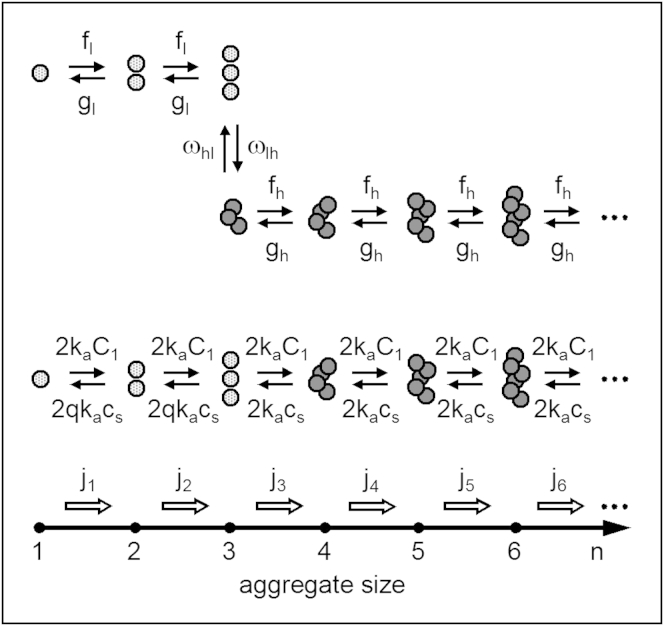
As illustrated by the first row of molecular aggregates in Fig. 1, CNT is based on the Szilard-Farkas model (55) according to which an aggregate of one-component new phase is characterized solely by the number n = 1, 2, 3, … of its molecules and evolves by randomly attaching and detaching only single molecules (monomers) with nonvanishing frequencies fn and gn, respectively (54).
Figure 1.
Schematic of the Szilard-Farkas model of aggregation (first row) and of the original and modified OK models of linear polymerization (second and third rows, respectively, with the trimer in the third row as fibril nucleus). The monomers (the circles) in the first row are clustered into two-dimensional crystallites with hexagonal symmetry. The monomers in the second and the third rows are assembled in one-dimension into linear fibrils, the only difference between the two rows being that in the third row the monomer detachment frequency for the dimer and the trimer is q times higher than that for the longer fibrils.
Knowing fn and gn allows determination of the work Wn to form an n-sized aggregate with the aid of the following exact expression (54):
| (1) |
Here W1 is the value of Wn at n = 1 (i.e., the work to form the smallest piece of the new phase), k is the Boltzmann constant, and T is the absolute temperature. When fn and gn are such that Wn has a maximum at a certain n = n∗ > 1, the system is in metastable equilibrium, i.e., it is supersaturated. The n∗-sized aggregate is the nucleus of the new phase, because it requires maximum work Wn∗ for its formation.
The monomer attachment to and detachment from aggregates gives rise to a net flux jn from size n to size n + 1 along the size axis. This flux is visualized by the open arrows in Fig. 1 and is of the form (54)
| (2) |
Here Cn is the number concentration of n-sized aggregates, and fnCn and gn+1Cn+1 are the forward and backward fluxes from size n and size n + 1 (the solid right- and left-handed arrows in the first row in Fig. 1), respectively.
According to the principle of detailed balance (or microscopic reversibility), the system is in thermodynamic equilibrium when jn = 0. This occurs when the aggregates have their equilibrium size distribution Ce,n given exactly by (54)
| (3) |
where C1 is the monomer concentration. The system is supersaturated if fn and gn are such that Ce,n diverges with n tending to infinity. For a solution, this is the case when C1 > cs, cs being the new-phase solubility, i.e., the monomer concentration at which a macroscopically large aggregate neither grows nor dissolves. For a supersaturated system, because of its divergence, Ce,n is only a thought size distribution of aggregates. The equilibrium size distribution Ce,n does really exist, however, when the system is saturated or undersaturated (for a solution, this is so when C1 = cs or C1 < cs, respectively).
A supersaturated system is in stationary state when jn = J for any n = 1, 2, 3,… , where J is the stationary nucleation rate. Then, rather than Ce,n, the corresponding stationary size distribution Cst,n of aggregates is what is really established in the system. For a system with number M of monomers that is large enough to allow using M = ∞, this distribution is given exactly by (54)
| (4) |
Here Ce,n is specified by Eq. 3, and J is expressed by the exact Becker-Döring formula (56), which can be represented as (54)
| (5) |
All Ce,n, Cst,n, and J from Eqs. 3–5 are t-independent when neither the monomer concentration C1 nor the frequencies fn and gn change with time t. If this is not the case, Ce,n and Cst,n are the quasi-equilibrium and quasi-stationary size distributions of aggregates, and J is the corresponding quasi-stationary nucleation rate (53, 54).
Finally, with jn from Eq. 2, the rate equations of the Szilard-Farkas model can be expressed in the form (n = 2, 3, 4,…) (54)
| (6) |
Importantly, these rate equations are self-contained in the sense that the only parameters in them are the monomer attachment and detachment frequencies fn and gn inherent to the model.
Results and Discussion
Before proceeding further, let us introduce some of the terms and symbols used hereafter. This seems expedient, as they may differ from those employed in the biophysical literature.
In formation of single-component protein fibrils at a given concentration C1 of monomeric protein, the supersaturation ratio S ≡ C1/cs characterizes the thermodynamic state of the protein solution when this is not too concentrated and activity effects are negligible. While for S < 1 the solution is stable because of the thermodynamically prohibited appearance of macroscopically long fibrils in it, for S > 1 the solution is metastable due to the thermodynamically favored formation of such fibrils in it. At S = 1, the solution is in phase equilibrium, as then it can coexist with the bulk fibrillar phase. The fibril solubility cs (termed also critical concentration (12, 15, 18, 19, 25)) is, therefore, simply the phase-equilibrium concentration of monomeric protein.
Within the OK model, the protein fibril itself is a one-dimensional straight or spiral chain of any number n = 1, 2, 3, … of protein monomers. The model is so simple that there is no need of specific terms for the short and the long protein chains, such as the often used protofibril and mature fibril, respectively. When S > 1, among the fibrils of all sizes there may be special ones, the fibril nuclei, each of them comprising n∗ monomers and requiring maximum work for its formation. Accordingly, the fibrils of sizes n < n∗ and n > n∗ are the fibril subnuclei and supernuclei, respectively. The subnuclei could be called oligomers (25), but we shall refrain from employing this term here, because rather than designating the short fibrils in relation to the nucleation process, it usually refers to idiosyncrasies in the physical structure and/or biological properties (such as cytotoxicity) of the smallest protein aggregates.
OK model of linear fibrils
The OK model (12) of protein fibrillation is a special case of the Szilard-Farkas model (55) of new-phase formation. Indeed, similar to what was done by Farkas (55) with respect to droplet nucleation, Oosawa and Kasai (12) considered the formation of fibrils as resulting solely from random attachment and detachment of monomers to and from them (other possible processes such as fibril fragmentation and association were not taken into account). Thus, the whole fibrillation process is controlled only by the frequencies fn and gn of monomer attachment to and detachment from the two ends of an n-sized fibril.
In the OK model of linear fibrils (the second row of aggregates in Fig. 1), fn and gn are considered as n-independent and are expressed as (12)
| (7) |
| (8) |
Here ka is the n-independent frequency (per unit monomer concentration) with which monomers from the protein solution are attached to one of the fibril ends, kd is the n-independent frequency of monomer detachment from one of the fibril ends, and the factor 2 accounts that a fibril has two ends. The solubility cs is defined by Oosawa and Kasai (12) as cs = kd/ka and is the C1 value at which the solution is saturated, for then fn = gn and the fibrils cannot lengthen or shorten.
Now, substituting fn and gn from Eqs. 7 and 8 in Eq. 1, we readily obtain the equality Wn + nkT ln S = W1 + kT ln S, which tells us that the sum Wn + nkT ln S has the same value for any n = 1, 2, 3,… . Denoting this value by ε, we thus arrive at the exact result (n = 1, 2, 3,… , S > 0):
| (9) |
Here, S is the supersaturation ratio, and the n-independent energy parameter ε can be determined by thermodynamic considerations showing that it is the sum of the energies of the two fibril ends (13, 15, 43).
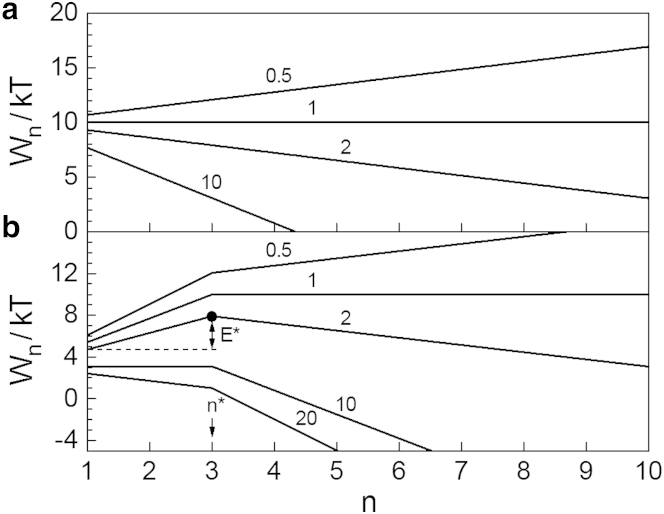
Equation 9 gives the work Wn to form an n-monomer-long linear fibril according to the OK model. This equation shows that when S > 1, i.e., for supersaturated solutions, Wn decreases linearly with the fibril size n. This is seen in Fig. 2 a in which lines 2 and 10 visualize Wn from Eq. 9 at S = 2 and 10, respectively, when ε = 10 kT. Because nucleation is operative only when Wn has a maximum at n = n∗ > 1, this decrease implies that the OK model of linear polymerization does not involve nucleation. Indeed, as the maximal Wn value is at n = 1 and, hence, each monomer in the solution is formally a nucleus, the nuclei are in the solution already at the very beginning of the polymerization process so that, at any S > 1, the process occurs in the so-called metanucleation (termed also supercritical (25)) regime (43, 47). This important feature of the OK model of linear fibrils is due to the n-independence of the monomer attachment and detachment frequencies fn and gn. For the linear protein polymerization to be nucleation-mediated, according to CNT, at least one of these frequencies should depend on n in a way leading to a maximum of Wn from Eq. 1 at n > 1. Fig. 2 a shows also that, within the OK model, no work is done on elongating or shortening the linear fibrils in saturated solutions (line 1), and that the formation of such fibrils in undersaturated solutions is not thermodynamically favored because of the unlimited increase of Wn with n (line 0.5). These two lines are drawn according to Eq. 9 with S = 1 and 0.5, respectively, and the above exemplary value of ε.
Figure 2.
Size dependence of the work Wn to form a linear fibril according to (a) the original and (b) the modified OK models: (lines) 0.5, 1, 2, 10, and 20 from Eqs. 9, 15 and 16 at S = 0.5, 1, 2, 10 and 20, respectively. (Arrows) Nucleus size n∗ and nucleation barrier E∗.
Employing fn and gn from Eqs. 7 and 8 in Eqs. 3–5 and invoking the geometric series formulae and , the latter being valid for |x| > 1, it is also a simple matter to determine Ce,n, Cst,n, and J for linear fibrils corresponding to the OK model. The exact result for Ce,n is (n = 1, 2, 3,… , S > 0),
| (10) |
and for Cst,n and J is (n = 1, 2, 3,… , S ≥ 1)
| (11) |
| (12) |
We note that at time-dependent monomer concentration C1 (i.e., supersaturation ratio S), these three expressions represent the quasi-equilibrium and quasi-stationary fibril size distributions and the quasi-stationary fibril nucleation (or, rather, metanucleation) rate. Also, Eq. 10 was obtained already by Oosawa and Kasai (12), and Eq. 12 coincides with that derived elsewhere (47) for formation of amyloid fibrils in metanucleation regime.
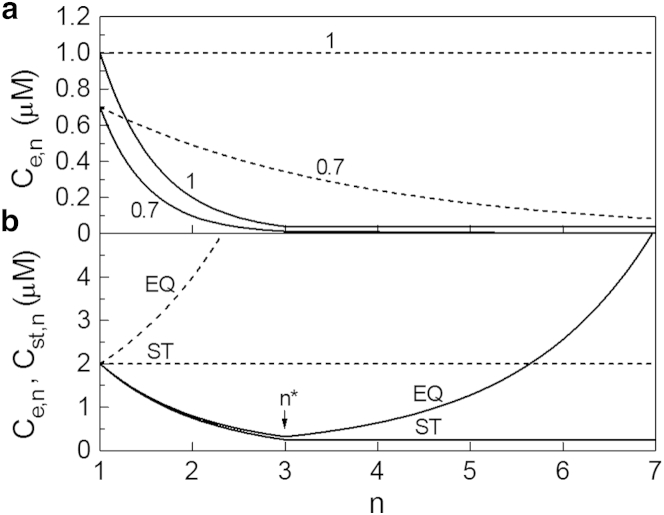
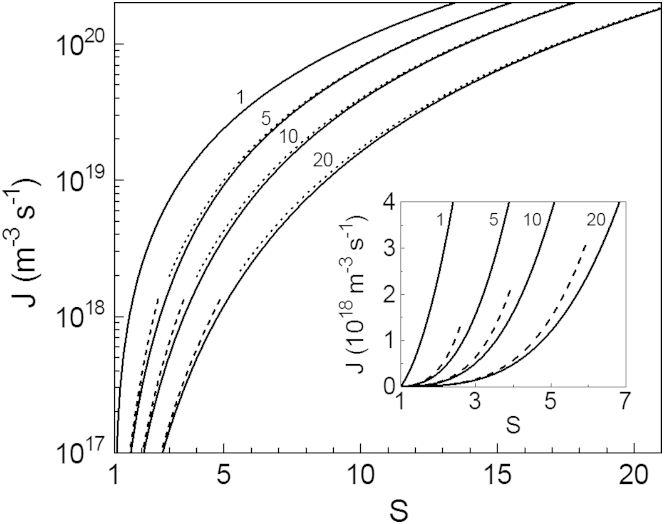
In Fig. 3, the dashed lines 0.7, 1, and EQ graph the function Ce,n from Eq. 10 for undersaturated (S = 0.7), saturated (S = 1), and supersaturated (S = 2) solution, respectively, for which cs = 1 μM (= 6 × 1020 m−3). In the latter case, as evidenced by line EQ in Fig. 3 b, Ce,n diverges with n so that it has no physical reality. The actually existing fibril size distribution then is Cst,n from Eq. 11: it is depicted by the dashed line ST in Fig. 3 b. This line shows that, according to the OK model, when the concentration C1 of monomeric protein in a supersaturated solution is maintained the same and the solution is in stationary state, regardless of their size, the linear fibrils in the solution are equally numerous. As to the S dependence of the corresponding fibril metanucleation rate J from Eq. 12, with exemplary ka = 103 M−1 s−1 (34) and the above cs value, it is displayed by line 1 in Fig. 4.
Figure 3.
Equilibrium (Ce,n) and stationary (Cst,n) size distributions of linear fibrils for (a) undersaturated or saturated, and (b) supersaturated solutions: (dashed lines) 0.7 and 1 – Ce,n from Eq. 10 of the original OK model at S = 0.7 and 1, respectively; (solid lines) 0.7 and 1 – Ce,n from Eqs. 19 and 20 of the modified OK model at S = 0.7 and 1, respectively; (dashed lines) EQ and ST, Ce,n from Eq. 10 and Cst,n from Eq. 11 of the original OK model at S = 2; (solid lines) EQ and ST, Ce,n from Eqs. 19 and 20 and Cst,n from Eqs. 21 and 22 of the modified OK model at S = 2.
Figure 4.
Dependence of the fibril stationary nucleation rate on the supersaturation ratio at q = 1, 5, 10 and 20 (as indicated): (solid lines) Eq. 23 (line 1 represents also Eq. 12); (dashed lines) Eq. 24; (dotted lines) Eq. 26; (inset) the dependence in linear coordinates.
The above analysis shows that, within the OK model, nucleation plays no role in the formation of linear fibrils, a result fully consonant with the CNT prediction for absence of one-dimensional nucleation when the end energy ε of the one-dimensional aggregates is n-independent (54). From a kinetic point of view, this independence of ε is equivalent to n independence of the monomer detachment frequency gn, because both ε and gn are functions of the binding energy of the aggregate end monomers. Thus, the question arises: can the OK model be modified in a way making it possible for nucleation to be involved in the formation of linear fibrils? The answer to this question is positive, and one such simple modification is considered below.
Modified OK model of linear fibrils
In the modified OK model of linear fibrils considered here, the attachment frequency ka remains unchanged and fn is therefore again specified by Eq. 7. The detachment frequency kd, however, is regarded as being q times higher for the short fibrils (those not surpassing a certain maximum size nm) than that for the long ones. The third row of aggregates in Fig. 1 illustrates the model in the case of nm = 3. Rather than by Eq. 8, gn is thus given by (nm = 1, 2, 3,…)
| (13) |
| (14) |
where the factor q ≥ 1 is the n-independent ratio between the frequencies of monomer detachment from short and long fibrils. The so-modified OK model is either the Hofrichter-Ross-Eaton model (37) or the Goldstein-Stryer model (18), each in the particular case of fn having the same value for all n = 1, 2, 3,… , or the Powers-Powers model (25) with nonvanishing , which is set equal to the size-independent gn of the longer fibrils.
Physically, the increased detachment frequency of the short linear fibrils is a kinetic manifestation of the fact that, due to fewer next-nearest, next-next-nearest, etc., neighbors, an end monomer of such a fibril is less strongly bound than an end monomer of a long enough fibril. The situation is analogous to that leading to increase in the evaporation rate of sufficiently small droplets. Also, the higher detachment frequency gn of the short fibrils may have a structural origin, e.g., such conformation and/or packing of the protein monomers in these fibrils that results in less strong binding of the fibril end monomers than in the long fibrils. A similar structural difference between short and long fibrils characterizes the helical polymerization (12, 25) when all fibrils of size n ≤ nm are linear, and those of size n > nm are helical. From a more general perspective, formation of helix is merely one of many possible scenarios to physically explain the increase in stability of large protein aggregates compared with small ones. The steplike change of gn represented by Eqs. 13 and 14 is a simplifying approximation to the expected gradual decrease of gn with increasing n. As seen from these equations (see also Fig. 1), at either q = 1 or nm = 1 the modified OK model passes into the original OK model in which, according to Eq. 8, all linear fibrils lose monomers with the same frequency gn.
We can now find the work Wn to form a linear n-sized fibril according to the modified OK model. Employing fn and gn from Eqs. 7, 13, and 14 in Eq. 1 leads to Wn + nkT ln (S/q) = W1 + kT ln (S/q) = εshort for 1 ≤ n ≤ nm and to for n ≥ nm. Here εshort and ε are the n-independent summary end energies of a short and a long fibril, respectively, the latter being equal to that in Eq. 9, because the long fibrils of the modified and the original OK models are identical. As according to the first of the above equations we have , from the second of them it follows that εshort = ε − nm kT ln q. Thus, using this expression for εshort and the above equations for Wn yields the exact result (S > 0)
| (15) |
| (16) |
Comparison of these two equations reveals that, via the detachment frequency ratio q, the increased frequency gn of monomer detachment from the short fibrils translates thermodynamically into: 1) decreased supersaturation ratio S/q at which these fibrils form, and 2) decreased summary end energy ε − nmkT ln q of these fibrils. Alternatively, it could be said that all fibrils form at the same supersaturation ratio S, but have n-dependent summary end energy εn: it increases linearly with n for the short fibrils (εn = (n − nm)kT ln q + ε for 1 ≤ n ≤ nm) and stays fixed for the long fibrils (εn = ε for n ≥ nm). We see also that at q = 1 or nm = 1, as it should be, Eqs. 15 and 16 reduce to Eq. 9 of the original OK model. When q > 1 and nm > 1, however, Eqs. 15 and 16 show that Wn is a broken linear function of n with a break at n = nm. This is seen in Fig. 2 b in which lines 0.5, 1, 2, 10, and 20 are drawn according to Eqs. 15 and 16 at S = 0.5, 1, 2, 10, and 20, respectively, and exemplary nm = 3, q = 10, and ε = 10 kT. We note that similar broken linear dependences of Wn on n were discussed in Powers and Powers (25) and Xue et al. (26), and that the minima of the amyloid fibril formation work in Fig. 2 b in Auer et al. (5) can be connected approximately also by a broken straight line with break at .
Importantly, when the protein solution is supersaturated and the S values are in the range between unity and q, Wn is maximal at its breaking point (the circle on line 2 in Fig. 2 b). As the Wn maximum is a hallmark of nucleation, this means that when 1 < S < q, according to the modified OK model, the formation of linear fibrils is nucleation-mediated. In Fig. 2 b, the nucleation range corresponds to the area between lines 1 and 10 (= q). When S > q, Wn has no maximum (see line 20 in Fig. 2 b) and the fibril formation is barrierless, i.e., as for the original OK model, the process occurs in metanucleation regime. Thus, the kinetic parameter q has a clear thermodynamic meaning: it is the value of the supersaturation ratio S at which nucleation turns into metanucleation and is thus analogous to the spinodal supersaturation ratio in nucleation of droplets in vapors. Naturally, for both the modified and the original OK models, as evidenced by the two lines 0.5 in Fig. 2, formation of macroscopically long fibrils is impossible when , i.e., when the solution is undersaturated, because then Wn increases unlimitedly with n.
Taking into account that the nucleus size n∗ coincides with the size nm and using Eq. 15, for n∗ and the energy barrier E∗ ≡ Wn∗−W1 to nucleation (see Fig. 2 b), we obtain (n∗ = 1, 2, 3,…, 1 ≤ S ≤ q)
| (17) |
| (18) |
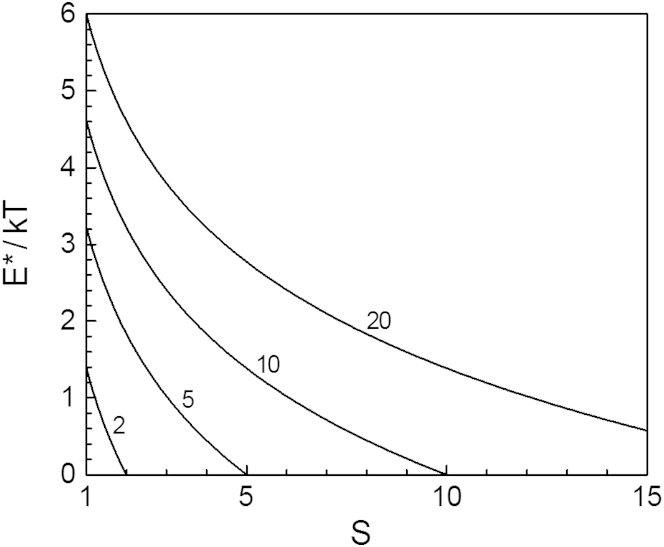
These two exact relations and Eq. 16 show that, like in CNT, E∗ is a decreasing function of S, and Wn∗ obeys the nucleation theorem in the form (54, 57) dWn∗/d(kT ln S) = −n∗. Unlike in CNT, however, n∗ does not depend on S, the reason being the steplike change of gn at n = nm, Eqs. 13 and 14, used in the modified OK model to approximate the decrease of gn with n. Considering gn as a gradually changing function of n, as done in CNT, would result in a certain dependence of n∗ on S (52, 54). Lines 2, 5, 10, and 20 in Fig. 5 display the S-dependence of E∗ from Eq. 18 at n∗ = 3 and q = 2, 5, 10, and 20, respectively. We observe that the greater the q value, the wider the S range in which fibril nucleation takes place and the greater the value of E∗ at a given S. The nucleation barrier E∗ vanishes at S = q so that when S > q, as already noted, the fibrils form in metanucleation regime. According to Eq. 18, E∗ increases linearly with increasing n∗ and is nil at q = 1 or n∗ = 1, the latter reiterating that nucleation is not involved in the original OK model of linear fibrils.
Figure 5.
Dependence of the fibril nucleation barrier E∗ on the supersaturation ratio at q = 2, 5, 10, and 20 (as indicated) according to Eq. 18.
We now turn to the equilibrium size distribution Ce,n of linear fibrils that corresponds to the modified OK model. With the aid of fn and gn from Eqs. 7, 13, and 14, in view of Eq. 17, from Eq. 3 we easily obtain the exact result (S > 0)
| (19) |
| (20) |
These equations are a particular case of those in Goldstein and Stryer (18) and, as required, at q = 1 or n∗ = 1 they turn into Eq. 10 for Ce,n of the original OK model. They reveal a strong dependence of Ce,n on n not only when the protein solution is undersaturated (then S < 1) and Ce,n is a really existing fibril size distribution because of its vanishing in the n → ∞ limit, but also when the solution is supersaturated (then S > 1) and Ce,n is only a thought size distribution, because it diverges in the same limit. This behavior of Ce,n is exhibited in Fig. 3, in which the solid lines 0.7, 1, and EQ graph the function Ce,n from Eqs. 19 and 20 for undersaturated (S = 0.7), saturated (S = 1) and supersaturated (S = 2) solutions, respectively, when q = 5, n∗ = 3, and cs = 1 μM. Comparison of these lines with the respective dashed lines resulting from the original OK model (for which q = 1) brings out the considerable drop in the entire fibril population caused by the only fivefold increase in the frequency of monomer detachment from the short linear fibrils (the dimers and the trimers). Importantly, this drop increases strongly with increasing q and n∗. We note as well that when the solution is supersaturated (Fig. 3 b), Ce,n has a minimum at the nucleus size n∗ = nm = 3. This minimum reflects the maximum of the fibril formation work Wn from Eqs. 15 and 16 (see Fig. 2 b), because Ce,n and Wn are related by the CNT expression Ce,n = C1 exp[−(Wn−W1)/kT] (54).
The last to determine are the stationary size distribution Cst,n and the stationary nucleation rate J of the linear fibrils corresponding to the modified OK model. Using fn and gn from Eqs. 7, 13, and 14 in Eqs. 4 and 5, owing to Eq. 17 and the two geometric series formulae presented earlier, we find that Cst,n and J are given exactly by (S ≥ 1)
| (21) |
| (22) |
| (23) |
As seen from these equations, they satisfy the requirement to pass into Eqs. 11 and 12 of the original OK model when q = 1 or n∗ = 1. It should be noted also that the J(S) dependence from Eq. 23 is different from that given in Hofrichter et al. (37).
The solid line ST in Fig. 3 b is a plot of Cst,n from Eqs. 21 and 22 for a supersaturated solution at fixed S = 2 (i.e., C1 = 2cs) when q = 5, n∗ = 3, and cs = 1 μM. We observe that the nucleus and supernucleus linear fibrils (those of size n ≥ n∗) 1) have the same concentration, and 2) are ∼10 times less numerous than the fibrils of the same size when the monomer detachment frequency is n-independent (then q = 1 and Cst,n is visualized by the dashed line ST of the original OK model). Also, the solid lines EQ and ST in Fig. 3 b evidence that when S is sufficiently smaller than q, Ce,n from Eq. 19 is a good approximation to Cst,n from Eq. 21 in the n ≤ n∗ range, i.e., for the nucleus and subnucleus linear fibrils. Physically, this means that when fibril formation is strongly nucleation-mediated (then 1 ≤ S << q), the imaginary equilibrium and the real stationary size distributions of these fibrils are virtually the same.
The S dependence of J from Eq. 23 of the modified OK model is displayed by the solid lines 1, 5, 10, and 20 in Fig. 4. The lines are drawn with the already used ka = 103 M−1 s−1, cs = 1 μM, n∗ = 3, and q = 1, 5, 10, and 20, respectively (line 1 also represents J from Eq. 12 of the original OK model). Seen in the figure and its inset is that the fibril nucleation rate J increases in a parabolic manner with the supersaturation ratio S (i.e., with the concentration C1 of monomeric protein) and that it diminishes substantially with increasing the ratio q between the frequencies of monomer detachment from the short (subnucleus and nucleus) and the long (supernucleus) linear fibrils. The J(S) function from Eq. 23 has no singularity at S = q, the S value which separates the nucleation (S < q) and the metanucleation (S > q) regimes of fibril formation.
The dashed lines in Fig. 4 visualize the simple J(S) dependence applicable to strongly nucleation-mediated linear polymerization (1 ≤ S << q)
| (24) |
This approximate relation follows from Eq. 23, provided the short linear fibrils lose monomers much more frequently than the long ones (then q >> 1) and the polymerization occurs by nucleation in sufficiently weakly supersaturated solutions (then S << q so that S – 1 << (q – 1)). It is seen in Fig. 4 that Eq. 24 approximates well Eq. 23 when S is sufficiently smaller than q. It is worth noting also that with the aid of the nucleation barrier E∗ from Eq. 18, J from Eq. 24 can be represented in the familiar CNT form (54)
| (25) |
where the preexponential factor A = 2kacs2S(S−1) is, physically, the rate of barrierless (E∗ = 0) formation of linear fibrils, i.e., the fibril metanucleation rate from Eq. 12.
In the opposite extreme, when the fibrils form in sufficiently strongly supersaturated solutions, Eq. 23 simplifies to (S >> 1, q >> 1),
| (26) |
which is the expression obtained by Powers and Powers (25). The dotted lines in Fig. 4 represent the J(S) dependence from Eq. 26 and show that this equation is a good approximation to Eq. 23 in the entire metanucleation range S ≥ q and, also, in the nucleation range S < q as long as S is sufficiently greater than unity. The approximate Eq. 26 reduces to J(S) = 2kacs2S(S–q) when the fibrils form in the metanucleation range and S is sufficiently greater than q to satisfy the condition << 1.
Rate equations of linear polymerization
The rate equations of linear polymerization within the modified OK model can be obtained by combining Eqs. 2 and 6 of the Szilard-Farkas model and using fn and gn from Eqs. 7, 13, and 14 with nm replaced by n∗. Doing that yields the equations (n = 2, 3,…,n∗−1)
| (27) |
for the fibril subnuclei, the equation
| (28) |
for the n∗-sized fibril nuclei, and the equations (n = n∗ +1, n∗ +2,…)
| (29) |
for the fibril supernuclei. When n∗ = 2, Eqs. 27 are superfluous. When q = 1, both Eqs. 27 and 28 are superfluous, and the remaining Eq. 29 describes the kinetics of nucleationless linear polymerization within the original OK model for which n∗ = 1. Importantly, Eqs. 27–29 are self-contained, because they include solely the four independent parameters ka, cs (or kd), n∗, and q of the modified OK model. Also, they are a particular case of those in Goldstein and Stryer (18).
Equations 27–29 are a set of ordinary differential equations of first order for the fibril size distribution Cn(t). This set parallels the one used first by Tunitskii (58) and Zeldovich (59) to describe nucleation at fixed supersaturation and later generalized (53, 54, 60) to also cover nucleation at variable supersaturation. The problem of solving Eqs. 27–29 is mathematically well posed when the set is supplemented with an equation for the monomer concentration C1(t) and when the initial fibril size distribution Cn(0) for n = 1,2,3,… is specified. In fibrillation at a given time-independent monomer concentration, an equation for C1 is not needed and, as can be verified by direct substitution, exact time-independent solutions of Eqs. 27–29 are Ce,n and Cst,n from Eqs. 19–22. Another important case is that of fibrillation in protein solutions with known fixed total concentration Ctot of protein. Then the equation for C1 is of the form , C1 is time-dependent, and Eqs. 27–29 are nonlinear and difficult to treat analytically (see, e.g., Goldstein and Stryer (18), Powers and Powers (25), and Michaels et al. (34) for important mathematical approaches and results).
It is instructive to compare Eqs. 27–29 with the rate equations used by Michaels et al. (34) for analysis of the kinetics of nucleation-mediated linear self-assembly of protein within the framework of the OK model. The analysis was carried out under the assumption of S-independent size nc ≥ 2 of the so-called growth nucleus (27, 28) which, in our terminology, is the smallest supernucleus, because it was shown (27) that nc is related to the size n∗ of the nucleus by
| (30) |
This equation implies that the analysis in Michaels et al. (34) is completely applicable to the modified OK model (recall that this model describes nucleation with S-independent n∗ from Eq. 17). Also, because the concentration of fibrils of size n < nc was considered as negligible, Eqs. 27 and 28 were not necessary for the analysis of Michaels et al. (34) so that only Eqs. 29 for the fibril supernuclei were used, the first of them in the form
| (31) |
(in writing Eq. 31, we have omitted the term in Eq. 1 in Michaels et al. (34) because of the considered vanishing smallness of ). In Eq. 31, the term is the so-called fibril nucleation rate, a quantity introduced ad hoc in the equation and defined by means of two free parameters: the S-independent nucleation rate constant kN and growth nucleus size nc. It is clear, however, that because does not vanish when the solution is saturated (i.e., at C1 = cs), it cannot be nucleation rate. To reveal the physical significance of the term and the parameter kN, we juxtapose the right-hand sides of Eq. 29 for n = n∗ + 1 and of Eq. 31. In view of Eq. 30, we thus find that Eq. 31 is identical to Eq. 29 for n = n∗ + 1 if . This result means that, indeed, is not the fibril nucleation rate, but merely an approximation to the forward flux 2kaC1Cn∗ through the nucleus size n∗.
If we now use Ce,n∗ from Eq. 19 to approximate Cn∗ in the above expression for kN, upon allowing for Eq. 30, we obtain (n∗ ≥ 2)
| (32) |
These equalities and Eq. 30 tell us that in analyses of protein fibrillation that are based on rate equations with the term in them (15, 20, 22, 27, 28, 29, 30, 31, 32, 33, 34, 35), when nc ≥ 3, kN and nc are related quite simply to the four independent parameters ka, cs (or kd), n∗ and q of the modified OK model that specify the monomer attachment and detachment frequencies fn and gn via Eqs. 7, 13, and 14.
Importantly, when the nc, kN, ka and cs (or kd) values are given in model theoretical studies or obtained from fit to experimental data, Eqs. 30 and 32 make it possible to determine the corresponding energy barrier E∗ and stationary rate J of nucleation of linear fibrils. This is so, because then the nucleus size n∗ and the detachment frequency ratio q can be calculated from these equations and used in Eqs. 18 and 23 for determination of E∗ and J. To illustrate this point, we can employ the exemplary ka = 103 M−1 s−1, kd = 10−3 s−1 (implying cs = 1 μM), kN = 102.5 M−2 s−1 and nc = 3 in Michaels et al. (34). Because in view of Eqs. 30 and 32, n∗ and q are given by (nc ≥ 3)
| (33) |
| (34) |
with the aid of the above parameter values we obtain n∗ = 2 and q = 6.3 × 106. Physically, this result means that in the case illustrated in the last figure in Michaels et al. (34): 1) the dimers are the fibril nuclei; 2) they lose monomers over a million times more frequently than the longer (supernucleus) linear fibrils; and 3) the fibrillation process is indeed nucleation-mediated in the considered S range from 1 to 10, because these S values satisfy the condition S < q. To check whether the above value of q is realistic, we can use it in Eqs. 18 and 23 to calculate the corresponding nucleation barrier E∗ and stationary nucleation rate J: the result is E∗/kT = 16–13 and J = 0 to 1.7 × 1014 m−3 s−1 (= 0.28 pM s−1) for S = 1–10. These E∗ and J values seem reasonable: typically, the nucleation barrier is between 10 and 40 kT, and a stationary nucleation rate of 1014 m−3 s−1 yields JVt = 108 supernuclei in volume V = 1 cm3 within time t = 1 s. We can, therefore, regard the above exemplary ka, kd, kN, and nc values as representing self-consistently the nucleation of linear fibrils within the modified OK model.
Helical polymerization
As schematized by the first and second rows of fibrils in Fig. 6 for the nm = 3 case, in the OK model of helical polymerization (12) the fibrils of size n < nm are linear, those of size n > nm are helical, and the nm-sized ones can be either linear or helical. While the linear fibrils are characterized by n-independent monomer attachment and detachment frequencies fl and gl, respectively, for the helical fibrils these (also n-independent) frequencies are fh and gh, respectively. In addition, Oosawa and Kasai (12) considered both the transformation of nm-sized linear fibrils into nm-sized helical ones and the reverse transformation as separate elementary events occurring with frequencies ωlh and ωhl, respectively.
Figure 6.
Schematic of the original (first and second rows) and simplified (third row) OK models of helical polymerization with the trimer as fibril nucleus. In the simplified OK model, the trimer line-to-helix and helix-to-line transformations are neglected, and the linear fibrils (dimers and trimers) lose monomers (the circles) q times more frequently than the helical fibrils (tetramers, pentamers, etc.).
Clearly, this model allows a simplification that makes it mathematically identical to the modified OK model of linear polymerization considered above. This simplification is illustrated by the third row of fibrils in Fig. 6 (see also Powers and Powers (25)). It consists of 1) neglecting the effect of the line-to-helix and helix-to-line transformations of the nm-sized fibrils on the nm → nm + 1 and nm + 1 → nm size transitions (this is feasible when the frequencies ωlh and ωhl are so high that they do not limit the rates of these transitions), and 2) setting fl = fh = 2kaC1 for all n, gl = 2qkacs for n ≤ nm and gh = 2kacs for n > nm, with cs now being the solubility of the helical fibrils. As these frequencies coincide with fn and gn from Eqs. 7, 13, and 14, mathematically, the so-simplified OK model of helical polymerization is indistinguishable from the modified OK model of linear polymerization. Therefore, the entire analysis and all results obtained above for linear fibrils in the framework of the modified OK model are fully applicable to helical fibrils describable within the simplified OK model. In particular, in the latter case, according to Eq. 17 the longest linear fibrils (the nm-sized ones) are the nuclei, the other linear fibrils are subnuclei, and all helical fibrils are supernuclei.
Conclusions
Several important points emerging from this nucleation-theory approach to protein polymerization into fibrils are worth bringing to the fore.
-
1)
The original OK model of linear polymerization does not involve nucleation. Instead, the polymerization occurs always in metanucleation regime, with no nucleation barrier and with the protein monomers playing the role of fibril nuclei.
-
2)
The analyzed modified OK model of linear polymerization admits of nucleation, but only when the protein solution is sufficiently weakly supersaturated. In a sufficiently strongly supersaturated solution, the polymerization takes place again in metanucleation regime.
-
3)
Within the modified OK model of linear polymerization, the fibril formation work Wn is a broken linear function of the fibril size n, and the nucleus size n∗ is independent of the supersaturation ratio S, because it is equal to the fixed fibril size nm at which the monomer detachment frequency changes abruptly. The energy barrier E∗ to nucleation decreases with S according to Eq. 18.
-
4)
Within the modified OK model, when the supersaturation ratio S is fixed and greater than unity, the stationary concentration Cst,n of the short (subnucleus) linear fibrils may be much higher than that of the long (supernucleus) fibrils and cannot be considered as vanishingly small. For the fibril subnuclei and nuclei, a good approximation to Cst,n from Eq. 21 can be their equilibrium concentration Ce,n from Eq. 19. Regardless of their length, the fibril supernuclei have the same stationary concentration, which is given by Eq. 22.
-
5)
Within the modified OK model, the stationary nucleation rate J increases with S according to Eq. 23 and has no singularity at the S value, which separates the nucleation and metanucleation regimes of linear polymerization. Under otherwise equal conditions, this rate decreases considerably when the subnucleus and nucleus linear fibrils lose monomers much more frequently than the supernucleus fibrils, a feature that should be born in mind when designing a strategy for stymying or stimulating fibril nucleation. The simple J(S) dependence from Eq. 24 is convenient for experimental verification and for use in rate equations describing strongly nucleation-mediated formation of OK-type protein fibrils.
-
6)
The rate equations of linear polymerization, Eqs. 27–29, describe the process within both the original and the modified OK models. Being self-contained because of not having ad hoc parameters, these equations reveal that the quantity used in the literature is not the fibril nucleation rate. Equations 30 and 32 relate the parameters nc and kN to the parameters of the modified OK model, and Eqs. 33 and 34 allow determination of the nucleus size n∗ and detachment frequency ratio q from data for nc and kN.
-
7)
The entire analysis and all results obtained for the modified OK model of linear polymerization are fully applicable to a simplified OK model of helical polymerization.
Acknowledgments
Fruitful discussions with Dr. Stefan Auer and his comments concerning this article are gratefully acknowledged.
Editor: Rohit Pappu.
References
- 1.Chiti F., Dobson C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 2.Invernizzi G., Papaleo E., Ventura S. Protein aggregation: mechanisms and functional consequences. Int. J. Biochem. Cell Biol. 2012;44:1541–1554. doi: 10.1016/j.biocel.2012.05.023. [DOI] [PubMed] [Google Scholar]
- 3.Gazit E. Self-assembled peptide nanostructures: the design of molecular building blocks and their technological utilization. Chem. Soc. Rev. 2007;36:1263–1269. doi: 10.1039/b605536m. [DOI] [PubMed] [Google Scholar]
- 4.Knowles T.P.J., Buehler M.J. Nanomechanics of functional and pathological amyloid materials. Nat. Nanotechnol. 2011;6:469–479. doi: 10.1038/nnano.2011.102. [DOI] [PubMed] [Google Scholar]
- 5.Auer S., Dobson C.M., Vendruscolo M. Characterization of the nucleation barriers for protein aggregation and amyloid formation. HFSP J. 2007;1:137–146. doi: 10.2976/1.2760023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vitalis A., Pappu R.V. Assessing the contribution of heterogeneous distributions of oligomers to aggregation mechanisms of polyglutamine peptides. Biophys. Chem. 2011;159:14–23. doi: 10.1016/j.bpc.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wu C., Shea J.-E. Coarse-grained models for protein aggregation. Curr. Opin. Struct. Biol. 2011;21:209–220. doi: 10.1016/j.sbi.2011.02.002. [DOI] [PubMed] [Google Scholar]
- 8.Morriss-Andrews A., Bellesia G., Shea J.-E. β-sheet propensity controls the kinetic pathways and morphologies of seeded peptide aggregation. J. Chem. Phys. 2012;137:145104. doi: 10.1063/1.4755748. [DOI] [PubMed] [Google Scholar]
- 9.Morriss-Andrews A., Shea J.-E. Simulations of protein aggregation: insights from atomistic and coarse-grained models. J. Phys. Chem. Lett. 2014;5:1899–1908. doi: 10.1021/jz5006847. [DOI] [PubMed] [Google Scholar]
- 10.Crick S.L., Ruff K.M., Pappu R.V. Unmasking the roles of N- and C-terminal flanking sequences from exon 1 of huntingtin as modulators of polyglutamine aggregation. Proc. Natl. Acad. Sci. USA. 2013;110:20075–20080. doi: 10.1073/pnas.1320626110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Powers E.T., Powers D.L. Mechanisms of protein fibril formation: nucleated polymerization with competing off-pathway aggregation. Biophys. J. 2008;94:379–391. doi: 10.1529/biophysj.107.117168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Oosawa F., Kasai M. A theory of linear and helical aggregations of macromolecules. J. Mol. Biol. 1962;4:10–21. doi: 10.1016/s0022-2836(62)80112-0. [DOI] [PubMed] [Google Scholar]
- 13.Oosawa F., Higashi S. Statistical thermodynamics of polymerization and polymorphism of protein. Prog. Theor. Biol. 1967;1:79–164. [Google Scholar]
- 14.Oosawa F. Size distribution of protein polymers. J. Theor. Biol. 1970;27:69–86. doi: 10.1016/0022-5193(70)90129-3. [DOI] [PubMed] [Google Scholar]
- 15.Oosawa F., Asakura S. Academic Press; London, UK: 1975. Thermodynamics of the Polymerization of Protein. [Google Scholar]
- 16.Buell A.K., Dobson C.M., Knowles T.P.J. The physical chemistry of the amyloid phenomenon: thermodynamics and kinetics of filamentous protein aggregation. Essays Biochem. 2014;56:11–39. doi: 10.1042/bse0560011. [DOI] [PubMed] [Google Scholar]
- 17.Frieden C., Goddette D.W. Polymerization of actin and actin-like systems: evaluation of the time course of polymerization in relation to the mechanism. Biochemistry. 1983;22:5836–5843. doi: 10.1021/bi00294a023. [DOI] [PubMed] [Google Scholar]
- 18.Goldstein R.F., Stryer L. Cooperative polymerization reactions. Analytical approximations, numerical examples, and experimental strategy. Biophys. J. 1986;50:583–599. doi: 10.1016/S0006-3495(86)83498-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hill T.L. Springer; New York: 1987. Linear Aggregation Theory in Cell Biology. [Google Scholar]
- 20.Flyvbjerg H., Jobs E., Leibler S. Kinetics of self-assembling microtubules: an “inverse problem” in biochemistry. Proc. Natl. Acad. Sci. USA. 1996;93:5975–5979. doi: 10.1073/pnas.93.12.5975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Masel J., Jansen V.A.A., Nowak M.A. Quantifying the kinetic parameters of prion replication. Biophys. Chem. 1999;77:139–152. doi: 10.1016/s0301-4622(99)00016-2. [DOI] [PubMed] [Google Scholar]
- 22.Collins S.R., Douglass A., Weissman J.S. Mechanism of prion propagation: amyloid growth occurs by monomer addition. PLoS Biol. 2004;2:e321. doi: 10.1371/journal.pbio.0020321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hall D., Edskes H. Silent prions lying in wait: a two-hit model of prion/amyloid formation and infection. J. Mol. Biol. 2004;336:775–786. doi: 10.1016/j.jmb.2003.12.004. [DOI] [PubMed] [Google Scholar]
- 24.Kunes K.C., Cox D.L., Singh R.R.P. One-dimensional model of yeast prion aggregation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:051915. doi: 10.1103/PhysRevE.72.051915. [DOI] [PubMed] [Google Scholar]
- 25.Powers E.T., Powers D.L. The kinetics of nucleated polymerizations at high concentrations: amyloid fibril formation near and above the “supercritical concentration”. Biophys. J. 2006;91:122–132. doi: 10.1529/biophysj.105.073767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xue W.-F., Homans S.W., Radford S.E. Systematic analysis of nucleation-dependent polymerization reveals new insights into the mechanism of amyloid self-assembly. Proc. Natl. Acad. Sci. USA. 2008;105:8926–8931. doi: 10.1073/pnas.0711664105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Knowles T.P.J., Waudby C.A., Dobson C.M. An analytical solution to the kinetics of breakable filament assembly. Science. 2009;326:1533–1537. doi: 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
- 28.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. Nucleated polymerization with secondary pathways. I. Time evolution of the principal moments. J. Chem. Phys. 2011;135:065105. doi: 10.1063/1.3608916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. Nucleated polymerization with secondary pathways. II. Determination of self-consistent solutions to growth processes described by non-linear master equations. J. Chem. Phys. 2011;135:065106. doi: 10.1063/1.3608917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. Nucleated polymerization with secondary pathways. III. Equilibrium behavior and oligomer populations. J. Chem. Phys. 2011;135:065107. doi: 10.1063/1.3608918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Prigent S., Ballesta A., Doumic M. An efficient kinetic model for assemblies of amyloid fibrils and its application to polyglutamine aggregation. PLoS One. 2012;7:e43273. doi: 10.1371/journal.pone.0043273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schreck J.S., Yuan J.-M. A kinetic study of amyloid formation: fibril growth and length distributions. J. Phys. Chem. B. 2013;117:6574–6583. doi: 10.1021/jp401586p. [DOI] [PubMed] [Google Scholar]
- 33.Hong L., Yong W.-A. Simple moment-closure model for the self-assembly of breakable amyloid filaments. Biophys. J. 2013;104:533–540. doi: 10.1016/j.bpj.2012.12.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Michaels T.C.T., Garcia G.A., Knowles T.P.J. Asymptotic solutions of the Oosawa model for the length distribution of biofilaments. J. Chem. Phys. 2014;140:194906. doi: 10.1063/1.4875897. [DOI] [PubMed] [Google Scholar]
- 35.Michaels T.C.T., Knowles T.P.J. Role of filament annealing in the kinetics and thermodynamics of nucleated polymerization. J. Chem. Phys. 2014;140:214904. doi: 10.1063/1.4880121. [DOI] [PubMed] [Google Scholar]
- 36.Gillam J.E., MacPhee C.E. Modelling amyloid fibril formation kinetics: mechanisms of nucleation and growth. J. Phys. Condens. Matter. 2013;25:373101. doi: 10.1088/0953-8984/25/37/373101. [DOI] [PubMed] [Google Scholar]
- 37.Hofrichter J., Ross P.D., Eaton W.A. Kinetics and mechanism of deoxyhemoglobin S gelation: a new approach to understanding sickle cell disease. Proc. Natl. Acad. Sci. USA. 1974;71:4864–4868. doi: 10.1073/pnas.71.12.4864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ferrone F. Analysis of protein aggregation kinetics. Methods Enzymol. 1999;309:256–274. doi: 10.1016/s0076-6879(99)09019-9. [DOI] [PubMed] [Google Scholar]
- 39.Perutz M.F., Windle A.H. Cause of neural death in neurodegenerative diseases attributable to expansion of glutamine repeats. Nature. 2001;412:143–144. doi: 10.1038/35084141. [DOI] [PubMed] [Google Scholar]
- 40.Galkin O., Vekilov P.G. Mechanisms of homogeneous nucleation of polymers of sickle cell anemia hemoglobin in deoxy state. J. Mol. Biol. 2004;336:43–59. doi: 10.1016/j.jmb.2003.12.019. [DOI] [PubMed] [Google Scholar]
- 41.Garai K., Sahoo B., Maiti S. Quasihomogeneous nucleation of amyloid beta yields numerical bounds for the critical radius, the surface tension, and the free energy barrier for nucleus formation. J. Chem. Phys. 2008;128:045102. doi: 10.1063/1.2822322. [DOI] [PubMed] [Google Scholar]
- 42.Zhang J., Muthukumar M. Simulations of nucleation and elongation of amyloid fibrils. J. Chem. Phys. 2009;130:035102. doi: 10.1063/1.3050295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kashchiev D., Auer S. Nucleation of amyloid fibrils. J. Chem. Phys. 2010;132:215101. doi: 10.1063/1.3447891. [DOI] [PubMed] [Google Scholar]
- 44.Cabriolu R., Kashchiev D., Auer S. Atomistic theory of amyloid fibril nucleation. J. Chem. Phys. 2010;133:225101. doi: 10.1063/1.3512642. [DOI] [PubMed] [Google Scholar]
- 45.Cabriolu R., Auer S. Amyloid fibrillation kinetics: insight from atomistic nucleation theory. J. Mol. Biol. 2011;411:275–285. doi: 10.1016/j.jmb.2011.05.032. [DOI] [PubMed] [Google Scholar]
- 46.Auer S., Ricchiuto P., Kashchiev D. Two-step nucleation of amyloid fibrils: omnipresent or not? J. Mol. Biol. 2012;422:723–730. doi: 10.1016/j.jmb.2012.06.022. [DOI] [PubMed] [Google Scholar]
- 47.Kashchiev D., Cabriolu R., Auer S. Confounding the paradigm: peculiarities of amyloid fibril nucleation. J. Am. Chem. Soc. 2013;135:1531–1539. doi: 10.1021/ja311228d. [DOI] [PubMed] [Google Scholar]
- 48.Kashchiev D. Protein fibrillation due to elongation and fragmentation of initially appeared fibrils: a simple kinetic model. J. Chem. Phys. 2013;139:105103. doi: 10.1063/1.4819496. [DOI] [PubMed] [Google Scholar]
- 49.Kashchiev D. Kinetics of protein fibrillation controlled by fibril elongation. Proteins. 2014;82:2229–2239. doi: 10.1002/prot.24586. [DOI] [PubMed] [Google Scholar]
- 50.Auer S. Amyloid fibril nucleation: effect of amino acid hydrophobicity. J. Phys. Chem. B. 2014;118:5289–5299. doi: 10.1021/jp411370y. [DOI] [PubMed] [Google Scholar]
- 51.Auer S. Nucleation of polymorphic amyloid fibrils. Biophys. J. 2015;108:1176–1186. doi: 10.1016/j.bpj.2015.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Abraham F.F. Academic Press; New York: 1974. Homogeneous Nucleation Theory. [Google Scholar]
- 53.Kashchiev D. The kinetic approach to nucleation. Cryst. Res. Technol. 1984;19:1413–1423. [Google Scholar]
- 54.Kashchiev D. Butterworth-Heinemann; Oxford, UK: 2000. Nucleation: Basic Theory with Applications. [Google Scholar]
- 55.Farkas L. Keimbildungsgeschwindigkeit in übersättigten dämpfen. Z. Phys. Chem. 1927;125:236–242. [Google Scholar]
- 56.Becker R., Döring W. Kinetische behandlung der keimbildung in übersättigten dämpfen. Ann. Phys. (Leipzig) 1935;24:719–752. [Google Scholar]
- 57.Kashchiev D. On the relation between nucleation work, nucleus size and nucleation rate. J. Chem. Phys. 1982;76:5098–5102. [Google Scholar]
- 58.Tunitskii N.N. O kondensatsii peresyshchennykh parov (On the condensation of supersaturated vapors) Zhur. Fiz. Khim. (Russia) 1941;15:1061–1071. [Google Scholar]
- 59.Zeldovich J.B. On the theory of new phase formation: cavitation. Acta Physicochim. URSS. 1943;18:1–22. [Google Scholar]
- 60.Kashchiev D. Nucleation at variable supersaturation. Surf. Sci. 1969;18:293–297. [Google Scholar]