Stable, Unstable and Metastable States of Equilibrium: Definitions and Applications to Human Movement

Dear Editor-in-chief

Human postural demands and balance control during locomotive and rotational motion are of primary interest for athletic performance and daily life. The equivocal use of terms and expressions such as equilibrium, balance, stability/instability obstruct a clear communication of scientific knowledge. In particular, the terms stability and balance and their different forms or word combinations are often used with various meanings and circular definitions not only in everyday language but in scientific communication as well. Further, stability and balance issues of human movement are often inadequately discussed in the literature in the form of equilibrium situations of rigid bodies. However, for animate systems, stable and unstable equilibrium approaches are too simplistic. As an alternative, the ‘metastability’ concept predominantly used as part of the dynamic systems theory should be applied to human movement.

Thus, the objectives of this letter to the editor are to define established and frequently used terms that describe responses to human movement behavior and to introduce and rationalize the use of a more appropriate and encompassing term entitled ‘metastability’.

Equilibrium: For most instances of athletic performance, stable states of equilibrium are in demand. Aside from net forces/torques to sum to zero, typically three states of mechanical equilibrium are distinguished by their response behavior to perturbations (Bartlett, 2007). For ‘stable’ equilibrium, a system will return to its original location if it is periodically displaced. In contrast, a system is in a state of ‘unstable’ equilibrium when it will not return into the original location when being displaced but instead passes into a new state of stable equilibrium such as an individual falling off a freely standing ladder (Hay, 1985). Objects showing neither tendency to return or move away from their initial state are said to be in ‘neutral’ equilibrium.

Balance: While the term equilibrium is typically used to describe the state of a body that is not changing its speed or direction when all forces/torques cancel out to zero, balance is conceived to be a fundamental requirement for athletic performance and everyday activities. Balance can be considered as an (task-specific) ability of an individual to control either static or dynamic equilibrium while maintaining a stable position (Knudson, 2007). Components of this balance ability are needed in both static equilibrium conditions (handstand on balance beam) and during dynamic movement (running). Individuals with good balance are able to adequately and continuously control their body position or center of mass (CoM) over the base of support (BoS) (Knudson, 2007). However, for dynamic movement, the projection of the CoM may periodically move from within the BoS to outside, as with running, while balance may continuously be maintained (Hof et al., 2005). Thus, balance is considered as an inversely related interplay of stability and mobility of the body with respect to its BoS (Hudson, 1996). The greatest potential for stability is represented by a large BoS, a low CoM, and the projection of the CoM centered in the BoS. However, mobility is restricted under these conditions. In turn, mobility is facilitated by a small BoS (push-off phase during ground contact while running) with the projection of the CoM located at the boundaries of the BoS or even outside. This interplay of stability and mobility is task-specific. An archer desires high stability and low mobility, a sprinter wants low stability and high mobility, and a ballerina seeks low stability and low mobility (Hudson, 1996).

Stability/Instability: For the human body, stability describes the body’s resistance to being moved out of the present state of motion, linear or rotary, by external forces or torques. Linear stability of a moving body is considered its resistance to being accelerated, stopped or having its direction changed. Linear stability is bound to a direction in space. A body may be stable in one direction but not necessarily in another. In contrast, rotary stability may be considered as a resistance to change the present state of angular motion by external torques accelerating or stopping the rotation about a given axis, or to change the angular motion from one axis to another. For upright postures with no angular motion, rotary stability would be associated with the resistance of the body to tripping over. Linear or rotary stability can be improved by various motor strategies. For example, a) extending the BoS, b) maintaining the projection of the CoM safely within the BoS, c) lowering the CoM, d) shifting the CoM and the line of gravity towards an incoming force, and/or e) extending the BoS towards an incoming force (Burkett, 2010).

As most definitions and conceptualizations of balance and stability in some way or other refer to equilibrium, a true equilibrium of forces/torques is practically non-existent in humans due to the ongoing mechanics of vital processes such as cardiorespiratory functioning and muscular activity. Even when attempting to stand as still as possible, these physiological processes will always ensure a certain degree of body sway, since the erect human body can be described as a constantly fluctuating inverted pendulum (Loram and Lakie, 2002). Instead, equilibrium is considered a virtual target condition of the mover who is attempting to control for body posture and static/dynamic balance during performance.

For individuals in motion, the term linear stability is often applied to dynamic/locomotive movements such as running (Burkett, 2010). Although during some phase of these movements, the objective of the individual may be to maintain dynamic equilibrium, be firmly established, resist change to their position, or minimize fluctuations, the individual will eventually want to change position by moving easily and sometimes suddenly. In this regard, individuals can be considered to move along a continuum of equilibrium states (Figure 1). Here, aside from the CoM projection to remain within the BoS, the CoM momentum must be accounted for as well (Hof et al., 2005). Hence, dynamic stability is achieved during locomotion since stance periods are continuously provided (CoM within BoS) while the CoM projection repetitively passes through the BoS.

Figure 1.

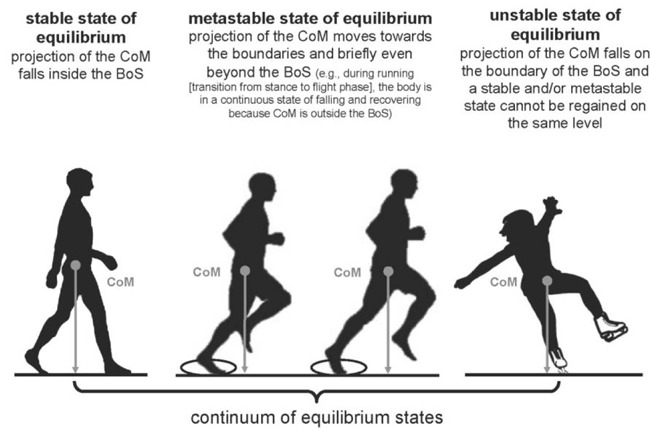
An illustration of the continuum of equilibrium states.

Stable, unstable, and neutral states of equilibrium are typically found in rigid bodies rather than in animate objects. However, humans are highly dynamic, animate, non-rigid bodies equipped by nature with physiological mechanisms to compensate for perturbations in stationary and locomotive environments. The term, ‘instability’ appears inadequate for the response behavior of biological systems to perturbations.

Metastability:Although stable instability may seem like an oxymoron, individuals are often in a state of flux, which allows them to transfer smoothly from relatively stable to relatively unstable conditions (change from stance to flight phase during running). Without some degree of instability, it would be impossible to move; however, without some degree of stability, it would be impossible to maintain equilibrium or to remain upright. Hence, a degree of stable instability or relative instability is aptly described by the term ‘metastability’.

Thus, the state of relatively stable or metastable equilibrium is defined as the state in which a system remains for a long period of time, and any slight disturbance causing the system to deviate from the metastable state does not result in the system passing into another state. As soon as the external disturbance is removed, the system will return into the initial metastable state (Tschoegl, 2000). A sufficiently strong disturbance, however, will put the system out of the metastable state, and the system will pass into a new state of stable equilibrium (Tschoegl, 2000).

Metastability and its application to human movement: For the individual, minor challenges of balance can be easily compensated for by conscious and unconscious motor control mechanisms. The mover will perceive his state of motion to be stable while his state of equilibrium is in fact metastable. For large challenges of balance, the mover may perceive his state of motion to be unstable while periodically approaching unstable states of equilibrium. Again, running is a good example of human locomotor metastability as the individual moves from a relative stable state (stance phase) by a muscular disturbance or perturbation (push-off phase) to achieve a new state of equilibrium (subsequent stance-phase). With locomotion, there are constant fluctuations in CoM relative to the BoS, which demand metastable control (Figure 1).

While metastability is considered to be a core feature of dynamic systems (den Hollander, 2009), the metastability concept should be applied to the issue of balance performance as well since the human body can be envisioned as a dynamic system with its response behavior following internal (breathing) and external (tackling during ball games) perturbations. Therefore, an athlete training on a commonly described ‘instability’ device (wobble board) would compensate for small to moderate disturbances to maintain a metastable state of equilibrium. Only a large disturbance will force the individual’s CoM projection to pass beyond the boundaries of the BoS such that the individual will leave the metastable state of equilibrium and eventually drop from the device.

In conclusion and in accordance with Kibele et al. (2014), we recommend to use the term ‘metastability’ in the fields of biomechanics and exercise science/physiology to adequately describe responses to human movement behavior.